Abstract
Motivation: Gene expression profiling technologies can generally produce mRNA abundance data for all genes in a genome. A dearth of proteomic data persists because identification range and sensitivity of proteomic measurements lag behind those of transcriptomic measurements. Using partial proteomic data, it is likely that integrative transcriptomic and proteomic analysis may introduce significant bias. Developing methodologies to accurately estimate missing proteomic data will allow better integration of transcriptomic and proteomic datasets and provide deeper insight into metabolic mechanisms underlying complex biological systems.
Results: In this study, we present a non-linear data-driven model to predict abundance for undetected proteins using two independent datasets of cognate transcriptomic and proteomic data collected from Desulfovibrio vulgaris. We use stochastic gradient boosted trees (GBT) to uncover possible non-linear relationships between transcriptomic and proteomic data, and to predict protein abundance for the proteins not experimentally detected based on relevant predictors such as mRNA abundance, cellular role, molecular weight, sequence length, protein length, guanine-cytosine (GC) content and triple codon counts. Initially, we constructed a GBT model using all possible variables to assess their relative importance and characterize the behavior of the predictive model. A strong plateau effect in the regions of high mRNA values and sparse data occurred in this model. Hence, we removed genes in those areas based on thresholds estimated from the partial dependency plots where this behavior was captured. At this stage, only the strongest predictors of protein abundance were retained to reduce the complexity of the GBT model. After removing genes in the plateau region, mRNA abundance, main cellular functional categories and few triple codon counts emerged as the top-ranked predictors of protein abundance. We then created a new tuned GBT model using the five most significant predictors. The construction of our non-linear model consists of a set of serial regression trees models with implicit strength in variable selection. The model provides variable relative importance measures using as a criterion mean square error. The results showed that coefficients of determination for our nonlinear models ranged from 0.393 to 0.582 in both datasets, providing better results than linear regression used in the past. We evaluated the validity of this non-linear model using biological information of operons, regulons and pathways, and the results demonstrated that the coefficients of variation of estimated protein abundance values within operons, regulons or pathways are indeed smaller than those for random groups of proteins.
Contact: weiwen.zhang@asu.edu; george.runger@asu.edu
Supplementary Information: Supplementary data are available at Bioinformatics online.
1 INTRODUCTION
The last decade has seen significant growth in technologies pertaining to molecular biological assays to measure gene expression profiles. These high-throughput technologies, such as DNA microarray and Serial Analysis of Gene Expression, have enabled the quantitative measurements of the abundance of various biological molecules and their variation between different states at the genome scale (Hermeking 2003; Horak and Snyder, 2002; Smith et al., 2002). However, evidence suggests that transcriptomic profiling is necessary but not sufficient to characterize biological system complexity (Gygi et al., 1999). For example, transcript levels detected by mRNA profiling do not reflect all regulatory processes in the cell, as post-transcriptional processes, such as synthesis, processing and modification of proteins, may affect active protein concentration but are not considered. Therefore, in addition to studying gene expression at the transcriptional level, large-scale proteomic analysis should be considered as a means to understand the systems and pathways in living organisms (Nie et al., 2007). Proteome-based expression analysis is generally performed by 2D-gel electrophoresis, in which proteins are separated according to their isoelectric point and mass. This technique requires intensive labor and time, and has proved effective in quantifying a cytoplasmic sub-set of the cellular proteome over a limited range of molecular weights and isoelectric points. In most cases, only a small set of proteins were detected (Alter and Golub, 2004; Mootha et al., 2003a, b). Recent advances in gel-free proteomics technologies facilitate large-scale characterization of the proteome. High-performance liquid chromatographic (HPLC) fractionation of protein tryptic digests, followed by automated tandem mass spectrometry (MS/MS) on the peptide fragments, allows identification of several hundred or even thousands of proteins simultaneously from cellular extract (Gygi et al., 1999). One of the major challenges in integrative analysis of large-scale transcriptomic and proteomic datasets is how to facilitate generation of new knowledge not accessible by analysis of either data type alone. In several recent studies in spite of sparse proteomic data, integrative analyses of genome-wide mRNA and protein expression patterns have enabled researchers to unravel global regulatory mechanisms and complex metabolic networks in living organisms (Alter and Golub, 2004; Hegde et al., 2003; Mootha et al., 2003a, b).
One of the key tasks for integrated transcriptomic and proteomic analysis is to identify relationships between protein abundance and their cognate mRNA concentrations. Although, one would hypothesize that the correlation between mRNA expression levels and protein abundance will be strong based on the central dogma of molecular genetics, support from early experimental data is not immediately apparent. Most recent studies have either failed to find a correlation between protein and mRNA abundances (Gygi et al., 1999) or have observed only a weak correlation (Greenbaum et al., 2002; Ideker et al., 2001; Washburn et al., 2003). In addition to various biological factors and limitations of current experimental protocols, it has been suggested that the poor correlation may stem from the inadequacy of available statistical tools to compensate for biases in the data collection methodologies.
While microarray analysis produces data on transcript levels for most genes in a given genome, proteomic datasets are often incomplete due to the imperfect identification of coding sequences within a genome and the limited sensitivity of current peptide detection technologies (Wilkins et al., 2006). Current technologies allow detection of only one-third to one-half of all coded proteins (Ideker et al., 2001; Scherl et al., 2006a, b; Zhang et al., 2006a). In prior comparisons of transcriptomic and proteomic data, undetected proteins were often assigned a concentration value of zero, and excluded from the correlation analysis. This unrealistic simplification could adversely affect interpretation of relationships between transcriptomic and proteomic data. For instance, current technologies for proteomic analysis tend to be biased towards detection of relatively abundant proteins. Correlation patterns between transcriptomic and proteomic data for these highly expressed genes are unlikely valid for the entire genome since correlation patterns may be different for lowly expressed genes. Hence, improved methods of coping with missing protein abundance values are necessary for integrative analysis of transcriptomic and proteomic datasets. To address issues with the missing proteomics data, one recent tactic was to integrate Gene Ontology (GO) information into the data imputation; the approach could enhance the imputation even when the missing fraction is large (Tuikkala et al., 2006). We also proposed a novel Zero-inflated Poisson (ZIP) regression model in which we assumed that 100×P% (0 < P < 1) of the genes with a proteomic abundance level of zero could be unexpressed genes or expressed genes that were undetected due to technical limitations (Nie et al. 2006a). Thus, the proteomic abundance (y) was distributed as a mixture of zeros with probability P and a Poisson regression distribution with probability (1 − P). Although, prediction of the missing proteomic data by both GO and ZIP models has improved biological interpretation, the models' assumption that correlation patterns of transcriptomic and proteomic data are linear at the whole-genome scale is not always true. For example, it has been suggested that correlations may vary in different functional categories in both prokaryotic and eukaryotic systems (Beyer et al., 2004; Nie et al., 2006b).
In this study, using two sets of cognate transcriptomic and proteomic data collected from Desulfovibrio vulgaris, we describe a non-linear data-driven model to predict abundance for undetected proteins for the two datasets. We demonstrate the application of stochastic gradient boosted trees (GBT) to uncover possible non-linear relationships between transcriptomic and proteomic data. The idea is to create regression boosted trees to predict protein abundance based on several relevant predictors in both datasets: mRNA abundance, cellular role, molecular weight, sequence length, protein length, GC content and triple codon counts in both datasets. To compare the general behavior of these factors across different experimental conditions within same species, the results are stratified into several parts: (i) variable (predictor) importance and partial dependency plots; (ii) construction of the model; and (iii) validation using biological information.
2 MATERIALS AND METHODS
2.1 Datasets
We analyzed two datasets from D.vulgaris. The experimental conditions differed between the datasets as they were obtained by independent research (Heidelberg et al., 2004; Mukhopadhyay et al., 2006; Zhang et al., 2006a, b). Brief description of both datasets is provided below. We normalized the raw intensity values from both datasets with a quantile normalization using an R package (caret) available through the R project (http://www.r-project.org/). Table 1 and the following sections provide a brief description of Datasets 1 and 2 used throughout this article.
Table 1.
Description of the datasets used in this study
| Dataset 1 | Dataset 2 | |
|---|---|---|
| References | Zhang et al., 2006a, b | Mukhopadhyay et al., 2006 |
| Conditions | Formate–Log (FL), Formate–Stationary (FS), Lactate–Log (LL), Lactate–Stationary (LS) | Control Time 0 h (CT0); Control Time 120 h (CT120); and Stressed NaCl Time 120 h (ST120) |
| Number of Variables | 70 | 70 |
| Number of genes analyzed | 456 (FL), 477 (FS), 440 (LL) and 462 (LS) | 2146 for all conditions |
| Number of replicates (mRNA abundance) | 4/gene | 3/gene except for ST120: 2/genes |
| Number of replicates (protein abundance) | 3/gene | 2/gene |
| Number of genes removed using a threshold t | 42 (FL), 477a (FS), 59 (LL) and 28 (LS) | 42 (CT0), 26 (CT120) and 19 (ST120) |
aThe condition FS was eliminated from further study based on biological knowledge provided by the experts. More details on Section 2.
2.1.1 Dataset 1
The dataset consists of the whole-genome mRNA expression and LC–MS/MS proteome abundance data from D.vulgaris in two different growth stages –log and stationary– and under two distinct types of media: lactate- or formate-based. To minimize variations between microarray and proteomic measurements, identical cell samples from each growth condition were split and used to isolate both the RNA and proteins for analyses. Complete descriptions of the experimental designs and microarray and proteomic data collection methods are given elsewhere (Nie et al., 2006b; Zhang et al., 2006a; b). Briefly, oligonucleotide microarrays containing 3507 open reading frames (ORFs) of the D.vulgaris genome were designed by NimbleGen Systems, Inc. (Madison, WI) (Nuwaysir et al., 2002; Heidelberg et al., 2004). For each experimental condition, mRNA abundances were determined from the average of four measurements for each gene: two replicates (each containing a pool of three biological replicates) that were each hybridized to duplicate microarrays (Zhang et al., 2006b). Proteomic analysis was performed on a Finnigan model LTQ ion trap mass spectrometer (ThermoQuest Corp., San Jose, CA). The relative protein abundance was estimated based on the number of peptide hits (Qian et al., 2005). The number of peptide hits for a given protein was the median of three LC-MS/MS measurements. The protein abundances ranged from one to several hundred (Zhang et al., 2006b).
2.1.2 Dataset 2
The dataset consists of the whole-genome mRNA expression and LC–MS/MS proteome abundance data from D.vulgaris grown under two stress conditions (250 mM NaCl or KCl) (Heidelberg et al., 2004; Mukhopadhyay et al., 2006). Briefly, spot signals, spot quality and background fluorescence intensities of the microarray were quantified with ImaGene, version 5.5 (Biodiscovery Inc., Los Angeles, CA) (Raw microarray data of this dataset can also be found in NCBI, GEO accession number GSE4447). Replicate cultures from a control (time zero and 120 min) and a stressed sample (120 min) were used to obtain total protein. A total of 1356 proteins were identified in all samples, and for 47 of these proteins there were reproducible changes between the control and the stressed sample (http://vimss.lbl.gov/SaltStress/) (Mukhopadhyay et al., 2006).
2.1.3 Quality of datasets
The quality of both datasets was assessed by calculating Pearson correlation coefficients among multiple replicates for microarray and protein measurements. Dataset 1 shows that correlation coefficients of the microarray experiments are from 0.97 to 0.99 among replicate samples (Nie et al., 2006a, b), and correlation coefficients of LC–MS/MS measurements normalized by amino acid composition are 0.86–0.92 among replicates, indicating good reproducibility. Similarly for Dataset 2, normalized microarray measurements showed correlation coefficients between 0.86 and 0.96 among replicates and a tight range of 0.96–0.98 for correlations between protein abundance samples for all conditions. In terms of correlation of mRNA and protein abundance using Pearson correlation, low values were found in both datasets. For Dataset 1, correlation between mRNA expression and normalized protein abundance was modest: 0.54 to 0.63 (P-value, 0.001) by Pearson correlation coefficient for all conditions. Dataset 2 reflected correlation values from 0.33 to 0.48. These correlation levels are similar to those previously reported for yeast (Ideker et al., 2001). The relatively poor correlation between mRNA and protein abundance suggests the fallacy of assumption of linearity in relationship between variables.
2.2 Genome information
2.2.1 Cellular functional category
The cellular functional categories of all genes in the D.vulgaris genome were downloaded from the Comprehensive Microbial Resource (CMR) of TIGR (http://cmr.tigr.org) (Heidelberg et al., 2004). On the basis of the original annotation, the genes and proteins are classified into 20 cellular functional categories. These categories were included in the model as possible predictors of protein abundance.
2.2.2 Other predictor factors
Gene annotated attributes such as sequence length, protein length, molecular weight, GC content and triple codon counts of all genes in the D.vulgaris genome were downloaded from the TIGR resource and included in our study. Continuous numerical values were gathered for the molecular weight of each gene. The GC content reflected the proportion of nucleotides G or C in the D.vulgaris genome. The triple codon information included counts for all 64 triple codon combinations in the genetic code.
2.2.3 Operon and pathway information
The complete genome of D.vulgaris and its ORF calls and annotation were downloaded from NCBI Genbank, the TIGR resource. Genes transcribed in the same direction having intergenic regions <15 bp were defined as one operon. Although, a new method has been proposed to define operons by combining intergenic distances with comparative genomic measures (Alm et al., 2005; Price et al., 2005), we opted for the distance-only approach, a relatively low threshold, to cover more of the possible operons. With this relatively low threshold, a total of 609 operons, ranging from 2 to 13 genes each, were identified in D.vulgaris (gene list of all operons is available upon request). The list of D.vulgaris regulons was kindly provided by Prof. Judy Wall and Dr Chris Hemme of the Department of Biochemistry at the University of Missouri at Columbia (the regulons were identified based on their homology to the known Escherichia coli regulons) (Hemme and Wall, 2004). Gene lists of 92 metabolic pathways defined for microbial genomes of interest were downloaded from the KEGG database (http://www.genome.jp/kegg/kegg2.html).
2.3 Construction of non-linear relationship model
To satisfy the need for a method amenable to mixed data types and capable of unraveling non-linear relationships between the data previously discussed, we applied stochastic GBT as described by Friedman (2002). These models have been used in a wide range of applications such as ecological modeling and prediction, chemical concentration on rocks and demographic survey data (De'ath, 2007; Elith et al., 2008; Friedman 2001). Our objective was to find an approximated function that could map a set of input variables x={x1,…, xn} to the response output y in such a way that the expected value of empirical loss was minimized as shown in (1). Boosting fits a weighted additive expansion composed of weak classifiers (e.g. regression trees) that approximates the response y as in (2) (Hastie et al., 2001). Gradient boosting sequentially applies regression trees to fit residuals while minimizing squared error loss, creating new models which are encouraged to become experts in cases misclassified by previous trees.
| (1) |
| (2) |
These individual trees partition the space of joint predictor variable values into disjoint regions Rj with constant predictor values γj assigned to each region. A single tree can be formally expressed as a piecewise constant function as described in (3). The parameter space delta is estimated by minimizing empirical risk as in (4). To find disjoint regions and constants that minimize a particular empirical risk is a large combinatorial problem. There are several optimization methods to achieve this. The method used in this study uses a gradient approach implemented from R.
| (3) |
| (4) |
The method described previously was implemented using the gbm R package available from the R project (http://www.r-project.org/). The required inputs include: loss function, number of trees, the depth of each tree, shrinkage rate and number of folds for cross validation (Ridgeway, 2007). Squared error loss was used as the loss function in the construction of the models for all conditions based on preliminary results where squared error and absolute loss performance were compared. The number of trees in each model was chosen to be 500, as this is considered sufficient iteration to achieve optimality (Friedman, 2001). To capture some degree of variable interaction a depth value of three was chosen to balance out the model complexity. For shrinkage rate, we chose the recommended default of 0.005 (Ridgeway, 2007) since we did not focus on the regularized aspect of the models. The models were specified to be built using five cross validated folds.
Cross validation is a technique for model assessment which includes randomization. Input data is partitioned into K equal parts where K – 1 sets are used to train the model and the other unseen set is used to calculate prediction errors (Hastie et al., 2001). This is repeated K times, yielding K prediction errors values, one computed at every fold. An average and standard deviation (SD) can be extracted to select the most representative model for future prediction. Once the best model has been selected based on cross validation, it is evaluated based on its coefficient of determination (R2) which represents the variation explained by the model. The coefficient of determination (R2) is a statistical measure representing the percentage of variance explained by the model. R2 values ranges from 0 to 1. The closer the R2 to 1 the better the model is explaining the variance of the data. Furthermore, as an alternative means to assess the goodness of the model, we studied the predictions of small sets of genes grouped based on pathway, operon and regulon information. In order to describe the variation within a dataset, such as ‘molar abundance’ of proteins within one operon, we computed the coefficient of variation (CV) for each set of proteins. The CV is defined as the ratio of the SD and the mean of the ‘molar abundance’ for a set of proteins (Johnson, 2005; Nie et al., 2006a) and is independent of the sample size. These CVs are computed for all pathway, operon and regulon groups and compared with a distribution of permuted CVs where permutation of genes is performed.
3 RESULTS AND DISCUSSION
3.1 Variable importance and partial variable dependence
The objective was to predict protein abundance based on the most relevant predictors. We used GBT model to uncover possible non-linear relationships between transcriptomic and proteomic data and to incorporate categorical predictors. In a previous study using multiple regressions, Nie et al. (2006b) found that mRNA abundance alone can explain only 20–28% of the total variation of protein abundance, suggesting mRNA–protein correlation can not be determined solely on the basis of mRNA abundance. Other possible predictors of protein abundance include cellular role of genes, GC content and codon usage of genes, length of genes and proteins and molecular weight of proteins (Nie et al., 2006b, 2006c, 2007).
GBT provided the implicit feature importance measures (for only the 10 top-ranked variables) shown in Table 2 for both Datasets 1 and 2. The relative importance measure is computed by measuring the contribution of an input variable based on its improvement on squared error loss at each tree for all trees and computing its average. This is done for all input variables. The relative influence value for a specific variable is presented as percentages of its relative contribution among all variables. Relative importance of variables measures for all 70 variables can be found in the Supplementary Tables 1–2. Cellular role and mRNA expression level were the best predictors of protein abundance across conditions and datasets. Some triple codon sequences appear to be more relevant in modeling protein abundance than sequence length, protein length and molecular weight. These triple codon counts differ in ranking across datasets but retain similar ranking within dataset conditions.
Table 2.
Measurements of relative importance of variables for the 10 top-ranked variables (after removing genes with high mRNA)
| Dataset 1 |
Dataset 2 |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| FL | LL | LS | CT0 | CT120 | ST120 | ||||||
| Variables | VRI (%) | Variables | VRI (%) | Variables | VRI (%) | Variables | VRI (%) | Variables | VRI (%) | Variables | VRI (%) |
| mRNAmean | 24.002 | mRNAmean | 28.877 | mRNAmean | 50.473 | mRNAmean | 38.398 | mRNAmean | 21.613 | mRNAmean | 25.149 |
| Cellular_role_I | 11.609 | Cellular_role_I | 16.694 | GCT | 14.916 | GGT | 17.351 | AAG | 13.941 | AAG | 15.046 |
| AAG | 9.105 | AAG | 7.785 | Cellular_role_I | 10.247 | AAG | 6.532 | Cellular_role_I | 11.590 | GGT | 10.861 |
| ACC | 8.879 | GGC | 5.277 | GTT | 5.912 | Cellular_role_I | 6.426 | GGT | 7.291 | ACC | 6.780 |
| GCT | 6.378 | GTT | 4.888 | AAG | 5.278 | GTT | 5.421 | GTT | 6.294 | Cellular_role_I | 6.637 |
| GGT | 4.379 | GCT | 4.536 | GGT | 2.595 | GGG | 3.596 | GGG | 3.977 | GCT | 3.720 |
| GGC | 3.208 | ACC | 3.561 | ACC | 1.103 | GAA | 2.641 | CGT | 3.408 | AAC | 2.545 |
| GTT | 3.140 | ATC | 2.992 | TGC | 1.031 | ACC | 1.980 | GCT | 3.289 | GGG | 2.053 |
| ATG | 2.194 | ATG | 2.444 | GAA | 0.986 | TAC | 1.869 | GAA | 2.442 | ACG | 2.047 |
| GCG | 2.069 | GCC | 2.041 | GTG | 0.904 | GCT | 1.744 | ACC | 2.264 | CCC | 1.983 |
Results show two datasets where VRI specifies variable relative importance. Relative influence is computed as the average of empirical improvements in squared error of splitting the decisions trees with corresponding variable. This measure is divided by the sum of the empirical improvement of all variables in the model. The percentage of this measure is VRI. More details are discussed in Section 3.
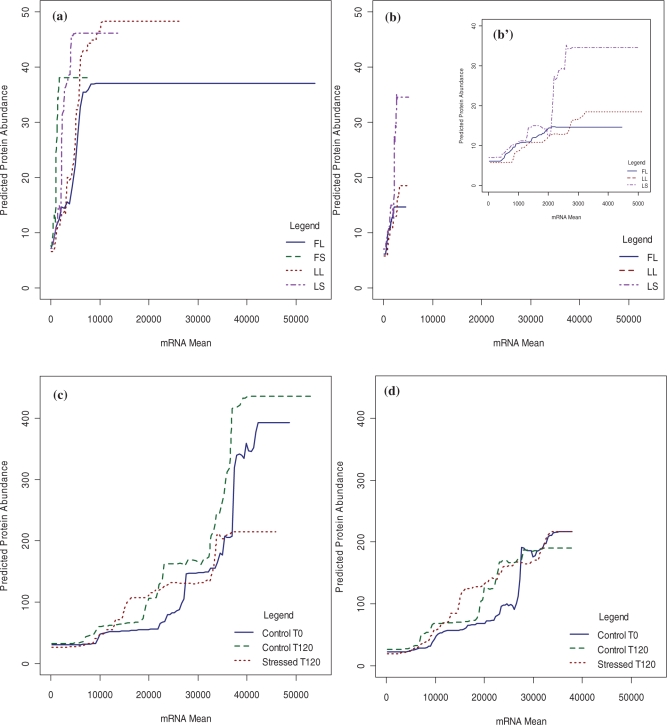
Our findings support the known correlation of mRNA and protein abundances. Besides the variable importance measures acquired from the boosted trees, partial dependency plots were studied to gain further insight into the association of mRNA abundance with protein measurements. The partial dependency plots provide a prediction model for a given predictor variable averaged across all other predictors. Figure 1 shows prediction values for given values of mRNA for different experimental conditions for Dataset 1 (Fig. 1a) and Dataset 2 (Fig. 1c). Though both datasets show increasing functions, slightly different relationships are observed across datasets, with similar behavior across conditions within a dataset. Both datasets exhibit a ‘plateau effect’ for high values of mRNA. The plateau occurs in regimens where protein abundance data is sparse with high variance where the tree models do not generate splits among the predictors. For example, in the region of high-mRNA values, there are a small number of genes/peptides whose protein values range from (0, 40) for Dataset 1 and (0, 500) for Dataset 2. This could reflect problems with the accuracy and sensitivity of current proteomic technologies.
Fig. 1.
Partial dependency plots. (a and c) Partial dependency prediction values for given values of mRNA for Datasets 1 and 2, respectively. (b and d) Partial dependency plots for mRNA values after eliminating genes with mRNA values higher than the corresponding cut-off threshold (for Datasets 1 and 2, respectively. (b′) A zoom view to partial dependency plot for plot (b).
After removing those genes/peptides with high-mRNA values, the model provided a more realistic fit. The cut-off threshold was obtained as the value where the plateau starts in partial dependency plots. A different threshold is obtained for each dataset. The minimal threshold value for all conditions is 5150 for Dataset 1 and 37975 for Dataset 2 (both in terms of absolute fluorescence intensity in the single color DNA array). Figure 1 shows partial dependency plots after eliminating genes with mRNA values higher than the corresponding cut-off threshold for Dataset 1 (Fig. 1b) and Dataset 2 (Fig. 1d). This provides a more realistic prediction model of protein based on mRNA. The partial dependency plots observed in Figure 1b and d, show an increasing predictive function for protein abundance as mRNA values increase. However, the curves exhibit variable slope, suggesting non-linear modifiers to the typical linear relationship. GBT were rebuilt using the five most important features across conditions and after removing genes/peptides having high-mRNA values. These modified models were used to predict protein abundance for genes/peptides with undetected protein values.
3.2 Construction of the non-linear correlation model
Initially, our GBT model was built using all variables to assess variable importance and to predict model behavior. Based on the plateau in regions of high-mRNA values, we removed genes in those areas based on thresholds estimated from the partial dependency plots where this behavior was captured. At this stage, our aim was to reduce model complexity by selecting the most relevant predictors of protein abundance. As discussed previously, mRNA abundance, main cellular functional categories and few triple codon counts were top-ranked after removing genes in the plateau region (Table 2). A new, tuned-GBT model was then built using the five most significant predictors. Protein abundance predictions using these newly tuned boosted trees for all conditions in both datasets are given in the Supplementary Tables 1–2.
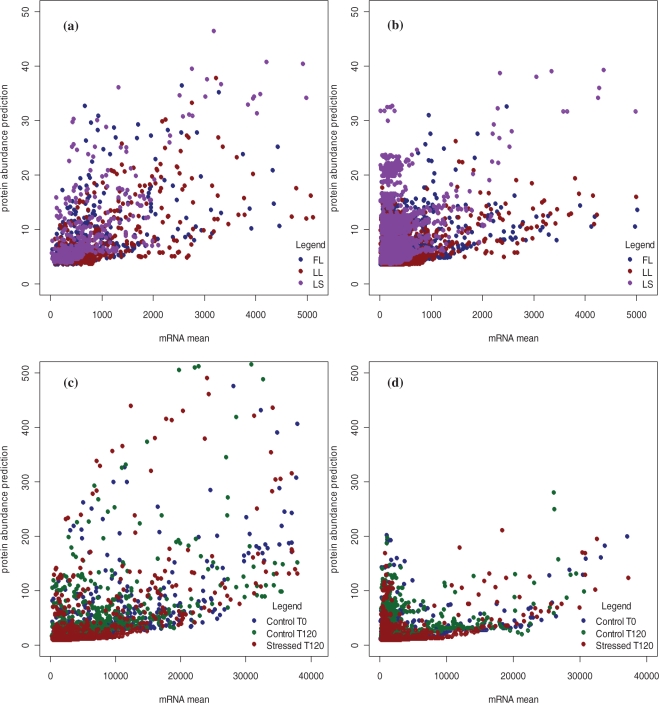
These predictions are depicted in Figure 2a and c, for Datasets 1 and 2, respectively. The behavior of both datasets predictions' when plotted only against mRNA is similar, showing a large number of genes/peptides with low-fitted protein values and less variability. For higher values of mRNA, the magnitude and variability of the predicted protein concentration increases. Similar behavior is noted in Figure 2b and d, were protein abundance measures where predicted for the genes/peptides with undetected values of protein abundance for both datasets.
Fig. 2.
Prediction plot for undetected proteins. (a and c) Protein prediction values for genes with protein values detected and used in model for Datasets 1 and 2, respectively. (b and d) Protein prediction values for genes with undetected protein values for Datasets 1 and 2, respectively.
3.3 Validation of prediction by external biological knowledge
External biological knowledge was invoked to validate the prediction of protein abundance values for the undetected proteins. The information used included gene organization information such as operon, and gene function information such as regulon and pathway. We tested the mode prediction by assuming that relationships between genes in operons, regulons and pathways are tighter than those between random gene sets. The information used for validation purposes is described in Section 2.2. The validation was conducted by calculating the CV within conditions for every operon, regulon and pathway of D.vulgaris for both Datasets 1 and 2. These groups of genes are thought to have less dispersion than a random set of genes by virtue of their intrinsic biological relationship. Table 3 provides an example of these results for the operon groups for both datasets. The complete data for operons, regulons and pathways is provided in the Supplementary Tables 1–2. To compare CV values we also performed a permutation test in the following way. A CV was computed from the protein prediction values for a set of randomly selected genes. This step was repeated a thousand times through resampling of genes without replacement.
Table 3.
Model validation: correlated expression of proteins in some operons groupsa
| Operons | Dataset 1 |
Dataset 2 |
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| FL |
LL |
LS |
CT0 |
CT120 |
ST120 |
||||||||
| CV | PCVmean | CV | PCVmean | CV | PCVmean | CV | PCVmean | CV | PCVmean | CV | PCVmean | ||
| 1: | DVU3025–DVU3033 | 0.515 | 0.634 | 0.417 | 0.735 | 0.441 | 0.771 | 0.582 | 1.107 | 0.579 | 0.973 | 0.751 | 1.122 |
| 2: | DVU2399–DVU2405 | 0.436 | 0.584 | 0.529 | 0.652 | 0.776b | 0.68 | 0.932 | 1.011 | 0.256 | 0.877 | 1.915b | 1.013 |
| 3: | DVU2072–DVU2078 | 0.368 | 0.61 | 0.508 | 0.691 | 0.755b | 0.73 | 1.490b | 1.011 | 1.438b | 0.915 | 0.618 | 1.013 |
| 4: | DVU1286–DVU1291 | 0.338 | 0.584 | 0.394 | 0.652 | 0.540 | 0.68 | 0.376 | 0.967 | 0.381 | 0.877 | 0.373 | 0.952 |
| 5: | DVU0429–DVU0434 | 0.470 | 0.584 | 0.417 | 0.652 | 0.601 | 0.68 | 0.504 | 0.967 | 0.501 | 0.877 | 0.481 | 0.952 |
| 6: | DVU0145–DVU0150 | 0.482 | 0.584 | 0.401 | 0.652 | 0.343 | 0.68 | 0.472 | 0.967 | 0.417 | 0.877 | 0.518 | 0.952 |
| 7: | DVU1080–DVU1085 | 0.329 | 0.584 | 0.313 | 0.652 | 0.497 | 0.68 | 0.307 | 0.967 | 0.423 | 0.877 | 0.382 | 0.952 |
| 8: | DVU2791–DVU2798 | 0.290 | 0.615 | 0.290 | 0.702 | 0.448 | 0.731 | 0.507 | 1.082 | 0.346 | 0.945 | 0.267 | 1.058 |
| 9: | DVU1627–DVU1634 | 0.588 | 0.615 | 0.441 | 0.702 | 0.732b | 0.731 | 0.675 | 1.082 | 0.837 | 0.945 | 0.778 | 1.058 |
| 10: | DVU1421–DVU1428 | 0.602 | 0.61 | 0.575 | 0.691 | 0.756b | 0.73 | 0.702 | 1.011 | 0.659 | 0.915 | 1.737b | 1.058 |
| 11: | DVU2978–DVU2985 | 0.296 | 0.615 | 0.311 | 0.702 | 0.417 | 0.731 | 0.685 | 1.082 | 0.599 | 0.945 | 1.567b | 1.058 |
| 12: | DVU1191–DVU1211 | 0.649 | 0.684 | 0.750 | 0.828 | 0.670 | 0.884 | 2.305b | 1.369 | 1.503b | 1.091 | 1.508b | 1.383 |
| 13: | DVU2558–DVU2563 | 0.383 | 0.584 | 0.530 | 0.652 | 0.395 | 0.68 | 0.682 | 0.967 | 0.600 | 0.877 | 0.594 | 0.952 |
| 14: | DVU1242–DVU1249 | 0.277 | 0.615 | 0.338 | 0.702 | 0.527 | 0.731 | 0.351 | 1.082 | 0.381 | 0.945 | 0.837 | 1.058 |
| 15: | DVU1552–DVU1560 | 0.689b | 0.634 | 0.828b | 0.735 | 0.711 | 0.771 | 1.002 | 1.107 | 0.905 | 0.973 | 0.943 | 1.122 |
| 16: | DVU0460–DVU0471 | 0.230 | 0.661 | 0.215 | 0.769 | 0.210 | 0.782 | 0.494 | 1.17 | 0.254 | 1.017 | 1.138 | 1.227 |
| 17: | DVU0646–DVU0651 | 0.223 | 0.584 | 0.316 | 0.652 | 0.426 | 0.68 | 0.133 | 0.905 | 1.480b | 0.877 | 1.589b | 0.952 |
| 18: | DVU1908–DVU1914 | 0.490 | 0.61 | 0.507 | 0.691 | 0.263 | 0.73 | 0.501 | 1.011 | 0.406 | 0.915 | 0.534 | 1.013 |
| 19: | DVU0861–DVU0872 | 0.198 | 0.661 | 0.335 | 0.769 | 0.333 | 0.782 | 1.199b | 1.17 | 0.771 | 1.017 | 0.552 | 1.227 |
| 20: | DVU1448–DVU1453 | 1.081b | 0.584 | 0.633 | 0.652 | 0.694b | 0.68 | 0.601 | 0.967 | 0.638 | 0.877 | 0.561 | 0.952 |
| 21: | DVU1038–DVU1044 | 0.670b | 0.61 | 0.787b | 0.691 | 0.712 | 0.73 | 0.661 | 1.011 | 0.776 | 0.915 | 0.998 | 1.013 |
| 22: | DVU1585–DVU1590 | 0.394 | 0.584 | 0.338 | 0.652 | 0.464 | 0.68 | 0.433 | 0.967 | 0.314 | 0.877 | 0.467 | 0.952 |
| 23: | DVU1045–DVU1052 | 0.675b | 0.615 | 0.751b | 0.702 | 0.667 | 0.731 | 1.278b | 1.082 | 0.800 | 0.945 | 0.854 | 1.058 |
| 24: | DVU1278–DVU1284 | 0.149 | 0.61 | 0.366 | 0.691 | 0.423 | 0.73 | 0.757 | 1.011 | 0.570 | 0.915 | 0.878 | 1.013 |
| 25: | DVU0807–DVU0813 | 0.712b | 0.61 | 0.739b | 0.691 | 0.614 | 0.73 | 1.052b | 1.011 | 1.061b | 0.915 | 1.042b | 1.013 |
| 26: | DVU1344–DVU1350 | 0.739b | 0.61 | 0.810b | 0.691 | 0.717 | 0.73 | 0.773 | 1.011 | 0.712 | 0.915 | 0.831 | 1.013 |
| 27: | DVU1301–DVU1330 | 0.529 | 0.695 | 0.733 | 0.855 | 0.733 | 0.948 | 0.753 | 1.499 | 0.628 | 1.123 | 0.925 | 1.526 |
| 28: | DVU2529–DVU2537 | 1.057b | 0.634 | 0.824b | 0.702 | 1.856b | 0.771 | 2.061b | 1.107 | 1.375b | 0.973 | 2.207b | 1.122 |
CV is computed by dividing SD by the mean of the prediction values for protein abundance for a specific set of genes (group). The protein prediction values were normalized by molecular weight before CV calculation. PCVmean is the mean of CV values computed through permutation test for selected operons. More details are provided in Section 2.
aCV values of selected operons based on predicted protein abundance from various experimental conditions are listed.
bCV values that are greater than the PCVmean.
For example, operon 19 contains twelve genes (DVU0861-DVU 0872). Its CV value was compared with a CV value generated through permutations where 12 genes were selected at random from the whole-genome dataset (without repeating any genes) and its condition-specific prediction values were used to calculate a single CV value. Repeating this calculation, a thousand times provided a CV-distribution to calculate mean, SD and percentile scores for groups with random genes per condition. As a result, the CV value for this operon was 0.335 for condition LL in Dataset 1 and the mean of the CV values through permutations was equal to 0.769 as shown in Table 3. Similarly, pathway path_dvu00052 (galactose metabolism) contains ten genes and its CV value was smaller than the mean of CV values through permutations (0.431 < 0.996) for condition ST120 in Dataset 2. This was done in the same way for all conditions in both datasets. As shown in Table 4, for Dataset 1, 75–79% of the operon groups had smaller CV values than those computed through permutation, and 79-88% of the pathway groups had smaller CV values than those computed through permutation. However, a shift to smaller proportions for regulon groups was observed with values between 50% and 67%. Similar results are presented Table 4 for Dataset 2. This shows that a large proportion of the biological-related groups are indeed less dispersed than unrelated groups of genes, providing some measure of validation for the predictions of our models. Furthermore, CV values from almost all operons groups were smaller than those by ZIP Regression Model (data not shown) (Nie et al., 2006a), suggesting the GBT model described the dataset better.
Table 4.
Percentages of groups with small CV value and percentile score
| Groups | Dataset 1 | Dataset 2 | ||
|---|---|---|---|---|
| Percentage of groups with CV <PCVmeana (%) | Percentage of groups with percentile score < 0.2 (%) | Percentage of groups with CV <PCVmeana (%) | Percentage of groups with percentile score < 0.2 (%) | |
| Operon | 75–79 | 36–50 | 75–82 | 32–54 |
| Pathway | 79–88 | 45–48 | 74–76 | 37–43 |
| Regulon | 50–67 | 8–33 | 58–83 | 25–33 |
CV is computed by dividing SD by the mean of the prediction values for protein abundance for a specific set of genes (group). The protein prediction values were normalized by molecular weight before CV calculation. More details are provided in Section 2.
aPCVmean is the mean of CV values computed through permutation test.
To gather more detailed information on how the CV compares with the distribution of the permuted CV, we also calculated the percentile score. Operon19 for LL condition in Dataset 1 showed a percentile score of 0.02 which provides information of the position of its CV across the CV values computed through permutations. The percentile score presented is a measure of the position of the biological group CV within the thousand CV values from permutations in percentage. Because operon19 had a percentile score of 0.02 this implies that 98% of the thousand CV values from permutations were greater than operon19 CV value. Likewise, pathway path_dvu00052 showed a small percentile score of 1% for ST120 condition in Dataset 2. Based on the thought that genes from pathway, operon and regulon groups should be less dispersed than permuted sets of genes, the percentile scores are expected to be very low. The calculated CV for most groups was less than the mean CV value for permuted sets of genes (Supplementary Tables 1–2). For the percentile scores about half of these groups fall within a percentile <0.20 as shown in Table 4. A similar trend was found when compared with the mean of permuted dispersion.
In addition, using the predicted values for each of the operon, pathway and regulon groups, we calculated the protein–mRNA correlation of these groups and compared it with the overall correlation at whole-genome level. The results showed relatively strong protein–mRNA correlation for most of gene/protein pairs within operons and pathways groups for both datasets (Supplementary Figs 1 and 2). Among them, pathway groups showed stronger correlation in general. About 10 of these pathways groups revealed perfect correlation. However, only a small percentage of regulon groups portrayed a solid correlation. The observation that regulon groups had greater percentile values than pathway and operon groups and smaller correlation values may reflect the fact that the relationship between genes/proteins in regulons is more complicated than those in operons and pathways, and that the regulon group information is less defined and validated experimentally.
4 CONCLUSION
High-throughput experimentation measuring mRNA and protein expression provides rich sources of information for better understanding of the metabolic mechanisms underlying complex biological systems. The goal of this investigation, as well as our previous study (Nie et al., 2006a) is to address the problem of incomplete proteomic datasets by using statistical approaches. In the two datasets we used in this analysis, the number of undetected proteins is 3050, 3061 and 3057 for FL, LL and LS conditions, respectively, for Dataset 1; and 2463, 2465 and 2463 for CT0, CT120 and ST120 for Dataset 2 (Mukhopadhyay et al., 2006; Zhang et al., 2006a, b). With only partial proteomic data, the power of integrative transcriptomic and proteomic analysis could be limited and the analyses could be biased. There exists, therefore, an urgent need to develop methodologies to accurately estimate missing proteomic data to provide deeper insight into metabolic mechanisms underlying complex biological systems. Estimating missing proteomic data is not a trivial task (Nie et al., 2006a, 2007). One of the major difficulties is that the correlation patterns between transcriptomic and proteomic data do not follow a linear relationship at the whole-genome scale. Recently, varying correlations between different functional groups of genes/proteins (Beck and Knecht, 2003; Beyer et al., 2004; Nie et al., 2006b), and varying strength of the correlation between different sampling times and growth conditions have been reported (Conrads et al., 2005). However, to our knowledge, no statistical method of capturing non-linearity of correlation has been published.
In this work, we employed stochastic gradient boosting trees as a non-linear model to understand a possible pair-wise constant relationship among transcriptomic data, proteomic data and other factors. The boosting tree procedure is one of the favorable predictive data mining tools for many reasons. From the regression trees characteristics, they inherit the positive features of robustness.
Boosted trees models are invariant under all monotone transformations of the individuals input variables, which eliminates the sensitivity to long-tailed distributions and outliers (Friedman, 2001). Moreover, implicit feature selection is intrinsic through the trees' construction and inherited by the boosting machinery. In contrast to a single tree, boosted tree models enhance stability by reducing the depth of the trees and averaging over many of them. Gradient boosting trees models may not produce exact description but they provide insights into the nature of the input-output relationship.
The GBT model constructed is a data-driven model where the input are the abundance measurements of all mRNA (∼3500) and qualified detected proteins (<∼800) and output are the predicted abundance levels for almost all proteins (∼3500) in the genome. This approach provides two major advantages over previous correlation methods. First, it allows undetected proteins (those with an assigned protein abundance value of 0) to be assigned a predicted abundance based on the mRNA levels. As output, the model provides predicted abundance levels for a large number of proteins which are undetected experimentally; and second, the model attempts to address the possible non-linearity property of the correlations between transcriptomic and proteomic data. Based on the coefficient of determination (R2) which is used to assess the cross validated models, R2 ranged from 0.393 to 0.582 in both datasets in this non-linear model, which provided slightly better results compared with results when multiple linear regression model is applied (R2 ranges from 0.27 to 0.33). Finally, we evaluated the validity of this model using bioinformatics approaches. For example, in a comparison of the predicted protein abundance patterns of genes belonging to the same operons (representing groups of proteins that are expected to have similar molar abundance values), the results demonstrated that the CV of estimated protein abundance values within operons are indeed smaller than that for random groups of proteins.
ACKNOWLEDGEMENTS
The authors would like to thank the Center for Ecogenomics at the Biodesign Institute.
Funding: National Institutes of Health (NIH) [National Human Genome Research Institute (NHGRI) Center of Excellence in Genomic Sciences (Grant No. 5 P50 HG002360)].
Conflict of Interest: none declared.
REFERENCES
- Alm EJ, et al. The MicrobesOnline web site for comparative genomics. Genome Res. 2005;15:1015–1022. doi: 10.1101/gr.3844805. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alter O, Golub GH. Integrative analysis of genomescale data by using pseudoinverse projection predicts novel correlation between DNA replication and RNA transcription. Proc. Natl Acad. Sci. USA. 2004;101:16577–16582. doi: 10.1073/pnas.0406767101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beck G.RJr, Knecht N. Osteopontin regulation by inorganic phosphate is ERK1/2-, protein kinase C-, and proteasomedependent. J. Biol. Chem. 2003;278:41921–41929. doi: 10.1074/jbc.M304470200. [DOI] [PubMed] [Google Scholar]
- Beyer A, et al. Posttranscriptional expression regulation in the yeast Saccharomyces cerevisiae on a genomic scale. Mol. Cell Proteomics. 2004;3:1083–1092. doi: 10.1074/mcp.M400099-MCP200. [DOI] [PubMed] [Google Scholar]
- Conrads KA, et al. A combined proteome and microarray investigation of inorganic phosphate-induced pre-osteoblast cells. Mol. Cell Proteomics. 2005;4:1284–1296. doi: 10.1074/mcp.M500082-MCP200. [DOI] [PubMed] [Google Scholar]
- De'ath G. Boosted trees for ecological modeling and prediction. Ecology. 2007;88:243–251. doi: 10.1890/0012-9658(2007)88[243:btfema]2.0.co;2. [DOI] [PubMed] [Google Scholar]
- Elith J, et al. A working guide to boosted regression trees. J. Anim. Ecol. 2008;77:802–813. doi: 10.1111/j.1365-2656.2008.01390.x. [DOI] [PubMed] [Google Scholar]
- Friedman JH. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001;29:1189–1232. [Google Scholar]
- Friedman JH. Stochastic gradient boosting. Comput. Stat. Data Anal. 2002;38:367–378. [Google Scholar]
- Greenbaum D, et al. Analysis of mRNA expression and protein abundance data: an approach for the comparison of the enrichment of features in the cellular population of proteins and transcripts. Bioinformatics. 2002;18:585–596. doi: 10.1093/bioinformatics/18.4.585. [DOI] [PubMed] [Google Scholar]
- Gygi SP, et al. Correlation between protein and mRNA abundance in yeast. Mol. Cell Biol. 1999;19:1720–1730. doi: 10.1128/mcb.19.3.1720. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hastie T, et al. The Elements of Statistical Learning-Data Mining, Inference, Prediction. New York, NY, USA: Springer; 2001. [Google Scholar]
- Hegde PS. Interplay of transcriptomics and proteomics. Curr. Opin. Biotechnol. 2003;14:647–651. doi: 10.1016/j.copbio.2003.10.006. [DOI] [PubMed] [Google Scholar]
- Heidelberg JF, et al. The genome sequence of the anaerobic, sulfate-reducing bacterium Desulfovibrio vulgaris Hildenborough. Nat. Biotechnol. 2004;22:554–559. doi: 10.1038/nbt959. [DOI] [PubMed] [Google Scholar]
- Hemme CL, Wall JD. Genomic insights into gene regulation of Desulfovibrio vulgaris Hildenborough. OMICS. 2004;8:43–55. doi: 10.1089/153623104773547480. [DOI] [PubMed] [Google Scholar]
- Hermeking H. Serial analysis of gene expression and cancer. Curr. Opin. Oncol. 2003;15:44–49. doi: 10.1097/00001622-200301000-00006. [DOI] [PubMed] [Google Scholar]
- Horak CE, Snyder M. Global analysis of gene expression in yeast. Funct. Integr. Genomics. 2002;2:171–180. doi: 10.1007/s10142-002-0065-3. [DOI] [PubMed] [Google Scholar]
- Ideker T, et al. Integrated genomic and proteomic analyses of a systematically perturbed metabolic network. Science. 2001;292:929–934. doi: 10.1126/science.292.5518.929. [DOI] [PubMed] [Google Scholar]
- Johnson RA. Miller And Freund's Probability and Statistics for Engineers. Pearson prentice hall; 2005. [Google Scholar]
- Mootha VK, et al. Integrated analysis of protein composition, tissue diversity, and gene regulation in mouse mitochondria. Cell. 2003a;115:629–640. doi: 10.1016/s0092-8674(03)00926-7. [DOI] [PubMed] [Google Scholar]
- Mootha VK, et al. Identification of a gene causing human cytochrome c oxidase deficiency by integrative genomics. Proc. Natl Acad. Sci. USA. 2003b;100:605–610. doi: 10.1073/pnas.242716699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mukhopadhyay A, et al. Salt stress in Desulfovibrio vulgaris Hildenborough: an integrated genomics approach. J. Bacteriol. 2006;188:4068–4078. doi: 10.1128/JB.01921-05. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nie L, et al. Integrated analysis of transcriptomic and proteomic data of Desulfovibrio vulgaris: zero-inflated Poisson regression models to predict abundance of undetected proteins. Bioinformatics. 2006a;22:1641–1647. doi: 10.1093/bioinformatics/btl134. [DOI] [PubMed] [Google Scholar]
- Nie L, et al. Correlation between mRNA and protein abundance in Desulfovibrio vulgaris: a multiple regression to identify sources of variations. Biochem. Biophys Res. Commun. 2006b;339:603–610. doi: 10.1016/j.bbrc.2005.11.055. [DOI] [PubMed] [Google Scholar]
- Nie L, et al. Correlation of mRNA expression and protein abundance affected by multiple sequence features related to translational efficiency in Desulfovibrio vulgaris: a quantitative analysis. Genetics. 2006c;174:2229–2243. doi: 10.1534/genetics.106.065862. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nie L, et al. Integrative analysis of transcriptomic and proteomic data: challenges, solutions and applications. Crit. Rev. Biotechnol. 2007;27:63–75. doi: 10.1080/07388550701334212. [DOI] [PubMed] [Google Scholar]
- Nuwaysir EF, et al. Gene expression analysis using oligonucleotide arrays produced by maskless photolithography. Genome Res. 2002;12:1749–1755. doi: 10.1101/gr.362402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Price MN, et al. OpWise: operons aid the identification of differentially expressed genes in bacterial microarray experiments. BMC Bioinformatics. 2005;7:19. doi: 10.1186/1471-2105-7-19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qian WJ, et al. Probability-based evaluation of peptide and protein identifications from tandem mass spectrometry and SEQUEST analysis: the human proteome. J. Proteome Res. 2005;4:53–62. doi: 10.1021/pr0498638. [DOI] [PubMed] [Google Scholar]
- Ridgeway G. Generalized boosted models: a guide to the gbm package. 2007 Available at http://cran.r-project.org/web/packages/gbm/vignettes/gbm.pdf. (last accessed date May, 2009) [Google Scholar]
- Scherl A, et al. Correlation of proteomic and transcriptomic profiles of Staphylococcus aureus during the post-exponential phase of growth. J. Microbiol. Methods. 2006a;60:247–257. doi: 10.1016/j.mimet.2004.09.017. [DOI] [PubMed] [Google Scholar]
- Scherl A, et al. Exploring glycopeptide-resistance in Staphylococcus aureus: a combined proteomics and transcriptomics approach for the identification of resistance-related markers. BMC Genomics. 2006b;7:296. doi: 10.1186/1471-2164-7-296. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith RD, et al. The use of accurate mass tags for high-throughput microbial proteomics. OMICS. 2002;6:61–90. doi: 10.1089/15362310252780843. [DOI] [PubMed] [Google Scholar]
- Tuikkala J, et al. Improving missing value estimation in microarray data with gene ontology. Bioinformatics. 2006;22:566–572. doi: 10.1093/bioinformatics/btk019. [DOI] [PubMed] [Google Scholar]
- Washburn MP, et al. Protein pathway and complex clustering of correlated mRNA and protein expression analyses in Saccharomyces cerevisiae. Proc. Natl Acad. Sci. USA. 2003;100:3107–3112. doi: 10.1073/pnas.0634629100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilkins MR, et al. Guidelines for the next 10 years of proteomics. Proteomics. 2006;6:4–8. doi: 10.1002/pmic.200500856. [DOI] [PubMed] [Google Scholar]
- Zhang W, et al. A proteomic view of Desulfovibrio vulgaris metabolism as determined by liquid chromatography coupled with tandem mass spectrometry. Proteomics. 2006a;6:4286–4299. doi: 10.1002/pmic.200500930. [DOI] [PubMed] [Google Scholar]
- Zhang W, et al. Global transcriptomic analysis of Desulfovibrio vulgaris on different electron donors. Antonie Van Leeuwenhoek. 2006b;89:221–237. doi: 10.1007/s10482-005-9024-z. [DOI] [PubMed] [Google Scholar]