Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2010 Oct 1.
Published in final edited form as: Neuropsychologia. 2009 May 3;47(12):2470–2479. doi: 10.1016/j.neuropsychologia.2009.04.024

Aberrant functional activation in school age children at-risk for mathematical disability: A functional imaging study of simple arithmetic skill

Nicole Davis 1,2, Christopher J Cannistraci 2, Baxter P Rogers 2,4, J Christopher Gatenby 2,4, Lynn S Fuchs 1, Adam W Anderson 1,2,3,4, John C Gore 1,2,3,4
PMCID: PMC2712586  NIHMSID: NIHMS115028  PMID: 19410589

Abstract

We used functional magnetic resonance imaging (fMRI) to explore the patterns of brain activation associated with different levels of performance in exact and approximate calculation tasks in well defined cohorts of children with mathematical calculation difficulties (MD) and typically developing controls. Both groups of children activated the same network of brain regions; however, children in the MD group had significantly increased activation in parietal, frontal, and cingulate cortices during both calculation tasks. A majority of the differences occurred in anatomical brain regions associated with cognitive resources such as executive functioning and working memory that are known to support higher level arithmetic skill but are not specific to mathematical processing. We propose that these findings are evidence that children with MD use the same types of problem solving strategies as TD children, but their weak mathematical processing system causes them to employ a more developmentally immature and less efficient form of the strategies.

Keywords: arithmetic, development, mathematical skill, numerical processing, school-age, mathematical disability

Some children with normal intelligence have a disability in mathematics (MD) that makes the acquisition of grade-level mathematical competencies a challenge, despite adequate instruction (Barrouillet, Fayol, & Lathuliére, 1997; Fayol, Barrouillet, & Marinthe, 1998; Geary 1990; Geary & Brown, 1991). Children with MD use the same types of strategies as their typically developing peers (Geary 1990; Geary, Hoard, & Hamson, 1999; Geary, Hamson, & Hoard, 2000; Hanich, Jordan, Kaplan, & Dick, 2001; Jordan, Hanich, & Kaplan, 2003a; 2003b). However, as early as first grade, children with MD use less mature strategies and make more calculation errors (Geary 1999; Geary, Hamson, & Hoard, 2000; Jordan et al., 2003a; Jordan & Montani, 1997). In particular, children with MD demonstrate a specific weakness in the ability to accurately and quickly retrieve mathematical facts to solve single digit arithmetic problems (Barrouillet et al., 1997; Garnette & Fleischner, 1983; Geary 1990; 1993; Hanich et al., 2001; Jordan et al., 2003a; Jordan & Montani, 1997; Temple & Sherwood, 2002). Although there have been substantial gains in the understanding of cognitive risk factors for MD at a behavioral level, its neural bases in children remain to be explained.

Studies with adults provide evidence of the brain regions involved in mathematical disability (Dehaene & Cohen, 1991; Kahn & Whitaker, 1991; McCloskey, Harley, & Sokol, 1991). For example, lesion studies demonstrated that an individual with a left subcortical lesion exhibited an inability to retrieve and manipulate math facts; whereas, an individual with a left parietal lesion suffered from problems with subtraction while the ability to retrieve math facts via rote memory was unimpaired. Functional differences between disabled and control groups are evident in these areas in imaging studies investigating mathematical disorders in individuals with genetically based disorders such as Turner Syndrome (Alexander & Money, 1966; Molko et al., 2003) and Fragile X (Burbaud et al., 1995; Menon, Rivera, White, Glover, & Reiss, 2000; Rickard, Romero, Basso, Wharton, Flitman, & Grafman, 2000). In particular, group differences that resembled the lesion studies’ findings were found in the parietal cortex. Although these studies provide critical neurobiological information on brain regions involved in mathematical ability within the populations under investigation, the relevancy of these results to children with MD is uncertain. Brain trauma in the lesion studies typically encompasses large anatomical regions, limiting the specificity with which one can link a particular brain region to a deficient cognitive process. Additionally, the cognitive correlates underlying mathematical ability in adults with a genetically-based mathematical disorder may differ from those that occur in MD.

According to these findings, children with poor mathematical skills ought to show functionally distinct profiles from children with good math skills in frontal and parietal regions during simple calculation tasks. A single functional imaging study investigating simple arithmetic skill has been published in which activation in children with MD was compared to activation in typically-developing controls (Kucian, Loenneker, Dietrich, Dosch, Martin, & von Aster, 2006). Using an ROI based approach, group differences were found in frontal and parietal regions during an approximate calculation task; children with MD had weaker activation. However, no group differences were found during an exact calculation task. The lack of group differences during the exact calculation task is inconsistent with the behavioral evidence that children with MD have a specific weakness in the ability to accurately retrieve math facts from long term memory (Barrouillet et al., 1997; Garnette & Fleischner, 1983; Geary 1990; 1993; Hanich et al., 2001; Jordan et al., 2003a; Jordan & Montani, 1997; Temple & Sherwood, 2002). A possible explanation for this result is that the mixture of grade level in school in the Kucian et al (2006) study may have diminished the power of the study to find group differences. Mathematical knowledge is significantly influenced by quantity and quality of instruction (Geary, Brown, & Samaranayake, 1991), and Kucian et al. (2008) maintained that functional differences between adults and children during simple arithmetic tasks were associated with a specialization for mathematical skill that occurs with schooling.

For our purposes, the results of these studies suggest important directions for research on children with MD. The aim of the current study was to describe quantitatively the patterns of brain activation associated with different levels of performance in exact calculation and estimation tasks in well defined cohorts of children with MD and normal controls (TD) in the same grade level in school. We hypothesized that we would find significant group differences in a largely left hemisphere network during fact retrieval and exact calculation and in frontal and parietal regions during an approximation task.

Materials and Methods

Participants

Participants were 48 children in the third grade, ranging in age from 8 years and one month of age to 9 years and one month of age (mean age = 8.2, SD = 2.9). We focused on third grade because basic skills that support exact and approximate calculation tasks are taught in first and second grade, creating a range of skill development by third grade. Children were recruited over a period of two years from a larger study investigating the effects of types of intervention in mathematics. Behavioral scientists within the intervention study assumed responsibility for recruitment in the schools, excluding children with a brain injury, other physical disabilities, severe emotional problems, uncorrected sensory disorders, ADHD, or an IQ of less than 80. Within this larger study, children were identified as TD or MD. To be in the present imaging study, children in the TD group had to score at or above the 49th percentile on the calculation screening measure described below and had to receive all math instruction in the regular classroom. A high ability was used as a cut-off to ensure that participants identified as TD had good calculation skills (see Shaywitz et al., 2002). Difficulty in math was defined as a skill at or below the 25th percentile on the screening measure. This percentile was chosen because children who exhibit mathematics difficulties include those performing in the low average range (e.g., at or below the 25%). Imaging data were collected from January to July on 36 MD and 27 TD children. Twelve MD and 3 TD children were removed from analyses because of excessive movement artifacts or failure to complete the in-magnet tasks. High resolution magnetic resonance scans indicated that none of the participants had any overt neuroanatomical abnormality. This study was approved by the Vanderbilt University Institutional Review Board. Written informed consent was obtained from the children’s guardians. Written assent was obtained from the children.

Screening Measure

As part of their screening process for inclusion in the larger study, trained examiners administered the calculation subtest of the Wide Range Achievement Test – Third Edition (WRAT-3, Wilkinson, 1993) to children during the first semester of their third-grade year. The WRAT-3 is a broadly used standardized measure of achievement. The calculation subtest involves the identification of numbers and computations that increase in difficulty. Means and standard deviations for the groups’ performance on the screening measure are shown in Table 1.

Table 1.

Group Descriptive

Group Male WRAT-M SS* Exact Calc. % Correct App. Calc. % Correct Exact Calc. RT (ms)* App. Calc. RT (ms)**
Control (N=24) 12 109.3 (8.9) 93.6 (8.5) 84.3 (8.6) 1863.3 (1027.9) 2658.5 (1010.6)
MD (N=24) 14 85.7 (3.8) 92.4 (6.5) 85.1 (7.8) 3140.1 (1303.1) 3432.4 (1353.3)
Open in a new tab
*

p < .01;

**

p < .05

RT = response time

Experimental Design and Procedure

Imaging stimuli and task

Children performed the imaging tasks on a computer outside of the MRI scanner to acclimate them to the structure and speed of the tasks. A subset of each task with novel equations was used for these practice sessions. Children were put in a mock scanner to simulate the in-magnet environment and to introduce them to the various noises made by the magnet. After completing the practice sessions, children performed the experimental tasks in the MRI scanner. During the scanning procedure, participants lay supine in the magnet, looking up at a mirror that reflected a screen on which computer-controlled stimuli were projected using E-Prime software (Psychology Software Tools, Inc.). At the beginning of each trial, participants saw a screen with written instructions, and the examiner read these instructions aloud to the participants. In a few cases, the child was unwilling or unable to complete a task. Data for those participants were not included in the present study.

The imaging paradigm was a standard block design. Each functional imaging run was five min in duration and consisted of three 40 s blocks of each experimental task (an exact and approximate calculation task), three 40 s blocks of the control task (Greek letter matching task) and three 20 s blocks of rest. The calculation tasks mirrored Dehaene et al. (1999). All task items were presented vertically with three response choices shown horizontally at the bottom. Participants chose the correct answer by pressing a button (on a MRI compatible response pad) corresponding to the location (left, middle, right) of the correct response. The items and response choices remained on the screen until the participant responded or the block ended after 40 s. Numeric and control tasks were self-paced; therefore, the number of trials that participants completed within each block varied. Rogers, Anderson, Gatenby, Cannistraci, and Gore (2007) demonstrated that paced and self-paced versions of the same mathematical task place comparable demands on calculation-specific and comparison-specific brain regions. Task presentation was randomized across all participants, and items were randomized within each block. In all trials, when not actively engaged in a task, participants were instructed to fixate on a gray square on the screen.

A Philips 3 Tesla Achieva (Philips Healthcare Inc) was used to acquire the MRI data. Anatomical scans were acquired for approximately 15 min prior to functional scans. The anatomical images were acquired with a T-1 weighted, 3D turbo field echo pulse sequence (170 slices, 1 mm3 voxels). A high-resolution 2D T1 anatomical series was also acquired at the same location and slice thickness as the functional data. All functional data were acquired using a gradient echo EPI sequence (FOV 220 mm, TE 35ms, TR 2000 msec, flip angle of 79 degrees, 80 × 80 acquisition matrix interpolated to 128 × 128 image matrix, 28 slices, 3.5 mm thick with a gap of .35 mm).

Data Analysis

All functional data were analyzed using Brainvoyager QX (Brain Innovations Inc). Each functional volume was motion corrected using 3D rigid body transformations to the first volume of the first functional run. Each subject’s fMRI data sets were adjusted for slice timing differences and temporal drifts were removed with a linear trend removal. Individuals’ functional data were coregistered to their own high-resolution 3D anatomic scan then normalized to Talairach standardized space (Talairach & Tournoux, 1988). The normalized volumes were smoothed with a 6 mm FWHM Gaussian kernel. Volumes where head motion exceeded 3 mm or 3° relative to the first volume were removed from the data set, with corresponding rows of the design matrix also removed prior to fitting. A general linear model was fit at each voxel in each subject to produce parametric maps of normalized signal change for each task condition. To investigate within-group activation, a second-level analysis was used to generate group-level statistical t-maps comparing each math task to its symbol-matching control task (for the MD and TD groups separately). MD and TD groups were compared directly in a 2-way analysis of variance (ANOVA) with a between-subject effect of group (MD versus TD) and a within-subject effect of condition (math task versus symbol-matching control). A voxelwise statistical threshold of p<.001 was applied to the statistical maps, which were then additionally corrected for multiple comparisons at the cluster level (p < .05, corresponding to a cluster size of 432 mm3). Talairach coordinates were derived from the local maxima of each cluster activated over the threshold. The Talairach Daemon (Lancaster et al., 2000) was used to identify the anatomical structures, considering those within 1 cm of the local maximum.

Results

Behavioral

Analysis with multivariate general linear model using SPSS 16.0 revealed no significant differences between children with versus without MD in accuracy levels on the exact calculation (F (1, 46) = .202, p =ns) and approximate calculation tasks (F (1, 46) = .103, p = ns). Group differences in the response time for correct items were found for the exact calculation (F (1, 46) = 15.895, p < .000) and the approximation task (F (1, 46) = 5.046, p < .03).

Functional MRI Results – Individual Group Activation

Our comparison of each group’s activation indicated several differences in the locations and levels of activation, especially during the approximation task. The regions identified as significantly activated from the group-level statistical t-tests comparing each math task to its symbol-matching task are shown in Tables 2–5. The tables provide the Talairach coordinates, cluster size, statistical maximum, significance values, percent signal change, and Brodmann’s Area (BA) for the clusters of activated voxels during the in-magnet tasks for each group. In addition, in the tables we show the other group’s percent signal change for the same clusters of voxels. All regions identified during this analysis showed an increase in signal change during the experimental task compared to its symbol matching control. Figures 1 and 2 show the individual groups’ brain activation patterns during the in-magnet tasks depicted on an inflated brain template.

Table 2.

Location, Size, and Magnitude of MD Group’s Activation during the Exact Calculation Task

Anatomical Region Talairach coordinates cluster size stat max (T) significance MD % Sig. Change 1 TD % Sig. Change 2 BA
X Y Z
LH middle frontal gyrus −39 35 19 1075 5.72 0.001 0.334 0.077 46
LH superior frontal gyrus −3 5 55 1833 5.39 0.001 0.348 0.174 6
Open in a new tab

cluster size in mm 3

1

= the MD group’s activation for the exact calculation task versus symbol matching control

2

= the TD group’s activation for the exact calculation task versus symbol matching control

Table 5.

Size, Location, and Magnitude of TD group’s Activation during the Approximate Calculation Task

Anatomical Region Talairach coordinates cluster size stat max (T) significance TD % sig change 1 MD % sig change 2 BA
X Y Z
RH medial frontal gyrus 18 8 55 4185 12.49 0.001 0.3067 0.2429 6
LH medial frontal gyrus 0 20 46 6843 7.87 0.001 0.3592 0.4033 8
RH precuneus 6 −67 43 7446 7.78 0.001 0.5927 0.5799 7
LH frontal lobe −24 5 55 2600 7.58 0.001 0.2945 0.3116 6
RH middle frontal gyrus 36 23 40 893 7.46 0.003 0.2396 0.2532 8
LH cuneus −27 −85 22 1423 6.93 0.001 0.3928 0.3945 19
RH cuneus 30 −82 31 1443 5.91 0.001 0.3552 0.2793 19
Open in a new tab

cluster size in voxels

1

= the TD group’s activation for the approximation task versus symbol matching control

2

= the MD group’s activation for the approximation task versus symbol matching control

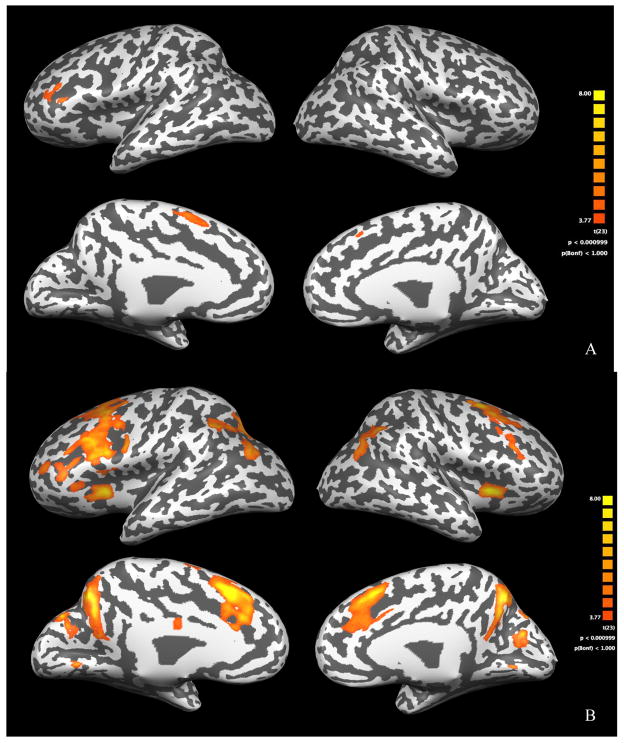
Figure 1.

Figure 1

Open in a new tab

Statistical maps of brain activation patterns for the MD group are depicted on an inflated brain template. A) Activation during the exact calculation task contrasted with its Greek symbol matching control task. B) Activation during the approximate calculation task contrasted with its Greek symbol matching control task. In each figure, the top row of figures shows the lateral view of the cortex and the lower row of figures shows the medial view, and the colored key provides significance levels for activation.

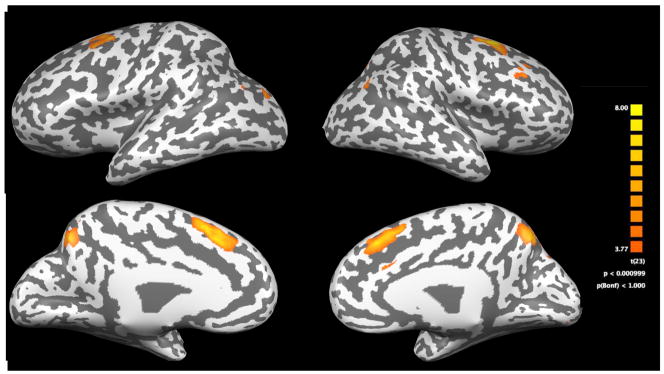
Figure 2.

Figure 2

Open in a new tab

Statistical maps of brain activation patterns for the TD group during the approximation task contrasted with its Greek symbol matching control are depicted on an inflated brain template. The top row of figures shows the lateral view of the cortex and the lower row of figures shows the medial view, and the colored key provides significance levels for activation.

MD Group

During the exact calculation task, children within the MD group had significant activation in the left hemisphere middle and superior frontal gyrus. As shown in Table 2, the TD group had little activation during the exact calculation task within these two regions. During the approximation task, children within the MD group showed activation in a network of brain regions typically reported during approximate calculation tasks, including biparietal, bilateral frontal, and left hemisphere cingulate cortices. As shown in the percent signal change column of Table 3, activation within these regions was decreased in the TD group compared with activation in the MD group.

Table 3.

Location, Size, and Magnitude of MD Group Activations during the Approximate Calculation Task

Anatomical Region Talairach coordinates cluster size stat max (T) significance MD % sig. change1 TD % sig. change2 BA
X Y Z
LH cingulated gyrus −6 20 40 40281 9.97 0.001 0.3369 0.1864 32
RH frontal lobe 27 2 52 8310 9.37 0.001 0.3406 0.2354 6
 RH middle frontal gyrus* 45 29 25 46
 RH frontal lobe* 27 2 52 6
RH claustrum 30 14 4 2502 9.17 0.001 0.2382 0.0971 -
LH precuneus 0 −64 40 18991 8.87 0.001 0.4433 0.2324 7
LH precuneus −27 −64 34 11281 7.44 0.001 0.3239 0.2213 7
RH inferior parietal lobe 39 −52 43 6250 7.29 0.001 0.2743 0.2151 40
 RH precuneus* 30 −67 37 19
LH IFG/caudate body −15 −1 19 4519 7.14 0.001 0.1961 0.0250 -
 LH middle frontal gyrus* −33 17 28 9
 LH middle frontal gyrus* −30 44 16 10
 LH claustrum* −24 20 7 -
 LH inferior frontal gyrus* −39 38 7 46
RH middle frontal gyrus 24 41 −2 655 5.95 0.004 0.3815 0.0592 11
LH medial frontal gyrus −3 2 58 615 4.88 0.008 0.5003 −0.0074 6
Open in a new tab

cluster size in mm3

*

regions are local maxima within the larger cluster of activation

1

= the MD group’s activation for the approximation task versus symbol matching control

2

= the TD group’s activation for the approximation task versus symbol matching control

TD Group

No regions reached significance level for the exact calculation condition in the TD group. Using a less conservative threshold of p < .001 and a cluster size of 108, activation was found in the right hemisphere insula and cingulate gyrus. Percent signal change within these regions in the MD group was comparable in the cingulate and distinct in the insula (Table 4). During the approximation task, children in the TD group activated an expected network in frontal and parietal regions. As shown in the percent signal change columns of Table 5, the MD group exhibited comparable percent signal change in several of the TD-group defined regions.

Table 4.

Size, Location, and Magnitude of TD group’s Activation during the Exact Calculation Task

Anatomical Region Talairach coordinates Cluster size stat max (T) TD % sig change 1 MD % sig change 2 BA
X Y Z
RH insula 30 23 13 133 5.36 0.2076 −0.0907 13
RH cingulate 9 17 40 369 4.56 0.2780 0.2715 32
Open in a new tab

Cluster threshold = 108, p < .001 (uncorrected)

1

= the TD group’s activation for the approximation task versus symbol matching control

2

= the MD group’s activation for the approximation task versus symbol matching control

Functional MRI Results – Group Contrasts

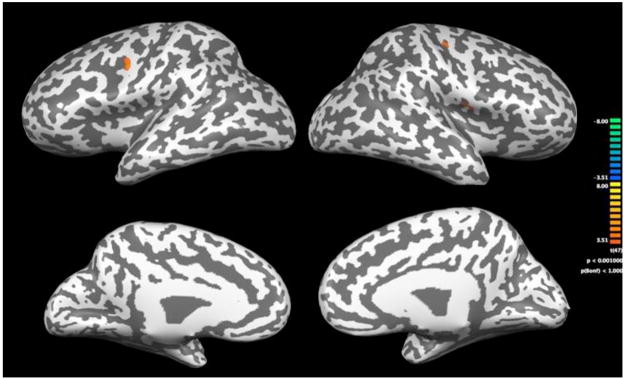
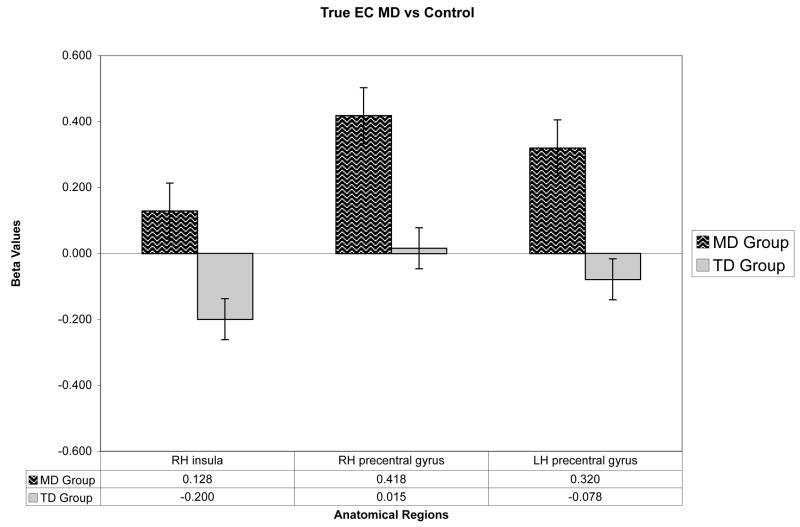
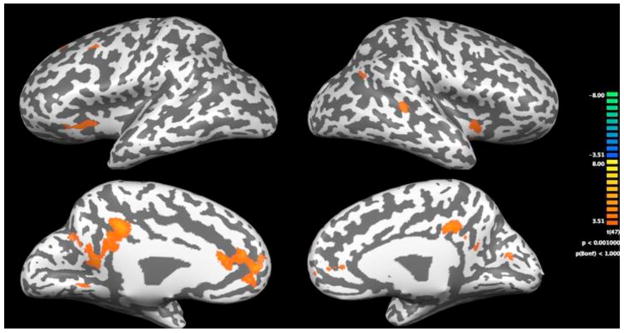
The 2-way ANOVA revealed significant group differences in primarily the bilateral frontal and cingulate cortex during the calculation tasks. At our significance level, the group comparisons yielded no evidence of decreased activation in the children with MD. Results are shown in tables 6 and 7 and figures 3–6. The tables give the Talairach coordinates, cluster size, statistical maximum, significance values, percent signal change, and Brodmann’s Area (BA) for the clusters of voxels that the two groups activate significantly differently during the in-magnet tasks. During the exact calculation task, group differences were seen in motor related regions within the bilateral precentral gyrus and also within the right hemisphere insula. Brain activation patterns in children with MD compared to the TD group during the exact calculation task are depicted on an inflated brain template in Figure 3. Each of the regions identified showed an increase in signal change during the exact calculation task compared to its symbol matching control. Figure 4 shows a bar graph of the percent signal change by group for the three regions identified as significantly different during the exact calculation task. As shown, children in the MD group on average had a positive signal change in the right hemisphere insula and left hemisphere precentral gyrus; whereas children in the TD group had a negative signal change within these regions.

Table 6.

Location, Size, and Magnitude of MD versus TD Contrasts for the Exact Calculation Task

Talairach coordinates cluster size Stat Max (T) Significance % Signal Change BA
X Y Z
LH precentral gyrus −45 −4 40 491 5.29 0.02 0.3982 6
RH insula 42 −4 10 811 4.29 0.001 0.3281 13
RH precentral gyrus 33 −22 52 517 4.24 0.019 0.4022 4
Open in a new tab

cluster size in mm3

Table 7.

Location, Size, and Magnitude of MD versus TD Contrasts for the Approximate Calculation Task

Anatomical Regions Talairach coordinates Cluster size Stat Max (T) significance % Sig Change BA
X Y Z
LH anterior cingulated −3 44 10 6150 5.78 0.001 0.4947 32
LH cingulate gyrus −3 −31 34 7376 5.46 0.001 0.3717 31
 LH posterior cingulate* −3 −49 7 5.00 0.6278 29
LH IFG/caudate −21 26 1 2389 5.40 0.001 0.3122 -
RH precuneus 36 −67 34 803 4.64 0.002 0.3012 39
RH prefrontal lobe 21 29 7 463 4.60 0.033 0.2411 -
LH inferior frontal gyrus −45 14 22 550 4.58 0.015 0.3479 9
RH claustrum 30 8 −2 516 4.47 0.019 0.2550 -
Open in a new tab

cluster size in mm3

*

submaxima of larger cluster, result of using a threshold of p<.0001 with a cluster of 200

Figure 3.

Figure 3

Open in a new tab

Statistical maps of increased signal change in the MD group versus children in TD group on the exact calculation task. Brain activation patterns are depicted on an inflated brain template. The top row of figures show the lateral view and the lower row of figures show the medial view. The colored key provides significance levels for activation.

Figure 6.

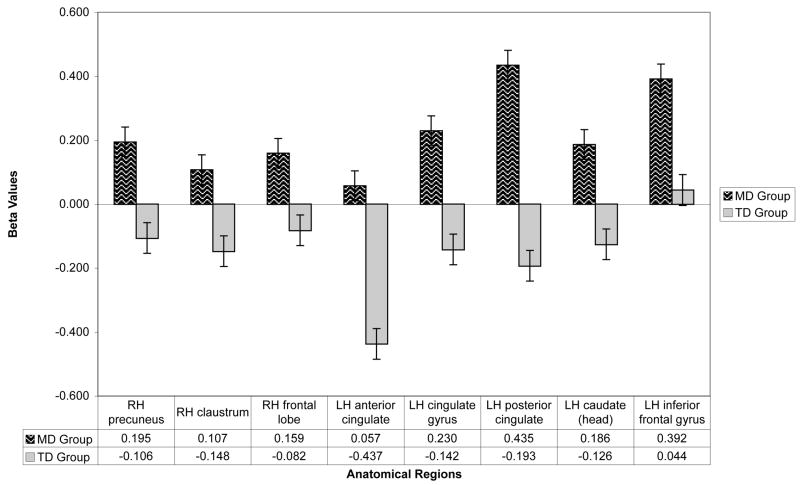
Figure 6

Open in a new tab

The signal changes for the brain regions shown in Figure 5 and listed in Table 7 are depicted. Error bars represent the SEM.

Figure 4.

Figure 4

Open in a new tab

The signal changes for the brain regions shown in Figure 3 and listed in Table 6 are depicted. Error bars represent the standard error of the mean (SEM).

To calculate the amount of variability in activation during the exact calculation task that was explained by number of solved trials by group, we performed an analysis of covariance (ANCOVA) to compare level of brain activation in the three regions listed in Table 6 by group using number attempted as a covariate. Number attempted did not reach statistical significance in the model for any of the three regions; however, its addition to the model caused the significance level of the right hemisphere precentral gyrus to decrease (F (1, 45) = 3.157, p < .082).

During the approximation task, group differences were found in left hemisphere cingulate (anterior and posterior) and inferior frontal gyrus (IFG) and in the right hemisphere precuneus, prefrontal cortex, and claustrum. Brain activation patterns in children with MD compared to the TD group during the approximation task are depicted on an inflated brain template in Figure 5. As shown in Figure 6, a similar pattern of group differences in the direction of activation (i.e. a positive versus negative magnitude) was found during the approximation task. The MD group had a positive signal change in all regions identified at our significance level. In contrast, the TD group had negative signal change in all regions, except for the left hemisphere IFG. Further analyses of these findings (consideration of the activations with respect to the fixation condition) indicated that the MD group’s positive signal in the cingulate regions were due to a greater negative signal during the symbol matching control task than the experimental task, suggesting that the group difference in these regions is related mostly to differences in activation during the control task.

Figure 5.

Figure 5

Open in a new tab

Brain activation of children in MD group versus children in TD group on the approximate calculation task. Brain activation patterns of children are depicted on an inflated brain template. The top row of figures show the lateral view, and the lower row of figures show the medial view. The colored key provides significance levels for activation.

To calculate the amount of variability in activation during the approximation task that was explained by number of solved trials by group, we performed ANCOVA to compare level of brain activation in the regions listed in Table 7 by group using number attempted as a covariate. Number attempted reached a statistically significant level in only one region, the left hemisphere caudate/IFG (F (1, 45) = 11.991, p < .001. Nevertheless, group difference in this region remained at a statistically significant level (F (1, 45) = 52.302, p < .000).

Discussion

The aim of the present study was to describe quantitatively the patterns of brain activation associated with performance in exact calculation and approximation tasks in well defined cohorts of children with MD and TD who were in the same grade in school. As predicted, we found group differences in activation during the exact and approximate calculation tasks. All of the regions identified in the group contrasts were due to significantly stronger activation in the MD group. Though these findings were in contrast to those from previous studies with adults and children, a majority of our differences were found in anatomical regions associated with domain general cognitive resources that support higher level arithmetic skill but are not specific to mathematical processing. Along with the behavioral evidence from the in-magnet tasks (comparable accuracy scores between groups and slower response times in the MD group), the increased activation in domain-general regions likely reflects greater cognitive processing demands in the MD group for successful task completion. Related to this, our findings are consistent with the evidence that children with MD employ the same types of strategies as TD children but use more developmentally immature and less efficient forms of these strategies (Geary et al., 1990; 1999; 2000; Hanich et al., 2001; Jordan et al., 2003a; 2003b).

In terms of the exact calculation task, our results showed that neither group of participants had significant activation in their parietal cortex while performing the task. In addition, the group contrast identified differences in the activation of domain-general anatomical regions that are not typically associated with mathematical processing skill. For example, children in the MD group had increased activation in the right insula, which may be associated with the fact that they performed a task that was difficult for them (Andreasen et al. 1995; Buckner & Carroll, 2006; Northoff, Heinzel, de Greck, Bermpohl, Dobrowolny, & Panksepp, 2006). The greater precentral gyrus activation found in the MD group may be functional evidence that they used strategies with greater executive functioning demands such as finger counting to complete the simple arithmetic tasks (Geary et al., 1992; 2000; Jordan et al., 2003a; Siegler & Jenkins, 1989; Siegler & Shrager, 1984). Our results are in contrast to those of adult imaging studies, in which the exact calculation task is associated with left lateralized activation. However, our findings are consistent with a growing body of evidence in the field that individual variability in functional activation during exact calculation tasks is related to developmental differences. Specifically, the parietal lobe may become specialized for mathematical tasks with schooling causing increased frontal lobe activation in young children related to compensatory strategy use (Ansari et al. 2005; Kucian et al. 2008; Rivera et al. 2005). Therefore, group differences during simple calculation tasks between good and poor math performers may arise predominantly in domain-general regions early in development and in domain-specific regions in adult populations.

With respect to the approximation task, both MD and TD groups activated a network of frontal and parietal brain regions reported in previous imaging studies on young children (Ansari et al., 2005; Cantlon et al., 2006; Kucian et al., 2008). Similar to the exact calculation task, we found greater activation in children with MD than the TD group. In particular, MD children had greater activation in a cluster of voxels in the right hemisphere inferior parietal lobe (Tal coords 36, −67, 34) near to a region reported by Pinel, Dehaene, Riviere, and LeBihan (2001) as associated with the “representation and manipulation of spatial information” (Tal coords 32, −64, 36). Spatial cognitive processes are employed during approximation tasks because individuals use a mental representation of a number line to estimate and manipulate magnitudes (Dehaene & Cohen, 1991). Individuals with MD may have less efficient mental representations of the number lines, which interferes with their processing speed and accuracy (Hanich et al., 2001; Siegler & Shrager, 1984). We propose that the MD group’s greater activation in this right hemisphere inferior parietal lobe is functional evidence of a group difference in numerical magnitude processing skill (Gallistel & Gelman, 1992).

Abnormal activation in the parietal cortex may cause a reallocation of cognitive resources to other compensatory brain regions to sustain performance on the approximation task. Accordingly, a majority of the regions with increased activation in the children in the MD compared to the TD group were prefrontal cortex regions. Prefrontal cortex is associated with domain general abilities such as attention and executive processes. Similarly, the children in the MD group had increased activation in the left hemisphere IFG near the caudate nucleus, a region that is also involved in cognition and executive functions (Cummings, 1993; Lewis, Dove, Robbins, Barker, & Owen, 2004; Masterman & Cummings, 1997; Rivera et al., 2005). The center of our activation was near a region that has been associated with working memory load in children (O’Hare, Lu, Houston, Bookheimer, & Sowell, 2008). Prior research has established the importance of the central executive components of working memory (Baddeley & Hitch, 1974) to the cognitive processes that maintain information “on line” for processing (Bull, Johnston, & Roy, 1999; Logie & Baddley, 1987). Although these findings are consistent with the proposal that children with MD have weak memory-based problem solving strategies (Geary, Widaman, Little, & Cormier, 1987; Ostad, 1997), the significant relationship between mathematical calculation skill and working memory disappears after accounting for individual differences in processing speed, phonological awareness, and inattentive behavior (Fuchs et al., 2006).

A novel finding in the current study was smaller negative task-related signal changes in the cingulate gyrus in the MD group during the approximation task. Most functional imaging studies focus on brain regions that exhibit task related positive increases in MRI signals. However, a network of brain regions exists that shows negative signal changes during a broad range of cognitive tasks. These have been termed the default mode network (Raichle, MacLeod, Snyder, Powers, Gusnard, & Shulman, 2001). In adults, an inverse relationship exists between this network and bilateral prefrontal regions, suggesting that the lateral prefrontal region recruits neural resources from the default mode brain regions to complete complex cognitive tasks (Greicius & Menon, 2004). Significant development occurs in the default network throughout childhood (Thomason, Chang, Glover, Gabrieli, Greicius, & Gotlib, 2008). Interestingly, the posterior cingulate appears to be part of the default mode network that develops early (Fair et al., 2007). Tentatively, our results may indicate that children with MD modulate the default mode network differently than TD children. Our activation in the anterior cingulate cortex is not identified as part of the early developing default mode network in children (Fair et al., 2007). However, it is located within a region of the anterior cingulate that has reciprocal connections with the lateral prefrontal cortex (Bush, Luu, & Posner, 2000), and it shows a negative signal in adults during cognitively demanding tasks (Bush et al., 1998). Since both groups had negative activation in these regions, the finding of a diminished negative signal in the MD group may be functional evidence of the relationship between attentive behavior and arithmetic skill (Ackerman & Dykman, 1995; Fuchs et al., 2005; 2006). Future studies should include tasks that measure the default mode network in children with and without mathematical difficulties to further investigate this finding.

Our results are not consistent with those of Kucian et al. (2006), in which weaker activations in children with developmental dyscalculia were found during the approximate calculation task. Results may differ because the behavioral task that we used, the method of analysis, or participant characteristics such as socio-economic status and severity of mathematical disability in the current study differed from those used by Kucian et al (2006). Related to this, a limitation to comparing the results of the two studies is that the calculation skill of our sample of children in the MD group was higher than that of Kucian et al. Recruitment of participants with significantly weaker mathematical skill might change our results.

Together, our results provide evidence that children with MD exhibit aberrant brain activations during exact and approximate calculation tasks. The significant group differences are consistent with behavioral studies indicating delayed calculation, approximation, attention, and working memory skills in children with MD. Although a significant group differences in activation during the approximation task was found in a domain-specific region of the parietal lobe, the majority of the group differences were located in domain-general regions. We propose that the difference in parietal lobe activation may be functional evidence of the MD group’s struggle to access the associated magnitudes of the numbers used during the approximation task (Gallistel & Gelman, 1992). However, the findings of increased activation in the prefrontal regions likely result from the allocation of a greater amount of cognitive resources to executive functioning and working memory processes for task completion in the MD group. A limitation in the current study may be the use of Talairach piecewise linear transformation to place all child brains in the same coordinate space. The precise correspondence between our coordinate space and the adult Talairach space is not well known because of differences between child and adult brains, but use of this transformation facilitates comparison with other published studies of children (e.g. Kucian et al. 2006; 2008).

Acknowledgments

This work was supported in part by the National Institutes of Health through the NIH Roadmap for Medical Research [T32 MH75883], the National Institute of Child Health and Development/Department of Education [HD046261], the National Institutes of Mental Health through the NIH Roadmap for Medical Research [T32 MH075883], and by the National Institute of Child Health and Development/Department of Education [HD046261]. We would like to thank Jack Fletcher and Whitney Schrader for their assistance during the course of this project.

Footnotes

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

References

  1. Ackerman PT, Dykman RA. Reading-disabled students with and without comorbid arithmetic disability. Developmental Neuropsychology. 1995;11:351–371. [Google Scholar]
  2. Alexander D, Money J. Turner syndrome and Gerstmann’s syndrome: neuropsychological comparison. Neuropsychologia. 1966;4:265–273. [Google Scholar]
  3. Andreasen NC, O’Leary DS, Cizadlo T, Arndt S, Rezai K, Watkins GL, Ponto LL, Hichwa RD. Remembering the past: two facets of episodic memory explored with positron emission tomography. American Journal of Psychiatry. 1995;152:1576–1585. doi: 10.1176/ajp.152.11.1576. [DOI] [PubMed] [Google Scholar]
  4. Ansari D, Garcia N, Lucas E, Hamon K, Dhital B. Neural correlates of symbolic number processing in children and adults. Neuroreport. 2005;16:1769–1773. doi: 10.1097/01.wnr.0000183905.23396.f1. [DOI] [PubMed] [Google Scholar]
  5. Baddeley AD, Hitch GJ. Working memory. In: Bower GH, editor. The psychology of learning and motivation: Advances in research and theory. New York: Academic Press; 1974. [Google Scholar]
  6. Barrouillet P, Fayol M, Lathuliére E. Selecting between competitors in multiplication tasks: An explanation of the errors produced by adolescents with learning disabilities. International Journal of Behavioral Development. 1997;21:253–275. [Google Scholar]
  7. Buckner RL, Carroll DC. Self-projection and the brain. Trends in Cognitive Science. 2006;11:49–57. doi: 10.1016/j.tics.2006.11.004. [DOI] [PubMed] [Google Scholar]
  8. Bull R, Johnston RS, Roy JA. Exploring the roles of the visual-spatial sketch pad and central executive in children’s arithmetical skills: Views from cognition and developmental neuropsychology. Developmental Neuropsychology. 1999;15:421–442. [Google Scholar]
  9. Burbaud P, Degreze P, Lafon P, Franconi JM, Bouligand B, Bioulac B, et al. Lateralization of prefrontal activation during internal mental calculation: A functional magnetic resonance imaging study. Journal of Neurophysiology. 1995;74:2194–2200. doi: 10.1152/jn.1995.74.5.2194. [DOI] [PubMed] [Google Scholar]
  10. Bush G, Luu P, Posner MI. Cognitive and emotional influences in anterior cingulate cortex. Trends in Cognition. 2000;4:215–222. doi: 10.1016/s1364-6613(00)01483-2. [DOI] [PubMed] [Google Scholar]
  11. Bush G, Whalen PJ, Rosen BR, Jenike MA, McInery SC, Rauch SL. The counting Stroop: an interference task specialized for functional neuroimaging – validation study with functional MRI. Human Brain Mapping. 1998;6:270–282. doi: 10.1002/(SICI)1097-0193(1998)6:4&#x0003c;270::AID-HBM6&#x0003e;3.0.CO;2-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Cantlon JF, Brannon EM, Carter EJ, Pelphrey KA. Functional imaging of numerical processing in adults and 4-y-old children. Public Library of Science Biology. 2006;4:e125. doi: 10.1371/journal.pbio.0040125. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Cummings JL. Frontal-subcortical circuits and human behavior. Archives of Neurology. 1993;50:873–880. doi: 10.1001/archneur.1993.00540080076020. [DOI] [PubMed] [Google Scholar]
  14. Dehaene S, Cohen L. Two mental calculation systems: a case study of severe acalculia with preserved approximation. Neuropsychologia. 1991;29:1045–1054. doi: 10.1016/0028-3932(91)90076-k. [DOI] [PubMed] [Google Scholar]
  15. Dehaene S, Spelke E, Pinel P, Stanescu R, Tsivkin S. Sources of mathematical thinking: behavioral and brain-imaging evidence. Science. 1999;284:970–974. doi: 10.1126/science.284.5416.970. [DOI] [PubMed] [Google Scholar]
  16. Fair DA, Cohen AL, Dosenbach NUF, Church JA, Miezin FM, Barch DM, Raichle ME, Petersen SE, Schlaggar BL. The maturing architecture of the brain’s default network. Proceedings of the National Academy of Science USA. 2007;105:4028–4032. doi: 10.1073/pnas.0800376105. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Fayol M, Barrouillet P, Marinthe C. Predicting arithmetical achievement from neuropsychological performance: a longitudinal study. Cognition. 1998;68:863–70. doi: 10.1016/s0010-0277(98)00046-8. [DOI] [PubMed] [Google Scholar]
  18. Fuchs LS, Compton DL, Fuchs D, Paulsen K, Bryant JD, Hamlett CL. The prevention, identification, and cognitive determinants of math difficulty. Journal of Educational Psychology. 2005;97:493–513. [Google Scholar]
  19. Fuchs LS, Fuchs DL, Compton D, Powell S, Seethaler PM, Capizzi AM, Schatschneider C, Fletcher J. The Cognitive Correlates of Third-Grade Skill in Arithmetic, Algorithmic Computation, and Arithmetic Word Problems. Journal of Educational Psychology. 2006;98:29–43. [Google Scholar]
  20. Gallistel CR, Gelman R. Preverbal and verbal counting and computation. Cognition. 1992;442:43–74. doi: 10.1016/0010-0277(92)90050-r. [DOI] [PubMed] [Google Scholar]
  21. Garnett K, Fleischner JE. Automatization and basic fact performance of normal and learning disabled children. Learning Disability Quarterly. 1983;6:223–230. [Google Scholar]
  22. Geary DC. A componential analysis of an early learning deficit in mathematics. Journal of Experimental Child Psychology. 1990;49:363–383. doi: 10.1016/0022-0965(90)90065-g. [DOI] [PubMed] [Google Scholar]
  23. Geary DC. Mathematical disabilities: Cognitive, neuropsychological, and genetic components. Psychological Bulletin. 1993;114:345–362. doi: 10.1037/0033-2909.114.2.345. [DOI] [PubMed] [Google Scholar]
  24. Geary DC, Bow-Thomas CC, Yao Y. Counting knowledge and skill in cognitive addition: A comparison of normal and mathematically disabled children. Journal of Experimental Child Psychology. 1992;54:372–391. doi: 10.1016/0022-0965(92)90026-3. [DOI] [PubMed] [Google Scholar]
  25. Geary DC, Brown SC. Cognitive addition: Strategy choice and speed-of- processing differences in gifted, normal, and mathematically disabled children. Developmental Psychology. 1991;27:398–406. [Google Scholar]
  26. Geary DC, Brown SC, Samaranayake VA. Cognitive addition: A short longitudinal study of strategy choice and speed-of processing differences in normal and mathematically disabled children. Developmental Psychology. 1991;27:787–797. [Google Scholar]
  27. Geary DC, Hamson CO, Hoard MK. Numerical and arithmetical cognition: A longitudinal study of process and concept deficits in children with learning disability. Journal of Experimental Child Psychology. 2000;77:236–263. doi: 10.1006/jecp.2000.2561. [DOI] [PubMed] [Google Scholar]
  28. Geary DC, Hoard MK, Hamson CO. Numerical and arithmetical cognition: Patterns of functions and deficits in children at risk for a mathematical disability. Journal of Experimental Child Psychology. 1999;74:213–239. doi: 10.1006/jecp.1999.2515. [DOI] [PubMed] [Google Scholar]
  29. Geary DC, Widaman KF, Little TD, Cormier P. Cognitive addition: Comparison of learning disabled and academically normal elementary school children. Cognitive Development. 1987;2:249–269. [Google Scholar]
  30. Greciuis MD, Menon V. Default-Mode activity during a passive sensory task: uncoupled from deactivation but impacting activation. Journal of Cognitive Neuroscience. 2004;16:1484–1492. doi: 10.1162/0898929042568532. [DOI] [PubMed] [Google Scholar]
  31. Hanich LB, Jordan NC, Kaplan D, Dick J. Performance across different areas of mathematical cognition in children with learning difficulties. Journal of Educational Psychology. 2001;93:615–626. [Google Scholar]
  32. Hitch GJ, McAuley E. Working memory in children with specific arithmetical learning disabilities. British Journal of Psychology. 1991;82:375–386. doi: 10.1111/j.2044-8295.1991.tb02406.x. [DOI] [PubMed] [Google Scholar]
  33. Jordan NC, Hanich LB, Kaplan D. Arithmetic fact mastery in young children: A longitudinal investigation. Journal of Experimental Child Psychology. 2003a;85:103–119. doi: 10.1016/s0022-0965(03)00032-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Jordan NC, Hanich LB, Kaplan D. Performance across different areas of mathematical cognition in children with learning disabilities. Journal of Educational Psychology. 2003b;93:615–626. [Google Scholar]
  35. Jordan NC, Montani TO. Cognitive arithmetic and problem solving: A comparison of children with specific and general mathematics difficulties. Journal of Learning Disabilities. 1997;30:624–634. doi: 10.1177/002221949703000606. [DOI] [PubMed] [Google Scholar]
  36. Kahn HJ, Whitaker HA. Acalculia: an historical review of localization. Brain and Cognition. 1991;17:102–115. doi: 10.1016/0278-2626(91)90071-f. [DOI] [PubMed] [Google Scholar]
  37. Kucian K, Loenneker T, Dietrich T, Dosch M, Martin E, von Aster M. Impaired neural networks for approximate calculation in dyscalculic children: a functional MRI study. Behavioral and Brain Functions. 2006;2:2–31. doi: 10.1186/1744-9081-2-31. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Kucian K, von Aster M, Loenneker T, Dietrich T, Martin E. Development of Neural Networks for Exact and Approximate Calculation: A fMRI Study. Developmental Neuropsychology. 2008;33:447–473. doi: 10.1080/87565640802101474. [DOI] [PubMed] [Google Scholar]
  39. Lancaster JL, Woldorff MG, Parsons LM, Liotti M, Freitas CS, Rainey L, Kochunov PV, Nickerson D, Mikiten SA, Fox PT. Automated Talairach Atlas labels for functional brain mapping. Human Brain Mapping. 2000;10:120–131. doi: 10.1002/1097-0193(200007)10:3&#x0003c;120::AID-HBM30&#x0003e;3.0.CO;2-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Lewis SJ, Dove A, Robbins TW, Barker RA, Owen AM. Striatal contributions to working memory: A functional magnetic resonance imaging study in humans. European Journal of Neuroscience. 2004;19:755–760. doi: 10.1111/j.1460-9568.2004.03108.x. [DOI] [PubMed] [Google Scholar]
  41. Logie RH, Baddeley AD. Cognitive processes in counting. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1987;13:310–326. [Google Scholar]
  42. McCloskey M, Harley W, Sokol SM. Models of arithmetic fact retrieval: An evaluation in light of findings from normal and brain-damaged subjects. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1991;17:377–397. [PubMed] [Google Scholar]
  43. Masterman DL, Cummings JL. Frontal-subcortical circuits: the anatomic basis of executive, social and motivated behaviors. Journal of Psychopharmacology. 1997;11:107–114. doi: 10.1177/026988119701100203. [DOI] [PubMed] [Google Scholar]
  44. Menon V, Rivera SM, White CD, Glover GH, Reiss AL. Dissociating prefrontal and parietal cortex activation during arithmetic processing. NeuroImage. 2000;12:357–365. doi: 10.1006/nimg.2000.0613. [DOI] [PubMed] [Google Scholar]
  45. Molko N, Cachia A, Riviere D, Mangin J, Bruandet M, Le Bihan D, Cohen L, Dehaene S. Functional and structural alterations of the intraparietal sulcus in a developmental dyscalculia of genetic origin. Neuron. 2003;40:847–858. doi: 10.1016/s0896-6273(03)00670-6. [DOI] [PubMed] [Google Scholar]
  46. Northoff G, Heinzel A, de Greck M, Bermpohl F, Dobrowolny H, Panksepp J. Self-referential processing in our brain--A meta-analysis of imaging studies on the self. NeuroImage. 2006;31:440–457. doi: 10.1016/j.neuroimage.2005.12.002. [DOI] [PubMed] [Google Scholar]
  47. O’Hare E, Lu LH, Houston SM, Bookheimer SY, Sowell ER. Neurodevelopmental changes in verbal working memory load-dependency: An fMRI investigation. NeuroImage. 2008;42:1678–1685. doi: 10.1016/j.neuroimage.2008.05.057. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Ostad SA. Developmental differences in addition strategies: A comparison of mathematically disabled and mathematically normal children. British Journal of Educational Psychology. 1997;67:345–357. doi: 10.1111/j.2044-8279.1997.tb01249.x. [DOI] [PubMed] [Google Scholar]
  49. Pinel P, Dehaene S, Riviere D, LeBihan D. Modulation of parietal activation by semantic distance in a number comparison task. NeuroImage. 2001;14:1013–1026. doi: 10.1006/nimg.2001.0913. [DOI] [PubMed] [Google Scholar]
  50. Raichle ME, MacLeod AM, Snyder AZ, Powers WJ, Gusnard DA, Shulman GL. A default mode of brain function. Proceedings of the National Academy of Science USA. 2001;98:676–682. doi: 10.1073/pnas.98.2.676. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Rickard TC, Romero SG, Basso G, Wharton C, Flitman S, Grafman J. The calculating brain: an fMRI study. Neuropsychologia. 2000;38:325–335. doi: 10.1016/s0028-3932(99)00068-8. [DOI] [PubMed] [Google Scholar]
  52. Rivera SM, Menon V, White CD, Glaser B, Reiss AL. Functional brain activation during arithmetic processing in females with fragile X syndrome is related to FMR1 protein expression. Human Brain Mapping. 2002;16:206–218. doi: 10.1002/hbm.10048. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Rivera SM, Reiss AL, Eckert MA, Menon V. Developmental changes in mental arithmetic: Evidence for increased functional specialization in the left inferior parietal cortex. Cerebral Cortex. 2005;15:1779–1790. doi: 10.1093/cercor/bhi055. [DOI] [PubMed] [Google Scholar]
  54. Rogers BP, Anderson AW, Gatenby JC, Cannistraci CJ, Gore JC. Effect of task pacing on activation of the horizontal intra-parietal sulcus during number comparison; 13th Annual Meeting of the Organization for Human Brain Mapping.Jun, 2007. [Google Scholar]
  55. Shaywitz BA, Shaywitz SE, Pugh KR, Mencl WE, Fulbright RK, Skudlarski P, Constable RT, Marchione KE, Fletcher JM, Lyon GR, Gore J. Disruption of posterior brain systems for reading in children with developmental dyslexia. Biological Psychiatry. 2002;52:101–110. doi: 10.1016/s0006-3223(02)01365-3. [DOI] [PubMed] [Google Scholar]
  56. Siegler RS, Jenkins E. Strategy Discovery and Strategy Generalization. In: Siegler R, Jenkins E, editors. How Children Discover New Strategies. Hillsdale, NJ: Lawrence Erlbaum Associates; 1989. pp. 1–20. [Google Scholar]
  57. Siegler RS, Shrager J. Strategy choice in addition and subtraction: How do children know what to do? In: Sophian C, editor. Origins of cognitive skills. Hillsdale, NJ: Erlbaum; 1984. pp. 229–293. [Google Scholar]
  58. Talairach J, Tournoux P. Co-planar stereotaxic atlas of the human brain: 3-dimensional proportional system: an approach to cerebral imaging. New York: Thieme; 1988. [Google Scholar]
  59. Temple CM, Sherwood S. Representation and retrieval of arithmetical facts: developmental difficulties. Quarterly Journal of Experimental Psychology A. 2002;55:733–752. doi: 10.1080/02724980143000550. [DOI] [PubMed] [Google Scholar]
  60. Thomason ME, Chang CE, Glover GH, Gabrieli JDE, Greicius MD, Gotlib IH. Default mode function and task-induced deactivation have overlapping brain substrates in children. NeuroImage. 2008;41:1493–1503. doi: 10.1016/j.neuroimage.2008.03.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
  61. Wilkinson GS. Wide Range Achievement Test–Revision 3. Wilmington, DE: Jastak Association; 1993. [Google Scholar]

RESOURCES