Model-driven Approaches for in Vitro Combination Therapy using ONYX-015 Replicating Oncolytic Adenovirus

Abstract

Replicating genetically modified adenoviruses have shown promise as a new treatment approach against cancer. Recombinant adenoviruses replicate only in cancer cells which contain certain mutations, such as the loss of functional p53, as is the case in the virus ONYX-015. The successful entry of the viral particle into target cells is strongly dependent on the presence of the main receptor for adenovirus, the coxsackie- and adeno-virus receptor (CAR). This receptor is frequently down-regulated in highly malignant cells, rendering this population less vulnerable to viral attack. It has been shown that use of MEK inhibitors can up-regulate CAR expression, resulting in enhanced adenovirus entry into the cells. However, inhibition of MEK results in G1 cell cycle arrest, rendering infected cells temporarily unable to produce virus. This forces a tradeo1. While drug mediated up-regulation of CAR enhances virus entry into cancer cells, the consequent cell cycle arrest inhibits production of new virus particles and the replication of the virus. Optimal control-based schedules of MEK inhibitor application should increase the efficacy of this treatment, maximizing the overall tumor toxicity by exploiting the dynamics of CAR expression and viral production. We introduce a mathematical model of these dynamics and show simple optimal control based strategies which motivate this approach.

1 Introduction

Widely used cancer therapies include surgery, radiation, and chemotherapies. Surgery and radiation represent good options for localized tumors without metastases, and chemotherapies can be used in combination to fight early-stage metastases. Unfortunately, in many forms of cancer, late-stage forms of the disease become chemotherapy resistant, and alternate approaches to therapy need to be developed.

One promising approach is the use of replicating, genetically modified viruses which specifically target cancerous cells. One such virus, ONYX-015, is a well-characterized modified adenovirus which differs from the wild-type adenovirus in that its E1B-55K gene is deleted. In wild-type viruses, the product of this gene inactivates normal p53, a molecule which inhibits viral replication and tumor development. Consequently, the ONYX-015 can only replicate in cells in which normal p53 function is otherwise suppressed (Bischo) et al. (1996), Ries et al. (2000)), as is the case in most cancers (Gallagher and Brown (1999)).

Phase-I and II studies have been done using ONYX-015 as a therapeutic agent for head and neck cancer, gastrointestinal cancer with liver metastases and pancreatic cancer (Khuri et al. (2000), Reid et al. (2001), Ries and Korn (2002), Mulvihill et al. (2001), Hecht et al. (2003)). The therapy was well tolerated, with the most common side effects being flu-like symptoms. Though the therapy showed some evidence of anti-tumor efficacy, the response was highly varied.

Further studies have shown that the expression of the coxsackie-adenovirus receptor (CAR), which is necessary for adenovirus entry into the cell (Bergelson et al. (1997), Wickham et al. (1994), Mathias et al. (1994), Hidaka et al. (1999)), is highly variable in certain cancer types (Rauen et al. (2002), Kanerva and Hemminki (2005)). The variability of response to the oncolytic virus therapy could therefore be related to this variability of CAR expression. MEK (MAP-kinase kinase) inhibitors have been shown to promote CAR expression, and could be used to increase the susceptibility of target cells to ONYX-015 infection. This could lead to a novel combined therapeutic approach, using MEK inhibitors and ONYX-015 in tandem to promote anti-tumor activity. However, MEK inhibitors induce temporary cell-cycle arrest, which inhibits the life-cycle of ONYX-015 (adenoviruses need to lock the cell in S-phase to replicate and lyse the cell). The competing effects of MEK inhibitors complicate the task of designing an effective synergistic therapy.

In order to develop an effective combination therapy, the ability of MEK inhibitors to promote susceptibility to infection must be intelligently balanced with their inhibition of virus production. This requires that we develop an understanding of the dynamic relationship of these processes. In this paper, we present a novel mathematical model of the effects of MEK inhibitor and ONYX-015 on a population of tumor cells. We analyze the model and discuss implications for therapy. We also discuss the potential for optimal control-based approaches to therapy design. The paper is organized as follows: In Section 2, we introduce the mathematical model and analyze its steady-state behavior. In Section 3, we analyze the therapeutic implications of the model, and use a simple optimal control strategy to compare the performance of static approaches with dynamic approaches. In Section 4, we summarize the implications of this work for the development of a synergistic therapeutic approach for oncolytic virus therapy. Because the systems described in this paper are both nonlinear and stiff, all simulations in this paper were performed using MATLAB’s ode23s variable-step low-order sti) solver with explicitly defined Jacobians.

2 Model

Over the last few years, we have presented a first and preliminary mathematical framework in order to analyze the concept of oncolytic virus therapy quantitatively (Wodarz (2001)). The model took into account the dynamical interactions between a growing population of tumor cells, a population of replicating viruses, and immune responses which can recognize viral antigen on tumor cells. We use this model as a basis for an expanded model which considers the specific challenges posed by CAR expression as modulate by MEK inhibitor application.

We start with a mathematical model that includes the following variables: The population of susceptible and uninfected tumor cells, x; the population of infected tumor cells, y; the population of free viruses, v; and the average expression level of CAR on the surface of the cells, r. The model is given by the following set of ordinary differential equations:

$$\begin{array}{l}\stackrel{.}{\mathbf{x}}=\rho \mathbf{x}(1-\mathbf{u})-d\mathbf{x}-\frac{\beta r\mathbf{xv}}{1+\epsilon \mathbf{v}}\\ \stackrel{.}{\mathbf{y}}=\frac{\beta \mathbf{rxv}}{1+\epsilon \mathbf{v}}-d\mathbf{y}-a(1-\mathbf{u})\mathbf{y}\\ \stackrel{.}{\mathbf{v}}=k(1-\mathbf{u})\mathbf{y}-b\mathbf{v}\\ \stackrel{.}{\mathbf{r}}=\eta \mathbf{u}(\gamma -\mathbf{r})-h\mathbf{r}\end{array}$$ (1)

It is explained verbally as follows. The intensity of MEK inhibitor application is captured in the parameter u. It ranges from zero to one. If u = 0, there is no drug treatment, that is no cells enter G1 arrest and there is no production of the CAR molecule. If u = 1, the drug has the maximum possible effect, all cells enter G1 arrest and the production of the CAR molecule is at its theoretical maximum. The population of uninfected tumor cells replicates with a rate ρ. The model assumes exponential growth, which can be slowed down by the inhibitor, captured in the expression 1 − u. The tumor cells are assumed to have a natural death rate, d. When the virus meets susceptible cells, infection can occur. This requires the interaction of free virus with a CAR receptor on a susceptible cell, which occurs at a rate βrxv. The infection rate is thus proportional to the average number of receptors on the cell surface, r, the concentration of free virus v, and the concentration of susceptible cells x. As the virus becomes hyper-abundant relative to the uninfected cells, multiple infections of already infected cells become more likely than infection of uninfected cells, so the infection rate saturates with v as the term $\frac{1}{1+\epsilon \mathbf{v}}$. The infected cells can die because of two reasons. The natural death rate, d, and the virus-induced death rate, a. The virus-induced death rate is proportional to 1 − u. That is, as the activity of the inhibitor is increased, the rate of virus-induced cell death declines. The reason is that virus-induced cell death requires virus production, and this does not occur in the presence of the inhibitor because the cells are arrested in G1. Infected cells produce new virus particles with a rate k, and this is again diminished in the presence of the inhibitor (proportional to 1 − u). Free virus particles decay with a rate b. We assume that CAR is produced by cells with a rate η, and production is related to inhibitor activity, u. That is, the stronger the inhibitor activity, the higher the production rate of CAR. The expression γ − r represents the saturation of CAR expression. That is, the cell cannot bear an infinite number of receptors, but production declines and stops as the number of receptors on the cell surface increases. CAR is lost from the cell surface with a rate h.

In the absence of virus, the tumor grows exponentially, with a trajectory of the form

$$\begin{array}{l}{\mathbf{x}}_{\mathbf{2}}(t)={\mathbf{x}}_{\mathbf{1}}(0)e^{t(\rho (1-\mathbf{u})-d)}\\ {\mathbf{y}}_{\mathbf{2}}(t)=0\\ {\mathbf{v}}_{\mathbf{2}}(t)=0\\ {\mathbf{r}}_{\mathbf{2}}(t)=\frac{\eta \gamma \mathbf{u}}{\eta \mathbf{u}+h}\end{array}$$ (2)

This accurately reflects the growth of a two-dimensional tumor in Vitro, since there are no saturating effects from limiting factors such as food or oxygen availability. The growth of a three-dimensional tumor in Vitro or in Vivo would be described by more complicated equations including spatially dependent terms.

We have written down the simplest possible dependencies of the dynamics on the intensity of drug treatment, u. As it is written in the above model, an increase in the intensity of drug treatment linearly decreases the cellular proliferation rate, ρ, the rate of virus production, k, and the virus-induced death rate, a. Similarly, an increase in the intensity of treatment results in a linear increase of the CAR production rate, η. These dependencies need not be linear, and in fact we do not know the exact form of this dependency. Therefore, we can re-write these terms in the following more general form: ρx(1 − F(u)), (1 − F (u))ay, (1 − F (u))ky, and ηG(u)(1 − r), where F (u) is a general function which describes how an increase in the intensity of treatment can down-regulate cell division, virus production, and virus-induced cell death. Similarly, G(u) is a general function which describes how an increase in the treatment intensity can up-regulate the rate of CAR production. The exact form of the functions F (u) and G(u) can be determined experimentally. For the purposes of the analysis in this paper, however, the simple forms will suffice.

If all parameters are assumed to be positive, and 0 ≤ u ≤ 1, then the nonnegative orthant is positively invariant, and we can restrict our analysis to the case when all states are nonnegative. The system of Equation 1 has two steady-state solutions, described by the equations:

$$\begin{array}{l}{\mathbf{x}}_{\mathbf{0}}=0\\ {\mathbf{y}}_{\mathbf{0}}=0\\ {\mathbf{v}}_{\mathbf{0}}=0\\ {\mathbf{r}}_{\mathbf{0}}=\frac{\eta \gamma \mathbf{u}}{\eta \mathbf{u}+h}\end{array}$$ (3)

and

$$\begin{array}{l}{\mathbf{x}}_{\mathbf{1}}=\frac{b(d+a(1-\mathbf{u}))}{k(-\rho \epsilon (1-\mathbf{u})+d\epsilon +\frac{\beta \eta \gamma \mathbf{u}}{\eta \mathbf{u}+h})(1-\mathbf{u})}\\ {\mathbf{y}}_{\mathbf{1}}=\frac{b(\rho (1-\mathbf{u})-d)}{k(-\rho \epsilon (1-\mathbf{u})+d\epsilon +\frac{\beta \eta \gamma \mathbf{u}}{\eta \mathbf{u}+h})(1-\mathbf{u})}\\ {\mathbf{v}}_{\mathbf{1}}=\frac{\rho (1-\mathbf{u})-d}{-\rho \epsilon (1-\mathbf{u})+d\epsilon +\frac{\beta \eta \gamma \mathbf{u}}{\eta \mathbf{u}+h}}\\ {\mathbf{r}}_{\mathbf{1}}=\frac{\eta \gamma \mathbf{u}}{\eta \mathbf{u}+h}\end{array}$$ (4)

The equilibrium described in Equation 3 is stable if $\mathbf{u}>1-\frac{d}{\rho }$. In fact, the entire nonnegative orthant converges to this equilibrium in this case. This implies that the tumor could be eradicated with a sufficiently high dose of MEK inhibitor; however, this is not feasible. It is unlikely that a tolerable dose of MEK inhibitor could so effectively lock the tumor in G1 arrest, and the natural death rate of the cells is likely to be too slow to result in effective clearance. For the purposes of this study, we will assume we cannot apply MEK inhibitor in a dose sufficient to result in eradication, that is, $\mathbf{u}<1-\frac{d}{\rho }$.

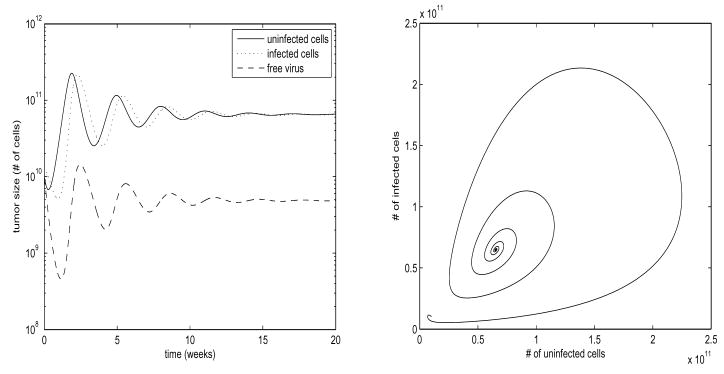
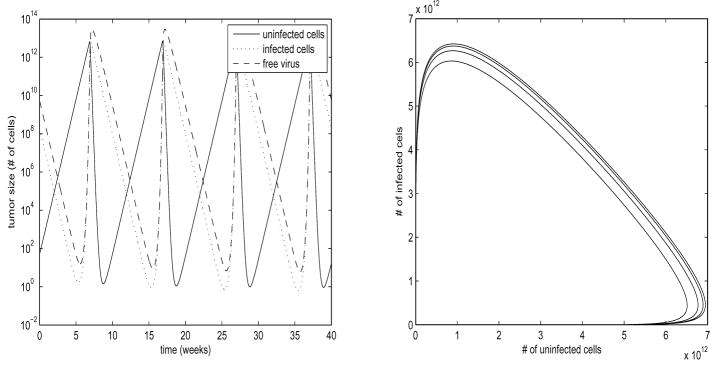
The equilibrium described by Equation 4 has stability which changes as a function of the parameters; it can be either a locally stable point, as in Figure 1, or the unstable center of a nonlinear limit cycle, as in Figure 2. A detailed bifurcation analysis of the stability of this equilibrium follows.

Fig. 1. Stable Steady State.

Parameter values are ρ= 5, β= 20, d = 0.01, a = 5, k = 0.5, b = 5, η = 1.2, h = 0.5, γ = 2, ε = 1.95, u = 0.25. States shown are x, y, v. Values are scaled by 10¹⁰ to correspond to number of cells. For constant u, r exponentially converges to its steady state value. Plot on left is log-scale. Trajectories converge in an oscillatory fashion to a stable steady state.

Fig. 2. Limit Cycle.

Parameter values are ρ = 5, β = 20, d = 0.01, a = 5, k = 0.5, b = 5, η = 1.2, h = 0.5, γ = 2, ε = 0.5, u = 0.25. States shown are x, y, v. Values are scaled by 10¹⁰ to correspond to number of cells. For constant u, r exponentially converges to its steady state value. Plot on left is log-scale. Oscillations form a nonlinear stable limit cycle.

In Figures 1 and 2, we have chosen parameter values which allow for numerically stable computations, while illustrating the various behaviors of the system. In order to better correlate this to the physical system, we use the following approximation: Pancreatic cancer patients presenting in stage I usually present with a tumor burden approximately 1–2cm in size, which corresponds to approximately 1 – 8 * 10¹² cells. End stage pancreatic cancer patients can present with several tumors reaching 7cm in size, which would correspond to a total tumor burden of approximately 10¹⁵ –10¹⁶ cells (Fortner et al. (1996)). With this reasonable range for tumor burden in mind, we scale our plots by 10¹⁰ so that the peak oscillation values under constant treatment correspond approximately to the average stage I tumor size. The use of this approximation is somewhat arbitrary, as we are modeling for in Vitro, not in Vivo. While pancreatic cancer in Vivo grows very slowly, we expect our in Vitro cultured cells to grow far more quickly, with doubling times on the order of days, which corresponds to the time scales in Figures 1 and 2 being on the order of weeks. Measured data values from future experiments will allow us to calculate actual parameter values, but these suffice for the the discussion in this paper.

2.1 Bifurcation Analysis

As we stated above, the equilibrium described in Equation 3 is stable if $\mathbf{u}>1-\frac{d}{\rho }$ and the entire nonnegative orthant converges to this equilibrium in this case. When $\mathbf{u}>1-\frac{d}{\rho }$, the equilibrium of Equation 4 has negative state values (so it is physically unrealistic) and is unstable.

The equilibrium of Equation 4 also can have negative state values when − ρε(1 − u) + dε + (βηγu)/(ηu + h) ≤ 0. In this circumstance, the equilibrium is unstable. Because the positive orthant is positively invariant for all positive sets of parameters, it is unnecessary to examine the behavior of the system about Equation 4 when its values lie outside the positive orthant, as the system will never approach those values.

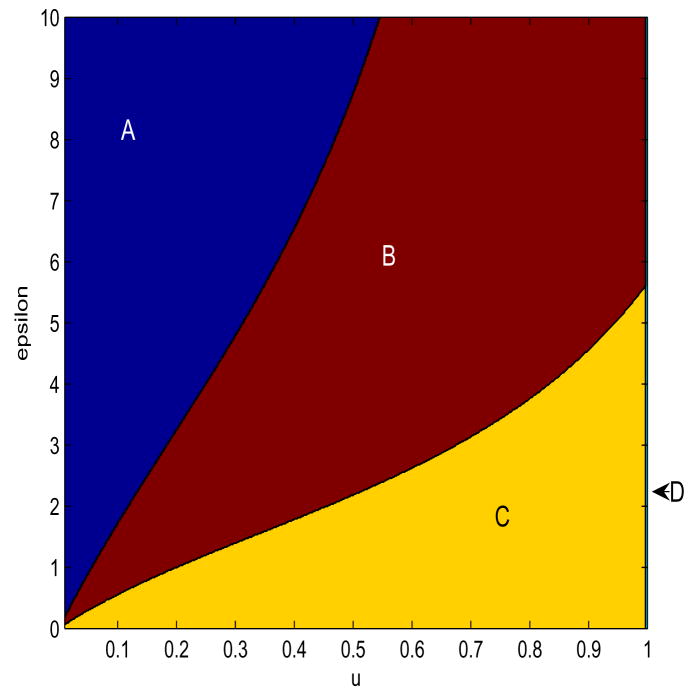
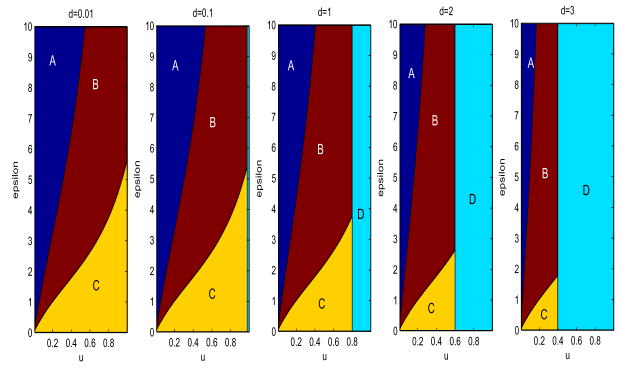
The stability of the equilibrium described by Equation 4 is nonlinear as a function of several parameters, and therefore no simple analytical formula can describe its stability. However, if we analyze the stability as a function of the two key parameters ε and u (stability for a fixed value of u), then we can plot the stability of the equilibrium of Equation 4 as a function of both ε and u. Figure 3 shows the bifurcation of the stability as a function of ε and u for nominal parameters, and Figure 4 shows how this bifurcation diagram changes for different values of the parameter d.

Fig. 3. Stability Bifurcations as u and ε.

Parameter values are ρ = 5, β = 20, d = 0.01, a = 5, k = 0.5, b = 5, η = 1.2, h = 0.5, γ= 2. ε ranges from 0 to 10, u ranges from 0.01 to 1. In bifurcation region A, there are no stable steady-states, and trajectories diverge. In bifurcation region B, the Equilibrium 4 is stable, and Equilibrium 3 is unstable. In bifurcation region C, Both Equilibria are unstable, and trajectories converge to a limit cycle. In bifurcation region D, Equilibrium 3 is stable, Equilibrium 4 is unstable, and all trajectories converge to Equation 3.

Fig. 4. Stability Bifurcations as u, ε, and d.

Parameter values are ρ = 5, β = 20, a = 5, k = 0.5, b = 5, η = 1.2, h = 0.5, γ = 2. ε ranges from 0 to 10, u ranges from 0.01 to 1. d takes values of 0.01, 0.1, 1, 2, and 3 from left to right respectively. Bifurcation regions are as in Figure 3

For high values of ε, low values of u (Region A), the equilibria corresponding to Equations 3 and 4 are both unstable, Equation 4 actually lies outside the positive orthant, and all trajectories which start within the positive orthant diverge, eventually approximating the trajectory described by Equation 2. For intermediate values of both ε and u (Region B), the equilibrium described by Equation 3 is unstable, the equilibrium described by Equation 4 is stable, and all trajectories starting in the positive orthant converge to it in decaying oscillations, as in Figure 1. For high values of u, low values of ε (Region C), both equilibria are unstable and in the non-negative orthant, and trajectories converge to a limit cycle as in Figure 2. A vertical separatrix at u = 1 − d/ρ divides the rest of the bifurcation space from Region D, in which the equilibrium defined by Equation 3 is stable, the equilibrium defined by Equation 4 is unstable and outside of the positive orthant, and all trajectories starting within the positive orthant converge to Equation 3.

When we allow d to vary, as in Figure 4, we see that increasing d causes this vertical separatrix to shift to the left, and additionally warps the curves which form the separatrices for the other regions.

Numerical analysis of the bifurcations is quite simple, as a linearization about the equilibrium points is sufficient to test stability, but analytical evaluation of the bifurcation separatrices is impossible due to the nonlinearity of the equation and the large number of parameters. Fortunately, it is not necessary, and numerical analysis is sufficient for our purposes.

3 Therapeutic Options

The behavior of the system described by Equation 1 suggests certain therapeutic approaches. The system of Equation 1 exhibits four distinct behaviors for reasonable values of u. We must avoid the case where trajectories diverge as in Equation 2, as this allows the cancer to grow unbounded. We cannot achieve the behavior in which the equilibrium of Equation 3 is stable, as it requires unrealistically high doses of u and a sustained efficacy of u which is also unrealistic, as discussed in Section 2. We examine treatment options in the parameter ranges of the remaining two system behaviors. In the case where the system exhibits a limit cycle, we can manipulate u in order to drive the oscillations to greater excursions than their limit cycle values, minimizing the tumor size at the nadir of the oscillations. In the case where the system exhibits damped oscillations which converge to a stable equilibrium, we can manipulate u to destabilize the steady-state, and drive the oscillations so that the nadir of the oscillations minimizes tumor size.

Finite-horizon optimal control provides a useful tool in determining patterns of MEK inhibitor application u(t) which achieve minimal tumor size in an economical fashion. This is a classical control tool successfully used in a variety of engineering applications. In this section, we use a simple optimal control formulation to determine useful pulsed treatment patterns, and compare the performance of these patterns to optimal constant MEK inhibitor application.

For the two parameter regions whose behaviors are shown in Figures 1 and 2, we applied a simple optimal control strategy. We found the constant concentration of 0 ≤ u ≤ 0.5 which minimized the lowest excursion of the total tumor size x + y during the optimization horizon. This restriction on the values of u insured that we did not allow concentrations of u so high that they would exhibit direct anti-tumor activity, as described in the case of $\mathbf{u}>1-\frac{d}{\rho }$. We then searched a space of switching controllers, which consists of schedules of u which can alternate between u(t) = 0 and u(t) = 0.5. We limited our search to a relatively coarse grid of schedules which switch only at fixed intervals of no faster than every two units of time. The finite horizon and fixed interval switching yields a finite space of controls, which guarantees that the optimization is well-formulated. This space of switching controllers is needlessly restrictive, but it serves the purpose of determining whether an optimized switching controller can show significant improvement over static approaches, and allows us to easily address the issue of computational complexity. We used an exhaustive search method for performing the optimizations.

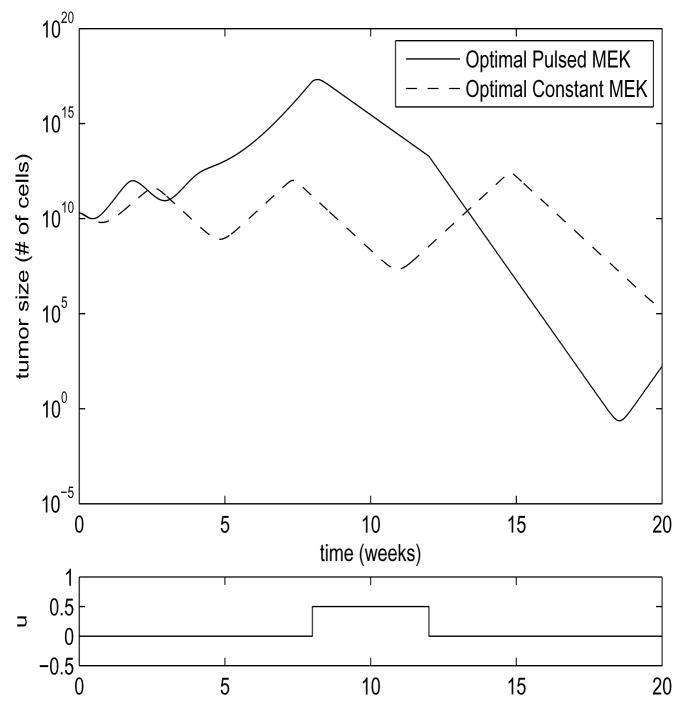
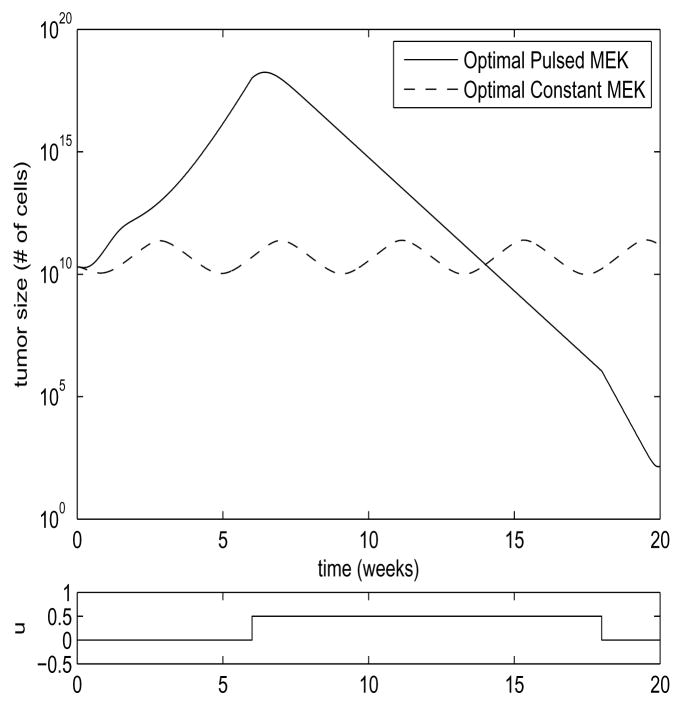
In Figure 6, we see the comparison between these two approaches for the system of Equation 1, for the parameter region in which the steady-state solution of Equation 4 is unstable, and the system exhibits limit cycle behavior. In this case, the switched strategy of MEK inhibitor application outperformed the optimal static approach by over 5 orders of magnitude. In Figure 5, we see the comparison between these two strategies for the system of Equation 1 for the parameter region in which the steady-state solution of Equation 4 is stable. In this case, the switched strategy outperformed the optimal static approach by 8 orders of magnitude. These results are summarized in Table 1. These results should not be seen as an entirely accurate portrayal of what would occur in Vitro, as the small number of tumor cells in the lower excursions of the graphs would violate our modeling assumptions, and the tumor size in Figure 6 actually dips below a value of one cell by our rough approximation. The models may also fail to reflect reality in their upper excursions. The large upper excursions of the tumor size in the switched strategies would certainly be unacceptable in Vivo, and may violate our assumptions of the growth-rate ρ being size-independent even in the in Vitro case. If this proves to be true after measurement of parameters through experiment, we will revise the model to introduce tumor size-dependent saturation of tumor growth. If large upper excursions prove to be a problem in therapy, it is trivial to include upper bounds on tumor growth as part of the optimal control criteria, at the cost of some performance. Nevertheless, it is clear that a dynamic approach to MEK inhibitor application can yield dramatic improvements in tumor shrinkage, and increase the odds of reducing the tumor size to a level where it can undergo stochastic extinction.

Fig. 6. Limit Cycle Comparison.

Parameter values are ρ = 5, β = 20, d = 0.01, a = 5, k = 0.5, b = 5, η = 1.2, h = 0.5, γ= 2, ε = 0.5. Shown are the plots of the sum x + y for the two strategies. Values are scaled by 10¹⁰ to correspond to number of cells. Optimal constant u = 0.3485. MEK inhibitor application for the pulsed treatment is shown in the lower plot.

Fig. 5. Stable Steady State Comparison.

Parameter values are ρ = 5, β = 20, d = 0.01, a = 5, k = 0.5, b = 5, η = 1.2, h = 0.5, γ = 2, ε = 1.95. Shown are the plots of the sum x+y for the two strategies. Values are scaled by 10¹⁰ to correspond to number of cells. Optimal constant u = 0.5. MEK inhibitor application for the pulsed treatment is shown in the lower plot.

Table 1. Results Comparison.

Minimum tumor size achieved through optimal constant MEK application compared with that achieved through optimal pulsed MEK application, for each of the two parameter regions of the model: Limit Cycle (ε = 0.5), and Stable Steady-State (ε = 1.95). Values are scaled by 10¹⁰ to correspond to number of cells.

	Limit Cycle	Stable Steady-State
Optimal Constant MEK	2.13 * 105	9.79 * 109
Optimal Pulsed MEK	1.17 * 10−1	1.38 * 102

4 Conclusions

In this paper, we have introduced a candidate model of the dynamics of interactions between genetically modified oncolytic adenovirus and cancer cells in Vitro, with the application of MEK inhibitor. We have analyzed the various behaviors of this model, and discussed the implications for therapy.

The model exhibited two distinct behaviors dependent upon parameter values; either a locally stable steady state, or a nonlinear limit cycle. Both of these behaviors suggested the use of therapies which manipulate the concentration of MEK inhibitor in order to drive these oscillations, which can drive tumor size to a desirable low level. We have used a simple finite-horizon optimal control strategy to find appropriate switched treatment strategies to achieve this, and compared these results to best-case constant MEK inhibitor applications. The improvement for these simple models ranged from five to seven orders of magnitude better tumor suppression for a dynamic optimal control approach as compared to a optimized static strategy. This strongly motivates the further investigation of dynamic, model-driven strategies for combined ONYX-015/MEK inhibitor cancer therapy.

The optimization technique used in this paper is needlessly restrictive. The sampling time was excessively coarse, and the discretization of the MEK inhibitor levels is not imposed by restrictions on the experimental implementation. These restrictions were used to limit the computational cost of this study, and the resulting system served the purpose of motivating further research into combined ONYX-015/MEK inhibitor cancer therapy. As experimental work allows us to refine the model and identify its parameters, we will revisit the optimal control formulation with a more realistic class of possible controls, replacing arbitrary restrictions with restrictions imposed by the experimental set-up.

Though the simulations and models here were not fitted to any data, the estimation of the parameters is not difficult in theory (at least in the in Vitro case), as most of the parameters can be isolated through experiment. Nondestructive live/dead assays in the absence of virus allow us to measure ρ and d, florescent CAR antibody measurements with varying concentrations of applied MEK inhibitor allow us to measure η, γ and h, and live/dead assays in the presence of virus allow us to measure the virus induced death rate a. The remaining parameters could then be fitted to time-sequence measurements using standard statistical methods.

The use of genetically modified viruses as anti-tumor therapies is a promising area of medical research, but interactions between the elements of this therapy can cause difficulties with the use of continuous application approaches. In this particular application, the dependence of ONYX-015 on CAR for successful infection and the viral production-inhibiting effect of the CAR promoter MEK inhibitor drugs create a dynamic trade-o), which requires a model-driven approach to effective use ONYX-015 in conjunction with MEK inhibitor as an anti-tumor therapy. The modeling and control work of this paper represent a first step in the development of such dynamic, model-driven therapies. This work will be continued through experimental model validation in cooperation with our experimental collaborators.