Natural scene statistics and the structure of orientation maps in the visual cortex

1. Introduction

Brain plasticity is crucial to brain development and function. Understanding the types and mechanisms of such plasticity is key to both treating human brain disorders and aiding recovery from neural trauma. Animal models have played a crucial role in uncovering the rules governing brain plasticity. In particular, the plasticity of maps in the primary visual cortex (V1) of animals such as cats, monkeys and ferrets provides a paradigm example of how brain structure can be altered by sensory input (Katz and Shatz, 1996; Sur and Leamey, 2001; Sengpiel and Kind, 2002). For instance, depriving one eye of visual stimulation during the critical period leads to a reduction in the amount of cortical territory occupied by that eye's representation of visual space, with a concomitant increase in the territory occupied by the open eye (Hubel et al., 1977; Shatz and Stryker, 1978). Similarly, raising a cat in an environment consisting mostly of stripes of only one orientation causes analogous changes in the orientation map in V1; the presented orientation expands its territory at the expense of other orientations (Blakemore and Cooper, 1970; Sengpiel et al., 1999; Tanaka et al., 2006). Complete removal of the map of one feature can also lead to changes in the periodicities and interrelationships of the remaining maps (Farley et al., 2007; Swindale, 2007).

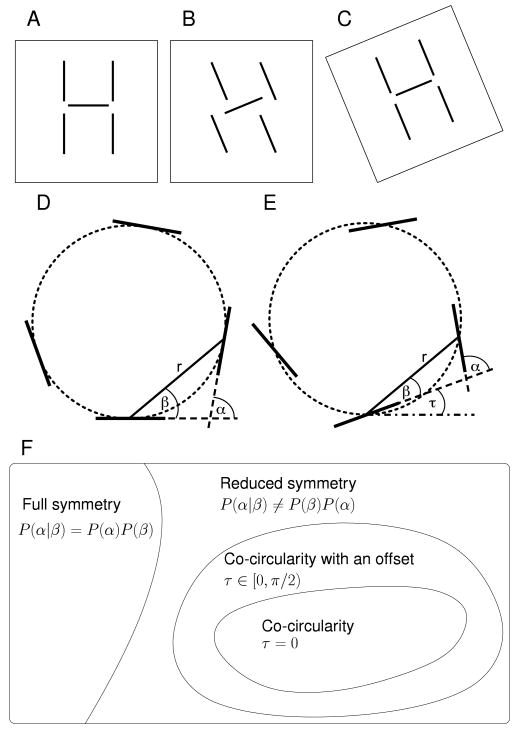
The geometric layout of orientation preferences in V1 can also be characterized by other statistical properties. In particular, by analyzing orientation maps in V1 from an individual macaque and an individual cat, Lee et al. (2003) discovered a higher-order statistical regularity of these maps. This was a weak but systematic dependence between the preferred orientations at pairs of cortical points and the angle of the line in the cortex joining that pair relative to a fixed but arbitrary set of axes (see also Lee and Kardar, 2006). Any such regularity means that map structure is not invariant to adding a fixed angle to the orientation preference at each position in the map, since this would change the relationship between orientation preferences and directions in the cortex. As invariance to addition of a fixed angle is a type of symmetry that orientation maps do not possess, Lee et al. (2003) referred to these maps as having “reduced symmetry” (Fig. 1A–C). Similar results have been reported for tree shrews, though so far only in abstract form, by Schnabel et al. (2004, 2006, 2007a). Within the class of all possible orientation maps with reduced symmetry there is a special subclass which is of particular interest. For these maps, the particular form of symmetry-breaking is that preferred orientations at different positions have a tendency to lie on a common circle: “co-circularity” (Sigman et al., 2001) (Fig. 1D).

Figure 1. Reduced symmetry, co-circularity and co-circularity with offset.

A In the natural world objects can be thought of as a group of line segments whose orientations are coupled to one another and to their positions in space (the retinotopy). Following Lee et al. (2003) we refer to coupling between orientation and spatial position as reduced symmetry. B This structure is modified if orientations are rotated independent of position. C When the particular reduced symmetry of A is maintained, by rotating the positions of the segments together with the rotation of the individual segments, the image retains its structure (Lee et al., 2003). D Coupling between the position and angle of oriented segments or orientation preferences can be described by α, the difference in orientation of the two segments, and β, the direction of one segment with respect to the orientation of the other segment. A feature of natural images is that segments tend to be tangent to a common circle (dotted line) which occurs when β = α/2 as shown here. E Co-circularity with offset, when β = α/2 − τ, is a more general form of coupling between relative positions and angles of oriented segments. Here τ is −20°. F A “set” diagram showing the relationship between full symmetry, reduced symmetry and co-circularity (with and without offset τ). The meaning of P(α, β) and τ is explained in the Methods section.

The reason why co-circularity is of particular interest is that it is a characteristic of the structure of natural images (Sigman et al., 2001; Geisler et al., 2001). Given one edge of a particular orientation at a particular position in the image, the most likely orientation for a second edge at a different position in the same image is one which lies on a common circle with the first edge (Fig. 1D). In addition, human performance at contour detection is well-described by a rule which groups nearby co-circular edges together along with a transitivity rule (Geisler et al., 2001). This demonstrates co-circularity is important for understanding how humans process visual scenes and group edges.

Establishing that co-circularity exists in a cortical orientation map is harder than just showing reduced symmetry. To show reduced symmetry one only needs to demonstrate some dependence between orientation difference α and relative position β (Fig. 1). To prove co-circularity is present it is necessary to also know the relationship between cortical directions and directions in visual space, since the latter is where orientation preferences are specified. Lee et al. (2003) did not have this information for the single macaque and cat map they analyzed, and so could only show that the maps had reduced symmetry. They postulated that the source of this may be the reduced symmetry from co-circularity in visual input, but since they could not establish that the reduced symmetry in the map had the form of co-circularity, the questions of whether co-circularity exists in orientation maps and whether this is driven by visual input are currently unanswered.

A slightly more general property than co-circularity, which is important for this paper, we will refer to as “co-circularity with offset” (Fig. 1E,F). By this we mean that the strongest relationship between preferred orientations at different cortical positions is that given by co-circularity with the addition of a specific offset angle we will call τ. The case of τ = 0 corresponds to co-circularity; however, determining the actual value of τ for a specific map requires knowledge of the transformation between visual field and cortical coordinates.

Given the strong influence of the structure of visual activity on visual map development in other contexts, and the role of V1 in edge detection, it is natural to hypothesize two things. Firstly, that orientation maps in V1 are indeed co-circular, and secondly that it is the co-circularity of natural images that drives the development of co-circularity in V1. In this paper, we present results suggesting that both of these attractive hypotheses are incorrect. In particular, we developed a quantitative measure for the reduced symmetry of maps, and used it to compare reduced symmetry in orientation maps from six normal, three dark-reared and four stripe-reared cats for which we estimated the overall mapping from visual field to cortical coordinates. This analysis confirmed Lee et al.'s (2003)n = 1 result that reduced symmetry exists in cat orientation maps. However, we found that for our maps the form of reduced symmetry was co-circular with offset (τ ≠ 0). In fact, τ appeared to take random values between different individuals, which is inconsistent with the hypothesis that the statistics are driven by natural scenes, for which τ = 0.

To further address whether natural scene statistics drive reduced symmetry we compared orientation map statistics between the three rearing paradigms. Despite the differences in image statistics that the cat experienced, there were few consistent differences between the co-circularity statistics, and in particular no correlation in τ values, again suggesting no influence of input statistics on this aspect of the maps. We also tested whether genetic relationships affected the form of reduced symmetry by comparing the variation in co-circularity statistics between hemispheres of the same cat, and found few significant genetic influences.

We then compared these results from the cats with two computational models of visual map development. These were “essentially-complex planar forms” (ECP), a simple analytical model of V1 layout (Wolf, 2005) and the elastic net model (Durbin and Mitchison, 1990; Goodhill and Willshaw, 1990; Carreira-Perpiñán and Goodhill, 2004; Carreira-Perpiñán et al., 2005). The ECP maps, which do not attempt to incorporate Hebbian developmental dynamics, showed minimal co-circularity or co-circularity with offset. Elastic net maps trained on co-circular inputs showed strong co-circularity at τ = 0. Moreover, this grouping at τ = 0 persisted even when driven with only weakly co-circular input. This suggests that purely activity-dependent development with even weakly co-circular inputs should produce co-circularity in V1. Surprisingly, elastic net maps trained on inputs with no co-circular structure showed co-circularity with offset (τ ≠ 0), with τ values that were distributed randomly, matching the result in the cat maps. Together, these results indicate that while V1 has reduced symmetry, it is not caused by co-circular natural scene inputs and instead may arise spontaneously.

2. Materials and Methods

Animals and rearing

All procedures were approved by local ethical review and were covered by the appropriate government licenses. Thirteen cats were used in this study. Six animals were reared normally in a colony room until 5–6 weeks of age. Three animals were kept in complete darkness, together with their mother, from the day of birth until five weeks of age, when optical imaging was performed. For stripe-rearing, four kittens and their mothers were reared in a darkroom from the day of birth. Starting at postnatal day 16/17 (P16/17), the kittens were placed in cylinders (2 m tall, 65 cm in diameter), which were painted with evenly spaced black and white stripes (3 or 4 cm wide) of a single orientation (0°, 90°, or 135°). Animals spent 3–5 hours a day (increasing with age) in this visual environment, and the rest of the time in the dark together with their mother. At P37–45, when the imaging experiment was performed, they had had a total exposure of 80 to 100 hours.

Surgery and optical imaging

Anesthesia was induced with an intramuscular injection of ketamine (20–40 mg/kg) and xylazine (2–4 mg/kg). Animals were intubated and artificially ventilated (50–60% N₂O, 40–50% O₂, and 0.9–1.2% halothane or 1.5–2.5% isoflurane). ECG, EEG, end-tidal CO₂, and rectal temperature were monitored continuously. Optical imaging of primary visual cortex was performed as described previously (Bonhoeffer and Grinvald, 1996; Schwarzkopf et al., 2007). Images were captured using either a cooled slow-scan CCD camera or an enhanced differential imaging system (ORA 2001 or Imager 2001, Optical Imaging Inc.), with the camera focused about 500 μm below the cortical surface. Visual stimuli, produced by a stimulus generator (VSG, Cambridge Research Systems), consisted of high-contrast, sinusoidally modulated gratings of two spatial frequencies (0.1 to 0.6 cycles/degree) and four different orientations (0°, 45°, 90° and 135°), drifting at a temporal frequency of 2 Hz. These were presented to the two eyes separately in randomized sequence, interleaved with trials in which the screen was blank. Single-condition responses (averages of 48–96 trials per eye and orientation) were added for the two eyes and divided (a) by responses to the blank screen, and (b) by the sum of responses to all four orientations (“cocktail blank”) to obtain iso-orientation maps. The actual signal used for subsequent quantitative analysis was reflectance change (ΔR/R) for each pixel, given at 16-bit precision.

As is standard (Frostig et al., 1990; Bosking et al., 1997; Sengpiel et al., 1999), the iso-orientation maps were then band-passed filtered to eliminate high-frequency noise and drifts in luminance. Polar orientation preference maps were then calculated by vectorial addition of four iso-orientation maps, and pseudo-color coded, with the vector angle represented by the hue and the length of the vector encoded as the brightness of the colors (Bonhoeffer and Grinvald, 1993). The maps were then masked for all subsequent analysis to select only pixels clearly belonging to V1 and specifically excluding any pixels on the V1/V2 border region. Some of the experimental maps have been previously published (Sengpiel et al., 1998, 1999; Zepeda et al., 2004); however, the analysis performed in this paper is novel.

Retinotopic information

A complete retinotopic map for the cats in these experiments was not obtained. However, all orientation maps were from the small, exposed section of V1 on the dorsal surface of the brain, just lateral of the midline, and the retinotopic map in this area in cat is stereotypical (Tusa et al., 1978; Diao et al., 1990; Payne and Peters, 2001). In addition, the comparison of responses to two spatial frequencies, one higher than the other, allows a functional estimate of the vertical meridian as the V1/V2 border, since the higher spatial frequency gives stronger V1 activation, and the lower spatial frequency stronger V2 activation (Bonhoeffer et al., 1995). Thus, since the approximate directions of the horizontal and vertical meridians were known, we rotated the orientation maps into alignment with the conventional visual field coordinate system. Examples of our estimated position for each map's vertical meridian are marked with white lines in Figure 2A–C. Rotation was performed by first separating any images containing both hemispheres into two separate images (for some cats both hemispheres were imaged simultaneously), and then manually selecting the vertical meridian by visual inspection. Bi-linear interpolation was then used to generate the rotated map. Maps were also flipped vertically to give a right-handed coordinate system. Based on our experience with retinotopic maps obtained by optical imaging from V1 of young cats (Zepeda et al., 2003), and maps obtained with single-cell recordings (Tusa et al., 1978), we are confident that our estimates of the vertical and horizontal meridians were correct to within 10°.

Figure 2. Illustrations of reduced symmetry in normal, stripe-reared and dark-reared cats.

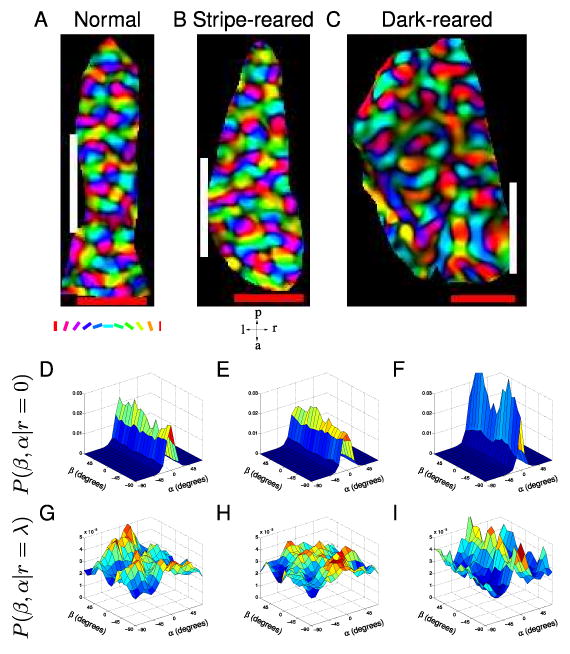
Representative examples of cat orientation preference maps and joint probability distributions P(β, α|r) at r/λ = {0,1} for the three rearing conditions. Orientation maps are polar; the colour encodes the orientation preference according to the key under A and the brightness encodes the orientation selectivity strength. Our estimate of the position of each map's vertical meridian, which was used to orientate the maps retinotopically, is marked with a white line. The red scale bars are 1 mm. These maps have been flipped vertically after rotation to give them a right-handed coordinate system and then masked to eliminate points outside V1. Only the unmasked points were used in all subsequent analysis. (A,D,G) Representative example from a normal cat. A Orientation preference map. D P(β, α|r = 0). At short distances there is little β-dependence in the probability distribution, with almost all the probability near α = 0 indicating that the orientation preferences of pixels close to another tend to be similar. G P(β, α|r = λ) demonstrates a β-dependence in the probability distribution, indicating that reduced symmetry exists at separations of approximately λ. (B,E,H) Representative example from a stripe-reared cat. This cat was reared in environment rich in 135° lines. B Orientation preference map. E P(β, α|r = 0). H Ridges in P(β, α|r = λ) indicate the presence of co-circularity with offset. While the proportions of the map preferring each orientation changes under stripe-rearing conditions, the joint probability distributions P(β, α|r) did not demonstrate qualitatively different properties to normally reared cats. (C,F,I) Representative example from a dark-reared cat. C Orientation preference map. F P(β, α|r = 0). I P(β,α|r = λ). Despite the maps of dark-reared cats showing visually obvious differences, such as less clearly defined pinwheels and a “blobbier” structure than those from normally reared cats, they also demonstrated reduced symmetry at separations of approximately λ.

While globally the retinotopic map is non-linear and anisotropic, in the small area we imaged it is on average linear and approximately isotropic (Tusa et al., 1978; Payne and Peters, 2001). Thus, we assumed that there was a linear, isotropic relationship between visual field and cortical coordinates so that, after rotation, the relative positions of cells in cortical coordinates were similar to the relative positions of their receptive fields. This simplification has been used in previous studies (Lee et al., 2003; Lee and Kardar, 2006; Schnabel et al., 2007a).

However, in order to test whether any uncorrected anisotropy or jitter in the retinotopic map could have a major effect on our conclusions regarding co-circularity, we also examined the sensitivity of our analyzes to the addition of these influences. Anisotropy was introduced by globally stretching or contracting the cortical maps by a factor ρ, which is equivalent to stretching or contracting the visual field representation by a reciprocal amount, and co-circularity statistics were then recalculated. To examine the effect of random jitter in receptive field position we added uniform noise from [−1, 1] pixels to each cortical position.

In general, overall map topography is determined by a combination of Eph/ephrin gradients and spontaneous waves of retinal activity (Cang et al., 2005a,b, 2008). Since there is no evidence that either of these sources of retinotopic information are disrupted in dark- or stripe-rearing, we assumed that overall map topography in these cases was the same as for the normal case. Additional post-hoc support for this assumption comes from the fact that we found no significant changes in co-circularity between the different rearing conditions.

Co-occurrence histograms for orientation maps

For each pair of points on the orientation preference maps, we defined the following (see Fig. 1D):

θ1	orientation preference of point 1;
θ2	orientation preference of point 2;
s1	orientation selectivity of point 1;
s2	orientation selectivity of point 2;
r	cortical distance between points 1 and 2;
φ	angle of the line from point 1 to point 2;
α = θ2 − θ1	relative orientation preference of the two points;
β = φ − θ1	angular position of the second point relative to the orientation preference of the first point.

The orientation preferences θ₁ and θ₂ are defined in real space where the stimulus is presented, relative to zero degrees along a horizontal x-axis. The selectivity of each point is between [0, 1] where 1 is a completely selective point and 0 implies lack of any orientation preference. The relative position of the cortical points φ is defined relative to the horizontal axis of the retinotopic map.

Reduced symmetry in natural images and orientation maps has previously been demonstrated by calculating joint histograms of the frequency at which different relative orientations α occur at different relative positions (r, β) (Sigman et al., 2001; Geisler et al., 2001; Lee et al., 2003; Lee and Kardar, 2006). We calculated a similar distribution P(β, α|r) for both experimental and simulated maps. A systematic relationship between α and β (or more precisely, that P(β, α|r) ≠ P(β|r)P(α|r)) at a particular length scale r indicates reduced symmetry.

All distances on the map were normalized by the wavelength λ of the map. As there is variation in column spacing between individuals (Kaschube et al., 2002), and the imaging of each map may be at different magnifications, the use of λ as the unit of length aims to ensure that the quantification of reduced symmetry is not affected by overall changes in map scaling. To calculate the mean wavelength for each map we first calculated the Fourier power spectrum. For the normal and stripe-reared cases most of the power was present in a narrow wavelength band, and we therefore calculated the mean wavelength as the mean of the Fourier spectrum averaged over all directions as previously described (Carreira-Perpiñán and Goodhill, 2004). For the dark-reared cases the power in the Fourier spectrum was much more diffusely distributed over wavelengths, making it harder to characterize these maps in terms of a single wavelength. While we again used the same averaging method to determine a wavelength, we note that wavelength calculations using any method will in general be less reliable for the dark-reared case.

For every pair of cortical points we measured r, φ, α and β. We then binned φ, α and β at intervals of 10°, restricting α and β to the interval [−90°, 90°) because they were periodic. We binned r at intervals centered every λ/4, where λ was the wavelength of the map. The first bin, referred to hereafter as r = 0, contained pairs where 0 ≤ r < 1/8λ, the r = 1/4λ bin contained the pairs where 1/8λ ≤ r < 3/8λ, and so on. The pairs were weighted according to their selectivity s₁s₂. From this we obtained H(r, φ, β, α), the joint probability distribution describing how often each selectivity-weighted combination of r, φ, α and β occurs over all pairs of points.

Next, we noted that there is a systematic non-uniformity in the spatial distribution of pairs

$$C(r,\phi )=\sum _{\beta }\sum _{\alpha }H(r,\phi ,\beta ,\alpha )$$ (1)

arising from the finite size of our maps, and the presence of more moderately separated than closely separated pairs. Since it has the potential to cause spurious correlations in P(r, β, α), a correction was made for this non-uniformity by normalizing H:

$$P_1(r,\phi ,\beta ,\alpha )=\{\begin{array}{cc}\frac{H(r,\phi ,\beta ,\alpha )}{C(r,\phi )}& \text{for}C(r,\phi )\ne 0\\ 0& \text{for}C(r,\phi )=0.\end{array}$$ (2)

We then marginalized over the unwanted φ-dimension:

$$P_2(r,\beta ,\alpha )=\sum _{\phi }{P}_1(r,\phi ,\beta ,\alpha )$$ (3)

and normalized to calculate the final probability distribution of interest:

$$P(\beta ,\alpha |r)=\frac{P_2(r,\beta ,\alpha )}{{\sum }_{\beta }{\sum }_{\alpha }{P}_2(r,\beta ,\alpha )}.$$ (4)

The procedure outlined above is slightly different from that used previously by Lee et al. (2003) and Lee and Kardar (2006), since we normalized for nonuniform C(r, φ) and restricted α, β and φ to the interval [−90°, 90°) instead of [0, 90°).

In natural scenes, oriented edges at angles θ₁ and θ₂ are most likely to be tangent to the same circle, which occurs along the lines β = α/2 and β = α/2 ± 90° where α and β are as defined above and in Figure 1D (Sigman et al., 2001; Geisler et al., 2001). Hence, if reduced symmetry in V1 orientation maps is caused by reduced symmetry in natural images, then we might expect ridges in the P(β, α|r) distribution along β = α/2 and β = α/2 ± 90°. If the directions of the retinotopic axes in the cortex are not known, then P(β, α|r) can still be calculated, as was done in Lee et al. (2003) and Lee and Kardar (2006). However, there may be a rotation between the axis from which φ is measured, and the axis from which θ₁ and θ₂ are measured. A rotation of τ between the two coordinate systems would cause P(β, α|r) to be shifted by τ along the β axis, and thus correlations would now be expected at β = α/2 − τ. The presence of these correlations is the definition of co-circularity with offset (Fig. 1E). In a following section we describe a method for finding the rotation τ_best which maximizes the correlations at β = α/2 − τ_best.

Measuring co-circularity in orientation maps

There are in principle many different types of reduced symmetry, i.e. P(β, α|r) ≠ P(β|r)P(α|r). We found it useful to restrict our quantitative analysis to an investigation of whether the reduced symmetry has the specific form of co-circularity (i.e. β = α/2), or co-circularity with offset (i.e. β = α/2 − τ, where τ is the angle of rotation of orientation needed to produce exact co-circularity, see Figure 1E,F).

While P(β, α|r) for a particular map is a useful method of visualizing directly whether α depends on β for a given separation r, it is hard to compare these multidimensional distributions between conditions. We therefore developed a scalar measure of co-circularity as a function of point separation to allow more direct comparisons. If point 1 has orientation preference θ₁, then at point 2, located at angle φ in the cortex relative to the first point, there is a unique orientation preference ${\theta }_2^{\text{cc}}$ that is co-circular to the first point:

$${\theta }_2^{\text{cc}}=2\phi -{\theta }_1.$$ (5)

The absolute difference between the actual orientation preference at point 2 θ₂, and the co-circular orientation ${\theta }_2^{\text{cc}}$, is a measure of the degree to which points 1 and 2 are co-circular. To average this over an entire map, we calculated the weighted average of this difference over all pairs of points in the map separated by distance r:

$$D_{\text{diff}}(r)=\frac{{\sum }_{\text{pairs}}{s}_1{s}_2|{\theta }_2-{\theta }_2^{\text{cc}}|}{{\sum }_{\text{pairs}}{s}_1{s}_2}$$ (6)

$$=\frac{{\sum }_{\text{pairs}}{s}_1{s}_2|{\theta }_1+{\theta }_2-2\phi |}{{\sum }_{\text{pairs}}{s}_1{s}_2}$$ (7)

D_diff(r) has the intuitively appealing property that it is 45° when no co-circularity is present (i.e. when the orientation preferences at all pairs of locations have no systematic dependence), and decreases if the relationship between the angles at the two positions becomes more co-circular. To calculate D_diff(r) we binned r in intervals of λ/4 as for the co-occurrence histograms. The first bin, referred to hereafter as r = 0, contained pairs where 0 ≤ r < 1/8λ, the r = 1/4λ bin contained the pairs where 1/8λ ≤ r < 3/8λ, and so on. This bin spacing balances the requirements of having a reasonable number of pairs in each bin to reduce noise, while allowing fine enough resolution to investigate trends with r.

Calculating the optimal rotation τ_best

We found that, while most of our experimental maps did not display co-circularity, they did display co-circularity with offset as defined above. In order to determine the offset τ_best at which co-circularity is most strongly represented, we calculated

$$D_{\text{diff}}(r,\tau )=\frac{{\sum }_{\text{pairs}}{s}_1{s}_2|{\theta }_1+{\theta }_2-2\phi -2\tau |}{{\sum }_{\text{pairs}}{s}_1{s}_2}$$ (8)

for τ = 0 to 85° in 5° increments. Since line elements are co-circular if they obey the relation β = α/2 or β = α/2 ± 90°, searching over this range covers all possible values for τ. The rotation that gave the best match, τ_best, was taken to be that which gave the minimum of ${\int }_{r=0.75\lambda }^{1.25\lambda }$D_diff (r, τ)dr (i.e. maximum reduced symmetry at a cortical separation of one wavelength). The range of integration was chosen because reduced symmetry is maximal over this range in the simulated maps (see Results). For each map we denote D_diff(r, τ_best) as D_best(r).

Statistics

Since the source of reduced symmetry statistics in the maps was the object of investigation, it was not clear a priori if these were likely to be normally distributed. Therefore, all statistical tests were performed using permutation tests similar to those in Kaschube et al. (2002). The only assumption these tests make about the data is that samples are independent. No knowledge of the source distribution is assumed.

In order to test for statistically significant differences in D_diff(r) or D_best(r) between sets of maps, the values at different r were treated independently. Given two sets of N measurements at a particular r, {D_i} and {D_j} (e.g. D_diff(r = λ) for normal and dark-reared cats), the difference in the mean values between the two sets was calculated:

$$\Delta Q=\frac{{\sum }_i{D}_i}{N_i}-\frac{{\sum }_j{D}_j}{N_j}$$ (9)

In order to determine if the difference in mean values between the sets was significant we calculated the likelihood of this difference in means arising if both sets are sampled from the same original source. This was done by generating pseudo-random permutations between the sets and examining how probable such a difference in means is for a randomly sampled permutation. If both sets are sampled from the same original source then randomly permuting the sets should give a similar difference in mean values. If, however, the sets are sampled from different sources then the permuted sets should tend to have a smaller difference in means. This is calculated as

$$p=<H\left(|\Delta Q|-|\Delta Q_t|\right){>}_t$$ (10)

where H(·) is the Heaviside function (i.e H(x) = 0 for x ≤ 0, H(x) = 1 for x > 0), ΔQ_t is the difference in means between the permuted sets t, and < · >_t is the ensemble average of pseudo-randomly generated permutations between the sets D_i and D_j. Permutations are created by grouping all the values of both sets together and then pseudo-randomly assigning each value to two pseudo-sets of equivalent sizes as the original sets. The use of the Heaviside function means this equation returns the fraction of permutations which have a mean difference greater than that of the original sets. Thus a low value indicates the original mean difference was significant. p-values were calculated using 10⁵ randomly generated permutations.

If reduced symmetry in the maps arose from the co-circularity of natural scenes one would expect D_best(r = λ) for each map to occur when τ_best = 0 (no rotation required to bring the P(β, α|r) distributions into alignment with co-circularity). A systematic error in orienting retinotopic axes in the cortex would result in τ_best clustering around another angle. A modified permutation test was therefore used to detect any significant clustering of τ_best. Given a set of τ_best values, the mean difference between pairs (over all N pairs) was calculated as

$$\Delta M=\frac{{\sum }_{\mathrm{pairs}}min({\tau }_1-{\tau }_2,{\tau }_2-{\tau }_1)}{N}$$ (11)

where τ₁ − τ₂ and τ₂ − τ₁ were calculated modulo 90°. This arrangement corrects for the 90° symmetry in τ when calculating the mean difference. In order to determine if this mean difference indicates any significant grouping the probability of observing such a grouping based on sampling from a uniform random spread of probabilities across all angles was calculated as

$$p=<H(\Delta M-\Delta M_t){>}_t$$ (12)

where < · >_t is the ensemble average across pseudo-random samples of sets of τ values the same size as the set of interest but randomly distributed across all angles. If the grouping of the sample is significant then the pseudo-set mean difference ΔM_t will tend to be greater than the sample set mean difference ΔM. Low p-values indicate statistically significant clustering. p-values were calculated using 10⁵ permutations.

Similarly, permutation tests were used to test the significance of hemispheric grouping. To test grouping of a value between hemispheres given two ordered sets of values A and B (where these values might be D_diff or D_best at a particular value of r or τ_best) where corresponding entries in each set are pairs of values from the same cat, the mean difference between pairs was calculated as

$$\Delta M=\frac{1}{N}\sum _i|A_i-B_i|$$ (13)

where N is the number of pairs. For τ_best the 90° symmetry was included when calculating the mean difference. The significance of the grouping was then calculated as the probability of such a difference arising randomly. This is given by

$$p=<H(\Delta M-\Delta M_t\text{)}{>}_t$$ (14)

where < · >_t is the ensemble average across pseudo-random pairing generated by permuting set B.

Essentially-complex planar form (ECP) maps

Essentially-complex planar forms are simple analytical models of orientation map layout that describe the attractors of time-evolving fields under particular symmetry considerations (Wolf, 2005) (others have also noted that orientation maps can be described simply in Fourier space (Niebur and Worgotter, 1994)). Here we use them as simple way of generating maps without consideration of training input. As commonly done (Swindale, 1996), we represent orientation maps as complex fields z(x) where the orientation preference at position x is given by arg(z(x))/2 and the selectivity |z(x)|. In this representation, ECP maps are defined by a sum of wavevectors as follows:

$$z(\text{x})=\sum _j^n{e}^{i{l}_j{\text{k}}_{j}x}$$ (15)

where the n wavevectors k_j are distributed equidistantly on the upper half of the circle and

$${\text{k}}_j=k_c(cos(j\pi /n),sin(j\pi /n)).$$ (16)

The binary variables l_j = ±1 determine whether the wavevector or its negative is used. We used n = 15 to generate the ECP maps in the paper. The values for l_j were assigned randomly. It can be shown by symmetry considerations that for n = 15 there are 612 different ECP maps (Wolf, 2005), although we only generate 40 distinct maps.

For comparison with the experimental maps, the ECP map wavelengths were scaled by adjusting to the length of the wavevectors k_c to generate wavelengths close to the experimental maps. The maps were truncated, after adding a 100 pixel offset, to 128 × 128 pixels, the same size as the elastic net maps (described next) and a similar size to the cat maps.

Elastic net maps

The elastic net is a feature-mapping model of visual map development (Swindale, 1996). From a computational point of view, feature-mapping models are relatively robust and efficient. From a biological point of view, they have been shown to produce a close match to much of the experimental data regarding the structure of ocular dominance, orientation, direction, and spatial frequency maps in V1, including their geometrical relationships (Erwin et al., 1995; Swindale, 1996; Swindale and Bauer, 1998; Goodhill et al., 1997; Goodhill and Cimponeriu, 2000; Carreira-Perpiñán et al., 2005). The elastic net in particular has also been shown to reproduce the experimentally observed effects on map structure of single orientation rearing (Carreira-Perpiñán et al., 2005) and monocular deprivation (Goodhill and Willshaw, 1994; Carreira-Perpiñán et al., 2005), including the co-localization of pinwheels with the center of deprived-eye patches that has been observed experimentally (Crair et al., 1997).

The low-dimensional version of the elastic net model used here treats each combination of input features, such as an oriented edge at a particular position in space, as a point in a ‘feature’ space. A net of points representing cortical cells occupies this feature space and the position of each cortical cell y_j represents its full receptive field i.e. (x-position, y-position, orientation preference, orientation selectivity). This abstraction speeds up computation while still producing results in good agreement with biological data (Erwin et al., 1995; Swindale, 1996).

At each iteration, training points which sample the feature space are presented to the elastic net. The ‘activity’ of each cortical cell y_i in response to the input x_i is related to the distance in feature space between the cell and the feature point, scaled by the parameter K:

$$\Phi (\Vert {\text{x}}_i-{\text{y}}_j\Vert ,K)=exp\left(-\frac{{\Vert {\text{x}}_i-{\text{y}}_j\Vert }^2}{2K^2}\right).$$ (17)

These activities are normalized so that each input elicits the same amount of activity in the cortex:

$$n_{ij}=\frac{\Phi (\Vert {\text{x}}_i-{\text{y}}_j\Vert ,K)}{{\sum }_p\Phi (\Vert {\text{x}}_i-{\text{y}}_p\Vert ,K)}.$$ (18)

The receptive field of each cortical cell y_j is then adapted towards the input by an amount proportional to the degree n_ij to which it responded to that input:

$$\Delta {\text{y}}_j=\gamma \left(\mu \sum _i{n}_{ij}({\text{x}}_i-{\text{y}}_j)+\nu K\sum _{j^{\prime }\in \text{N}(j)}({\text{y}}_{j^{\prime }}-{\text{y}}_j)\right)$$ (19)

where N(j) refers to the set of cells in the cortical sheet that are neighboring j. The second term in equation 19 models the effect of lateral interactions which move neighboring cortical points towards each other in feature space to keep the receptive fields of neighboring cortical cells similar to each other.

The mapping procedure attempts to improve a trade-off between good coverage and good continuity, two properties of real cortical maps (Swindale, 1996). The cortical points must adequately sample the feature space in order to avoid perceptual blind spots (good coverage) and neighboring cortical points must be close together in feature space to produce the smooth maps observed in the primary visual cortex (good continuity). The weighting of the coverage and continuity terms is controlled by the constants μ and ν, while γ is an overall rate constant. The parameter K is reduced over the course of the simulation so that the effect of each input is increasingly local and the attraction between neighboring cortical points decreases.

Since we wished to examine whether co-circular inputs affected the overall structure of the orientation maps, we trained the elastic net on manufactured “images” containing curves. These “images” were constructed in the four-dimensional feature space described above. Hence, images were not described by a set of pixel intensities, but by the features which made up the image. Each image consisted of a subset of points in the four-dimensional feature space with dimensions for x-position, y-position, orientation preference and orientation selectivity. The (x, y)-coordinates and orientations described curves of random radii.

At each iteration, a 1 × 1 unit training image was randomly selected from a 100 × 100 unit master image and presented to the elastic net. To create the master image, a position (x, y) was chosen randomly within the 100 unit square and an orientation chosen randomly from the interval [−90°, 90°). This feature point acted as a seed for a curve with a radius chosen randomly in the interval [0.1, 1] and a sign also chosen randomly. Starting from the seed point, additional points were added to the master image by extending the arc until it had a length of one. Points along an arc were spaced 1/64 units apart. This process was then repeated until the master image had an average density of 400 feature points per unit square. In order to control the strength of the training input correlations these highly correlated “images” were modified by adding uniform noise of magnitude ε to the orientations. ε was set between [0,1] where ε = 0 is maximally correlated input (no noise added) and at ε = 1 the input had entirely randomly distributed orientations (no correlation).

At each of 4000 iterations, a point was chosen randomly in the interval [1,98] to be the origin of a 1 × 1 unit training image selected from the master image. The use of the interval [1, 98] rather than the full range [0, 99] left a border around the master image which eliminated edge effects. The x and y dimensions of the training image were populated by translating the x- and y-coordinates of points in the selected area of the master image into the range [0, 1]. The orientation preference and selectivity dimensions of the training images were in polar coordinates. The polar angles of the training points were the orientations of the line segments in the selected area of the master image. The polar radius was 0.11 for all points. This polar radius was chosen to generate maps of similar wavelength to the cat maps.

Each four-dimensional “image” in the training set had an average of 400 feature points forming up to 20 arcs, some extending off the edge of the image at both ends, some terminating within the image. The probability of observing any given angle at any particular location was approximately equal over the set of training images.

For all simulations, the annealing parameter K was reduced from 0.2 to 0.01 over the course of the 4000 iterations. The continuity constant, ν, was 10 and the coverage constant, μ was 1. The overall learning rate, γ, was 0.1. The cortical net consisted of 128 × 128 points. For each value of ε = 0, 0.2, 0.4, 0.6, 0.8, 1.0, 40 maps were simulated.

Retinotopic information for simulated maps

For the simulated maps the transformation between visual field and cortical coordinates was globally linear and isotropic on average, and hence we used the relative positions of pairs of cells in cortical space as approximations to the relative positions of their receptive field centers. The effect of anisotropy and jitter on co-circularity statistics was examined for the elastic net maps in the same way as described above for the experimental maps.

3. Results

Experimental maps show reduced symmetry but not co-circularity, and reduced symmetry is not affected by rearing condition

We analyzed data obtained from thirteen individual cats. For some cats both hemispheres were imaged so that a total of eleven normal, seven stripe-reared and six dark-reared hemispheres were available. Some animals used in this study were litter-mates. For this analysis we treated the hemispheres of the animals as independent (see later for justification). Figure 2A–C shows a sample orientation preference map from each of these three experimental conditions.

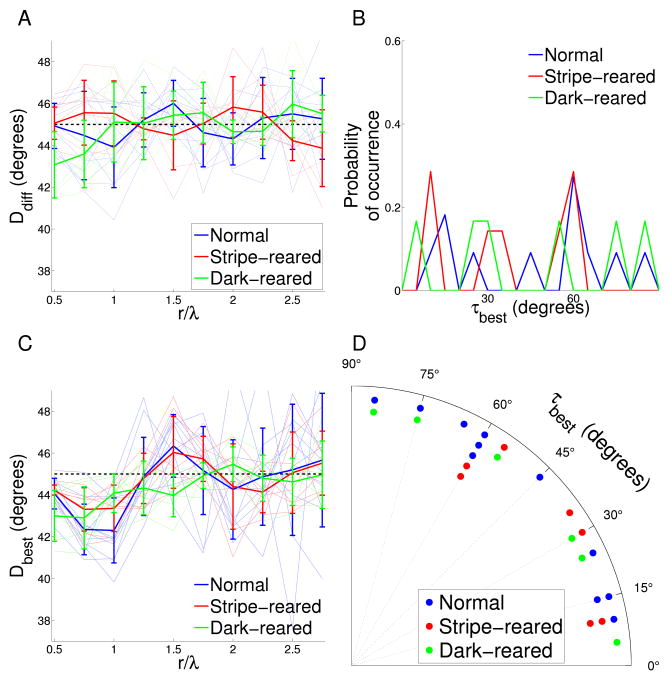
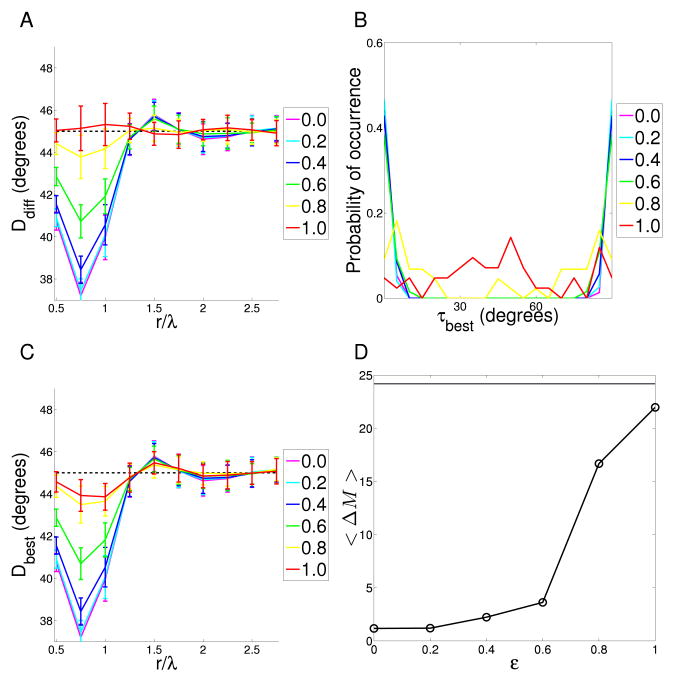
For each cat we calculated the probability that different relative orientations α occur at different relative positions (r, β) (see Figure 1D and Methods for angle definitions). Figure 2D–I shows example distributions for each experimental condition. These joint probability distributions provide a visualization of any reduced symmetry; in particular, any systematic relationship between α and β (the presence of which is the definition of reduced symmetry) is apparent in the shape of these plots. Co-circularity with offset τ would be visible as diagonal ridges, spaced 90° apart, running along the lines β = α/2 − τ and β = α/2 − τ ± 90°. The smoothness of orientation maps meant that at close range (r < λ/8, where λ is the wavelength of the orientation map), α was independent of β, indicating an absence of reduced symmetry (Fig. 2D–F). This independence can be seen in the figures; every slice along α (constant β) is identical to the other slices (modulo noise). For points separated by around one wavelength, we found reduced symmetry of varying strength in individual maps from all three experimental conditions (Fig. 2G–I). This can be seen in the figures; for each slice along α, the shape depends on the choice of β, so α and β are not independent. However, we did not find the high probability ridges at β = α/2 and β = α/2 ± 90° that are the signature of co-circularity. The absence of co-circularity was confirmed by examining the measure D_diff(r) for each rearing condition (Fig. 3A). For each map we generated a control map by pseudo-randomly permuting the positions of the pixels. This destroyed any reduced symmetry and ensured that for these maps, α and β were independent. We used these control maps to test for significance of D_diff(r). No rearing condition had a D_diff(r) significantly different from control near r = 1λ. In addition, there was no significant differences between rearing conditions except at r = 0.5 for normal compared to dark-reared and r = 2.5 for stripe-reared compared to dark-reared.

Figure 3. Analysis of reduced symmetry in experimental maps.

A Co-circularity strength D_diff(r) calculated for varying pair separations for the cat orientation preference maps under different rearing conditions. Thin lines are the results from individual cats; thick lines are the means for the different rearing conditions. The dashed black line at 45° shows the expected mean value when no co-circularity is present. There is no significant difference in the mean D_diff(r) for any r between any rearing condition and their randomly permuted controls except at r = 1.5λ (p = 0.01) for normal maps, r = 2.5λ (p = 0.05) for stripe-reared and r = 0.5, 2.5 (p = 0.01, 0.01) dark-reared. This indicates that no rearing condition shows significant co-circularity at r = λ, where it would be expected if the reduced symmetry in the maps was driven by co-circularity in natural scene input. Between normal and stripe-rearing, the only positions displaying significant difference in D_diff is r = 1.5, 2.0λ (p = 0.03). There are significant differences between normal and dark-reared cats at r = 0.5 (p = 0.01) and stripe-reared and dark-reared cats r = 2.5 (p = 0.01). B Density plot showing the distribution of τ_best, the angle of rotation of each orientation map required to bring it into maximal agreement with co-circularity for r = λ. There is no significant grouping of τ_best, either by rearing condition or cumulatively (p > 0.6). This indicates that the reduced symmetry in the maps is unlikely to have arisen due to natural scene input, since this would have defined a consistent coupling between retinotopic and cortical axes. Because τ is circularly symmetric at 90°, the ends of the x-axis can be thought of as joined and τ values near 90° are also close to 0. C Maximum co-circularity strength D_best(r) after rotation by τ_best for all rearing conditions. The dashed black line at 45° shows the expected mean value when no co-circularity is present. There are significant differences between normal results and control (randomly shuffled) maps at r = 0.5, 0.75, 1,1.5λ (p < 0.01), between stripe-reared and control maps at r = 0.5, 0.75, 1, 2.25λ (p < 0.03), and between dark-reared and control maps at r = 0.5, 0.75, 1, 1.5λ (p < 0.01). This indicates that all rearing conditions demonstrate statistically significant reduced symmetry near 1λ, but not co-circularity (as demonstrated in B). There is no significant difference in the mean D_best(r) between normal and stripe-reared cats for any r. There are significant differences in the mean D_best(r) between normal and dark-reared cats at r = 0.5, 1, 1.5λ (p < 0.04), and between stripe- and dark-reared cats at r = 0.5, 1.5λ (p = 0.01, 0.02 respectively). The differences may be due to difficulties in defining a value for λ in the dark-reared maps. Note that the minimum value for D_best is similar for the dark-reared cats compared to the other rearing conditions, indicating that the overall strength of reduced symmetry in the maps is not changed by rearing condition. D The same data (τ_best) as in (B) but presented as a polar histogram. All statistical tests as described in Methods section.

To confirm that a fixed rotation of cortical axes relative to visual field axes (as would arise from, for instance, a systematic error in our estimate of the vertical meridian in the cortex) could not produce significant co-circularity, we found the offset angle for each map, τ_best, which maximized our measure of co-circularity, D_diff(r), between r = 0.75λ and r = 1.25λ. The angle of rotation required for each individual map is plotted in Figure 3B,D. The rotation needed to match the co-circularity of natural images was not clustered at a constant value for all maps in any one experimental condition, or overall. This indicates that, while our experimental data display co-circularity with offset, there was no consistent offset angle that might arise from, for example, a systematic error in our estimate of visual field axes in the cortex.

Figure 3C shows D_best(r), the form of D_diff(r) after rotation by τ_best, for the different rearing conditions. All the maps demonstrated co-circularity with offset as shown by the significant dip in each rearing condition near r = λ. The significance of this dip was established by comparing each rearing condition with the permuted control maps. Although there were significant differences in D_best(r) between dark-reared cats and the other rearing conditions at some r values, the deviation from 45° was approximately the same, and we believe these differences are due to the difficulty in calculating the average wavelength of maps for the dark-reared cats.

Maps from the same cat are no more similar than maps from different cats

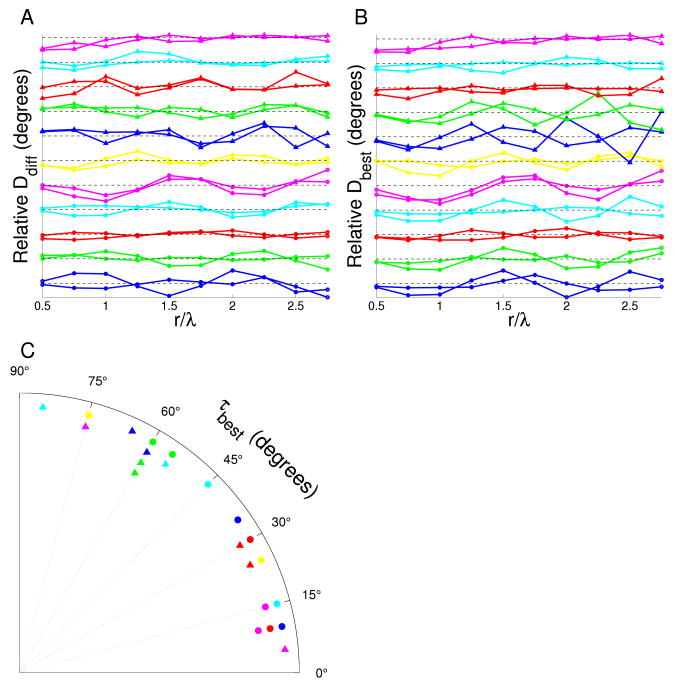
We hypothesized that reduced symmetry in V1 orientation maps may be directly genetically encoded, as an alternative to being driven by co-circularity in natural scenes. For a total of eleven cats, maps of both hemispheres were obtained. (To maximize the number of pairs for comparison, rearing condition were pooled for this analysis.) Since these paired maps are more genetically similar than unpaired maps, we tested for grouping of reduced symmetry properties between hemispheres of the same individual. The results are shown in Figure 4. While there was a statistically significant grouping in the strength of co-circularity between pairs at r = 0.5, 1.75, 2.25λ (Fig. 4A), this grouping was not near a separation of one wavelength, where co-circularity is strongest. The grouping may be due to the small sample size. There was no significant grouping in co-circularity with offset between pairs except at r = 0.5λ (Fig. 4B). Similarly, there was also no statistically significant grouping in τ_best between hemispheres from the same cat (Fig. 4C). Overall, the results indicate that genetics have little effect on reduced symmetry at the cortical range at which it is expected to be strongest. Although some cats were littermates, there were not enough data to allow a robust comparison of these more subtle genetic relationships. However, one would expect a genetic component of co-circularity to be demonstrable by hemispheric clustering.

Figure 4. Influence of genetics on reduced symmetry.

A Co-circularity strength D_diff(r) for the cat orientation preference maps classified by individual. Each pair of lines represents the results of both hemispheres from one cat. The dashed black line at 45° shows the expected mean value when no co-circularity is present. There is statistically significant grouping between pairs at r = 0.5, 1.75, 2.25λ (p = 0.02, 0.01 and 0.01 respectively). B Maximum co-circularity strength D_best(r) after rotation by τ_best for all hemispheres. The line colors are labeled as in A and again, the dashed black line at 45° shows the expected mean value when no co-circularity is present. There is no significant grouping effect between pairs at any r except at r = 0.5 (p = 0.03). C Polar histogram of τ_best, the angle of rotation of each orientation map required to bring it into maximal agreement with co-circularity for r = λ. Each pair of symbol type and color represents the results of both hemispheres from one cat. Although some pairs are grouped, overall there is no statistically significant grouping (p > 0.13). All statistical tests as described in Methods section.

Anisotropy and jitter in the retinotopic map do not strongly affect co-circularity statistics in experimental maps

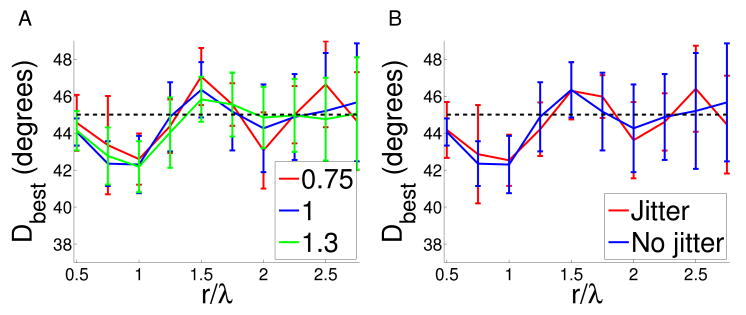
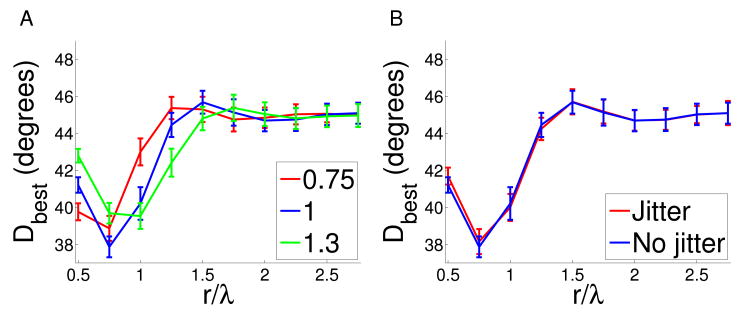
There is substantial experimental evidence from other studies to support our assumption of a smooth and isotropic retinotopy in the small region of cortex we are analysing (see Methods and Discussion). However, since retinotopy was not directly measured for the animals used in the present study, we cannot definitively eliminate the possibility that there existed a global anisotropy and/or jitter in receptive field locations. To investigate whether such uncorrected anisotropy or jitter might significantly influence our calculations of co-circularity statistics we therefore introduced explicitly them into the maps (see Methods). Fig. 5 shows that in neither case were the overall form of co-circularity statistics strongly affected. This argues that, even if small uncorrected distortions in retinotopy exist in our maps, this is not the reason we did not find co-circularity with zero offset.

Figure 5. The effect of anisotropy and jitter on cat map co-circularity with offset.

A We calculated co-circularity with offset D_best in the normal cat maps when anisotropy was added by stretching the x direction by a factor ρ. If there is existing anisotropy in the map we would expect this to correct for it. We examined ρ = 0.75 and ρ = 1.3. We found no significant changes in the strength of co-circularity with offset D_best or τ_best, indicating that our results are robust to these perturbations. B Similarly, we added jitter consisting of uniform random noise between [−1,1) pixels, to the normal cat maps. There was no significant change to co-circularity with offset D_best or τ_best, indicating the measurements are robust to jitter.

Co-circularity in maps is not a purely geometric feature of orientation maps

Since co-circularity with offset was found in all the experimental maps and all rearing conditions it was important to establish that it was not arising purely from inherent geometrical constraints for maps of this size. Therefore, we analyzed reduced symmetry in the ECP model of map development, a simple analytical model based on map symmetries. This model is not driven by specific patterns of input activity and is not Hebbian. Nonetheless, it reproduces many qualitative and quantitative features of map layout (Wolf, 2005). The maps it generates are a useful control for testing whether the co-circularity with offset is a geometric feature of all maps of this size. Figure 6 shows three example ECP maps and corresponding P(β, α|r) distributions. The distributions (Fig. 6G–I) and measurements of D_best (not shown) show minimal co-circularity with offset for the maps, as expected.

Figure 6. ECP maps.

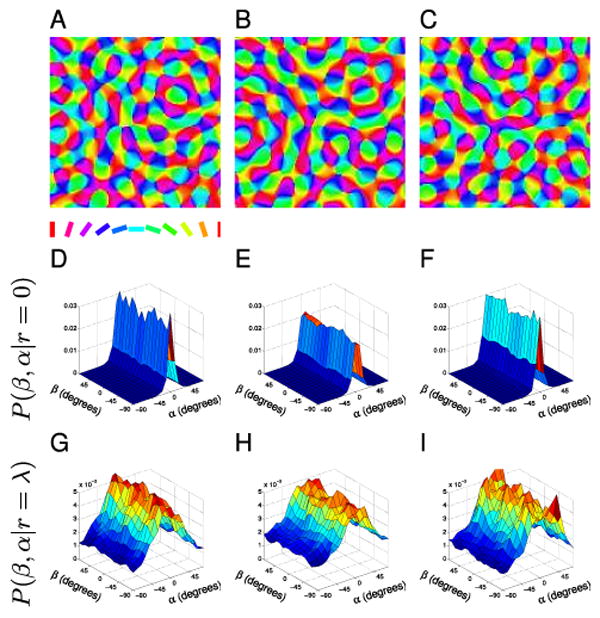
(A–C) Sample ECP orientation maps. (D–F) The associated P(β, α|r = 0) distributions for cortical points with small separation do not have reduced symmetry since pairs tend to be orientated similarly regardless of direction β. (G–I) The P(β, α|r = λ) distributions for cortical points separated by one wavelength also do not show any clear co-circularity.

Co-circular inputs to a Hebbian model produces maps with co-circularity while uncorrelated inputs to a Hebbian model produce maps that best match experimental data

Many computational models of visual map development have been proposed which learn inputs according to Hebbian mechanisms (for reviews, see Erwin et al., 1995; Swindale, 1996; Goodhill, 2007). In these models, a set of visual inputs is mapped onto a two-dimensional array of cells representing V1. Training on co-circular inputs allows us to examine the potential of input statistics to influence map development.

We used one such dimension-reduction or feature-mapping model, the elastic net. We simulated maps trained on synthesized images with varying amounts of co-circularity. Figure 7A–D shows example orientation maps. They are all periodic, feature pinwheels, saddle points and linear zones, and the degree of co-circularity in the input cannot be determined by visual inspection of the resulting map. As in the experimental maps, α and β are independent at close range for all inputs (Fig. 7E–H) because the maps are smooth.

Figure 7. Elastic net maps.

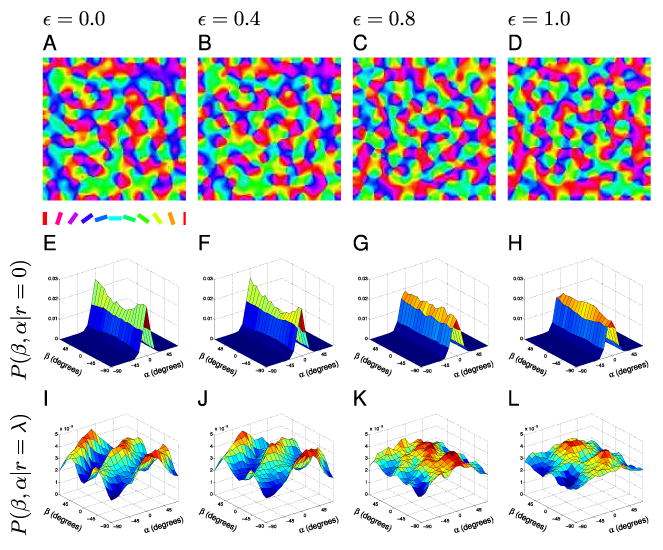
(A–D) Sample orientation maps trained on images of varying degrees of co-circularity (ε). ε = 0.0 corresponds to maps trained on highly co-circular inputs while ε = 1.0 signifies maps trained on inputs without co-circular correlations. (E–H) The associated P(β, α|r = 0) distributions for cortical points with small separation do not have reduced symmetry since pairs tend to be orientated similarly regardless of direction β. (I–L) The P(β, α|r = λ) distributions show forms of reduced symmetry. In the highly correlated training condition (I, ε = 0.0) the maps are strongly co-circular at τ = 0. As the training input correlations are reduced the strength of the co-circularity is reduced (J,K), but even with no correlation (L, ε = 1.0) the maps still exhibit reduced symmetry. However, with no input correlation, the maps show co-circularity with offset rather than co-circularity and the values for τ are randomly distributed.

In sharp contrast to the experimental maps, highly correlated inputs (ε = 0.0) produced a strong coupling between α and β for cortical points about one wavelength apart (Fig. 7I and 8A). Furthermore, the coupling is the same in all maps and is consistent with co-circularity, with signature ridges along β = α/2 and β = α/2 ± 90° (Fig. 7I) (and thus τ_best = 0, Fig. 8B,D). This illustrates that co-circular inputs can influence the layout of orientation columns; however, this influence does not appear in the cat maps.

Figure 8. Analysis of reduced symmetry in elastic net maps.

A Co-circularity strength D_diff(r) for elastic net maps trained on varying input correlation strength, ε. ε = 0.0 corresponds to maps trained on highly co-circular inputs while ε = 1.0 signifies maps trained on inputs without co-circular correlations. As input correlations are reduced the strength of co-circularity is also reduced. B Density plot of τ_best, the angle of rotation of each orientation map required to bring it into maximal agreement with co-circularity for maps with varying input correlation, ε. Because τ is circularly symmetric at 90° the ends of the x-axis can be thought of as joined and τ values near 90° are also close to 0. For uncorrelated input ε = 1.0), there are no significant areas of high density (p = 0.12), however, for all other conditions the density is concentrated near τ = 0 (p < 0.01). This indicates that even a small amount of reduced symmetry in the input is enough to cause symmetry breaking along the initially defined axis. C D_best for elastic net maps trained on varying strengths of input correlations ε. Since for most maps τ_best is near 0 this plot is similar to (A). As input correlations are reduced the strength of the map co-circularity is also reduced. D The mean distance between pairs of τ_best, < ΔM > (a measure of how grouped the τ values are). Each point on the plot is the mean of 40 elastic net maps. The horizontal line indicates the mean < ΔM > for the normal cat maps. As ε increases (inputs become less correlated) the maps exhibit more variability in τ_best and reduced co-circularity. The best agreement in the variability of τ_best values occurs when ε = 1.0. All statistical tests as described in Methods section.

Real visual input is likely to be less strongly co-circular than the highly correlated input used to train the ε = 0.0 maps. Indeed, maps driven with partially correlated input (Fig. 7B–C) showed reduced co-circularity strength closer to that of the cat maps (Fig. 8A). However, even for only weakly correlated input, τ_best is still clustered near 0 (Fig. 8B,D), unlike in the cat maps which do not show any preferred τ_best (Fig. 3B,D). This demonstrates that even a small amount of co-circularity in the input causes strong clustering of τ_best near zero, which is not observed experimentally.

Interestingly, reduced symmetry arose spontaneously at r = λ in maps trained on inputs without co-circular correlations (ε = 1.0, Fig. 7L, 8D). There was a significant difference in D_best between ECP and the ε = 1 elastic net maps at all distances examined (p < 0.04) except at r = 0.5, 2.0, 2.5, 2.75λ. The strength of this spontaneous co-circularity with offset was greater than that in ECP maps, demonstrating that it is significant and not a constraint of geometry. Furthermore, the offset τ was not grouped (Fig. 8B) which also matches the cat maps. The elastic net maps with spontaneous co-circularity and random offsets model the characteristics of the experimental maps. This indicates the co-circularity with offset found in the experimental maps may be arising as a form of spontaneous symmetry breaking.

Anisotropy and jitter in the retinotopic map do not strongly affect co-circularity statistics in simulated maps

Our elastic net simulations allowed us to approach the issue of anisotropy and jitter from the reverse direction: if co-circularity with zero offset exists, is it easily destroyed by uncorrected retinotopic distortions? In the same way as for the experimental maps described above, we therefore introduced anisotropy and jitter into elastic net maps which had strong co-circularity with zero offset (ε = 0). Fig. 9 shows that this had very little effect on the co-circularity statistics in this case, and the presence of co-circularity was still reliably detected.

Figure 9. The effect of anisotropy and jitter on elastic net map co-circularity.

To test whether true underlying co-circularity could be destroyed by uncorrected anisotropy or jitter, we added these to the elastic net maps in the same way as for the experimental maps (Fig. 5). In particular we investigated the case ε = 0, where the simulated maps display strong co-circularity with zero offset. A The maps were stretched or contracted in the x-direction by ratio ρ. As before we examined ρ = 0.75 and ρ = 1.3. The value of D_best was shifted when anisotropy was introduced. However, even under significant anisotropy the presence of co-circularity was reliably detected. Importantly, under all conditions for all the samples the measured value of τ_best was within 5° of the true origin (data not shown). This indicates that any anisotropy in the cat maps would not impede the detection of co-circularity or the origin τ_best. B We examined co-circularity with offset D_best and τ_best for maps when jitter was added to cortical positions. The jitter consisted of uniform random noise between [−1, 1) pixels. The jitter did not significantly affect measured co-circularity or the value of τ_best.

4. Discussion

Natural images display co-circularity, a particular form of reduced symmetry (Sigman et al., 2001; Geisler et al., 2001). Previous analysis of orientation maps from a cat and a monkey showed that reduced symmetry existed in these maps (Lee et al., 2003; Lee and Kardar, 2006), and preliminary data suggest a similar result in tree shrews (Schnabel et al., 2004, 2006, 2007b). Lee et al. (2003) proposed that co-circularity in the visual world was the likely source, but a lack of knowledge of the absolute axes of visual space in the maps they analyzed prevented these authors confirming that the reduced symmetry they observed was indeed co-circularity. We analyzed reduced symmetry in several cat orientation maps with known retinotopic axes. We found that, while reduced symmetry of the form of co-circularity with offset (τ_best ≠ 0) was present in each case, both its strength and the angular offset required to bring it into alignment with co-circularity differed apparently randomly between individuals. We also compared the reduced symmetry in maps from normal, stripe-reared and dark-reared cats. We found no strong relationships between rearing condition and the strength or co-circularity offset τ_best, both of which again appeared to be randomly distributed across rearing conditions and hemispheres. These results lead us to conclude that the co-circular coupling between position and orientation in natural scenes is not the cause of coupling between these dimensions in orientation maps in cat cortex.

To probe whether one would expect co-circularity in visual input to be reflected in orientation maps in V1 under standard Hebbian learning rules, we simulated map development using two different models. ECP maps were produced using a simple non-Hebbian analytical model. They displayed minimal co-circularity with offset, which was significantly weaker than that in cat maps. These maps acted as a control, demonstrating that it was possible to have maps which reproduced other important orientation map features whilst exhibiting minimal reduced symmetry. This finding established that the strength of co-circularity with offset found cat maps was significant. The elastic net (see also Schnabel et al., 2005) was used as a more realistic Hebbian model of development. This model, when trained with co-circular inputs produced orientation maps displaying robust co-circularity at τ = 0. The clustering at τ = 0, which didn't occur for cat maps, occurred for elastic net maps even when the training input was only weakly co-circular. However, when trained on inputs without any co-circularity (ε = 1), weak reduced symmetry with random offsets still emerged in the maps, apparently spontaneously, and was a closer magnitude to that found the cat maps. Hence, the elastic net maps trained on images without co-circular correlations most closely model the cat maps.

Assumptions about the retinotopic map

As in previous work (Lee et al., 2003), we have assumed that the mapping from visual space to the cortex is isotropic, smooth and continuous over the lengths we calculate correlations. We imaged only the small exposed dorsal surface of V1 approximately 5 mm × 5 mm in size, spanning both hemispheres. This area covers −5° to +5° of elevation and from the vertical meridian to +5°(−5°) of azimuth in the left(right) hemisphere (Tusa et al., 1978; Payne and Peters, 2001). However, within this area, we calculate correlations over a range of only 0 to 2.75 wavelengths which corresponds to a cortical distance of up to 1.3 mm. We will first discuss the validity of our assumption of isotropy, followed by smoothness, over these length scales in this area of cat V1.

Evidence for isotropy in cat V1 comes from microelectrode recordings by Tusa et al. (1978) which showed that in this small central portion of the visual field, the cortical magnification factor is close to constant and isotropic. Meanwhile, evidence from primates is conflicting. Tootell et al. (1988) and Blasdel and Campbell (2001) found an anisotropic magnification factor in macaque with the vertical magnification factor up to 1.5 times the horizontal magnification factor. However, the magnification factor in marmoset monkey is reported to be remarkably isotropic (Schiessl and McLoughlin, 2003).

Evidence for smoothness in mammalian V1 in general comes from several studies using optical imaging. In ferret, Yu et al. (2005) found a smooth map with no evidence of local distortions due to the orientation map. In tree shrew, Bosking et al. (2002) found that the spatial map was smooth down to the limit of resolution of their optical imaging technique, about 0.5° or 100 μm, and again they found no evidence for disruption of local retinotopy due to the orientation map. A similar result was found in marmoset monkeys (which have greater visual acuity) by McLoughlin et al. (2005), except that these authors reported smoothness down to a remarkable scale of 0.03°.

In contrast, Das and Gilbert (1997) suggested that cat maps are locally non-uniform and reported systematic distortions in local map retinotopy that were correlated with changes in orientation preference. However, more recent studies have found results more consistent with the data for other species described above. Using tetrode recordings, Hetherington and Swindale (1999) showed that receptive field scatter in cats was of the order of 0.5°, and that there was no correlation between this and orientation preferences. Using both optical imaging and electrophysiological recording in cat, Buzás et al. (2003) concluded that “our findings are compatible with a locally smooth and linear representation of visual space that is not coupled to the representation of stimulus orientation.” Thus, although there may be some variations between species, the weight of evidence supports our assumption of a locally smooth and continuous retinotopy in cat, at least for the small region of cortex on which our analysis is based.

However, in order to investigate the sensitivity of our results to potential uncorrected anisotropy or jitter that might be present we added artifically generated anisotropy and jitter to both the experimental and elastic net maps. We found in the former case that co-circularity with zero offset did not emerge, and in the latter case that co-circularity with zero offset was not destroyed. Thus even if anisotropy or jitter is present in the experimental maps it is unlikely to significantly affect our results and conclusions.

Our analysis relies on an estimate of the vertical retinotopic axis based on an assumption of the existence of a stereotypical retinotopic map in cat V1 as suggested by the literature (Payne and Peters, 2001). We found that the coupling between orientation and retinotopic maps indicated by τ_best was independent in different individuals. This result could only occur with co-circular coupling of the retinotopic and orientation maps if the vertical axis of the retinotopic map was randomly oriented in each hemisphere. Recordings in cat (Albus, 1975; Tusa et al., 1978; Diao et al., 1990) and other animals (Tootell et al., 1988; Schuett et al., 2002; Adams and Horton, 2003) have never found inter-individual variability to be this great. We estimate that errors of up to 10° exist in our estimations of the vertical axes, and these could introduce systematic errors in each calculation of D_best and the consequent selection of τ_best. However, the distribution of τ_best would still be clustered around zero degrees if co-circular coupling was occurring between the retinotopic and orientation maps. This finding is robust even if there was anisotropy in the maps that was unaccounted for.

Genetic influences on map structure

Kaschube et al. (2002) found an activity-independent contribution to the specification of column layout by comparing orientation maps in cats in the two hemispheres of individual brains, in littermates and in unrelated colony-mates. In particular they found significant similarities in column size and shape in the two hemispheres of individual brains, and in littermates. However, we found that the rotation of the cortical coordinates that best aligns our experimental maps with co-circularity is not correlated between hemispheres in individuals. This suggests that, unlike low-order properties, higher-order details of column layout, such as reduced symmetry, are not influenced by genetics. This is supported by our simulation studies, showing that while properties such as average map wavelength are robust to changes in initial conditions, reduced symmetry is not.

Due to both practical and ethical considerations, experiments involving rearing cats with controlled visual stimulation are generally restricted to small n-values, and this limits the strength of some of our conclusions, particularly those concerning genetic influences. A related issue is the difficulty of defining wavelengths for the orientation maps in our dark-reared cats. For instance, Figure 3C might be interpreted as showing a subtle stretching of the length-scale of reduced symmetry in dark-reared cats compared to the normal and stripe-reared cases. However, given the ambiguity in defining an appropriate length scale over which to normalize the variation of reduced symmetry with distance for maps without a sharp peak in their Fourier spectra, in conjunction with small n values, we suggest that it would be unwise to attach strong weight to such subtle effects. While there are clearly differences between the general structure of the maps in dark-reared versus normal animals, a thorough analysis of these differences beyond their potential effects on co-circularity statistics is outside the scope of this paper.

Lateral connections and map stability

Our results concern only the geometric layout of orientation columns rather than patterns of lateral connections. Initial work examining how natural scene statistics influence cortical maps was stimulated by the experimental findings in cat that, while short-range lateral connections are isotropic, long-range connections occur preferentially between co-oriented columns whose receptive fields are aligned along the axis of that orientation preference (Nelson and Frost, 1985; Bosking et al., 1997). Sigman et al. (2001) speculated that V1 may use such mechanisms to either decorrelate co-circular input, or oppositely, reinforce responses to probable configurations. This latter postulate is consistent with a Hebb-type learning rule encoding the high probability of co-circular edge segments in natural scenes into the lateral connections of maps (Ben-Shahar and Zucker, 2004). Subsequent modeling work has included re-creating these patchy lateral connections in networks with suitable training (Choe and Miikkulainen, 2004), creating orientation maps using models that incorporate co-circular lateral connections (Lee et al., 2003; Lee and Kardar, 2006; Schnabel et al., 2007a), and analyzing what the structure of visual hallucinations reveals about the symmetry of long-range intracortical connections (Bressloff et al., 2002). However, since we focused entirely on the geometric layout of columns, our results do not conflict with the evidence that lateral connections in V1 have reduced symmetry, or that their structure may be caused by the co-circularity of natural images.

Using theoretical modeling, Lee et al. (2003) and Lee and Kardar (2006) (see also Schnabel et al., 2007b) also aimed to demonstrate that the coupling of orientation and position is necessary for the development of stable maps containing pinwheels. In their model, maps with isotropic lateral connections produce a stable rainbow pattern containing no pinwheels, while maps in which orientation and position are coupled through anisotropic lateral connections evolve to a stable pattern containing pinwheels. Analysis of these two types of simulated maps revealed that maps with pinwheels and anisotropic connections had reduced symmetry while rainbow maps with isotropic connections had full symmetry. The authors concluded that the existence of pinwheels in a stable map implies that orientation and position are coupled in the inputs. They acknowledge though that stable maps containing pinwheels may occur biologically without coupled inputs due to other mechanisms, such as developmental freezing. However, they did not look for reduced symmetry in a simulated map with isotropic connections that was frozen so that it still contained pinwheels. We have verified here that reduced symmetry does occur in stable, biologically-realistic maps containing pinwheels, but we have also shown that it can occur without explicitly coupling position and orientation in the inputs.

An issue related to map stability is the fact that we examined only maps from young cats (ages 5–6 weeks) rather than adults. It is thus conceivable that the reason we did not find co-circular structure consistent with that in natural images was simply that it had not developed yet, and that adult animals would show such structure. However, imaging of orientation maps in both cat (Gödecke et al., 1997) and ferret (Chapman et al., 1996) at several developmental time-points in individual animals has shown that once the map is detectable it is highly stable and does not change with time. Thus we think it is unlikely that co-circular structure would only emerge later in development. In addition, one of the normal reared cats was optically imaged at two time points (5 and 6 weeks), and we found no significant differences in reduced symmetry statistics between these two time points (data not shown). Furthermore, Sengpiel et al. (1999) and White et al. (2001) previously demonstrated that dark- and stripe-rearing have definite first-order effects on map structure. Therefore, it is reasonable to look for higher-order effects in these animals.

In summary, our results suggest that some statistical properties of cortical map structure are determined neither by genetics, nor by the statistics of visual input during the critical period. Rather, they may arise spontaneously, as a result of more general rules for self-organizing cortical development. Consequently, these statistical properties may not have a significant functional role in adult. This is similar to the situation suggested for the cortical column (Swindale, 1990, 1998; Horton and Adams, 2005), which has much greater appeal as a candidate fundamental principle of cortical organisation. However, even without a functional role, each demonstrated statistical feature of cortical maps provides a useful constraint for developmental mechanisms.