A Sparse Marker Extension Tree Algorithm for Selecting the Best Set of Haplotype Tagging Single Nucleotide Polymorphisms

Abstract

Single nucleotide polymorphisms (SNPs) play a central role in the identification of susceptibility genes for common diseases. Recent empirical studies on human genome have revealed block-like structures, and each block contains a set of haplotype tagging SNPs (htSNPs) that capture a large fraction of the haplotype diversity. Herein, we present an innovative sparse marker extension tree (SMET) algorithm to select optimal htSNP set(s). SMET reduces the search space considerably (compared to full enumeration strategy), therefore improves computing efficiency. We tested this algorithm on several datasets at three different genomic scales: (1) gene-wide (NOS3, CRP, IL6 PPARA, and TNF), (2) region-wide (a Whitehead Institute's inflammatory bowel disease dataset and a UK Graves’ disease dataset), and (3) chromosome-wide (chromosome 22) levels. SMET offers geneticists with greater flexibilities in SNP tagging than lossless methods with adjustable haplotype diversity coverage (ϕ). In simulation studies, we found that (1) an initial sample size of 50 individuals (100 chromosomes) or more is needed for htSNP selection; (2) the SNP tagging strategy is considerably more efficient when the underlying block structure is taken into account; and (3) htSNP sets at 80−90% ϕ are more cost-effective than the lossless sets in term of statistical power, relative risk ratio estimation, and genotyping efforts. Our study suggests that the novel SMET algorithm is a valuable tool for association tests.

Introduction

Surveys of variations at different genomic scales have revealed block-like patterns of haplotype structures in European, Asian, and African populations. Examples include chromosomes 5q31 [Daly et al., 2001], 6 in the MHC class II region [Jeffreys et al., 2001], 19 [Phillips et al., 2003], 21 [Patil et al., 2001], 22 [Dunning et al., 2000], and 51 autosomal regions spanning 13.4 Mb [Gabriel et al., 2002]. This has motivated the launch of the HapMap project to assess the haplotypic structure of the entire human genome. Once haplotype block structure is deciphered, a small fraction of SNPs – called “haplotype tagging” SNPs (htSNPs) -- can be used to represent a large fraction of the haplotype diversity. Various testing schemes, including haplotype-based and multiple-marker methods, have been proposed to utilize htSNPs in capturing genetic association [Akey et al., 2002; Clark, 2004; Roeder et al., 2005; Schaid, 2004]. In order to identify the best htSNP set, we first need to nail down a proper measure of “haplotype diversity”. Several metrics, such as $R_h^2$ [Stram et al., 2003], heterozygosity (H) [Zhang and Jin, 2003], and entropy (E) [Ackerman et al., 2003; Hampe et al., 2003] have been proposed. A computer program called “Best Enumeration of SNP Tags” (BEST) picks the optimal htSNP set distinguishing all haplotypes [a.k.a., lossless htSNP set, where H=E=100%] [Sebastiani et al., 2003].

In genetic association studies, it is of great interest to determine the best threshold of haplotype diversity coverage, denoted as ϕ. In particular, it is critical to ascertain how much power is lost and how much bias is introduced in estimating the disease risk ratio when the htSNP set only captures 80−90% (as opposed to 100%) of the haplotype diversity. To address these issues, we conducted both simulation and empirical studies using a new algorithm, sparse marker extension tree (SMET), which allows for flexibility in selecting the optimal htSNP set at any given haplotype diversity coverage. We also assessed the impacts of sample size on panel development and the utilization of haplotype block structures.

Materials and Methods

Definition of a minimum htSNP set

Let K denote the number of the original SNPs and W the total number of distinct haplotypes formed by the original SNPs. Let ϕ_N denote the haplotype diversity coverage captured by the N (K≥N) candidate htSNPs. The selection of minimum htSNP set for a pre-defined threshold, ϕ_T, requires identification of the minimum of all N that satisfy ϕ_N ≥ ϕ_T. We calculate ϕ_N using either E or H.

(1) Heterozygosity, H, is a classic statistic measuring genetic marker diversity, and the H of all K SNPs is defined as:

$${\mathit{H}}_{full}=\frac{n}{n-1}(1-\sum _{i=1}^W{p}_i^2),$$ (1)

where p_i denotes the frequency of the W haplotypes, ${\sum }_{i=1}^W{p}_i=1$, and n denotes the total number of chromosomes in the study sample. Consider that N htSNPs reconstruct L distinct haplotypes with frequencies f₁,...,f_L (Note that ${\sum }_{j=1}^L{f}_j=1$), respectively. ϕ_N of the N htSNPs can be derived as

$${\varphi }_N=\frac{{\mathit{H}}_{htSNP}}{{\mathit{H}}_{full}}=\frac{\frac{n}{n-1}(1-\sum _{j=1}^L{f}_j^2)}{\frac{n}{n-1}(1-\sum _{i=1}^W{p}_i^2)}=\frac{1-\sum _{j=1}^L{f}_j^2}{1-\sum _{i=1}^W{p}_i^2},$$ (2)

(2) Entropy, E, is also a commonly used measurement of information diversity, defined as

$${\mathit{E}}_{full}=-\sum _{i=1}^W{p}_i{\log }_2\left(p_i\right)$$ (3)

Thus, ϕ_N can be defined as:

$${\varphi }_N=\frac{{\mathit{E}}_{htSNP}}{{\mathit{E}}_{full}}=\frac{-\sum _{j=1}^L{f}_j{\log }_2\left(f_j\right)}{{\mathit{E}}_{full}}$$ (4)

Reconstructing haplotype phase and partitioning haplotype blocks

For reconstructing haplotype phases of unrelated subjects, we applied the partition-ligation Gibbs sampling algorithm [Niu et al., 2002]. For pedigree data, we used the transmission disequilibrium test function of GeneHunter 2.0 [Daly et al., 2001] and Clark's method [Clark, 1990]. We did not attempt to perform block partitioning for gene-wide datasets, because the physical lengths (<300 kb) and the number of SNPs for each gene are relatively small. For Whitehead Institute's IBD dataset, we used haplotype blocks from the original report [Daly et al., 2001]. For the UK Graves’ disease dataset and the chromosome 22 dataset, we applied block partitioning algorithms based on the confidence intervals of D’ [Gabriel et al., 2002; Schulze et al., 2004]. Specifically, we calculated 95% confidence bounds for all pairwise D’ using a bootstrap resampling technique [Gabriel et al., 2002]. Two criteria were used: (1) for the SNP pair comprising both the left-most and right-most SNPs, the D’ needs to have a 95% upper bound (ub) > 0.95 and a 95% lower bound (lb) > 0.7; and (2) among all the possible SNP pairs within the block, the fraction of SNP pairs with both ub >0.95 and lb >0.50 should be >80%.

Sparse Marker Extension Tree (SMET) algorithm

For any initial set of K SNPs (K≥2) and a given threshold ϕ_T, our algorithm selects the minimum htSNP set(s). As described above, ϕ_N can be defined on the basis of either H or E. Our algorithm follows a stepwise forward selection procedure that begins with all possible pairs of SNPs and sequentially adds SNPs until the minimum htSNP set(s) is found (i.e. when ϕ_N exceeds threshold ϕ_T).

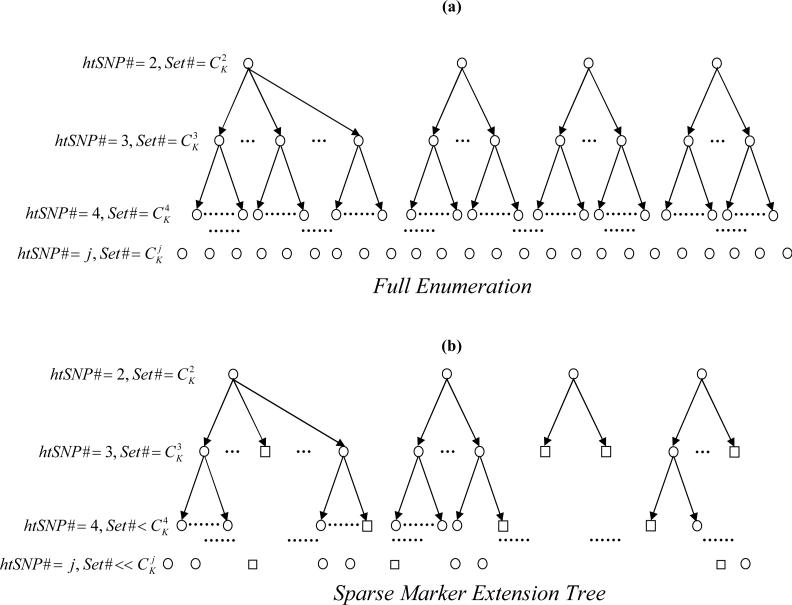
Figure 1 provides a tree representation of the algorithm. Each tree node (denoted as either a circle or a square) represents a candidate SNP set. At the j^th level of the tree, for each SNP set of size j, one additional SNP is added to form a new set at the (j+1)^th level. Computationally enumerating all possible SNP sets (tree nodes), as shown in the upper panel of Figure 1, is prohibitively expensive when K is large. In contrast, SMET produces only a sparse tree comprising non-singular nodes. A singular node (denoted as a square) is a node at least one of whose member SNPs’ information is entirely redundant with the information of the haplotypes formed by other member SNPs of that node. A nonsingular node (denoted as a circle) contains no SNP whose information is fully redundant with the haplotypes formed by other SNPs. Any higher-level node that extends from a singular node must also be singular. Therefore, such singular nodes constitute “terminals” of their respective branches, and there is no further “growth” of such branches.

Figure 1.

A schematic diagram illustrating the contrast between (a) the full enumeration algorithm, and (b) the sparse marker extension tree (SMET) algorithm for htSNP selection. SNP sets were represented as tree nodes (circles or squares). Two types of nodes were distinguished - singular (square) nodes and nonsingular (circle) nodes. Because SMET only enumerates a sparse tree instead of a full tree, it is computationally much more efficient. When a node becomes singular (i.e. the node already contains redundant SNPs), any derivative nodes from this singular node will also be singular; therefore, singular nodes constitute the terminal nodes of their respective branches. In (a), all nodes have to be enumerated in screening for the minimum htSNP set; in (b) only non-singular nodes were taken into consideration in screening for the minimum htSNP set.

The essence of SMET is that all calculations are made only for nonsingular nodes, resulting in a significant reduction in computational cost when K is large. Below we describe the algorithmic details of SMET: Let A_k denote the nonsingular nodes at the k^th level of the tree, and a_i denote the member sets of A_k. S denotes the original K SNPs. Also, a_max,k denotes the node(s) carrying the largest haplotype diversity coverage among all a_i. The SMET can be written as,

While (ϕ (a_max,k) < ϕ_T) {

$A_{k+1}=\varnothing$;

For each tree node $a_i\in A_k$ {

add each SNP m_j ∈ S\a_i individually to a_i, such that if $a_i’=a_i\vee \left\{m_j\right\}$ is a new, nonsingular node, then add a_i' to A_k+1;

}

k ← k + 1;

}

return a_max,k.

Empirical Datasets

We compared the performance of our algorithm with the BEST algorithm on datasets that represent different genomic scales.

1. SeattleSNPs dataset: a total of 118 SNPs on 4 diabetes candidate genes NOS3, CRP, IL6, and PPARA were genotyped in 24 African Americans and 23 European Americans.

2. TNF dataset: a total of 12 SNPs located at the TNF gene locus were genotyped in unrelated Gambian (N=212) and Malawian (N=84) adults [Ackerman et al., 2003].

3. Whitehead Institute's IBD dataset: a total of 103 SNPs in a 500 kb region of chromosome 5q31 were genotyped in 129 family trios of European descent [Daly et al., 2001].

4. UK Graves’ disease dataset: a total of 108 SNPs distributed in a 317 kb region containing CD28, CTLA-4, and ICOS genes were genotyped among Graves’ disease cases (N=384) and controls (N=652) from the UK [Ueda et al., 2003].

5. Chromosome 22 dataset: a total of 656 SNPs [minor allele frequency (MAF) ≥ 5%] distributed across chromosome 22 were genotyped in 54 unrelated individuals. This dataset was generated using Affymetrix Gene Mapping 100K SNP Array.

Evaluation based on simulations

(1) Assessing the impact of the sample size of the developing panel on htSNP selection adequacy

Researchers often genotype an initial grid of densely spaced SNPs on a developing panel with a sample size - N_d, followed by haplotype block partitioning and htSNP selection; afterwards, only those htSNPs (derived from the developing panel) are genotyped in large samples. Therefore, it is critical to evaluate the impact of N_d on the efficiency of htSNP selection. We generated our simulated datasets based on (1) the TNF haplotypes in the Gambian sample [Ackerman et al., 2003] and (2) the UK Graves’ disease dataset [Ueda et al., 2003]. In each dataset, we randomly sampled an N_d of (1) 25 and (2) 50 individuals as our developing panel, based upon which we identified the respective minimal htSNP sets using SMET, then evaluated the haplotype diversity coverage of these htSNP sets on simulated large cohorts, comprising 324 chromosomes (i.e. 162 individuals) derived from the TNF Gambian dataset and 324 chromosomes (i.e. 162 individuals) from the UK Graves’ disease dataset, respectively. Specifically, in each resampling-based dataset, we resampled 50 or 100 haplotypes from this “haplotype pool” [e.g. the”haplotype pool” of the UK Graves’ disease dataset (N=652) contained 1,304 chromosomes] to serve as the “development panel” in SNP tagging. For each parameter set, we conduct 1,000 resamplings to ensure reliable inferences. Also, the resampling was performed within individual haplotype blocks.

(2) Assessing the dependency of htSNP selection efficiency on a genuinely LD-based haplotype block structure

The efficiency of htSNP selection using “haplotype-block-tagging” approach depends on whether the underlying haplotype block structure is truly based on LD [Stram et al., 2003]. To evaluate the extent of this dependency, we devised a simulation scheme similar to that of Lin et al. [2004]. In brief, suppose n SNPs are located linearly on the chromosome, denoted as SNP₁ to SNP_n from 5’ → 3’. A haplotype block can be denoted as an interval [j, k], where n ≥ k > j ≥ 1, so that j^th through k^th SNPs form a haplotype block. We reshuffle the order of these SNPs by moving the first t (t is a randomly generated integer) SNPs to the end of the list, which results in a new list: SNP_t+1, SNP_t+2,..., SNP_n, SNP₁,..., SNP_t. By still treating j^th through k^th SNPs in the new list as a haplotype block, we generated arbitrarily-defined, non-LD based pseudo-blocks without destroying the “local” LD relations of neighboring SNPs (except for SNP_t). A total of 1,000 simulations were conducted for each set of parameters.

(3) Assessing the impact of genetic diversity on htSNP selection efficiency

We used the coalescent model to simulate data to evaluate the impact of genetic diversity (haplotypic diversity). The program HUDSON [Schierup and Hein, 2000a; Schierup and Hein, 2000b] was applied. In our simulations, we specified the population mutation rate (θ = 4Nμ) as 0.05 and the population recombination rate (ρ = 4Nν) as 1.0, where N designates the effective population size, and μ and ν designate the per-locus mutation and recombination rates per generation [Wall and Hudson, 2001], respectively. We simulated two populations (denoted as Pop I and Pop II, respectively), and their only difference was that Pop II had a longer (two times) evolution history than Pop I. Therefore, Pop II would possess more historical recombinations and a higher genetic diversity than Pop I. A total of 500 pairs (i.e. for Pop I and Pop II respectively) of simulated datasets were generated, and in each pair of simulated datasets, 50 individuals from each population were sampled for SNP tagging.

(4) Statistical power and relative risk ratio estimation in haplotype association tests using htSNPs at various ϕ

The choice of ϕ may affect the power of haplotype-based association tests. We investigated two datasets: (1) TNF dataset in the Gambian sample [Ackerman et al., 2003] and (2) the 5^th, 8^th and 9^th block in UK Graves’ disease dataset. We used these datasets because of their relatively large sample sizes and SNP numbers, and we only considered the most frequent haplotype in each dataset as the disease haplotype. The power was evaluated through simulations. To assess the impacts of different disease models using different parameter settings, we performed the following simulations. We set the number of cases and number of controls each to be 200, respectively, and specified a disease-susceptible haplotype with a penetrance of 0.1, 0.2, and 0.4 for subjects carrying 0, 1, and 2 susceptible haplotypes, respectively. For each simulation dataset, we (1) generated the data by a random sampling from each respective real dataset and by assigning the disease status to each individual according to that individual's haplotype configuration and penetrance, (2) identified htSNPs using N_d = 50 at ϕ of 80%, 90% and 100% levels, (3) conducted association tests in a contingency table setting, which compares the haplotype frequencies between cases and controls, and (4) estimated power at α (Type I error) = 0.0001. We generated 5,000 simulation datasets for each set of parameters.

Results

Empirical Studies

We compared the performance of SMET with BEST at various genomic scales.

Gene-wide (< 300 kb) scale

(a) SeattleSNPs databsets

We studied a total of 40, 17, 16, and 45 SNPs on NOS3, CRP, IL6, and PPARA, respectively (Table I). The analysis included all haplotypes that appeared at least twice in the dataset. As shown in Table I, based on either E or H, an htSNP set containing 6−9 SNPs at ϕ = 100%. Based on E alone, an htSNP set containing 4−6 SNPs at ϕ = 90% (please note, according to our studies using both simulated and real data sets, H is not a sensitive measure of haplotype diversity coverage, and we recommend the use of E).

Table I.

Gene htSNP Selection^*

			SeattleSNPs Dataset				TNF Dataset
			NOS 3	CRP	IL6	PPARA		TNF
E Criteria	Total SNP #	White (N=23 individuals)	40	17	16	45	Gambia (N=212 individuals)	8
	Full E		4.293	2.655	2.509	3.283		2.698
	htSNP # at ϕ = 100%		9	7	6	7		8
	htSNP # at ϕ = 90%		6	4	4	5		5
H Criteria	Full H		0.935	0.783	0.751	0.805		0.763
	htSNP # at ϕ = 100%		9	7	6	7		8
	htSNP # at ϕ = 90%		3	2	2	3		4
E Criteria	Full E	Black (N=24 individuals	4.524	3.125	3.567	5.038	Malawi (N=84 individuals)	2.813
	htSNP # at ϕ = 100%		7	7	7	7		6
	htSNP # at ϕ = 90%		5	5	5	5		4
H Criteria	Full H		0.934	0.878	0.834	0.964		0.814
	htSNP # at ϕ = 100%		7	7	7	7		6
	htSNP # at ϕ = 90%		3	3	3	3		3

^*E, entropy; H, heterozygosity.

(b) TNF dataset

Prior to the analysis, we removed 4 SNPs with MAF <10%, as well as rare haplotypes that appeared only once. When the study sample size was large (N=212; the Gambian sample), all SNPs were needed to from the lossless (i.e. ϕ=100%) htSNP set. When the study sample size was small (N=84; the Malawi sample), 6 out of 8 SNPs were needed. To achieve ϕ = 90%, the minimal htSNP set included only 3−5 of the 8 SNPs (Table I).

Region-wide (300 − 500 kb) scale

(a) Whitehead Institute IBD dataset

Among the 103 SNPs distributed on a 500 kb region of 5q31, 99 SNPs were located within 11 haplotype blocks, and 4 SNPs did not belong to any blocks. Infrequent haplotypes, which appeared only once in the sample, were excluded prior to analysis. Based on E, we found that to achieve ϕ = 100%, 29−100% SNPs were needed. 16.3−80.0% SNPs were needed at ϕ = 90% (Figure 2).

Figure 2.

The haplotype block structure, D’, and htSNP selection of the Whitehead Institute IBD dataset. E, entropy; H, heterozygosity.

(b) UK Graves’ disease dataset

Among the 108 SNPs distributed over a 317 kb region containing CD28, CTLA-4, and ICOS genes, a total of 107 frequent SNPs (MAF ≥ 10%) were used. By applying D’-based block partitioning [Gabriel et al., 2002], 10 haplotype blocks were revealed. The size and the average D’ value for each block are shown in Figure 3. 101 SNPs were located in haplotype blocks and the remaining 6 SNPs were block-free. Blocks varied greatly in terms of both the number of SNPs (range: 2−26) and physical sizes (range: 31 bp – 55.8 kb). We applied SMET to the 5 haplotype blocks containing > 10 SNPs (all others contained 2−4 SNPs), and found that to achieve ϕ = 100%, 95.2−100% SNPs were needed. Based on E, 35.3−50.0% SNPs were needed at ϕ = 90% (Figure 3).

Figure 3.

The haplotype block structure, D’, and htSNP selection of the UK Graves’ disease dataset. E, entropy; H, heterozygosity.

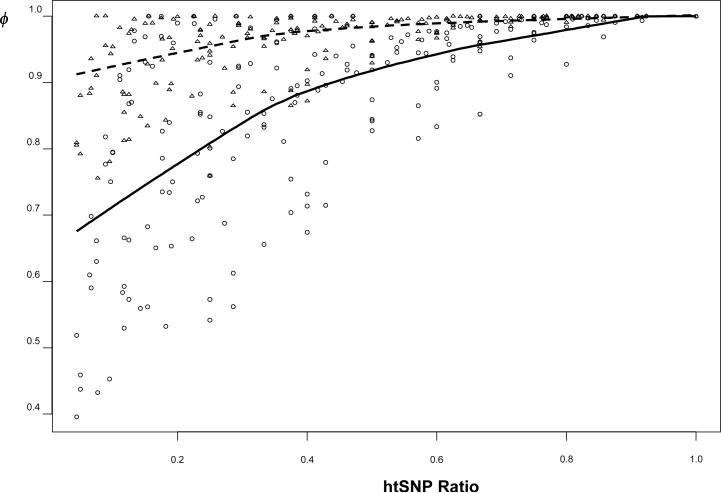
Combining the gene- and region-wide SNP datasets, we plotted ϕ as a function of htSNP ratio (defined as the size of the htSNP set/the size of the lossless htSNP set), based on either E or H (Figure 4). Both curves had a plateau phase before reaching the lossless htSNP set. E clearly provides a better sensitivity than the conventional H.

Figure 4.

The relationship between the htSNP ratio (i.e. the size of the htSNP set/the size of the lossless htSNP set) using SMET algorithm and the information capturing ratio defined by either the percentage of coverage based heterozygosity (triangles and the broken line) or based on entropy (circles and the solid line). The datasets used were from SeattleSNPs datasets on NOS3, CRP, IL6, PPARA, the TNF datasets of Ackerman et al. [2003], as well as two region-wide datasets [Daly et al., 2001; Ueda et al. 2003]. The two curves were fit using LOWESS smoothing function with f=2/3. The two curves converge when htSNP ratio = 1 (i.e. when the lossless htSNP set is found).

Chromosome-wide (33.4 Mb) scale

By applying the D’-based block partitioning method [Gabriel et al., 2002], a total of 150 blocks were revealed for 656 SNPs in the chromosome 22 dataset. The distributions of the physical sizes of the haplotype blocks are shown in Figure 5. Among the 656 SNPs, 452 (68.8%) SNPs were located inside haplotype blocks, and 205(31.2%) SNPs were block-free. We performed htSNP selection on the 4 largest haplotype blocks (size > 7). At ϕ = 100%, 50−66.7% SNPs were needed. Based on E, 37.5−55.6% SNPs were needed at ϕ = 90% (Table II).

Figure 5.

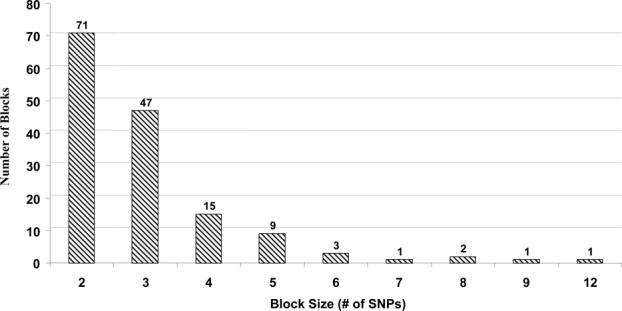
The distribution of the haplotype block sizes in chromosome 22. A total of 656 SNPs were partitioned into 150 haplotype blocks [452 (68.8%) SNPs were located inside haplotype blocks] based on minor modifications of the Gabriel's LD-based algorithm (please see the Materials and Methods section for details). The x-axis denotes the size of the blocks, in terms of SNP number. The y-axis denotes the number of haplotype blocks of respective sizes.

Table II.

Haplotype Block Partitioning and htSNP Selection in the 4 Largest Haplotype Blocks of the Chromosome 22 Dataset^*

Block No.		1	2	3	4
# SNPs in the Block		8	8	9	12
Physical Size (bp)		392640	101759	266306	146449
Average Pairwise D’		0.821	0.848	0.861	0.826
SNP Tagging
E Criteria	Full E	2.757	1.823	2.483	2.483
	htSNP # at ϕ = 100%	5	4	6	6
	htSNP # at ϕ = 90%	4	3	5	5
H Criteria	Full H	0.810	0.659	0.797	0.708
	htSNP # at ϕ = 100%	5	4	6	6
	htSNP # at ϕ = 90%	3	3	3	3

^*E, entropy; H, heterozygosity.

For all the above datasets, we also used the program BEST version 1.0, and confirmed that the lossless htSNP sets identified by SMET were identical to those identified by BEST.

Simulation Studies

Impact of N_d on htSNP selection adequacy

Figure 6 showed the results using resampled datasets of the TNF and the UK Graves’ disease datasets. When N_d = 25 (i.e. 50 chromosomes), based on E, the htSNP sets at ϕ = 100% in the developing panel achieve ϕ = 73.9−87.9% in the large cohort (324 chromosomes); the htSNP sets with ϕ = 90% in the developing panel achieve ϕ = 68.7−87.1%. When the N_d = 50 (i.e. 100 chromosomes), based on E, the htSNP sets with ϕ = 100% in the developing panel achieve ϕ = 84.5−95.0% in the large cohort; the htSNP sets with ϕ = 90% in the developing panel achieve ϕ = 78.7−89.9%. An N_d = 25, such as that used by Sebastiani et al. [2003], may result in a htSNP set with unsatisfactorily low ϕ, insufficient for large-scale studies. N_d ≥ 50 is needed to identify htSNP sets with reliable and adequate ϕ.

Figure 6.

The impact of the sample size on the efficiency of htSNP selection in the developing panel. We generated our simulated sets based on (1) TNF SNP data in the Gambian sample [Ackerman et al., 2003] and (2) the UK Graves’ disease dataset [Ueda et al., 2003]. In each dataset, we randomly selected 50 (N_d = 25) or 100 (N_d = 50) chromosomes in our developing panel. Based on this developing panel, we applied SMET to choose the minimum htSNP set. Then, we applied the selected htSNP set to two resampling-derived large-scale cohorts comprising 324 chromosomes based on the TNF SNP dataset and 324 chromosomes based on the UK Graves’ disease dataset, respectively. (A) results using E criterion; (B) results using H criterion. The x-axis denotes the size (in terms of the total number of chromosomes) of the developing panel, and y-axis denotes the coverage ratio. Bars denote the developing scheme of the htSNPs: shaded bars, ϕ=100%; open bars, ϕ=90%; 1,000 simulations were conducted for each set of parameters, and in each simulation, haplotypes were randomly sampled without replacement.

Efficiency comparison of htSNP selection based on a genuinely LD-based block structure vs. an arbitrarily-defined pseudo-block structure

We used the 5 largest blocks (size > 10) in the UK Graves’ disease dataset in our comparison experiment. The lossless (ϕ = 100%) htSNP set contained an average of 5.04 SNPs/block chosen by the SMET algorithm based on a predefined genuinely LD-based block structure, which is smaller than the lossless (ϕ = 100%) htSNP set (5.51 SNPs/block) chosen by the SMET algorithm based on an arbitrarily-defined pseudo-block structure, assuming that they share exactly the same “physical” haplotype block structure (i.e. the same width for each respective block and the same block order) (Figure 7). In other words, we applied the same “haplotype-block-tagging approach” – SMET on truly LD-based blocks vs. arbitrarily-defined, non-LD based, pseudo-blocks for the same set of linked SNPs. As shown in Figure 3, for the UK Graves’ disease dataset, blocks 5 and 8 are moderate-LD blocks with an average D’ of 0.785 and 0.777, respectively; blocks 4, 6, and 9 are high-LD (i.e. average D’ > 0.80) blocks with an average D’ of 0.981, 0.824, and 0.836, respectively. For the three high-LD blocks, the application of the genuinely LD-based block structure considerably reduced the size of htSNPs set/block than the application of arbitrarily-defined, pseudo-block structure (4.07 SNP/block vs. 5.33 SNP/block). For the two moderate-LD blocks, the difference of the htSNP set size between considering LD-based block vs. non-LD based pseudo-block structure is less dramatic. As a conclusion, htSNP selection based on previously partitioned genuinely LD-based blocks is a more efficient, especially when such blocks are high-LD blocks.

Figure 7.

Efficiency of htSNP selection for a genuinely LD-based haplotype block structure vs. an arbitrarily-defined, non-LD-based pseudo-block structure. The x-axis denotes different parameter settings and the y-axis denotes the average number of htSNPs in the five studied blocks (blocks 4, 5 ,6, 8, and 9 in the UK Graves’ disease dataset). shaded bars, considering haplotype blocks; open bars, ignoring haplotype blocks; 1,000 simulations were conducted for each set of parameters. N, size of developing panel (in terms of number of chromosomes); and ϕ, haplotype diversity coverage. (A) results using E criterion; (B) results using H criterion.

Impact of genetic diversity on htSNP selection efficiency

Two populations, denoted as Pop I and Pop II respectively, were simulated using the HUDSON program. The only difference between Pop I and Pop II was that Pop II had a two times longer evolution history than Pop I. Therefore, Pop II would possess more historical recombinations and hence a higher genetic diversity than Pop I. A total of 500 pairs (i.e. for Pop I and Pop II respectively) of simulated datasets were generated, and in each pair of simulated datasets, 50 individuals from each population were sampled for SNP tagging. On average, Pop II required 1.51 times more computational steps than Pop I.

Impact of haplotype diversity coverage on statistical power and relative risk ratio estimation

The choice of ϕ had small-to-moderate impact on statistical power and relative risk ratio estimation (Figure 8). In comparison with the lossless htSNP set, the test using htSNPs derived at ϕ = 80 and 90% achieved an average power of 87.0 and 95.1%, respectively. Because we set the true relative risk ratio > 1 in the simulation, using htSNPs at ϕ <1 reduces relative risk ratio. On average, htSNPs at ϕ = 80 and 90% achieved an average relative risk ratio of 95.1 and 98.4%, respectively, comparing to the lossless htSNP set.

Figure 8.

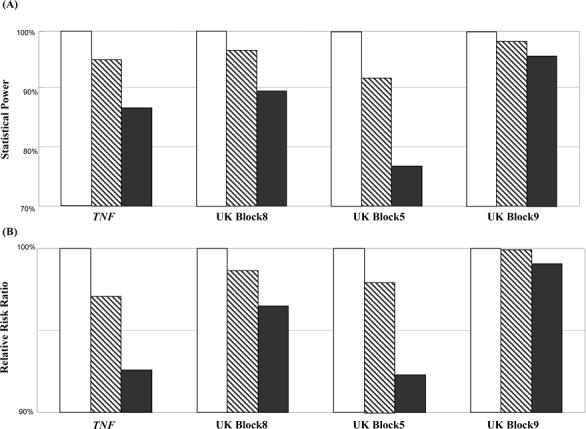
(A) Relative power and (B) relative risk ratio of haplotype-based association test at various levels of haplotype diversity coverage. We set the power and relative risk ratio using lossless (i.e., ϕ =100%) htSNP sets (open bars) as reference group. ϕ =80% (solid bars) and 90% (shaded bars) htSNPs introduced random misclassification into the tests and estimations, hence, reduced the power and attenuated the estimate of relative risk ratio.

Discussion

In this article, we propose a new sparse tree-based method, SMET, for finding the optimum htSNP set with ϕ exceeding a user-defined threshold ϕ_T. The idea of SMET is in essence similar to the sparse binary trees used represent patterns of gene flow in pedigrees used by Abecasis et al. [2002]. We applied SMET to empirical datasets at (1) gene-wide, (2) region-wide, and (3) chromosome-wide levels. Our results demonstrate that when ϕ is set to be 100%, the SMET algorithm selects the same htSNPs as the method named “BEST” [Sebastiani et al., 2003], which is a lossless-only method. For example, in the 8^th block of the UK Graves’ disease dataset, both SMET and BEST identified the same 25 out of the original 26 SNPs as the lossless htSNP set. However SMET is more flexible than BEST that allows users to impose coverage thresholds. As shown in Figure 4, a fraction of the total number of SNPs usually can capture over 90% of the haplotype information.

To identify the optimum htSNP set for a given ϕ_T, the full enumeration strategy is a straightforward approach, but is computationally very intensive (Discussed by Dr. David Clayton, please see Electronic Database Information Section [1]). The greedy methods [Carlson et al., 2004; Stram et al., 2003] dramatically lighten the computational burden by reducing the number of SNP sets to be considered, which can also accommodate various user-specified ϕ levels. Similar to SMET, these approaches organize the search space into tree structures, but only grow the branch with the largest ϕ at each level of the tree. Therefore, these greedy methods traverse a much smaller subspace than the entire space of the full tree. Although the greedy algorithms can run faster than SMET due to its heuristic nature (note than the SMET algorithm traverses a sparse version of the full tree), their drawbacks include (1) there is no mathematical guarantee that the greedy algorithm can identify the optimal htSNP sets; and (2) when there are multiple optimum htSNP sets, the greedy algorithm may not identify them all. Recently, principle component analysis (PCA) has been applied in assessing multivariate SNP correlations to identify htSNPs [Horne and Camp 2004; Lin and Altman 2004].

However, the PCA algorithm does not directly take haplotypes into account and cannot guarantee finding the optimal sets. In contrast, SMET traverses all non-singular tree nodes (i.e. SNP sets) with the potential to be optimal htSNP set(s), and mathematically guarantees the global optimum. Moreover, SMET can identify multiple optimal htSNP sets if they exist. Recently, Ding et al. [2005] developed a computer program named htSNPer1.0 with a graphical user interface for characterizing the haplotype block structure and for selecting htSNPs. Similar to SMET, htSNPer1.0 first estimates haplotypes within each haplotype block, and based on the estimated haplotypes, htSNPs are selected according to three htSNPs performance criteria (α-percent coverage [Patil et al., 2001], explained proportion of Clayton's haplotype diversity (please see Electronic Database Information Section [2]), and weighted-average haplotype r² [Weale et al., 2003]) and four haplotype block definitions [chromosome coverage [Weale et al., 2003], average pairwise LD |D’| [Reich et al., 2001], estimated pairwise LD confidence limits [Gabriel et al., 2002] with minor modifications by Wall and Prichard [2003], and no historical recombination [Wang et al., 2002]). The htSNPer1.0 software package takes advantages of a novel tree-based heuristic algorithm called the Generalized Branch-and-Bound (GBB) algorithm to search the minimal htSNPs set. However, the GBB algorithm of htSNPer 1.0 does not use the exactly same ϕ criterion for htSNP selection as we used in SMET.

The reduction of computational steps by SMET over the full enumeration strategy becomes more substantial as the search tree depth becomes greater. This is because there is an exponential growth of the number of nodes (and hence the search space) for the exhaustive enumeration method to traverse when tree depth increases linearly. Generally speaking, the tree depth correlates with the haplotype block size (measured by the number of SNPs within the block). Thus, the advantage of SMET algorithm over the full enumeration method was more evident for htSNP selection for large haplotype blocks such as the two largest blocks of the UK Graves’ disease dataset. In comparison with the full enumeration method (e.g. htSNP program, please see Electronic Database Information Section [3]), the factor of computational step reduction by SMET becomes as large as 18 for the largest block in the UK Graves’ disease dataset - Block 8 with 26 SNPs and an average D’ of 0.777.

In our study, D’, a measure of LD between pairs of sites [Lewontin 1964], was chosen for defining haplotype blocks because it is directly related to the goal of detecting historical recombination, which is pivotal to the block concept, and because it can be applied directly to unphased diploid data. Two widely-cited previously performed studies - Reich et al. [2001] and Gabriel et al. [2002], used similar D’-based block definitions as that of ours. In particular, our haplotype block definition is based on minor modifications of Gabriel et al. [2002], which appears to perform reasonably well by controlling the random noise inherent in D’. In contrast, the r² measure of LD is typically used for tagging SNP selection rather than for block partitioning [Ahmadi et al., 2005; Goldstein et al., 2003].

As shown in Figure 4, ϕ measured by H sometimes cannot clearly distinguish different htSNP sets because of its narrow range of values. Comparatively speaking, the Shannon entropy (E) is a more sensitive measure of haplotype diversity coverage than H. Besides H and E, another metric of haplotype diversity, $R_h^2$, was used in the tagSNP program [Stram et al., 2003]. Zhang et al. [2004] surveyed the choices of diversity measurements (e.g., E or $R_h^2$), and found they led remarkably consistent results. The tagSNP algorithm employs the “greedy stepwise inclusion method”, instead of an exhaustive search. Therefore, the tagSNP inherits the two drawbacks discussed in last paragraph. As acknowledged by Stram et al. [2003], this stepwise procedure does not fully explore the entire search space, and thus does not guarantee the finding of the globally “best pick” of htSNPs [Stram et al., 2003]. Figure 4 also shows that, when the htSNPs ratio (the size of the htSNP set/the size of the lossless htSNP set) increases, ϕ rises rapidly at the early stage, and then enters a plateau phase before reaching the maximum value. In the plateau phase, we gain little extra information and statistical power (Figure 8) by adding more tagging SNPs. Thus, appropriate haplotype diversity coverage is a key factor to be considered in designing cost-effective association studies.

Figure 6 presents the results of the assessment of the impact of the sample size for the developing panel, N_d, as an important parameter to be taken into consideration for htSNP selection. There are several reasons to choose an adequately large N_d. First, a small N_d leads to an instability in the performance of various haplotype phasing algorithms [Niu et al., 2002]. Second, when N_d is small, certain common haplotypes in the large-scale cohort may appear only once or may not even be sampled in the developing panel. Such “unlucky” haplotypes thus may be inadvertently removed before the htSNP selection step. Our simulation study suggested a N_d at least 50 (i.e. 100 chromosomes) in order to ensure a sufficient coverage of common haplotypes in the large-scale sample.

As shown in Figure 7, we found that selecting htSNPs based on a predefined, genuinely LD-based block structure could be more efficient than selecting htSNPs based on an arbitrarily-defined, pseudo-block structure. The gain in efficiency becomes more noticeable for high-LD blocks. The findings of this simulation are reasonable because the haplotype diversity for each pseudo-block is higher than that of its corresponding genuinely LD-based haplotype block, and the total number of htSNPs needed to tag each pseudo-block would be greater than the total number of htSNPs needed to tag each corresponding genuinely LD-based block. We regard the SMET algorithm to be more appropriately applied within LD-based blocks after the genomic segment of interest (regardless of gene-wide, region-wide, or chromosome-wide scales) was partitioned into LD-based blocks. The rationales are: (1) LD-based blocks typically represent haplotype blocks of common ancestry [Halldorsson et al., 2004], which are transmitted from generation to generation with little evidence of historical recombination. Thus, the LD-based “haplotype block model” has important implications for association mapping, because it implies that, by identifying htSNPs for each LD-based block, it is possible to predict the likely configurations of alleles at an unobserved SNP site within the same block. Indeed, this is one of the motivations of the International HapMap Project, which aims to produce a genomewide haplotype map that can be used for genomewide haplotype block detection and to streamline association mapping. (2) For an increasing number of linked SNPs, the accuracy of haplotype phasing results of various statistical algorithms of haplotype inference is decreasing [Niu et al., 2002], because the number of possible phases grows exponentially with an increasing number of SNPs [Niu, 2004]. This is especially the case when N_d (i.e. the size of the developing panel) is as small as 25 or 50, because the phasing accuracy also decreases pronouncedly with a decreasing sample size [Niu et al., 2002]. To overcome this obstacle, pairwise LD-based haplotype block partitioning was performed as a first step, and then SMET algorithm was applied just within each LD-based block such that the haplotype reconstruction is only necessary within each LD-based block of limited haplotype diversity, and the phasing results would be reasonably accurate for each individual block. However, if we consider each region or each entire chromosome as a single block (i.e. we totally disregard the underlying block structure) for selecting htSNPs using SMET, we have to directly reconstruct the haplotype phase for a large region or even a whole chromosome. The accuracy of haplotype reconstruction for such large blocks would then be computationally unstable which can lead to untenable results. Recently, Ahmadi et al. [2005] developed a “block-free” tagging SNP selection strategy based on a multiple-marker criterion – haplotype r², which selects tagging SNPs independently of any underlying haplotype block structure [Goldstein et al., 2003]. Their strategy required the minimum estimated r² between the tagged and tagging SNP set to be at least 0.85. Halldorsson et al. [2004] similarly developed a “block-free” tagging SNP selection strategy based on finding neighborhoods of a target SNP, which uses a metric that is in spirit similar to haplotype r². Although ignoring heuristically defined block boundaries, “long-range” LD can be captured by “block-free” tagging SNP selection strategies, such approaches also have a limitation: to achieve a high r² value, the frequencies of the SNPs must be matched that could be difficult to achieve in a “SNP-by-SNP” manner or even between the haplotypes defined by the tagging SNPs and the other SNPs, thus requiring an excessively large number of htSNPs [Goldstein et al., 2003].

We used the program HUDSON [Schierup and Hein, 2000a; Schierup and Hein, 2000b], which is based on the coalescent model, to simulate data to assess the impact of genetic diversity (haplotypic diversity) on htSNP selection efficiency. We found that the Pop II, the population with a longer evolution history and thus a greater genetic diversity, required 1.51 times more computational steps than Pop I. Thus, haplotypic diversity will determine the proportion of non-singular nodes in the dataset, i.e., a highly diverse population (e.g. the African sample) will have fewer redundant SNPs, and therefore the number of nodes traversed by the SMET algorithm will approach the number in the full enumeration approach.

What is the cost-effectiveness, in term of statistical power in association study, between htSNP sets of ϕ=80 or 90% and the lossless sets? We found that htSNP sets with a ϕ of 80% or 90% can achieve 87−95% of the statistical power attained by the lossless htSNP sets. More importantly, htSNP sets with ϕ = 80 or 90% incurred relatively insubstantial biases in relative risk ratio estimation (Figure 8). Because the size of the htSNP set is much smaller at ϕ = 80 or 90% than that of a lossless set (Figure 2), scientists can save considerable genotyping cost without much reduction of the statistical power or the relative risk ratio in detecting a haplotype-based association. It should be noted that the disease model and the association test we chose in our paper are both simple and straightforward, which solely serve the purpose of demonstrating the application of htSNPs selected based on the SMET algorithm. Thus, these were not necessarily the most realistic ones among all possible disease models and all possible types of association tests, and further extensive evaluations of the performances of the htSNPs under a spectrum of disease models using a variety of different association tests are clearly needed (such extensive evaluations would go beyond the scope of our paper).

Practically speaking, whether or not haplotype tests are more powerful than single-marker tests remains a highly debatable topic [Akey et al., 2002; Clark, 2004; Roeder et al., 2005; Schaid, 2004]. Using simulated case-control data sets, Nielsen et al. [2004] demonstrated that either approach has its merits: when moderate to high levels of multilocus LD exist, haplotype tests tend to be more powerful, which could be by a very large degree. Single-marker tests tend to prevail when pairwise LD is high (note that the power of the single-marker tests can be seen to rely on pairwise LD of the observed marker with the functional site). If single-marker tests are to be used, Nielsen et al. [2004] pointed out that a multiple-testing adjustment should be applied, which would reduce the power of single-marker tests. Based on standard chi-square statistics, the simulation studies of Akey et al. [2001] showed that the power of haplotype tests is influenced by critical population genetic parameters, such as genetic distances between the observed markers and the causative mutation, maker allele frequency, age of the causal mutation. Given a single founder mutation and the absence of phenocopy, haplotype tests are more powerful and more robust than single-marker tests in case-control studies. An example of the superiority of haplotype tests over single-marker tests is a study of the adenine phosphoribosyltransferase (APRT) deficiency [Kuno et al., 2004]. In single-SNP analyses, even at SNP loci close to the mutation site (APRT*J), no significant results were found; however, the use of haplotypes based on the haplotype block data gave sufficient significance, and thus, haplotype tests based on the haplotype-block structure is more powerful than single-marker analyses for the detection of disease-related loci. Because of the lack of consensus as to which (haplotype vs. single-marker) tests are more powerful in case-control studies, the trade-off between these two types of tests need to be weighed carefully on a case-by-case basis.

Taken together, we describe a novel algorithm, SMET, which elegantly achieves (1) flexibility in haplotype diversity coverage, (2) computational efficiency, and (3) mathematical optimum. We applied SMET on various simulated and empirical datasets, and validated this novel algorithm by an existing method – BEST [Sebastiani et al., 2003]. Furthermore, we investigated several important issues related to htSNP selection and association testing, including (1) the impact of N_d on htSNP selection, (2) the impact of a predefined, genuinely LD-based block structure vs. an arbitrarily-defined, pseudo-block structure on SNP tagging, (3) the impact of genetic diversity, and (4) the relationship of haplotype diversity coverage and statistical power. These results, as well as the SMET algorithm, will provide helpful guidance to scientists in choosing their htSNPs and in conducting haplotype-based genetic studies.