Abstract
We present a method for discovering patterns of activation observed through fMRI in experiments with multiple stimuli/tasks. We introduce an explicit parameterization for the profiles of activation and represent fMRI time courses as such profiles using linear regression estimates. Working in the space of activation profiles, we design a mixture model that finds the major activation patterns along with their localization maps and derive an algorithm for fitting the model to the fMRI data. The method enables functional group analysis independent of spatial correspondence among subjects. We validate this model in the context of category selectivity in the visual cortex, demonstrating good agreement with prior findings based on hypothesis-driven methods.
1 Introduction
In contrast to early fMRI studies that commonly used a simple task-versus-fixation setup to localize functional areas of interest, modern fMRI experiments aim to explore and understand brain activations induced by an increasing number of tasks or stimuli. In this paper, we introduce a representation for fMRI activations that naturally lends itself to exploratory analysis of the space of observed activation patterns. We demonstrate a method for such analysis in individual subjects and in a population, using visual fMRI experiments to validate our approach.
Our motivation comes from fMRI studies of category selectivity in visual cortex (high level vision) where subjects are presented with several categories of visual stimuli. Using hypothesis-driven localization methods [1], investigators discovered regions with specific category selectivity which consistently appear in most subjects. For instance, the well-known fusiform face area (FFA) is associated with higher response to faces when compared to other visual stimuli. In addition, the parahippocampal place area (PPA), and extrastriate body area (EBA) exhibit high selectivity for places, and body parts, respectively [2].
While hypothesis-driven methods provide a convenient tool for testing highly specific hypotheses about activations, they usually consider and compare only two experimental conditions (categories) at a time. Spatial consistency of the localization maps across subjects serves as evidence for the validity of the corresponding hypothesis. With the increasing number of conditions or tasks, it becomes more challenging with these methods to search the entire set of possible activations, for instance, all hypothetical areas activated by more than one condition. Moreover, this approach leaves out the question of what constitutes a good hypothesis. This is in stark contrast with the goals of a fMRI experiment aiming to model visual processing in the brain by finding structure in the space of activations due to visual stimuli.
An alternative approach is to employ exploratory, unsupervised learning methods, which can be broadly grouped into two classes. The first class of methods works on the raw time courses and uses clustering [3,4,5] or Independent Component Analysis [6,7] to estimate a decomposition of the data into a set of distinct time courses of interest and their localization maps. However, this framework offers no clear mechanism for characterizing the relationship between the multitude of experimental conditions and the noisy representative time courses identified in such analysis. The second group of exploratory methods uses the information from the experimental setup to define a measure of similarity between voxels, effectively projecting the original high-dimensional time courses onto a low dimensional feature space, followed by clustering in the new space [3,8,9].
Here, we present an exploratory method that aims to identify patterns of activation (e.g., patterns of category selectivity in high level vision) in complex experimental setups. We introduce an activation profile, a low-dimensional representation that directly reflects the effects of experimental conditions. Working in the space of activation profiles, we employ mixture modeling to find the strongest patterns of activation present in the data. Rather than relying on spatial consistency to establish the validity of the detected activation pattern, we employ functional consistency across subjects to evaluate the robustness, and therefore relevance, of the detected profiles. Thus, we obtain a fully functional characterization of the data.
We emphasize that our goal is to find patterns of activation in complex experimental setups, unlike previous feature-based clustering methods [8,9] that mainly focused on identifying the “active” voxels in simple experiments. In the case of high level vision, our results agree with the findings in the field that were established as a result of numerous hypothesis-driven fMRI studies.
2 Methods
We present our method in three steps. First, we introduce the space of activation profiles, our representation of fMRI data. Then, we describe our mixture model which finds the prototypical activation profiles and their corresponding localization maps. Finally, we discuss our approach to group analysis.
2.1 Space of Activation Profiles for Category Selectivity
We define an activation profile to be a vector whose components describe selectivity to different categories. Given a set of raw fMRI time courses, we apply a General Linear Model (GLM) analysis [1] at each voxel and form a vector containing the estimated regression coefficients of the experiment stimuli. The norm of these vectors is mainly a byproduct of irrelevant variables such as distance from major vessels or, the overall magnitude of response to the type of stimuli used in the experiment. Moreover, it is widely accepted that only relative values of responses are important in characterizing selectivity to different stimuli. To reflect these two properties in our representation, we choose to normalize the activation profiles to be unit length vectors. This removes the effect of the magnitude of activation while preserving the relative strength of activation across categories. With D categories of visual stimuli present in the experiment, our space of activation profiles is a unit sphere SD−1 in a D-dimensional space. A unit vector in this space represents a specific form of category selectivity. For instance, a profile completely parallel to a single dimension represents perfect selectivity to the corresponding category.
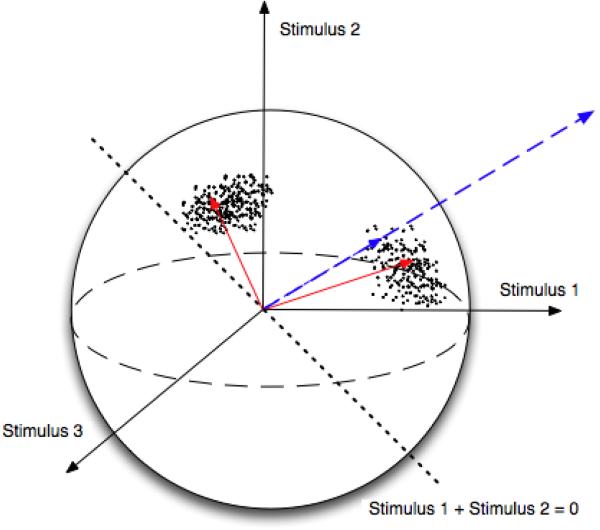
When represented in the space of activation profiles, an fMRI data set becomes a population of vectors on a unit sphere. Naturally, the interesting patterns of selectivity in this population correspond to the directions with highest concentration of data points around them (Fig. 1). It is easy to see that finding these patterns can be thought of as clustering the activation profiles and estimating the corresponding cluster means as described in the next section.
Fig 1.
An artificial population of voxels illustrating the space of activation profiles. The experiment presents three stimuli and evokes two distinct profiles. The blue, dashed line shows an original vector of regression coefficients. A hypothesis test comparing the first and second stimuli projects the vector of regression coefficients onto the dotted line; the significance is a function of the projection coefficient. The red vectors are the cluster mean profiles.
2.2 Estimating Patterns of Category Selectivity
Let be a set of activation profiles of V brain voxels on a SD−1 sphere. We devise a mixture model based on correlation as the natural measure of similarity for unit vectors. We assume the vectors are i.i.d. samples from a mixture distribution
| (1) |
where denotes the weights of K model components and f(y; m, μ) is a distribution defined on a unit sphere. We choose the simplest such distribution, von Mises-Fisher distribution [10]
| (2) |
where 〈·, ·〉 denotes the inner product of two vectors the normalizing constant CD(μ) is defined in terms of the γ-th order modified Bessel function of the first kind Iγ. This distribution is an exponential function of the correlation between voxel activation vector y and the cluster activation profile m. The concentration parameter μ controls the concentration of the distribution around the mean direction m. In general, mixture components can have distinct concentration parameters but in this work, we use the same parameter for all the clusters to ensure a more robust estimation.
We use the EM algorithm [12] to solve the corresponding maximum likelihood estimation. We define p(t)(k|yv) to be the posterior probability that voxel v is associated with the mixture component k at step t. Through a bit of algebra, we the update rules:
| (3) |
| (4) |
| (5) |
where , , and μ(t+1) are the parameter estimates at step t. We normalize vectors in each step to unit length. The nonlinear equation (5) for the estimation of μ(t+1) can be solved with a simple zero-finding algorithm. We note that this model was independently developed previously in the context of clustering text data [11].
Using the above algorithm, we find K representative activation profiles mk and a set of soft assignments p(k|yv). The assignments define localization maps of different activation profiles.
2.3 Group Analysis of the Activation Profiles
Since we aim to discover activation patterns that robustly appear in brain activations, it is reasonable then to assume that the space of activation profiles is shared across subjects.
We denote a voxel in an experiment with S subjects by , where s ∈ {1, … ,S} is the subject label and v is the voxel index as before. If the set of vectors mk truly descbribes all noteworthy activation profiles of the brain, each voxel could be thought of as an independent sample from the same distribution (1). Thus, we can combine the data from several subjects to form the group data, i.e., , to perform our analysis across subjects. Applying the same algorithm on the group data, the resulting defines the localization map of activation profile k in subject s. We note that no spatial registration of subjects is required for this step.
3 Experimental Results
We demonstrate our method on the data from a block design fMRI experiment on 9 subjects using five categories of images: bodies, faces, objects, scenes, and scrambled images. Each block lasts 16 seconds and contains 20 images from one category with an interval of fixation separating it from other blocks. Each run contains two blocks of each category; blocks of the same category do not share images. We perform motion-correction, spike detection, intensity normalization, and Gaussian smoothing with a kernel of 3-mm width using the standard package FreeSurfer. We apply General Linear Model [1] to estimate 5 regression coefficients for the stimulus categories and form a 5-dimensional vector for each voxel. To discard the voxels not activated by any of the visual categories, we run a t-test comparing the response of each voxel to fixation, keeping only the voxels which show significance with p ≤ 10−4. The resulting data is a set of 5-dimensional vectors corresponding to the voxels that demonstrate significant response to at least one category of presented images.
3.1 Activation Profiles
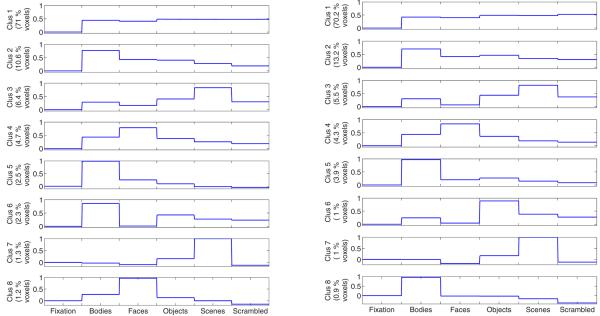
Since our main goal is to discover important patterns of activation, we first examine the resulting cluster profiles. Fig. 2 (Left) shows the selectivity profiles for the clusters found in the data from one of the subjects found for K = 8. The largest cluster corresponds to the visually responsive voxels that do not show differential response to the variety of categories presented in this experiment. Such a cluster appears in all our results from single-subject and group data sets. The smaller clusters exhibit the selectivity patterns expected based on the previous studies. According to the rough definition commonly used in the field, the response of a selective region to its category is at least two times stronger than that of any other category. We find such selective clusters for bodies (clusters 2, 5, and 6,) scenes (clusters 3 and 7,) and faces (clusters 4 and 8,) corresponding to the EBA, PPA, and FFA, respectively. These profiles only differ in their strengths of selectivity. The interesting aspect of this result is that we do not find clusters corresponding to the types of category selectivity not observed before. For instance, no scrambled-image-selective region or double-category selectivity is observed.
Fig 2.
Cluster profiles for (Left) a single subject and (Right) group data for 9 subjects. The clusters are ordered based on their estimated weight in the model.
Using the data from all 9 subjects, we run a group data analysis. Fig. 2 (Right) shows the resulting group profiles. The group profiles are very similar to the ones found in the single subject data, supporting our assumption that the space of activations is shared across subjects. However, we also expect to see some differences due to factors such as subject variablitity and noise. Group data yields more robust estimates of the cluster profiles by providing more samples per cluster.
3.2 Spatial Maps
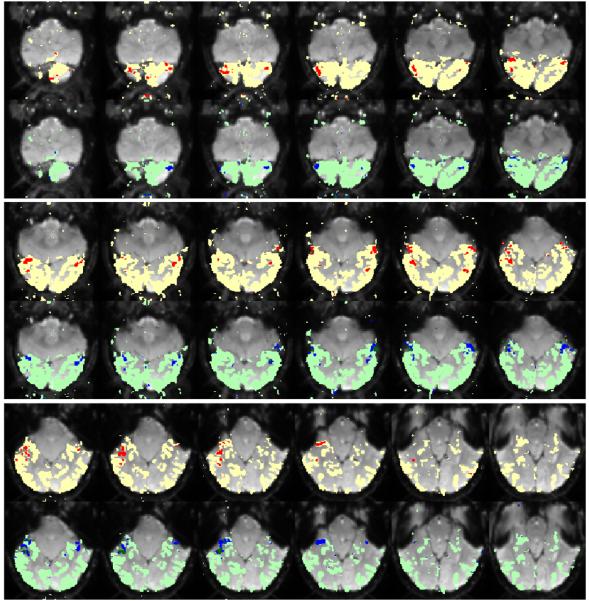
We examine the spatial maps our algorithm associates with cluster profiles by comparing them with the standard maps of FFA, PPA, and EBA. To find these standard maps, we apply t-tests comparing each voxel's response for faces, scenes, and bodies, to its response for objects, and threshold the resulting significance maps at p = 10−4. From our algorithm's results, we accept any profile whose component for one of the three categories of interest is at least 1.5 times all other components. The cluster assignments found in our method represent probabilities over cluster labels. Here, we assign each voxel to its corresponding MAP cluster label to find a binary map. Fig. 3 shows the standard map of face selective region (FFA) for the same subject in Fig. 2 (Left). It also shows the voxels assigned by our method to clusters 4 and 8 in Fig. 2 (Left). These clusters are face-selective according to the above definition. Although the two maps are derived with very different assumptions, they clearly agree.
Fig 3.
Spatial maps of the face selective regions found by the statistical test (red) and the mixture model (dark blue). The same slices from the two maps are presented in alternating rows. The mask of visually responsive voxels is shown in different colors (yellow for the hypothesis test, and light green for ours) in the backgound of the two maps to help the visual comparison.
We quantify the agreement between these binary, spatial maps by measuring their uncentered correlation. For example, the correlation between the two maps presented in Fig. 3 is 0.29. We also form the map associated with the largest cluster as another case for comparison and call it the non-selective profile. Table 1 shows the resulting correlation values averaged across all subjects for K = 7, 8, and 9.
Table 1.
Correlation between the spatial maps constructed with our method and those from the t-test. Values are averaged across all 9 subjects in the experiment.
| Group K = 7 | FFA | PPA | EBA | Group K = 8 | FFA | PPA | EBA |
|---|---|---|---|---|---|---|---|
| Face Profile | 0.37 ± 0.09 | 0.00 | 0.04 ± 0.03 | Face Profile | 0.37 ± 0.10 | 0.00 | 0.04 ± 0.03 |
| Scene Profile | 0 | 0.31 ± 0.14 | 0.00 ± 0.01 | Scene Profile | 0 | 0.31 ± 0.14 | 0.00 ± 0.01 |
| Body Profile | 0.04 ± 0.03 | 0.00 | 0.51 ± 0.07 | Body Profile | 0.05 ± 0.04 | 0.00 | 0.47 ± 0.08 |
| Non-sel. Profile | 0.05 ± 0.04 | 0.06 ± 0.04 | 0.04 ± 0.04 | Non-sel. Profile | 0.05 ± 0.04 | 0.06 ± 0.04 | 0.02 ± 0.03 |
| Group K = 9 | FFA | PPA | EBA | Indiv. K = 8 | FFA | PPA | EBA |
| Face Profile | 0.36 ± 0.10 | 0.00 | 0.04 ± 0.03 | Face Profile | 0.31 ± 0.13 | 0.00 | 0.02 ± 0.02 |
| Scene Profile | 0 | 0.31 ± 0.14 | 0.00 ± 0.01 | Scene Profile | 0 | 0.30 ± 0.13 | 0.00 |
| Body Profile | 0.03 ± 0.03 | 0.00 | 0.48 ± 0.08 | Body Profile | 0.03 ± 0.04 | 0.00 | 0.49 ± 0.09 |
| Non-sel. Profile | 0.05 ± 0.04 | 0.06 ± 0.04 | 0.02 ± 0.03 | Non-sel. Profile | 0.04 ± 0.04 | 0.06 ± 0.04 | 0.02 ± 0.01 |
We first note that the correlation between the functionally related regions is significantly higher than the other ones. Moreover, the spatial correlation is insensitive to the number of clusters. In genereal, we observed that increasing the number of clusers results only in the split of some clusters, and does not significantly alter the pattern of the discovered profiles. In the table, we also present the spatial correlations obtained from subject-specific activation profiles. The correlation values are quite similar to the group analysis, which suggests that by forming the group data, we have not lost the accuracy of our method in identifying the functional areas in individual subjects. Moreover, we have established correspondence among these functionally defined areas, as all of them are now associated with the same profile of activation in the group data.
We emphasize that from our perspective, the statistical significance maps are not the ground truth but rather a competing hypothesis for explaining the data. In fact, the neuroscientific definition of the selective regions only includes a subset of the standard map, identified by the experts based on prior knowledge of the approximate locations. Therefore, we do not seek a perfect agreement between the spatial maps.
4 Conclusion
We presented a mixture-model algorithm which finds the profiles of fMRI activation due to different experimental condition. It enables group analysis without spatial co-registration of subjects. Our algorithm promises benefits in discovering new category selective regions in high level vision and other problems with complex experimental setup. Representing the fMRI data in the space of activation profiles makes it possible to define the consistency of a discovered profile aross subjects as an alternative for the traditionally used registration-based spatial consistency. We are currently working on methods for investigating cross-subject consistency in this space.
Acknowledgements
This research was supported in part by NIH grants NIBIB NAMIC U54-EB005149, and NCRR NAC P41-RR13218, and by the NSF CAREER grant 0642971.
References
- 1.Friston KJ, et al. Statistical parametric maps in functional imaging: a general linear approach. Hum. Brain Mapp. 1995;2:189–210. [Google Scholar]
- 2.Kanwisher NG. The ventral visual object pathway in humans: evidence from fMRI. In: Chalupa L, Werner J, editors. The Visual Neurosciences. MIT Press; Cambridge: 2003. [Google Scholar]
- 3.Goutte C, et al. On clustering fMRI time series. NeuroImage. 1999;9:298–310. doi: 10.1006/nimg.1998.0391. [DOI] [PubMed] [Google Scholar]
- 4.Baumgartner R, et al. Fuzzy clustering of gradient-echo functional MRI in the human visual cortex. J. Magnetic Resonance Imaging. 1997;7(6):1094–1108. doi: 10.1002/jmri.1880070623. [DOI] [PubMed] [Google Scholar]
- 5.Golland P, et al. Detection of spatial activation patterns as unsupervised segmentation of fMRI data. In: Ayache N, Ourselin S, Maeder A, editors. MICCAI 2007, Part I. LNCS. Vol. 4791. Springer; Heidelberg: 2007. pp. 110–118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.McKeown JM, et al. Analysis of fMRI data by blind separation into independent spatial components. Hum. Brain Mapp. 2000;10:160–178. doi: 10.1002/(SICI)1097-0193(1998)6:3<160::AID-HBM5>3.0.CO;2-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Beckmann CF, Smith SM. Tensorial extensions of independent component analysis for group fMRI data analysis. NeuroImage. 2005;25(1):294–311. doi: 10.1016/j.neuroimage.2004.10.043. [DOI] [PubMed] [Google Scholar]
- 8.Goutte C, et al. Feature-space clustering for fMRI meta-analysis. Hum. Brain Mapp. 2001;13:165–183. doi: 10.1002/hbm.1031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Thirion B, Faugeras O. Feature detection in fMRI data: the information bottleneck approach. In: Ellis RE, Peters TM, editors. MICCAI 2003. LNCS. Vol. 2879. Springer; Heidelberg: 2003. pp. 83–91. [Google Scholar]
- 10.Mardia KV. Statistics of directional data. J. R. Statist. Soc. Series B. 1975;37:349–393. [Google Scholar]
- 11.Banerjee A, et al. Clustering on the unit hypersphere using von Mises-Fisher distribution. J. Mach. Learn. Res. 2005;6:1345–1382. [Google Scholar]
- 12.Dempster A, et al. Maximum likelihood from incomplete data via the EM algorithm. J. R. Statist. Soc. Series B. 1977;39:1–38. [Google Scholar]