A single charged voltage sensor is capable of gating the Shaker K⁺ channel

Abstract

We sought to determine the contribution of an individual voltage sensor to Shaker's function. Concatenated heterotetramers of Shaker zH4 Δ(6–46) wild type (wt) in combination with a neutral S4 segment Shaker mutant (mut) with stoichiometries 2wt/2mut and 1wt/3mut were studied and compared with the 4wt concatenated homotetramer. A single charged voltage sensor is sufficient to open Shaker conductance with reduced delay (<1 ms) and at more hyperpolarized voltages compared with 4wt. In addition, the wt-like slow inactivation of 1wt/3mut was almost completely eliminated by mutations T449V-I470C in its single wt subunit, indicating that the subunits bearing a neutral S4 were unable to trigger slow inactivation. Our results strongly suggest that a neutral S4 segment of Shaker's subunit is voltage insensitive and its voltage sensor is in the activated position (i.e., ready for pore opening), and provide experimental support to the proposed model of independent voltage sensors with a final, almost voltage-independent concerted step.

INTRODUCTION

The Shaker K⁺ channel (Papazian et al., 1987) is a homotetramer in which each monomer has two ion-selective pore-forming helices (S5 and S6 connected by a P-loop) and a voltage-sensing domain (S1 to S4) that contains the charged residues responsible for voltage-dependent channel opening. Charge neutralization and histidine scanning established that the first four arginine residues (R362, R365, R368, and R371) in the S4 and only one acidic group in the S2 (E293) segments of Shaker contribute to gating charge movement upon depolarization (Aggarwal and MacKinnon, 1996; Seoh et al., 1996; Starace et al., 1997; Starace and Bezanilla, 2001, 2004). Although there is clear indication of movement of the first four charges in the S4 segment (Starace et al., 1997; Starace and Bezanilla, 2001, 2004), there is no evidence for such movement for E293. This result indicates that the role of E293 might be in shaping the electric field sensed by the moving S4 charges, and consequently it should contribute no gating charge when the S4 charges are neutralized. The other charges in S2 through S4 (E283 in S2, D316 and D310 in S3, and K374 and R377 in S4) are involved in electrostatic interactions stabilizing the voltage-sensing domain tertiary structure (Papazian et al., 1991, 1995; Perozo et al., 1994; Tiwari-Woodruff et al., 1997). It has been found that simultaneous neutralization of only three arginines (R362, R365, and R371) in Shaker produces a voltage-insensitive channel with reduced open probability (Bao et al., 1999). Therefore, it is expected that the neutralization of the first four charges in the S4 segment makes a nonfunctional voltage sensor.

Although the tetrameric nature of Na⁺ and Ca²⁺ channels is encoded by four highly homologous DNA repeats, the four identical K⁺ channel subunits are assembled in the ER. Major progress in understanding the molecular mechanism of K⁺ channels has been made using homotetrameric channels, taking advantage of the fact that a site-directed mutation represents changing four residues at the protein level with radial symmetry. However, addressing some questions required the construction of heterotetrameric channels. Thus, coinjection of a mixture of cRNAs encoding for different members of the Shaker family suggested the existence of a tetramerization domain (McCormack et al., 1990), and tandems of K⁺ channel cDNA provided strong experimental evidence in favor of K⁺ channels' homo- or heterotetrameric stoichiometry (Isacoff et al., 1990; Hurst et al., 1992; Liman et al., 1992). The molecular identity of the TEA binding site (Kavanaugh et al., 1992; Pascual et al., 1995), intersubunit interactions (Tytgat and Hess, 1992; Krovetz et al., 1997; Yang et al., 1997; Holmgren et al., 1998), and the mechanism by which the mutation W434F renders Shaker “non-conducting” (Yang et al., 1997) have also been elucidated by the expression of heterotetramers encoded by concatenated cDNA.

Interestingly, the tetrameric nature of K⁺ channels was implicit in the first kinetic model of K⁺ channel function (Hodgkin and Huxley, 1952b) in which four n voltage-dependent particles needed to be in the proper position to allow ion permeation. Although this formalism is still useful to our comprehension of K⁺ channel function, it is now accepted that a more complex model is needed to explain detailed aspects of Shaker activation. Namely, the observed delay for opening of the channel when the holding potential (HP) is very negative is underestimated in Hodgkin and Huxley's formalism (Cole and Moore, 1960). Several kinetic models containing 12–20 free parameters explaining the activity of Shaker have been proposed (Bezanilla et al., 1994; Zagotta et al., 1994a; Schoppa and Sigworth, 1998b; Ledwell and Aldrich, 1999). In the consensus view of voltage-dependent channel activation, the four subunits contribute to activation and act concertedly in the last step of channel activation (Zagotta et al., 1994a; Schoppa and Sigworth, 1998b; Ledwell and Aldrich, 1999; Horn et al., 2000). However, the contribution of four subunits to channel activation makes it difficult to study the movement of a single voltage sensor and to establish a kinetic model coherent with the gating, ionic conduction, and single-channel analysis.

To determine the contribution of a single voltage sensor in Shaker's function, we studied heterotetrameric channels expressed from concatemerized cDNAs of “wild-type” (wt) Shaker non-inactivating (IR) (Hoshi et al., 1990) and of a quadruple mutant (mut) in which the first four arginine residues in the S4 segment have been neutralized. The heterotetramer containing a single charged voltage sensor activates faster and at more hyperpolarized voltages, presents a reduced delay for channel opening after a hyperpolarized pulse (Cole-Moore shift), and displays subconductance levels but slow inactivates with wt-like kinetics. Our results indicate that there is no cooperativity between voltage sensors upon activation and provide direct experimental evidence supporting the proposed model in which the movement of the voltage sensors is independent and followed by an essentially voltage-independent step.

MATERIALS AND METHODS

Molecular biology

Site-directed mutagenesis.

Site-directed mutations were introduced following the method of Fisher and Pei (1997) and confirmed by dideoxy DNA sequencing (University of Chicago Cancer Research Center, DNA sequencing facility). The charge-neutralizing mutations R362Q, R365Q, R368N, and R371Q were all simultaneously introduced in the template Shaker zH4 Δ6-46 or IR (Hoshi et al., 1990). For the sake of simplicity, Shaker zH4 IR and the quadruple mut will be referred to as wt and mut, respectively.

VENUS constructs.

The VENUS tag (Nagai et al., 2002), a green fluorescent protein isoform, was introduced on the N terminus of Shaker and mut. VENUS was subcloned on the N terminus of CiVSP-pBSTA from VENUS in vector pCS2 (provided by A. Miyawaki, Brain Science Institute, RIKEN, Saitama, Japan). To construct the clone N-terminal VENUS Shaker, CiVSP was removed by digestion with SpeI/XbaI. Shaker was amplified by PCR using primers that each contain a site for NheI, which is compatible with SpeI and XbaI, for an undirected cloning.

Concatenated cDNA construction.

The tetramer tandem cDNA constructs were designed to have a unique six-bases restriction site between each protomer. The C terminus of domain I was linked to the N terminus of domain II by a proline residue creating an AvrII restriction site (CCTAGG) (see Fig. S1). Domain II C terminus and domain III N terminus were linked with a histidine residue and are thus separated by an NdeI restriction site (CATATG) and domains III and IV with an aspartic acid, which gives an AatII restriction site (GACGTC). The first methionine residue of domains II and IV were mutated into arginine and valine, respectively.

First, dimers were constructed by digestion of the insert and vector cDNA, removal of 5′ phosphates on the vector DNA, followed by extraction and purification on agarose gel (gel extraction kit; QIAGEN), and ligation using Quick ligase (New England Biolabs, Inc.). 10 µl of the ligation reaction was used to transform competent cells, colonies were selected the next day and screened using restriction mapping, and the positive clones' cDNA was verified by sequencing of the full sequence. QIAGEN or Macherey-Nagel maxi-prep or midi-prep kits were used to extract DNA. Finally, the tetramer tandems were created using the same methodology, by linking in tandem dimers with different linkers.

Expression in Xenopus oocytes

cDNA was linearized using NotI (New England Biolabs, Inc.), and in vitro mRNA transcription was performed using mMESSAGE mMACHINE T7 kit (Applied Biosystems). 50 ng mRNA was injected in Xenopus oocytes, and measurements were done 1–3 d after injection. The oocytes were kept at 18°C in a solution containing (in mM): 100 NaCl, 2 KCl, 1 MgCl₂, 1.8 CaCl₂, 5 HEPES, and 0.1 EDTA supplemented with 50 mg/ml gentamicin or 100 U/ml penicillin and 0.1 mg/ml streptomycin.

Electrophysiology

Function of the expressed tetramers channels was evaluated with the cut-open voltage clamp and patch clamp techniques. All measurements were done at room temperature unless otherwise noted.

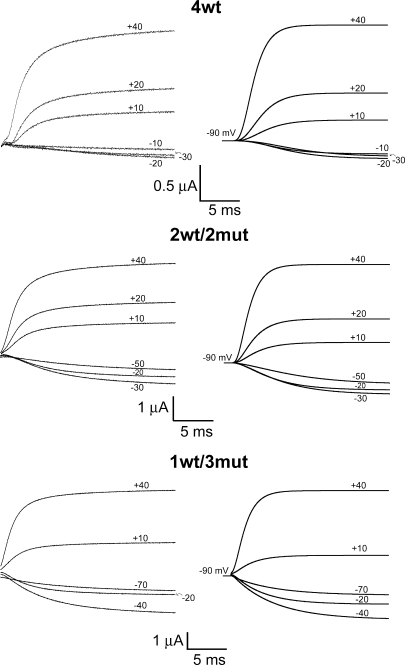
Cut-open recording was essentially done as described previously (Cha and Bezanilla, 1998). In brief, the agar bridges were filled with 1 M NMDG–methanesulfonic acid (MS). The current microelectrode was filled with CsCl 3M and had a resistance of ∼0.1–0.3 MΩ. Data were filtered at 10 kHz and sampled at 50 kHz. The linear leak and the remaining non-compensated capacitance were either subtracted online using the standard P/4 protocol with subtracting pulses from an HP of −120 mV for 4wt and 2wt/2mut, or −160 mV for 1wt/3mut, or analogically compensated for capacitance but non-subtracted, as noted in the figure legends. The HP was varied to account for the differences in voltage dependence of the channel constructs. Traces shown are non-subtracted unless otherwise noted.

The cell-attached configuration of the patch clamp technique was used to record macroscopic currents or single-channel activity using 2–5-MΩ pipettes with borosilicate glass (WPI, Inc.) in symmetrical 120 K⁺ using the Axopatch 200B amplifier (MDS Analytical Technologies). The resting potential of oocytes was in average −1.4 ± 1.7 mV (n = 25), as estimated with the instantaneous I-V. Data were filtered at 20 kHz and sampled at 100 kHz for macroscopic currents or filtered at 5 kHz and sampled at 50 kHz for single-channel measurements. The HP was −100 mV. Fluctuation analysis was performed from patches with macroscopic currents. From an HP of −100 mV, 25-ms duration depolarization pulses (from −20 to +70 mV) were applied ∼150–600 times, depending on the maximal current of the patch. Acquisition of currents at depolarizing voltage pulse was stopped every 50–150 pulses for acquisition of subtracting pulses according to the P/−4 subtraction protocol. Subtraction was done offline. Single-channel transitions were measured on patches containing one to five channels, and the HP was set to inactivate some channels to observe single-channel openings and closings. Blank traces (containing no activity) were averaged for offline subtraction of linear capacitance. All-points histograms were constructed and fitted with Gaussian distributions to determine the single-channel current.

Solutions

In the cut-open oocytes technique, the solutions were composed, respectively, of (in mM): internal solution: 120 K-MS, 20 HEPES, and 2 EGTA (120 K⁺); external solutions: 103 NMDG-MS, 12 K-MS, 20 HEPES, and 2 Ca-(MS)₂ (12 K⁺), or 120 K-MS, 20 HEPES, and 2 Ca-(MS)₂ (120 K⁺), or 70 NMDG-MS, 50 K-MS, 20 HEPES, and 2 Ca-(MS)₂ (50 K⁺) as noted.

In patch clamp experiments, the pipette (external) solution was (in mM): 120 K-MS, 20 HEPES, and 2 CaCl₂. The oocytes were bathed with 120 mM K-MS and 20 mM HEPES. The pH of each solution was 7.4.

Data analysis

The G-V curves were obtained from the amplitude of the tail currents at a constant return potential (see legends of Figs. 1 and 3) or calculated as G = I/(E−E_r). The G-V curve of 1wt/3mut was fitted with Origin version 7.5 or 8 (Microcal Software, Inc.) by a simple Boltzmann, whereas that of 2wt/2mut and 4wt were fitted with a Boltzmann to the “n^th” power (i.e., Q = [1/(1 + exp(V − V_1/2)zF/RT)]ⁿ) using the voltage dependence parameters (V_1/2, z) of the 1wt/3mut. The fits with Origin were done using the Levenberg-Marquardt algorithm and the instrumental weighting method.

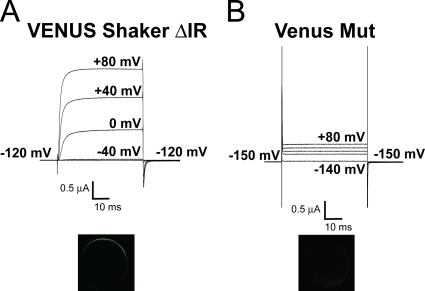
Figure 1.

The homotetrameric Shaker quadruple mut R362Q/R365Q/R368N/R371Q expresses poorly at the plasma membrane in Xenopus oocytes. (A) Ionic current (top) and confocal image (bottom) of a typical oocyte injected with VENUS-Shaker zH4 IR (monomers). (B) Ionic current (top) and confocal image (bottom) of a typical oocyte injected with the VENUS-Shaker quadruple mut R362Q/R365Q/R368N/R371Q (monomers). Cut-open voltage clamp measurements. The internal and external solutions contained 120 and 12 mM K⁺, respectively.

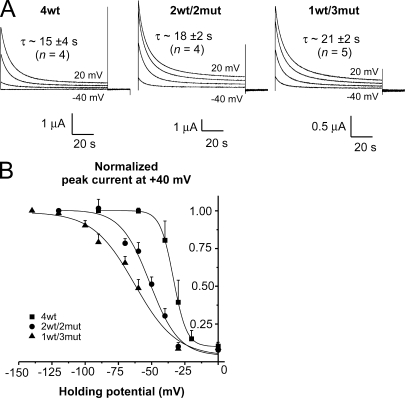
Figure 3.

Slow inactivation occurs with the same time constant but with shifted voltage dependence in the heterotetramers compared with the 4wt tetramer. (A) Time course of slow inactivation during a 100-s pulse. Current traces, at the indicated voltages, from representative oocytes expressing 4wt (left), 2wt/2mut (middle), and 1wt/3mut (right). The weighted time constants represent an average from four to five experiments. The internal and external solutions contained 120 and 12 mM K⁺, respectively. (B) Voltage dependence of slow inactivation. The normalized peak tail current at +40 mV is plotted as a function of the HP and fitted to a Boltzmann distribution: G_m = G_min + G_max/(1 + exp[−z(V_1/2 −V_m)F/RT]). 4wt data are shown as filled squares, 2wt/2mut data are shown as filled circles, and 1wt/3mut data are shown as filled triangles. Cut-open voltage clamp measurements. The internal and external solutions both contained 120 mM K⁺.

Time constants of slow inactivation, activation, and deactivation were obtained by fitting a single or double exponential with an in-house program using the Levenberg-Marquardt algorithm, which is a minimization of the χ² to the currents as noted in the legends of Figs. 4 and 5. When two time constants were necessary for the fit, weighted time constants were shown and calculated as τ = (A_fastτ_fast + A_slowτ_slow)/(A_fast + A_slow). Uncertainty on weighted τ was calculated using propagation of error.

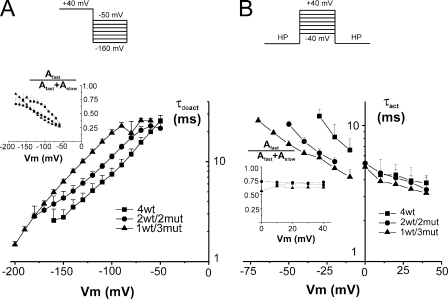
Figure 4.

Time constant of activation and deactivation. (A) Deactivation time constants of heterotetramers compared with the 4wt tetramer. The currents were fitted with two exponentials. The weighted time constant is shown, and the inset represents the contribution of the fast time constant. 4wt data are shown as filled squares (n = 5), 2wt/2mut data are shown as filled circles (n = 8), and 1wt/3mut data are shown as filled triangles (n = 4). (B) Activation time constants of the heterotetramers compared with 4wt. The currents could be fitted with a single exponential for V_m lower than 0 mV but required two exponentials in the positive region. The weighted time constant is shown, and the inset represents the contribution of the fast component in the positive region. 4wt data are shown as filled squares (n = 3), 2wt/2mut data are shown as filled circles (n = 4), and 1wt/3mut data are shown as filled triangles (n = 5). The HP was −90 mV for 4wt and −120 mV for 2wt/2mut and 1wt/3mut. Note the log scale vertically. The applied voltage routine is shown in the top panel. Points are connected with lines for clarity. Cut-open voltage clamp measurements. For activation time constants, the experiments were performed at room temperature and in symmetrical 120 mM K⁺ to have larger currents in the negative region of voltage. Deactivation time constants were measured at 6–8°C; the internal and external solutions contained 120 and 50 mM K⁺, respectively.

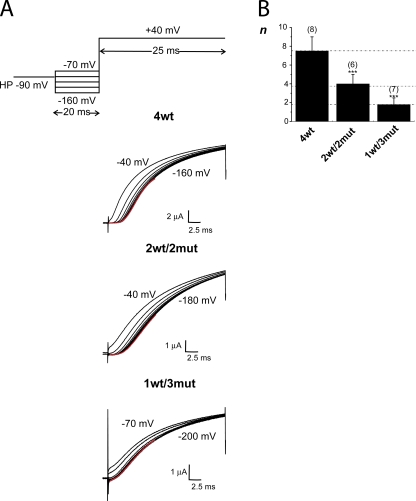
Figure 5.

The Cole-Moore shift is reduced in the heterotetramers compared with 4wt. (A) The family of K⁺ current traces from representative oocytes expressing 4wt (top), 2wt/2mut (middle), and 1wt/3mut (bottom). The pulse protocol is represented in the top panel. The currents are the ones measured a +40 mV in each case, preceded by various prepulses in 20-mV increments. For 4wt, the 20-ms prepulse ranges from −160 to −40 mV, and for 2wt/2mut, it ranges from −180 to −40 mV (20-ms duration). For 4wt and 2wt/2mut, HP was −90 mV, and subtracting HP was −120 mV. For 1wt/3mut, HP was either −120 or −100 mV, and subtracting HP was −160 mV. In that case, a 200-ms prepulse (from −200 to −70 mV) was applied. The red line represents the fit to the data for the first 10 ms of the lower trace with Eq. 1. (B) The averaged exponent n of the fit of the data indicated by the red line in part A to Eq. 1 for the heterotetramers compared with 4wt. The number of oocytes is shown in parentheses. The dotted lines are located at an abscissa value of 4wt (7.5 ± 1.5); half of this value and a quarter of this value. Cut-open voltage clamp measurements. Experiments were performed at 6–8°C. The internal and external solutions contained 120 and 12 mM K⁺, respectively. *, P ≤ 0.05; **, P ≤ 0.01; ***, P ≤ 0.001.

In the Cole-Moore shift experiments, the first 10 milliseconds of the current traces were fitted with Origin with the following relation:

(1)

in which I is the current, A is the amplitude, t is the time, τ is a time constant, and n is a number that is proportional to the number of closed states in a sequential model (Fitzhugh, 1965; Armstrong, 1969).

For fluctuation analysis, the variance was corrected for the background variance measured at zero current. The mean variance data were fitted with Origin with a parabolic equation as follows:

(2)

in which σ² is the variance, i is the single-channel current, I is the mean current, and N is the number of channels in the patch. Knowing the mean maximal current I_max, the maximal open probability (P_omax) could be estimated with the relation:

(3)

Kinetic model

The kinetic model was programmed using Simulation Control Program (SCoP; version 3.5; http://www.simresinc.com/scopinfo.html). For the fitting, SCoP searches for the lowest standard error value; it is a least square or χ² fit. The optimization algorithm is called PRAXIS for “principal axis method.” The global fitting routine was used to fit the data to the model. 20 sets of data were fit at once: 7 from 4wt, 7 from 2wt/2mut, and 6 from 1wt/3mut from selected voltage steps, allowing the description of the G-V curve of each concatemer.

Statistics

The experiments were performed on at least three oocytes obtained for a minimum of two different donors. Data are reported as mean ± SEM. The statistical difference was tested using an ANOVA test in Origin, which assumes a normal distribution of error. The statistical significance was set at P < 0.05.

Online supplemental material

Fig. S1 provides more details about concatemer construction. Fig. S2 shows the gating currents and the Q-V curves of the two concatemers, 4wt-W434F and 2wt/2mut-W434F. Fig. S3 illustrates the current traces and G-V for the dimers wt/mut or mut/wt with two different linkers, as well as comparison of 1wt/3mut and mut/wt/2mut. Figs. S4 and S6 provide the two components of the channel's voltage-dependent inactivation and voltage dependence of channel activation and deactivation, respectively. Fig. S5 shows the recovery from inactivation data. The current traces and G-V curves for the concatemers wtTVIC/3wt and wtTVIC/3mut are provided in Fig. S7. Figs. S1–S7 are available at http://www.jgp.org/cgi/content/full/jgp.200810082/DC1.

RESULTS

Homotetrameric Shaker R362Q/R365Q/R368N/R371Q is poorly expressed at the plasma membrane of Xenopus oocytes

mRNA of the Shaker quadruple mut with the four gating charges neutralized (R362Q/R365Q/R368N/R371Q or mut) was injected as monomers in Xenopus oocytes, but the amplitude of ionic currents measured was similar to the ones measured in uninjected oocytes in the same conditions. Two hypotheses sustained this finding from the homotetrameric mut: (1) a mistrafficking and (2) an impaired function of the channels. A VENUS tag (Nagai et al., 2002) was added on the N terminus of Shaker wt and mut, allowing for detection of membrane expression with the use of confocal imaging. Although VENUS-tagged wt Shaker expressed in oocytes displayed robust currents (Fig. 1 A, top), no ionic current could be detected in oocytes expressing the VENUS-tagged mut upon depolarization (Fig. 1 B, top). Confocal imaging of VENUS-tagged wt Shaker–expressing oocytes showed an intense signal at the plasma membrane (Fig. 1 A, bottom), whereas VENUS-tagged mut displayed an extremely low signal at the surface of the oocyte (Fig. 1 B, bottom), comparable to that observed in uninjected oocytes. These results support the hypothesis that the channels may be retained in the ER.

A first attempt to study heterotetramers formed from wt and mut subunits was made by coinjecting mRNA in Xenopus oocytes with a ratio of 1 wt:10 mut, statistically favoring a 1wt:3mut stoichiometry of the channels. Ionic currents of several µA in amplitude were measured in cut-open, and interestingly, the activation of the channel population occurred at more hyperpolarizing potentials compared with Shaker IR. However, using the coinjection method, the possible presence of several populations of heterotetramer channels with different stoichiometries prevents reaching definitive conclusions. To fix the channels' stoichiometry, we constructed cDNA concatemers with either two or three domains with a neutral S4 (stoichiometries of 2wt/2mut and 1wt/3mut). Functional activity of these heterotetramer constructs was assessed after the injection of mRNA in Xenopus oocytes and compared with a wt tetramer constructed similarly (see Materials and methods).

Shaker zH4 IR and 4wt are functionally undistinguishable

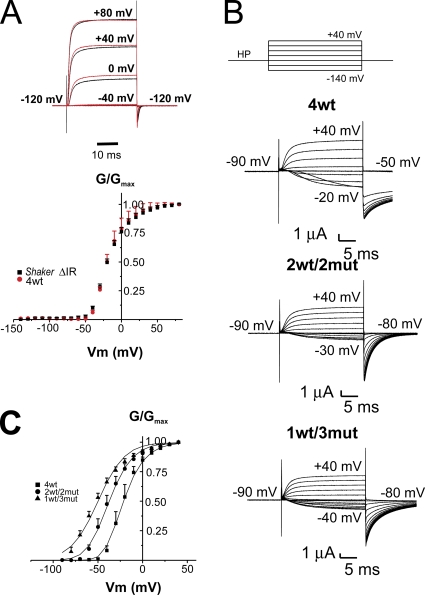
Tandem assembly of the four wt protomers had no major influence on Shaker activation. Fig. 2 A (top) shows a family of ionic currents from an oocyte expressing either Shaker zH4 IR (black line) or the tetramer 4wt (red line) from an HP of −90 mV with a 20-ms prepulse at −120 mV, followed by depolarization to +80, +40, 0, and −40 mV, as indicated, with 12 and 120 mM K⁺ in the external and internal solutions, respectively. The bottom panel of Fig. 2 A shows the normalized G-V curve for both Shaker zH4 IR (filled black squares) and the tetramer 4wt (filled red circles). The G-V relation of the tetramer construct 4wt is centered at −20 ± 1 mV (n = 4) compared with −17 ± 1 mV (n = 4) for Shaker zH4 IR injected as monomers. The kinetics of activation and deactivation were also similar. The homotetramer 4wt-W434F (non-conducting) is also undistinguishable from Shaker W434F zH4 IR injected as monomers (see Fig. S2).

Figure 2.

Ionic currents and G-V curve of Shaker tetramers wt (4wt), with two (2wt/2mut) or three subunits (1wt/3mut) with neutralized S4 gating charges. (A; Top) Scaled ionic currents from oocytes expressing Shaker zH4 IR (black line) or our tetramer 4wt (red line) for selected membrane potentials, as indicated. The maximal current recorded at +80 mV was around 5 µA for each oocyte. (Bottom) Averaged normalized conductance (G)-membrane potential (V) relation taken from the tail currents, Shaker zH4 IR (n = 4; filled black squares) and tetramer 4wt (n = 4; filled red circles). Holding membrane potential was −90 mV, and each depolarization was preceded by a 20-ms prepulse to −120 mV. The internal and external solutions contained 120 and 12 mM K⁺, respectively. (B) Ionic currents from oocytes expressing 4wt, 2wt/2mut, or 1wt/3mut heterotetramers. The voltage pulse protocol is shown on top. The HP was −90 mV. Pulse from −140 to +40 mV in 10-mV increments was applied, and the tail currents were measured at −50 mV for 4wt and at −80 mV for 2wt/2mut and 1wt/3mut. (C) Normalized G-V curve for 4wt (filled squares), 2wt/2mut (filled circles), and 1wt/3mut (filled triangles). The lines represent the global fit of a simple Boltzmann distribution for 1wt/3mut and Boltzmann distribution taken to the “n^th” power for 2wt/2mut and 4wt, all sharing the parameters V_1/2 and z. The HP was −90 mV for 4wt and −120 mV for 2wt/2mut and 1wt/3mut, and depolarization from −70 to +40 mV was applied for 4wt and from −120 to +40 mV for 2wt/2mut and 1wt/3mut. The conductance was measured using the tail currents. The internal and external solutions both contained 120 mM K⁺. Cut-open voltage clamp measurements.

Shaker heterotetramers with three neutralized voltage sensors still gate

Typical recordings of ionic currents in symmetrical 120 mM K⁺ measured in cut-open oocytes expressing the heterotetramers with neutralized voltage sensors are illustrated in Fig. 2 B. Compared with 4wt, 2wt/2mut and 1wt/3mut opened at more hyperpolarized voltages, consistent with the results obtained with the mRNA coinjection experiments. Fig. 2 C shows the normalized conductance (G/G_max)-V curve for the 4wt, 2wt/2mut, and 1wt/3mut. It is clear that although 4wt is almost completely closed at −50 mV, a quarter of the 2wt/2mut and half of the 1wt/3mut is opened. This is reflected by the left-shift of the G/G_max-V curve, from a V_1/2 of approximately −22 mV (n = 4) for 4wt, −39 mV (n = 4) for 2wt/2mut, and −52 mV (n = 6) for 1wt/3mut. As expected, in heterotetramers with neutralized gating charges in a given number of domains, the slope of the curve reflecting the apparent valence of the transferred charge is also reduced in the 1wt/3mut (1.7 ± 0.1) and in the 2wt/2mut (2.0 ± 0.1) compared with 4wt (2.5 ± 0.2). A global fit of the three G-V curves was performed using a simple Boltzmann distribution for 1wt/3mut (exponent set to a fixed value of 1) and Boltzmann distribution taken to the “n^th” power (i.e., Q = [1/(1 + exp(V − V_1/2)zF/RT)]ⁿ) for 2wt/2mut and 4wt, each sharing V_1/2 and z, as represented by the curves in Fig. 2 C. The exponents for 2wt/2mut and 4wt were 1.93 and 4.97, respectively, which are not too far from the expected values.

The position of the wt subunit in the heterotetrameric tandems seems to have no major influence on channel function, as two tetramers of stoichiometry 1 wt:3 mut (wt/mut/mut/mut and mut/wt/mut/mut) were statistically not different (G/G_max Boltzmann parameter V_1/2 was compared using an ANOVA test; n = 7 for both 1wt/3mut and mut/wt/mut/mut injected in the same batches of oocytes; P = 0.33) when injected in the same batches of oocytes (see Fig. S3). Similarly, the channels' function of the four dimers wt/mut (which should assemble with a 2wt:2mut stoichiometry) and the tetramer wt/wt/mut/mut were statistically not different (n = 3 for wt/mut, n = 3 for mut/wt [dimers with linker AatII], and n = 4 for wt/mut and n = 3 mut/wt [dimers with linker AvrII] compared with 2wt/2mut, n = 7, injected in the same batches of oocytes; P = 0.87). These findings suggest that the position of the subunits wt and mut has little effect on the functional properties of the heterotetramers. Larger samples and alternative permutations (such as wt/mut/mut/mut vs. mut/mut/mut/wt) would be required to be certain that there are no differences owing to concatemer ordering. Differences due to such ordering have been previously reported for Shaker concatemers with somewhat different design (McCormack et al., 1990). We note here that, although the tandem tetramers studied in this work show the expected behavior of a corrected assembled and translated functional channel, it does not constitute proof that indeed they are assembled as expected.

Slow (C/P type) inactivation

As the heterotetramers were constructed with the Shaker zH4 IR (Δ6−46) that does not exhibit fast (N-type) inactivation, there is no evidence of channel inactivation during a short 50-ms depolarization in either of the heterotetramers (see Fig. 2 B). However, Shaker zH4 IR slowly inactivates when a long-duration depolarization is applied. Slow inactivation is also referred to as C- and P-type inactivation (Hoshi et al., 1990; Olcese et al., 1997; Loots and Isacoff, 1998). Slow inactivation was also observed in the heterotetramers 2wt/2mut and 1wt/3mut, similarly to that observed in 4wt, as illustrated in Fig. 3 A. When a 100-s pulse is applied, with 12 and 120 mM K⁺ in the external and internal solutions, respectively, the currents of 4wt decayed with two exponentials of equal amplitudes as previously reported for Shaker IR expressed as monomers (Olcese et al., 1997; Larsson and Elinder, 2000). The weighted time constant (see Materials and methods; Fig. S4) was not statistically different between 4wt, 2wt/2mut, and 1wt/3mut (τ ∼15–21 s at +20 mV; see Fig. S5 and the associated Results and Discussion sections for recovery from inactivation).

Assuming that the time constant of slow inactivation was the same for 4wt and the heterotetramers, steady-state voltage-dependent slow inactivation was studied as reported previously (Olcese et al., 1997). The conductance was measured after at least 2 min at different HPs, and the peak tail currents at +40 mV were plotted as a function of the HP to obtain the steady-state inactivation voltage dependence. The voltage dependence of steady-state inactivation for the heterotetramers 2wt/2mut and 1wt/3mut was left-shifted compared with the 4wt (see Fig. 3 B). The V_1/2 of a simple Boltzmann equation fitted to the points is −34.0 ± 0.5 mV (n = 4) for 4wt, −53 ±2 mV (n = 4) for 2wt/2mut, and −65 ±3 mV (n = 5) for 1wt/3mut. Moreover, the apparent valence is also reduced in the 2wt/2mut (2.4 ± 0.4) and 1wt/3mut (1.9 ± 0.4) compared with that of 4wt (5.3 ± 0.1).

Gating kinetics

The voltage dependence of channel activation and deactivation is shown in Fig. 4. To increase the resolution in the negative region of membrane potentials, channel activation was measured in symmetrical 120 mM K⁺ at room temperature, whereas channel deactivation was measured in 50 mM of external K⁺ at 6–8°C to have a better time resolution of tail current kinetics. Activation and deactivation kinetics are thus shown on separate graphs. As described before for channel deactivation, a single exponential was insufficient to fit current decay (Bezanilla et al., 1994). Thus, Fig. 4 A shows the weighted time constant of heterotetramer deactivation compared with that of 4wt. Deactivation was slightly slower for 1wt/3mut compared with 4wt at any given repolarization V_m. At −120 mV for instance, 4wt and 1wt/3mut decayed with a τ of ∼5.5 and ∼10.5 ms, respectively. 1wt/3mut deactivated in ∼5.5 ms at −160 mV, suggesting a shift in the time constant versus voltage curve of ∼−40 mV. To estimate the kinetics of activation, we fitted the currents to two exponentials excluding the current that was below 20% of the maximum to skip the activation delay (see below). Only for voltages lower than 0 mV, current activation followed a single exponential. The weighted τ (see also Fig. S6) is shown as well as the contribution of the fast component in the inset (Fig. 4 B). 4wt and the heterotetramers activated at similar rates in the range of voltages at which the G/G_max curve has saturated (above 0 mV). However, below 0 mV, 4wt activated slower than 1wt/3mut and 2wt/2mut. At −30 mV, 4wt and 1wt/3mut activated with a τ of ∼10 and ∼5 ms, and 1wt/3mut activated with a τ of ∼10 ms at a V_m of −70 mV. The first milliseconds after channel activation were analyzed in more detail at a lower temperature, as described below.

Reduced delay for activation in the 1wt/3mut

Voltage-dependent K⁺ channels exhibit a delay for activation (Hodgkin and Huxley, 1952a), which increases when hyperpolarizing prepulses are applied (Cole and Moore, 1960). In addition to the delay for activation, known as the Cole-Moore shift, Shaker also displays a change in sigmoidicity of the current with the prepulse voltage (Bezanilla and Stefani, 1994; Stefani et al., 1994; Zagotta et al., 1994b). The kinetics of current activation was thus analyzed with an exponential function to the “n^th” power (Eq. 1); this “n^th” power is roughly proportional to the number of closed states in a sequential model equivalent to that proposed by Hodgkin and Huxley (Fitzhugh, 1965; Armstrong, 1969).

The voltage pulse protocol applied for 4wt is shown in Fig. 5 A (top); the heterotetramers were submitted to a similar protocol, except for the range of prepulses tested and for the HPs (see the figure legend). Fig. 5 A shows typical current recordings from oocytes expressing 4wt (top), 2wt/2mut (middle), and 1wt/3mut (bottom). The delay for activation was measured by extrapolating a double exponential curve to zero current. For 4wt, the observed delay for opening was ∼2.5 ms with a prepulse at −160 mV and ∼1.5 ms with a prepulse to −60 mV. This is consistent with the previous ∼2–3-ms delay for activation measured by Zagotta et al. (1994b) and Rodriguez et al. (1998) in various conditions. At the prepulse of −40 mV, some channels were already opened and no delay is observed. In the heterotetramers, the longest delay for channel activation measured was ∼1.75 ms with 2wt/2mut and <1 ms with 1wt/3mut. For the 2wt/2mut, the length of the delay for activation was reduced until a prepulse at −60 mV (Fig. 5 A, middle). Remarkably, with the 1wt/3mut, this shift with the prepulse value almost completely disappeared. Actually, the current traces measured with prepulses from −200 to −120 mV superimposed (Fig. 5 A, bottom). As some channels were opened at −90 and −110 mV, the current traces were slightly shifted compared with the prepulse at −130 mV. The exponential function (Eq. 1) was fitted to the currents preceded by a prepulse to −160, −180, and −200 mV for 4wt, 2wt/2mut, and 1wt/3mut, respectively. (The current traces from each oocyte were fitted independently, and the average value of the exponent of the function was averaged and is shown in Fig. 5 B.) Dotted lines were drawn to illustrate the proportion of the n value for 4wt versus the one of 2wt/2mut and 1wt/3mut. The values of n for 2wt/2mut and 1wt/3mut are 50 and 25% of the value for 4wt, respectively. This strongly suggests that the 1wt/3mut has a reduced number of closed states that approaches the theoretical expected value of one quarter of the number of states for wt Shaker.

Fluctuation analysis reveals a lower open probability for 1wt/3mut

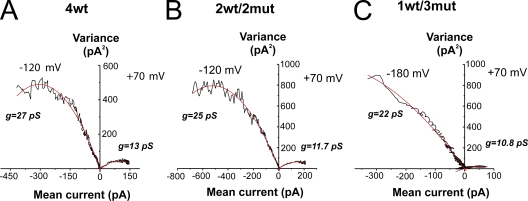
To get estimates of the single-channel conductance and open probability, non-stationary noise analysis (Sigworth, 1980) of an ensemble of current traces recorded in cell-attached patches of oocytes expressing 4wt, 2wt/2mut, or 1wt/3mut was performed. Graphs of variance–mean are shown in Fig. 6. A series of 300 (4wt), 450 (2wt/2mut), and 600 (1wt/3mut) pulses of 20-ms depolarization to +70 mV, followed by repolarization to −120 mV (−180 mV for 1wt/3mut), was applied to compute the single-channel current and the number of channels in the patch as described in Materials and methods. The single-channel conductance (g) computed as i/(V−V_rev) was found to be very similar for 4wt, 2wt/2mut, and 1wt/3mut at +70 mV, giving values of 13 and 10.8 pS for 4wt and 1wt/3mut, respectively. In addition, the conductance at −120 mV was 27 and 25 pS for 4wt and 2wt/2mut, and the conductance at −180 mV was 22 pS for 1wt/3mut. The maximal open probability was around 0.73 for 4wt, 0.67 for 2wt/2mut, and slightly lower than 0.50 for the 1wt/3mut. Overall, the single-channel conductance seemed to be similar for the heterotetramers 2wt/2mut and 4wt, but the lower open probability and slightly lower single-channel conductance measured with 1wt/3mut required further analysis because this behavior can be associated with the occurrence of subconductance levels. We then measured single-channel activity of the heterotetramer 1wt/3mut.

Figure 6.

Variance–mean plot for the heterotetramers compared with the 4wt. (A) Fluctuation analysis from an ensemble of current traces (n = 300 pulses) for a 20-ms depolarization to +70 mV, followed by repolarization to −120 mV in a cell-attached patch of an oocyte expressing 4wt. The data were fitted with Eq. 2, and the single-channel current i and the number of channels N in the patches were estimated. The corresponding conductance was estimated to be of 13 and 27 pS at +70 and −120 mV, respectively. The number of channels in the patch was 213. Eq. 3 allows for the calculation of the P_omax (maximal open probability), which was calculated to be 0.73 (n = 8). (B) Fluctuation analysis from a cell-attached patch of an oocyte expressing 2wt/2mut. 450 current traces of 20-ms depolarizations to +70 mV and repolarizations to −120 mV were used for noise analysis. The number of channels in the patch was estimated at 374, the single-channel conductance to 11.7 and 25 pS at +70 and −120 mV, respectively, and the P_omax to 0.67 (n = 7). (C) Fluctuation analysis from an oocyte expressing 1wt/3mut in a cell-attached configuration. 600 current traces of a 20-ms depolarization to +70 mV and repolarization to −180 mV were averaged and analyzed. The single-channel conductance was estimated at 10.8 and 22 pS at +70 and −180 mV, respectively. The number of channels in the patch could not be estimated accurately because of the open probability of 0.47 (n = 3). The black lines are the data, and the red lines are the fitted curve. Patch clamp experiments. The external and internal solutions both contained 120 mM K⁺.

Occurrence of intermediate current levels with 1wt/3mut in single-channel recordings

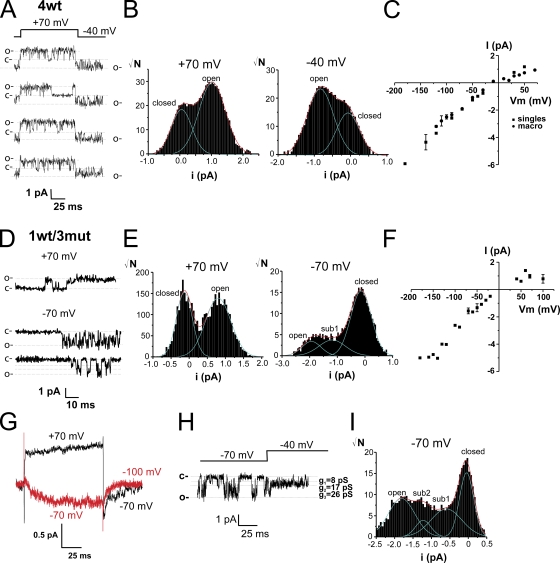
Single-channel transitions were recorded in the cell-attached configuration in symmetrical 120 mM K⁺. Fig. 7 A shows four single-channels traces for 4wt for a pulse from an HP of −40 to +70 mV. The single-channel current amplitude was determined with the all-points histograms for the group of traces in Fig. 7 A (Chapman and VanDongen, 2005) shown in B at +70 mV (left) and −40 mV (right). The single-channel current was 0.97 and 0.76 pA at +70 and −40 mV, respectively. The single-channel current amplitudes of all single-channel patches were plotted against voltage (Fig. 7 C) together with the estimates of single-channel current amplitudes obtained from the noise analysis of macro patches. The single-channel conductance was ∼22 ± 1 pS for the conductive range of voltage and 30 ± 5 pS at more hyperpolarized voltages. This confirms the results from previous studies on Shaker (Solc et al., 1987; Heginbotham and MacKinnon, 1993; Shao and Papazian, 1993; Hoshi et al., 1994; Li and Correa, 2001). The heterotetramer 1wt/3mut exhibits wt-like single-channel behavior at depolarizing voltages, as shown for +70 mV in Fig. 7 D, and has single-channel current identical to the one of the wt channel (0.97 pA), as calculated from the all-points histogram (Fig. 7 E, left). Interestingly, this heterotetramer clearly shows intermediate current levels at voltages at which the wt Shaker is normally found in the closed state (−70 mV; Fig. 7, D and H, taken from different patches). Intermediate current levels were also observed at −90 mV and below (not depicted). The single-channel current amplitudes of all single-channel and macro patches were plotted against voltage (Fig. 7 F), and the conductance was identical to that of 4wt (∼25 pS). They were observed in all patches from oocytes expressing 1wt/3mut (n = 6), with more prolonged and shorter durations on ∼10% of the number traces with activity. Assuming that these intermediate current levels indeed represent subconductances, they would be 8 and 17 pS. As predicted by fluctuation analysis, if the fully open channel has a conductance of 25 pS at hyperpolarized voltages (−180 mV), these subconductance levels would correspond to ∼32 and ∼68% of the fully open-channel conductance. The ensemble average of the single-channel traces (Fig. 7 G) reproduces the gating kinetics found in cut-open voltage clamp. Although the existence of subconductances states in 1wt/3mut patches seems certain, additional experiments will be required to further assess their biophysical properties (open probability of each conductance states, voltage dependence, and dwell time).

Figure 7.

Single-channel activity of 1wt/3mut reveals subconductance levels in a range of voltage at which the wt Shaker subunit is closed. (A) Single-channel recordings measured in an oocyte expressing 4wt from an HP of −40 to +70 mV. (B) All-points histograms from the selected traces shown in A at +70 mV (left) and −40 mV (right). (C) Single-channel current amplitude versus voltage relationship of single channels and macro patches of 4wt (n = 6–15; n = 7 of single-channel recordings). (D) Single-channel recordings taken from an oocyte expressing 1wt/3mut at +70 and −70 mV. (E) All-points histograms from selected traces as shown in D at +70 mV (middle) and −70 mV (right). (F) Single-channel current amplitude versus voltage relationship of single channels and macro patches of 1wt/3mut (n = 6–9; n = 6 from single-channel recordings). (G) Ensemble average of the single-channel recordings from the patch shown in D for depolarizations from an HP of −70 to +70 mV (black line) and from an HP −100 to −70 mV (red line). (H) Single-channel recordings taken from another patch of an oocyte expressing 1wt/3mut from an HP of −40 to −70 mV. (I) All-points histogram of the recording shown in H. The dotted lines indicate the level of current in the closed or open channel. Patch clamp experiments. The external and the internal solutions both contained 120 mM K⁺.

Effect of double mutations T449V-I470C on slow inactivation

The large left-shift in the voltage dependence of activation, the time course of activation, and the reduced delay for activation in addition to the occurrence of subconductance levels in 1wt/3mut heterotetramer suggest that the subunits with a neutral S4 are in the activated state. As inactivation proceeds preferentially from this activated state (Olcese et al., 2001), and if independence of the subunits in the inactivation process is assumed, contrary to our observation (see Fig. 3), a faster inactivation would be expected for 1wt/3mut compared with 4wt because three subunits would be one step closer to the inactivated state. The results reported above agree with a cooperative step of the four subunits for channel inactivation (Ogielska et al., 1995; Panyi et al., 1995; Larsson and Elinder, 2000; for review on Kv inactivation see Kurata and Fedida, 2006).

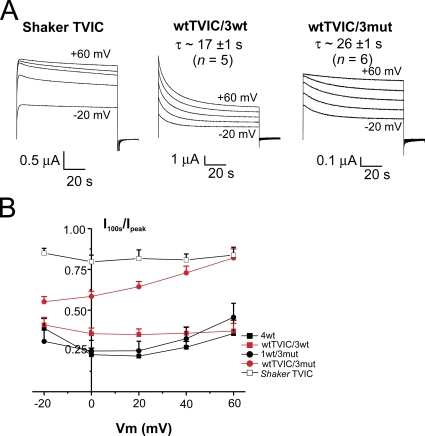
To further address cooperativity and voltage sensor contribution in the inactivation process, we constructed heterotetramers in which the inactivation is impaired by the simultaneous mutations T449V and I470C (TVIC) (Lopez-Barneo et al., 1993; Holmgren et al., 1997; Olcese et al., 2001) introduced in only one wt monomer. The function of these constructs was also assayed in cut-open oocytes. Fig. 8 A displays traces elicited by 100-s duration pulses to voltages ranging from −20 to +60 mV in oocytes expressing Shaker IR injected as monomer (left) and heterotetrameric channels with the TVIC mutations introduced in the first domain, the wtTVIC/3wt (middle), and the wtTVIC/3mut (right; see also Fig. S7). The time course of wtTVIC/3wt inactivation was indistinguishable from that of 4wt (see also Fig. 3 A, left). The time constant for inactivation at +20 mV of the wtTVIC/3wt (17 ± 1 s; n = 5) was not significantly different than the 4wt (15 ± 4 s), whereas the 26 ± 2-s (n = 6) time constant observed in the wtTVIC/3mut was significantly different than that of the wt/3mut 21 ± 1 s (P = 0.01). At −20 mV, wtTVIC/3wt inactivates with a τ of 15 ± 2 s, whereas wtTVIC/3mut inactivates in 22 ± 3 s (P < 0.05). The fraction of non-inactivated channels after a 100-s depolarizing pulse (I_100s/I_peak) is shown in Fig. 8 B. It is clear that ∼22–25% of the channels 4wt and 1wt/3mut remain non-inactivated even after a 100-s depolarization, whereas this proportion is slightly higher for wtTVIC/3wt (∼35%). In contrast, ∼80% of the wtTVIC/3mut channels do not inactivate at +60 mV (P = 0.005 against 1wt/3mut), similarly to that observed in the Shaker IR TVIC injected as monomers.

Figure 8.

The double mutation T449V-I470C in one wt subunit impairs slow inactivation in 1wt/3mut, but not in 4wt. (A) Time course of slow inactivation. Representative current traces from oocytes expressing Shaker IR TVIC injected as monomers (left), wtTVIC/3wt (middle), and wtTVIC/3mut (right) from an HP of −90 mV to voltages from −20 to +60 mV in 20-mV intervals for 100 s. Cut-open voltage clamp measurements. The internal and external solutions contained 120 and 12 mM K⁺, respectively. (B) Ratio of the remaining current after a 100-s depolarizing pulse over the peak current (I_100s/I_peak) for Shaker TVIC injected as monomers (open black squares), 4wt (filled black squares), wtTVIC/3wt (filled red squares), 1wt/3mut (filled black circles), and wtTVIC/3mut (filled red circles).

DISCUSSION

A heterotetrameric Shaker K⁺ channel containing one wt voltage sensor and three neutral S4 segments (mut) is capable of permeating K⁺ ions and gating in a voltage-sensitive manner, but with largely modified voltage dependence. This single-charged voltage sensor Shaker channel activates with almost no delay and at more negative voltage, but slow inactivates as the wt Shaker. Its number of closed states is also approximated to be a quarter of the number of closed states of wt Shaker. Our results strongly suggest that neutralization of the four gating charges in the S4 of Shaker K⁺ channel renders such an S4 segment voltage insensitive and in the active position (the S4 having moved out and the pore being ready to open).

It is reasonable to ask whether neutralization of the four gating charges (R362Q/R365Q/R368N/R371Q) completely abolishes the sensor's voltage sensitivity. Unfortunately, function of the neutralized homotetrameric Shaker could not be assessed because of its poor membrane expression in Xenopus oocytes (Fig. 1). Nonetheless, Bao et al. (1999) showed that a homotetramer Shaker mut channel with three neutralized gating charges (R362Q/R365Q/R371Q) is voltage insensitive, and that additional neutralization of the arginine at position 380 had no further effect. Thus, it is unlikely that a voltage sensor with four neutralized arginines is still voltage dependent, and that the other charged residues of the voltage-sensing domain (Aggarwal and MacKinnon, 1996; Seoh et al., 1996) contribute to voltage sensitivity in the absence of the four first arginines in S4.

Activation of a Shaker channel with a single charged voltage sensor

The heterotetrameric 1wt/3mut Shaker channel opens at more hyperpolarized voltages compared with wt, and its apparent valence of transferred charge is reduced (Fig. 2). It opens twice as fast as the wt and deactivates twice as slowly (Fig. 4), and it has a reduced delay for opening due to a reduced number of closed states, which approaches a quarter of those of wt Shaker (Fig. 5).

Our results demonstrate that it requires less energy to open the heterotetrameric channels containing less gating charges per channel than for opening wt Shaker (Fig. 2). As expected by neutralizing the gating charges in two and three subunits, the apparent valence of the transferred charge (z) of the G-V of the heterotetramers 2wt/2mut and 1wt/3mut compared with that of wt (Fig. 2) was reduced, which is consistent with the reduced number of gating charges per channel. (Instability of the patches at negative voltages necessary to reach open probabilities of <10⁻⁶ with 1wt/3mut has made the limiting-slope method [Seoh et al., 1996; Sigg and Bezanilla, 1997] difficult to perform.) At negative voltages, in addition to stabilization by anions and water, interactions of the gating charges with residues of the other transmembrane segments of the voltage sensing domain (Treptow and Tarek, 2006; Campos et al., 2007; Yang et al., 2007) and/or with the membrane (Long et al., 2007; Xu et al., 2008) stabilize the position of the voltage sensor in its resting state. The energy provided by depolarization disrupts these interactions; the voltage sensors move to the activated position triggering the conformational changes leading to channel opening. It is probable that neutralization of the gating charges destabilizes these interactions in such a way that the neutral S4 segment position differs from that of wt voltage sensor at hyperpolarized voltages. Most likely, the neutral S4 position in the activated state is in the range of voltage at which the wt voltage sensor is closed; otherwise, more energy would be required to open the channels with neutral S4 compared with wt Shaker.

The simple Boltzmann distribution for the G-V of 1wt/3mut taken to the power of 1.93 and 4.97 gave a reasonable fit to the ones of 2wt/2mut and 4wt, respectively (Fig. 2). This suggests that the observed voltage sensitivity is directly related to the number of subunits per channel actually sensing voltage, and that the voltage dependence of the wt subunit in the 1wt/3mut allows for the explanation of Shaker voltage dependence with a model of independent subunits (see below).

The heterotetramer 1wt/3mut opens twice as fast and closes twice as slow as 4wt, whereas the 2wt/2mut has intermediate opening/closing time constants (Fig. 4). We have also shown that the 1wt/3mut has a shorter delay for activation and less sigmoidicity in its currents compared with 4wt (Fig. 5). These results are expected if neutralized subunits are found in the active state and do not respond to voltage: the kinetics of opening will be faster because there is less subunit to activate, and closure will be slowed down because the number of subunits that can close the channel is reduced compared with 4wt. Change in sigmoidicity of the current with more depolarizing prepulse voltage is observed and reflects the presence of multiple closed states and rate-limiting steps (Cole and Moore, 1960; Bezanilla et al., 1994; Klemic et al., 1998) that is characteristic of most delayed rectifiers, including Shaker.

The number of closed states that was estimated with the power function of the exponential function described by Fitzhugh (1965) and Armstrong (1969) was reduced to exactly a quarter of that of 4wt (Fig. 5). It was shown that more than five unequal transitions must occur during channel activation and that at least one concerted step exists (Bezanilla et al., 1994; Zagotta et al., 1994a; Schoppa and Sigworth, 1998b; Ledwell and Aldrich, 1999; Horn et al., 2000). Tytgat and Hess (1992) used tandem tetramers to challenge cooperativity and independence of the subunits in RCK1 K⁺ channel by neutralizing only one of the four gating charges in three of the subunits. Their approach, which only considered steady-state conductance, could not discriminate between cooperativity and concerted action, nor could it decide in which step there was the inferred cooperativity. Pathak et al. (2005) concluded from voltage dependence of fluorescence changes from TMRM-labeled wt or V369I+I372L+S376T mutant (ILT) subunits in Shaker that S4 plays a role in cooperativity in gating and opening. The approach adopted, although interesting, still could not discriminate between cooperativity and concerted action.

Our results are consistent with the notion that the voltage sensors operate independently and that the opening step is concerted, thus producing an apparent cooperativity in the opening of the conductance. In addition, our results provide the first evidence that the natural state of a subunit that is no longer sensitive to voltage is to be in the active (almost open) state and that the fourth subunit, which is voltage controlled, opens and closes the channel. This heterotetramer 1wt/3mut allows us to address the voltage dependence of the last step of the four subunits upon the final activation step.

Model of Shaker activation with independent voltage sensors

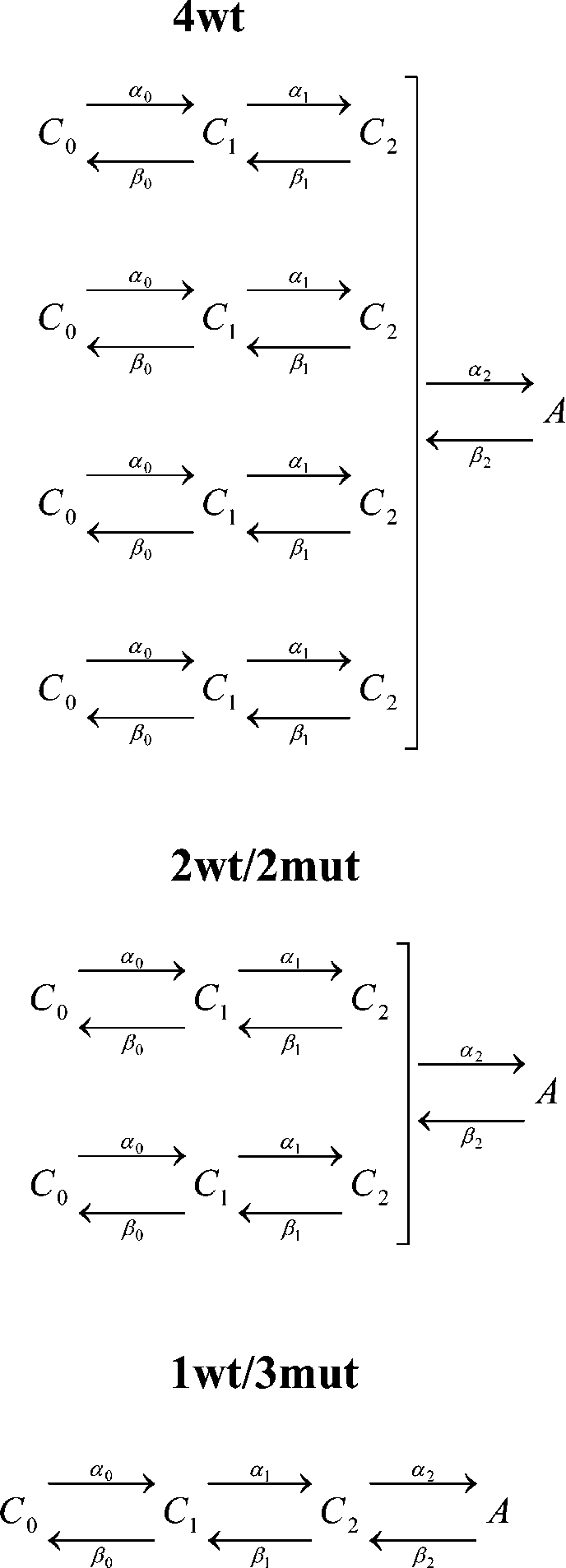(SCHEME 1)

A kinetic model of channel activation by independent voltage sensors with a concerted step preceding pore opening has been proposed (Zagotta et al., 1994b; Schoppa and Sigworth, 1998b; Ledwell and Aldrich, 1999; Horn et al., 2000). We used this model, shown in Scheme 1, in which each wt voltage sensor transits between three closed states (C₀, C₁, and C₂) before all four subunits simultaneously undergo the final transition to the open state (A) to globally fit the steady-state voltage dependence and activation kinetics of our heterotetramers (1wt/3mut, 2wt/2mut, and 4wt) in symmetrical 120 mM K⁺. It was assumed that a neutral S4 subunit would be in state C₂, whereas a wt subunit would undergo voltage-dependent transitions according to the values of α's and β's that are affected by the membrane potential. This assumption is supported by the characteristics of 1wt/3mut's function described above. It is also assumed that the charge carried by the last concerted step does not involve movement of the S4 segment. This will provide the valence of the charge and rate constants of each transition that are actually only due to the wt subunit(s) movement. The parameters in Table I provide an adequate fit to the data, as shown by the simulated ionic currents in Fig. 9. The kinetics and the G-V of 1wt/3mut and 2wt/2mut are almost perfectly reproduced by the model, whereas the ones of 4wt are fairly well accounted for. The model also predicts very well their delay for activation after leak correction (in 1wt/3mut particularly) while ignoring the contamination by gating currents of 4wt, as shown in Fig. 9. As expected, the maximal open probability (∼α₂₀/β₂₀) at 0 mV is 0.7. In our model, the charge carried by the last concerted step represents 0.6% of the total charge, which is smaller than in the model proposed by Ledwell and Aldrich (1999) (13%) based on the homotetramer Shaker ILT electrophysiological properties. Understanding this difference requires a more detailed analysis of the effect of the ILT mutations in our heterotetramer 1wt/3mut and its mechanism of action. Gating currents should provide more constraints on the model, but because of the presence of an omega-like current, it has been extremely difficult to accurately measure gating in 2wt/2mut and 1wt/3mut (see Fig. S2). The success of the model in describing the data obtained with one, two, and four wt subunits supports the conclusion that the gating of Shaker subunits acts independently. Moreover, the data are consistent with the conclusion that we have been able to isolate the functioning of a single voltage sensor in a heterotetrameric Shaker (1wt/3mut).

TABLE I.

Parameters of the kinetic model

Rate constant	k0	zk
	ms−1	e0
α00	0.3659	0.3965
β00	0.0001	2.5084
α10	2.9902	0.0037
β10	0.4255	1.1015
α20	0.2586	0.0001
β20	2.4364	0.0261

The rate constants are given for the model presented in Scheme 1. Forward and backward rate constants are α and β, respectively, and follow exponential voltage dependence as α₀ = α₀₀exp(z_0fV_mF/RT) and β₀ = β₀₀exp(z_0bV_mF/RT). The k₀ column gives each of the rates at 0 mV, and the z_k column indicates the equivalent valence in electronic charge units assigned to the transition. F is the Faraday constant, Vm is voltage, R is the universal gas constant, and T is the temperature in Kelvin.

Figure 9.

Predictions of the model for ionic currents in symmetrical 120 mM K⁺ at room temperature (19–20°C) for 4wt, 2wt/2mut, and 1wt/3mut compared with experimental data. Experimental data are shown on the left, and the right panel illustrates the predictions of the kinetic model illustrated in Scheme 1. The artifacts of pulse subtraction and compensation measured at the beginning of the pulses (first ms) are not shown. The HP was −90 mV, and steps were elicited to the annotated V_m. The rate constants and equivalent valence in electronic charge units are shown in Table I.

Single-channel properties of a Shaker channel controlled by one voltage sensor

The single-channel openings of the heterotetramer Shaker channel 1wt/3mut revealed the occurrence of subconductance levels at voltages at which the wt subunit should be found in the closed state (Fig. 7), consistent with the fluctuation analysis findings (Fig. 6). It has been proposed that when not all of the subunits are in the active state, the channels allow ion permeation but with lower single-channel conductance, and that entry and exit from this conductance level reflect fluctuation of the voltage sensors between the active and closed positions (Chapman et al., 1997; Zheng and Sigworth, 1997, 1998; Chapman and VanDongen, 2005). The observed subconductances were 37 and 70% of the fully open-channel conductance. This is similar to that described by Chapman et al. (1997) and Chapman and VanDongen (2005) in a slowly activating large-conductance Kv2.1 mut named drk1-LS and also by Zheng and Sigworth (1997, 1998) in a Shaker B chimera containing the T442S mutation. The Shaker chimera has a single-channel conductance of ∼95 pS at −100 mV and a G-V curve left shifted by ∼40 mV compared with wt Shaker IR. Some subconductances of a different kinetic nature were occasionally observed in wt Shaker IR by Hoshi et al. (1994), Zheng and Sigworth (1997), and Schoppa and Sigworth (1998a). In the positive range of voltage, no subconductance was observed with 1wt/3mut. If the neutral S4 segment were free to fluctuate, we might expect to see subconductances independently of the applied voltage; however, their movement might still require the concerted step described above, and thus, the probability of activation of the mut subunits is ultimately linked to the position of the wt voltage sensor. Although it is expected to observe a third subconductance level, neither we nor Chapman observed this subconductance state. The reason for this could be its short lifetime, its low occupancy or filtering, and/or its noise level.

Subunit cooperativity and role of a charged voltage sensor in slow inactivation

The voltage dependence of slow inactivation was decreased in the neutralized S4 heterotetramers (Fig. 3). The slow inactivation inherits its voltage dependence from the activation process (Olcese et al., 1997, 2001), a result that is consistent with the findings on the voltage dependence of activation as shown in Fig. 2 (see above).

An interesting result was that we observed equal kinetics of slow inactivation with 1wt/3mut (and 2wt/2mut) channels when compared with 4wt (Fig. 4 A). Panyi et al. (1995) and Ogielska et al. (1995) studied the inactivation kinetics of the heterotetramer channels of Kv1.3 and Shaker, respectively, formed by wt and mut subunits with a several-fold difference between the inactivation kinetics of the homotetramer. A cooperative mechanism, as opposed to an independent model of slow inactivation, was coherent with their measured inactivation kinetics. Later, Larsson and Elinder (2000) also supported this mechanism in Shaker. Although it was impossible to estimate the inactivation kinetics of the homotetramer with the four gating charges neutralized, it is clear that the kinetics expected by an independent model would differ from our observation. If the independent model was to be considered, a constitutively activated subunit would move further into the inactivated state, and thus a faster time constant of slow inactivation would be expected with 1wt/3mut. Our results support a cooperative mechanism of slow inactivation in which a permanently open subunit has to wait for the voltage-controlled subunit to move to its activated position to inactivate the channel conductance.

Even more striking is our result regarding the double mut, T449V-I470C (or TVIC), which removes slow inactivation (Lopez-Barneo et al., 1993; Holmgren et al., 1997; Olcese et al., 2001). Introducing the TVIC mutations in Shaker's monomers left-shifts the G-V curve by ∼35 mV, whereas it left-shifts by 10–15 mV in both wtTVIC/3wt and wtTVIC/3mut, which in any case remains as shifted compared with each other as 4wt and 1wt/3mut are (see Fig. S7). When the TVIC mutations were introduced in only one subunit of the wt Shaker, it barely affected inactivation (Fig. 8). In contrast, the wtTVIC/3mut heterotetramer inactivates slower and to a markedly lower extent than the wt tetramer, but similarly to homotetrameric Shaker TVIC (Fig. 8), most specifically at higher depolarization (>+40 mV). At lower voltages, wtTVIC/3mut inactivates more than Shaker TVIC but less than 4wt, which might be an effect similar to that of U-type inactivation, usually described to be more profound in the intermediate range of activation (near or below V_1/2) than at higher voltages. In this case, −20 mV is already saturating in the G-V curve of wtTVIC/3mut. However, these results suggest that subunits bearing a neutral S4 segment were unable to go into the inactivated state by themselves.

Elinder's group proposed that E418 in Shaker, located at the end of the S5 segment, lays close to and interacts with the S4 charges (Elinder and Arhem, 1999) and found that cysteines introduced at E418 and at either two residue locations on the P-loop (V451 or G452) stabilize the open or the inactivated state by disulfide bridge formation (Larsson and Elinder, 2000). The proximity between the S4 segment and the pore in the activated conformation was directly demonstrated by Laine et al. (2003), who found that cysteines introduced at positions R362 and A419 in Shaker spontaneously form disulfide bridges. Electrostatic interaction between the negative charge at E418 and the positive charges of S4 was suggested to be involved in breaking the hydrogen-bound network between S5-P-S6 loops after channel activation, which would trigger pore constriction during slow inactivation (Larsson and Elinder, 2000). The lack of inactivation triggered by the IR wt subunit or the neutral S4 subunits in the wtTVIC/3mut construct does not contradict this hypothesis. However, our results ultimately suggest that inactivation seems to come about when all four subunits are in the activated position.

Conclusion

Our results indicate that a single voltage sensor is capable of gating the Shaker's pore, and that neutralization of the four gating charges in S4 renders such a subunit voltage insensitive and constitutively active, although still under the wt subunit's movement influence through a nearly voltage-independent concerted step. This provides experimental evidence of Shaker's subunit independence in the early transitions toward the final concerted step that fully opens the channel for ion conduction. The neutral S4 subunits were shown not to go into the inactivated state by themselves, which also provides support to the proposal that the charges in S4 interact with the pore region (E418) upon activation triggering slow inactivation.