Abstract
The synchronous movement of chromosomes during anaphase ensures their correct inheritance in every cell division. This reflects the uniformity of spindle forces acting on chromosomes and their simultaneous entry into anaphase. Although anaphase onset is controlled by the spindle assembly checkpoint, it remains unknown how spindle forces are uniformly distributed among different chromosomes. In this paper, we show that tension uniformity at metaphase kinetochores and subsequent anaphase synchrony in Drosophila S2 cells are promoted by spindle microtubule flux. These results can be explained by a mechanical model of the spindle where microtubule poleward translocation events associated with flux reflect relaxation of the kinetochore–microtubule interface, which accounts for the redistribution and convergence of kinetochore tensions in a timescale comparable to typical metaphase duration. As predicted by the model, experimental acceleration of mitosis precludes tension equalization and anaphase synchrony. We propose that flux-dependent equalization of kinetochore tensions ensures a timely and uniform maturation of kinetochore–microtubule interfaces necessary for error-free and coordinated segregation of chromosomes in anaphase.
Introduction
The sense and purpose of mitosis is revealed in its climax during anaphase, when sister chromatids migrate synchronously toward opposite poles. This critical task is accomplished by a highly dynamic microtubule (MT)-based apparatus: the mitotic spindle, which interacts with specialized structures at the centromere of each chromosome termed kinetochores (Maiato et al., 2004a). Anaphase synchrony prevents the occurrence of lagging chromosomes that could lead to the formation of micronuclei after nuclear envelope restoration or reversion of cleavage furrow ingression during cytokinesis. These cytological features may lead to aneuploidy or polyploidy, and have been associated with elevated risk of cancer in mammalian models and humans (Tucker and Preston, 1996; Ganem et al., 2007). In higher eukaryotic cells, anaphase synchrony is ensured by the strategic positioning of all chromosomes at the cell equator during metaphase and the strict coordination of sister chromatid separation. Although anaphase onset is regulated by the spindle assembly checkpoint (SAC), which ensures that all kinetochores are properly attached to the spindle before loss of sister chromatid cohesion (Musacchio and Salmon, 2007), the mechanism responsible for the uniform action of spindle forces at kinetochores remains to be elucidated.
During metaphase, many animal and plant spindles are characterized by a conspicuous “flux” activity due to continuous MT poleward translocation, while maintaining steady-state length (Mitchison, 1989; Rogers et al., 2005). Spatio-temporal scales of flux dictate that spindle MTs are fully recycled before anaphase, which results from continuous incorporation of tubulin subunits at kinetochores (Maiato et al., 2005) balanced by MT depolymerization at the poles (Rogers et al., 2004). In addition, sister kinetochores on metaphase chromosomes are pulled toward opposite poles by spindle forces that stretch the interconnecting centromeric chromatin. This tension is thought to control the maturation (King and Nicklas, 2000) and correction (Nicklas and Ward, 1994) of kinetochore–MT attachments before cells enter anaphase.
Simultaneity of tension and MT translocation/flux relative to the kinetochore suggests that the flux-driving force is not generated at the kinetochore–MT interface. Indeed, any mechanical event at this interface that hypothetically pushes kinetochore MTs (kMTs) poleward (e.g., a kinesin power stroke) would react against the kinetochore structure, leading to centromere compression, not stretching. MT poleward flux may be driven by active MT minus-end depolymerization at the poles (Waters et al., 1996; Rogers et al., 2004; Ganem et al., 2005) or by motors acting along the length of kMTs (Mitchison, 2005; Forer et al., 2008). Growing emphasis in several cell types is being given to kinesin-5 motors, which slide apart antiparallel interpolar MTs (ipMTs), as the main flux-driving force (Miyamoto et al., 2004; Goshima et al., 2005; Brust-Mascher et al., 2009). Polymerization and depolymerization at MT plus and minus ends, respectively, are viewed as downstream responses to MT poleward translocation that regulate spindle length (Gaetz and Kapoor, 2004; Maiato et al., 2005). In this framework, kinesin-5 motors may drive kMT flux by directly cross-linking kMTs to ipMTs of opposite polarity (Mitchison, 2005) or, indirectly, by laterally transmitting the force generated by sliding ipMTs to kMTs within the same half spindle (Brust-Mascher et al., 2009). The key ingredient in both models is that ipMT sliding may prompt kMT poleward translocation through force transmission via a mechanical coupler, which in a more general view may consist of proteins with MT cross-linking activity (Manning and Compton, 2007) or a viscoelastic network (Brangwynne et al., 2006). The existence of such mechanical coupler may be heuristically inferred by the fact that spindles rotate and translate as a unified structure, which ultimately means that all chromosomes are mechanically connected.
The conservation and energetic cost of flux during metaphase, together with its dispensability for chromosome segregation in systems where it is normally present (Ganem et al., 2005; Buster et al., 2007), poses obvious questions regarding its functional roles. Besides, MT poleward translocation relative to the kinetochore (i.e., kMT flux) reflects the relaxation of the kinetochore–MT interface (implying a certain loss of tension), which may be seen as an apparent disadvantage to the cell. Here, we used Drosophila S2 cells to test whether the existence of flux represents a way to redistribute excess tensions on metaphase chromosomes, thereby contributing to the equalization of forces acting at kinetochores and anaphase “quality.”
Results
Experimental attenuation of kMT flux in Drosophila S2 cells
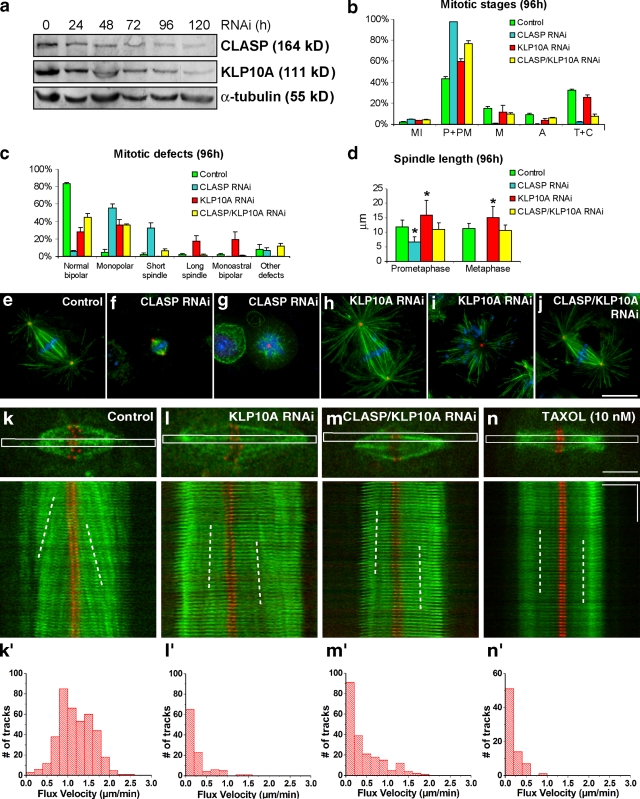
The poleward flux of kMTs requires a corresponding rate of MT polymerization and slippage at the kinetochore. To test whether flux-associated slippage at the kinetochore–MT interface contributes to a uniform distribution of forces acting on kinetochores, we started by experimentally reducing kMT flux on bipolar spindles. In Drosophila S2 cells, kMT flux requires cytoplasmic linker associated protein (CLASP)-mediated incorporation of tubulin subunits at kinetochores (Maiato et al., 2005) balanced by KLP10A-dependent MT depolymerization at the poles (Rogers et al., 2004; Buster et al., 2007). Although CLASP RNAi causes kMT shortening and a strong accumulation of prometaphase cells with monopolar or short spindles (Fig. 1, a–g; Maiato et al., 2005), KLP10A RNAi increases spindle length without precluding bipolar spindle formation and function (Fig. 1, a–e, h, and i; Goshima et al., 2005; Buster et al., 2007). Simultaneous knockdown of CLASP and KLP10A significantly restores normal spindle bipolarity, length, and morphology (Fig. 1, a–e, and j; Laycock et al., 2006). To verify that bipolar spindles after KLP10A or CLASP/KLP10A RNAi undergo slower kMT flux, we used S2 cells stably expressing GFP–α-tubulin under the control of an inducible promoter and the kinetochore marker mCherry–centromere identifier (CID)-mCherry. The leaky expression of GFP–α-tubulin can be used to measure kMT flux by fluorescent speckle microscopy (FSM; Goshima et al., 2005; Danuser and Waterman-Storer, 2006). KMT flux in control metaphase cells is 1.2 µm/min (median) at 25°C, with only 2% of the speckles moving slower than 0.2 µm/min relative to kinetochores (Fig. 1, k and k′; Table I). After KLP10A or CLASP/KLP10A RNAi, kMT flux drops to 0.2 µm/min (Fig. 1, l–m′; Table I), which is comparable to the velocity of kMT flux observed after MT stabilization with 10 nM taxol (Fig. 1, n and n′; Table I). Although flux velocity is slow, these slowly fluxing spindles satisfy the SAC, enter anaphase, and segregate chromosomes. We conclude that KLP10A or CLASP/KLP10A RNAi represent valid strategies to reduce kMT flux, while allowing the formation of functional bipolar spindles in S2 cells.
Figure 1.
Phenotypic analyses of CLASP, KLP10A, and CLASP/KLP10A RNAi in Drosophila S2 cells. (a) Western blot analysis after CLASP and KLP10A RNAi at different time points revealed a 70–90% reduction in protein levels after 96 h of RNAi treatment. α-tubulin was used as loading control. (b) Quantification of mitotic parameters reveals a significant rescue of the CLASP phenotype by simultaneous depletion of KLP10A. Note that metaphases and anaphases were restored in the double RNAi experiments. (c and d) Quantification of mitotic defects in controls and after CLASP, KLP10A, and CLASP/KLP10A RNAi show that simultaneous depletion of CLASP and KLP10A significantly restored spindle bipolarity and length. Plotted values in panels b–d represent the mean from three experiments, and error bars represent the respective standard deviations. Asterisks in panel d indicate statistically significant differences when compared with controls (P < 0.001; Mann-Whitney test). (e–j) Immunofluorescence analysis of mitotic spindles from control, CLASP, KLP10A, and CLASP/KLP10A RNAi. MTs (green) and centrosomes (red) were, respectively, revealed with anti–α- and γ-tubulin antibodies, whereas DNA (blue) was counterstained with DAPI. S2 cells stably expressing low levels of GFP-α-tubulin (green) and CID-mCherry (red) were used to analyze kMT poleward flux by FSM. Bar, 10 µm. (k–n) Control (k), KLP10A RNAi (l), CLASP/KLP10A RNAi (m), and Taxol-treated cells (n). Speckle poleward velocity was determined by measuring the slopes obtained from the kymographs (white broken lines). (k′–n′) Distribution of flux velocity in control, KLP10A RNAi, CLASP/KLP10A RNAi, and Taxol-treated cells, respectively. Horizontal bar, 5 µm; vertical bar, 1 min. All treatments were statistically different from controls (P < 0.05; Dunn's test).
Table I.
Summary of measured mitotic parameters
| Experiment | Metaphase flux velocity | Anaphase kMT minus-end depolymerization velocity | Inter-KT distance measured from fixed cells | Pixel intensity BubR1/CID | Inter-KT distance measured from live imaging | Chromosome poleward velocity [Vch] | Half-spindle elongation velocity [Vpole] | KMT shortening velocity [Vch-Vpole] |
| µm/min | µm/min | µm | µm | µm/min | µm/min | µm/min | ||
| Control | ||||||||
| M | 1.2a | 0.4a | 1.0a | 1.1 | 0.9a | 1.7 | 0.9 | 0.8 |
| SD | 0.4 | 0.4 | 0.2 | 0.6 | 0.1 | 0.5 | 0.2 | 0.4 |
| IQR | 0.6 | 0.5 | 0.2 | 0.8 | 0.2 | 0.7 | 0.2 | 0.6 |
| n | 392 tracks; 23 cells | 43 tracks; 8 cells | 207 tracks; 34 cells | 59 tracks; 9 cells | 198 tracks; 21 cells | 88 tracks; 30 cells | 30 cells | 88 tracks; 30 cells |
| Control + colchicine | ||||||||
| M | 0.7 | |||||||
| SD | 0.1 | |||||||
| IQR | 0.2 | |||||||
| n | 56 tracks; 8 cells | |||||||
| Control + MG132 | ||||||||
| M | 1.1a | 1.2 | ||||||
| SD | 0.2 | 0.6 | ||||||
| IQR | 0.4 | 0.7 | ||||||
| n | 125 tracks; 20 cells | 57 tracks; 9 cells | ||||||
| Control (Prophase) | ||||||||
| M | 0.4a | |||||||
| SD | 0.1 | |||||||
| IQR | 0.2 | |||||||
| n | n = 102; 3 cells | |||||||
| KLP10A RNAi | ||||||||
| M | 0.2a | 0.9a | 1.6 | 0.8a | 1.3 | 0.4 | 0.9a | |
| SD | 0.3 | 0.2 | 0.9 | 0.1 | 0.6 | 0.2 | 0.6 | |
| IQR | 0.2 | 0.2 | 1.2 | 0.2 | 0.9 | 0.3 | 0.9 | |
| n | 105 tracks; 6 cells | 137 tracks; 16 cells | 50 tracks; 8 cells | 267 tracks; 25 cells | 186 tracks; 32 cells | 32 cells | 186 tracks; 32 cells | |
| KLP10A RNAi + MG132 | ||||||||
| M | 0.9 | |||||||
| SD | 0.2 | |||||||
| IQR | 0.2 | |||||||
| n | 50 tracks; 7 cells | |||||||
| KLP10A RNAi + (Prophase) | ||||||||
| M | 0.4a | |||||||
| SD | 0.1 | |||||||
| IQR | 0.1 | |||||||
| n | n = 79; 3 cells | |||||||
| CLASP/KLP10A RNAi | ||||||||
| M | 0.2a | 0.2a | 1.0 | 1.7a | 0.8a | 1.1 | 0.4 | 0.7a |
| SD | 0.4 | 0.4 | 0.2 | 1.7 | 0.2 | 0.4 | 0.2 | 0.4 |
| IQR | 0.6 | 0.4 | 0.2 | 1.4 | 0.2 | 0.6 | 0.2 | 0.6 |
| n | 208 tracks; 13 cells | 51 tracks; 10 cells | 159 tracks; 23 cells | 51 tracks; 9 cells | 241 tracks; 25 cells | 219 tracks; 33 cells | 33 cells | 219 tracks; 33 cells |
| CLASP/KLP10A RNAi + MG132 | ||||||||
| M | 1.1a | 1.4a | ||||||
| SD | 0.2 | 0.7 | ||||||
| IQR | 0.2 | 1.0 | ||||||
| n | 129 tracks; 20 cells | 44 tracks; 8 cells | ||||||
| CLASP/KLP10A RNAi (Prophase) | ||||||||
| M | 0.4a | |||||||
| SD | 0.1 | |||||||
| IQR | 0.1 | |||||||
| n | 22 tracks; 2 cells | |||||||
| Mad2 RNAi | ||||||||
| M | 0.8a | |||||||
| SD | 0.2 | |||||||
| IQR | 0.2 | |||||||
| n | 122 tracks; 12 cels | |||||||
| Mad2 RNAi (Prophase) | ||||||||
| M | 0.4a | |||||||
| SD | 0.1 | |||||||
| IQR | 0.1 | |||||||
| n | 54 tracks; 3 cells | |||||||
| KLP10A/SAS4 RNAi | ||||||||
| M | 1.6 | 0.7 | 0.9 | |||||
| SD | 0.6 | 0.2 | 0.5 | |||||
| IQR | 0.6 | 0.2 | 0.7 | |||||
| n | 84 tracks; 14 cells | 14 cells | 84 tracks; 14 cells | |||||
| Taxol | ||||||||
| M | 0.1a | 0.7 | 3.3a | |||||
| SD | 0.2 | 0.1 | 2.0 | |||||
| IQR | 0.2 | 0.1 | 3.4 | |||||
| n | 73 tracks; 5 cells | 44 tracks; 7 cells | 42 tracks; 7 cells | |||||
Blank cells indicate that the value was not determined. KT, kinetochore; M, represents the mean, except for the distributions that do not follow a normal distribution; IQR, interquartile range; n, the number of measurements (in the prophase situation, n represents the number of interkinetochore distances measured before nuclear envelope breakdown).
Distrubutions that do not follow a normal distribution, where median is represented.
Flux-associated kMT minus-end depolymerization is down-regulated at anaphase onset and has a minor role in anaphase chromosome-to-pole motility in Drosophila S2 cells
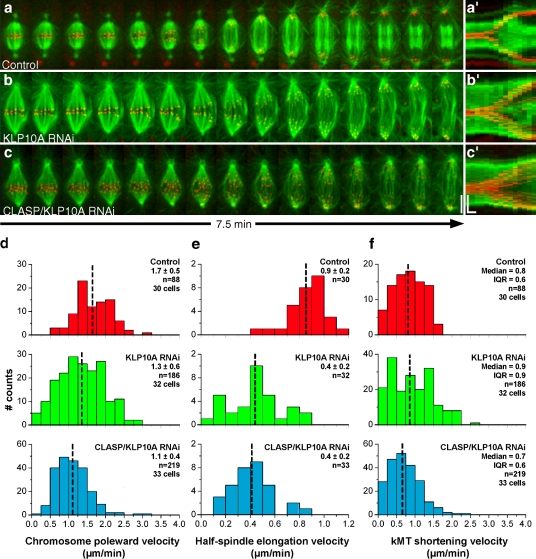
We next used dual-wavelength spinning-disk confocal microscopy to investigate the impact of reduced kMT flux on chromosome segregation. Anaphase poleward velocity of sister chromatids after KLP10A or CLASP/KLP10A RNAi was reduced by ∼0.5 µm/min relative to controls. This reduction was essentially caused by a KLP10A-dependent decrease in the velocity of spindle elongation and not reduced kMT shortening velocity (Fig. 2, a–f; Table I). Because KLP10A is apparently not required for the formation of the spindle midzone or recruitment of kinesin-5 motors to this location (unpublished data), we reasoned that the slower spindle elongation could be caused by increased resistance due to cortical interactions with the abnormally long astral MTs observed after perturbation of KLP10A (Fig. 1, h and j). Indeed, codepletion of KLP10A with Sas4, a protein required for the formation of functional centrosomes and astral MTs (Basto et al., 2006), restores normal spindle elongation velocity (Table I and Fig. S1, a–d).
Figure 2.
Analysis of chromosome and spindle dynamics during anaphase. (a–c) S2 cells stably expressing GFP–α-tubulin (green) and CID-mCherry (red) were used to track kinetochore movement and spindle elongation during anaphase. Control (a), KLP10A RNAi (b), and CLASP/KLP10A RNAi cells (c). Bar, 5 µm. (a′–c′) Corresponding collapsed kymograph analysis. Horizontal bar, 60 s; vertical bar, 5 µm. (d) Distribution of chromosome poleward velocity in control, KLP10A, and CLASP/KLP10A RNAi. All RNAi treatments are statistically different from control (P < 0.05; Dunn's test). (e) Distribution of spindle elongation velocity. All RNAi treatments were statistically different from controls (P < 0.001; Student-Newman-Keuls test). (f) Distribution of kMT shortening velocity in control, KLP10A, and CLASP/KLP10A RNAi. The differences were not statistically significant. The mean ± SD or median and interquartile range are indicated for each distribution. The mean or median values are marked with a broken vertical line.
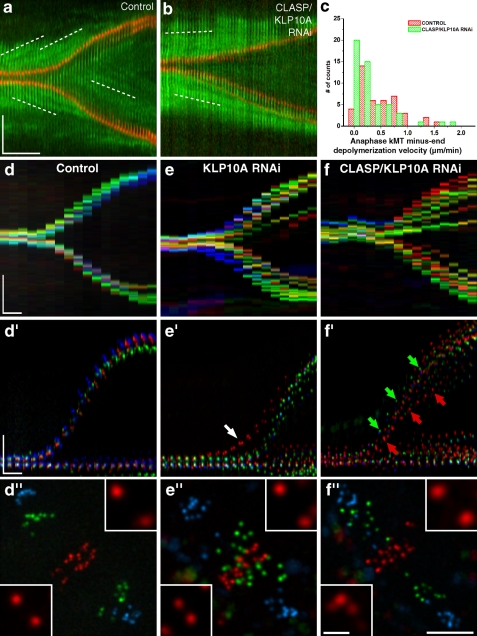
Our results show that a substantial decrease in metaphase flux velocity does not significantly affect the mean velocity of kMT shortening in anaphase. This finding is surprising in light of the recent proposal that MT minus-end depolymerization associated with flux is the main force driving chromosome-to-pole movement during anaphase in S2 cells (Buster et al., 2007). One important difference between this previous report and our study was our inclusion of a kinetochore marker and collection of z stacks through the entire volume of the cell, which allowed us to directly measure kMT shortening velocities for the full chromosome set. To investigate this further, we performed FSM in control anaphase cells and found that kMT translocation velocity is equivalent to that observed in metaphase, as revealed by the constant slope of speckle tracks on kMTs (Fig. 3 a and Table I). Because spindles elongate immediately after anaphase onset at ∼0.9 µm/min in S2 cells, this indicates that MT minus-end depolymerization must be attenuated by an equivalent rate. Indeed, we found that >50% of the speckles move slower than 0.4 µm/min relative to spindle MT minus ends (Fig. 3, a and c; and Table I), which is consistent with a model where the extent of down-regulation of MT minus-end depolymerization governs the rate of spindle elongation during anaphase (Brust-Mascher et al., 2004). Finally, the rate of speckle movement relative to kMT minus ends in anaphase is only marginally affected after RNAi depletion of CLASP/KLP10A, which suggests that their flux-associated activities during metaphase in untreated cells are significantly down-regulated at anaphase onset (Fig. 3, b and c; and Table I). These results support the finding that, as in human cells (Gorbsky et al., 1987; Ganem et al., 2005), kinetochore motility coupled to MT plus-end depolymerization (“Pac-Man” activity) is the main driver of anaphase chromosome-to-pole movement in Drosophila S2 cells (Fig. 3 a).
Figure 3.
Analysis of chromosome segregation during anaphase. (a and b) S2 cells stably expressing low levels of GFP–α-tubulin (green) and CID-mCherry (red) were used to track tubulin speckle movement (white broken lines) relative to spindle MT minus ends by FSM. (a) Control cell. (b) CLASP/KLP10A RNAi cell. Note that in both cases, kinetochores approach the speckles. (c) Distribution of kMT minus end depolymerization velocity in control and CLASP/KLP10A RNAi cells. The differences are statistically significant (P < 0.05; Mann-Whitney test). (d–f) Chromo-kymograph analysis of kinetochores in control, KLP10A RNAi, and CLASP/KLP10A RNAi cells at the metaphase–anaphase transition. (d′–f′) Overlay of guided kymographs showing three kinetochore pairs color coded red/green/blue. Arrows indicate precocious entry of anaphase (white) or differential poleward migration (green/red). (d′′–f′′) Respective projections of three different time frames. Red/green/blue frames correspond to 1, 3.5, and 7 min after anaphase onset. Insets highlight the kinetochore pairs where interkinetochore distances were maximum and minimum. Bars: (space) 5 µm; (time) 1 min; (inset) 1 µm.
KMT flux ensures anaphase synchrony in Drosophila S2 cells
Although experimental attenuation of flux has only a minor effect on mean kinetochore-to-pole velocity, we discovered that it significantly impaired anaphase synchrony (Fig. 2, a–c′). To measure the uniformity of chromosome segregation after attenuation of flux, we developed a chromo-kymograph algorithm to show the movements of multiple kinetochores as a function of time through the metaphase–anaphase transition. In control cells, we generally observed 2 main kinetochore tracks during anaphase, which indicated synchronous segregation of chromosomes (Fig. 3, d and d′; n = 30 cells). After KLP10A or CLASP/KLP10A RNAi, we typically found 3–12 kinetochore tracks per cell (Fig. 3, e, e′, f, and f′; n = 31 cells for each RNAi), despite the formation of normal metaphase plates. Closer inspection of the chromo-kymographs revealed marked asynchrony in the entry and/or poleward migration during anaphase (Fig. 3, d–f′′). One plausible explanation for the observed asynchrony during anaphase could be the presence of kinetochores with merotelic attachments (Cimini et al., 2004). Indeed, members of the kinesin-13 family were implicated in correcting kinetochore–MT attachments in human cells (Ganem et al., 2005; Bakhoum et al., 2009). Therefore, it is possible that KLP10A, which localizes to centromeres in addition to spindle poles (Rogers et al., 2004), is also involved in this process. Analysis of KLP10A RNAi spindles revealed the persistence of cold-resistant kMTs that were indistinguishable from controls, which suggests normal kinetochore function (Fig. S1, e–g). Because the correction of merotelic attachments involves mechanisms acting before and during anaphase (Cimini et al., 2003), we quantified merotelic attachments after KLP10A RNAi using two criteria: accumulation of Aurora B at the inner centromere during metaphase (Knowlton et al., 2006) and stretching of the merotelic kinetochore during anaphase (Cimini et al., 2004). We were unable to detect a significant enrichment of Aurora B on metaphase plates after knocking down KLP10A (Fig. S1, h–j). In contrast, our live-cell analysis of anaphase did reveal a two-to-three–fold increase in the percentage of KLP10A (n = 31)- and CLASP/KLP10A (n = 29)-depleted cells with merotelic attachments in anaphase (13% and 10%, respectively, as opposed to 4% of control cells [n = 25]). However, we never found more than one chromosome or chromatid with merotelic-attached kinetochores per depleted cell, which is too infrequent to account for the observed level of asynchrony in anaphase cells depleted of KLP10A or CLASP/KLP10A. Still, it remains possible that these numbers represent an underestimate of the full complement of merotelic attachments, especially more subtle cases, which cannot be resolved by the abovementioned methods. We conclude that molecular players involved in kMT flux may be implicated in correcting erroneous kinetochore–MT attachments invisible to the SAC and somehow help in ensuring the coordinated movement of chromosomes during anaphase.
Anaphase synchrony reflects the uniformity of forces acting on metaphase kinetochores
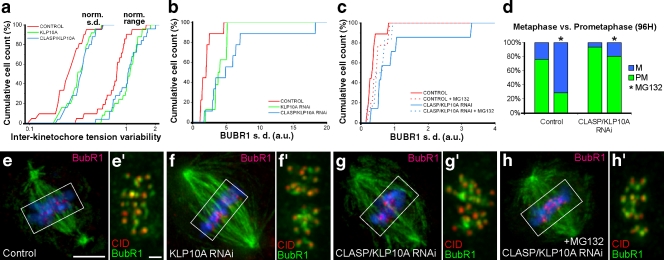
Flux players may promote anaphase synchrony by mediating the equalization of forces acting at kinetochores of metaphase chromosomes. Indeed, measurement of interkinetochore distances as a readout of centromere tension in living metaphase cells revealed that tension was highly variable between sister kinetochore pairs after KLP10A or CLASP/KLP10A RNAi (Fig. 4 a). In agreement, live-cell imaging of the tension-sensitive protein BubR1 in KLP10A or CLASP/KLP10A-depleted cells revealed that several kinetochores retain abnormal high levels of BubR1, which correlated with a delayed initiation of poleward migration and local degradation of the cohesin subunit Scc1 (Fig. S2). Quantitatively, we confirmed that flux reduction by these methods causes an increase in the variability of BubR1 at metaphase kinetochores, which is attenuated if cells are allowed to stay in metaphase for 2 h by incubation with the proteasome inhibitor MG132 (Fig. 4, b–h′).
Figure 4.
Experimental analysis of tension uniformity during metaphase. (a) Cumulative histogram for the normalized standard deviation (left) and range (right) of intracellular interkinetochore distances along a metaphase plate for control (n = 21), KLP10A RNAi (n = 25), and CLASP/KLP10A RNAi (n = 25), where n is the number of cells. CLASP/KLP10A RNAi is statistically different from control but not KLP10A RNAi (P < 0.05; Dunn's test). (b) Cumulative histograms for the standard deviation of BubR1 fluorescence intensity for control (n = 10), KLP10A RNAi (n = 7), and CLASP/KLP10A RNAi (n = 7) cells. Both treatments cause a statistically significant variability relative to controls (P < 0.05; Dunn's test). (c) Cumulative histograms for the standard deviation of BubR1 fluorescence intensity on metaphase kinetochores in control and CLASP/KLP10A RNAi before and after incubation with MG132 for 2 h. Note the approximation of the control and CLASP/KLP10A RNAi distributions after MG132 treatment. Only CLASP/KLP10A RNAi is statistically different from controls (P < 0.05; Dunn's test). (d) Quantification of prometaphase and metaphase figures in fixed cells before and after MG132 treatment. Note that CLASP/KLP10A RNAi-treated cells have problems aligning chromosomes at the metaphase plate, which is slightly attenuated if additional time is provided by incubation with MG132. The asterisks indicate the presence of MG132. (e–h) Mitotic spindles from control, KLP10A RNAi, CLASP/KLP10A RNAi, and CLASP/KLP10A RNAi after MG132 treatment, respectively. α-tubulin is shown in green, BubR1 in red, and DNA in blue. Bar, 5 µm. (e′–h′) Insets of the respective metaphase plates indicated in e–h, where CID is shown in red and BubR1 in green. Only cells with aligned chromosomes after CLASP/KLP10A RNAi were used for all quantitative analyses of metaphase. Bar, 1 µm.
Force equalization by flux can be explained by an MT-coupling model
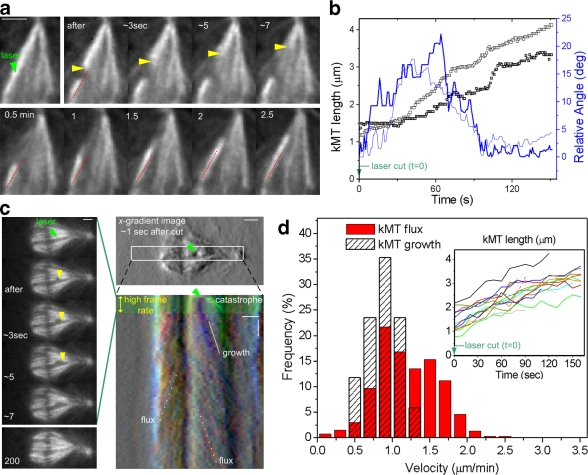
In an attempt to explain how kMT flux contributes to the uniformity of forces on metaphase kinetochores, we developed a minimal mathematical model for the metaphase spindle, which assumes that kMT flux is driven by forces that are laterally transmitted through a mechanical coupler cross-linking kMTs with sliding ipMTs. In this context, antiparallel ipMT sliding may be driven either by plus end–directed bipolar motors (Brust-Mascher et al., 2009; Goshima et al., 2005) or by active depolymerases at ipMT minus ends (Rogers et al., 2004). We support the finding that forces are laterally transmitted to kMTs based on the uninterrupted poleward translocation at near flux rates of laser-severed kMTs (Fig. 5, a–d; kMT growth = 0.9 ± 0.2 µm/min, n = 17; Table I), which don't reach near the poles and whose minus ends are not depolymerizing (Maiato et al., 2004b), suggesting that kMT minus-end depolymerization by itself is not a major flux-driving force.
Figure 5.
KMT fiber regrowth after laser microsurgery at near-flux velocity. (a) Selected frames of a laser microsurgery experiment on a kMT fiber during metaphase. The readouts for a successful laser cut are (1) a catastrophe of newly created kMT plus ends (∼20 µm/min) and (2) reorientation of the kinetochore-associated MT fiber after a laser cut (red lines have equal length and slope). (b) kMT fiber length and orientation over time after microsurgery. Data points correspond to two high-speed acquisitions (light and dark lines) in kMT fibers associated with chromosomes positioned at the periphery of the metaphase plate. The relative angle corresponds to the fiber deviation from the initial (presurgery) orientation. (c) FSM during metaphase after laser microsurgery on a kMT fiber. A first high-speed acquisition phase (∼1 s interval) is used to confirm the catastrophe of newly created kMT plus ends (left). After the catastrophe, images are acquired at a 10-s interval to observe kinetochore-associated MT fiber growth and intact kMT fiber flux, as revealed by the chromo-kymograph. The kymograph is based on intensity-gradient images along the horizontal direction, which helped observation of the minus ends of a growing kMT fiber. Green arrowheads in a and c indicate the location of the laser cut. Yellow arrowheads indicate the catastrophe of newly created kMT plus ends after surgery. (d) Velocity distributions of growing kMT fibers after laser microsurgery and of poleward flux, i.e., translocating intact kMT fibers. The elongation of kMT fibers was tracked and is shown in the inset. Bars: (space) 2 µm; (time) 1 min.
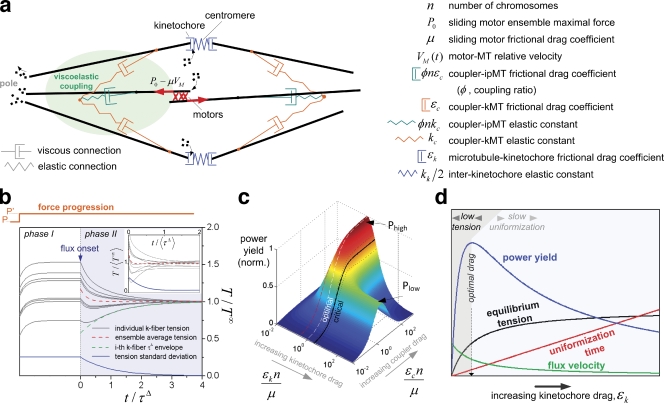
We next simulated the mechanical behavior of the proposed fluxing metaphase spindle model (Fig. 6 a; see Materials and methods for details), where ipMTs translocate poleward driven by a force P (a generalization for non-ipMT forces is discussed in Materials and methods). In this context, motor force decreases with sliding velocity (Valentine et al., 2006), a dependence that is assumed to be linear. ipMT sliding is not free; instead, it is resisted by MT cross-linking or coupling, here modeled as a serial linkage of viscous and elastic elements. This viscoelastic coupler cross-links spindle MTs, and therefore acts as a mechanical mediator that allows force transference between ipMTs and kMTs. As a result, kMTs are pulled poleward, exhibiting flux, which is primarily resisted by friction at the kinetochore–MT interface. We represent this friction as a viscous interaction, T(t) = εkV+(t), where T is the centromeric tension, εk is the friction drag coefficient associated with kinetochore-MT affinity, and V+ is the slippage/flux velocity of the MT relative to the kinetochore. Finally, the centromere is assumed to be linearly elastic, with tension given by T(t) = kkEk(t), where kk is the elastic constant characterizing centromere stiffness and Ek is the interkinetochore elongation resulting from an applied tension T. In parallel, all n chromosomes are described by equivalent interdependent equations. The mechanical coupling between adjacent MTs integrates the system, which will react globally to local events on individual chromosomes. For simplicity, this model disregards position and velocity-dependent forces driving chromosome oscillation. It is plausible, however, that it applies to systems where chromosomes do oscillate, given that MT poleward translocation is independent of the directional state (poleward or antipoleward) of metaphase chromosomes (Cameron et al., 2006).
Figure 6.
MT coupling leads to tension uniformity in the presence of flux. (a) Spring-dashpot (elastic-viscous) functional representation of the coupled spindle. Viscous and elastic elements describe both coupler–MT and MT–chromosome interactions. (b) Normalized centromeric tensions as a function of normalized time without flux (phase I) and with flux (phase II). A force P generates initial (random) tension values. A step-increased force (P′) is applied to the system (see “force progression” above the graph). First, to simulate a nonfluxing spindle, phase I shows the system dynamics when no slippage is allowed at the viscous connections, i.e., totally rigid kinetochore–MT and coupler–MT attachments. The system reaches a static (stretched) state when elastic force balances the applied force. Tension heterogeneity (as measured by the standard deviation, blue line) does not decrease because slippage-mediated tension redistribution does not occur. At t = 0, viscous drag coefficients drop to a finite value, allowing slippage to begin (phase II). Throughout phase II, tensions converge with timescale τΔ to the mean tension, which itself decreases (red broken line) to a new asymptotic level T∞. The inset shows the system behavior when kinetochore–MT attachment drags are variable among chromosomes on the same metaphase plate, following a normal distribution with full width equal to 10% of the mean. (c) Power yield of the mechanical system as a function of normalized MT–coupler drag and normalized kinetochore–MT drag. The system reaches a plateau of highest efficiency (Phigh) when kMTs are tightly coupled to ipMTs (high coupler drag) but only partially coupled to kinetochores (intermediate kinetochore drag). A secondary plateau (Plow) is found if kinetochore drag is higher than a critical value (black line; sub- and supracritical black broken lines are also shown), a condition in which it is beneficial to have a finite coupler drag and infinite kinetochore drag (no kMT flux). Critical kinetochore drag represents an unbiased estimate of the maximal drag expectable for fluxing spindles; i.e., the minimum flux. The critical point-associated power may be used to define the low end of expected drag (red broken line). (d) Summary of the system behavior as a function of kinetochore–MT drag in the high-coupling regime. High kinetochore drag maximizes tension at equilibrium, but it comes at the expense of a long equalization time. The reverse happens for low kinetochore drag, suggesting optimal behavior in an intermediate situation (maximal power yield), where flux velocity is not zero and not as high as it could be if generated by free ipMT motors.
Analytical solution of the model shows that two characteristic time scales fully describe the system dynamics (Fig. 6 b; and Materials and methods). First, mean interkinetochore tension at the metaphase plate tends exponentially to an equilibrium tension. Second, individual tensions converge exponentially to the evolving mean tension within the timescale
| (1) |
hereafter referred as the equalization time, which in the high coupling regime (εc = ∞ and kc = ∞) is simply εk/kc. Importantly, τΔ is also the characteristic decay time of the tension standard deviation on the entire chromosome set, and therefore represents a global measure of the tension equalization time in the spindle. λ and f are, respectively, typical elastic deformation and flux velocity scales of the metaphase spindle. The magnitude for λ lies between interkinetochore stretch (typically around 0.5 µm; Waters et al., 1996; Maddox et al., 2003; Meraldi et al., 2004; Maiato et al., 2006) and MT–coupler stretch, which should be less than one half the spindle length (typically 5–15 µm; Waters et al., 1996; Gaetz and Kapoor, 2004; Goshima et al., 2005; Bird and Hyman, 2008). Using f of ∼1 µm/min we get from Eq. 1, τΔ = 0.5–15 min. This estimate is in agreement with metaphase duration in several systems (Rieder et al., 1994; Meraldi et al., 2004; Maiato et al., 2005; Brust-Mascher et al., 2009), regardless of the different number of chromosomes (note the independence of n), and is not affected by the introduction of a tension-assisting force (e.g., due to dynein; Yang et al., 2007) at the kinetochore–MT interface (see Materials and methods).
Using dimensional analysis, a trade-off between low kinetochore–MT affinity (resulting in low tension) and high kinetochore–MT affinity (leading to high tension but slow equalization) may be found in the form of a centromeric power yield, reflecting the fact that centromeric elastic energy should maximally and uniformly accumulate in the metaphase plate in the shortest possible time (Fig. 6, c and d; and Materials and methods). An optimal flux regime is found for high coupling and when kinetochore–MT attachments are strong/weak enough to allow metaphase flux at a velocity between one and three eighths of the unloaded velocity of motors that slide ipMTs (note that these figures are strongly dependent on the shape of the force–velocity relation characterizing motor activity). Finally, the model predicts that ipMT flux is faster than kMT flux as a result of imperfect force transmission, a feature indeed observed in several systems (Maddox et al., 2003; LaFountain et al., 2004; Yang et al., 2008; see Materials and methods).
The SAC extends the duration of mitosis to allow the uniform distribution of forces acting on metaphase kinetochores
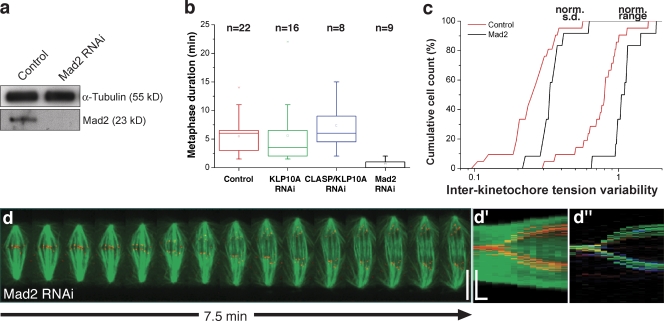
If cells require time for a uniform distribution of tension on metaphase chromosomes, one would predict that acceleration of mitosis prevents this equalization. Mad2 is a key signaling component of the SAC that extends the duration of mitosis until all kinetochores are attached to the spindle (Meraldi et al., 2004). Indeed, RNAi depletion of Mad2 in S2 cells (Fig. 7 a) significantly accelerated mitosis so that cells entered anaphase prematurely (Fig. 7 b; see Orr et al., 2007). Additionally, Mad2-depleted cells that were able to form a metaphase plate showed increased interkinetochore tension variability (Fig. 7 c) and underwent asynchronous chromosome segregation during anaphase (Fig. 7 d–d′′). These results support our theoretical prediction that cells require time for a uniform distribution of forces acting on kinetochores.
Figure 7.
Tension uniformity and synchrony analysis after acceleration of mitosis. (a) Western blot showing Mad2 depletion 96 h after RNAi. α-tubulin was used as loading control. (b) Cumulative histogram for the normalized standard deviation (left) and range (right) of intracellular interkinetochore distances along a metaphase plate for control (n = 21) and Mad2 RNAi (n = 12), where n is the number of cells. Mad2 RNAi is statistically different from controls (P < 0.05, Student t test). (c) Metaphase duration in control, KLP10A RNAi, CLASP/KLP10A RNAi, and Mad2 RNAi cells, where n represents the number of cells capable of forming a metaphase plate. The box plot determines the interquartile range, the line inside the box represents the median, the point inside the box represents the mean, and the whiskers determine the limits of the distribution disregarding outliers. Mad2 RNAi is the only treatment that is statistically different from controls (P < 0.001, Mann-Whitney test). (d–d′′) Kymograph (d), collapsed kymograph (d′), and cromo-kymograph (d′′) analysis of a representative Mad2-depleted cell. Vertical scale bar, 10 µm; horizontal time bar, 1 min.
Discussion
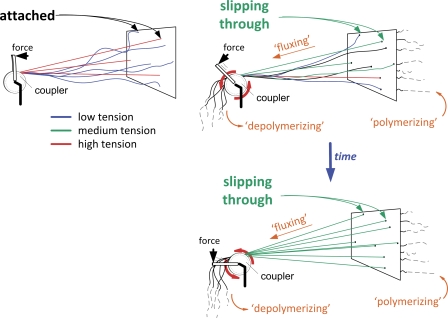
In this paper, we propose that flux-associated slippage of MTs at kinetochores allows spindle forces to become evenly distributed along the metaphase plate. The rationale behind this model is that MT slippage at a given kinetochore interface reflects a mechanical relaxation event that allows ipMT sliding motors to do further work, thus providing extra tension to other chromosomes. Sustained slippage events occurring along the metaphase plate eventually drive the spindle to an equilibrium state characterized by homogeneous tension. An analogy to this tension redistribution mechanism is illustrated in Fig. 8. Tension equalization during metaphase ensures that any mechanism relying on tension, such as the maturation and correction of kinetochore–MT attachments (Nicklas and Ward, 1994; King and Nicklas, 2000; Liu et al., 2009), recruitment of SAC proteins (Pinsky and Biggins, 2005; Musacchio and Salmon, 2007), or even the coordination of cohesin degradation between sister chromatids (this study) operates uniformly along the metaphase plate.
Figure 8.
Schematic representation of the flux-dependent tension redistribution principle. Several cables (representing kMTs) with random lengths are firmly attached to the wall (representing chromosomes at the metaphase plate). Cables are connected to a coupler, which is subjected to a “rotating force” (torque). In the “no flux” condition (left), the coupler will only rotate up to the point where the first cables become under tension, a point in which they resist further rotation: the system reaches a static equilibrium characterized by large tension heterogeneity. In the strict analogy of inextensible cables, a maximum of three cables experience tension. The “flux” condition (right) is characterized by a single modification: instead of being firmly attached, cables are now passing through tight holes in the wall and thereby slip, although not freely, in response to the applied force. Cable “growth” by slippage allows the coupler to keep rotating, eventually leading to stretching (i.e., development of tension) in previously relaxed cables. The system eventually reaches a dynamic equilibrium, characterized by tension homogeneity, although at the expense of diminished mean tension. For clarity, we represent a point-coupler instead of an extended structure. Rotation of the motorized coupler emulates the linear “hand-over-hand” dynamics that characterize permanent attachment/detachment dynamics of system motors/cross-linkers, which allows maintenance of the coupler “position.”
The close match found between equalization time and metaphase duration is, in our opinion, the strongest support for a flux-dependent mechanism for tension equalization. However, such correlation poses a delicate question regarding the relationship between equalization time and the SAC. One possibility is that SAC silencing requires that all chromosomes overcome a given tension threshold. In fact, a uniform distribution of tension maximizes the probability of globally surpassing any threshold. Alternatively, SAC satisfaction may rely only on MT occupancy at kinetochores. A cell with a satisfied SAC in the absence of such tension equalization mechanism would be expected to segregate its chromosomes at distinct times and/or with distinct velocities. Because metaphase duration is not significantly affected after experimental perturbation of flux, and acceleration of mitosis precludes tension equalization, a plausible explanation for the observed asynchronous chromosome segregation is the reduced capacity to evenly mature and correct kinetochore–MT attachments that nevertheless satisfy the SAC. Recent works support the finding that interkinetochore tension is dispensable in satisfying the SAC (O'Connell et al., 2008; Maresca and Salmon, 2009; Uchida et al., 2009). However, tension may provide an important readout to allow the detection and correction of potential errors before anaphase onset (Pinsky and Biggins, 2005). Indeed, application of tension to kinetochores is known to promote its saturation with MTs (King and Nicklas, 2000), possibly by increasing MT stability due to spatial separation of kinetochore substrates from Aurora B at centromeres (Liu et al., 2009). However, maximizing tension by firmly grabbing MTs at their kinetochore attachment sites would not only prevent the release of erroneous attachments, but also hinder kMT flux/slippage, which could lead to chromosome segregation defects (Ganem and Compton, 2006; Bakhoum et al., 2009). Therefore, at the expense of some local loss of tension, MT affinity at kinetochores must be regulated to allow MTs to slip and possibly detach. According to our MT-coupling model, the system will respond globally to equilibrate tensions, and, consequently, all tension-dependent processes, precluding the need for tight spatial regulation of force distribution.
Our experimental perturbation of kMT flux involved down-regulation of CLASP and KLP10A, which appeared not to be implicated in force production but rather on how the spindle responds to it. Localization of CLASP at the kinetochore and its requirement for kMT flux away from the kinetochore (Maiato et al., 2005) suggest that its main function is to regulate the affinity of kMT attachments by decreasing the frictional drag (εk). In support of this conclusion, preventing Hec1 phosphorylation by Aurora B increases the affinity of the Ndc80 complex to MTs, which impairs kMT flux and turnover, while causing a 50% reduction of CLASP levels at kinetochores in Ptk1 cells (DeLuca et al., 2006). It is interesting to note that, although in this cell type the described perturbation leads to hyperstretching of the centromere without affecting spindle bipolarity, CLASP RNAi in S2 cells leads to spindle collapse without any obvious increase in interkinetochore tension (Maiato et al., 2005). These different responses might reflect mechanical peculiarities associated with each cell type. KLP10A depletion likely prevents MT depolymerization at the poles, leading to increased resistance to kMT poleward translocation and consequent flux reduction (see Materials and methods). Similar to polymerization at the kinetochore, depolymerization at the pole seems essentially a reactive mechanism that regulates kMT length upon translocation. Additionally, localization of KLP10A at the centromeres may account for the observed role in the correction of erroneous attachments described in this paper, which may be intrinsically coupled to its role in flux.
One important outcome of asynchronous chromosome segregation is the increased risk of aneuploidy. Recent work in budding yeast, which lack any detectable flux (Maddox et al., 2000), provided a molecular explanation for the abrupt degradation of cohesins at anaphase onset (Holt et al., 2008). It is noteworthy that budding yeast do not align their chromosomes at the cell equator and rely heavily on spindle elongation for accurate chromosome segregation (Straight et al., 1997). In contrast, animal and plant cells establish a metaphase plate, a high-order state that is only justified if the subsequent synchronous migration of sister chromatids is ensured, where a mechanism involved in force equalization may be essential. The emergence of flux in higher eukaryotes and its contribution to anaphase “quality” may play particularly important roles in the prevention of chromosomal abnormalities observed in cancers or in several human syndromes, many of which result from defects in chromosome segregation during meiosis, where flux is indeed maintained at high rates.
Materials and methods
Model description
We supported in the main text the finding that poleward translocation of spindle MTs allows the spindle to relax by passively redistributing excess tensions, thereby smoothening initial deviations from average tension. The underlying model is defined by the mechanical circuit in Fig. 6 a in the main text and in the scheme below, which represents a “half-spindle,”
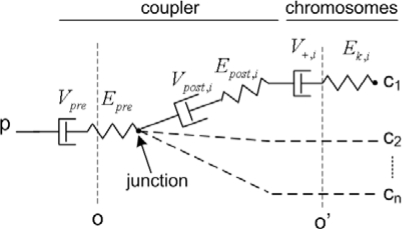 |
where Vpre is the pre-junction coupler dashpot slippage velocity, Vpost,i is the post-junction coupler dashpot slippage velocity (chromosome-indexed), Epre is the pre-junction spring strain, Epost,i is the post-junction spring strain (chromosome-indexed), V+,i is microtubule-kinetochore relative velocity (chromosome-indexed), and Ek,i is the interkinetochore strain (chromosome-indexed). To represent the system mathematically, we first use the homogeneous stress condition, i.e., the sum of forces along o is equal to that along o′ or along any other parallel plane. Assuming linearity of the motor force–velocity (F-V) relation and of all elastic and viscous responses in the spindle we get
| (2) |
where Ti ≡ kkEk,i is the centromeric tension at the i-th chromosome. Second, using the additive strain condition along a path connecting p to the i-th chromosome ci,
| (3) |
Using Eq. 2 to substitute the terms in Eq. 3, we get the ordinary differential equation (ODE) that governs the system dynamics. The j-th centromere tension is given by
| (4) |
To gather an intuitive understanding of the system behavior, we separate the problem in two parts. First we follow the evolution of the ensemble-averaged centromeric tension and then focus on how individual centromere tension levels approach the evolving mean tension. For the first step we simply need to calculate (Eq. 4), giving
a first-order ODE with a solution given by a single exponential that decays in a characteristic time
to the equilibrium tension
| (5) |
where ε* is defined as the friction drag coefficient coupling ipMTs to kinetochores. At equilibrium, kMT fiber slippage velocity (or flux velocity) is As ε* increases, T∞ tends to its maximum value P0/n, a condition in which flux velocity would drop to zero. If ε* decreases, kMT flux velocity tends asymptotically to V0/2, where V0 is the free motor velocity.
For the second step, we study how any individual centromere tension Ti approaches the evolving mean tension 〈T〉E, where the subscript denotes that averaging is done along the chromosome ensemble. The timescale of the decay of Ti − 〈T〉E is equal to that of ΔTij ≡ Ti − Tj, where i and j are any distinct chromosomes. We calculate ΔTij using Eq. 4, where the summation terms vanish, yielding
Thus, individual tension levels redistribute by approaching each other (and the mean tension) in the timescale defined by
the equalization time.
We assumed throughout that the system's viscous and elastic properties may be characterized by bulk magnitudes for both MT–kinetochore and MT–coupler interactions. Regarding coupling, the model assumes that all kMT fiber pairs are (1) equally coupled to each other and (2) equally coupled to the ipMTs. However, we let the coupling efficiencies 1 and 2 be different, which is reflected by the coupling ratio parameter φ. This factor allows variation of ipMT number or its substitution by other (non–MT dependent) motorized structures. For example: φ = 1 represents a spindle in which ipMT-coupler total drag is equivalent to kMT-coupler total drag; φ = ∞ may represent a situation in which the number of ipMTs is very large, with its connections to the coupler being dominant relative to kMT connections to the coupler, or the case of a non-ipMT–based force generation mechanism, which is tightly bound to the coupler.
Ratio between ipMT and kMT poleward translocation velocities
At equilibrium, the ratio between the translocation/flux velocity of ipMTs and kMTs, R, is given by
where we used Eq. 5 along with the relations and In general R > 1 unless the perfect-coupling regime strictly holds (εc = ∞). We did not determine this factor experimentally because of the low number of fluxing ipMTs that we were able to measure, but it has been consistently shown in several systems, including Drosophila S2 cells, that R > 1 (Maddox et al., 2003; LaFountain et al., 2004; Goshima et al., 2005).
Optimal performance of the model mechanical system
We now study the trade-off between loose and tight attachment at the microtubule–kinetochore interface. In search of a compromise, we maximize tension and minimize redistribution time by defining a dimensionally meaningful parameter to be maximized, (Fig. 6 c), which is a measure of centromeric power. Power maximization reflects the fact that the physical system is tuned to allow the largest fraction of the available energy in the spindle to be uniformly accumulated in the form of elastic energy at the metaphase plate within the shortest possible time. The optimal regime is found to occur for high coupling (εc = ∞) but with intermediate εk (see Fig. 6 c). Optimal εk is independent of φ and given by which leads to an equilibrium tension equal to half its maximum value T∞ = P0/(2n), or a flux velocity equal to V0/4. A critical value of
which corresponds to a flux velocity of V0/[4(1 + φ−1)], may be found above which εk = ∞ always maximizes Ω, a condition in which equalization is achieved solely by slippage at the coupler–MTs interface but at the expense of a reduced power yield: Ωmax,high-coupling/Ωmax,high-attachment = 1 + φ−1.
In summary, the mechanical system in Fig. 6 a will behave most efficiently if kMTs are strongly coupled to the poleward force-generating structures (and therefore between them), whereas their attachment to kinetochores allows kMT flux velocity between one and three eighths of the maximal motor velocity when ipMTs and kMTs have comparable attachments to the coupler (φ of ∼1). This range is broadly consistent with the observed magnitude of flux velocities in different systems if it is assumed that motors with ∼5 µm/min free velocity are responsible for ipMT sliding. We stress that nonlinearities in the motor F-V relation will shift this optimal regime.
Effect of polar resistance to microtubule poleward translocation
We have presented a model for the “wild-type” spindle. To study the possible effect of KLP10A depletion on metaphase spindle tension and dynamics, we introduced a set of polar viscous elements antagonizing microtubule sliding. We assume these dashpots to be anchored (e.g., by astral MTs at the cortex). Adding such viscous term εpV−,i, where is the depolymerization velocity, to Eqs. 2 and 3 yields a second-order ODE with overdamped solutions that tend to an equilibrium tension given by
where εp is the viscous drag at the poles. As expected, an increase in εp leads to decreased centromeric tension, which, however, may be recovered by an increase in εk. This is in broad agreement with mean tension recovery (as measured by interkinetochore distance) in KLP10A RNAi followed by codepletion of CLASP (Table I). However, flux velocity at equilibrium, given by will drop upon increased εp or εk. Polar resistance will in general lead to an increased equalization time, which for stiff coupling (kc → ∞) is given by
Effect of an active tension-generating mechanism at the kinetochore
An offset force component, Fk, may be introduced in the model to account for kinetochore-based tension generation, possibly by minus end–directed motors like dynein (Howell et al., 2001; Yang et al., 2007). Tension is then given by Ti(t) = εkV+,i(t) + Fk. For clarity, we describe Fk as a fraction f of the maximum tension deliverable by an equilibrated spindle, Fk = f Po/n. Only the constant term in Eq. 4 is modified, with the RHS becoming which naturally doesn't change the timescales that describe the system, τΔ or τ∞. However, equilibrium tension is now increased to
To first order in f, optimal behavior (see “Optimal performance of the model mechanical system”) occurs for valid for f ≪ 1, with εc = ∞. This means that introduction of an active tension-assisting component at the kinetochore shifts the optimal behavior to the slightly increased flux velocity V0(1 + f)/4.
RNAi
RNAi depletion of Drosophila CLASP, KLP10A, and Mad2 in S2 cells was performed as described previously (Rogers et al., 2004; Maiato et al., 2005; Orr et al., 2007). Phenotypes were quantified by light microscopy every 24 h over 7 d. Protein knockdown was monitored by Western blotting using the following antibodies and dilutions: rabbit anti-CLASP and anti-Mad2 (gifts from C. Sunkel, Instituto de Biologia Molecular e Cellular, University of Porto, Portugal) 1:600 and 1:3,000, respectively; rabbit anti-KLP10A (gift from J. Scholey, University of California, Davis, Davis, CA) 1:1500; and mouse anti–α-tubulin clone B512 (Sigma-Aldrich) 1:10,000. Secondary antibodies were visualized using the ECL system (GE Healthcare).
Drug treatments
To suppress MT dynamics in S2 cells, we used 10 nM taxol for 10 min before time-lapse recording or immunofluorescence processing. Whenever indicated, the proteasome inhibitor MG132 was used at 20 µM for 2 h. To determine the interkinetochore rest length, we treated S2 cells with 30 µM colchicine for 2 h to induce MT depolymerization.
Immunofluorescence microscopy
S2 cells were grown on 0.5 mg/ml concanavalin A (Sigma-Aldrich)-coated coverslips and processed for immunofluorescence as described previously (Maiato et al., 2004b). Primary antibodies were rabbit anti–γ-tubulin (1:500; gift from A. Debec, Institut Jacques Monod, Paris, France); mouse anti–α-tubulin clone B512 (1:1500; Sigma-Aldrich); rabbit anti-BubR1 and anti-Scc1 (1:2,000 and 1:500, respectively; gifts from C. Sunkel); chicken anti-CID (1:300; gift from G. Karpen, University of California, Berkeley, Berkeley, CA); rabbit anti-Aurora B (1:500; a gift from M. Carmena and B. Earnshaw, University of Edinburgh, Edinburgh, Scotland, UK). All fluorescent-conjugated secondary antibodies were from the Alexa Fluor series (Invitrogen). Quantitative 3D datasets were collected using a wide-field microscope (Imager.Z1; Carl Zeiss, Inc.) equipped with a charge-coupled device (CCD; Axiocam MRm) and using a 100×, 1.4 NA oil immersion objective lens at 0.25 µm z steps, using Axiovision software. For an imaging medium, we used 89.5% glycerol, 10% 1 M Tris-HCl, pH 8.5, and 0.5% N-propyl-gallate. Images were subsequently blind deconvolved with AutoDeblur X2 software (Media Cybernetics) and processed for publication using Photoshop CS3 (Adobe).
Time-lapse microscopy
S2 cells stably expressing GFP–α-tubulin (a gift from R. Vale, University of California, San Francisco, San Francisco, CA) and CID-mCherry (the mCherry cDNA was provided by R. Tsien, University of California, San Diego, La Jolla, CA) or mRFP-BubR1 (mRFP-BubR1 construct was modified from a vector provided by R. Karess, Institut Jacques Monod, Paris, France) were grown on concanavalin A–coated coverslips and mounted in modified Rose chambers with Schneider's medium (Sigma-Aldrich) containing 10% FBS. 4D datasets covering the entire cell volume were collected every 30 s with 1-µm z steps with a 100× 1.4 NA Plan-Apochromatic objective at 25°C with a Revolution Spinning Disk confocal system (Andor) equipped with an electron multiplying CCD (EMCCD) iXonEM+ camera, two laser lines (488 and 561 nm), and a Yokogawa CSU-22 unit based on an inverted microscope (IX81; Olympus) and driven by Andor IQ.
Fluorescent speckle microscopy
To measure flux rates, we used S2 cells stably expressing GFP–α-tubulin under the control of a leaky inducible metallothionein promoter (a gift from R. Vale) and CID-mCherry. Without induction, low levels of GFP–α-tubulin are expressed. Time-lapse images were collected every 5 s at 25°C with an inverted microscope (TE2000U; Nikon) equipped with a CoolSNAP HQ2 CCD camera (Photometrics) using a 100× 1.4 NA Plan-Apochromatic objective, and driven by NIS elements (Nikon). Images were subsequently blind-deconvolved with AutoDeblur X2 (Media Cybernetics).
Guided kymography
In order to either kymograph the entire spindle or to prepare the data for local kymograph analysis, we used a custom routine written in Matlab (The MathWorks, Inc.) to compensate for spindle rotation and translation described by the following steps: (1) 2D tracking of spindle poles, (2) region-of-interest (ROI) dimensions definition, and (3) thick-kymograph generation with the ROI being automatically translated and rotated every frame according to the 2D coordinates of the two reference objects in step 1. The direct output is a whole-spindle kymograph that can be used to generate a set of aligned images that are the basis for all subsequent analysis. For a detailed description see Pereira and Maiato, 2009.
Chromo-kymography
Chromo-kymograph generation was implemented using Matlab by assigning different colors to the n pixel rows of the n × m ROI by defining a color-gradient filter along the vertical axis (n rows). For the color filter, we used linearly varying red/green/blue components. A sum projection is performed on the n × m × 3 matrix to obtain an m × 3 output. For each time-lapse image, this transformation generates a 90° “tilted” 2D matrix with dimensions 1 × m × 3, where the three layers are weighed red/green/blue contributions. Final chromo-kymograph dimensions are: (number of time-lapse images) × m × 3. For a detailed description see Pereira and Maiato, 2009.
Collapsed kymography
Raw kymographs are composed of an image stack at different time points, each with dimensions n × m. Collapsed kymographs are projections of the raw kymograph that result from conversion of each time point image matrix into a vector, according to some weighed combination (e.g., mean or maximum) of the pixels along each column of the ROI. Chromo-kymographs are a generalization of collapsed kymographs on which three different weight functions are applied, each one generating an RGB channel of the output chromo-kymograph.
Laser microsurgery
We use the second harmonic (532 nm) of a Nd:YAG laser to generate quasi-single mode (M2 < 1.5) 8-ns pulses. Pulse energy for kMT surgery is 1–2 μJ. The laser beam was steered onto a microscope (TE2000U; Nikon) with “stage up-kit,” which allows the laser beam to overlap the microscope optical axis in the infinite-conjugated section. The laser beam diameter is adjusted to fill the objective back aperture to minimize spot diameter at the sample (<0.5 μm). The details of the optical system have been described previously (Pereira et al., 2009).
Quantifications
Spindle length in fixed material was measured for each bipolar spindle as the distance between opposite poles revealed by γ-tubulin immunostaining.
Flux velocities were measured by kymograph analysis in which a long thin rectangular region covering the entire spindle length is extracted from each image in the time-lapse series and sequentially aligned with reference to the poles. The position of the rectangular region is chosen by the presence of a kinetochore pair and correspondent kMTs. On these collapsed kymographs, slopes corresponding to the movement of bright or dark speckles over time (equivalent to the flux velocity) are directly measured. Results obtained by this method reveal slightly faster kinetochore MT flux velocities than those obtained by other techniques such as photobleaching or photoactivation of spindle MTs (Maiato et al., 2005; Rogers et al., 2005; Buster et al., 2007).
Chromosome poleward velocity relative to the equator was measured after each CID-mCherry track obtained from chromo-kymographs covering the entire cell volume. Velocity was determined measuring the slope of the fastest linear movement after anaphase onset within each half spindle. The distribution shown in the histogram represents each track measured in the total number of cells.
Spindle elongation velocity was measured after spindle MT minus ends. Slopes were determined for the same period of time when chromosome poleward velocity was measured. Each value shown in the histogram is the mean from the slopes of both half spindles per cell.
KMT shortening velocity was measured as the difference between each measurement of poleward chromosome velocity and the corresponding half-spindle elongation velocity. Given the observed asynchrony after perturbation of flux, each value represented in the histogram represents individual kMT shortening measurements.
MT minus-end depolymerization rates in anaphase were quantified by subtracting the MT minus-end slope to the speckle slope. MT minus ends were determined using collapsed kymographs, which gather all MT minus ends converging to a common focus.
Interkinetochore distances measured from fixed samples were obtained after immunofluorescence as the distance between centroids of CID-labeled kinetochore pairs through metaphase z stacks using ImageJ 1.30 software (National Institutes of Health). Interkinetochore distances measured from living cells represent the distance between centroids of opposite CID-mCherry pairs through metaphase z stacks 2 min before anaphase onset. Anaphase onset was inferred as the moment where at least two kinetochore pairs were at a distance higher than 1.2 µm. Intracellular tension variability was quantified upon calculation of the coefficient of variation, σT/〈T〉, which for a linear spring is equal to σd/(〈d〉 − d0), where d is the interkinetochore distance in metaphase and d0 is the interkinetochore distance in prophase (rest length).
Quantification of BubR1 fluorescence at kinetochores was performed relative to CID fluorescence as described previously (Hoffman et al., 2001) using ImageJ 1.30 software and a partially automated tool written in Matlab. In brief, an inner and an outer ROI are defined so that the first fully encloses the kinetochore and the second additionally encloses a small peripheral area, which is used to estimate intensity background. If the integrated signal is Si in an inner ROI with dimensions i × j and So in an outer ROI with dimensions k × l, then the background-subtracted signal is S = Si − (So − Si) × (i × j)/(k × l − i × j). For kinetochore quantification, we used 9 × 9 pixel and 13 × 13 pixel ROIs (1 pixel = 65 nm). To measure Aurora B signal in the metaphase plate, we quantified both Aurora B and CID in the entire metaphase plate with a fixed ROI. Background intensity was estimated from an area contiguous to the spindle.
Cold stable kMTs were quantified by immunofluorescence after 10 min at 4°C.
Metaphase duration was defined from the moment of alignment of the last chromosome at the metaphase plate until anaphase onset.
Regrowth of laser-cut kMT fibers was only measured when the newly created kMT plus ends underwent clear catastrophe. The minus ends of the growing kinetochore-associated fibers were manually tracked using a Matlab script. A linear fit was done to the data points of kMT length over time to obtain growth velocity.
Statistical analyses
Statistical analysis was performed using either parametric one-way (ANOVA) or nonparametric analysis of variance (Kruskal-Wallis) for multiple group comparisons according to the normality of the distribution as determined by Kolmogorov-Smirnov test. All pairwise multiple comparisons were subsequently analyzed using either post hoc Student-Newman-Keuls (parametric) or Dunn's (nonparametric) tests. A parametric t test or nonparametric Mann-Whitney was used for two group comparisons. We used both standard deviation and interquartile range as measures of the distribution spread. All statistical analysis was performed using SigmaStat 3.5 (Systat Software).
Online supplemental material
Fig. S1 shows analysis of spindle elongation and kinetochore–MT attachments after KLP10A RNAi. Fig. S2 shows analysis of sister chromatid separation in anaphase and BubR1 levels at kinetochores. Online supplemental material is available at http://www.jcb.org/cgi/content/full/jcb.200904153/DC1.
Acknowledgments
We thank J. Scholey for communicating results before publication and for a gift of antibodies; R. Vale, G. Karpen, R. Tsien, R. Karess, Mar Carmena, Bill Earnshaw, and C. Sunkel for the gift of reagents; M.S. Belsley, F.P. Ferreira, J.V. Gomes, and P.A. Coelho for discussions; and A. Khodjakov and V. Magidson for advice on the set up of our laser microsurgery system.
I. Matos and M. Lince-Faria hold fellowships (SFRD/BD/22020/2005 and SFRH/BPD/26780/2006) from Fundação para a Ciência e a Tecnologia (FCT) of Portugal, and A.J. Pereira was supported by Crioestaminal/Viver a Ciência. Work in the laboratory of H. Maiato is supported by grants PTDC/BIA-BCM/66106/2006 and PTDC/SAU-OBD/66113/2006 from FCT, and the Gulbenkian Programmes for Research Stimulation and Frontiers in the Life Sciences.
Footnotes
Abbreviations used in this paper: CID, centromere identifier; CLASP, cytoplasmic linker associated protein; FSM, fluorescent speckle microscopy; ipMT, interpolar MT; kMT, kinetochore MT; MT, microtubule; ROI, region of interest; SAC, spindle assembly checkpoint.
References
- Bakhoum S.F., Thompson S.L., Manning A.L., Compton D.A. 2009. Genome stability is ensured by temporal control of kinetochore-microtubule dynamics.Nat. Cell Biol. 11:27–35 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Basto R., Lau J., Vinogradova T., Gardiol A., Woods C.G., Khodjakov A., Raff J.W. 2006. Flies without centrioles.Cell. 125:1375–1386 [DOI] [PubMed] [Google Scholar]
- Bird A.W., Hyman A.A. 2008. Building a spindle of the correct length in human cells requires the interaction between TPX2 and Aurora A.J. Cell Biol. 182:289–300 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brangwynne C.P., MacKintosh F.C., Kumar S., Geisse N.A., Talbot J., Mahadevan L., Parker K.K., Ingber D.E., Weitz D.A. 2006. Microtubules can bear enhanced compressive loads in living cells because of lateral reinforcement.J. Cell Biol. 173:733–741 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brust-Mascher I., Civelekoglu-Scholey G., Kwon M., Mogilner A., Scholey J.M. 2004. Model for anaphase B: role of three mitotic motors in a switch from poleward flux to spindle elongation.Proc. Natl. Acad. Sci. USA. 101:15938–15943 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brust-Mascher I., Sommi P., Cheerambathur D.K., Scholey J.M. 2009. Kinesin-5-dependent poleward flux and spindle length control in Drosophila embryo mitosis.Mol. Biol. Cell. 20:1749–1762 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buster D.W., Zhang D., Sharp D.J. 2007. Poleward tubulin flux in spindles: regulation and function in mitotic cells.Mol. Biol. Cell. 18:3094–3104 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cameron L.A., Yang G., Cimini D., Canman J.C., Kisurina-Evgenieva O., Khodjakov A., Danuser G., Salmon E.D. 2006. Kinesin 5-independent poleward flux of kinetochore microtubules in PtK1 cells.J. Cell Biol. 173:173–179 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cimini D., Moree B., Canman J.C., Salmon E.D. 2003. Merotelic kinetochore orientation occurs frequently during early mitosis in mammalian tissue cells and error correction is achieved by two different mechanisms.J. Cell Sci. 116:4213–4225 [DOI] [PubMed] [Google Scholar]
- Cimini D., Cameron L.A., Salmon E.D. 2004. Anaphase spindle mechanics prevent mis-segregation of merotelically oriented chromosomes.Curr. Biol. 14:2149–2155 [DOI] [PubMed] [Google Scholar]
- Danuser G., Waterman-Storer C.M. 2006. Quantitative fluorescent speckle microscopy of cytoskeleton dynamics.Annu. Rev. Biophys. Biomol. Struct. 35:361–387 [DOI] [PubMed] [Google Scholar]
- DeLuca J.G., Gall W.E., Ciferri C., Cimini D., Musacchio A., Salmon E.D. 2006. Kinetochore microtubule dynamics and attachment stability are regulated by Hec1.Cell. 127:969–982 [DOI] [PubMed] [Google Scholar]
- Forer A., Pickett-Heaps J.D., Spurck T. 2008. What generates flux of tubulin in kinetochore microtubules? Protoplasma. 232:137–141 [DOI] [PubMed] [Google Scholar]
- Gaetz J., Kapoor T.M. 2004. Dynein/dynactin regulate metaphase spindle length by targeting depolymerizing activities to spindle poles.J. Cell Biol. 166:465–471 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ganem N.J., Compton D.A. 2006. Functional roles of poleward microtubule flux during mitosis.Cell Cycle. 5:481–485 [DOI] [PubMed] [Google Scholar]
- Ganem N.J., Upton K., Compton D.A. 2005. Efficient mitosis in human cells lacking poleward microtubule flux.Curr. Biol. 15:1827–1832 [DOI] [PubMed] [Google Scholar]
- Ganem N.J., Storchova Z., Pellman D. 2007. Tetraploidy, aneuploidy and cancer.Curr. Opin. Genet. Dev. 17:157–162 [DOI] [PubMed] [Google Scholar]
- Gorbsky G.J., Sammak P.J., Borisy G.G. 1987. Chromosomes move poleward in anaphase along stationary microtubules that coordinately disassemble from their kinetochore ends.J. Cell Biol. 104:9–18 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goshima G., Wollman R., Stuurman N., Scholey J.M., Vale R.D. 2005. Length control of the metaphase spindle.Curr. Biol. 15:1979–1988 [DOI] [PubMed] [Google Scholar]
- Hoffman D.B., Pearson C.G., Yen T.J., Howell B.J., Salmon E.D. 2001. Microtubule-dependent changes in assembly of microtubule motor proteins and mitotic spindle checkpoint proteins at PtK1 kinetochores.Mol. Biol. Cell. 12:1995–2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holt L.J., Krutchinsky A.N., Morgan D.O. 2008. Positive feedback sharpens the anaphase switch.Nature. 454:353–357 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Howell B.J., McEwen B.F., Canman J.C., Hoffman D.B., Farrar E.M., Rieder C.L., Salmon E.D. 2001. Cytoplasmic dynein/dynactin drives kinetochore protein transport to the spindle poles and has a role in mitotic spindle checkpoint inactivation.J. Cell Biol. 155:1159–1172 [DOI] [PMC free article] [PubMed] [Google Scholar]
- King J.M., Nicklas R.B. 2000. Tension on chromosomes increases the number of kinetochore microtubules but only within limits.J. Cell Sci. 113:3815–3823 [DOI] [PubMed] [Google Scholar]
- Knowlton A.L., Lan W., Stukenberg P.T. 2006. Aurora B is enriched at merotelic attachment sites, where it regulates MCAK.Curr. Biol. 16:1705–1710 [DOI] [PubMed] [Google Scholar]
- LaFountain J.R., Jr., Cohan C.S., Siegel A.J., LaFountain D.J. 2004. Direct visualization of microtubule flux during metaphase and anaphase in crane-fly spermatocytes.Mol. Biol. Cell. 15:5724–5732 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laycock J.E., Savoian M.S., Glover D.M. 2006. Antagonistic activities of Klp10A and Orbit regulate spindle length, bipolarity and function in vivo.J. Cell Sci. 119:2354–2361 [DOI] [PubMed] [Google Scholar]
- Liu D., Vader G., Vromans M.J., Lampson M.A., Lens S.M. 2009. Sensing chromosome bi-orientation by spatial separation of aurora B kinase from kinetochore substrates.Science. 323:1350–1353 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maddox P., Straight A., Coughlin P., Mitchison T.J., Salmon E.D. 2003. Direct observation of microtubule dynamics at kinetochores in Xenopus extract spindles: implications for spindle mechanics.J. Cell Biol. 162:377–382 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maddox P.S., Bloom K.S., Salmon E.D. 2000. The polarity and dynamics of microtubule assembly in the budding yeast Saccharomyces cerevisiae.Nat. Cell Biol. 2:36–41 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maiato H., DeLuca J., Salmon E.D., Earnshaw W.C. 2004a. The dynamic kinetochore-microtubule interface.J. Cell Sci. 117:5461–5477 [DOI] [PubMed] [Google Scholar]
- Maiato H., Rieder C.L., Khodjakov A. 2004b. Kinetochore-driven formation of kinetochore fibers contributes to spindle assembly during animal mitosis.J. Cell Biol. 167:831–840 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maiato H., Khodjakov A., Rieder C.L. 2005. Drosophila CLASP is required for the incorporation of microtubule subunits into fluxing kinetochore fibres.Nat. Cell Biol. 7:42–47 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maiato H., Hergert P.J., Moutinho-Pereira S., Dong Y., Vandenbeldt K.J., Rieder C.L., McEwen B.F. 2006. The ultrastructure of the kinetochore and kinetochore fiber in Drosophila somatic cells.Chromosoma. 115:469–480 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manning A.L., Compton D.A. 2007. Mechanisms of spindle-pole organization are influenced by kinetochore activity in mammalian cells.Curr. Biol. 17:260–265 [DOI] [PubMed] [Google Scholar]
- Maresca T.J., Salmon E.D. 2009. Intrakinetochore stretch is associated with changes in kinetochore phosphorylation and spindle assembly checkpoint activity.J. Cell Biol. 184:373–381 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meraldi P., Draviam V.M., Sorger P.K. 2004. Timing and checkpoints in the regulation of mitotic progression.Dev. Cell. 7:45–60 [DOI] [PubMed] [Google Scholar]
- Mitchison T.J. 1989. Polewards microtubule flux in the mitotic spindle: evidence from photoactivation of fluorescence.J. Cell Biol. 109:637–652 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitchison T.J. 2005. Mechanism and function of poleward flux in Xenopus extract meiotic spindles.Philos. Trans. R. Soc. Lond. B Biol. Sci. 360:623–629 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miyamoto D.T., Perlman Z.E., Burbank K.S., Groen A.C., Mitchison T.J. 2004. The kinesin Eg5 drives poleward microtubule flux in Xenopus laevis egg extract spindles.J. Cell Biol. 167:813–818 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Musacchio A., Salmon E.D. 2007. The spindle-assembly checkpoint in space and time.Nat. Rev. Mol. Cell Biol. 8:379–393 [DOI] [PubMed] [Google Scholar]
- Nicklas R.B., Ward S.C. 1994. Elements of error correction in mitosis: microtubule capture, release, and tension.J. Cell Biol. 126:1241–1253 [DOI] [PMC free article] [PubMed] [Google Scholar]
- O'Connell C.B., Loncarek J., Hergert P., Kourtidis A., Conklin D.S., Khodjakov A. 2008. The spindle assembly checkpoint is satisfied in the absence of interkinetochore tension during mitosis with unreplicated genomes.J. Cell Biol. 183:29–36 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Orr B., Bousbaa H., Sunkel C.E. 2007. Mad2-independent spindle assembly checkpoint activation and controlled metaphase-anaphase transition in Drosophila S2 cells.Mol. Biol. Cell. 18:850–863 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pereira A.J., Maiato H. 2009. Improved kymography tools and its applications to mitosis.Methods. In press [DOI] [PubMed] [Google Scholar]
- Pereira A.J., Matos I., Lince-Faria M., Maiato H. 2009. Dissecting mitosis with laser microsurgery and RNAi in Drosophila cells.Methods Mol. Biol. 545:145–164 [DOI] [PubMed] [Google Scholar]
- Pinsky B.A., Biggins S. 2005. The spindle checkpoint: tension versus attachment.Trends Cell Biol. 15:486–493 [DOI] [PubMed] [Google Scholar]
- Rieder C.L., Schultz A., Cole R., Sluder G. 1994. Anaphase onset in vertebrate somatic cells is controlled by a checkpoint that monitors sister kinetochore attachment to the spindle.J. Cell Biol. 127:1301–1310 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rogers G.C., Rogers S.L., Schwimmer T.A., Ems-McClung S.C., Walczak C.E., Vale R.D., Scholey J.M., Sharp D.J. 2004. Two mitotic kinesins cooperate to drive sister chromatid separation during anaphase.Nature. 427:364–370 [DOI] [PubMed] [Google Scholar]
- Rogers G.C., Rogers S.L., Sharp D.J. 2005. Spindle microtubules in flux.J. Cell Sci. 118:1105–1116 [DOI] [PubMed] [Google Scholar]
- Straight A.F., Marshall W.F., Sedat J.W., Murray A.W. 1997. Mitosis in living budding yeast: anaphase A but no metaphase plate.Science. 277:574–578 [DOI] [PubMed] [Google Scholar]
- Tucker J.D., Preston R.J. 1996. Chromosome aberrations, micronuclei, aneuploidy, sister chromatid exchanges, and cancer risk assessment.Mutat. Res. 365:147–159 [DOI] [PubMed] [Google Scholar]
- Uchida K.S., Takagaki K., Kumada K., Hirayama Y., Noda T., Hirota T. 2009. Kinetochore stretching inactivates the spindle assembly checkpoint.J. Cell Biol. 184:383–390 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Valentine M.T., Fordyce P.M., Krzysiak T.C., Gilbert S.P., Block S.M. 2006. Individual dimers of the mitotic kinesin motor Eg5 step processively and support substantial loads in vitro.Nat. Cell Biol. 8:470–476 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Waters J.C., Mitchison T.J., Rieder C.L., Salmon E.D. 1996. The kinetochore microtubule minus-end disassembly associated with poleward flux produces a force that can do work.Mol. Biol. Cell. 7:1547–1558 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang G., Cameron L.A., Maddox P.S., Salmon E.D., Danuser G. 2008. Regional variation of microtubule flux reveals microtubule organization in the metaphase meiotic spindle.J. Cell Biol. 182:631–639 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang Z., Tulu U.S., Wadsworth P., Rieder C.L. 2007. Kinetochore dynein is required for chromosome motion and congression independent of the spindle checkpoint.Curr. Biol. 17:973–980 [DOI] [PMC free article] [PubMed] [Google Scholar]