Viscoelasticity imaging using ultrasound: parameters and error analysis

Abstract

Techniques are being developed to image viscoelastic features of soft tissues from time-varying strain. A compress-hold-release stress stimulus commonly used in creep-recovery measurements is applied to samples to form images of elastic strain and strain retardance times. While the intended application is diagnostic breast imaging, results in gelatin hydrogels are presented to demonstrate the techniques. The spatiotemporal behaviour of gelatin is described by linear viscoelastic theory formulated for polymeric solids. Measured creep responses of polymers are frequently modelled as sums of exponentials whose time constants describe the delay or retardation of the full strain response. We found the spectrum of retardation times τ to be continuous and bimodal, where the amplitude at each τ represents the relative number of molecular bonds with a given strength and conformation. Such spectra indicate that the molecular weight of the polymer fibres between bonding points is large. Imaging parameters are found by summarizing these complex spectral distributions at each location in the medium with a second-order Voigt rheological model. This simplification reduces the dimensionality of the data for selecting imaging parameters while preserving essential information on how the creeping deformation describes fluid flow and collagen matrix restructuring in the medium. The focus of this paper is on imaging parameter estimation from ultrasonic echo data, and how jitter from hand-held force applicators used for clinical applications propagate through the imaging chain to generate image noise.

1. Introduction

Phase-sensitive imaging modalities such as ultrasound, MRI and OCT are frequently used to image mechanical properties of soft biological tissues (Greenleaf et al 2003, Ko et al 2006). The value of diagnostic elasticity imaging stems from the contrast observed in viscoelastic features that correlate with important changes in stroma and other connective tissues that are characteristic of disease processes (Sarvazyan 1998, Krouskop et al 1998). Our goal is to understand the molecular basis for the viscoelastic contrast observed in order to develop reliable breast elasticity imaging techniques. There are many different approaches to imaging mechanical features of tissues (Lerner and Parker 1988, Ophir et al 1991, Fatemi and Greenleaf 1998, McKnight et al 2002, Sharma et al 2004, Sinkus et al 2005). The information provided by each approach varies with the bandwidth of the deformation stimulus. For example, at the lowest stress frequencies in the stimulus bandwidth of quasi-static elasticity imaging, elastic strain images can be formed that can be valuable for differentiating benign and malignant palpable breast masses (Garra et al 1997, Hall et al 2003). However, recent studies on early-stage non-palpable masses show that elastic strain can also be non-specific for cancer (Lorenzen et al 2003, Insana et al 2004, Pellot-Barakat et al 2006). In those cases, lesion discriminability may be enhanced by adding strain information from slightly higher stress stimulus frequencies; e.g., by imaging viscoelastic features from time-varying strain following a compress-hold-release stress stimulus. The motivation for this approach comes from the pathology literature on the ultrastructure of the extracellular matrix (ECM) in breast lobules (Losa and Alini 1993). Profound changes in the ECM were found to occur in malignant tissues that exhibit lower extracellular fluid viscosity as compared with that of benign lesions. Spatial variations in fluid permeability generate contrast in viscoelastic features that aid in discriminating lesion types.

The approach to viscoelastic imaging is a straightforward extension of elastic strain imaging using quasi-static compression. A linear array ultrasound transducer is pressed into one surface of the medium to induce an approximately uniaxial stress field. The applied force is small enough to assume a linear viscoelastic response. Ultrasonic RF frames are recorded before and after compression, and correlation-based (Chaturvedi et al 1998) algorithms are applied to the echo data to estimate a time series of strain images. Strain is computed from the displacement component along the axis of the ultrasound beam. To estimate viscoelastic features, the compressive force is held constant for 10–2000 s while RF echo frames are recorded. If constant uniaxial stress is achieved, the time series of RF frames allows us to image the spatial distribution of viscous creep in the medium. Creep is the measure of time-varying strain for a medium under a constant load. Hydro-polymers creep because the full strain is delayed in time (retarded) by viscoelastic properties that are characteristic of the chemical structure of the polymer. While variations in boundary conditions add uncertainty to the estimated parameters used as pixel values, the effects are offset by typically large object contrast.

Time-dependent creep curves can be measured for each strain pixel. We fit the multi-exponential creep curves to a low-order discrete Voigt model to estimate two retardance times per pixel. This paper describes how (a) the retardance times are computed from the creep curves and (b) deviation of the stress field from the assumed constant value generates noise in retardance time images.

The test media for this study were animal-hide gelatin hydrogels (Hayes et al 1997, Madsen et al 2005, Ward 1954). Gelatin was selected to develop viscoelastic imaging methods because of its known and relatively simple molecular structure (Djabourov et al 1993), and, in our experience, it has demonstrated inter-sample reproducibility of mechanical response. Mechanical properties of gelatin gels and breast-tissue stroma are both determined by a high molecular-weight, type I collagen matrix that is saturated in water. The dense electric charge concentration of the matrix peptide side-chains gives gelatin hydrophilic properties that determine its viscoelastic behaviour (Ferry 1980). Stromal breast tissues, however, also have a negatively charged polysaccharide gel surrounding the collagen molecules. The polysaccharide gel plays a major role in determining the viscoelastic properties of the stroma and is responsible for material properties (Fung 1993, Gordenne et al 1985, Stoeckelhuber et al 2002). Gelatin does not have a polysaccharide gel, and yet its mechanical properties can be adjusted to approximate those of soft tissues by adding chemical cross-linkers (Madsen et al 2005) or by adjusting pH to vary the ionic concentration (Sridhar and Insana 2005). In addition, gelatin properties are much more sensitive to thermal and mechanical histories (Ward and Courts 1977, Hoffman 1991) than living stroma because the aggregate structure of denatured collagen molecules in gelatin is less stable than the triple helical structure of collagen in stromal ECM. Despite structural differences, the viscoelastic spectra for the two media have similar shapes, suggesting that similar mechanisms control viscoelastic behaviour. Structural differences between the media appear to only change features of the same basic spectral shape (Sridhar et al 2006a, 2006b). Consequently, gelatin is a reasonable physical model to aid in the development of viscoelastic breast imaging techniques.

2. Methods

The methods section has four major parts. In the first part, the imaging experiment with gelatin samples is outlined. In the second part, imaging parameters extracted from creep curves are described briefly in the context of constitutive equations assumed for the imaging geometry. Details of the analysis may be found elsewhere (Sridhar et al 2007). Third, curve-fitting and filtering methods used to estimate viscoelastic parameters from creep curves are described. This processing generates physically descriptive imaging parameters based on the retardation-time distribution. Fourth, parametric errors are estimated from experimental uncertainties.

2.1. Imaging techniques

Frames of RF echo data are recorded while a force is suddenly applied to the top surface of a sample, held for a specified time and released. The basic technique is the same as with other strain imaging methods that use quasi-static compression stimuli. Stress was applied using a precise motion controller system or with a jittery freehand technique; the former minimized stress stimulus uncertainties. Both methods are described below.

2.1.1. Computer-controlled stress

A linear array transducer (Siemens Sonoline Antares system and VF10-5 linear array transmitting at 8 MHz) is flush mounted to a compression plate and positioned with a computer-controlled motion system (Galil Inc., Rocklin, CA) as depicted in figure 1. A small pre-load is applied to acoustically couple the probe to the gelatin block. Then a short-duration (~1 s) ramp stress of amplitude 500 Pa is applied along the beam axis and normal to the top surface. The force is held to initiate creep measurements. Force is measured using a digital balance (Denver Instruments Co., Model TR-6101, Denver, CO) and maintained at a constant value by feeding the force-balance signal back to the motion controller. The effects of the stress ramp rate are discussed in (Sridhar et al 2007). Mineral oil is applied to all exposed gelatin surfaces to minimize desiccation and allow contact boundaries to freely slip under the load.

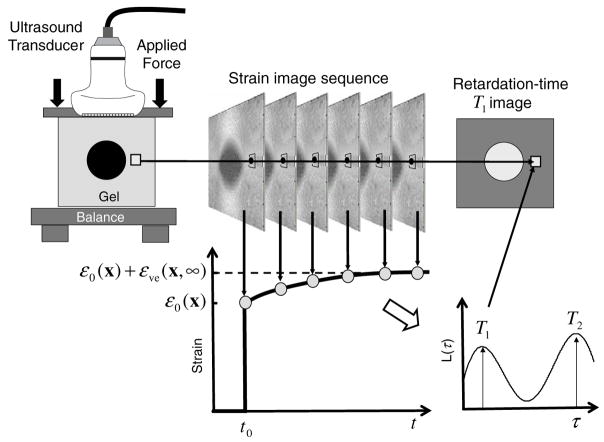
Figure 1.

A technique for imaging viscoelastic properties of a gelatin phantom is illustrated. The object (top-left) is compressed from above and held while the ultrasound system records a series of RF echo frames from which a sequence of strain images (top-centre) is computed. Pixels from the strain-image sequence (bottom-left) are fitted to viscoelastic models to compute retardation-time (T_ℓ) images (top-right) that correspond to retardance spectral distribution L(τ) peaks (bottom-right).

Echo frames are recorded synchronous with the transducer motion at a rate between 1 and 4 fps for up to 2000 s. The URI feature of the Antares provides digitized RF echo frames that can be triggered using an external waveform generator connected to the ECG trigger feature on the Antares (Brunke et al 2006). Since on-board memory is limited, multiple acquisition bursts of 300 s were acquired and aligned using the time stamp on a recorded frame. An RF echo-data frame acquired just after applying the compression at t = t₀ becomes the reference to which subsequent RF frames acquired at discrete times t[n] = nT are recorded at intervals of T s. Strain images are produced using constant reference multi-resolution cross correlation strain imaging techniques (Chaturvedi et al 1998). Viscoelastic images were generated using methods described in the following sections.

Figure 1 shows a typical creep curve for a pixel in the strain sequence. With the applied stress comes the instantaneous elastic strain response (sharp strain increase at t = t₀) followed by an exponential increase in strain over time (creep curve). The continuous distribution of exponential constants from a decomposition of the creep curve is shown on the lower right-hand side of figure 1.

2.1.2. Freehand stress

Freehand experiments are essentially the same as that using the motion controller system except that forces were applied by operators holding the transducer without restraint, as they do in clinical scanning. Three operators participated by applying a constant force of approximately 5 N for 120 s with and without the help of force feedback. When feedback was permitted, operators were asked to keep a force plot constant while watching a real-time force display.

2.2. Constitutive equations for viscoelastic imaging

A creep curve is measured for each strain pixel (or group of pixels) as illustrated in figure 1. From the curves, imaging parameters are estimated based on the constitutive equation for uniaxial polymer compression (Sridhar et al 2007, Tschoegl 1989). Constitutive equations reveal how material properties of the medium interact with applied mechanical stimuli to generate mechanical responses. In imaging experiments, stress σ(x, t) is often the stimulus, strain ε(x, t) is the response, and compliance D(x, t) defines material properties of the medium that relate the two. All three quantities can vary in space, x, and time, t. In our creep experiment, a compressive stress is suddenly applied to one surface of the sample. The stimulus is approximated by a step function σ_a(x)u(t − t₀), where σ_a is the temporally constant applied stress and u(t) = 1 for t ≥0 and 0 otherwise. The linear constitutive equation is

$$\epsilon (\mathbf{x},t)=D(\mathbf{x},t){\sigma }_a(\mathbf{x})u(t-t_0).$$ (1)

Equation (1) acknowledges that each factor can vary in space and time depending on material heterogeneity and boundary conditions.

Conceptually, compressive compliance may be decomposed into three terms describing time-independent elastic, time-varying viscoelastic and purely viscous responses, respectively; D(x, t) = D₀(x) + D_ve(x, t) + D_v (x, t) for t > t₀. The elastic response D₀(x), which is assumed to be the only significant term in strain imaging using quasi-static stimuli (Ophir et al 1991, Chaturvedi et al 1998, O’Donnell et al 1994), is inversely related to the elastic modulus (Tschoegl 1989). The viscous response, D_v = (t − t₀)/η₀, is measured and removed from the data during the process of estimating viscoelastic parameters. Gelatin gels are hydrophilic, which binds the water tightly to the matrix to increase the steady-state viscosity η₀ (O(10⁷) Pa·s (Sridhar et al 2007)).

This paper is focused on the viscoelastic response, D_ve. It can be expressed in different ways to emphasize various aspects of its continuous distribution. For example,

$$\begin{array}{l}{D}_{ve}(\mathbf{x},t)={\int }_{-\infty }^{\infty }\text{d}\tau D_{ve}^{\prime }(\mathbf{x},\tau )[1-exp(-(t-t_0)/\tau )]\\ =\frac{1}{{\sigma }_a(\mathbf{x})}{\int }_{-\infty }^{\infty }\text{d}\tau {\epsilon }_{ve}(\mathbf{x},\tau )[1-exp(-(t-t_0)/\tau )]\\ ={\int }_{-\infty }^{\infty }\text{d}ln\tau L(\mathbf{x},\tau )[1-exp(-(t-t_0)/\tau )]\text{for}t>t_0,\end{array}$$ (2)

where τ are time constants for components, $L(\tau )=\tau D_{ve}^{\prime }$ and d ln τ = dτ/τ. $D_{ve}^{\prime }={\epsilon }_{ve}/{\sigma }_a$ are component amplitudes. The polymer mechanics literature prefers the third form since distributions are typically very broad thus requiring a log axis (Ferry 1980, Tschoegl 1989, Schwarzl and Staverman 1953). Integration over τ (or ln τ) gives the observed compliance D_ve.

D_ve summarizes material properties of the medium that determine the amplitude and duration of the delayed strain in a creep response. Components are interpreted as weak chemical cross links (mostly hydrogen bonds and structured water molecules) producing frictional forces in the polymer that retard strain. Components in equation (2) are represented by exponential Voigt units, $D_{ve}^{\prime }[1-exp(-(t-t_0)/\tau )]$. Randomness in the chemical structure generates a broad range of cross-link energies that is likely to be responsible for the continuous distribution of time constants τ. Retardance time distributions are estimated from creep curves using methods described in (Sridhar et al 2007) from the analysis of (Tschoegl 1989).

When stress relaxation experiments (measured stress response from a strain stimulus) are conducted, relaxation-time distributions H (τ) are found analogous to L(τ) using similar techniques. There is no direct relationship between the two functions (Tschoegl 1989) although their shapes are highly correlated. Some investigators (Ferry 1980, Tschoegl 1989) plot L(τ) and H(τ) distributions as frequency spectra L̃(ω) and H̃(ω). In that case, they assume ω = 1/τ. However, in this paper we use L(τ) and H(τ).

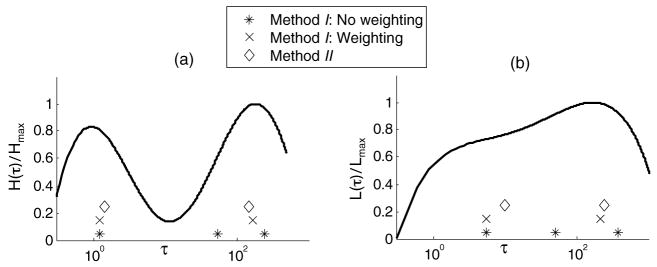
Figure 2(a) is an example of a relaxation distribution H(τ) in a confined measurement geometry as taken from (Sridhar et al 2007). It was computed from a stress relaxation curve measured from a gelatin sample. Figure 2(b) is a retardation distribution L(τ) also measured for gelatin in an unconfined measurement geometry. Both distributions are bimodal although clearly the peak locations and modal widths depend on the boundary conditions. We hypothesize that time constant within the short-time modal peak, near 1 s, describes polymer matrix relaxation acting over a short spatial range that is impeded by viscous fluid flow. We also hypothesize that the modal peak for the longer time constant, near 200 s, represents matrix relaxation over longer spatial ranges (entanglement coupling (Ferry 1980)).

Figure 2.

(a) Normalized H (τ) distribution for gelatin undergoing uniaxial compression in a confined geometry. (b) Normalized L(τ) distribution for uniaxial compression of gelatin in an unconfined geometry, similar to imaging experiments. Both curves are reproduced from data in Sridhar et al (2007), where details of the experiments are described. Markers along the τ axes indicate estimates of peak respondance times by applying method I with and without weighting and method II as described in section 2.2.

2.3. Parameterizing creep data for imaging

For each pixel in the time series of strain images there is a distribution of retardance times. Thus there is a 3D data set for each image plane in the medium. The goal for viscoelastic imaging is to find the most diagnostic features of the distribution and map those into images. A problem common to all spectroscopic imaging methods, e.g., colour Doppler spectra and MRS, is how to reduce the dimensionality of data for imaging without sacrificing task-essential information. We propose to parameterize the data by estimating retardance times corresponding to the two peaks of the bimodal distributions. The rationale is that these times indicate the principal components of the data corresponding to the two physical mechanisms responsible for creep—fluid-dominated matrix relaxation and relaxation of entanglement couplings.

If the hypothesis is true, then we can approximate the integral of equation (2) with a second-order discrete model to convey essential features of these two processes. Combining equations (1) and (2), the Pth-order discrete approximation to the continuous distribution in terms of viscoelastic strain is

$${\epsilon }_{ve}(\mathbf{x},t)=\sum _{\ell =1}^P{\epsilon }_{\ell }(\mathbf{x})[1-exp(-(t-t_0)/T_{\ell }(\mathbf{x}))]\text{for}t>t_0.$$ (3)

T_ℓ for 1 ≤ ℓ ≤P are discrete retardation times analogous to τ of the continuous representation. The model is expressed in terms of measured strain to avoid having to estimate the stress field σ_a. This is acceptable provided the goal is to consistently generate tissue specific image contrast rather than estimate material properties. The task now is to estimate ε_ℓ and T_ℓ and assess their suitability as diagnostic imaging parameters.

2.3.1. Method I: least squares

Previously we applied a maximum likelihood approach to fitting model functions to creep data that is based on minimizing a χ² statistic (Sridhar et al 2007). Although the physical model for the bimodal spectrum suggests a second-order sum, we allow some flexibility in selecting P. Time-varying strain measurements ε̂ sampled on the ultrasonic frame-rate interval T include zero-mean white Gaussian noise (WGN): ε̂[n] = ε_ve[n] + w[n] for t₀ ≤ nT ≤ (N − 1)T + t₀. These are compared to the discrete model function ε_ve[n; θ] from equation (3) that depends on 2P fit parameters θ = (ε₁, T₁, …, ε_P, T_P). At each location in the medium x and for P = 1, 2,…, we compute for t₀ = 0

$${\chi }_P^2=\sum _{n=1}^N\frac{{(\widehat{\epsilon }[n]-{\epsilon }_{ve}[n;\theta ])}^2}{var(\widehat{\epsilon }[n])}0\le n\le N-1,$$ (4)

where var(ε̂[n]) is the sample variance. We compute the probability $Q\left({\chi }_P^2;\xi \right)$ that chi-square should exceed the particular value ${\chi }_P^2$ by chance, where ξ = N − 2P is the number of degrees of freedom, and select P from the lowest order model for which Q > 0.1. Although the threshold is arbitrary, probabilities greater than 0.1 suggest the model is an acceptable representation of the data given that the errors are normally distributed. The algorithm for estimating time constants for each mode in the retardation distribution using method I is outlined in table 1.

Table 1.

Algorithm for method I.

Estimate L(τ) from the time-varying strain data of a creep experiment. Record the number of peaks in L(τ) as the number of modes M. Model the strain response using equation (3) and compute χ2 and Q estimates via equation (4). The order of the model is the lowest value of P for which Q > 0.1. Matlab function LSQCURVEFIT is used for fitting. If P > M, identify the peaks associated with each distribution mode and compute the weighted mean Tm = Σℓ(εℓTℓ)/Σℓεℓ as the time constant for the mode. For stress-relaxation data, substitute H (τ) for L(τ).

2.3.2. Method II: Hankel-SVD

There are several parametric modelling approaches (Marple 1987). One promising method employed in MR spectroscopy is a state-space approach called the Hankel-SVD method (Vanhamme et al 2001). It assumes signals such as creep curves can be modelled as a linear superposition of exponentials: $s[n]={\sum }_{\ell }{s}_{\ell }{z}_{\ell }^{n-1}+w[n]$ where z_ℓ = exp(−T/T_ℓ). We adapt the method by modifying the creep data to the form

$$s[n]=\widehat{\epsilon }[\infty ]-\widehat{\epsilon }[n]\simeq \widehat{\epsilon }[N]-\widehat{\epsilon }[n]0\le n\le N-1$$ (5)

assuming a steady-state response has been achieved, i.e., (N − 1)T > 2(T_ℓ)_max.

Signal samples s[n] are arranged into a matrix of dimension (N − R) × (R + 1) with Hankel structure,

$$\mathbf{S}=\left(\begin{array}{cccc}s[0]& s[1]& \cdots & s[R]\\ s[1]& s[2]& \cdots & s[R+1]\\ ⋮& ⋮& \ddots & ⋮\\ s[N-R-1]& s[N-R]& \cdots & s[N-1]\end{array}\right),$$ (6)

where we choose P ≤R ≤N/2 but typically R ≤N/3. (See table 2 for details.) The rank of S equals the prediction order R + 1.

Table 2.

Algorithm for method II.

Compute s[n] from (5) and arrange into the Hankel matrix S of (6). Apply the HLSVD-PRO algorithm (Laudadio et al 2002). Select R = 2n such that n equals the value that minimizes (τmax/(5T)) − 2n. Also set P = M and truncate the creep curve at nT = 2τmax to compute U′. τmax is the largest value of τ at which L(τ) peaks. Apply equations (8) and (9) to compute retardance time values Tℓ for 1 ≤ ℓ ≤ M.

S is decomposed into its singular values (Marple 1987) via

$$\mathbf{S}=\mathbf{U}\mathbf{\Lambda }{\mathbf{V}}^{†},\text{where}\mathbf{\Lambda }=\left(\begin{array}{cc}\mathbf{D}& \mathbf{0}\\ \mathbf{0}& \mathbf{W}\end{array}\right)$$ (7)

and V^† is the conjugate transpose of V. U and V are unitary matrices of order (N −R)×(N −R) and (R + 1) × (R + 1), respectively, and Λ is a diagonal matrix containing singular values λ₁ ≥···≥λ_R+1. The task is to partition Λ into a P × P signal-space matrix D and a (R + 1 − P) × (R + 1 − P) noise-space matrix W. When the signals are noisy and P is unknown, model order is estimated by locating the largest difference between two successive singular values. However, our experience with measured spectra suggests a second-order model (P = 2). Consequently, we choose the dimension of the signal space, P, to equal the number of modes in the L(τ) distribution, M; i.e., P = M = 2.

Noise is suppressed by truncating the Hankel matrix: S′ = U′DV′^†, where U′ is of order (N − R) × P and V′ is (R + 1) × P. U′ provides a relationship between the singular values in D and the corresponding eigenvalues Z = diag (z₁,… z_ℓ,… z_P) that are related to the model in equation (3) from which T_ℓ are found. Define ${\mathbf{U}}_{\text{top}}^{\prime }$ to be U′ with the top row removed, ${\mathbf{U}}_{\text{bot}}^{\prime }$ to be U′ with the bottom row removed, u is the bottom row of U′, and I is the identity matrix. Then (Hoch and Stern 1996)

$${\mathbf{Z}}^{\prime }=\left(\mathbf{I}+\frac{\mathbf{u}{\mathbf{u}}^{†}}{1-{\mathbf{u}}^{†}\mathbf{u}}\right){\mathbf{U}}_{\text{top}}^{\prime †}{\mathbf{U}}_{\text{bot}}^{\prime }.$$ (8)

The relation between Z and Z′ is Z′ = QZQ⁻¹. Although we do not know Q, it can be shown that the eigenvalues of Z′ from equation (8) equal those for the diagonal matrix Z that we seek. From the eigenvalues of Z′, z_ℓ = exp(−T/T_ℓ), and therefore

$$T_{\ell }=-\frac{T}{ln{z}_{\ell }},\text{for}\ell \le P.$$ (9)

A more computationally efficient algorithm HLSVD-PRO was used in this study as obtained from the authors of Laudadio et al (2002). It uses the Lanczos algorithm to speed SVD computation (Millhauser et al 1989) with extensions that exploit the orthogonality among the Lanczos vectors. Method II procedures are summarized in table 2.

2.3.3. Imaging parameters

Candidates for imaging parameters resulting from a second-order discrete model are the elastic strain ε₀, the four viscoelastic parameters ε₁, T₁, ε₂, T₂, and the viscous flow parameter σ_a/η₀. The elastic strain image ε₀ can be computed from the RF frames recorded immediately before and after application of the stress or from ε₀ estimates determined from a simultaneous estimation of all parameters; the difference is in the amount of image noise generated.

2.4. Simulations

Our initial investigation of methods I and II was through Monte Carlo simulations of creep experiments. Assuming that L(τ) follows a log-normal distribution (Tschoegl 1989), we generated a single-mode, broadband input function L(nDelta;τ) as illustrated by the points in figure 3. From equations (1) and (2), we simulated measurement signals ε̂(t) and added signal-independent WGN. Noise was added at low power to simulate creep curves at high signal-to-noise ratio (SNR = 40 dB), representative of materials testing measurements (Sridhar et al 2007). Low SNR (15–20 dB) data were also simulated to represent imaging measurements. Values were calculated using SNR (dB) =10log₁₀(ρ²/(1 − ρ²)), where ρ is the correlation coefficient between noisy and noiseless data (Walker 2001). SNR was varied by changing the amplitude of the WGN. We also varied the width of the input L(τ) distribution over the range 70–500 s to observe how modal bandwidth affects estimates of the peak retardation time constant.

Figure 3.

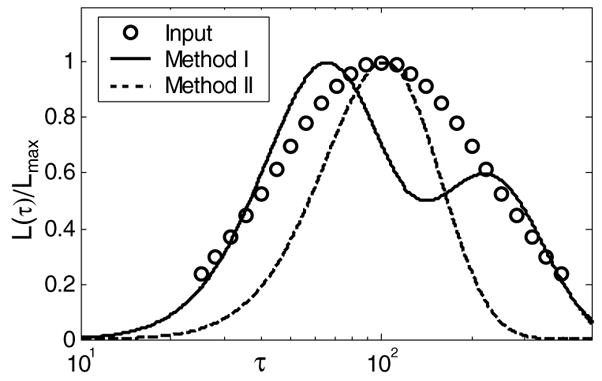
Points marked (○) are the log-normal retardation spectra input into the simulation (peak value is 100 s and the bandwidth is 220 s). The lines are estimates of the spectrum from equation (3) fitted to the data using method I (solid line) and method II (dashed line).

Method I was applied to data simulated from the broadband, unimodal input distribution where we set the peak value for L(τ) at τ = 100 s. As seen in figure 3, the best fit gave a bimodal estimate. Such performance is typical of χ² methods, because they add terms to the model as needed to achieve the best fit. Nevertheless, a weighted mean of the two peaks gives the estimate 123 s. Method II, conversely, reduces the size of the signal space according to prior information about the number of distribution modes. Therefore method II estimates a single peak value at 103.5 s despite the fact that this all-pole technique underestimates the bandwidth of L(τ). The order of the discrete model approximation should be determined from a physical model of the process rather than curve fitting.

2.5. Retardation-time error analysis

Strain errors can be significant when the applied stress σ_a is not the constant we assume. Uncertainty in σ_a becomes an issue when stress is applied by hand as in clinical applications. We now show how stress errors affect the variance of T_ℓ and ε_ℓ estimates for method I.

We seek model parameters θ that satisfy ε̂[n] = ε_ve[n; θ]. Consider the discrete viscoelastic model representation of equation (3) while dropping the spatial notation and setting t₀ = 0 for convenience. The first-order (P = 1) model yields

$$\widehat{\epsilon }[n]={\epsilon }_0+{\epsilon }_1[1-exp(-nT/T_1)].$$ (10)

Linearizing the equation and arranging terms gives

$$y[n]=c+m\times nT,$$ (11)

where y[n] = ln(ε₀ + ε₁ − ε̂[n]), the intercept is c = ln(ε₁) and the slope is m = −1/T₁.

Maximum likelihood estimates of model parameters are obtained by minimizing the χ² metric of equation (4), i.e.,

$$\frac{\partial {\chi }_P^2}{\partial \theta }=-2\sum _{n=1}^N\frac{(\widehat{\epsilon }[n]-{\epsilon }_{ve}[n;\theta ])}{var(\widehat{\epsilon }[n])}\frac{\partial }{\partial \theta }{\epsilon }_{ve}[n;\theta ]=0.$$ (12)

In terms of the linearized model we have

$$\begin{array}{l}\frac{\partial {\chi }_1^2}{\partial c}=-2\sum _{n=1}^N\frac{(y[n]-c-\mathit{mnT})}{var(y)}=0\\ \frac{\partial {\chi }_1^2}{\partial m}=-2\sum _{n=1}^N\frac{nT(y[n]-c-\mathit{mnT})}{var(y)}=0.\end{array}$$ (13)

The pair of simultaneous equations can be solved to give an equation for slope m in terms of data y and its variance var(y),

$$m=\frac{{\sum }_n\frac{1}{var(y)}{\sum }_n\frac{\mathit{nTy}[n]}{var(y)}-{\sum }_n\frac{nT}{var(y)}{\sum }_n\frac{y[n]}{var(y)}}{{\sum }_n\frac{1}{var(y)}{\sum }_n\frac{{(nT)}^2}{var(y)}-{\left({\sum }_n\frac{nT}{var(y)}\right)}^2}.$$ (14)

Propagating the error (Bevington and Robinson 1992) and applying equation (14), we find

$$var(m)=var(y){\left(\frac{\partial m}{\partial y}\right)}^2=\frac{{\sum }_n\frac{1}{var(y)}}{{\sum }_n\frac{1}{var(y)}{\sum }_n\frac{{(nT)}^2}{var(y)}-{\left({\sum }_n\frac{nT}{var(y)}\right)}^2}.$$ (15)

Also m = −1/T₁, and therefore var(T₁) = var(m)/m⁴.

Next, we relate var(y) to the stress stimulus variance var(σ). In equation (1), we assumed a constant applied stress, σ (t) = σ_a for t > t₀. We now allow σ(t) to be a normally distributed random variable, 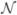(σ_a, var(σ)). From equation (11),

$$var(y)=var({\epsilon }_0){\left(\frac{\partial y}{\partial {\epsilon }_0}\right)}^2+var({\epsilon }_1){\left(\frac{\partial y}{\partial {\epsilon }_1}\right)}^2+var(\widehat{\epsilon }){\left(\frac{\partial y}{\partial \widehat{\epsilon }}\right)}^2,$$ (16)

where the covariances are assumed negligible. Since ε_ℓ = D_ℓσ_a, the variance in strain constants on the right-hand side of equation (16) can be related to stress variance via D_ℓ, where we assume compliance is a deterministic property of the media. Consequently,

$$\begin{array}{l}var(y)=\frac{var(\sigma )(D_0^2+D_1^2)+var(\widehat{\epsilon })}{{({\epsilon }_0+{\epsilon }_1-\widehat{\epsilon })}^2}\\ =\frac{var(\sigma )(D_0^2+D_1^2+m^{\prime })}{{({\epsilon }_0+{\epsilon }_1-\widehat{\epsilon })}^2}\text{for}t>t_0.\end{array}$$ (17)

The last form uses the constant m′ = var(ε̂)/var(σ). This variance ratio can be assumed approximately constant because measurements show var(ε̂) and var(σ) (see figure 9) do not strongly depend on time. Notice that all the quantities in equation (17) are functions of time via the discrete variable n except D₀ and D₁.

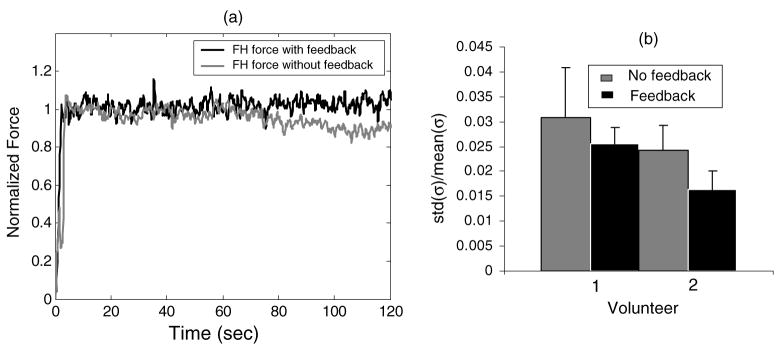
Figure 9.

(a) Freehand force applied over time to a gelatin sample with and without feedback. (b) Relative stress variability as recorded from two volunteers that apply forces with and without feedback.

Combining equations (15), (17) and the relation $var(T_1)/T_1^2=var(m)/m^2$, we have the proportionality

$$\frac{var(T_1)}{T_1^2}={\alpha }^2\frac{var(\sigma )}{{\sigma }_a^2},$$ (18)

where

$${\alpha }^2={\left(\frac{T_1}{T}\right)}^2\frac{{\sigma }_a^2(D_0^2+D_1^2+m^{\prime }){\sum }_n{({\epsilon }_0+{\epsilon }_1-\widehat{\epsilon })}^2}{{\sum }_n{({\epsilon }_0+{\epsilon }_1-\widehat{\epsilon })}^2{\sum }_n{n}^2{({\epsilon }_0+{\epsilon }_1-\widehat{\epsilon })}^2-{({\sum }_{n}n{({\epsilon }_0+{\epsilon }_1-\widehat{\epsilon })}^2)}^2}.$$

Similarly we can show that the variance of the intercept c from equation (11) is

$$var(c)=\frac{{\sum }_n\frac{{(nT)}^2}{var(y)}}{{\sum }_n\frac{1}{var(y)}{\sum }_n\frac{{(nT)}^2}{var(y)}-{\left({\sum }_n\frac{nT}{var(y)}\right)}^2}.$$

Since ε₁ = exp(c), propagation or error gives $var({\epsilon }_1)/{\epsilon }_1^2=var(c)$ and therefore

$$\frac{var({\epsilon }_1)}{{\epsilon }_1^2}={\beta }^2\frac{var(\sigma )}{{\sigma }_a^2},$$ (19)

where

$${\beta }^2=\frac{{\sigma }_a^2(D_0^2+D_1^2+m^{\prime }){\sum }_n{n}^2{({\epsilon }_0+{\epsilon }_1-\widehat{\epsilon })}^2}{{\sum }_n{({\epsilon }_0+{\epsilon }_1-\widehat{\epsilon })}^2{\sum }_n{n}^2{({\epsilon }_0+{\epsilon }_1-\widehat{\epsilon })}^2-{({\sum }_{n}n{({\epsilon }_0+{\epsilon }_1-\widehat{\epsilon })}^2)}^2}.$$

The closed form expressions of equations (18) and (19) are for first-order rheological models obtained by linearizing equation (3). They predict that the coefficient of variation for T₁, i.e., CV (T₁) = std(T₁)/mean(T₁), and CV (ε₁) are each proportional to CV (σ). Consequently, jitter from hand-held stress applicators linearly increases parametric uncertainty.

To validate the expressions, we obtained analytical predictions for α and β using equations (18) and (19) and compared them to commensurate values computed using numerical methods for Monte Carlo simulations of creep curves as described above. The analytical and computational values for α are 2.97 and 3.1, respectively. The corresponding values for β are 2.01 and 1.83. Since the analytical and computational values agree closely for P = 1, numerical methods using simulated creep data were used for predictions for a second-order model where closed form expressions are not available. Plots of the coefficient of variation for the five parameters of a second-order model, θ = (ε₀, ε₁, ε₂, T₁, T₂), were all approximately proportional to CV (σ). The constants of proportionality were 0.17, 1.84, 1.24, 3.68, 1.79, respectively. These values can be combined with contrast estimates to select the most promising features for viscoelastic imaging. For example, a long duration strain series can increase object contrast significantly (figure 6) and parametric errors moderately and yet still be unacceptable for clinical imaging because of breathing motions. Thus the relative merits of each parameter must be evaluated for specific imaging situations.

Figure 6.

(a) Variation in retardance time estimates with acquisition time for method I and a gelatin phantom. (b) Variation in retardance time contrast with acquisition time.

2.6. Acquisition parameters

Ultrasonic frame rate, total strain acquisition time and the average stress amplitude σ_a each influence viscoelastic contrast. We studied these effects for gelatin previously (Sridhar et al 2007), and we found that frame rates between 1 and 4 fps acquired over at least 1000 s were adequate to sample the creep-response bandwidth of gelatin. Acquisition time determines the frequency resolution and therefore the longest retardance times. σ_a < 860 Pa ensured a linear stress–strain relationship for soft gels (5.5% gelatin) and σ_a < 2600 Pa for stiffer gels (10% gelatin). σ_a < 30 Pa was necessary to ignore the D_v term.

2.7. Gelatin phantom preparation

A 5 cm cubic block of gelatin was prepared with a 0.8 cm diameter cylindrical inclusion centred in the block as illustrated in figure 1. The gelatin block material was manufactured (Hall et al 1997) by combining 26 ml of propyl alcohol, 13.5 g of type A, 275 bloom, animal-hide gelatin (Fisher Scientific, Chicago, IL) and 200 ml distilled water to produce a 5.5% by weight gelatin gel. The solution was heated to 60 °C for ~30 min until visually clear before adding 0.3 ml of formaldehyde to increase collagen cross linking. 9.1 g of graphite powder was added to the molten gelatin and thoroughly mixed. Graphite provided tissue-like ultrasonic absorption and backscatter. For the inclusion, 20 g of gelatin powder was used to give 8% gelatin concentration by weight. Since Young’s modulus for gelatin gels is proportional to the square of gelatin concentration (Hall et al 1997, Gilsenan and Ross-Murphy 2001), the inclusion was approximately (0.08/0.055)² = 2.1 times stiffer than the background. Samples were stored at room temperature 4 days prior to measurements.

3. Results

3.1. Method comparisons

The data in figure 4 were simulated (section 2.4) assuming a unimodal distribution of retardance times peaked at 100 s. For both estimation methods, bias in the peak value increases with the bandwidth of the input distribution. However, method II generates significantly less bias than method I. The bias in method I comes from the increase in model order required to minimize χ². Method II estimates singular values for the assumed model order, which effectively seeks the peak time without attempting to fit all the data. Since our goal is to track the distribution peaks, method II is preferred. However to apply the error analysis of section 2.5, subsequent results employ method I. Figure 4 also shows that increases in creep noise do not affect estimation bias for peak retardation times. Precision is affected by noise as described in section 2.5.

Figure 4.

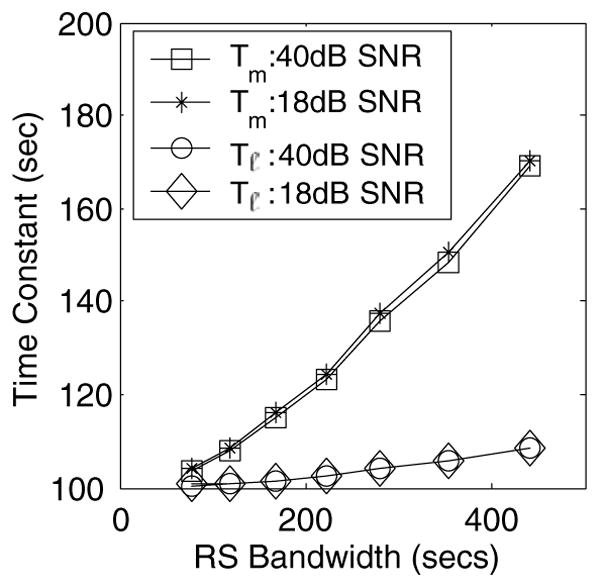
(a) T_m (method I) and T_ℓ (method II) at two SNR values, 18 dB and 40 dB, and for varying L(τ) bandwidth are shown. The peak value input is 100 s.

Methods I and II were next used to parameterize the experimental gelatin distribution in figure 2. Method I yielded a P = 3 model order for both cases although the number of peaks observed was two, common with χ² based methods. However, peak retardance times, T_m, calculated in accordance with table 1 coincided closely with spectral peaks. Method II values for P = 2 yielded estimates close to that of method I with some overestimation of T₁. This is because of the restriction placed on the signal space. If more flexibility was given, P > 2, values coinciding with the peaks were obtained in addition to other low-medium amplitude poles. Assessing the importance of each pole then becomes challenging.

3.2. Retardance time images

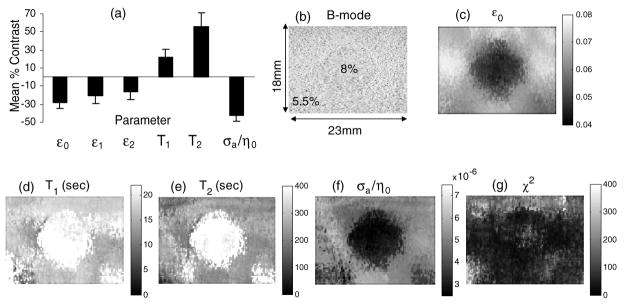
Figure 5 displays contrast estimates and images of viscoelastic parameters obtained experimentally for the gelatin phantom. A uniaxial compression of 533 Pa was applied to the top of the phantom and held constant for 2000 s using the motion controller. A second-order model was found to minimize χ², and we estimated SNR = 15–20 dB for the data. All parameters were estimated simultaneously using method I. The uniformly low values seen in the χ² map suggest that equation (3) is representative of the experimental creep data.

Figure 5.

Results for method I. (a) Mean % contrast for viscoelastic images. Error bars denote 1 standard deviation of the mean. (b) B-mode image showing 0.8 cm dia inclusion, (c) elastic strain image ε₀, (d) T₁ image, (e) T₂ image, (f) σ_a/η₀ image and (g) χ² map from equation (4). σ_a/η₀ can be interpreted as a fluid flow image; flow is high when viscosity is low.

Figure 5(a) shows a plot of the mean contrast for parametric images calculated from three separate acquisitions. Contrast for parameter θ between the inclusion and background regions is found from spatial averages of the parameter,

$$C_{\theta }=({\overline{\theta }}_i-{\overline{\theta }}_b)/{\overline{\theta }}_b.$$ (20)

Here θ̄_i is the spatial mean of the parameter within the inclusion area and θ̄_b is the mean parametric estimate for the background over small regions. The mean contrast and standard deviation of the mean for three data sets with unequal uncertainties are (Bevington and Robinson 1992)

$${\overline{C}}_{\theta }=\frac{{\sum }_{k=1}^3{(C_{\theta }/var(C_{\theta }))}_k}{{\sum }_{k=1}^{3}1/var{(C_{\theta })}_k}\text{and}\text{std}({\overline{C}}_{\theta })={\left(\sum _{k=1}^{3}1/var{(C_{\theta })}_k\right)}^{-1/2}.$$ (21)

Parameters ε₁ and ε₂ provided the lowest image contrast for the phantom.

To check for consistency of our data with that in the literature, we made two comparisons. First, the measured value for elastic strain contrast C̄_ε0 was used to estimate strain contrast transfer efficiency for comparisons with predictions for this phantom geometry (Ponnekanti et al 1995). The contrast transfer efficiency is defined as CTE (dB) = 20 (|log(C̄_ε0+ 1)| − |log (C_E0+ 1)|) where C_E0 is the Young’s modulus contrast. We found that C̄_ε0 in figure 5(c) is −0.305 as computed from equation (20). Also since Young’s modulus is proportional to the square of gelatin concentration, as described in section 2.5, C_E0 = (0.08² − 0.055²)/0.055² = 1.11 for our phantom. Therefore CTE = −3.3 dB, which is close to the prediction of −3.1 dB reported by (Ponnekanti et al 1995).

Another experimental study suggested that the viscosity of gelatin gels varies with gelatin concentration according to the power law η₀ ∝ Conc^1.1 (Higgs and Ross-Murphy 1990). The predicted contrast for our phantom, therefore, is (0.08^1.1 − 0.055^1.1)./0.055^1.1 = 0.51, and the contrast observed from figure 5(f) is 0.43. Given that there could be a loss of efficiency in transferring viscosity contrast into an image, as there is for strain, the agreement is reasonable.

Elastic strain patterns surrounding a stiff inclusion, as in figure 5(c), are strongly influenced by boundary conditions when quasi-static stress stimuli are applied. Stress concentration effects on strain patterns are well understood (Goodier 1933, Bilgen and Insana 1998). However, the background patterns in the T₁ and T₂ images of figures 5(d), (e) are different, and in our broader experience they seem less dependent on boundary factors. The central bright regions in retardance time images are consistent with the inclusion region creeping slower than the background region because the higher density polymer increases the fluid viscosity and provides more inter-fibre hydrogen-bonded cross links (Ferry 1980).

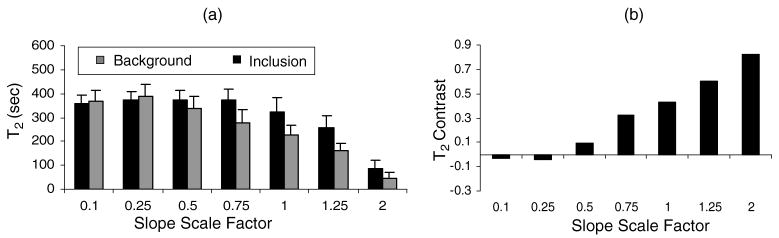
3.3. Acquisition time and contrast

Images in figure 5 were estimated using method I from data acquired over 1400 s. At shorter acquisition times, figure 6(a) shows that parameters are underestimated. For gelatin, stable retardance times require acquisition times as large as 800 s. Since T₁ and T₂ are estimated simultaneously, stabilization times are similar.

More importantly for imaging, we investigated the contrast in T_ℓ images for gelatin phantoms (see figure 6(b)). T₁ image contrast stabilizes quickly for acquisition times greater than 120 s. However T₂ contrast is negligible below about 300 s. It grows to 40% when the acquisition time T_a > 4T₂. The results need to be repeated for tissue imaging to guide scanning techniques. However preliminary results have shown that T₁ in normal breast tissue is on the order of 3 s and T₂ is of order 60 s (Sridhar et al 2006a), and the viscoelastic amplitudes ε₁ and ε₂ are several times greater than for gelatin. Together these findings help explain why we have been able to obtain T₁ images in breast patient studies with 20 s acquisitions but not T₂ (Sridhar and Insana 2005).

3.4. Linear viscous creep

Significant biases occur when estimating viscoelastic parameters for large stresses if the linear-in-time viscosity term σ_a/η₀ is ignored or inaccurately determined. For example, see figure 5(f). Figure 7(a) shows T₂ values estimated when the linear term was scaled up or down by the factor indicated on the abscissa. Underestimation of σ_a/η₀ affects the background region surrounding the inclusion to a greater degree, resulting in a loss of T₂ contrast (figure 7(b)). Overestimation of σ_a/η₀ preserves contrast but underestimates T₂ thus increasing image noise. Consequently, σ_a/η₀ errors greatly influence T₂ estimates.

Figure 7.

(a) T₂ background and inclusion estimates at different scaled σ_a/η₀ values, (b) corresponding contrast values.

The effects of σ_a/η₀ on T₁ can be less pronounced as seen in figure 8. Solid points are obtained when compensating for the linear term exactly and open points are uncompensated. No significant differences were found for acquisition times <90 s indicating that the linear term can be ignored. This is the range of most clinical imaging (Pellot-Barakat et al 2006). We assumed a first-order discrete model for these gelatin phantom measurements, resulting in stable T₁ values for 20 s ≤ T_a ≤50 s and biased estimates for longer acquisition times (figure 8). Unbiased estimates for acquisition times >90 s are found by switching to a second-order model, as we did in figure 6(a).

Figure 8.

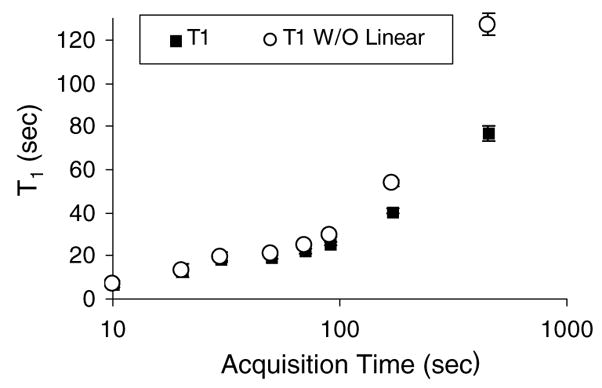
T₁ variation over short acquisition times with and without compensating for linear viscous creep via σ_a/η₀.

3.5. Stress variance

For all the data above, precise stresses were applied using a computer-controlled motion system. However, for a clinical setting, stresses need to be applied freehand. Figure 9(a) provides two examples of hand-held stress applied to a gelatin sample over time with and without the help of force feedback. With feedback, the stresses in the hold phase are steady except for the random variability seen. With no feedback, stresses are maintained for the first 60 s. After that time drift occurs.

Stress application errors were further quantified by measuring the variance of two volunteers attempting to hold an ultrasonic transducer while applying a constant 6 N force to the gelatin phantom (see figure 9(b)). Volunteer 1 had no training and volunteer 2 practiced more than 10 h before measurement. Clearly both training and feedback can reduce the variance in the stress stimulus.

4. Summary and conclusion

The creep response from gelatin gels has been modelled as a sum of exponentials where the time constants are continuously distributed and bimodal (e.g., figure 2). The model is derived from the constitutive equation for a step stimulus but agrees with experimental gelatin creep measurements even though a short-duration ramp-and-hold stress function is applied. The principal effect of increasing ramp times is to reduce the amplitudes of high-frequency (short-duration) retardance times (Sridhar et al 2007).

The objective of viscoelastic imaging is to maximize contrast for diagnostic targets. With this goal, interpretation of images for the assumptions made in the constitutive equations is reasonable. If the objective was to accurately estimate viscoelastic properties, this approach would fail because the true stress tensors at each voxel location in the medium are unknown. A second-order generalized Voigt model is able to parameterize experimental creep measurements in gelatin for imaging. Based on the molecular theory of polymer dynamics (Ferry 1980) we interpret T₁ images as descriptive of the viscoelastic response regulated by fluid viscosity and T₂ images as descriptive of the solid collagen matrix response.

Estimating viscoelastic properties in this manner is an ill-posed inverse problem. For example, we have generated broadband L(τ) distributions as inputs into Monte Carlo simulations of creep data in noise (forward problem) and then attempted to estimate the distribution from the simulated data (inverse problem). Depending on the quality of our initial guesses at parameters using least-squares methods (method I, table 1), the bandwidth of L(τ), and the strain SNR, the quality of the parametric estimates was highly variable. Limiting our interest to the peaks of the distribution (instead of attempting to back out the entire distribution) yields acceptable parametric precision and accuracy for imaging applications. Method II offers the advantage of providing SVD filtering for the strain data and model-based exponential estimation that can efficiently detect retardation times at or near the distribution peaks. However, it too is sensitive to parametric initialization and requires the operator to select operational parameters (see table 2). Considering the differences in computational load and the resulting parametric errors, this early stage of development provides no clear advantage of one method over the other.

A different approach to viscoelastic modelling that is gaining momentum models the constitutive equation as a fractional derivative (Tschoegl 1989, Bagley 1983). Instead of exponential time dependences, strain retardation (or stress relaxation) is modelled as algebraic decays (Schiessel and Blumen 1993). Mathematically, we use ε_ve(x, t) = D₁(x)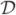 ^α{σ (x, t)} in place of equation (3), where 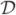^α is the fractional derivative operator applied to the stimulus and 0 < α< 1. The fractional derivative result is simplified in the Laplace domain as ε̃_ve(x, s) = D₁(x)s^ασ̃ (x, s), and has the desirable feature of concise representation by two parameters: D₁(x) and α(x). Since both can vary with position, they are natural imaging parameters. As (Schiessel and Blumen 1993) show, the ladder models of a continuous retardation distribution are interpreted as series equations approximated by a fractional derivative. There is also a molecular basis for interpreting these parameters in polymer solutions (Bagley 1983). However the interpretation in cross-linked polymeric solids with arrheodictic behaviour, like gelatin and soft connective tissues, is still empirical in the sense that α is a characteristic parameter not directly connected to molecular structures. Our proposal is to use T₁ and T₂ from second-order Voigt units (equation (3)) as parameters describing, respectively, short-range fluidic structure and long-range entanglements of the polymer.

Our experience with viscoelastic imaging suggests that stimulus variability is a major source of noise when applying freehand stimuli, that is when applying a force to a sample by manually pressing the transducer into its surface. The results of section 2.5 parametric uncertainties are proportional to stress stimulus variability. Also, figure 9 provides an estimate of stress errors in freehand stress applications. Comparisons with predicted values indicate <12% errors in T₁ estimates.

The analysis of viscoelastic imaging developed in this paper and the results in gelatin phantoms provide a framework for investigating creep properties of breast tissues for linear deformations. Images of elastic strain ε₀, retardation times T₁ and T₂, and linear viscous response σ_a/η₀ form a concise feature set for investigation and may be interpreted in terms of the underlying polymeric structure.