Spectroscopic and Density Functional Theory Studies of the Blue–Copper Site in M121SeM and C112SeC Azurin: Cu–Se Versus Cu–S Bonding

Abstract

S K-edge X-ray absorption, UV–vis absorption, magnetic circular dichroism (MCD), and resonance Raman spectroscopies are used to investigate the electronic structure differences among WT, M121SeM, and C112SeC Pseudomonas aeruginosa (P.a) azurin. A comparison of S K-edge XAS of WT and M121SeM azurin and a Cu^II–thioether model complex shows that the 38% S character in the ground state wave function of the blue–copper (BC) sites solely reflects the Cu–S_Cys bond. Resonance Raman (rR) data on WT and C112SeC azurin give direct evidence for the kinematic coupling between the Cu–S_Cys stretch and the cysteine deformation modes in WT azurin, which leads to multiple features in the rR spectrum of the BC site. The UV–vis absorption and MCD data on WT, M121SeM, and C112SeC give very similar C₀/D₀ ratios, indicating that the C-term MCD intensity mechanism involves Cu-centered spin–orbit coupling (SOC). The spectroscopic data combined with density functional theory (DFT) calculations indicate that S_Cys and Se_Cys have similar covalent interactions with Cu at their respective bond lengths of 2.1 and 2.3 Å. This reflects the similar electronegativites of S and Se in the thiolate/selenolate ligand fragment and explains the strong spectroscopic similarities between WT and C112SeC azurin.

1. Introduction

Azurin belongs to the family of bacterial type I, blue–copper (BC) proteins and is involved in long-range electron transfer.^1–6 The structure of Pseudomonas aeruginosa (P.a.) azurin is very similar to those of other BC proteins.^7–10 The active site contains a mononuclear Cu center that is in a trigonally distorted tetrahedral geometry containing a short Cu–S_Cys bond at ~2.1 Å and two typical Cu–N_His bonds at ~1.95 Å. These three ligands lie in the equatorial plane. A weak axial Cu–S_Met interaction is present at ~2.9 Å. In addition to these four ligands, a weak ionic interaction from an axial carbonyl oxygen of a glycine residue trans to the S_Met ligand is also present in azurins, which is absent in other BC proteins (plastocyanin, amicyanin, etc.).¹¹

This unusual geometric structure of the BC sites lends to its unique spectroscopic features. The absorption spectrum is dominated by an intense S_Cys pπ → Cu charge-transfer transition at ~600 nm (ε = 5000 cm⁻¹ M⁻¹), which imparts the brilliant blue color to the protein.^4,12 The electron paramagnetic resonance (EPR) spectrum has a much lower hyperfine coupling value (A_|| ≤ 80 × 10⁻⁴ cm⁻¹) relative to normal Cu sites (A_|| ≈ 160 × 10⁻⁴ to 200 × 10⁻⁴ cm⁻¹).¹² These unusual spectral features of the BC site derive from a highly covalent Cu–S_Cys bond resulting from the strong interaction between the Cu 3d_x²−y² acceptor orbital and the S 3pπ donor orbital. Resonance Raman (rR) data have indicated a high Cu–S stretching frequency of ~400 cm⁻¹ supporting a strong Cu–S_Cys bond.¹³ A direct estimate of the Cu–S_Cys covalent interaction (amount of S character in the ground state wave-function) has been obtained from S K-edge X-ray absorption spectroscopy (XAS).¹⁴ The high intensity of the XAS pre-edge transition at ~2469 eV indicates that ~38% S character is mixed into the Cu 3d_x²−y² orbital in the ground state. This strong anisotropic covalency of the Cu–S_Cys bond activates the blue–copper site for its biological function of long-range, rapid, directional electron transfer.^{10,12,15–17}

Recently, the expressed protein ligation (EPL) technique has been developed that allows facile incorporation of natural and unnatural amino acids into proteins.^18,19 Lu et al. have recently incorporated Se_Met (M121SeM mutant) and S_Cys (C112SeC mutant) into the active site of P.a. azurin.^20,21 The UV–vis absorption, EPR, and extended X-ray absorption fine structure (EXAFS) spectra of these mutants have been measured and compared to that of WT P.a. azurin.²² These spectroscopic data were very similar for M121SeM and WT, indicating similar geometric and electronic structures of the two proteins. This was consistent with previous results, which showed that the axial S_Met ligand does not significantly contribute to the ground-state wave-function.⁴ EXAFS studies on C112SeC indicated a Cu–Se_Cys bond length of ~2.3 Å (relative to ~2.14 Å for the Cu–S_Cys in WT P.a. azurin), consistent with an increase in the size of Se relative to S.²² EPR studies showed that the spin–orbit coupling (SOC) of Se had a large effect on the spectrum but were inconclusive in determining the change in bond strength between Cu–S_Cys and Cu–Se_Cys.

In this study, a combination of UV–vis absorption, magnetic circular dichroism (MCD), rR, S K-edge XAS, and density functional theory (DFT) calculations are applied to WT, M121SeM, and C112SeC P.a. azurin to quantitatively probe the electronic structure differences due to replacement of S_Met and S_Cys with Se_Met and Se_Cys, respectively. S K-edge data on M121SeM and WT, combined with data on a Cu^II–thioether complex, help uncouple the contribution of S_Met and S_Cys to the ground-state wave-function and show that the S K-pre-edge intensity at ~2469 eV solely reflects the Cu–S_Cys bond. rR data on C112SeC and WT have been used to experimentally probe and compare the Cu–Se_Cys and Cu–S_Cys bonds. EPR and MCD data are both affected by SOC. In this study, the effect of ligand SOC (Se = 1690 cm⁻¹, S = 382 cm⁻¹) on MCD data is investigated. The very similar C₀/D₀ ratios in WT and C112SeC P.a. azurin indicate that only the SOC of the Cu center (828 cm⁻¹) determines the MCD intensity. Finally, these results are coupled with DFT calculations to determine that the Cu–S_Cys and Cu–Se_Cys bonds are, in fact, very similar and to elucidate the factors affecting the nature of metal–Se versus metal–S bonding.

2. Experimental Section

2.1. Sample Preparation

WT azurin samples were purified from Pseudomonas aeruginosa (P.a.) as previously described.^23,24 The C112SeC and M121SeM proteins were prepared using the expressed protein ligation (EPL) method as previously described.^20,22 All samples were purified by anion-exchange chromatography, on a POROS 20HQ anion-exchange resin with a BioCad Sprint high-performance liquid chromatograph (HPLC) (Per-Septive Biosystems, Farmingham, MA) or an AKTA basic (GE Healthcare, Piscataway, NJ) system after copper incorporation liquid chromatography–mass spectroscopy (LC–MS) mass spectral data were collected for WT and M121SeM azurin, and show a single peak in the mass spectrum corresponding to the weight of the full-length protein (wild-type or variant) with no evidence of residual contamination from other proteins or synthetic peptides in the WT and ~4% contamination from unligated apoprotein. The degree of copper incorporation was assessed by comparison of the 280 nm and the 625 or 677 nm peak in the electronic absorption spectrum and from EPR spin quantitation. WT and M121SeM mutant azurin were prepared in NH4OAc buffer at pH 5.1 while C112SeC was prepared in TrisHCl buffer at pH 8.0 owing to the increased stability of this variant at elevated pH. All protein solutions were ~2.5 mM. Samples were transferred into MCD and S K-edge XAS cells for spectroscopic characterization and kept under liquid N₂ conditions until data collection.

2.2. S K-edge X-ray Absorption

S K-edge spectra were measured using the SSRL 54-pole wiggler beamline 6–2 in high magnetic field mode of 10 kG with a Ni-coated harmonic rejection mirror and a fully tuned Si(111) double-crystal monochromator. Details of the optimization of this beam line for low-energy fluorescence measurements and the experimental setup have been described previously.^25,26 S K-edge measurements were made at ~4 °C. Protein samples were pre-equilibrated in a water-saturated He atmosphere for ~0.5–1 h to minimize bubble formation in the sample cell. Protein solutions were loaded via syringe into a Pt-coated Al block sample holder with a 6.35 μm thick polypropylene window. The data were measured as fluorescence excitation spectra utilizing an ionization chamber as a fluorescence detector. All protein samples were monitored for potential effects of photoreduction throughout the course of data collection. The partially beam-reduced WT, C112SeC, and M121SeM samples were oxidized with a 10-fold excess of K₃[Fe(CN)₆], which allowed 8-, 4-, and 8-scan averages, respectively, to be obtained with no further indication of photoreduction. The energy was calibrated from S K-edge spectra of Na₂S₂O₃·5H₂O, run at intervals between sample scans. Data normalization was performed as described in earlier publications.²⁶ The area under the pre-edge peak was quantified by fitting the data using EDG_FIT.²⁷ The pre-edge and rising-edge features were modeled with pseudo-Voigt line-shapes with a fixed 1:1 Lorentzian/Gaussian ratio. The reported intensity and half-width values are based on averages over simultaneous fits that accurately modeled the data and their second derivative. Normalization procedures introduce ~3% error in the value of the integrated area under the pre-edge peak.

2.3. UV–Vis Absorption and Magnetic Circular Dichroism

Absorption spectra at temperatures between 5 and 300 K were measured using a computer-interfaced Cary-500 spectrophotometer modified to accommodate a Janis Research Super Vari-Temp cryogenic dewar mounted in the light path. Low-temperature magnetic circular dichroism spectra were obtained using two Jasco spectropolarimeters. Each is equipped with a modified sample compartment to accommodate focusing optics and an Oxford Instruments SM4000-7T superconducting magnet/cryostat. This arrangement allows data collection at temperatures ranging from 1.6 to 290 K and fields up to 7 T.²⁸ A Jasco J810 spectropolarimeter operating with a S-20 photomultiplier tube was used for the ultraviolet and visible spectral regions. A Jasco J200 spectropolarimeter operating with a liquid nitrogen cooled InSb detector was used for the near-infrared region. Depolarization of the light by the MCD samples was monitored by the differences in the circular dichroism spectra of nickel (+)-tartarate placed before and after the sample. In all cases, the depolarization was less than 5%.²⁹ MCD samples were run in cells fitted with quartz disks and a 0.3 cm rubber gasket spacer. Simultaneous Gaussian fitting of the absorption and MCD spectra was performed using the commercially available Peak-Fit program.

2.4. Resonance Raman

Resonance Raman (rR) spectra were collected with a Princeton Instruments ST-135 back-illuminated charge-coupled device (CCD) detector on a Spex 1877 CP triple monochromator with 1200, 1800, and 2400 grooves/mm holographic gratings. Continuous wave coherent Kr ion (Innova90C-K) and an Ar ion (Sabre-25/7) visible and UV laser lines were used as variable excitation sources. A polarization scrambler was used between the sample and the spectrometer. The Raman energy was calibrated with Na₂SO₄. Frequencies are accurate to within <2 cm⁻¹. Samples were loaded in 4 mm NMR tubes and stored in liquid nitrogen.

2.5. Computational Details

Density functional theory (DFT) calculations were performed on a 141-atom molecular model of the blue–copper site derived from the 1.5 Å resolution structure of oxidized P.a. azurin (PDB code 1JZF). This model for the azurin was optimized, keeping the backbone C and N atom coordinates constrained to their crystallographic positions. To model the M121SeM and C112SeC azurin mutants, the WT active site was modified by replacing the corresponding S atom by Se and the resulting structures were reoptimized, keeping the backbone atoms constrained. In addition, the DFT calculations have been performed on the BC model complexes [Cu(tpz)(XC₆F₅)], where X = S and Se and tpz is the tris(1-pyrazolyl)hydroborate ligand.

Spin-unrestricted DFT calculations were performed using the Gaussian 03 program³⁰ (Revision C.02) with the B3LYP exchange-correlation functional,³¹ which provides a reasonable orbital description of the copper sites in the model complexes. The triple-ζ TZVP basis set³² on the Cu, S, and Se atoms and the double-ζ 6-31G* basis set^33–35 on the O, N, C, and H atoms were used. Extending the basis set to TZVP for the O, N, C, and H atoms did not change the calculated spin density distribution in the blue–copper site of azurin. For the [Cu(tpz)(XC₆F₅)] complexes, the 6-311+G* basis set was used for the geometry optimization. Harmonic frequency calculations were performed on the [Cu(tpz)(XC₆F₅)] model to obtain the Cu–X normal modes and the nuclear mass effect (by changing M_Se of 80 to 32 a.u. (M_S)) on their frequencies. Then, the single-point calculations at B3LYP/TZVP level were used to evaluate bonding between the metal fragment and the XC₆F₅⁻ ligand. Tight self-consistent field (SCF) convergence criteria (10⁻⁸ a.u.) were used for all calculations. Wave-function stability calculations were performed (using the STABLE keyword) on all optimized wave-functions to confirm that they corresponded to the true ground state.

Molecular orbital (MO) compositions were calculated with the AOMix program^36,37 using the Mulliken population analysis (MPA).^38–41 Atomic charges and spin densities were calculated using natural population analysis methods (NPA),⁴² as implemented in Gaussian 03, and the Mayer bond orders,^43–46 as implemented in AOMix-L.

Force constants were calculated by fitting the Cu–X_thiolate potential surface to the polynomial function:

$$E=E_0+\frac{1}{2}k{(d-d_0)}^2+k_{\text{a}}{(d-d_0)}^3$$ (1)

Time-dependent density functional theory (TD–DFT) was used to calculate the energies and intensities of the 35 lowest-energy spin-allowed electronic transitions. These were transformed with the SWizard program into simulated spectra as described before, using Gaussian functions with half-widths of 3000 cm⁻¹.

The time-dependent density functional theory (TD–DFT) framework implemented in ORCA⁴⁷ was used to compute Cu K pre-edge (Cu 1s → ψ*_β–LUMO) and S K pre-edge (S 1s → ψ*_β–LUMO) transition energies. Single-point calculations were performed on CuL1 and [(Im)₂Cu(SMe)(SMe)₂]⁺ (modified from the crystal structure of P.a. azurin) in Gaussian03 using the BP86^31,48–50 with the 6-311G*^51–53 basis set on Cu and S and 6-31G* basis set^33–35 on the rest of the atoms. Single-point ground-state DFT calculations with the BP86 functional were performed using the geometry-optimized coordinates obtained from Gaussian03. The Ahlrichs’ triple-ξ valence basis TZVP³² was used on all atoms. The DFT calculations were repeated on the geometry-optimized structures of CuL1 (with the tertiary butyl groups replaced by H atoms) and the azurin model, and similar energy shifts were obtained.

3. Results and Analysis

3.1. S K-edge XAS

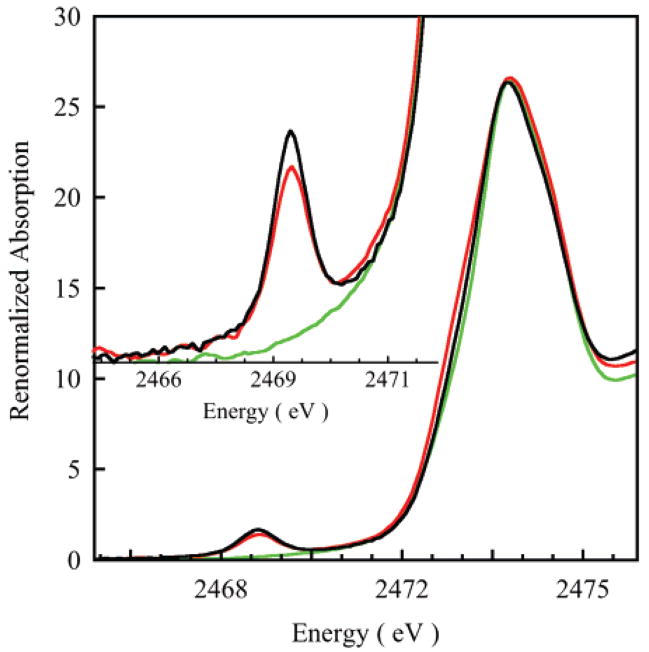
The renormalized⁵⁴ S K-edge X-ray absorption spectra of WT, C112SeC, and M121SeM mutants of P.a. azurin are shown in Figure 1. The WT and M121SeM spectra have a low-energy transition at ~2469 eV, which is absent in the C112SeC azurin spectrum. This pre-edge feature, which appears below the onset of the sharp-edge transition, is associated with the Cys S 1s → ψ*_β–LUMO transition (the lowest unoccupied β-spin molecular orbital in a spin-unrestricted description).^26,55–57 Because of the localized nature of the S 1s orbital, this transition is observed if ψ*_β–LUMO contains significant S 3p character and gains intensity as the S 3p character in this orbital increases. Thus, the pre-edge intensity is proportional to the S 1s → 3p transition intensity weighted by S_thiolate contribution to ψ*_β–LUMO. Integrating the area under the pre-edge peak and using the area obtained from the S K-pre-edge transition of plastocyanin as a reference (well-characterized from various spectroscopies with 38% S character in ψ*_β–LUMO), ¹⁴ a direct estimate of the Cu 3d–S 3pπ contribution to Cu–S bond covalency can be obtained. Table 1 gives the % S character and the energies of the pre-edge and edge features of WT, C112SeC, and M121SeM azurin. The pre-edge energy reflects a combination of $Q_{\text{mol}}^{\text{Cu}}$ (charge on Cu in the molecule), $Q_{\text{mol}}^{\text{S}}$ (charge on S in the molecule), and the ligand field (LF) felt by the central Cu atom.⁵⁶ The pre-edge occurs at 2469 and 2468.9 eV in WT and M121SeM azurin, respectively. The similarity in the pre-edge energy positions in WT and M121SeM indicates comparable $Q_{\text{mol}}^{\text{S}},Q_{\text{mol}}^{\text{Cu}}$, and Cu LFs in these two proteins. The edge energy reflects the $Q_{\text{mol}}^{\text{S}}$ in the molecule. However, azurin contains two cysteines and five methionines (in addition to the coordinating Cys and Met residues), which are not bound to the Cu center but contribute to the energy and the total intensity of the S 1s → 3p edge transition.⁷ This precludes an estimation of $Q_{\text{mol}}^{\text{S}}$ from the edge energy position.

Figure 1.

S K-edge X-ray absorption spectra of WT azurin (black line), M121SeM (red line), and C112SeC (green line) azurins. Inset shows the expanded pre-edge region. The spectra have been renormalized in each case to account for noncoordinating S-containing amino acids in the proteins.

Table 1.

Sulfur K-Edge XAS Results

azurin	pre-edge energya (eV)	1s → 4p transition energyb (eV)	% S character in ψ*β–LUMOc
WT	2469.0	2473.4	40%
M121SeM	2469.0	2473.4	37.5%
C112SeC		2473.5

^aThe error in the energy position is estimated to be ±0.1 eV.

^bDetermined from the second derivative spectra.

^cError in % S character due to data processing and fitting is ±3%.

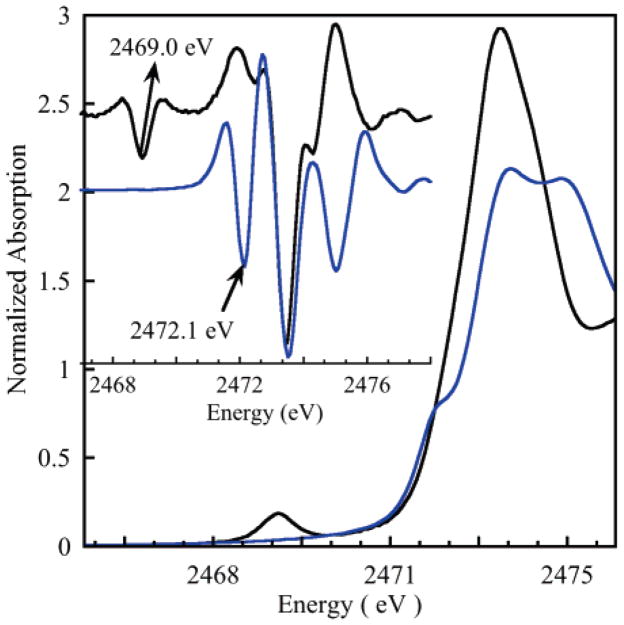
It has been shown that the ground state S character in blue–copper proteins predominantly comes from the covalent Cu–S_Cys interaction.⁴ This is consistent with the absence of the pre-edge feature in C112SeC in which S_Cys has been replaced by Se_Cys.⁵⁸ In WT and M121SeM azurin, the % S character in the ψ* _LUMO is 40 ± 3% and 37.5 ± 3%, respectively (Table 1), indicating a small decrease in S character in M121SeM azurin.⁵⁹ Although the S characters in the ground states of WT and M121SeM are quite similar (within error), in principle, a small decrease could reflect loss of a small contribution of the S_Met to the pre-edge intensity. Alternatively, the larger size of Se relative to S can potentially increase the charge donation from Se_Met to Cu and consequently decrease the S_Cys contribution to ψ*S_Cys bond _β–LUMO. EXAFS studies have shown that the Cu–distance does, in fact, increase from 2.14 to 2.18 Å on going from WT to M121SeM azurin.²⁰ In order to evaluate the contribution of the S_Met to ψ*_β–LUMO, the S K-edge spectrum of a Cu–S_thioether model complex, CuL1 (where H₂L1 = 2,6- bis[S-(3,5-di-tert-butyl-2-hydroxyphenyl)sulfanylmethyl]pyridine),⁶⁰ was obtained (see Supporting Information, Figure S1). The structure of CuL1 is five-coordinate with two Cu–S_thioether bond lengths of 2.4 Å. DFT calculations on CuL1 give a ψ*_β–LUMO with ~13% S_thioether character, therefore predicting a S K-pre-edge feature with significant intensity. Figure 2 shows the S K-edge data of CuL1, which exhibits a pre-edge transition at 2472.1 eV. Figure 2 also compares the normalized S K-edge spectra of WT azurin with that of CuL1. The pre-edge feature due to the Cu 3d–S_thiolate covalent interaction in WT azurin occurs at 2469.0 eV, while that due to the Cu 3d–S_thioether covalent interaction in CuL1 occurs 3.1 eV to higher energy at 2472.1 eV. The S K pre-edge energy position shifts to higher energy with an increase in $Q_{\text{mol}}^{\text{S}}$ and LF and to lower energy with an increase in $Q_{\text{mol}}^{\text{Cu}}$. In order to estimate the differences in $Q_{\text{mol}}^{\text{Cu}},Q_{\text{mol}}^{\text{S}}$, and ligand field, DFT and Cu 1s → ψ*_β–LUMO and S 1s → ψ*_β–LUMO TD–DFT calculations were performed on CuL1 and the azurin model. Calculations show that the energies of S K pre-edge (S 1s → ψ*_β–LUMO) and Cu K pre-edge (Cu 1s → ψ*_β–LUMO) transitions are, respectively, 2.1 and 0.7 eV higher in CuL1 than in the azurin model (Figure S2). It has been previously shown that the 1s → 3d transition energy at the Cu K-edge dominantly reflects the ligand-field strength felt by the Cu center. Thus, an ~1.4 eV increase in the S K-pre-edge energy in CuL1 is due to a combination of $Q_{\text{mol}}^{\text{Cu}}$ and $Q_{\text{mol}}^{\text{S}}$. DFT calculations show that $Q_{\text{mol}}^{\text{Cu}}$ is lower in the azurin active site compared to that in CuL1. This is consistent with a very covalent Cu–S_thiolate in azurin, which leads to only 41% Cu character in the ground state (Cu L-edge XAS)⁶¹ compared to the significantly weaker Cu–S_thioether bonds in CuL1, which results in ~70% Cu character in the ground state (DFT calculations).⁶⁰ Since an increase in $Q_{\text{mol}}^{\text{Cu}}$ decreases the pre-edge energy position, the increase in the pre-edge energy, due to changes in $Q_{\text{mol}}^{\text{S}}$ on going from a Cu–S_thiolate system to a Cu–S_thioether system, is expected to be significantly higher than ~1.4 eV. This is consistent with the fact that the rising-edge of CysNa (Na salt of cysteine thiolate) is ~1.8 eV lower in energy than that of methionine, reflecting an increase in $Q_{\text{mol}}^{\text{S}}$ in methionine.^62,63 Thus, any contribution of the S_thioether to the ground-state wave-function in azurin would be to higher energy than the pre-edge transition at ~2470 eV. Since no corresponding feature is observed to higher energy, the results confirm that Cu–S_Met covalent interaction is very small in azurin64 and give experimental evidence for the fact that the pre-edge intensity is a direct reflection of the Cu–S_thiolate covalency in azurin, and the similar pre-edge intensities in WT and M121SeM reflect very similar covalent interactions.⁶⁵

Figure 2.

S K-edge X-ray absorption spectra of WT azurin (black line) and the Cu–S_thioether complex (CuL1) (blue line). Inset shows the second-derivative spectra. The pre-edge energy positions have been marked in both cases.

3.2. UV–Vis Absorption and Magnetic Circular Dichroism

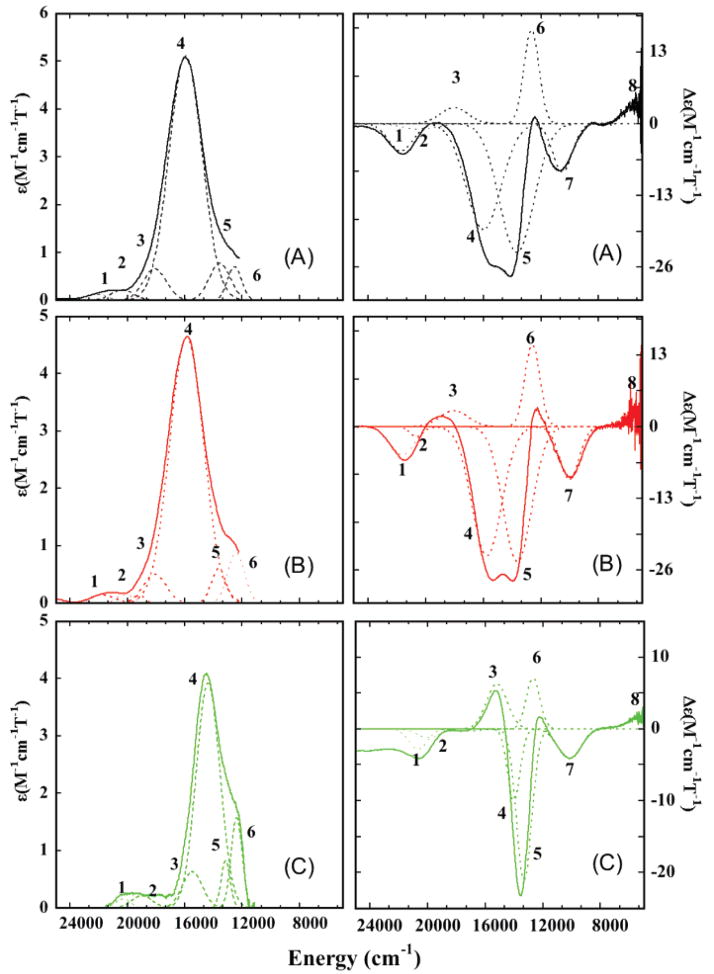
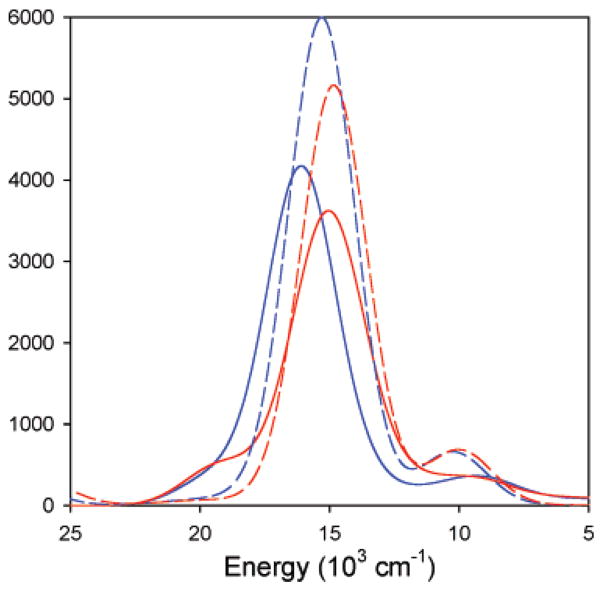
Low-temperature absorption and MCD spectra between 5000 and 30 000 cm⁻¹ for WT, M121SeM, and C112SeC azurin are presented in Figure 3. The transition energies and ε and Δε values obtained from the simultaneous Gaussian fits are presented in Table 2. The absorption and MCD spectra of azurin have been shown to be similar to plastocyanin, and hence, the following analysis is based on the band assignments in plastocyanin.^4,5 The Gaussian resolution of the absorption and MCD data require eight bands to adequately fit the spectra for each protein and have been included using dashed lines. For all three proteins, bands 1–4 in the high-energy region (>16 000 cm⁻¹) have high absorption intensity and low MCD intensity. The low-energy region (5000–15 000 cm⁻¹) also consists of four bands (only two are observed in the absorption spectra) that show low absorption intensity and high MCD intensity. On the basis of the spectral assignments of plastocyanin,^12,66 the four high-energy bands in azurin, M121SeM, and C112SeC are assigned as ligand-to-metal charge-transfer transitions, while the four lower energy bands are assigned to metal-based d → d (LF) transitions.^5,67,68 The blue–copper site has been found to have a relatively small splitting of the d_xz,yz orbitals.⁶⁹ This close-to-degenerate orbital set exhibits a pseudo-A term with the higher-energy transition having a negative sign (band 5) and the lower-energy transition (band 6) having a positive sign.⁶⁶ Band 7 is assigned to the d_xy → d_x²−y² transition and at lowest energy, band 8, is assigned to the d_z² → d_x²−y² transition. The charge-transfer region (14 000–25 000 cm⁻¹) is dominated by an intense transition, band 4, which is responsible for the blue color of these proteins. In analogy to other well-characterized blue–copper proteins, this band involves the strong Cu 3d-S pπ interaction and is assigned as the S_thiolate 3pπ → Cu d_x²−y² charge-transfer (CT) transition. To higher energy, a low-intensity transition is observed (band 3), which is assigned to the S 3p pseudo σ → d_x²−y² charge-transfer transition. The intense π, weak σ CT intensity inverted from that observed for normal Cu complexes and was attributed to the fact that the lobes of the half-occupied Cu 3d_x²−y² orbital bisect the S–Cu bond. The weak transitions band 1 and band 2 have been assigned to transitions from His (π) and S_Met to Cu d_x²−y² CT transitions. The intensities in the absorption spectra,⁶⁶ ENDOR studies,⁷⁰ and DFT calculations^4,5,71 have shown that the two His (π) and S_Met valence orbital overlaps with the half-occupied Cu d_x²−y² orbital are low.

Figure 3.

Electronic absorption (left panel) and magnetic circular dichroism (right panel) spectra of (A) WT (black line), (B) M121SeM (red line), and (C) C112SeC (green line) azurins. Simultaneous Gaussian fits require eight bands to fit the data, which have been depicted with dashed lines. The bands have been labeled 1–8 for all three proteins.

Table 2.

Experimental Absorption and MCD Parameters for WT, M121SeM, and C112SeC Azurin

	energy (cm−1)			ε (M−1 cm−1)			Δε (M−1 cm−1 T−1)			C0/D0
band & assignment	WT	M121SeM	C112SeC	WT	M121SeM	C112SeC	WT	M121SeM	C112SeC	WT	M121SeM	C112SeC
8a dz2	5430	5420	5400				+3.5	+2.0	+1.5	+b	+b	+b
7a dxy	10 700	9960	10 100				−8.8	−9.3	−4.1	−b	−b	−b
6 dxz+yz	12 600	12 400	12 500	730	740	460	+16.9	+16.9	+7.1	+0.25	+0.24	+0.16
5 dxz−yz	13 700	13 600	13 200	740	700	820	−23.3	−24.2	−22.2	−0.34	−0.37	−0.29
4 Cys pπ	15 900	15 800	14 200	5070	4700	4000	−19.2	−22.3	−8.3	−0.04	−0.05	−0.02
3 pseudo pσ	18 100	18 000	15 300	510	400	630	+2.9	+1.9	+3.4	+0.06	+0.05	+0.06
2 His π	20 100	20 600	17 200	160	180	170	−0.8	−1.0	−0.9	−0.05	−0.06	−0.05
1c Met	21 900	22 000	20 100	170	190	200	−5.0	−1.6	−1.3	−0.06	−0.05	−0.07

^aBands 7 and 8 are not observed in the absorption spectra.

^bOnly signs can be determined from the data for these parameters; however, the C₀/D₀ ratios should be >0.1 based on the relative magnitude of MCD to upper ε limit in absorption.

^cThis involves the Met b₁ orbital.

3.2.1. Comparison of WT and M121SeM Azurin

The absorption and MCD spectra of WT and M121SeM azurin are very similar with only small quantitative differences (Table 2). The ligand-field bands are lower in energy in M121MSe compared to WT by an average value of ~170 cm⁻¹. This difference is very small, indicating similar ligand-field strengths at the Cu center in both systems. Band 8, which is assigned as the d_z² → ψ*_β–LUMO d →d transition, occurs at 5430 cm⁻¹ and 5420 cm⁻¹ in WT and M121SeM, respectively. The energy of the d_z² orbital is tuned by two factors, the strength of the axial S/Se_Met–Cu interaction and the extent of Cu 4s mixing into the d_z² orbital. Cu 4s mixing with the d_z² orbital decreases while the axial donor interaction increases the energy of the d_z² orbital. As the energy of band 8 is the same in WT and M121SeM, replacement of the axial S_Met by Se_Met does not significantly perturb the axial interaction. The intense charge-transfer transition, band 4, occurs at 15 900 cm⁻¹ (ε = 5070 M⁻¹ cm⁻¹) for WT and is slightly lower in energy and intensity for M121SeM at 15 800 cm⁻¹ (ε = 4700 M⁻¹ cm⁻¹). This is consistent with the small decrease in the S character in ψ*_LUMO of M121SeM relative to WT observed from S K-edge XAS (vide supra) and supports the above analysis that the decrease in pre-edge intensity is due to weakening of the Cu–S_Cys bond. Band 1, which is assigned as the S_Met → Cu CT transition, is very similar in WT and M121SeM. This indicates that, going from S_Met to Se_Met, the Cu–S/Se axial donor interaction is not significantly perturbed. This is consistent with the strong similarity between the Cu–S_Cys/Se_Cys interaction described below.

3.2.2. Comparison of WT and C112SeC Azurin

A comparison of the absorption and MCD spectra of C112SeC with WT and M121SeM azurin is shown in Figure 3C (see also Figure S3 in Supporting Information) and Table 2. Gaussian fits to the LF region indicate that bands 5–8 are lower in energy by an average of only ~200 cm⁻¹ in C112SeC relative to WT. The energy of band 8 is comparable for WT (5430 cm⁻¹) and C112SeC (5400 cm⁻¹), indicating similar axial interaction between the S_Met and the Cu d_z² orbitals. This similarity in the d–d transition energy indicates comparable LF strengths in the two proteins. In the charge-transfer region, the intense blue band, band 4, is shifted to lower energy by 1700 cm⁻¹ in C112SeC relative to WT and results in the overlap of band 4 and band 5 in the absorption and MCD spectra (Figure 3). While the DFT calculations in Section 4.2 show that the electronegativity of Se relative to S is diminished in the cysteine thiolate fragments, there is still a decrease in ψ*_HOMO/ψ*_β–LUMO energy gap (see fragment calculations shown in Figure 8 and Supporting Information) on going from SCys⁻ to SeCys⁻, resulting in the decrease in CT energies. However, the d–d bands are more metal-centered and mixed with several ligand fragments and are, thus, less sensitive to the Se vs S difference relative to purely ligand-based orbitals, which are affected by the resulting change in the ψ_HOMO*/ψ*_β–LUMO energy gap. However, the striking similarity in the MCD spectra of WT and C112SeC azurin indicates that the two active sites have very similar geometric and electronic structures.

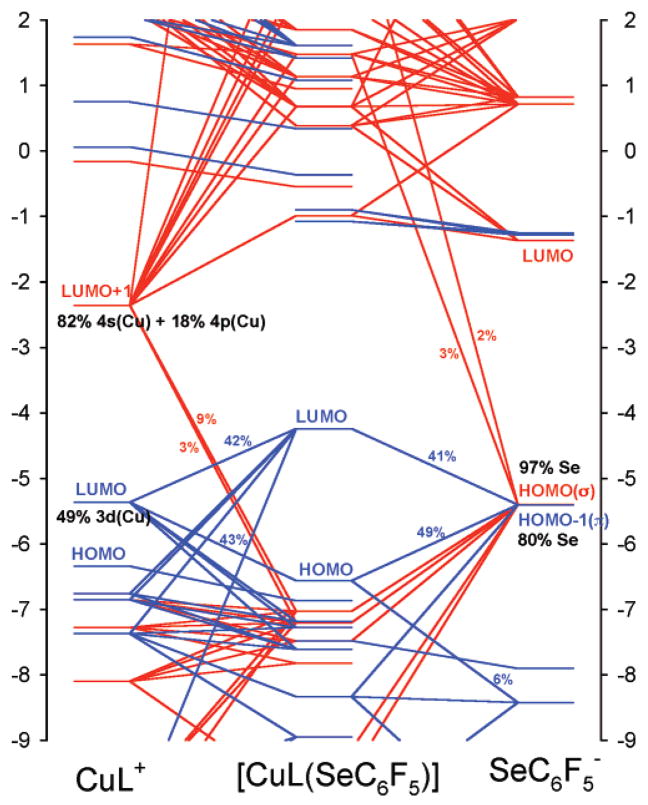
Figure 8.

Interaction diagram for β-spin molecular orbitals of [Cu^II(tpz)-(SeC₆F₅)] with [CuII(tpz)]⁺ and SeC₆F₅⁻ as fragments and the corresponding σ and π interactions are shown in red and blue. The molecular orbitals of the Cu(tpz)⁺ and SeC₆F₅⁻ fragments are shifted by 4.0 and −4.5 eV, respectively. The interaction diagram for β-spin molecular orbitals of [Cu^II-(tpz)(SC₆F₅)] is presented in Figure S4.80 The interaction diagram for α-spin molecular orbitals is very similar. However, since the α-spin Cu d_x²−y² fragment orbital is occupied, there is no net contribution to bonding from the π ligand-to-metal donation from this spin-orbital.

It is interesting to note that EXAFS analysis of WT and C112SeC azurin indicates that the Cu–Se_Cys bond distance in C112SeC is 2.3 Å, 0.16 Å longer than the Cu–S_Cys bond distance in WT, which is due to the larger covalent radius of Se compared to S (difference in the covalent radius is 0.135 Å).²² Despite this difference in bond distance, the electronic structure of the two proteins is very similar. The larger radial distribution of the valence 4p orbitals of Se compensate for the increase in bond distance, which results in a bonding interaction similar to that in WT azurin. The similarity of the MCD CT band intensities in WT and C112SeC azurin raises an interesting issue. Transitions observed in the LT absorption and MCD spectra were assigned as LF or CT transitions based on their relative intensity ratios.^66,72,73 This is given by the C₀/D₀ ratio, where C₀ is the low-temperature MCD C-term intensity and D₀ is the dipole strength obtained from the absorption spectrum, which is calculated using the following equation,^66,74

$$\frac{C_0}{D_0}=\frac{kT}{{\mu }_{\text{B}}B}{\left(\frac{\mathrm{\Delta }\epsilon }{\epsilon }\right)}_{\text{Max}}$$ (2)

where T is the temperature, B is the applied external magnetic field strength, k is the Boltzmann constant, μ_B is the Bohr magneton, ε is the absorption maximum in M⁻¹ cm⁻¹, and Δε is MCD intensity maximum measured in M⁻¹ cm⁻¹ K⁻¹. In a low-symmetry system, such as in azurin (C₁ symmetry), the orbital degeneracy of all states is lifted; hence, all electronic transitions are polarized in one molecular direction. However, MCD intensity requires two perpendicular transition moments. In such cases, low-temperature C-term MCD intensity derives from spin–orbit coupling (SOC), which can mix the two orthogonal transition dipole moments of different states. Hence, the C₀/D₀ will depend on the magnitude of SOC occurring at the centers involved in the transitions. Since the SOC parameter for Cu is greater than that for N or S (ξ_3d(Cu) ≈ 828 cm⁻¹ >≈ ξ_3p(S)382 cm⁻¹ > ξ_2p(N) ≈ 70 cm⁻¹), the Cu d → d transitions are expected to exhibit greater C₀/D₀ ratios than the ligand-based CT transitions in WT azurin. However, since in C112SeC azurin the corresponding S_Cys → Cu CT transitions are replaced by Se_Cys→Cu CT transitions, these bands might be expected to have larger C₀/D₀ ratios relative to WT since the SOC of Se is more than twice that of Cu (ξ_4p(Se) ≈ 1690 cm⁻¹). The experimentally determined C₀/D₀ ratios for both the d → d (LF) and CT transitions are, however, comparable in WT, M121SeM, and C112SeC azurin (Table 2). This insensitivity of the MCD intensity to the ligand SOC relates to the mechanism of low-temperature MCD intensity in the blue–copper site and is addressed in the Discussion section.

3.3. Resonance Raman

The resonance Raman (rR) spectra of blue–copper proteins obtained with excitation into the ~600 nm CT band (S_Cys 3pπ + Cu d_x²−y² → ψ*_β–LUMO transition) produces strong enhancement of three or more fundamental vibrational modes in the 330–460 cm⁻¹ region.^13,75 It has been suggested that the multiplicity of these modes is due to coupling of the Cu–S stretch with internal modes of the cysteine ligand.^76,77 The intensity-weighted average energy of these vibrations (〈ν_Cu–S〉), where 〈ν_Cu–S〉 = Σ_i(I_iν²)/Σ_i(I_iν), has been used as an indicator of the Cu–S_Cys bond strength with a higher 〈ν_Cu–S〉, indicating a stronger Cu–S bond.⁷⁵

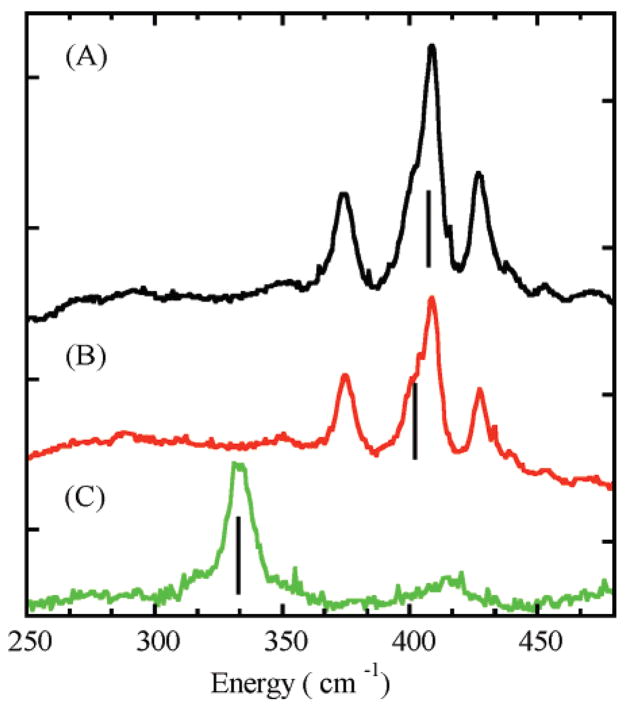
3.3.1. Comparison of WT and M121SeM Azurin

Figure 4 presents the rR spectra of WT and M121SeM azurin obtained with excitation at 647.1 nm, into the intense S(Cys) 3pπ → Cu CT transition (band 4). The spectra for WT and M121SeM are very similar and show three bands centered around 410 cm⁻¹. The intensity-weighted average energies of the Cu–S_Cys stretch were 407 and 402 cm⁻¹ for WT and M121SeM, respectively. The variation of stretching force constant for an atom-pair can be correlated to the bond distance between them using Badger’s rule.⁷⁸

Figure 4.

Resonance Raman spectra obtained upon excitation at 647.1 nm for WT (black line), M121SeM (red line), and C112SeC (green line) azurins. Lines mark the position of the intensity-weighted average of the Cu–S vibrations.

$$k=1.86{(r_{\text{e}}-d_{ij})}^{-1/3}$$ (3)

where k is the force constant, r_e is the equilibrium bond length, and the constant d_ij is fixed for bonds between atoms of rows i and j of the Periodic Table. Using the bond distances obtained from EXAFS data and WT 〈ν_Cu–S〉 as reference, the Cu–S_Cys bond distance estimated from Badger’s rule for M121SeM is 2.16 Å, which is within error of the experimentally (EXAFS) obtained Cu–S_Cys distance of 2.18 Å. These results are indicative of a small decrease in the Cu–S_Cys force constant on going from WT to M121SeM azurin, consistent with a small decrease in the S K-pre-edge intensity.

3.3.2. Comparison of WT and C112SeC Azurin

A comparison of the rR spectra of WT and C112SeC with excitation at 647.1 nm is also included in Figure 4. The spectrum of C112SeC consists of one band at 333 cm⁻¹ in contrast to the three-band spectrum of WT. Using the reduced masses of the Cu–Se and Cu–S pair in C112SeC and WT, respectively, and the WT 〈ν_Cu–S〉 (407 cm⁻¹) as a reference, a 〈ν_Cu–Se〉 value of 317 cm⁻¹ would reflect the mass change effect with no change in the Cu–X force constant. The experimental value of 333 cm⁻¹ indicates, at most, a small increase in the Cu–Se force constant in C112SeC.

3.4. Density Functional Theory

3.4.1. Geometry Optimization

The results of the geometry optimization of the 141-atom models of WT, M121SeM, and C112SeC azurin are presented in Table 3. The structures of the M121SeM mutant and WT are very similar, and the Cu–ligand distances are perturbed only slightly (Δd ≤ 0.02 Å, Table 3). The structural changes are more significant in the C112SeC mutant. The calculated Cu–Se_Cys distance is 2.31 Å, 0.1 Å longer relative to the calculated Cu–S_Cys distance in the WT (Table 3). Alternatively, the Cu–S_Met distance is ~0.1 Å shorter relative to that in WT. The Cu–N_His and Cu–O_Gly distances undergo only very small changes upon Se_Cys substitution.

Table 3.

Calculated Cu–Ligand Distances (Å) in the 141-Atom Azurin Models

	Cu–NHis1	Cu–NHis2	Cu–XCys	Cu–XMet	Cu–Oax
WT	2.06	2.03	2.21	3.06	2.68
M121SeM	2.06	2.04	2.22	3.07	2.66
C112SeC	2.06	2.02	2.31	2.97	2.69

3.4.2. Comparison of Wave-functions

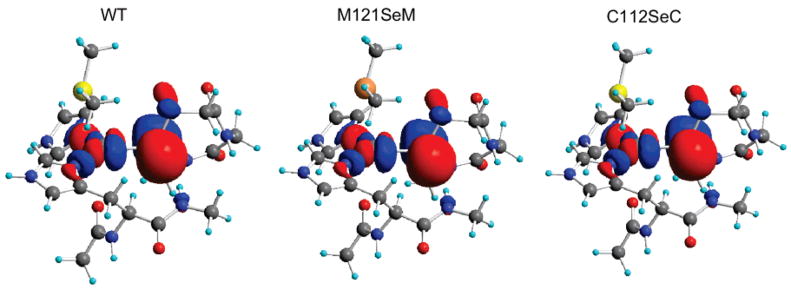
The DFT calculations on WT, M121SeM, and C112SeC azurin give a ground-state description that indicates a highly covalent Cu–S/Se_Cys bond in all three structures, which is reflected in the composition of the β-spin ψ*_LUMO (Table 4, Figure 5). In the WT model, the Cu and S_Cys contributions to ψ*_LUMO are 43.4% and 35.5%, respectively (Table 4). As a result, the spin density is almost equally shared between these two atoms (Cu and S_Cys MPA- and NPA-derived spin densities are ~43% and 38–39%, respectively). This description is in agreement with the experimental S K-edge XAS data (Table 1). The spin density of the Cu and S_Cys atoms accounts for ~79% of the total spin density of the system. The remaining 21% is mostly delocalized over the imidazole rings of the histidine ligands and the β-methylene H-atoms of the Cu-bound Cys residue. The contribution of S_Met is very small (0.1%), reflecting a very weak interaction between the half-occupied Cu 3d_x²−y² orbital and the S_Met donor orbital, consistent with the approximately perpendicular orientation of the Cu–S_Met with respect to the Cu d_x²−y² plane.

Table 4.

ψ*_β–LUMO Compositions in Terms of Cu, S/Se of Cys and Met, and N_His Contributions in the 141-Atom Azurin Models

	orbital contributions to ψ*LUMO, %
	Cu	2NHis1	XCysa	XMet	Oax
WT	43.4	4.2	35.5 (35.3)	0.1	0.1
M121SeM	43.0	5.8	34.7 (34.6)	1.8	0.2
C112SeC	39.1	4.1	41.2 (40.9)	0.3	0.1

^aThe S 3p orbital contribution.

Figure 5.

ψ*_β–LUMOof the 141-atom azurin model (the isocontour value is 0.03 a.u.). The contour plots indicate very similar ground-state wave-functions of the three proteins with only small quantitative differences.

Figure 5 shows a contour plot comparison of the WT with M121SeM azurin. The overall spin-density distribution (Table 4) is very similar to that in the WT; however, the contribution of the Se_Met to ψ*_β–LUMO (1.8%) is greater than the contribution of S_Met. There is no structural distortion in M121SeM, which indicates that the increased S_Met donation to the ground state is because of the larger radial distribution of the Se 4p relative to the S 3p orbital. The small increase in the Cu–Se_Met interaction leads to a slightly weaker Cu–S_Cys covalent interaction, as reflected in the changes in the ψ*_β–LUMO composition (decreased by ~1%) (Table 4).

In C112SeC, the ground-state wave-function is qualitatively very similar to that of the WT protein (Figure 5). The Se_Cys and Cu contributions to ψ*_β–LUMO are ~41% and 39% (Table 4). This indicates that C112SeC has the strongest covalent interaction between unoccupied Cu 3d_x²−y² orbital and X_Cys relative to WT and M121SeM. The highly covalent Cu–Se_Cys bond description obtained from DFT calculations is consistent wih the small increase in the covalent component of the Cu–Se_Cys bond observed in the rR data. However, the increase incovalent interaction upon replacement of S_Cys with Se_Cys is very small (only ~5%), resulting in only a small perturbation to the ground-state wave-function.

3.4.3. TD–DFT

TD–DFT calculations were performed on WT azurin and the C112SeC mutant to compare to the experimental electronic absorption spectra. The results are presented in Figure 6 and are in good agreement with the experimental data (Figure 3). Both the calculated spectra contain an intense charge-transfer band (~16 200 cm⁻¹ for the WT and 15 200 cm⁻¹ for the C112SeC), which corresponds to a β-spin electron transition from the Cu 3d_x²−y² + X_Cys pπ occupied orbital to ψ*_β–LUMO. The calculated oscillator strength of this CT band in the C112SeC mutant is slightly less than the corresponding oscillator strength in the WT. This small decrease in intensity is linked to a slightly smaller Cu–X_Cys overlap population (OP) in the C112SeC mutant relative to WT azurin due to the longer Cu–X_Cys bond (OP_Cu–X are −0.070 and −0.063 for the WT and C112SeC, respectively). The d–d transitions in C112SeC relative to WT are less shifted than the corresponding CT bands, since they are dominantly metal based and are mixed with several ligand fragments.

Figure 6.

TD–DFT-calculated spectra of WT azurin (black dotted line), the C112SeC mutant (red dotted line), [Cu^II(tpz)(SC₆F₅)] (black solid line), and [Cu^II(tpz)(SeC₆F₅)] (red solid line).

These results coupled with the experimental data indicate that replacement of S_Cys with Se_Cys leads to a surprisingly small electronic structure perturbation. Although, as expected, the Cu–Se bond does become stronger and more covalent relative to WT, the overall S character only increases by ~5%. This is even more intriguing given that a structural perturbation occurs on going from WT to C112SeC (Cu–X_Cys is longer by 0.1 Å and the Cu–X_Met is shorter by ~0.1 Å). This is addressed in the next section.

4. Discussion

4.1. Unique Spectroscopic Features of Blue–Copper Proteins

BC proteins have been extensively studied by a wide range of spectroscopic methods, which have helped define the ligand field of the Cu center and quantify its covalent bonding interaction. However, there are several interesting issues related to these spectroscopies that have remained elusive. The mutation of S to Se in the equatorial cysteine and axial methionine has provided an excellent opportunity to probe these interactions and resolve a number of key spectroscopic issues.

4.1.1. S_Met Contribution to S K-edge XAS

S K-edge XAS provided the first quantitative measure of the S character in ψ*_β–LUMO of a BC protein (~38%).¹⁴ However, since blue–copper proteins contain a weak Cu–S_Met bond and LT abs and MCD spectra (consistent with other spectroscopic studies and DFT calculations) show a small contribution of the S_Met ligand to the ground-state wave-function, it has remained important to evaluate whether the 38% S character in the ground state observed from the S K-pre-edge intensity quantifies the CuS_Cys interaction. In this study, although the pre-edge of M121SeM at 2469.0 eV is very similar to that of the WT protein, the intensity is decreased by a small amount (~1–3%) (Figure 1). However, the S K-edge XAS spectra of CuL1, which has a Cu^II–S_thioether bonding interaction, was also measured, which indicates that the pre-edge of a Cu–S_Met complex occurs at 2472.1 eV, ~3.1 eV above the Cu–S_thiolate pre-edge transition observed in BC proteins. This clearly shows that the Cu–S_Met bond does not contribute to the pre-edge intensity at ~2469 eV in BC proteins and the 38% S character in the ground-state wave-function only involves S_Cys.

4.1.2. Kinematic Coupling in Resonance Raman Spectroscopy

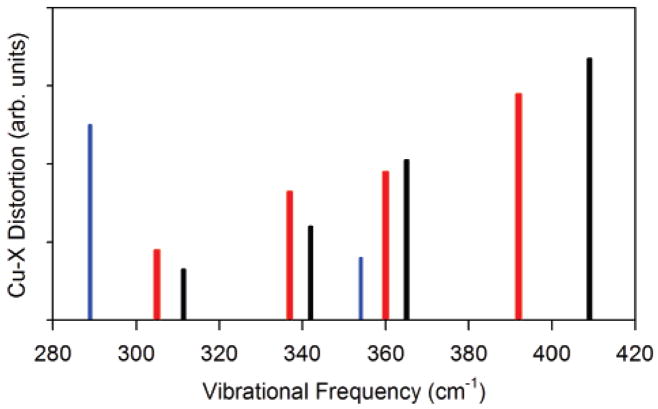
X-ray crystal structures of BC proteins show that the dihedral angle formed by the S_Cys is highly conserved as are the Cu–S_γ–C_β–C_α and the S_γ–C_β–C_α–N dihedral angles (~170°).¹³ This leads to near coplanarity of the Cu–S_Cys bond with the cysteine side-chain and part of the polypeptide backbone. It has been suggested that this results in coupling between the Cu–S_Cys vibration and the cysteine deformation modes.^13,77,79 Because of the mass effect, for the C112SeC mutant, the Cu–X_Cys stretching frequency decreased from 410 to 333 cm⁻¹. Interestingly, the three-peak vibrational pattern observed in the rR spectrum of WT is replaced by a single peak in the rR spectrum of C112SeC (Figure 4), even though DFT calculations suggest minimal structural change upon Se_Cys mutation (the calculated active=site geometries of the 141-atom WT and C112SeC azurin are very similar (see Figure 5)). To evaluate the factors resulting in the loss of kinematic coupling in C112SeC azurin, frequency calculations were performed on the small-molecule analogues; [(tpz)Cu(XC₆F₅)] (X = Se and S). Figure 7 shows the calculated magnitude of Cu–X motion contributing to the vibrational normal modes between 280 and 420 cm⁻¹. The frequencies of these modes for [(tpz)Cu(SC₆F₅)] are in reasonable agreement with the observed spread of frequencies in the published rR data.⁸⁰ In contrast to the calculated mixing of Cu–S distortion over four normal modes in [(tpz)Cu(SC₆F₅)] (311, 342, 365, and 409 cm⁻¹), the calculated Cu–Se distortion is mostly restricted to a single low-frequency normal mode (~290 cm⁻¹) in [(tpz)Cu(SeC₆F₅)] (Figure 5). Finally, frequency calculations were also performed on the hypothetical [(tpz)Cu(³²SeC₆F₅)] complex in which the mass of Se is modified to be equal to S. Interestingly, the calculations reveal that, similar to the Cu–S motion in [(tpz)-Cu(SC₆F₅)], the Cu–³²Se distortion is mixed into four normal modes (305, 337, 360, and 393 cm⁻¹). This indicates that the low Cu–Se stretching frequency eliminates mechanical coupling of the Cu–Se distortion with other ligand normal modes, and when the mass of Se is lowered, the mixing is reestablished. Thus, the absence of multiple bands in the rR spectrum of C112SeC indicates that the lower frequency of the Cu–Se_Cys stretch uncouples it from the cysteine deformation modes and results in a single vibrational feature. These results support the kinematic coupling between the Cu–S_Cys and the cysteine deformation modes in BC proteins.

Figure 7.

DFT calculated Cu–X distortion (arbitrary units) along normal modes for [(tpz)Cu(XC₆F₅)]; X = S (black line), X = Se (blue line), and X = ³²Se (red line).

4.1.3. Effect of Ligand Spin–Orbit Coupling on MCD C-Terms

At low temperature, the C-term dominates the MCD spectrum of paramagnetic systems. Two mechanisms contribute to nonzero C-term intensity: (i) SOC between two nearby excited states |J> and |K> to which orthogonal transitions are made from the ground state |A> and (ii) SOC between the ground state |A> and a low-lying excited state |K> from which two orthogonal transitions can be made to a single excited state |J>. The first mechanism leads to oppositely signed C-terms with equal intensities (pseudo-A term), while the second leads to deviation from the MCD sum-rule. Both these mechanisms involve two perpendicularly polarized CT transitions, which have SOC along a third, mutually orthogonal direction. Defining the molecular coordinate system in azurin such that the S/Se_Met is along the z-direction, the Cys- and His-based ligand-to-metal CT transitions are x,y-polarized and require the SOC along the z-axis (L_z). The C₀ term associated with two such CT transitions is given by^74,81,82

$$\begin{array}{l}{C}_0(A\to J)=\\ -\frac{1}{6}\sum _{K\ne A,J}{g}_z{{\mathrm{\Delta }}_{KJ}}^{-1}(D_x^{KA}{D}_y^{AJ}-D_y^{KA}{D}_{\text{x}}^{AJ})L_z^{KJ}\end{array}$$ (4)

where g_z is the effective g-value in the z-direction, Δ⁻¹_KJ is the energy difference between the two excited states, |J〉 and |K>, $D_x^{JA}$ is the component of the transition dipole moment between |A〉 and |J〉 in the x-direction, and $L_z^{KJ}$ is the spin–orbit coupling operator. Since $L_z^{KJ}$ is effectively a localized, single-center, one-electron operator, the center involved in SOC around the z-direction must be simultaneously present in both orthogonal CT transitions. This can only involve the central Cu atom, which overlaps both donor orbitals. Hence, nonzero ligand-to-metal charge transfer C-term intensity involves a metal-based SOC mechanism. This explains the similar C₀/D₀ ratios in WT, M121SeM, and C112SeC azurin (Figure 3). Although the donor orbitals are dominantly ligand-based with very different SOC parameters on S versus Se, this difference does not affect the C-term intensity. The effect of this metal-centered SOC mechanism can be seen in the previously observed MCD spectra of Pf AOR, a W(V) containing enzyme with dithiolato ligands in comparison to the data on Rs DMSOR, a structurally similar enzyme with a Mo(V) center.^83,84 The C-term intensity is an order of magnitude higher for Pf AOR since the SOC of W_5d is ~4 times higher than that of Mo_3d.

4.2. Cu–S Versus Cu–Se Bonding

Resonance Raman data and DFT calculations reveal that the ground-state wave-functions (ψ*_β–LUMO) of WT and C112SeC are very similar, with only a small increase in the Cu–X_Cys covalency in C112SeC. A similar trend in metal–S/Se covalency has been previously observed in [Fe₂Se₂(SPh)₂]²⁻ and [Fe₂S₂(SPh)₂]²⁻ where the Fe–S and Fe–Se covalencies were found to be similar.⁸⁵ This is surprising, since the larger and “softer” Se might have been expected to have a much stronger Se–Cu (4pπ–Cu 3d_x²−y²) interaction relative to S–Cu (3pπ–Cu 3d_x²−y²). To analyze the factors affecting M–S vs M–Se bonding, DFT calculations were performed on [Cu^II(tpz)(XC₆F₅)] model complexes (tpz = trispyrazolyl borate, X = S, Se) to correlate interaction energies and bond lengths and to quantify the nature of chemical bonding.^86,87 The TD–DFT calculated absorption spectra (Figure 6) of [Cu^II(tpz)(SC₆F₅)] and [CuII(tpz)(SeC₆F₅)] are very similar to those of WT azurin and the C112SeC mutant, respectively, and show the same shifts in energy and intensity as in the proteins. This indicates that a reasonable theoretical comparison of the two models can be made to interpret the protein experimental data.

Relevant calculated parameters for [Cu^II(tpz)(SC₆F₅)] and [Cu^II(tpz)(SeC₆F₅)] are summarized in Table 5. The electronic interaction energy between the Cu^II–tpz fragment and the SeC₆F₅⁻ ligand in [Cu^II(tpz)(SeC₆F₅)] is calculated to be 0.8 kcal mol⁻¹ smaller than the electronic interaction energy between the [Cu^II(tpz)]⁺ fragment and the SC₆F₅⁻ ligand in [Cu^II(tpz)(SC₆F₅)]. Such a small difference in the interaction energies in the two systems originates from the fact that Cu–X covalency in the two is very close (27% S character in [Cu^II-(tpz)(SC₆F₅)] and 32% Se character in [CuII(tpz)(SeC₆F₅)] and the Cu–S and Cu–Se bond orders are 1.07 and 1.08, respectively; see Table 5). In these two complexes, the covalent bonding between the XC₆F₅⁻ ligand and Cu^II is limited to σ and π ligand-to-metal donation. There are only two donor orbitals involved: the near-degenerate, highest occupied pσ, and pπ orbitals of the XC₆F₅⁻ ligand (see the orbital interaction diagram, Figure 8, right). In the [Cu^II(tpz)(SC₆F₅)] model, the α-spin Cu^II(tpz)⁺–SC₆F₅⁻ orbital interactions involve only the pσ orbital of the thiolate, which donates 0.16 electrons to the metal fragment. The β-spin orbital interactions involve both pσ and pπ and 0.16 and 0.41 electrons are transferred to the metal fragment from these two orbitals, respectively. In the [Cu^II(tpz)-(SeC₆F₅)] model, the situation is very similar: pσ donates 0.17 electrons (α-spin) and 0.17 electrons (β-spin) to the metal fragment and pπ donates 0.44 electrons (β-spin).

Table 5.

Cu–X Bond Distance and Mayer Bond Order (B_Cu–X), [Cu^II(tpz)]⁺–XC₆F₅⁻ Electronic Interaction Energy, Composition of β-spin LUMO (ψ*_β–LUMO), Energies of HOMO and HOMO-1 of the XC₆F₅⁻ Ligand, and the Overlap Integral (S) between the β-spin Cu d_x²−y² Fragment Orbital and the pπ Orbital of XC₆F₅⁻ in the [Cu^II(tpz)(XC₆F₅)] Complexes (X = S and Se)

ligand	dCu–X (Å)	BCu–X	Eint(kcal· mol−1)	% X (and % XC6F5) in ψ*β–LUMO	εHOMO (eV)	εHOMO−1 (eV)	S
SC6F5−	2.204	1.07	−144.0	26.7 (39.0)	−0.94	−1.04	0.063
SeC6F5−	2.316	1.08	−143.2	31.9 (41.7)	−0.90	−0.90	0.061

There are two factors that influence the extent of Cu–X covalent bonding. The first is the fragment orbital overlap (which determines the magnitude of the corresponding Fock matrix element 〈ψ_i|F|ψ_j〉), and the second is the relative energies between the interacting orbitals (ψ_i and ψ_j) of the two fragments,

$$E_{i\to j}=-\theta \frac{{\langle {\psi }_i\mid F\mid {\psi }_i\rangle }^2}{E_j-E_i}$$ (5)

where θ is the electron occupation of the resulting bonding orbital (2 for a doubly occupied MO and 1 for a singly occupied MO). DFT calculations show that, for ψ*_β–LUMO, the Cu d_x²−y² fragment orbital involved in the π ligand-to-metal donation has the same orbital overlaps, 0.06 (Table 5) with the pπ orbitals of SC₆F₅⁻ and SeC₆F₅⁻ in the corresponding complexes (in which the Cu–S and Cu–Se distances are 2.20 and 2.32 Å, respectively) (Table 5). In addition, the fragment calculations show that the donor orbitals (HOMO and HOMO-1) of the free ligands have very similar energies (Table 5). Since both the orbital overlap and the relative fragment energies are very similar, the corresponding bonding interactions between the donor orbitals of the ligand and the acceptor orbitals of the metal result in very similar orbital stabilization energies and covalencies for the two complexes.

The result that the donor orbitals of SC₆F₅⁻ and SeC₆F₅⁻ are so close in energy (which indicates that the electronegativities of the Se and S atoms in SC₆F₅⁻ and SeC₆F₅⁻ are very close) is not obvious considering that free S and Se have significantly different atomic electronegativities χ (Mulliken values of χ are 6.22 eV for S and 5.89 eV for Se).^88,89 On the basis of the electronegativity of free atoms, the energies of S-based donor orbitals are expected to be significantly lower (by at least 0.3 eV) compared to the Se-based donor orbitals. Insight into this deviation from the atomic electronegativities comes from the fact that, although local atomic electronegativity is a function of atomic charge, the hardness η (η_S= 4.14 eV and η_Se = 3.86 eV) indicates how sensitive the electronegativity is with respect to change in atomic charge. In the ligand XC₆F₅⁻, the charge is distributed over the entire ligand framework to equalize the chemical potential. DFT calculations indicate that the S atom in SC₆F₅⁻ has the same charge as the Se atom in SeC₆F₅⁻ (q_NPA = −0.45 a.u.). This similarity in S and Se charges in the ligand molecular framework results in very similar local electronegativities of S and Se (2.08 eV for S and 2.03 eV for Se). Thus, the corresponding S- and Se-donor orbitals (pσ and pπ of the XC₆F₅⁻ ligand) have very similar energies, allowing for similar bonding interactions as observed experimentally in the WT and C112SeC mutant of azurin.

This study shows that the M-thiolate/selenolate bond strengths are very similar in Cu–S_Cys and Cu–Se_Cys systems and provides important insight into other M–X_Cys (X = S, Se) containing proteins involved in redox processes. These include the heterometallic NiFeSe hydrogenases^90,91 (which contain a Ni–Se_Cys bond) and the Mo/W containing formate dehydrogenases (FDHs) (which contain a Mo/W–Se_Cys bond).^92–94 This study reveals that the frontier molecular orbitals (FMOs) of RSe⁻ and RS⁻ are very similar, which explains the similarity in the active-site electronic structures and the catalytic rates of NiFeSe and NiFe (S_Cys instead of Se_Cys), both of which occur naturally.⁹⁵ In FDHs, however, replacing the WT Mo–Se_Cys bond by Mo–S_Cys leads to only 0.3% catalytic rate.⁹⁶ Interestingly, although the bond strength and electronic structure of the active site Mo–S/Se are very similar, the intrinsic pKa of the Se_Cys and S_Cys are significantly different (5.2 and 8.3, respectively).^97,98 These results indicate that the presence of Se_Cys in lieu of S_Cys does not tune the redox reactivity of the metal center, but instead, the pKa of the selenolate could be required for efficient catalysis.

In summary, a spectroscopic and DFT investigation of WT, M121SeM, and C112SeC azurin has been performed, which has elucidated interesting spectroscopic issues. S K-edge XAS on WT, M121SeM, and the Cu^II–S_thioether model CuL1 show that the 38% S character in the ψ*_β–LUMO only reflects the SCys ligand. Resonance Raman data on WT and C112SeC azurin support the model that mechanical coupling of the Cu–S stretch with the cysteine deformation modes in WT result in the multiple-peak rR spectrum in the 400 cm⁻¹ region. The much lower stretching frequency of the Cu–Se mode (333 cm⁻¹) decouples it from the protein vibrational models, resulting in a single peak. UV–vis and MCD data on WT, M121SeM, and C112SeC give similar C₀/D₀ ratios, which show that it is the SOC on the metal center that determines MCD intensity. The spectroscopic data show that the Cu–S_Cys and Cu–Se_Cys bonds have very similar covalencies at the bond distances of 2.1 and 2.3 Å, respectively, which is supported by DFT calculations. These calculations indicate that fragment orbital overlaps and energies are very similar for the S and Se in their thiolate/selenolate fragment environment, which leads to very similar ground-state covalencies and overall bonding.