Abstract
Gas diffusion from an encapsulated microbubble is modeled using an explicit linear relation for gas permeation through the encapsulation. Both the cases of single gas (air) and multiple gases (perfluorocarbon inside the bubble and air dissolved in surrounding liquid) are considered. An analytical expression for the dissolution time for an encapsulated air bubble is obtained; it showed that for small permeability the dissolution time increases linearly with decreasing permeability. A perfluorocarbon-filled contrast microbubble such as Definity was predicted to experience a transient growth due to air infusion before it dissolves in conformity with previous experimental findings. The growth phase occurs only for bubbles with a critical value of initial partial mole fraction of perfluorocarbon relative to air. With empirically obtained property values, the dissolution time of a 2.5 micron diameter (same as that of Definity) lipid coated octafluoropropane bubble with surface tension 25 mN/m predicts a lifetime of 42 minutes in an air saturated medium. The properties such as shell permeability, surface tension, relative mole fraction of octafluoropropane are varied to investigate their effects on the time scales of bubble growth and dissolution including their asymptotic scalings where appropriate. The dissolution dynamics scales with permeability, in that when the time is nondimensioanlized with permeability, curves for different permeabilities collapse on a single curve. Investigation of bubbles filled with other gases (non-octafluoropropane perfluorocarbon and sulfur hexafluoride) indicates longer dissolution time due to lower solubility and lower diffusivity for larger gas molecules. For such micron size encapsulated bubbles, lifetime of hours is possible only at extremely low surface tension (<1mN/m) or at extreme oversaturation.
Keywords: Microbubble, Ultrasound Contrast Agents, Dissolution, Permeability, Encapsulation, Epstein-Plesset, Gas Transport
INTRODUCTION
Encapsulated microbubbles are used for improved contrast of ultrasound images (Chang et al 1996, Dejong et al 1994, Dejong & Hoff 1993, Dejong et al 1992, Ferrara et al 2007, Klibanov et al 2006, Pollard et al 2004, Simpson et al 1999) and drug and gene delivery (Klibanov 2006, Price et al 1998, Shohet et al 2000). The encapsulation, typically made of proteins, lipids and other surface active materials, stabilizes a bubble against dissolution in the blood stream. A stable microbubble with good scattering characteristics is critical for achieving good image contrast. Dissolution of free bubbles has been investigated in detail since the pioneering study of Epstein and Plesset (1950), where they showed that an air bubble’s growth (dissolution) in oversaturated (undersaturated) liquid is modified by the surface tension (see Duncan and Needham (2004) for a review of the literature). Surface tension generates a higher pressure inside the bubble and the equation of state for the gas predicts a higher gas concentration there. Consequently, a higher gas concentration at the bubble wall drives the outward diffusion of gas in the liquid. In pure water, micron-size free air-bubbles would dissolve in 30 milliseconds [see Eq. (13) below], while an encapsulated microbubble would last much longer depending on the surface properties. Replacing air with sparingly soluble perfluorocarbon (PFC) gas (also called osmotic agent) has also contributed to increased lifetime of these bubbles (Ferrara et al 2007).
Here we develop a mathematical model for the effects of encapsulation, incorporate it into the boundary value problem of the gas diffusion, and investigate resulting bubble dynamics in presence of perfluorocarbon inside and air dissolved in the liquid outside (air could also be initially present inside the microbubble). This investigation is motivated by our investigation of Definity® (Bristol Myers Squibb Medical Imaging, N. Billerica, MA, USA) destruction process (Chatterjee et al 2005). Under ultrasonic excitation, we saw an increase in total attenuation from a Definity solution with time for relatively low levels of excitations, the maximum being reached around 10 min. We inferred that the encapsulation becomes slightly permeable and leads to initially more inward diffusion of air than outward diffusion of less soluble octafluoropropane (OFP). The increased bubble size causes the increased attenuation. At intermediate excitation levels, the attenuation decreased with time with decrease-rate increasing with excitation level; it indicated a far larger permeability where outward diffusion of OFP becomes the limiting step leading to slow dissolution of bubbles. At even higher levels of excitations, attenuation decreased at much faster rate, and the rate did not depend on excitation level indicating a total destruction of the encapsulation. Both at intermediate and higher value of excitations, the time scale for the process 6–10 minutes. Such transient growth (also with 5–10 minute time scale) was inferred by Shi and Forsberg (2000), when they observed a shift in the maximum of the attenuation spectrum of ultrasound from Optison® (GE Healthcare, Princeton, NJ, USA) agent. Guan and Matula (2004) in their investigation of Sonazoid® (GE Healthcare, Oslo, Norway) under ultrasonic pulse excitation and Chen et al (2002) in their destruction study of Optison and biosphere® observed a temporary increase in scattered signals. They used a model developed by Kabalnov et al. (1998b). The model is an adapted version of the one developed by Epstein and Plesset (1950) for presence of both air and PFC. Kabalnov et al (1998a, 1998b) showed that diffusivity and solubility critically affect the lifetime of contrast microbubbles. These models of contrast microbubbles did not account for the effects of encapsulation.
Recently, Duncan and Needham (2004) performed a careful test of the Epstein-Plesset dissolution model using an air bubble (of radius~15 μm) supported on a micropipette. They concluded that the model predicts bubble dissolution time to 10% accuracy. There has not been any model to take into account the effect of the encapsulation for air bubble except for the one by Borden and Longo (2002) (the same model was also discussed in the review article by Ferrara et al (2007)), where they assumed an additional resistance due to a shell of lipid monolayer for the bubble (of radius ~ 25 μm) and incorporated it along with the resistances due to a polyethylene glycol (PEG) layer and the surrounding water. We see below that our model can be used to obtain the shell resistance parameter Rshell.
In this work we first develop a model for the effects of the encapsulation on the gas diffusion. In the subsequent subsections, we develop the single and multiple gas cases in presence of encapsulation. Wherever possible, theoretical results are related with those presented elsewhere. We then concentrate on a bubble representative of Definity contrast agent (2.5 micron diameter and containing octafluoropropane). It has a lipid encapsulation; lipid coating and gas permeation through it have been investigated quite extensively recently, making it an excellent choice for finding how the property values determine its lifetime and dissolution. The material properties such as diffusivities, Ostwald coefficients of air and octafluoropropane were determined from the literature. We investigate the time varying behavior and dissolution time. Later we present a parametric study of the effects of variation in surface tension, permeability, radius, Ostwald coefficient and air saturation on dissolution time. We also investigate the effects of different gas contents—perfluorocarbons and sulfur hexafluoride. We discuss our results and its implications on contrast microbubbles. Final section summarizes our findings.
MATHEMATICAL FORMULATION
Gas diffusion through permeable shell
For an encapsulated bubble, the dissolution time is much longer than the time scale for diffusion R0/hg through the encapsulation, where R0 is the initial bubble radius and hg is the permeability of gas through the membrane (see also nomenclature at the end of text for symbols). Thus a pseudo steady state can be assumed. Neglecting the fast transients and convective transport term, the gas concentration C in moles/volume outside the bubble of radius R satisfies steady state diffusion equation, which in spherically symmetric case is
| (1) |
with boundary condition C→C(∞) at r → ∞, where C(∞) is the concentration of the dissolved gas in the liquid very far away from the bubble (Figure 1). The boundary condition at the liquid side of the bubble wall is that the flux in the liquid side is matched by the diffusion through the membrane. The diffusion through the membrane is modeled as proportional to the concentration difference across the membrane Cw−C (R), where Cw is the gas concentration at the inner wall of the membrane in contact with the gas inside (Figure 1):
| (2) |
Figure 1.
Schematic for an encapsulated microbubble.
Here kg is the coefficient of diffusivity of the gas through the liquid. The mass flux through the encapsulation is modeled by a coefficient hg which can be thought of as , where is the diffusivity of the gas through the encapsulation and δ the thickness of encapsulation. However, Fickian diffusion might be inappropriate for a monolayer encapsulation. An energy barrier model of gas permeation through membrane would also give rise to such a linear relation (Blank & La Mer 1962, Borden & Longo 2002). Solving (1) with boundary condition(2), we obtain
| (3) |
The bubble contains gas at a concentration Cg. Its growth is determined by the mass flux at the bubble wall
| (4) |
We assume that the membrane is completely hydrated. Therefore, the dissolved gas concentration Cw at the membrane wall in contact with the inside gas is related to the inside gas concentration by the Ostwald coefficient Lg:
| (5) |
Note that for an ideal gas, it is equivalent to the Henry’s law, , (H is Henry’s constant) that relates the wall concentration to the gas partial pressure pg. The partial pressure in turn is proportional to the concentration Cg by the gas law, giving rise to
| (6) |
where T and RG are temperature and the universal gas constant. Using (3), we obtain for the evolution of bubble radius:
| (7) |
Single gas
For a single gas content such as air, we investigate the behavior of the bubble for both cases when the gas is air (identical to the case considered by Epstein and Plesset except for the effect of the shell), or other low solubility gas such as perfluorocarbons. C(∞) is determined by the level of saturation of the liquid with the gas at the atmospheric pressure, i.e.
| (8) |
The factor f describes whether the liquid is saturated (f=1), undersaturated (f<1) or oversaturated (f>1) with the gas. The pressure inside the bubble is higher than the atmospheric pressure by the Laplace pressure due to surface tension γ:
| (9) |
Replacing C(∞) and Cg (from Eq (9)) in Eq (7) we obtain:
| (10) |
This is the same equation obtained by Borden and Longo (2002) (their equation (13) when one identifies Rshell=1/hg); they obtained it by an entirely different consideration of various resistances in the mass diffusion circuit. (The review article (Ferrara et al 2007) in their Eq. 1.2 has a minor typographical error of 3/4 instead of 4/3 in the first factor of the denominator). In the limit of a free bubble hg → ∞, we obtain the familiar Epstein-Plesset equation [Eq. (15) in (Duncan & Needham 2004)]. Note that a non-zero surface tension γ, and undersaturation (1− f > 0) drives dissolution. Small hg (less permeable membrane) and small Lg (low solubility) hinder bubble dissolution. One can integrate the equation, but the result is algebraically complex to provide any additional insight. However for the saturated case (f = 1), we obtain:
| (11) |
and
| (12) |
where dissolution time tdiss (when bubble radius R becomes zero) is non-dimensionalized by the time scale of diffusion (R2/kg); γ/patm R0 is the nondimensional Laplace overpressure. hg R0/kg is the analogue of Sherwood number which appears in convective mass transfer. It is the ratio of the resistance due to gas diffusivity through bulk liquid to that due to hindered permeability of the encapsulation. The dissolution time is inversely proportional to the Ostwald coefficient Lg. However note that finite permeability, i.e. finite Sherwood number, destroys the inverse proportionality with the gas diffusivity kg. In the limit of hg R0/kg → ∞, we obtain
| (13) |
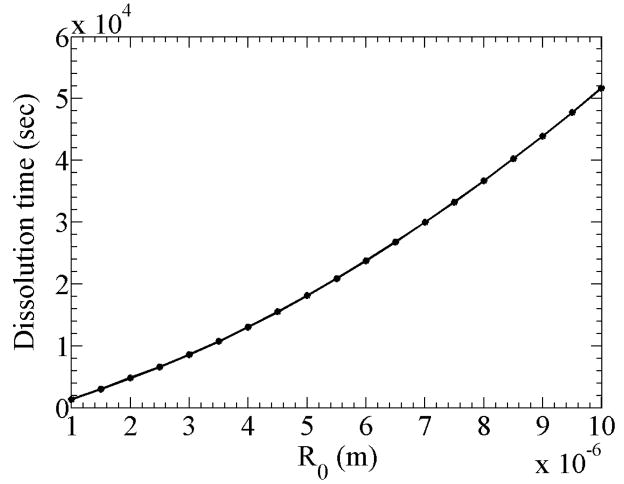
same as in Duncan and Needham (2004). In Figure 2, we plot the dissolution time for an encapsulated air bubble of diameter 2.5μm as a function of encapsulation permeability. The reference permeability used is for air through a lipid encapsulation (see Appendix and Table 1). Other property values are given in Table 1. It shows that for small hg the dissolution time decreases inversely with hg, finally reaching the limiting case of (13) for large enough hg. The limiting value for the dissolution time for this 2.5 micron encapsulated air bubble is 53 milliseconds. Note that using an encapsulation with hg = 2.785×10 −5 m/s increases the dissolution time to 5 seconds (a hundred fold increase in life-time). The analytical expression (12) of dissolution for a single gas clearly shows the importance of the permeability barrier of the encapsulation, in that the effects of permeability adds two terms which are inversely proportional to the Sherwood number O(kg/hgR), which is ~100 (from Table 1). The relatively moderate value of the inverse of Sherwood number indicates that the resistance due to the encapsulation dominates over the one due to diffusivity through bulk liquid. In Figure 3, we plot the dissolution time as a function of R0 with property values from Table 1. The rate of increase of dissolution time with initial radius is steeper than linear. For example an increase from two to twenty micron in bubble radius approximately increases the dissolution time by hundred.
Figure 2.
Variation of dissolution time with permeability for an encapsulated 2.5 micron diameter air bubble, h* = 2.785 × 10−5 m/s.
Table 1.
Physical properties of contrast microbubbles (see Appendix for references to literature and determination procedure)
| Initial bubble radius (R0) | 1.25 ×10−6 m |
| Atmospheric pressure (patm) | 101325 Pa |
| Coefficient of diffusivity of air in water (kA) | 2.05 ×10−9 m2 s−1 |
| Coefficient of diffusivity of SF6 in water | 1.2 ×10−9 m2 s−1 |
| Coefficient of diffusivity of C3F8 in water (kF) | 7.45 ×10−10 m2 s−1 |
| Coefficient of diffusivity of C4F10 in water | 6.9×10−10 m2 s−1 |
| Coefficient of diffusivity of C5F12 in water | 6.3 ×10−10 m2 s−1 |
| Coefficient of diffusivity of C6F14 in water | 5.8 ×10−10 m2 s−1 |
| Surface tension (γ) | 0.025 N/m |
| Ostwald coefficient of SF6 | 5.4 ×10−3 |
| Ostwald coefficient of C3F8 (LF) | 5.2 ×10−4 |
| Ostwald coefficient of C4F10 | 2.02 ×10−4 |
| Ostwald coefficient of C5F12 | 1.17 ×10−4 |
| Ostwald coefficient of C6F14 | 2.3 ×10−5 |
| Ostwald coefficient of air (LA) | 1.71 ×10−2 |
| Permeability of air through the encapsulation (hA) | 2.857 ×10−5 m s−1 |
| Permeability of SF6 through the encapsulation | 8.7 ×10−6 m s−1 |
| Permeability of C3F8 through the encapsulation (hF) | 1.2 ×10−6 m s−1 |
| Permeability of C4F10 through the encapsulation | 2.57 ×10−7 m s−1 |
| Permeability of C5F12 through the encapsulation | 9.04 ×10−8 m s−1 |
| Permeability of C6F14 through the encapsulation | 4.44 × 10−8 m s−1 |
Figure 3.
Variation of dissolution time with initial radius for an encapsulated microbubble of air. Inset shows a shorter range (1–2 μ) radius variation.
Multiple gas content
The above analysis indicates that using a gas with lower solubility and diffusivity will result in enhanced microbubble stability, as is indeed the case with second generation contrast microbubbles made with perfluorocarbon. The non-air filling gas is often called an osmotic agent. However, due to the presence of air dissolved in the liquid outside, air also plays a role in the dynamics. We therefore consider diffusion of two components: air A and the sparingly soluble perfluorocarbon F. One correspondingly gets two equations for these two components. We assume CF (∞) = 0, i.e. the gas is only introduced into the liquid through the bubbles, but CA (∞) is determined by the fact that the liquid is in contact with air at atmospheric pressure patm, i.e. CA (∞) = fLA patm/RGT, as in equation (8). The factor f as before determines the air saturation level of the liquid. The two equations are then
| (14) |
| (15) |
For a free bubble hA,F→ ∞ or more appropriately the nondimensional number hA,F R/kA,F → ∞, we obtain the same equations of Kabalnov et al (1998b) in absence of the encapsulating membrane. The pressure inside the bubble arises from partial pressures due to the osmotic agent and the air:
| (16) |
We non-dimensionalize various variables (Kabalnov et al 1998b):
where R0 is a initial bubble radius, equations (14), (15) and (16) become
| (17) |
| (18) |
| (19) |
Using the constraint (19) we eliminate F to obtain
| (20) |
Corresponding initial conditions are
| (21) |
where XF is the initial mole-fraction of the insoluble gas F. One arrives at
| (22) |
MATERIAL PROPERTIES
As a reference case, we take an FDA approved ultrasound contrast agent, Definity. Definity microbubbles contain Octafluoropropane (OFP; n-C3F8) and have a fairly narrow radius distribution with a mean diameter of 2.5 micron (Quaia 2005, Sboros et al 2001). They have a lipid (DPPA, DPPC, MPEG5000 DPPE) encapsulation. An interfacial tension value of 0.025 N/m reduced from its pure air-water interface value of 0.072 N/m is assumed for the lipid monolayer (Duncan & Needham 2004). Note that for C16 lipids the collapse phase surface tension was measured as 0.010N/m (Borden & Longo 2002). The exact value of the surface tension for the encapsulation is hard to determine especially for a micron size bubble. Recently, we have developed an inverse procedure to measure such interfacial rheological properties.(Chatterjee & Sarkar 2003, Sarkar et al 2005). We also note that by suitably choosing the encapsulation, one can completely eliminate surface tension for a waxy solid like layer (Duncan & Needham 2004, Kim et al 2003). Later in this paper, we investigate the effects of surface tension variation. The values of diffusivities kA,F of air and OFP are provided in Table 1. Determining the value of permeability hA,F poses difficulty. Fickian model assumes which requires accurate estimation of diffusivity through encapsulation material and the encapsulation thickness. The thickness of the Definity encapsulation has been reported with wide variation: 1–2 nm (Goertz et al 2007), 4 nm (Chen et al 2004) and a much larger value of 15 nm (Cheung et al 2008). Encapsulation thickness varies between contrast microbubbles, e.g. 15 nm for Optison (Christiansen et al 1994), 200–300 nm for Quantison, 600–1000 nm for Myomop (Quaia 2005). The air diffusivity in bulk lipid is 10−14 m2/s giving hg ~ 10−5 m/s for δ ~ 1nm which seems more appropriate for a lipid monolayer ((Borden & Longo 2002). On the other hand for a thin monolayer, a continuum description of diffusion through a finite layer with bulk material properties may not be appropriate. The monolayer acts more like a barrier which only sufficiently energetic gas molecules can overcome. Such an energy barrier model for gas penetration through a thin layer has been developed by Blank (Blank 1962, Blank 1964, Borden & Longo 2004, Borden et al 2006). The energy barrier depends on the gas molecules’ collision diameter, and surface pressure, the later being determined by the constituent surface active molecule’s geometry and packing in the layer. The resistance consequently becomes an exponential function (through the Arrhenius factor) of the layer thickness as opposed to a linear one characteristic of Fickian diffusion. Borden and Longo (2002) investigated such dependence by varying the chain length of encapsulation molecules. However the measurement failed to conclusively determine in favor of either the Fickian diffusion or energy barrier models. We use the energy barrier model for determining the values of encapsulation permeability. The values are found in the Appendix to be hA = 2.857×10−5 m/s, hF = 1.2×10−6 m/s. The other parameters are listed in Table 1. The procedure for determining the properties are detailed in the Appendix. These are used except when explicitly stated otherwise. Note that both the models of gas permeation give permeability values of the same order of magnitude. Note that the encapsulation is characterized mechanically only by a surface tension—Newtonian interfacial rheology (Chatterjee & Sarkar 2003). A more complex interfacial rheology will introduce other interfacial parameters (Katiyar et al 2009, Sarkar et al 2005).
RESULTS AND DISCUSSION
As can be seen by the nondimensional equations (17)–(22), the dependent variables R̂(τ), F(τ) and A(τ) are functions of nondimensional variables R̂0, γ̂, LF, LA, λ, αF, αA and XF. We present our results in terms of dimensional quantities for ease of use. MATLAB is used to solve the system of equations. Figure 4 shows the dissolution of a Definity microbubble with properties inferred as above (Table 1). The bubble initially grows to a maximum and then experiences slow dissolution. Note that the logarithmic time scale, used to delineate the transient dynamics exaggerates the transient time scale (see Figure 5). The bubble reaches the maximum around 50 seconds and the total dissolution time is approximately 2500s. The initial growth of the bubble is due to more air diffusing into the bubble than OFP coming out, which in turn is due to the higher diffusivity of air than that of OFP. The temporary growth of contrast microbubbles was previously inferred from acoustic experiments, albeit under acoustic excitation (Chatterjee et al 2005, Shi & Forsberg 2000). The predicted time scale of growth ~ 2min is of the same order as the experimentally inferred one (~ 10 minutes) at low acoustic excitation. The total dissolution time as well is of the same order as that observed under intermediate and higher acoustic excitations. It indicates that acoustic excitation degrades the encapsulation making way for the increased gas transfer. In such a process, encapsulation permeability plays a critical role in determining the bubble behavior.
Figure 4.
Dissolution of an encapsulated 2.5 micron diameter OFP bubble in an air-saturated medium.
Figure 5.
Variation of R/R0 with time for different OFP mole fractions; in the inset dissolution time vs OFP mole fraction.
Figure 4 also plots the partial pressures of air and OFP. The partial air pressure inside the bubble increases rapidly to the value of the atmospheric pressure outside at which point the right-hand side of Eq.(15) becomes zero. The partial pressure of OFP first decreases as OFP diffuses out and air diffuses into the bubble, but then it rises explosively in the final phase as the bubble radius shrinks to zero. Kabalnov et al predicted a life time of 40 seconds for a perfluorobutane (n-C4F10) filled unencapsulated bubble of radius 2.5 micron (Kabalnov et al 1998b). The OFP-filled Definity bubble despite having half the size and a smaller perfluorocarbon has approximately sixty times longer lifetime primarily because of the encapsulation.
Figure 5 shows the bubble evolution as a function of initial mole fraction of OFP. The bubble’s initial growth is controlled by the initial composition of gases in the bubble; as the amount of initial air fraction increases, the initial growth of the bubble reduces, being almost zero for the mole fraction of 0.28. For lower initial OFP content, the radius first decreases sharply for a short time interval, and after the air partial pressure inside reaches its equilibrium value of the atmospheric pressure, more gradually. In the inset, the dissolution time is seen to vary significantly with initial OFP content, especially for an air bubble (XF = 0) with small addition of OFP. In the presence of sparingly soluble OFP, diffusion of air is dominated by the slower diffusion of OFP, and a higher dissolution time is observed. Figure 6 shows the effects of initial radius distribution of Definity on any particular bubble’s dissolution behavior. The dissolution time increases sharply with bubble radius similar to the behavior seen for the air bubble in Figure 3.
Figure 6.
Variation of dissolution time with initial bubble radius of an encapsulated OFP microbubble.
We then consider bubbles containing non-branched perfluorocarbon gas other than octafluoropropane—C4F10, C5F12, and C6F14—and sulfur hexafluoride (SF6). SF6 has been used as an osmotic agent in experimental contrast agents such as BR1 (Schneider et al 1995) and ST44 (Forsberg et al 1999). The gas properties are listed in Table 1; some are taken from Kabalnov et al (1998b) (their Table 1 had a typographical error in the diffusion coefficient unit—D×1010 m2/s—revealed when values are calculated from their Appendix). The properties for SF6 listed in Table 1 are found from previous measurements (see Appendix). SF6 is the smallest molecule, with correspondingly largest diffusivity, permeability and solubility. Therefore in Figure 7, it shows the shortest dissolution time. For perfluorocarbons, with increasing carbon chain length, solubility, diffusivity and permeability reduce leading to increased dissolution time; they show similar growth and dissolution pattern. The dissolution times are reported in Table 2.
Figure 7.
Variation of R/R0 with time for an encapsulated 2.5 micron diameter bubble with different gas content in an air-saturated medium.
Table 2.
Dissolution time for a 2.5 micron encapsulated microbubbles with different gases in an air-saturated medium
| Osmotic agent | Dissolution time, tdiss |
|---|---|
| SF6 | 35 seconds |
| C3F8 | 42 minutes |
| n-C4F10 | 83 hours |
| n-C5F12 | 17 days |
| n-C6F14 | 17 days 14 hours |
Next, we analyze the effects of other parameters such as permeability and surface tension on its dissolution behavior. We already noted the difficulties in ascertaining their values. Furthermore, under ultrasound excitation and in suspension over time the encapsulation would show structural deterioration, resulting in different property values (Chen et al 2002, Chomas et al 2000, Shi & Forsberg 2000). Therefore knowledge of the effects of property variation would be useful in interpreting experimental results and in designing better contrast agents. Figure 8 shows the dynamics of an OFP bubble in a saturated medium for different surface tension values. Nonzero surface tension via Laplace pressure causes the bubble to dissolve, as the inside pressure is always higher than the outside pressure driving the gradient. The zero surface tension on the other hand predicts a final non-zero radius. OFP diffuses out of the bubble reducing its partial pressure to zero, but air diffuses into the bubble, and the bubble can finally reach a nonzero equilibrium radius when inside pressure equals the outside pressure. The inset shows the increase in dissolution time as surface tension decreases from its pure air-water interface value of 0.072 N/m. The increase is initially gradual, and only below 1 mN/m it is much sharper reaching hours of lifetime.
Figure 8.
Variation of R/R0 of an encapsulated OFP microbubble with time for different surface tension values; dissolution time variation with surface tension in the inset.
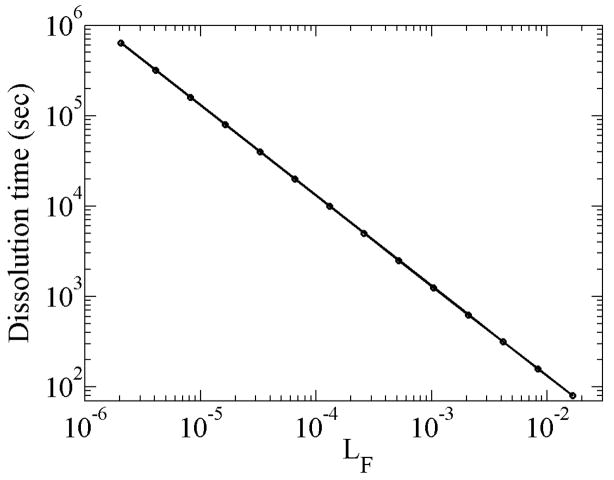
Figure 9a shows the effects of encapsulation permeability on bubble dissolution. For the parametric study, we vary both air and OFP permeability by the same multiplicative factor assuming that air and OFP interact similarly with the encapsulation constituents. This assumption can easily be relaxed. As expected increasing the permeability delays the growth and the dissolution process. As with the case of an air bubble in Figure 2, the OFP bubble with very high permeability reaches the limiting value of dissolution time of about 4.75 seconds (Figure 9b), in contrast to 53 milliseconds for an air bubble. For low permeability, the dissolution time seems to scale with permeability. Indeed when the time is scaled with permeability as in the inset of Figure 9b, all curves for different permeability (from Figure 9a) collapse on to a single curve. Figure 10 shows that there is an inverse relation between dissolution time and Ostwald coefficient as also shown by equation (12) for single-gas bubbles, the minimum value of the coefficient in the figure being close to that of air.
Figure 9.
(a) Variation of R/R0 of an encapsulated OFP microbubble with time for different permeability values, . (b) Dissolution time variation of an encapsulated OFP microbubble with permeability; variation of R/R0 with non-dimensional time in the inset.
Figure 10.
Variation of dissolution time with Ostwald coefficient of osmotic agent
We note here that only extremely low values of surface tension or unusually low encapsulation permeability would lead to a relatively stable (hours of life time) bubble. Typically for the second generation microbubbles, several hours of lifetime has been suggested. In the model presented, a non-zero surface tension and undersaturation (1−f>0) drive the dissolution. Undersaturation plays a role in physiological situations. We therefore study the effects of undersaturation in Figure 11 with a surface tension value of zero. We observe that even for zero surface tension, the undersaturation is an extremely efficient mechanism for driving towards dissolution. Only for extremely low values (~10−3) of (1−f), we obtain microbubble lifetime greater than a day.
Figure 11.
Variation of R/R0 and dissolution time with saturation level for zero surface tension.
SUMMARY
We have developed and investigated a new model for gas diffusion from encapsulated contrast microbubbles. A new linear permeability model is assumed for the gas diffusion through the encapsulating shell, which is appropriate for both Fickian diffusion and energy barrier models. With typical values for material constants, layer thickness, and molecular parameters, both theories give rise to permeability values of the same order of magnitude.
Both air and perfluorocarbon bubbles are modeled. In the latter case, diffusion of perfluorocarbon as well as air dissolved in the liquid is accounted for. We have developed an analytical relation for the dissolution time of an air bubble which shows an inverse relation with encapsulation permeability. For an air bubble a hundred-fold increase and for an OFP bubble a five-hundred-fold increase in dissolution time compared to free bubbles is predicted with encapsulation. The relative importance of the encapsulation permeability compared to bulk diffusion in determining the life time of an encapsulated bubble as exemplified by the low value of Sherwood number underscores the choice of appropriate encapsulating material for optimal design of contrast agents. The dissolution time also rises sharply with initial radius.
We investigate an encapsulated octafluoropropane-filled microbubble with the physical properties representative of the Definity contrast agent. We find that such a bubble dissolves in 2500 seconds. But before dissolution, the bubble experiences a transient growth due to more air going into the bubble from surrounding liquid than OFP going out. Increasing initial air content of the bubble reduces the growth part, making it negligible for OFP mole fraction of 0.28. The simulated time scale of growth and complete dissolution match in order of magnitude with what can be inferred from experiments under acoustic excitation.
The dissolution curves for different permeabilities collapse onto a single curve when the time is appropriately scaled with permeability. We also investigated the effects of the filling gas—perfluorocarbons of increasing chain length and sulfur hexafluoride. Increased size of gas molecule results in lower water solubility and lower diffusivity both through encapsulation and water leading to longer lifetime. Decreasing surface tension also lengthens the lifetime, giving a stable bubble at zero surface tension. However, we note that one has to really reach extremely low surface tension before one reaches more than couple of hours of lifetime. Duncan and Needham (2004) showed that solid waxy encapsulation is possible under careful preparation that has effectively a zero surface tension. It remains to be determined if the commercially available contrast agents have such an encapsulation. For a zero surface tension case, we further find that slight undersaturation is sufficient to result in reduced bubble life. Noting the difficulty in determining the material properties of the encapsulation the parametric study presented here can be an effective tool in designing better contrast agents. Different constitutive properties of the encapsulation with added explicit interfacial elasticity results in different dissolution dynamics (Katiyar et al 2009).
Acknowledgments
The authors acknowledge financial support from NSF CBET-0651912. KS acknowledges fruitful discussion with Professor Mark Borden in Columbia University and Flemming Forsberg in Thomas Jefferson University.
Nomenclature
- C
Concentration of the gas (mol m−3)
- Cg
Concentration of the gas in the bubble (mol m−3)
- Cw
Concentration of the gas at the bubble wall (mol m−3)
- CA
Concentration of the air in the bubble (mol m−3)
- CF
Concentration of the OFP in the bubble (mol m−3)
- f
Saturation level constant
- hg
Permeability of gas through the membrane (m s−1)
- hA
Permeability of air through the membrane (m s−1)
- hF
Permeability of OFP through the membrane (m s−1)
- kg
Coefficient of gas (air/OFP) diffusivity through the liquid (m2 s−1)
Coefficient of gas (air/OFP) diffusivity through the membrane (m2 s−1)
- kA
Coefficient of diffusivity of the air through the liquid (m2 s−1)
- kF
Coefficient of diffusivity of the OFP through the liquid (m2 s−1)
- Lg
Ostwald coefficient of gas
- LA
Ostwald coefficient of air
- LF
Ostwald coefficient of OFP
- m
Mass of the gas inside the bubble (kg)
- patm
Atmospheric pressure (kg m−1 s−2)
- pg
Pressure of the gas inside the bubble (kg m−1 s−2)
- pA
Partial pressure of air inside the bubble (kg m−1 s−2)
- pF
Partial pressure of OFP inside the bubble (kg m−1 s−2)
- R
Bubble radius (m)
- R0
Initial bubble radius (m)
- RG
Universal gas constant (kg m2 s−2 mol−1K−1)
- Rshell
Shell resistance (s m−1)
- XF
mole fraction of a gas in the bubble
- r
Radial distance (m)
- t
Time (s)
- T
Temperature (K)
- α
Non-dimensional number involving diffusivity, permeability and R0
- γ
Surface Tension (kg s−2)
- δ
Shell thickness (m)
- λ
Ratio of the diffusivities of air and OFP
- τ
Non-dimensional time
APPENDIX
The oxygen permeability of phospholipid monolayer as a function of domain boundary density has been determined (Pu et al 2005). The mean value of shell resistance for oxygen through a C16 lipid monolayer is 350 s/cm. We use shell resistance of air to be the same as that of oxygen and therefore its inverse hA = 2.857×10−5 m/s. Using the energy barrier model for diffusion, the shell resistance of two gases are related to their collision diameters and the surface pressure (Blank & La Mer 1962, Ciani et al 2004, Ferrara et al 2007):
The collision diameters for OFP and oxygen are aOFP = 6.95A°, aOxygen = 3.6A° (Siebert & Knobler 1971). Π is the surface pressure (47 mN/m; the difference in air-water interfacial tensions for the free interface, 72 mN/m, and the adsorbed interface, 25 mN/m). We get hF = 1.2×10−6 m/s. Similarly, we obtain permeability for non-octafluoropropane perfluorocarbons and sulfur hexafluoride using their collision diameters from Siebert & Knobler (1971). The diffusion coefficient of air in water has been calculated to be kA = 2.05×10−9 m2s−1 by the molar average of the diffusivities of oxygen (2.20×10−9 m2s−1) and nitrogen (2.01×10−9 m2 s−1) at 25°C (Ferrell & Himmelblau 1967). The diffusion coefficient of OFP in water is calculated using an empirical correlation (Hayduk & Laudie 1974, Kabalnov et al 1998b)
where Vm is the molar volume in cm3/mol. The molar volume of OFP is calculated using group additive method and the molar volumes of CF3 and CF2 groups (Lawson et al 1978). We find kF = 7.45×10−10 m2/s. The Ostwald coefficient of air is also calculated as LA = 1.71×10−2 by the molar average of the Ostwald coefficients of nitrogen (1.448×10−2) and oxygen (2.773×10−2) following Lide (1998). The solubility of non-branched fluorocarbons in the homologous series decrease by a factor of ~ 8 (Kabalnov et al 1990). The solubility of OFP is then obtained by those of C2F6 (1.272×10−3) and C4F10 (2.02×10−4) to be LF = 5.2 ×10−4. The diffusivity of SF6 (1.2. × 10−9 m2 s−1) listed in Table 1 was obtained using a correlation provided by King & Saltzman (1995) based on their measurement, the value being very similar to the one predicted by the above correlation due to Hayduk & Laudie with Vm = 77.69 cm3/mol. The Ostwald coefficient of SF6 (5.4 ×10−3) is measured by Morrison & Johnstone (1955).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Blank M. Monolayer Permeability to Gases and Properties of Cell Membranes. Federation Proceedings. 1962;21:151. [Google Scholar]
- Blank M. Approach to Theory of Monolayer Permeation by Gases. Journal of Physical Chemistry. 1964;68:2793. [Google Scholar]
- Blank M, La Mer VK. Retardation of Evaporation by Monolayers. 1962:59–66. [Google Scholar]
- Borden MA, Longo ML. Dissolution behavior of lipid monolayer-coated, air-filled microbubbles: Effect of lipid hydrophobic chain length. Langmuir. 2002;18:9225–33. [Google Scholar]
- Borden MA, Longo ML. Oxygen permeability of fully condensed lipid monolayers. Journal of Physical Chemistry B. 2004;108:6009–16. [Google Scholar]
- Borden MA, Martinez GV, Ricker J, Tsvetkova N, Longo M, et al. Lateral phase separation in lipid-coated microbubbles. Langmuir. 2006;22:4291–7. doi: 10.1021/la052841v. [DOI] [PubMed] [Google Scholar]
- Chang PH, Shung KK, Levene HB. Quantitative measurements of second harmonic Doppler using ultrasound contrast agents. Ultrasound in Medicine and Biology. 1996;22:1205–14. doi: 10.1016/s0301-5629(96)00146-9. [DOI] [PubMed] [Google Scholar]
- Chatterjee D, Jain P, Sarkar K. Ultrasound-mediated destruction of contrast microbubbles used for medical imaging and drug delivery. Physics of Fluids. 2005;17:100603. [Google Scholar]
- Chatterjee D, Sarkar K. A Newtonian rheological model for the interface of microbubble contrast agents. Ultrasound in Medicine and Biology. 2003;29:1749–57. doi: 10.1016/s0301-5629(03)01051-2. [DOI] [PubMed] [Google Scholar]
- Chen WS, Lu XC, Liu YB, Zhong P. The effect of surface agitation on ultrasound-mediated gene transfer in vitro. Journal of the Acoustical Society of America. 2004;116:2440–50. doi: 10.1121/1.1777855. [DOI] [PubMed] [Google Scholar]
- Chen WS, Matula TJ, Crum LA. The disappearance of ultrasound contrast bubbles: Observations of bubble dissolution and cavitation nucleation. Ultrasound in Medicine and Biology. 2002;28:793–803. doi: 10.1016/s0301-5629(02)00517-3. [DOI] [PubMed] [Google Scholar]
- Cheung K, Couture O, Bevan PD, Cherin E, Williams R, et al. In vitro characterization of the subharmonic ultrasound signal from Definity microbubbles at high frequencies. Physics in Medicine and Biology. 2008;53:1209–23. doi: 10.1088/0031-9155/53/5/004. [DOI] [PubMed] [Google Scholar]
- Chomas JE, Dayton PA, May D, Allen J, Klibanov A, Ferrara K. Optical observation of contrast agent destruction. Applied Physics Letters. 2000;77:1056–8. [Google Scholar]
- Christiansen C, Kryvi H, Sontum PC, Skotland T. Physical and Biochemical-Characterization of Albunex(Tm), a New Ultrasound Contrast Agent Consisting of Air-Filled Albumin Microspheres Suspended in a Solution of Human Albumin. Biotechnology and Applied Biochemistry. 1994;19:307–20. [PubMed] [Google Scholar]
- Ciani I, Burt DP, Daniele S, Unwin PR. Effect of surface pressure on oxygen transfer across molecular monolayers at the air/water interface: Scanning electrochemical microscopy investigations using a mercury hemispherical microelectrode probe. Journal of Physical Chemistry B. 2004;108:3801–9. [Google Scholar]
- Dejong N, Cornet R, Lancee CT. Higher Harmonics of Vibrating Gas-Filled Microspheres.1. Simulations. Ultrasonics. 1994;32:447–53. [Google Scholar]
- Dejong N, Hoff L. Ultrasound Scattering Properties of Albunex Microspheres. Ultrasonics. 1993;31:175–81. doi: 10.1016/0041-624x(93)90004-j. [DOI] [PubMed] [Google Scholar]
- Dejong N, Hoff L, Skotland T, Bom N. Absorption and Scatter of Encapsulated Gas Filled Microspheres - Theoretical Considerations and Some Measurements. Ultrasonics. 1992;30:95–103. doi: 10.1016/0041-624x(92)90041-j. [DOI] [PubMed] [Google Scholar]
- Duncan PB, Needham D. Test of the Epstein-Plesset model for gas microparticle dissolution in aqueous media: Effect of surface tension and gas undersaturation in solution. Langmuir. 2004;20:2567–78. doi: 10.1021/la034930i. [DOI] [PubMed] [Google Scholar]
- Epstein PS, Plesset MS. On the Stability of Gas Bubbles in Liquid-Gas Solutions. Journal of Chemical Physics. 1950;18:1505–9. [Google Scholar]
- Ferrara K, Pollard R, Bordeni M. Ultrasound microbubble contrast agents: Fundamentals and application to gene and drug delivery. Annual Review of Biomedical Engineering. 2007;9:415–47. doi: 10.1146/annurev.bioeng.8.061505.095852. [DOI] [PubMed] [Google Scholar]
- Ferrell RT, Himmelblau DM. Diffusion Coefficients of Nitrogen and Oxygen in Water. Journal of Chemical and Engineering Data. 1967;12:111–115. [Google Scholar]
- Forsberg F, Basude R, Liu JB, Alessandro J, Shi WT, et al. Effect of filling gases on the backscatter from contrast microbubbles: Theory and in vivo measurements. Ultrasound in Medicine and Biology. 1999;25:1203–11. doi: 10.1016/s0301-5629(99)00079-4. [DOI] [PubMed] [Google Scholar]
- Goertz DE, de Jong N, van der Steen AFW. Attenuation and size distribution measurements of definity (TM) and manipulated definity (TM) populations. Ultrasound in Medicine and Biology. 2007;33:1376–88. doi: 10.1016/j.ultrasmedbio.2007.03.009. [DOI] [PubMed] [Google Scholar]
- Guan JF, Matula TJ. Using light scattering to measure the response of individual ultrasound contrast microbubbles subjected to pulsed ultrasound in vitro. Journal of the Acoustical Society of America. 2004;116:2832–42. doi: 10.1121/1.1795334. [DOI] [PubMed] [Google Scholar]
- Hayduk W, Laudie H. Prediction of Diffusion-Coefficients for Nonelectrolytes in Dilute Aqueous-Solutions. Aiche Journal. 1974;20:611–5. [Google Scholar]
- Kabalnov A, Bradley J, Flaim S, Klein D, Pelura T, et al. Dissolution of multicomponent microbubbles in the bloodstream: 2. Experiment. Ultrasound in Medicine and Biology. 1998a;24:751–60. doi: 10.1016/s0301-5629(98)00033-7. [DOI] [PubMed] [Google Scholar]
- Kabalnov A, Klein D, Pelura T, Schutt E, Weers J. Dissolution of multicomponent microbubbles in the bloodstream: 1. Theory. Ultrasound in Medicine and Biology. 1998b;24:739–49. doi: 10.1016/s0301-5629(98)00034-9. [DOI] [PubMed] [Google Scholar]
- Kabalnov AS, Makarov KN, Shcherbakova OV. Solubility of Fluorocarbons in Water as a Key Parameter Determining Fluorocarbon Emulsion Stability. Journal of Fluorine Chemistry. 1990;50:271–84. [Google Scholar]
- Katiyar A, Sarkar K, Jain P. Effects of Encapsulation Elasticity on the stability of an Encapsulated Microbubble. Journal of Colloid and Interface Science. 2009 doi: 10.1016/j.jcis.2009.05.019. submitted. [DOI] [PubMed] [Google Scholar]
- Kim DH, Costello MJ, Duncan PB, Needham D. Mechanical properties and microstructure of polycrystalline phospholipid monolayer shells: Novel solid microparticles. Langmuir. 2003;19:8455–66. [Google Scholar]
- King DB, Saltzman ES. Measurement of the Diffusion-Coefficient of Sulfur-Hexafluoride in Water. Journal of Geophysical Research-Oceans. 1995;100:7083–8. [Google Scholar]
- Klibanov AL. Microbubble contrast agents - Targeted ultrasound imaging and ultrasound-assisted drug-delivery applications. Investigative Radiology. 2006;41:354–62. doi: 10.1097/01.rli.0000199292.88189.0f. [DOI] [PubMed] [Google Scholar]
- Klibanov AL, Rychak JJ, Yang WC, Alikhani S, Li B, et al. Targeted ultrasound contrast agent for molecular imaging of inflammation in high-shear flow. Contrast Media & Molecular Imaging. 2006;1:259–66. doi: 10.1002/cmmi.113. [DOI] [PubMed] [Google Scholar]
- Lawson DD, Moacanin J, Scherer KV, Terranova TF, Ingham JD. Methods for Estimation of Vapor-Pressures and Oxygen Solubilities of Fluorochemicals for Possible Application in Artificial Blood Formulations. Journal of Fluorine Chemistry. 1978;12:221–36. [Google Scholar]
- Lide DR. CRC Handbook of Chemistry and Physics 1998 [Google Scholar]
- Morrison TJ, Johnstone NBB. The Salting-out of Non-Electrolytes.3. The Inert Gases and Sulphur Hexafluoride. Journal of the Chemical Society. 1955:3655–9. [Google Scholar]
- Pollard RE, Garcia TC, Stieger SM, Ferrara KW, Sadlowski AR, Wisner ER. Quantitative evaluation of perfusion and permeability of peripheral tumors using contrast-enhanced computed tomography. Investigative Radiology. 2004;39:340–9. doi: 10.1097/01rli.0000124456.82985.35. [DOI] [PubMed] [Google Scholar]
- Price RJ, Skyba DM, Skalak TC, Kaul S. Delivery of colloidal particles and red blood cells to tissue through microvessel ruptures resulting from microbubble destruction by ultrasound. Circulation. 1998;98:570. doi: 10.1161/01.cir.98.13.1264. [DOI] [PubMed] [Google Scholar]
- Pu G, Longo ML, Borden MA. Effect of microstructure on molecular oxygen permeation through condensed phospholipid monolayers. Journal of the American Chemical Society. 2005;127:6524–5. doi: 10.1021/ja051103q. [DOI] [PubMed] [Google Scholar]
- Quaia E. Contrast media in Ultrasoinography 2005 [Google Scholar]
- Sarkar K, Shi WT, Chatterjee D, Forsberg F. Characterization of ultrasound contrast microbubbles using in vitro experiments and viscous and viscoelastic interface models for encapsulation. Journal of the Acoustical Society of America. 2005;118:539–50. doi: 10.1121/1.1923367. [DOI] [PubMed] [Google Scholar]
- Sboros V, Moran CM, Pye SD, McDicken WN. Contrast agent stability: A continuous B-mode imaging approach. Ultrasound in Medicine and Biology. 2001;27:1367–77. doi: 10.1016/s0301-5629(01)00440-9. [DOI] [PubMed] [Google Scholar]
- Schneider M, Arditi M, Barrau MB, Brochot J, Broillet A, et al. Br1 - a New Ultrasonographic Contrast Agent Based on Sulfur Hexafluoride-Filled Microbubbles. Investigative Radiology. 1995;30:451–7. doi: 10.1097/00004424-199508000-00001. [DOI] [PubMed] [Google Scholar]
- Shi WT, Forsberg F. Ultrasonic characterization of the nonlinear properties of contrast microbubbles. Ultrasound in Medicine and Biology. 2000;26:93–104. doi: 10.1016/s0301-5629(99)00117-9. [DOI] [PubMed] [Google Scholar]
- Shohet R, Chen S, Zhou YT, Wang ZW, Meidell RS, et al. Targeted gene delivery to the left ventricular myocardium using ultrasound-triggered microbubble destruction. Journal of the American College of Cardiology. 2000;35:444A-A. [Google Scholar]
- Siebert EMD, Knobler CM. Interaction Virial Coefficients in Hydrocarbon-Fluorocarbon Mixtures. Journal of Physical Chemistry. 1971;75:3863. [Google Scholar]
- Simpson DH, Chin CT, Burns PN. Pulse inversion Doppler: A new method for detecting nonlinear echoes from microbubble contrast agents. Ieee Transactions on Ultrasonics Ferroelectrics and Frequency Control. 1999;46:372–82. doi: 10.1109/58.753026. [DOI] [PubMed] [Google Scholar]