Dynamic pressure–flow relationship of the cerebral circulation during acute increase in arterial pressure

Abstract

The physiological mechanism(s) for the regulation of the dynamic pressure–flow relationship of the cerebral circulation are not well understood. We studied the effects of acute cerebral vasoconstriction on the transfer function between spontaneous changes in blood pressure (BP) and cerebral blood flow velocity (CBFV) in 13 healthy subjects (30 ± 7 years). CBFV was measured in the middle cerebral artery using transcranial Doppler. BP was increased stepwise with phenylephrine infusion at 0.5, 1.0 and 2.0 μg kg⁻¹ min⁻¹. Phenylephrine increased BP by 11, 23 and 37% from baseline, while CBFV increased (11%) only with the highest increase in BP. Cerebrovascular resistance index (BP/CBFV) increased progressively by 6, 17 and 23%, demonstrating effective steady-state autoregulation. Transfer function gain at the low frequencies (LF, 0.07–0.20 Hz) was reduced by 15, 14 and 14%, while the phase was reduced by 10, 17 and 31%. A similar trend of changes was observed at the high frequencies (HF, 0.20–0.35 Hz), but gain and phase remained unchanged at the very low frequencies (VLF, 0.02–0.07 Hz). Windkessel model simulation suggests that increases in steady-state cerebrovascular resistance and/or decreases in vascular compliance during cerebral vasoconstriction contribute to the changes in gain and phase. These findings suggest that changes in steady-state cerebrovascular resistance and/or vascular compliance modulate the dynamic pressure–flow relationship at the low and high frequencies, while dynamic autoregulation is likely to be dominant at the very low frequencies. Thus, oscillations in CBFV are modulated not only by dynamic autoregulation, but also by changes in steady-state cerebrovascular resistance and/or vascular compliance.

Continuous measurement of cerebral blood flow (CBF) velocity with transcranial Doppler (TCD) combined with non-invasive measurement of arterial pressure has made the study of the dynamic pressure–flow relationship of the cerebral circulation practical in humans (Aaslid et al. 1989; Diehl et al. 1995; Panerai et al. 1998; Zhang et al. 1998).

Typically, a linear transfer function method has been used to estimate the magnitude and the phase relationship between spontaneous changes in arterial blood pressure (BP) and CBF velocity to assess dynamic cerebral autoregulation, a concept implicating that cerebrovascular resistance responds rapidly to changes in BP to attenuate changes in CBF on a beat-to-beat basis (Aaslid et al. 1989; Zhang et al. 1998). In addition, a second-order linear differential equation has been used to describe the dynamic BP–CBF velocity relationship during induced transient changes in BP using a thigh cuff method (Tiecks et al. 1995). Application of these methods in clinical studies showed that assessment of dynamic autoregulation may provide valuable information for management of patients with cerebrovascular diseases (Haubrich et al. 2003; Reinhard et al. 2004).

Despite these developments, the physiological mechanisms underlying the dynamic pressure–flow relationship of the cerebral circulation are not well understood. In particular, the currently used methods assume that beat-to-beat changes in CBF velocity in response to BP are determined mainly, if not solely, by the mechanisms of dynamic autoregulation.

However, blood flow in the cerebrovascular bed, besides dynamic autoregulation, is governed by the basic principles of fluid mechanics and the dynamic pressure–flow relationship may thus be affected by alterations in steady-state cerebrovascular resistance and/or vascular compliance. Indeed, the dynamic pressure–flow relationship can be described by a Windkessel model (Nichols & O’Rourke, 1990; Olufsen et al. 2002). Thus, changes in steady-state cerebrovascular resistance and/or vascular compliance, for example, during steady-state (static) cerebral autoregulation may influence beat-to-beat changes in CBF independent of dynamic autoregulation.

In a previous study, we found that transfer function gain between spontaneous changes in BP and CBF velocity was increased after BP lowering in patients with hypertension and that these changes were associated with reduction in steady-state cerebrovascular resistance (Zhang et al. 2007). In this study, we tested the hypothesis that transfer function gain and phase are reduced during cerebral vasoconstriction induced by acute increase in BP. Furthermore, we used a three-element Windkessel model to simulate the effects of changes in steady-state cerebrovascular resistance and/or vascular compliance on the estimation of transfer function gain and phase during acute increases in BP.

Methods

Subjects

Thirteen healthy young subjects (10 men, 3 women) with a mean age of 30 ± 7 years, height of 174 ± 9 cm and weight of 71 ± 10 kg participated in this study. No subject smoked, or had known medical problems. Subjects were screened carefully with a medical history and a physical examination with 12-lead ECG. All subjects signed an informed consent form approved by the Institutional Review Boards of the University of Texas Southwestern Medical Center and Presbyterian Hospital of Dallas and the study conformed to the Declaration of Helsinki.

Instrumentation

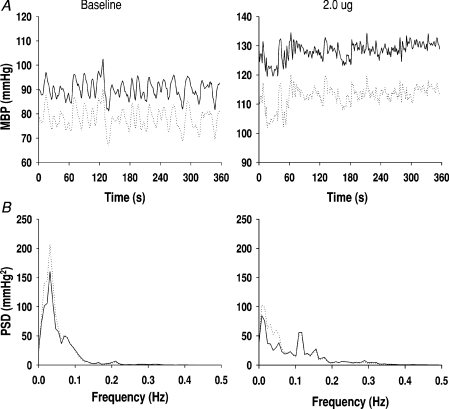
In four subjects, arterial pressure was measured simultaneously with a radial arterial catheter (Abbott Critical Care System) and non-invasive finger photoplethysmography (Finapres, Ohmeda, Colorado, USA). After a negative Allen's test, the catheterization was performed under local anaesthesia with 2% lidocaine. The pressure transducer of the catheter was calibrated and zeroed to heart level. The Finapres pressure transducer was positioned also at heart level and placed on the middle finger ipsilaterally to the arterial catheter. In these four subjects, beat-to-beat changes in arterial pressure measured with the Finapres tracked well those measured with the arterial catheter both at baseline and during phenylephrine infusion (Fig. 1). To reduce the burden and discomfort of the subjects, arterial pressure was measured only with the Finapres in the other nine subjects. Data from all subjects were combined for statistical analysis because no differences were observed between the invasive and non-invasive measurements. Finally, to corroborate Finapres measurement during phenylephrine infusion, intermittent cuff blood pressure was measured at the upper arm using electrosphygmomanometry (SunTech, BP Monitor, USA).

Figure 1. Invasive and non-invasive arterial pressure recordings at baseline and during phenylephrine infusion.

A, beat-to-beat mean blood pressure (MBP) from a subject at baseline and during phenylephrine at 2 μg kg⁻¹ min⁻¹. B, averaged power spectra from 4 subjects. Continuous lines are from the arterial line recordings. Dotted lines are from the Finapres. Similar data were observed during 0.5 and 1 μg kg⁻¹ min⁻¹ infusion.

Cerebral blood flow velocity was measured in the middle cerebral artery (MCA) using transcranial Doppler (Multiflow, DWL, Germany). A 2 MHz probe was placed over the subject's temporal window. After an optimal Doppler signal was obtained, the probe position and angle of the insonation were fixed with a custom made mold to fit each subject's facial bone structure (Giller & Giller, 1997). Heart rate was monitored using an electrocardiogram. End-tidal CO₂ (ETCO₂) was monitored via a nasal cannula using a mass spectrometer (Marquette Electronics, Wisconsin, USA).

Experimental protocol

All experiments were performed in the morning at least 2 h after a light breakfast in an environmentally controlled laboratory with an ambient temperature of 22°C. The subjects refrained from heavy exercise and caffeinated or alcoholic beverages at least 24 h before the tests. After at least 30 min of supine rest, 6 min of baseline data were collected during spontaneous breathing. Following baseline data collection, intravenous infusion of phenylephrine was begun at a rate of 0.5 μg kg⁻¹ min⁻¹. After waiting for 5 min to reach a steady-state increase in arterial pressure, 6 min of data were collected. The same procedures were repeated when the rate of infusion was increased to 1 and 2 μg kg⁻¹ min⁻¹.

Data analysis

Arterial pressure and the spectral envelope of CBF velocity were sampled at 100 Hz and digitized at 12 bits for off-line data analysis. Beat-to-beat mean arterial pressure and CBF velocity were obtained by integration of arterial pressure and CBF velocity waveforms within each cardiac cycle. The beat-to-beat data were then linearly interpolated and resampled at 2 Hz for spectral and transfer function analysis.

For steady-state data, beat-to-beat arterial pressure, heart rate, CBF velocity and breath-by-breath ETCO₂ were calculated as the average of the 6 min data. A cerebrovascular resistance index (CVRI) was calculated by dividing mean blood pressure (MBP) by mean CBF velocity. Steady-state arterial pressure also was obtained by the average of 2–3 cuff pressure measurements at baseline and during each level of phenylephrine infusion.

For dynamic data analysis, the cross-spectrum between changes in arterial pressure and CBF velocity was estimated, and then divided by the auto-spectrum of arterial pressure to obtain the transfer function. Coherence function also was estimated to quantify the linear relationship between changes in arterial pressure and CBF velocity (Zhang et al. 1998).

Spectral power of arterial pressure and CBF velocity, mean value of transfer function gain, phase and coherence function were calculated in the very low (VLF, 0.02–0.07 Hz), low (LF, 0.07–0.20 Hz) and high (HF, 0.20–0.35 Hz) frequency ranges, respectively. These ranges were chosen to reflect the high-pass filter characteristics of the dynamic pressure–flow relationship (Zhang et al. 1998). In addition, normalized transfer function gain was derived as the percentage changes in CBF velocity (beat-to-beat changes divided by the mean values) in relation to the percentage changes in arterial pressure (gain × CVRI).

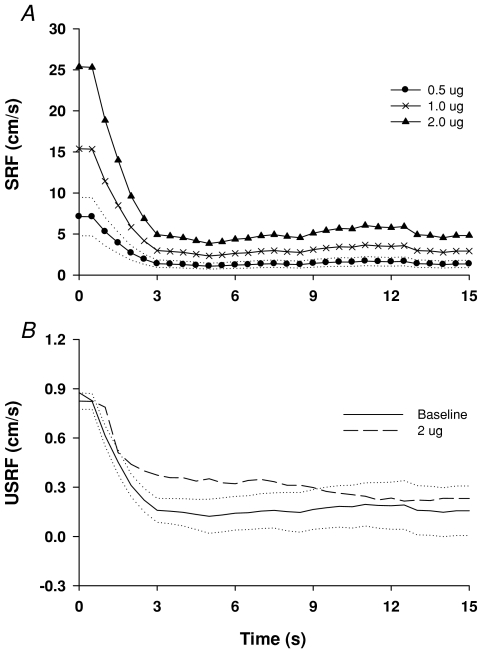
Finally, a step-response function (SRF) was estimated to describe dynamic autoregulation in the time domain (Zhang et al. 1998; Panerai et al. 1999). First, three step-functions of BP were derived from the magnitude of stepwise increases in BP during each level of phenylephrine infusion. Then, they were convolved with the impulse response function (IRF, the inverse Fourier transform of the transfer function) obtained at baseline. The SRFs obtained in this way were used to determine whether the transfer function obtained at baseline could predict changes in CBF velocity under steady-state conditions during phenylephrine infusion. Second, unit step response functions (USRFs) were derived by convolving of a unit change in BP (1 mmHg) with the impulse response functions obtained at baseline and during phenylephrine infusion at 2.0 μg kg⁻¹ min⁻¹ to reveal the effects of cerebral vasoconstriction on dynamic autoregulation in the time domain.

Windkessel model

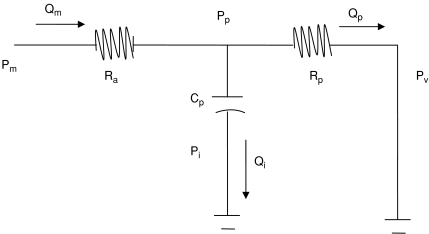
A three-element Windkessel model was used (Fig. 6, Appendix). The model parameters of cerebral arterial resistance (R_a) and peripheral vascular resistance (R_p) were derived from the experimentally estimated CVRI at baseline and during phenylephrine infusion. The peripheral vascular compliance (C_p) was derived from the estimated phase (see Appendix). The simulation was conducted with stepwise increases in CVRI and to allow C_p to change from 0 (rigid vessels without compliance) to 0.5 ml mmHg⁻¹ (vasodilatation, 2.5 times of the C_p values estimated at baseline) to reveal effects of changes in steady-state cerebrovascular resistance and/or vascular compliance on the transfer function gain and phase. Results of the model simulation are presented at the frequency of 0.1 Hz, where transfer function gain and phase were reduced markedly during acute increases in BP. Similar results of the model simulation were observed at the frequencies of 0.05 and 0.2 Hz. However, to reduce the redundancy, these data are not shown.

Figure 6. Schematic diagram of the three-element Windkessel model.

R_a, cerebral arterial resistance; R_p, peripheral vascular resistance; C_p, peripheral vascular compliance.

Statistics

The steady-state haemodynamics, spectral power of arterial pressure and CBF velocity, transfer function gain and phase at baseline and during each level of phenylephrine infusion were compared using one-way repeated ANOVA. Student–Newman post hoc tests were performed if significant main effects of drug infusion were detected (SigmaStat, version 3.1). Log transformation and Mann-Whitney rank tests were performed if the variables were not normally distributed. Data are expressed as means ±s.e.m. The significance level was P < 0.05.

Results

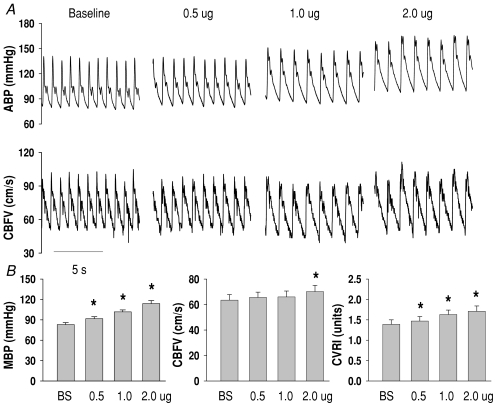
Representative BP and CBF velocity waveforms at baseline and during phenylephrine infusion are presented in Fig. 2. During infusion at 0.5, 1.0 and 2.0 μg kg⁻¹ min⁻¹, mean BP increased by 11%, 23% and 37% from baseline, while CBF velocity was unchanged until the highest increases in BP (Fig. 2 and Table 1). CVRI increased progressively by 6, 17 and 23%, indicating cerebral vasoconstriction and effective autoregulation under steady-state conditions (Fig. 2 and Table 1).

Figure 2. Changes in arterial pressure, cerebral blood flow velocity and cerebrovascular resistance during phenylephrine infusion.

A, representative arterial pressure (ABP) and cerebral blood flow velocity (CBFV) waveforms from a subject at baseline and during phenylephrine infusion. B, group averaged mean blood pressure (MBP), CBFV and cerebrovascular resistance index (CVRI) from 13 subjects. The error bars are standard errors of the mean (s.e.m.). *P < 0.05 from baseline.

Table 1.

Steady-state haemodynamics during phenylephrine infusion

	Baseline	0.5 μg	1.0 μg	2.0 μg
HR (bpm)	59 ± 3	55 ± 4*	48 ± 3*	43 ± 2*
SBP (mmHg)	119 ± 4	130 ± 4*	142 ± 4*	159 ± 6*
DBP (mmHg)	66 ± 3	72 ± 3*	79 ± 3*	87 ± 4*
MBP (mmHg)	83 ± 3	92 ± 3*	102 ± 3*	114 ± 4*
SBPC (mmHg)	115 ± 4	122 ± 4*	130 ± 5*	155 ± 7*
DBPC (mmHg)	65 ± 3	71 ± 3*	78 ± 2*	90 ± 3*
MBPC (mmHg)	82 ± 3	88 ± 3*	95 ± 3*	111 ± 4*
CBFV (cm s−1)	63 ± 4	66 ± 4	66 ± 5	70 ± 5*
CVRI (mmHg cm−1 s−1)	1.39 ± 0.11	1.47 ± 0.11*	1.63 ± 0.11*	1.71 ± 0.13*
ETCO2 (mmHg)	39 ± 1	40 ± 1	40 ± 1	39 ± 1

Values are means ±s.e.m., n= 13. HR, heart rate; SBP, systolic pressure; DBP, diastolic pressure; MBP, mean blood pressure measured in the finger using Finapres. SBP_C, DBP_C and MBP_C are cuff pressures measured in the arm using Suntech BP monitor. CBFV, cerebral blood flow velocity in the middle cerebral artery; CVRI, cerebrovascular resistance index (CVRI = MBP/CBFV); ETCO₂, end-tidal CO₂.*P < 0.05, compared with baseline. Infusion rate of phenylephrine was 0.5, 1.0 and 2.0 μg kg⁻¹ min⁻¹.

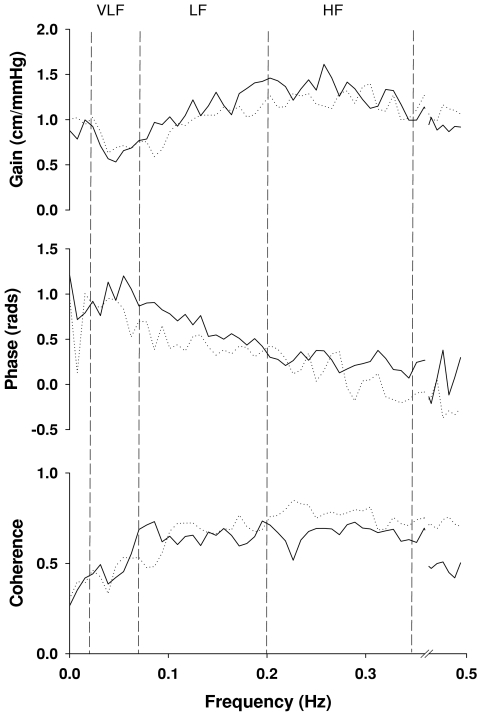
The results of spectral and transfer function analysis are summarized in Table 2. BP variability at the very low frequencies was decreased substantially by 50% and 49% during phenylephrine infusion at 1.0 and 2.0 μg kg⁻¹ min⁻¹ (Fig. 1, Table 2). However, corresponding reductions in CBF velocity variability were not observed at 2.0 μg kg⁻¹ min⁻¹ infusion (Table 2). Transfer function gain in the LF range was reduced by 15, 14 and 14%, and phase was reduced by 10, 17 and 31% during phenylephrine infusion (Fig. 3 and Table 2). A similar trend of changes was observed in the HF range, but gain and phase were unchanged in the VLF range (Fig. 3 and Table 2). In addition, normalized transfer function gain did not change during acute increases in BP (Table 2).

Table 2.

Spectral and transfer function analysis of spontaneous changes in arterial pressure and CBF velocity during phenylephrine infusion

	Baseline	0.5 μg	1.0 μg	2.0 μg
MBPVLF (mmHg2)	6.07 ± 1.15	4.32 ± 1.09	3.03 ± 1.15*	3.11 ± 0.75*
MBPLF (mmHg2)	2.15 ± 0.53	1.47 ± 0.38	1.29 ± 0.56	1.93 ± 0.67
MBPHF (mmHg2)	0.31 ± 0.15	0.24 ± 0.07	0.32 ± 0.10	0.52 ± 0.12
CBFVVLF (cm s−1)2)	5.86 ± 1.94	4.53 ± 1.09	3.83 ± 1.43	7.17 ± 3.71
CBFVLF (cm s−1)2)	2.50 ± 0.58	1.84 ± 0.54	1.56 ± 0.52	2.16 ± 0.59
CBFVHF (cm s−1)2)	0.62 ± 0.27	0.47 ± 0.14	0.49 ± 0.11	0.88 ± 0.19
GainVLF (cm s−1 mmHg−1)	0.68 ± 0.06	0.81 ± 0.09	0.67 ± 0.07	0.77 ± 0.09
GainLF (cm s−1 mmHg−1)	1.11 ± 0.06	0.94 ± 0.05*	0.96 ± 0.06*	0.96 ± 0.06*
GainHF (cm s−1 mmHg−1)	1.32 ± 0.07	1.16 ± 0.07	1.04 ± 0.05	1.21 ± 0.09
NGainVLF (units)	0.90 ± 0.08	1.19 ± 0.16	1.04 ± 0.10	1.31 ± 0.16
NGainLF (units)	1.51 ± 0.11	1.38 ± 0.10	1.54 ± 0.11	1.60 ± 0.10
NGainHF (units)	1.79 ± 0.14	1.69 ± 0.13	1.68 ± 0.13	1.95 ± 0.09
PhaseVLF (rad)	1.00 ± 0.12	0.92 ± 0.13	0.72 ± 0.19	0.83 ± 0.11
PhaseLF (rad)	0.66 ± 0.07	0.59 ± 0.07*	0.55 ± 0.07*	0.45 ± 0.09*
PhaseHF (rad)	0.25 ± 0.06	0.13 ± 0.11	0.11 ± 0.08	0.10 ± 0.06
CohereneVLF	0.46 ± 0.05	0.53 ± 0.04	0.38 ± 0.03	0.46 ± 0.04
CoherenceLF	0.66 ± 0.04	0.56 ± 0.05	0.57 ± 0.04	0.66 ± 0.05
CoherenceHF	0.67 ± 0.03	0.62 ± 0.04	0.63 ± 0.05	0.77 ± 0.05

Values are means ±s.e.m., n= 13. MBP_VLF, MBP_LF, MBP_HF, CBFV_VLF, CBFV_LF and CBFV_HF, mean blood pressure (MBP) and cerebral blood flow velocity (CBFV) at the very low, low and high frequencies. Gain_VLF, Gain_LF, Gain_HF, NGain_VLF, NGain_LF, NGain_HF, transfer function gain and normalized gain at the very low, low and high frequencies. Phase_VLF, Phase_LF, Phase_HF, Coherence_VLF, Coherence_LF, and Coherence_HF, phase and coherence at the very low, low and high frequencies.*P < 0.05, compared with baseline. Infusion rate of phenylephrine was 0.5, 1.0 and 2.0 μg kg⁻¹ min⁻¹.

Figure 3. Group averaged transfer function gain, phase and coherence function from 13 subjects at baseline (continuous lines) and during phenylephrine infusion at 2 μg kg⁻¹ min⁻¹ (dotted lines).

Dashed lines indicate the very low (VLF), low (LF) and high frequency ranges (HF). Similar changes were observed during 0.5 and 1 μg kg⁻¹ min⁻¹ infusion (For simplicity, these data are not shown). Statistical data analysis of changes in gain, phase and coherence are represented in Table 2.

Step-response functions (SRF) derived by convolving of the step increases in BP during phenylephrine infusion with the impulse response function obtained at the baseline are shown in Fig. 4A. After a transient period of about 3 s, all three SRFs reached the stead-steady values, consistent with the changes in CBF velocity measured under steady-state conditions (Table 1). Unit SRFs derived at baseline and during 2 μg kg⁻¹ min⁻¹ infusion are presented in Fig. 4B. Note a slightly delayed return to the baseline during phenylephrine infusion.

Figure 4. Step response function during phenylephrine infusion.

A, step response functions (SRF) derived by convolving of increases in BP during phenylephrine infusion with the impulse response function (IRF) obtained at the baseline. B, unit step response functions (USRF) derived at the baseline and during phenylephrine infusion at 2.0 μg kg⁻¹ min⁻¹. Dotted lines are standard errors of the mean (s.e.m.) for the SRF at 0.5 μg kg⁻¹ min⁻¹ (A), and for the USRF at the baseline (B). Group averaged data from 13 subjects. The temporal patterns of the USRFs for 0.5 and 1 μg kg⁻¹ min⁻¹ infusion were similar to that at the baseline.

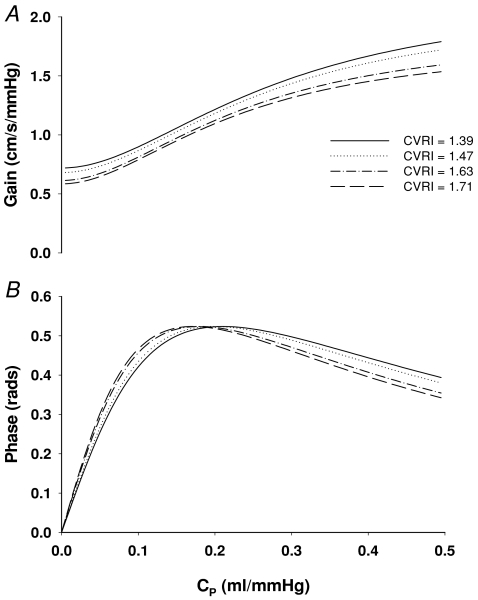
Windkessel model simulation showed that increases in cerebrovascular resistance (CRVI) and/or decreases in vascular compliance (C_P) from baseline (∼0.2 ml mmHg⁻¹) lead to reductions in gain and phase (Fig. 5). Notably, the bimodal feature of changes in phase suggests that either decreases or increases in C_P would lead to a reduction in phase depending on the baseline level of cerebrovascular compliance (Fig. 5).

Figure 5.

Windkessel model simulation of the effects of changes in steady-state cerebrovascular resistance index (CVRI) and/or vascular compliance (C_P) on the transfer function gain (A) and phase (B).

Discussion

The main findings of this study are that transfer function gain and phase between spontaneous changes in BP and CBF velocity in the LF range from 0.07 to 0.20 Hz were reduced during acute increases in arterial pressure. In contrast, gain and phase were unchanged in the VLF range from 0.02 to 0.07 Hz, where dynamic autoregulation is likely to be most effective. Furthermore, Windkessel model simulation suggests that increases in steady-state cerebrovascular resistance and/or decreases in vascular compliance may contribute to the reductions in transfer function gain and phase. Taken together, these findings indicate that changes in cerebrovascular resistance and/or vascular compliance due to steady-state (static) cerebral autoregulation modulate the dynamic pressure–flow relationship of the cerebral circulation.

Steady-state cerebral haemodynamics

Phenylephrine is an α₁-adrenorecepor agonist. Intravenous infusion of phenylephrine increases arterial pressure acutely, but is unlikely to have a direct effect on the cerebral blood vessels since it does not pass the blood–brain barrier (Olesen, 1972; Bevan et al. 1998). In addition, the density of α₁-adrenorecepors in the cerebral blood vessels is likely to be low in humans (Olesen, 1972; Bevan et al. 1998).

In this study, CBF velocity did not change during moderate increases in BP. Progressive increases in cerebrovascular resistance (CVRI) demonstrate the effectiveness of static autoregulation. Increases in CBF velocity by 11% during large increases in BP by 37% from the baseline (about 30 mmHg) are not unexpected. Increases in CBF by 3–5% per 10 mmHg increases in BP have been observed in the context of intact autoregulation using other methods for measuring CBF directly (Heistad & Kontos, 1983). Notably, these findings are in contrast with the classic model of static cerebral autoregulation which suggests a CBF plateau with a rise only at much higher BP levels (> 150 mmHg) than that in this study (Lassen, 1959).

During phenylephrine infusion intracranial pressure (ICP) is unlikely to change when autoregulation is intact (Watts et al. 2002). Thus, increases in cerebrovascular resistance are likely to be mediated mainly by a myogenic mechanism due to increases in transmural pressure (Schubert & Mulvany, 1999). In addition, sympathetic withdrawal during acute increases in BP as indicated by the markedly reduced BP variability at the very low frequencies is likely to reduce rather than increase cerebral vasoconstriction (Zhang et al. 2002).

Dynamic autoregulation, transfer function gain and phase

The diameter of small cerebral arteries and arterioles responds to changes in arterial pressure rapidly in a few seconds to alter vascular resistance to buffer changes in blood flow (Symon et al. 1973; Kontos et al. 1978). These earlier studies in animals have forged the concept of dynamic autoregulation (Aaslid et al. 1989). Similar to autoregulation under steady-state conditions, quantification of the dynamic pressure–flow relationship may reveal autoregulatory ability of the cerebral vasculature during transient changes in BP.

However, few studies have been conducted to determine the underlying mechanisms of the dynamic autoregulation. In animal studies, inhibition of vascular myogenic response with Ca²⁺ channel blockade eliminated beat-to-beat changes in cerebrovascular resistance during dynamic changes in BP (Kolb et al. 2006). These changes in turn have led to an increase in transfer function gain and a decrease in phase at the low frequencies below 0.1 Hz (Kolb et al. 2006). These findings, if confirmed in humans, support the use of the transfer function method to quantify dynamic cerebral autoregulation.

In this study, we calculated step response functions (SRFs) to describe dynamic autoregulation in the time domain. Consistent with previous studies, estimation of SRFs predicted that CBF velocity would increase immediately after a step-wise increase in BP, and then return back to the pre-stimulus baseline after a brief period of a few seconds (Zhang et al. 1998; Panerai et al. 1999). Notably, a parallel upward shift of the SRFs was observed for stepwise increases in the magnitude of BP step-functions (Fig. 4). These findings suggest that the rate of autoregulatory responses (the slope of initial fall of the SRFs) increases with the magnitude of increases in BP.

We also found that relative to rest conditions, the unit step-response function (USRF) during phenylephrine infusion at 2 μg kg⁻¹ min⁻¹ showed a slightly delayed return back to the baseline, suggesting a slowed vascular response to dynamic changes in BP.

Transfer function gain and phase in the LF range were reduced during acute increases in BP. Reduction in phase was not expected. For example, increases rather than decreases in phase have been observed during cerebral vasoconstriction induced by hypocapnia (Birch et al. 1995). In addition, reductions in phase have been observed during hypercapnic vasodilatation and these changes have been interpreted to indicate impaired autoregulation (Diehl et al. 1995).

The mechanistic link between changes in cerebrovascular tone and phase is not clear. Effects of changes in arterial CO₂ on the vascular tone and phase may be different from those induced by changes in BP (Lavi et al. 2003). The bimodal relation between changes in phase and vascular compliance identified with the Windkessel model simulation also may shed light on this issue. According to this model, either cerebral vasoconstriction or vasodilatation can lead to a reduction in phase depending on the baseline level of vascular compliance (Fig. 5). Thus, it is possible that changes in phase in previous studies induced by arterial CO₂ may reflect changes in cerebrovascular compliance rather than dynamic autoregulation.

Of note, the positive phase between changes in BP and CBF velocity observed in this study is consistent with previous studies (Birch et al. 1995; Diehl et al. 1995; Panerai, 2008). However, it should be noted that for a dynamic system, estimation of phase between the input (BP) and output variables (blood flow) does not necessarily reflect a cause–effect relationship (Nichols & O’Rourke, 1990; Van de Vegte, 1994). Furthermore, for compliant blood vessels, changes in blood flow indeed may lead changes in BP as revealed by the Windkessel model simulation.

Windkessel model simulation also suggests that either increases in steady-state cerebrovascular resistance or decreases in vascular compliance may lead to reductions in transfer function gain. Consistent with these results, normalized transfer function gain (gain × CVRI) did not change during acute increases in BP. However, the results of model simulation cannot explain why gain and phase remained unchanged in the VLF range during acute increases in BP. In addition, reduction in gain in the LF range did not progress further despite progressive increases in cerebrovascular resistance.

It is possible that changes in steady-state cerebrovascular resistance or vascular compliance may have less effects on the dynamic autoregulation in the VLF frequency range. Alternatively, an enhanced autoregulation during cerebral vasoconstriction may overcome the effects of changes in vascular resistance or compliance on the transfer function gain and phase. However, assuming a linear pressure–flow relationship, increases in steady-state vascular resistance would attenuate oscillations in blood flow regardless of the frequencies of changes in perfusion pressure. Furthermore, a stronger autoregulation would have led to a reduced CBF velocity variability at the VLF, which was not observed in this study.

Thus, it is more likely that counteracting (or counterbalancing) effects of increases in cerebrovascular resistance and a less effective rather than enhanced dynamic autoregulation may have led to the unchanged gain and phase in the VLF range. That is, complex interactions between changes in vascular resistance/compliance and the transfer function analysis outcome may mask changes in dynamic autoregulation. This possibility also explains why the reduction in gain in the LF range did not progress further despite progressive increases in vascular resistance.

Clinical implications

Changes in transfer function gain and/or phase have been observed under a variety of clinical conditions such as cerebrovascular diseases, hypertension and diabetes, suggesting altered dynamic autoregulation (Cencetti et al. 1999; Haubrich et al. 2003; Immink et al. 2004; Reinhard et al. 2004). In particular, reductions in transfer function gain in patients with mild to moderate hypertension have been interpreted to reflect a better dynamic autoregulation (Serrador et al. 2005). Moreover, transfer function gain was increased after BP lowering associated with a reduction in steady-state cerebrovascular resistance (Zhang et al. 2007). In this regard, Windkessel model simulation suggests that for compliant cerebral blood vessels (C_p > 0.2 ml mmHg⁻¹), decreases in steady-state cerebrovascular resistance would lead to increases in both gain and phase, while increases in gain and reductions in phase may occur for less compliant blood vessels (C_p < 0.15 ml mmHg⁻¹) (Fig. 5). Thus, these factors should be considered in the study of dynamic autoregulation where sustained cerebral vasoconstriction or dilatation may occur.

Notably, assessment of dynamic autoregulation using transfer function and other methods also suggests that it was preserved in the elderly with or without hypertension (van Beek et al. 2008). Given the well-known facts that CBF is reduced with ageing associated with increases in cerebrovascular resistance and/or arterial stiffness through vascular remodelling or vascular degenerative changes, these observations should be interpreted with caution since changes in vascular resistance or compliance may mask impairment of autoregulation with ageing as suggested in this study (Kety, 1956; Kalaria, 1996).

Study limitations

First, like other studies using transcranial Doppler, CBF velocity rather than volumetric blood flow was measured. Changes in CBF velocity equal changes in blood flow only if the diameter of the insonated blood vessels does not change. The relatively constant CBF velocity during acute increases in BP is remarkably consistent with other studies of cerebral autoregulation using different methods for measuring CBF directly (Heistad & Kontos, 1983; Paulson et al. 1990). Thus, the diameter of the insonated middle cerebral artery (MCA) in this study was unlikely to change. Otherwise, either an active myogenic vasoconstriction or a passive vasodilatation of the MCA during increases in BP would lead to an increase or decrease in CBF velocity if cerebral blood flow was maintained constant via autoregulation.

Second, it must be recognized that the results of the model simulation only suggest, but do not prove, the underlying vascular mechanism. In particular, the mechanism of dynamic autoregulation, that is, changes in cerebrovascular resistance and/or vascular compliance in response to changes in BP on a beat-to-beat basis was not reflected in the Windkessel model. In addition, changes in cerebrovascular compliance (C_p) during acute increases in BP were estimated based on the Windkessel model (Appendix). Given the potential limitations of the model used, reductions in C_p may reflect qualitatively rather than quantitatively increases in cerebrovascular stiffness during cerebral vasoconstriction.

Finally, findings from this study suggest that dynamic autoregulation may interact with changes in steady-state cerebrovascular resistance and/or vascular compliance leading to changes in transfer function gain and phase. In this regard, a more comprehensive model to include both the autoregulatory mechanisms and steady-state vascular parameters should be explored to improve the precision of the model prediction.

In summary, during acute increases in arterial pressure, transfer function gain and phase were reduced in the LF range from 0.07 to 0.20 Hz, but were unchanged in the VLF range from 0.02 to 0.07. Windkessel model simulation suggested that increases in steady-state cerebrovascular resistance and/or decreases in vascular compliance contributed to the changes in transfer function gain and phase. Taken together, these results reveal the complexity of the dynamic pressure–flow relationship of the cerebral circulation and suggest that spontaneous oscillations in CBF velocity in response to changes in BP are modulated not only by dynamic autoregulation, but also by changes in steady-state cerebrovascular resistance and/or vascular compliance during acute cerebral vasoconstriction.

Glossary

Abbreviations

BP

blood pressure

CBFV

cerebral blood flow velocity

CVRI

cerebrovascular resistance index

ETCO₂

End-tidal CO₂

MCA

the middle cerebral artery

SRF

step-response function

TCD

transcranial Doppler

VLF

the very low frequency range from 0.02 to 0.07 Hz

LF

the low frequency range from 0.07 to 0.20 Hz

HF

the high frequency range from 0.20 to 0.35 Hz

Appendix: Windkessel model simulation

A three-element Windkessel model was used to reveal the effects of changes in steady-state cerebrovascular resistance and vascular compliance on the transfer function gain and phase during acute increase in BP (Fig. 6). In this model, P_m represents beat-to-beat changes in cerebral perfusion pressure, which can be approximated by changes in mean arterial pressure assuming that intracranial pressure (P_i) and cerebral venous pressure (P_v) were relative small and constant (∼0). Q_m represents beat-to-beat changes in CBF velocity in the middle cerebral artery (MCA). Q_i, Q_p and P_p represent intermediate flow and pressure. We assumed that R_a represents the resistance of the large cerebral arteries branching from the MCA leading to the small pial arteries, while R_p represents peripheral vascular resistance. C_p represents peripheral vascular compliance. The transfer function relating Q_m to P_m can be derived as:

(1)

where S is the Laplace transform variable.

Equation (1) provides a convenient way to study the impact of changes in the arterial resistance (R_a), peripheral vasculature resistance (R_p) and vasculature compliance (C_p) on the transfer function gain and phase.

The transfer function gain can be obtained as:

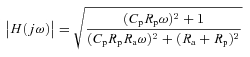(2)

and the phase is given by:

(3)

where ω depicts the angular frequency (ω= 2 π f).

For simulation, the model parameters (R_a, R_p and C_p) need to be known. We estimated the values of R_a and R_p from the experimentally measured steady-state cerebrovascular resistance index (CVRI, Table 1). We assumed the internal diameter of the MCA to be 3 mm (Newell & Aaslid, 1992). Therefore, the internal area of the MCA can be calculated as A=π(1.5/10)²= 0.0707 cm² and the total cerebrovascular resistance (R) can be estimated from the measured CVRI as R= CVRI ×A. Furthermore, we assume that R can be apportioned to R_a and R_p (Heistad & Kontos, 1983). C_p was estimated from eqn (2), given the phase and R_a and R_p at a specific frequency. We use eqn (2) rather than eqn (1) because phase is likely to be more sensitive than gain to changes in cerebrovascular tone (Panerai, 2008). The values of C_p at 0.1 Hz estimated at baseline and during phenylephrine infusion at 0.5, 1.0 and 2.0 μg kg⁻¹ min⁻¹ were 0.21, 0.20, 0.18 and 0.13 ml mmHg⁻¹ respectively, suggesting decreases in vascular compliance during acute increases in BP.

For the results in Fig. 5, R_a was apportioned to be 1/3 of R and R_p to be 2/3 of R. The frequency was selected to be 0.1 Hz to reflect that gain and phase in the LF range were reduced during increases in BP. However, we also explored the effects of lowering and raising frequencies (0.05 and 0.2 Hz) and apportioning of R as 1/4 to R_a and 3/4 to R_p on the gain and phase using the model simulation. In all cases, the overall pattern of changes in gain and phase remained the same as shown in Fig. 5, suggesting that changes in steady-state cerebrovascular resistance and/or vascular compliance influence gain and phase similarly in the VLF, LF and HF ranges. However, as expected, the rate of increases in gain and the location and magnitude of the peak phase were changed depending on the specific parameters used for simulation.

Author contributions

R.Z. contributed to the study design, experiments, data analysis and interpretation of this study, and drafted the manuscript. K.B. contributed to the Windkessel model simulation, data analysis and interpretation of this study, and contributed critically to the revision of this article. B.L. contributed to the study design, experiments, data analysis and interpretation of this study, and contributed critically to the revision of this article. All authors has approved the final version of this article. The experiments of this study were conducted at the Institute for Exercise and Environmental Medicine, Presbyterian Hospital of Dallas, TX 75231, USA.