Contribution of whole-cell optimization via cell body rolling to polarization of T cells

Abstract

Directed secretion of cytotoxins or cytokines by T cells during immune response depends on migration of the centrosome in the T cell to the interface with the target cell. The mechanism of the centrosome translocation has been elusive. The presented computational analysis demonstrates that the centrosome should be positioned at the interface if the T cell attempts simultaneously a) to minimize its surface area, b) to maximize the interface area, c) to maintain the cell volume, and d) to straighten the microtubules. Live three-dimensional microscopy and measurements show that the optimal position of the centrosome is achieved in large part (by about 40%) via rolling of the entire T cell body on the target surface, which movement appears to entrain the centrosome. The theoretical and experimental results draw attention to the previously unrecognized role of the whole-cell structure and whole-cell movements in the T cell polarization.

1. Introduction

T-helper and T-killer cells of the immune system perform their functions via direct interactions with other cells. Upon contacting a cell that is a target of the immune response, such as a virus-infected cell, a T cell displays a drastic reorganization of its structure that ensures specificity of the immune response. Most remarkably, an extended contact area between the two cells is developed via deformation of the T cell, and the T cell centrosome is positioned next to this interface area [1,2]. The centrosome is an intracellular body that was defined by T. Boveri as the “dynamic center of the cell.” In T cells, in particular, it determines the location of the vesicles that store the effectors of the immune response, for example the cytotoxic compounds that destroy the cells that harbor viruses. Upon binding of the T cell to the target cell, the vesicles fuse with the plasma membrane, releasing the effector compounds [3]. The extended interface area between the T cell and the target cell (called immunological synapse) should serve to prevent diffusion of the effectors into the surrounding tissue. At the same time, the positioning of the centrosome next to the interface with the target cell is thought to ensure that the release of the effectors is directed at the target cell and not at the bystander cells in the tissue [4]. This type of centrosome positioning is characteristic not only of killing interactions of T cells with infected or tumorous cells, but also of interactions between T cells with other cell types in the immune system that can be stimulatory in nature [2], as well as of the action of natural killer cells [5] that are different from T cells in other respects. Thus, the centrosome positioning (called polarization) is an intracellular event that is crucial for both the efficiency and specificity of the immune response.

The mechanism of the centrosome polarization remains unknown. The aster of the microtubule fibers of the T cell cytoskeleton, which are attached with one end to the centrosome, seems to be involved, because if the microtubules are disassembled in an experiment, the centrosome does not polarize [3]. Hypotheses were put forward that related the polarization of the cytoskeleton to either microtubule shortening or stabilization at the site of contact with the target [6,7], but these hypotheses did not prescribe the actual mechanism for the centrosome reorientation. An observation of microtubule deformation in T cells next to the interface with the target cell suggested that molecular motors might be involved that could pull on the microtubules, dragging the centrosome to the contact site [8]. Direct evidence, however, is lacking.

Given the present difficulties of establishing the mechanism of the centrosome polarization in T cells interacting with their immunological targets, it is intriguing to observe that a very similar polarization behavior is exhibited by cells of various types in a different experimental situation. These experiments have not so far been considered of relevance to the study of the immunological cell-cell interactions: When allowed to sediment from suspension onto plain glass, T cells as well as macrophages, neutrophils, fibroblasts, and epithelial cells spread on this inert, artificial substrate and position their centrosomes next to the cell-glass contact area [9–11]. Irrespective of its molecular-level cause, the attachment to the substrate in these cases appears to be essentially the same cellular activity as the attachment of a T cell to the target cell. In fact, the T cell polarization has been successfully studied in experimental models that replace the target cell with a biomimetic surface. The artificial substrate that mimics the target cell surface can be, for example, glass coated with antibodies binding to the T cell receptor [12,13], which protein on the T cell surface normally mediates the interaction with the target cell. It is striking that the centrosome polarization to the attachment site is observed in each situation, be it the cell-cell interaction, the interaction mediated by the highly specific molecular recognition, the interaction with the plain glass, or even the interaction with the plain glass of a cell very different from a T cell. One may hypothesize that a mechanism should exist that is at least partly responsible for the emergence of the functionally important centrosome orientation in the T cell-target cell interaction, and that should not be identified with any of the pathways or processes specific to T cells. A mechanism of centrosome positioning might exist that could be as intrinsic to the cell structure as to be exhibited by a generic cell that develops a contact with a generic substrate to which it has affinity, the molecular cause of such affinity notwithstanding.

In this paper, we address the following questions. What position of the centrosome can be expected from the most generic considerations in a cell that is attached to some surface? In what parsimonious kinematical manner can this position be achieved? How does the theoretical expectation as to the kinematics of polarization compare to experimental measurements made on the polarizing T cells?

A fuller description of the geometry of the biomimetic system to study T cell polarization should be illuminative of both the theory and experiments presented in this paper. The T cells in this setup are allowed to settle from the growth medium on the optical-glass bottom of the observation chamber, immediately above the objective lens of an inverted microscope that is used for observation. These cells are normally non-adherent and grow in suspension. The chamber bottom, however, is coated with antibodies that bind and stimulate the T cell receptor on the cell surface. This triggers attachment and the centrosome polarization as if the chamber bottom were the target cell. The centrosomes are oriented randomly in cells that have come in contact with the bottom. In 15 min, however, most attached cells have already spread slightly and positioned their centrosomes next to the substrate, commonly in the middle of the attachment site [14,15]. This is known from fixed specimens. Here we employ this experimental system for dynamic observations to probe some of the theoretical expectations.

The basic theoretical approach will be structural optimality. To introduce this method, a familiar example will be useful: the body of a given volume that has the minimum surface area is a ball. A free drop of liquid with surface tension spontaneously becomes round. Of course, application of this rule to the cell falls short of predicting the specific shapes of various cell types. Also, the nature of the surface tension and volume maintenance in the case of the cell is different from that in a liquid drop, being, rather, active contraction of the actomyosin cell cortex and osmotic effects of ion pumps [16]. Their complex biophysics and limited applicability notwithstanding, the volume maintenance and surface minimization explain well the most primitive cell shape, the roughly round one which is acquired by freely suspended animal cells in culture, so long as the cell body is concerned but not the thin protrusions. While the geometrical shape which is optimal with respect to these two principles is well known, the rigorous proof of its being optimal is rather involved. With additional structural elements and optimality principles needed to approximate the polarizing T cell, neither intuition nor analytical mathematics can be relied on. The optimal shape can nonetheless be found numerically.

The centrosome positioning was illuminated from the numerical optimization standpoint in a study that dealt with microtubule asters assembled in vitro around artificial centrosomes in microfabricated cell-size chambers [17]. The centrosome position was successfully calculated as the one corresponding to the minimum bending energy of the microtubules constrained by the chamber walls. Remarkably, when the microtubules were sufficiently long (considerably longer than the radius of the chamber), their simultaneous unbending positioned the centrosome off center in the round chamber. This result might not be intuitive, but it demonstrates that at least the fact that the position of the T cell centrosomes is eccentric can be understood from first principles. Having dealt with the flat, round chambers, however, this theory cannot be applied to the problem of why the centrosome in the activated T cells becomes positioned not only off center, but specifically in the direction of the target surface.

The liquid-drop model predicts the primitive shape of a flexible, empty “cell,” whereas the microtubule-unbending model predicts the centrosome position within a given, rigid boundary. Integrating these approaches, we begin with predicting the centrosome position inside a flexible cell in the geometrical framework of the experimental model of T cell polarization. The kinematical implication of the theoretical algorithm for the centrosome positioning is then compared with live measurements of the T cell polarization.

2. Methods

2.1. Computational details

Microtubules are approximated as chains of straight, freely jointed segments of constant length and number. (The assumption of the constant length is experimentally validated and discussed below.) The surface of the free-floating cell is defined as the minimal convex hull enclosing all the microtubule segments. The structure of the free-floating cell is determined by the set X of the direction angles of all the microtubule segments - two angles, azimuth and declination, for each segment. The optimal structure is the one that minimizes the following energy function: F_f(X) = ∏(V(X) – V_g) – ∏V_glog(V(X)/V_g) + γS(X) + κB(X)/2. In this formula, V_g is the goal cell volume, and V(X), S(X), and B(X) are respectively the actual cell volume, cell surface area, and microtubule bending as functions of X. The constant coefficients are ∏ = 25 mm Hg = 3.4 fJ/µm³, the osmotic pressure characteristic of mammalian tissues [18], γ = 0.035 dyn/cm = 35 aJ/µm², the cortical (surface) tension in leukocytes [19], and κ = 88 aJ µm, the flexural rigidity of microtubules. We obtain the latter value by multiplying 2.2×10⁻²³ N m² = 22 aJ µm [20], the mid-range value of for pure microtubules [21], by 4, to reflect the fact that even though the absolute values for pure microtubules are controversial, the four-fold increase was seen consistently with the addition to the pure microtubules of microtubule-associated proteins that co-polymerize with them in vivo [22]. The terms involving the volume and the osmotic pressure can be derived from the consideration of work done against the osmotic pressure difference across the cell boundary by expanding or contracting the cell volume, which would be accompanied by diluting or concentrating the proteinaceous osmogenic solutes within the cell [16]. The bending term B(X) represents the integral, over the length of all the microtubules, of the squared curvature, to which the bending energy is proportional. It is computed by summation, over all the segment joints, of the inverse square radius of curvature, which the joined segments define. Precisely, if the direction of two joined segments of length s differs by the angle α, then it is assumed that they approximate a radius of curvature s/2*tan((π–α)/2) over the arc length s. The same applies to the differences of the directions of the first segments of each microtubule and the equally spaced directions along which unstrained microtubules should emanate from the centrosome. Optimization was performed using the sequential quadratic programming algorithm of the MATLAB software package by Mathworks, Inc. An aster of straight microtubules was used as the starting configuration, randomized by adding a pseudorandom number between 0 and 0.1 to each segment direction angle.

For the attached cell, the microtubule aster is projected onto the horizontal plane that passes through the lowermost point in the aster. The area of the minimal convex polygon enclosing the projection is the area of contact with the target, S_c. The cell surface is calculated as the minimal convex hull that encloses the projection as well as the microtubule aster. The aster configuration is given by the set of the segment joint angles, which was found optimal in the free-floating cell. The aster is rotated by two rigid-body rotation angles, θ and ϕ. The optimal orientation of the aster is found as the θ,ϕ pair that minimizes the energy function F_a(θ,ϕ) = ∏(V(θ,ϕ) – V_g) – ∏V_glog(V(θ,ϕ)/V_g) + γS(θ,ϕ) – γ_adhS_c(θ,ϕ), where γ_adh= 2.5×10⁻⁵ J/m² = 25 aJ/µm² is the mid-range estimate of the typical total (nonspecific plus receptor-mediated) adhesion energy density [23].

2.2. Experimental details

Jurkat cells (a gift of Dr. L. Kane, University of Pittsburgh) were grown and prepared for observation essentially as described [24]. The temperature, 37 °C, was maintained using a Nevtek air curtain incubator. The cells were incubated with 500 nM Oregon Green 488 TubulinTracker (Molecular Probes) in the culture medium for 25 min before being injected into the chambers. For image registration, a Nikon TE 200 inverted microscope was equipped with a Hamamatsu ORCA II ERG cooled interline camera, and the Nikon Plan Apo 60x objective with numerical aperture 1.4 was driven by a piezo-positioner PIFOC 721 (Physik Instrumente). The camera, the objective driver, and an illumination shutter (Uniblitz) were coordinated by the IPLab software. 76 fluorescence images of the optical sections were taken over 7.5 s beginning at the end of every 5 min until 25 min after injection of the cells into the chambers. The formal resolution (voxel size) was 0.22, 0.22, and 0.4 µm in X, Y, and Z dimensions, Z being along the optical axis and orthogonal to the glass forming the bottom of the observation chamber. The acquisition of each Z-series of the fluorescence images was immediately followed by capturing the image in phase contrast.

The three-dimensional reconstruction from the near-simultaneously taken optical sections was calculated using a ray-casting algorithm for fluorescence images and measured in the same software. The geometrical center (centroid) of the cell was calculated as the midpoint between the X, Y, and Z bounds of the cell. The position of the centrosome was determined as the point of convergence of the fluorescent microtubules, usually corresponding to the point of the maximum brightness due to this convergence. For each cell, only the time points after the cell begins displaying flat, phase-contrast lamellipodial protrusions were used to make certain that the cell is attached to the substrate and its movements are active. After the attachment was assured from the phase-contrast images, the vertical coordinates measured in the three-dimensional reconstructions of the fluorescence images were adjusted to compensate for focus drift between the time points by subtracting the current vertical coordinate of the bottom cell boundary from the vertical coordinates of the centrosome and the top of the cell.

For immunofluorescence, 4% paraformaldehyde (Sigma) was used to fix the cells at room temperature for 30 min. The cells were then permeabilized with 0.5% Triton (Sigma) for 5 min and stained with goat anti-tubulin antibody (Sigma) and TRITC anti-goat antibody (Invitrogen, Carlsbad, CA).

2.3. Prediction of centrosome displacements from cell rolling

For each measured displacement of the cell between the successive observations, the predicted centrosome displacement due to cell rolling was calculated as follows. The angle by which the cell rotates during the time interval is found by dividing the displacement of the centroid by the half-height of the cell as the idealized rolling radius. The centrosome moves within the plane which is a) orthogonal to the plane on which the cell is rolling and b) parallel to the centroid displacement. The initial center of rotation of the centrosome is the point on its plane of rotation that also lies on the initial axis of the cell rotation. This axis is horizontal, orthogonal to the centroid displacement, and passes through the initial centroid position. The distance from the initial position of the centrosome to its initial rotation center is the radius of the centrosome rotation. The initial phase angle of the centrosome is determined as the angle between 1) the direction from the initial centrosome rotation center to the initial centrosome position and 2) the direction of the centroid displacement. The final phase is the initial phase plus the angle by which the cell rotates. The predicted new position of the centrosome is obtained by displacing the initial center of the centrosome rotation in parallel with the cell centroid and by adding to this displacement 1) a displacement in the same direction that is equal to the centrosome rotation radius multiplied by the cosine of the final phase angle and 2) a vertical displacement that is proportional to the same radius multiplied by the sine of the final phase. The calculation must be done individually for each cell and each time interval. The calculated displacements of the centrosome in a given cell can then be summed up for all the time intervals to get the prediction where the centrosome would be at the end of the time sequence if it were entrained in the rolling cell.

3. Results and Discussion

3.1. Theoretical optimality of a free T cell

We begin by computing the optimal structure of the free-floating cell with the microtubule aster inside. This corresponds to the T cell structure in the experimental model before the cell comes in contact with the target-like surface and undergoes the polarization of the centrosome to that surface. Refer to the Methods section for the computational details. Microtubules in the theoretical model begin at the common point corresponding to the centrosome. They have constant length, but can bend arbitrarily. (The assumption of the constant length is experimentally validated and discussed below.) Numerically, the microtubules are represented by chains of straight segments. The cell surface is shrink-wrapped around the microtubule aster. Mathematically, it is defined as the minimum convex hull enclosing the microtubules. (This surface does not represent the extremely wrinkled plasma membrane, but rather the contractile submembrane actomyosin cortex that actually bounds the leukocyte cell contents [19].) The numerical optimization begins from a random configuration (i.e., all the joint angles between the microtubule segments are randomized). The optimization algorithm then attempts to simultaneously minimize the cell surface and straighten the microtubules while keeping the cell volume as close as possible to a set value.

One can observe that these are conflicting goals: straighter microtubules can only be enclosed in a cell surface with a larger area, and shrinking the surface would decrease the volume, too. We need to determine what configuration of the microtubule aster will be optimal with respect to all these objectives simultaneously. To approach this problem, we can put in correspondence to each possible configuration an energy value that would reflect the bending energy of the microtubules, the energy of the cell surface stretching, and the energy of deviation of the cell volume from the one dictated by the osmotic equilibrium with the physiological medium. Then we can postulate that the optimal configuration minimizes this energy function.

Two distinct cell structures that are optimal in this sense are found depending on the ratio of the microtubule length to the goal cell volume. If the microtubules are short and the cell volume large, the cell acquires a configuration one could expect: an almost round cell with an aster of microtubules, which extend from the centrosome near the cell center and bend slightly under the cell surface. Tightening the volume constraint on the microtubules, however, causes dislocation of the centrosome in the optimal structure from the center. This spontaneous symmetry breaking is also not surprising, being very similar to the one seen in the experiments in vitro and explained by the optimality theory for the microtubules constrained in the flat, rigid chambers [17]. Remarkably, we were not able to obtain the asymmetric structure with the mid-range value of the microtubule flexural rigidity measured for pure microtubules, 22 aJ µm [20,21], but only when we multiplied it by 4, which four-fold increase was the measured effect of microtubule-associated proteins (MAPs) co-polymerizing with the microtubules in vivo [22]. Even beginning with the same initial configuration, separate runs of the optimization algorithm terminate on slightly different optimal configurations. At the same time, even starting from completely different initial configurations leads to essentially the same final structure. This structure becomes clearly asymmetric when the microtubules are at least 1.5 times as long as the radius of a ball that would have the goal cell volume (figure 1a).

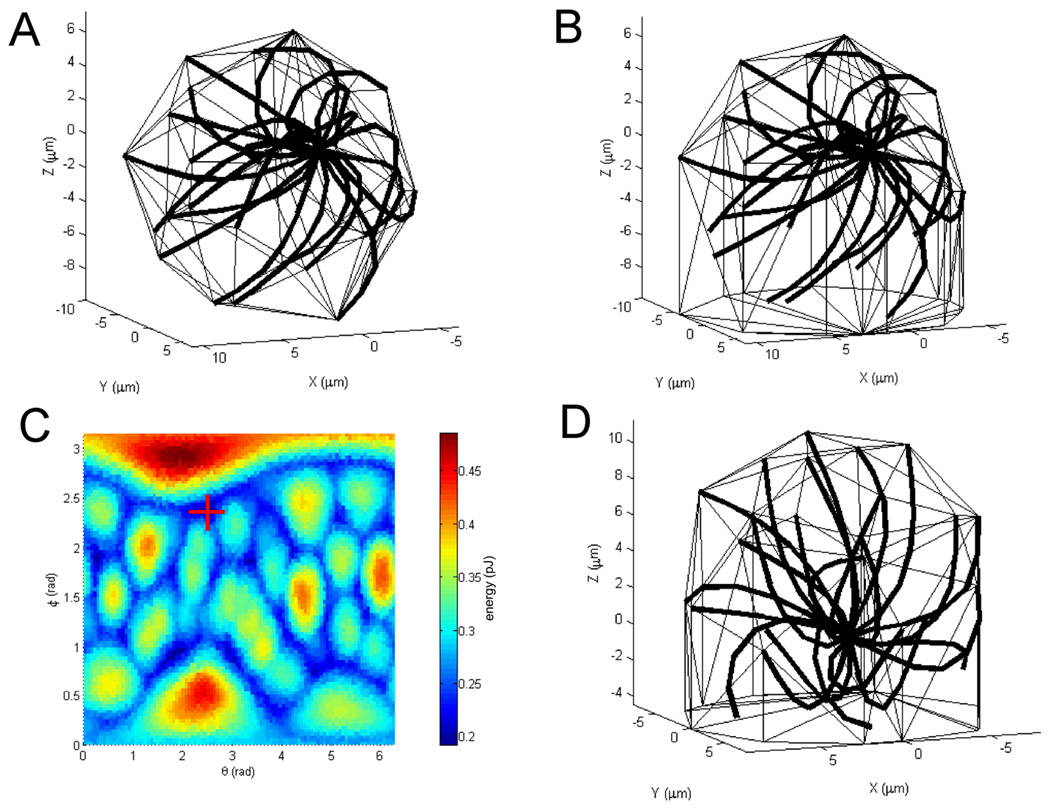
Figure 1.

Theoretical optimality analysis of the T cell structure and orientation. (A) The optimal structure of a free-floating cell. Microtubules are thick lines converging on the centrosome, the cell surface is triangulated. (B) The same microtubule aster in a cell attached to the target substrate plane below. (C) The landscape of the energy function of the attached cell. On the axes, the tilt and azimuth of rotation of the microtubule aster, on the color bar, the values of the energy function. The global minimum is marked with a red cross. (D) The optimal structure of the attached cell, corresponding to the minimum in part C. In this simulation, there are 24 microtubules, each with 6 2 µm-long segments, and the target cell volume is that of a ball with a radius of 8 µm.

This structure (figure 1a) shares the following critical features with the structure of real T cells [8]: the rounded and somewhat onion-shaped cell outline, the microtubules converging on the eccentric centrosome, the microtubules running around the cell body as well as through the cell interior. The most characteristic of the capacity of the model to capture the nontrivial T cell morphology are those microtubules that are predicted to extend from the centrosome first outwards, and then bend where they meet the cell boundary and follow the cell outline toward the “pole” of the cell that is opposite the centrosome (figure 1a). This distinctive morphological feature has been given attention in the high-resolution experimental studies of T cells [8].

3.2. Algorithm for optimization upon attachment to the target

The asymmetric microtubule aster configuration predicted from the first principles for a suspended cell (figure 1a) is almost the same as the one seen in polarized T cells in contact with the target, in that the microtubules emanate from the centrosome on the side of the cell. The aster of microtubules is similarly asymmetric before as well as after the polarization response to the target binding [3]; the difference is in the orientation of the asymmetric microtubule system. The essential difference of the microtubule cytoskeleton in a suspended cell from the one seen in T cells polarized to the target is that the cytoskeleton orientation in the free cell should be arbitrary. There is no external reference for the free cell in our theoretical as well as experimental model that would make different orientations of the aster distinguishable to the cell or preferred by the optimization algorithm. The orientation selected by the algorithm is essentially random, which can also be expected of the aster orientation in a cell in suspension. (Strictly speaking, the computed orientation is not random but depends on the pseudorandom starting configuration, because our optimization algorithm is deterministic. However, the deterministic search passes through a quasi-chaotic regime before a near-optimal configuration is found. This effectively erases the dependence on the starting configuration.) The polarized T cell in a conjugate with the target is most obviously different from one in suspension in that it is attached to the target on one side. This could potentially make the different orientations of the asymmetric structure already found in the free cell nonequivalent, some being more optimal structurally than others. Next we will explore the possibility of deriving the polarized structure of the T cell from the freely floating configuration parsimoniously by optimizing only the orientation of the microtubule aster while leaving its configuration proper as constant.

To model the T cell attachment to the target surface, which would introduce the extracellular asymmetry with which the intracellular one could potentially be aligned, we assume that the microtubule aster will sit on the target plane and be canopied by the T cell surface. Geometrically, the aster will touch the plane, and the orthogonal projection of the aster onto the plane will be enclosed together with the aster in the minimal convex hull designated as the surface of the cell. The area on the target plane covered by the microtubule aster will be the area of contact of the T cell with the target. A structure that is obtained in this manner from the free-floating structure in the same arbitrary orientation is shown in figure 1b. The overall shape of the attached model cell can be described very crudely as a hemisphere on top of a short upright cylinder sitting on the substrate plane. This geometry also describes reasonably well the general shape of an attached T cell as seen in three-dimensional experimental images [14,25]. Evaluating the fidelity of the model, it is important to note that T cells do not flatten upon attachment to the substrate nearly as much as fibroblasts, epithelioid and other generic cultured cell types do. The T cells do send out very flat protrusions over the substrate, but most of the cell body retains the dome-on-a-turret shape as seen in confocal reconstructions [14,25]. Most significantly for this study, microtubules in general do not enter the extremely flat lamellipodial protrusions [26], the volume of the protrusions is insignificant, and the surface area minimization arises not from the physical surface tension per se but from the active cortex contraction [16] and is therefore restricted to the compact cell body as modeled, not involving the protrusions. In the light of these considerations, the geometrical construction of the attached cell model appears adequate.

It can be seen in the theoretical structure (figure 1b) that the volume and the total surface area of the attached cell depend on the orientation of the microtubule aster, because the latter is asymmetric. This dependency alone is sufficient to make the different orientations of the microtubule cytoskeleton inherited from the free-floating cell nonequivalent. Some orientations would conserve the volume and keep the surface minimal after the attachment better than others. These more optimal configurations may therefore more readily be adopted by a T cell attaching to the target. It can also be observed from figure 1b that the area of contact with the target will depend on the microtubule aster orientation as well. We will require that the model T cell maximize the area of contact with the target, as this should be favored by the negative surface energy density associated with receptor-mediated adhesion [23].

Remarkably, the whole-cell optimality associated with the microtubule aster orientation is a function of only two variables, the tilt and azimuth angles needed to specify the rigid-body rotation of the aster in three dimensions. This makes it possible to visualize the relative optimality of all orientations in a single graph. One graphical convention that can be exploited is the energy landscape from studies of molecular conformations, where the energy minimum corresponding to the most optimal configuration can be found on plots that are similar to topographic maps. Utilizing this convention, we can find the optimal orientation of the microtubule aster in the polarized T cell as the lowest point on a map obtained by plotting the structural penalty (energy function) as altitude with the two rotation angles as the longitude and latitude. The coordinates of the lowest point on such a landscape will be the two angles of rotation necessary to bring the aster from the unattached cell (whose orientation was arbitrary) into the optimal (lowest-energy) orientation in the attached cell. In this operational way, the coordinates of the global minimum will specify the optimal orientation.

The energy landscape calculated for the microtubule aster from figure 1 parts a and b is shown in figure 1 part c. It is essentially the same, although not identical, for the slightly different asters that, as discussed above, the optimization algorithm can find for the unattached cell instead of the sample in figure 1. Alongside some irregular features, the structural penalty landscape displays a creeks-into-the-lake pattern leading to the deepest point of the global minimum. Taking the aster from figure 1a, rotating it by the angles given by the coordinates of the global minimum, and canopying it by the cell surface as defined above produces the optimal structure of the T cell attached to the target. It is shown in figure 1d. The centrosome in the optimal structure can be seen over the center of the interface with the target, quod erat demonstrandum.

3.3. Hypothesis of coupling of optimization to whole-cell movement

One aspect of the optimization procedure leading to the functional position of the centrosome should be easily observable because it implies whole-cell movement. The hypothetical rotation of the extended microtubule aster through the dense interior of the cell is unlikely because of the resisting drag force this movement would induce. The rotation prescribed by the model should therefore involve the entire cell. The T cell, however, adheres firmly to the target surface. In the experimental model where the surface is the antibody-coated glass, the adhesion is especially likely to preclude any slippage. The microtubule aster rotation under these conditions should be manifested as whole-cell rolling. The striking implication of this hypothesis is therefore that the cell should move laterally as the centrosome migrates to the substrate.

3.4. Experimental measurement and estimation

To compare the theoretical expectation with the experiment, we followed the course of polarization of a living T cell by tracking the cell outline as well as the centrosome position in three dimensions and in time. The position of the centrosome was determined by fluorescently labeling the microtubules that converge on it, and recording at successive time points three-dimensional images of the cells.

To validate our live-cell set-up against the previous work done with fixed cells, we fixed and immunostained the cells 12 min into one of our live experiments, set up as usual including the incubation with the fluorescent probe. 96%, n=121, cells were polarized in 12 min, compared to 85% in 15 min as reported before [15], validating our set-up.

In the live experiments, the cells exhibited a firm attachment to the target surface inside the time period used for measurements, excluding the possibility that convection, turbulence, etc., add a passive component to the cell movements that are registered. The active attachment was distinguished from passive settlement by the presence of lamellipodial protrusions of the cells on the substrate surface. The protrusions were monitored in phase-contrast images acquired near-simultaneously with each three-dimensional fluorescence image in the time sequence. 25 cells were tracked in detail.

Microscopy shows that the cells settle on the biomimetic substrate that mimics biochemically the surface of the target cell and exhibit an active polarization response as described before [12–15,25]. The cells attach to the substrate and demonstrate a downward migration of the centrosome towards it. After attachment, a cell was observed for 15 ± 1 min on average (±SE, n=25 everywhere). During this time, it did not display any significant alteration in the outline of its body, which is protruding over the substrate and is distinct from the thin skirt of lamellipodial protrusions, as previously described [14,15,25]. The diameter of the round cell body as viewed from the top comprised initially 14.5 ± 0.5 µm, and the cell height, slightly less than that, 10.6 ± 0.5 µm. At the end of the observation period, the diameter was 14.4 ± 0.6 µm, and the height, 10.3 ± 0.5 µm. The centrosome migrated down by 2.4 ± 0.5 µm. Being about 1/4 of the cell height, this displacement is nearly 1/2 of what would be needed on average for translocating the centrosome from a random position to the very substrate. The centrosome in T cells, however, stays away from the very margin of the cell, as discussed above, limiting the possible range of its vertical positions to less than the vertical dimension of the cell. This suggests that our observation window captures most of the centrosome translocation that takes place.

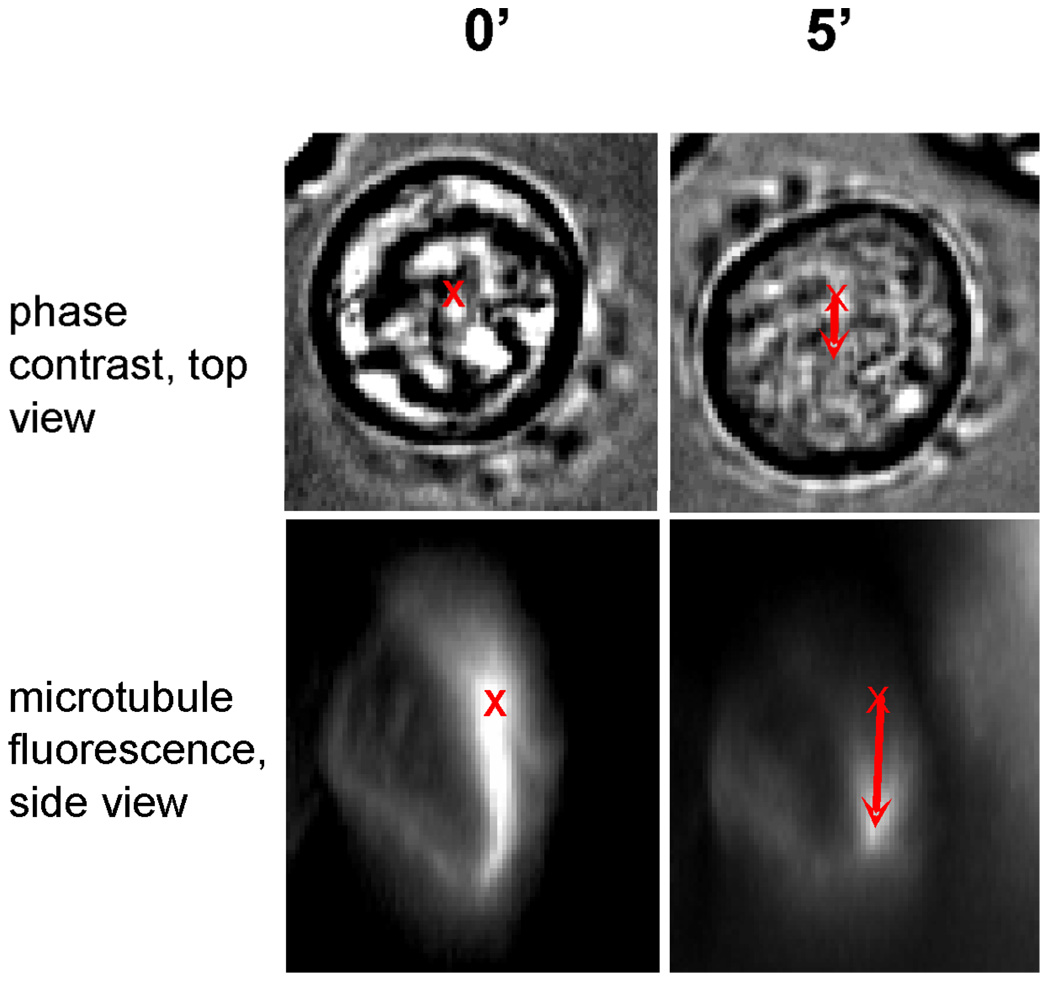
Most remarkably, the downward migration of the centrosome is indeed accompanied by lateral migration of the cell on the target substrate. The lateral displacement of the cell centroid was 2.9 ± 0.4 µm. This is very close in magnitude to the vertical displacement of the centrosome. At the same time, being only about 1/5 of the cell diameter, this lateral migration hardly qualifies as cell locomotion and is easy to overlook. The quantitative measurements, however, confirm that the centrosome polarization is accompanied by the lateral movement of the entire cell. Sample top-view and side-view snapshots in figure 2 illustrate this.

Figure 2.

Real-time observation of the coupled centrosome polarization and cell movement. All the images show the same T cell attached to the substrate coated with antibodies to the T cell receptor. The images in the right column were taken 5 min after the images in the left column. The images in the top row are phase-contrast images showing a top view of the cell. A skirt of thin lamellipodia is seen around thick, round cell body. The initial position of the cell centroid is marked with a cross, and the arrow on the right shows the lateral displacement of the cell centroid five minutes later. The images in the bottom row are side views of three-dimensional images of fluorescently labeled microtubules. Microtubules diverge like rays from the centrosome, making the latter the brightest spot. The initial position of the centrosome is marked with a cross, and the arrow on the right shows the vertical displacement of the centrosome towards the transparent underlying substrate five minutes later.

Quantitative evaluation of the involvement of the whole-cell movements in the centrosome polarization requires comparing the actual downward migration of the centrosome with one that could be expected of a point embedded into the cell moving as a whole. A geometric formalism will be needed for deriving the passive component of the centrosome movements from the movements of the cell. This formalism, effectively a kinematic hypothesis about the T cell polarization, will be used to quantify the theoretically expected contribution of the actual whole-cell movements to the actual centrosome migration. In the complexity of the simultaneous dynamics of the cell and its centrosome, we will attempt to discern the component of simple, idealized whole-cell rolling that could entrain the centrosome.

The geometrical calculation of the trajectory expected of the embedded centrosome (see the Methods section) is a three-dimensional generalization of the curtate cycloid curve that is described by a point anywhere along a radius on a rolling wheel. The vertical displacement of such an eccentric point can be found given the horizontal displacement of the wheel. The no-slip condition between the wheel and the substrate stipulates that the horizontal translocation of the wheel equals the radius of the wheel multiplied by its rotation angle. Thus, knowing the horizontal displacement and the rolling radius, the rotation angle can be found. Any point on the wheel undergoes rotation around the hub by the same angle. This makes it possible to find the vertical displacement of any such point. In the special case of a point that is initially directly behind the axis, the vertical displacement will be its distance from the hub times the sine of the rotation angle. This calculation strategy is generalizable to the rolling of a three-dimensional ball and the movement of any off-center point in it (details provided in the Methods section).

The attached T cell does not have the shape of a ball. The cell therefore cannot roll without internal deformations that would complicate the movement of the embedded point, such as the centrosome in our hypothesis. However, if the complications are secondary to the main movement which is rolling, one can expect that the movement of the centrosome can be calculated to a useful precision from the lateral movement of the cell by following the above strategy. Given the deviation of the cell from a ball, it becomes an assumption that the rolling radius as used in the calculation of the rotation angle should be the half-height of the cell, and that the rotation angle of the cell is also the rotation angle of the centrosome around the axis passing through the cell centroid. We will calculate the centrosome movement that would be expected under this idealized cell rolling from the actual lateral movement of the cell, and compare it quantitatively with the actual centrosome movement.

Applying the formalism individually and then averaging over the cells, we obtain that the centrosome would be 1.0 ± 0.3 µm lower than initially due to the cell body rolling. The contribution of cell body rolling to the centrosome polarization can be calculated as the ratio of the vertical displacement of the centrosome that is expected based on rolling to its actual vertical displacement (2.4 µm). We obtain that cell body rolling can be responsible for 43% of the centrosome polarization in our experiments.

3.5. Discussion

In this paper, we have formulated a quantitative theory that explains the centrosome polarization in activated T cells. The simple geometric principles in the basis of this theory would be applicable to any cell that possesses a microtubule aster and adheres to a surface after being initially suspended freely. The theory thus explains the T cell polarization induced by the molecular recognition of the specific target cell [1] as well as the orientation of the centrosome to the non-specific substrate displayed by T cells, macrophages, neutrophils, fibroblasts, and epithelial cells that sediment from suspension in culture [9–11]. This broad applicability is seen here as an advantage of the theory and in fact a requirement for any theory of the process, but it may raise the question whether our theory accounts for the specificity of the T cell response. The answer is that our theory applies whenever its geometrical conditions are met by the cell, but the T cells normally meet the condition of attachment when the target surface induces the specific molecular recognition, such as between the T cell receptor and the antigen displayed on the target cell. More generally, however, it appears that the polarization response of the T cells sometimes has to be induced by the specific recognition, as probably is the case in vivo, and sometimes, at least in the artificial circumstances of an experiment, it need not. The development of the experimental model employed in this study is an illustration. Plain glass induces attachment of T cells and polarization of the centrosome to the glass substrate [9]. Coating glass with poly-lysine abrogates attachment of T cells [14], which cannot be rescued by adsorbing various kinds of antibodies over the poly-lysine layer, for example, of antibodies against the LFA-1 integrin, a T cell surface adhesion molecule [14]. Specific clones of antibodies to the T cell receptor, however, may be used for coating over the poly-lysine, and the surface so prepared induces both the T cell attachment and the centrosome polarization again [14]. Triggering of specific intracellular signaling pathways downstream from the T cell receptors is seen as evidence that binding of these specific antibodies mimics, to a degree, the normal recognition of antigen by the receptors [14]. The real interaction between a given T cell and a potential target cell is induced by recognition of a specific antigen on the surface of the potential target cell; if the antigen is not the one which this specific T cell recognizes, the polarization response is not induced [3]. The polarization in a cell-cell interaction can, however, be induced experimentally by non-specific lectin-mediated binding as well [3]. Comparing the effects of plain glass, poly-lysine, antibodies against the LFA-1 integrins, antibodies against the T cell receptors, and of the specific and non-specific antigens or non-specific lectins on the target cell, one can conclude that there are biochemically specific surfaces that induce the attachment and polarization and those that do not, as well as that there are biochemically non-specific surfaces that do and do not. That the polarization is induced by the highly specific molecular recognition in the natural setting does not imply that an explanation of polarization must account for the specificity of response.

In our theory, polarization of the centrosome is linked geometrically to spreading of the T cell to the target surface. The cell spreading and centrosome polarization co-occur in the variety of the discussed experiments with different cell types and different substrata. While the spreading of T cells is known to be driven by actin cytoskeleton dynamics [12,14], the molecular mechanism of the centrosome polarization has not been formulated with certainty. According to the present work, a large part of centrosome migration may not have a specific molecular mechanism. To be precise, it may not have a molecular mechanism that would be separate from those that are behind the forces that shape the geometry of our model, which exhibits the centrosome polarization. Among them there are the basic elasticity of microtubules, osmotic volume maintenance mechanisms involving ion pumps, and actomyosin cortex contraction responsible for the effective cell surface tension [16]. The geometry-shaping mechanism that is the most specific of all to the cell-cell interaction at hand is the actin polymerization dynamics responsible for spreading of the T cell on the target. Thus, our model, although it does not deal explicitly with molecular mechanisms, implies that the actin-driven spreading is part of the molecular mechanism of the polarization of the microtubule cytoskeleton. The existing evidence for this role of the actin cytoskeleton comes from the study of signaling in T cells. The signaling cascades that trigger the centrosome polarization and the T cell spreading, although they have not been described in their entirety, appear to overlap to a significant degree. The T cell receptor engagement can induce both [27,28,12,14], acting through the same, relatively upstream adaptors and kinases [14,29,15]. The second messenger Ca⁺⁺ is involved in triggering both events, too [14,30]. The most suggestive is that the relatively downstream cytoskeleton regulator Cdc42, whose role in regulating the actin-driven protrusion is comparatively well understood [31] appears to affect both the spreading and centrosome polarization [6]. Lastly, as T cell precursors develop and express more T cell receptors on their surface, their spreading and centrosome polarization co-vary: improved centrosome polarization comes with improved spreading [25]. Taken together with the mentioned co-occurrence of spreading and centrosome polarization in various cell types on various substrata, this molecular evidence substantiates the implication of our model that the centrosome polarization is a consequence, among other factors, of the T cell spreading on the target surface.

Attachment to the target without the centrosome polarization was seen in 50% of interactions with a non-specific target cell [3], indicating that the attachment is not sufficient for polarization. Sufficiency is not argued here either, only contribution. However, it is important for the present discussion that the natural killer cells in the cited experiments were attached to the target cells and simultaneously to the glass substrate. The spreading on the glass clearly dominated. This would explain the absence of orientation of the centrosome to the target cell, precisely if attachment does direct the orientation, as argued here. Another elegant experiment was performed to refute the hypothesis that the actin-driven spreading is involved in the centrosome polarization [32]. Engaging different receptors on different sides of the same T cell causes the centrosome to go to the site of T cell receptor engagement while strong accumulation of actin is seen at the site of integrin engagement. Is the T cell spreading on the side next to which the centrosome is observed in fixed specimens still the dominant one, quantitatively? This is possible especially because the T cell receptors are engaged there by antibodies coating a rigid bead, while the other target surface belongs to a cell expressing the integrin ligands [32]. In the absence of the clear predominance of one attachment site over the other, the situation in this experiment may be similar to engagement of several target cells with a single T cell. Live observations showed that the centrosome then visits the separate contact areas stochastically [8]. In the framework of our optimality landscape for the orientation of the microtubule aster, the situation in these experiments with multiple and different targets would lead to appearance of multiple attraction basins of different depth and size, between which the centrosome orientation can jump analogously to a molecule between its alternative conformations. Attempting to predict which orientation would be preferred would require precise, model-guided measurements.

According to our calculations, of the actual centrosome displacement to the target substrate, only about 40% can be accounted for by the cell body rolling. The rest of the centrosome polarization is not explained by the current model. It should be noticed that our calculations contain a significant error due to the fact that they assume rolling at a straight line inside the time interval between the consecutive observations when the measurements of the cell position are taken. The so-determined direction of movement, however, changes between the consecutive intervals, indicating that inside the intervals the cell in fact deviates from the straight line assumed in the calculations. It is possible therefore that with improved time resolution, the movement of the centrosome will be more fully explained by cell rolling. The better approximation could also be aided by accounting, in the calculations of the expected centrosome movement from the cell movement, for the deformations that should accompany rolling of the cell that is not entirely round. It is our expectation, however, that the residual unexplained movement of the centrosome is not on the whole due to the imprecision of the measurements and of the theory of whole-cell movements. Rather, proper intracellular motility of the centrosome may exist and contribute significantly to the centrosome polarization. For example, as proposed earlier, the movement of the microtubule aster could be driven by the pulling action of molecular motors anchored at the cortex [8]. Discerning the quantitative contribution of such additional mechanisms in the future would be difficult without first determining the large contribution of whole-cell movements driven by whole-cell optimization as described here.

Quantitative test of our theory relied on tracking the centrosome in three dimensions in living, responding T cells. The observations of the centrosome movements in living T cells that had been accomplished prior to this work had been essentially two-dimensional and qualitative. When multiple optical sections of these cells were acquired, only one per time frame was nonetheless selected to monitor the centrosome movement, reducing the latter to two dimensions [15]. In this case as well as in the others [8,33], interaction of T cells with antigen-presenting cells was followed. The centrosome movements were accompanied by large displacements of the entire T cell, possibly on the inert substrate as well as on the target cell, and the target cell itself was not entirely immobile. Coupling between the movements of the T cell and its centrosome was not analyzed. Here we employed an experimental model in which the only cellular movements are those of the T cell on the target surface, and followed them as well as the centrosome movements in three dimensions. This allowed us to discern the previously disregarded lateral movement of the T cell on the target surface. Earlier, qualitative examination of videomicroscopy data obtained on natural killer-target cell conjugates did not appear to support the similar hypothesis of lateral crawling, which therefore was rejected [5]. Our measurements not only revealed this unusual type of movement, but also allowed us to deduce its kinematical connection to the polarization of the centrosome through the apparent entrainment of the centrosome by the cell body rolling as a whole. It is an open question whether the “vectorial translocation” of the centrosome seen in the previous two-dimensional data [8] is different from the rolling that we see in ours, or whether rolling only looked like linear movement in the two-dimensional projection. The vectorial translocation was considered consistent with bending of microtubules as seen in still images next to the interface with the target, both observations pointing at the possibility that molecular motors are situated at the T cell cortex near the interface and pull on the microtubules to translocate the centrosome [8]. Our computational model, however, explains both the centrosome positioning and the very characteristic microtubule bending at the interface without invoking any molecular motors (cf. figure 6 of ref. [8] and figure 1d here).

For labeling the microtubules in our experiment, we used taxol conjugated with a fluorophore. At the submicromolar concentrations used, taxol suppresses microtubule dynamics, abrogating normal rearrangements of the microtubule cytoskeleton that depend on the microtubule dynamics, arresting cells in mitosis [34]. In our experiments, the centrosome polarization was not inhibited compared to previous studies not involving taxol. This is consistent with the fact that other drastic reorientations of the microtubule cytoskeleton in leukocytes, such as its polarization diring the initiation of migration in neutrophils [35] and retraction into the uropod in T cells [36], are not affected by abrogation of the microtubule dynamics by taxol. This result validates not only our live experimental setup, but also the simplifying assumption in the model that the microtubules do not change their length. In contrast, microtubule dynamics may influence the centrosome position during other processes in other cell types, which has been also subject to theoretical investigation [37,38].

4. Conclusions and Outlook

The theoretical and experimental findings in this paper can be summarized as follows. The eccentric position of the centrosome in T cells can be explained quantitatively as the one stipulated by whole-cell optimization in the sense of a compromise between microtubule unbending and cell surface area minimization under the constraint of cell volume maintenance. The position of the centrosome in activated T cells next to the interface with the immunological target can in theory be obtained parsimoniously by rotating the asymmetric but arbitrarily oriented microtubule aster present in the T cell before stimulation. The orientation of the microtubule aster that brings the centrosome to the interface is quantitatively optimal in the sense of simultaneous cell surface minimization, volume maintenance, and interface area maximization. Rotation of the microtubule aster should involve the entire cell because of the drag resistance, while the adherence of the cell to the target should transform the rotation into rolling. The lateral movement of the T cell on the target surface as expected under rolling is indeed observed in the experiment simultaneously with the centrosome migration to the interface. Measurements suggest that rolling accounts for 43% of the centrosome migration to the target. An entirely novel picture of T cell polarization emerges from these findings. In this picture, the whole-cell structural optimization directs the whole-cell movement that entrains the centrosome, reorienting it to the target cell as required for the immunological function of the T cell.

Certain aspects of the polarization mechanism suggested by our computational and experimental analysis appear to have deep parallels in seemingly unrelated cell-biological phenomena. Cell body rolling with partial slippage on the substrate was observed in keratocytes [39], an experimental model of the adherent cell with rapid and highly persistent locomotion. The centrosome was not monitored in the migrating keratocytes, but the organelles that were, moved around the cell center similarly to the T cell centrosome in our experiments. If the lateral movements of T cells on the target surface can be seen as extremely limited locomotion, it seems natural that the cell body rolling mechanism would be involved in this case also. The difference between the keratocytes and T cells is then not in how they move their organelles around the cell center by coupling them passively to the whole-cell migration through rolling, but in that the keratocytes migrate indefinitely in an apparently random direction and continue cycling their organelles as they move. The T cells, according to our analysis, migrate only slightly and on the whole in the direction dictated by the asymmetry of the microtubule aster, and stop when the centrosome achieves its location next to the substrate.

Similarly to the microtubule aster polarization in the T cells, the self-organization of the microtubule aster in cytoplasts devoid of centrosomes had also been long believed to arise from intracellular transport of the microtubules by molecular motors [40]. When the measurements were taken, they demonstrated immobility of the microtubules in the cytoplasm [41], also excluding the possibility that pushing and pulling associated potentially with assembly and disassembly of the microtubules might be involved. Exclusion of the microtubule movement with respect to the surrounding cytoplasm is the conceptual basis for translating the abstract rotation of the microtubule aster in our model into rotation of the whole cell body, which in turn is predicted to translate into rolling because of the perceived no-slip condition on the T cell-target interface. The sequence from the aster rotation to cell body rotation to rolling is purely conceptual; the causal sequence is probably the opposite: T cell rolling on the target surface entrains the microtubule aster inside, including the eccentric hub of the aster, which is the centrosome. The phenomenon of entrainment of microtubules by a bulk movement of cytoplasm during cell motility is known from the observations in optically favorable regions of motile epithelioid cells, where so-called retrograde flow takes with it microtubules that extend into these lamellar regions [26]. The retrograde flow is driven by the actomyosin cytoskeleton, whose organization and the cell shape determine the direction of the flow. During the polarization of the T cell microtubule cytoskeleton, according to our view, the microtubules are similarly entrained by the motion of the bulk of the cell body. The roles, however, are then distributed between the microtubule and actomyosin cytoskeletons. Whereas the movements are driven by actin, as reviewed above, their direction, on the whole, is dictated by the asymmetry of the microtubule cytoskeleton. Although the geometry of the T cells conjugated with the target is different from the typical motile cell, this microtubule-actin role distribution would be the same as suggested by experiments where disassembly of microtubules left intact the motility per se, but abrogated its directionality in fibroblasts [42].

Taken together with the possible identical basic mechanism of T and non-T cell polarization response that motivated this work, these parallels with cell locomotion seem to point at the fundamental simplicity and universality of cell behavior. We submit that although the quantitative principles proposed here are far from an exhaustive explanation of the T cell polarization, the whole-cell movements and whole-cell structural optimization should play an important role in it, subordinating the underlying molecular mechanisms.