Scaling properties of European research units

Abstract

A quantitative characterization of the scale-dependent features of research units may provide important insight into how such units are organized and how they grow. The relative importance of top-down versus bottom-up controls on their growth may be revealed by their scaling properties. Here we show that the number of support staff in Scandinavian research units, ranging in size from 20 to 7,800 staff members, is related to the number of academic staff by a power law. The scaling exponent of ≈1.30 is broadly consistent with a simple hierarchical model of the university organization. Similar scaling behavior between small and large research units with a wide range of ambitions and strategies argues against top-down control of the growth. Top-down effects, and externally imposed effects from changing political environments, can be observed as fluctuations around the main trend. The observed scaling law implies that cost-benefit arguments for merging research institutions into larger and larger units may have limited validity unless the productivity per academic staff and/or the quality of the products are considerably higher in larger institutions. Despite the hierarchical structure of most large-scale research units in Europe, the network structures represented by the academic component of such units are strongly antihierarchical and suboptimal for efficient communication within individual units.

The size and structure of academic research units have been the subject of both scientifically and politically motivated investigations (1–3). The general goal of such units is “to advance learning and perpetuate it to posterity” (Harvard University 1643 mission statement). However, it is not clear that research units are optimally organized to support science and education.

Organizational infrastructure is often linked to how organizations grow. Stanley et al. (4) and Buldyrev et al. (5) studied scaling behavior during the growth of manufacturing companies and concluded that the growth rate is affected by a tendency to retain an “optimal” size. These authors presented a hierarchical model where imperfect top-down management is a key factor. Both papers are, however, concerned with the distribution of annual growth rates, and it is not clear how this applies to the internal structure and growth of research organizations over much longer periods of time.

On the basis of research and development expenditure and research output data from 719 United States Universities, Plerou et al. (2) concluded that the distribution of growth rates displays a “universal” form, independently of the size of the university. Although these authors did not address how research units actually grow and how the organizational infrastructure evolves, the observed similarities across scales hint at an underlying scale-independent “growth principle.” We have further investigated this by studying the distribution of academic versus support staff for European research units, including entire universities and subunits within the universities. Our results demonstrate a striking scaling behavior that can hardly be explained by a common “global” optimization principle. This is directly relevant for the ongoing discussion of the pros and cons of merging research institutions into larger units.

Scaling Properties.

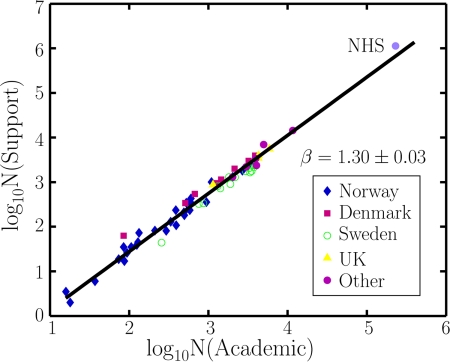
Employment data were obtained from 49 Scandinavian and 10 non-Scandinavian research units and separated into 2 categories: academic staff (actively conducting research and/or teaching) and other staff (hereafter referred to as support staff). All Danish, Norwegian, and Swedish universities are included. For the largest Norwegian universities, separate data have been obtained for the largest faculties and a random set of departments and research centers. The smallest units were not extensively sampled because the amount and nature of the support that they receive from their host university vary greatly, depending on factors such as how laboratory intensive their research is. Ten non-Scandinavian universities are included to determine if the trend established for Scandinavian universities applies elsewhere and extends to very large units. Data from the U.K. National Health System, another complex and extremely large public unit, are included for comparison. In this case the staff was split into medical and nonmedical staff. Fig. 1 demonstrates that the data define a linear trend when the logarithm of the number of support staff, N(Support), is plotted versus the logarithm of number of academic staff, N(Academic). This indicates a power-law scaling relationship between these 2 groups,

where C is a constant (≈0.07) and the exponent is β ≈ 1.30 ± 0.03. The Danish data fall above the linear fit to all of the data while the Swedish data fall below. Swedish universities have ≈10% less support staff than Norwegian and Danish universities with a similar number of total staff.

Fig. 1.

Diagram showing the distribution of academic and support staff for Scandinavian and a few other research units, including 4 U.K. universities. The data in this log-log plot were fitted to a power law, using an orthogonal distance regression. We used simple bootstrap sampling with repetition to seek the spread in the data and found a close to Gaussian distribution in the values for the exponents. Confidence intervals on the slopes were estimated using bootstrapping. Slopes for individual data sets (with confidence intervals): Norway, 1.32 (1.24–1.40); Denmark, 1.34 (1.19–1.39); Sweden, 1.39 (1.07–1.51). The analyses were carried out in Past, version 1.89, Hammer et al. (6). Sources of data: Norwegian data (from around 1990) can all be found in the database for the statistics of higher education in Norway (http://dbh.nsd.uib.no/dbhvev/ansatte/tilsatte_rapport.cfm). Data for the University of Oslo from before 1990 are available from annual reports. Data from Swedish, Danish, and other research units are found at the individual university's web pages, usually with references to the respective annual reports. The National Health Service (NHS) data are published at http://www.ic.nhs.uk/pubs/nhsstaff. No data have been excluded from the diagram. All data are provided in Tables S1 and S2.

The observed power-law behavior, which covers a range of >3 orders of magnitude (decades), reflects that the larger the units are, the higher the number of support staff is relative to the academic staff. Data points for subunits within Norwegian universities follow the same power-law trend and point to a hierarchical organization of the larger research units. The scale-free (power-law) relationship suggests that units of all sizes may be equally well (or poorly) organized to promote the research and education production with available resources. In principle, this could be the result of rational individual decision making within units of all sizes.

The data for the U.K. National Health System (NHS), with 1.36 million employees, are also plotted in Fig. 1. Extrapolation of the ratio between academic and support staff to the size of the NHS is strikingly similar to the ratio between NHS medical and nonmedical staff.

A Hierarchical Model.

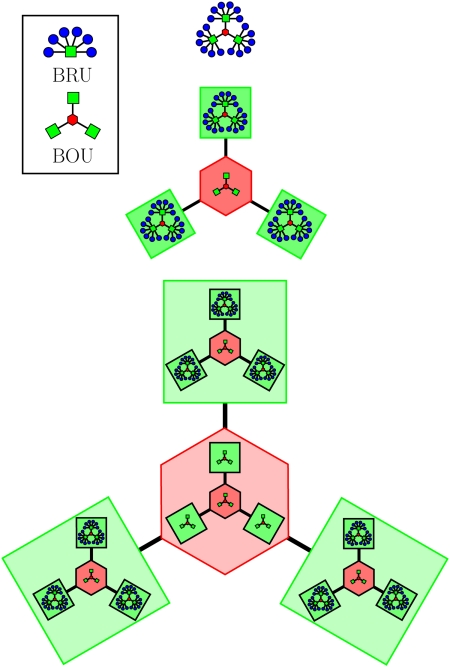
The observed power-law scaling behavior shown in Fig. 1 may not be surprising for individual research units given the hierarchical structure of most European universities. Fig. 2 shows a simple hierarchical model that results in scaling behavior similar to that observed. The basic organizational unit in the hierarchy is composed of 3 “basic research units.” Each research unit is composed of 1 “support staff” and a number of academic staff (6 in Fig. 2; typically this would be 1 or 2 professors and a number of postdocs and postgraduates). Fig. 1 shows that for N(Support) ≈ 1, N(Academic) will typically be on the order of 5–10. In addition, the smallest organizational unit requires 1 additional support staff to “administrate” both the academic and the support staff of the groups. Iteration of this structure to generate larger organizations results in a power-law scaling relation between academic and support staff, with a scaling exponent of [β = log(X1)/log(X1 − X2)], where X1 is the total number of research units (each having 1 support staff) and additional“central administrative” units in the basic organizational unit, and X2 is the number of central support staff in the basic organizational unit. In the model shown in Fig. 2, we have chosen X1 = 4 and X2 = 1. Thus β = log (4)/log (3) = 1.26, which is consistent with the observed exponent, within statistical and observational uncertainties. In general, X1 and X2 may have noninteger values because individual units of the same size within a large organization may be organized differently. Somewhat different exponents may be obtained from other models (for example: X1 = 6 and X2 = 2 gives β = 1.29). The important point is, however, that for any reasonable aggregation of a small number of individual basic research units into a “research center” with a central administration of 1–2 additional support staff, similar values are obtained for β. β-Values outside the range of 1.1< β <1.5 would be highly exceptional during any irreversible growth process (i.e., during mergers where the entire support staff from the merging units is kept).

Fig. 2.

A simple deterministic hierarchical model for the structure of a research unit. Three levels of the self-similar hierarchical organization are shown. The basic organizational unit (BOU) consists of 1 central administrator (pink hexagon) and 3 administrators (green square) dealing directly with the academic staff (blue circles). The iterative step in the construction of the hierarchy is to assume that the growth of the administration follows the pattern of the basic unit. Hence we obtain 1 central administrative unit, which has contact with 3 basic research units (BRU). The exponent for this construction is log(4)/log(3) ∼ 1.26. In general, the exponent is given by log(X1)/log(X1 − X2), where “X1” is the total number of support staff and “X2” is the number of “central support staff.” A general feature of these models is that the central support becomes increasingly distant from the basic research units, as the research unit grows in size. Note also that the number of academic staff in the BRU represents the point where the regression line in Fig. 1 intersects the x-axis (and thus gives the number of academic staff required for the first man year's support staff), but does not influence the scaling behavior.

Hierarchical networks such as the one illustrated in Fig. 2 may at first glance appear effective in terms of information transfer. However, when a research organization is divided into academic staff on one hand and support staff on the other, it becomes evident that the network composed of the academic staff is very poorly connected. Highly connected researchers will normally be surrounded by a group of less well connected postdocs and students, but few connections exist between active researchers across the traditional disciplinary divides. Thus, in the jargon of complex network science, the hubs (i.e., centers of activity) are poorly connected and the network of producers is strongly antihierarchical (7). In this respect, research networks resemble some biological systems, such as the interacting and regulatory network of proteins in yeast cells as described by Maslov and Sneppen (8). It is also interesting that the number of genes involved in the transcription regulation of eukaryotes shows a power-law dependence on the number of genes in the genome with an exponent of 1.26 (9). This is similar to the slope in Fig. 1 and close to an allometric scaling behavior with an exponent of 4/3. The origin of the frequently observed allometric scaling in biological systems has been explained in terms of the idea that life is sustained by a variety of hierachical branching networks optimized by natural selection processes (10–12).

Time Evolution.

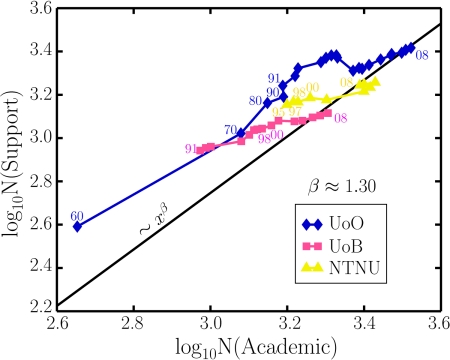
Time-series data may provide important clues about the relative roles of top-down versus bottom-up decisions in a complex organization. The time evolution of the support staff to academic staff ratio for the 3 largest Norwegian universities is shown in Fig. 3. Until recently, the ratio at all these universities was above the regression line shown in Fig. 1. The longest time series is available from the University of Oslo where the rapid growth of total staff in the 1960s did not significantly change the fraction of support staff compared to academic staff. A break in this trend occurred around 1970. From 1970 until the mid-1990s, the fraction of support staff relative to academic staff rose above the regression line in Fig. 1. From the mid-to-late 1990s onward, the fraction of support staff at the University of Oslo was reduced from about ≈54% in 1995 to 44% in 2008. A similar, albeit less radical decrease in the fraction of support staff from the 1990s is also seen for the 2 other universities shown in Fig. 3.

Fig. 3.

Time evolution in support versus academic staff for the 3 largest Norwegian universities: University of Oslo (UoO), University of Bergen (UoB), and the Norwegian University of Science and Technology (NTNU) for the periods 1960–2008, 1991–2008, and 1996–2008. The best-fit regression from Fig. 1 is also shown.

Discussion

The research units studied in this paper cover a size range that spans >3 orders of magnitude in terms of total staff, and the data include units with a wide range in ambitions and strategies. It would be surprising if the scaling behavior resulted from a common global optimization principle. Whereas biological systems may be globally optimized by natural selection, global optimization principles for social systems are often less obvious. Whereas commercial enterprises may be optimized to maximize income and may become “extinct” in the course of evolution if unsuccessful, academic institutions (at least in Europe) have been less exposed to “natural selection” through competition. Until the mid-1990s or so, the budgets of the Scandinavian universities were only to a very limited extent affected by performance. This is reflected by the autonomy of most research groups and university departments in the hiring of both academic and support staff. These observations suggest that the observed power-law relation (Fig. 1) reflects unregulated or “natural” growth (cf. ref. 13). Natural growth would, in this context, represent a process controlled by a multitude of local decisions (decisions would be intended to optimize the conditions for research and education in groups consisting of only a few staff members). Thus, any optimization “principle” is likely to operate locally. By reference to our simple model, this optimization would result in a hierarchical organization in which each unit consists of an “optimal” number of subunits.

However, like biological systems, a large-scale organization needs pathways for communication across the system. Two basic assumptions that are used in models for allometric scaling in biological systems (11, 12) are also fulfilled in our simple model of the university organization: (i) A space-filling hierarchical branching pattern connects the entire volume of the organism/university and (ii) the basic organizational unit (BOU) is size invariant (see Fig. 2). A third optimization principle, included in West et al.'s (10) model for allometric scaling in biological systems, is that the energy required to distribute resources is minimized, i.e., the hydrodynamic resistance in systems depending on transport of water, blood, or other fluids. Alternatively, Banavar et al. (11) suggested that in the transportation network the total volume of blood (or whatever “fluid” fills the transportation network) is minimized. Either of these optimization principles leads to the conclusion that the volume of the transport network V_net scales linearly with mass M and that the metabolic rate B scales with mass to the 4/3 power. Thus V_net∝B^4/3. It is tempting to suggest an analogy to research units by claiming that they attempt to minimize support staff to maximize production of research and education. Today, when a substantial fraction of university income depends on performance (for example, 40% of the total income to the University of Oslo is performance dependent), such an assumption may be partly justified. However, although the effect of this new “global optimization principle” is visible in the evolution of the largest Norwegian universities, the rate of “cultural changes” in academia seems far too slow for this to explain the main scaling behavior seen in Fig. 1.

An alternative local “optimization” principle for social systems was proposed in 1949 by George Kingsley Zipf (14), who in his Human Behavior and the Principle of Least Effort wrote “… a person in solving his immediate problems will view these against the background of his probably future problems, as estimated by himself. Moreover he will strive to solve his problems in such a way as to minimize the total work that must be expected in solving both his immediate problems and his probably future problems.” A possible consequence of such a principle would be the hiring of as many support staff as could be supported in an organization with a performance-independent income. Zipf's optimization principle would then easily lead to another famous principle: C. Northcote Parkinson's “law of multiplication of subordinates” (15). Although many would claim that these principles are universally applicable, their scaling consequences are not obvious—unless, as assumed in our hierarchical model, there is an optimum (or at least characteristic) number of subordinates at all levels of the hierarchy.

Another argument for local controls on the growth process behind the observed scaling behavior is that deviations from the main trend can be explained by top-down strategies or external/environmental forcing. Fig. 3 shows that the fastest growth of the University of Oslo (UoO) occurred between 1960 and 1970 when the number of staff almost tripled. Following the “fall of the dons” in the late 1960s and early 1970s (cf. Halsey, ref. 16), UoO and many other universities experienced a period of bureaucratization initially intended to democratize the universities (Gornitzka et al., ref. 1). This caused a sharp rise in the ratio of administrative to scientific staff. Similar trends were seen elsewhere. At the University of California at Los Angeles, the number of faculty members decreased by 7% from 1977 to 1987, while administrative employees increased by 36%. At MIT, administrative personnel rose by 37% from 1981 to 1989, with a modest increase of 8% in the number of faculty members (Leslie and Rhoades, ref. 17). Despite this increase in administrative staff, survey data from Great Britain showed that the proportion of administrative work performed by academic staff increased from 19 to 24% of total work hours between 1976 and 1989 (16). A Norwegian study from 1983 found that 38% of academic staff members reported that excess administration was the main obstacle to academic progress (18). Thus, there is very little evidence that an increased fraction of support staff in larger units promotes higher scientific production for the individual researcher.

An explanation for this in Norwegian Universities could be that there was a simultaneous change in the profile of administrative staff. During the early to mid-1990s there was a marked relative increase in staff with a high educational level at the expense of clerical staff. From 1987 to 1999 clerical staff was reduced by 28%, whereas the number of higher administrative staff increased by 215% (13). In any case, the increased bureaucratization from about 1970 to the 1990s was a result of an externally controlled political process rather than internal (local or top-down) decisions meant to promote academic output.

Increased expenditures to support administrative staff during this period generated a resistance among the academic personnel, and from the mid 1990s onward, the number of support staff relative to academic staff at UoO was reduced, resulting in a clear deviation from the “natural trend.” This was a direct result of a top-down process to improve the effectiveness of UoO's support functions. In the UoO strategic plan for 1995–1999 it was explicitly stated (point 8.1 in the plan) that it was a goal of the university to make sure that the resources devoted to support functions should be neither more nor less than those required to sustain the university's primary functions (research and education). This top-down (nonlocal) decision clearly resulted in a strong negative deviation from the “natural slope” seen in Fig. 1. Thus, the evolution of academic and support staff employment at UoO suggests that clear deviations from the general scaling behavior shown in Fig. 1 are a result of “nonlocal” effects (or a change in the “objective function” that is locally maximized or minimized because of top-down decisions and/or changes in the environment in which the university operates). Whether this behavior stops at the University level or continues across the entire research enterprise (including research councils, states, nations, etc.) is an open yet interesting question.

An important question arising from this work is whether the growth of larger research organizations at the expense of smaller ones can be justified in terms of cost–benefit arguments, where the critical outcome is the quality and costs of individual products related to research and education. There is little support for that outcome in the current data. However, a more thorough analysis of the research output and its impacts on society for research units of varying size would have to be undertaken before conclusive statements could be made about such issues. Interestingly though, the trends found for the research units studied here may also apply to other large-scale state organizations such as health systems. It may in fact be justified to ask if an increase in the number of support staff relative to those directly involved in production of goods, education, research, etc., is justified by its benefit to society as a whole because it provided rewarding employment to individuals who might otherwise be unemployed. It may also be possible that various “economies of scale” more than offset the cost of a larger support staff to “production staff” ratio in larger organizations.

It remains an empirical fact, however, that the hierarchical and strongly discipline-oriented organization of European research units is a challenge for efficient “lateral” communication between the scientific hubs. This fact represents a potential problem for effective organization of cross-disciplinary research and it may reduce the ability to attract large-scale external funding. It is also reasonable to anticipate that organizations that have grown by bottom-up decisions may have a built-in resistance to the implementation of top-down strategies.