Skip to main content
NCBI home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2009 Jul 23.
Published in final edited form as: J Neurochem. 2009 May;109(Suppl 1):73–79. doi: 10.1111/j.1471-4159.2009.05844.x

Cerebral oxygen demand for short-lived and steady-state events

Peter Herman 1,2,3,8, Basavaraju G Sanganahalli 1,2,3, Hal Blumenfeld 2,4,5,6, Fahmeed Hyder 1,2,3,7
PMCID: PMC2714475  NIHMSID: NIHMS106247  PMID: 19393011

Abstract

Due to importance of oxidative energetics for cerebral function, extraction of oxygen consumption (CMRO2) from blood oxygenation level dependent (BOLD) signal using multi-modal measurements of blood flow (CBF) and volume (CBV) has become an accepted functional magnetic resonance imaging (fMRI) technique. This approach, termed calibrated fMRI, is based on a biophysical model which describes tissue oxygen extraction at steady-state. A problem encountered for calculating dynamic CMRO2 relates to concerns whether the conventional BOLD model can be applied transiently. In particular, it is unclear whether calculation of CMRO2 differs between short and long stimuli. Linearity was experimentally demonstrated between BOLD-related components and neural activity, thereby making it possible to use calibrated fMRI in a dynamic manner. We used multi-modal fMRI and electrophysiology, in α-chloralose anesthetized rats during forepaw stimulation to show that respective transfer functions (of BOLD, CBV, CBF) generated by deconvolution with neural activity are time invariant, for events in the millisecond to minute range. These results allowed extraction of a significant component of the BOLD signal that can be ascribed to CMRO2 transients. We discuss the importance of minimizing residual signal, represented by the difference between modeled and raw signals, in convolution analysis using multi-modal signals.

Keywords: glia, glucose, glutamate, mitochondria, oxygen transport, signaling

INTRODUCTION

Despite advancements to measure neural activity, e.g., electroencephalography (EEG) and magnetoencephalography (MEG), these techniques still have limited spatial resolution and localization problems (Srinivasan et al. 2006). Alternative methods of brain mapping are based on secondary signals, such as changes in blood oxygenation level dependent (BOLD) signal and blood flow (CBF) or volume (CBV). However another estimation of brain activity, based on thermodynamic principles, can be obtained by measuring the energy consumption (Hyder et al. 2002). The main energy source for brain is glucose which is stoichiometrically oxidized in mitochondria to produce ATP efficiently (Riera et al. 2008). Cerebral oxygen consumption (CMRO2) is measured with 13C or 17O magnetic resonance spectroscopy (MRS) (Hyder et al. 2006; Zhu et al. 2008) as well as with 11C and 15O positron emission tomography (PET) (Vafaee and Gjedde 2000; Kudomi et al. 2005). Since these methods require expensive/radioactive isotopes, alternative ways of CMRO2 estimation are widely sought for brain mapping.

Functional magnetic resonance imaging (fMRI) is used for non-invasive mapping of brain activity. It provides an indirect measure of neural activity by sensing hyperemic changes. Since BOLD signal has both an energetic and hemodynamic basis, CMRO2 can be extracted by calibrating fMRI with additional measurements of CBF and CBV. The BOLD image-contrast depends on changes of magnetic properties of blood: oxy-hemoglobin is diamagnetic, while deoxy-hemoglobin is paramagnetic (Ogawa et al. 1993). At steady-state, based on the Fick’s principle (Kety and Schmidt 1948), the fractional change of BOLD signal (ΔS/S) is given by

ΔSS=A(ΔCBFCBF−ΔCMRO2CMRO21+ΔCBFCBF−ΔCMVCMV) (1)

where A is a field dependent constant and the biophysical and physiological basis of Eq. 1 have been described (Kennan et al. 1994; Hyder et al. 2001). Therefore high spatial resolution CMRO2 maps can be obtained by calibrated fMRI using multi-modal but concurrent measurements of BOLD, CBF, and CBV (Supplementary Fig. 1), where each parameter is measured independently (in the same session) with different MRI contrasts (i.e., BOLD with gradient or spin echo; CBF with arterial spin labeling; CBV with exogenous contrast agent). Furthermore the calculated CMRO2 can be validated by comparison with MRS or PET measurements (Kida et al. 2000; Zhang et al. 2004; Ito et al. 2005).

An alternative for dynamic calibrated fMRI is to test the linearity of the multi-modal signals within short-lived and steady-state stimuli. If each BOLD-related component in Eq. 1 is demonstrated to be linear across various stimulus durations, then the respective transfer functions generated by deconvolution with the neural signal should be time invariant and thus used for calculating CMRO2 dynamics. For CMRO2 transients associated with neural events, underlying BOLD-related components were measured and combined with electrophysiology data, over a range of brief and long stimuli. Transfer functions generated for brief stimuli with convolution analysis could be successfully used to model responses for long stimuli within the range of the uncertainty of the real measurements.

MATERIALS and METHODS

Animal preparation and stimulus presentation

All experiments were conducted on artificially ventilated (1–2% halothane during surgery, plus 70%N2O/30%O2) adult male rats (n = 26; Sprague-Dawley; 200–300 g; Charles River, Wilmington, MA). Femoral artery and vein were cannulated respectively for monitoring physiologic parameters (pCO2, pO2, pH, blood pressure) and for infusion of iron oxide contrast agent for measuring CBV changes (Kida et al. 2000). The α-chloralose (∼40 mg/kg/h) and D-tubocurarine chloride (∼0.3 mg/kg/h) were administered intraperitoneally. Stimulus parameters consisted of 2mA amplitude pulses of 0.3ms duration where multiple pulses were separated by 333ms and the number of pulses varied from 1 to 90. A resting period of 300s was allowed between repeated stimulation trials (at least four trials per rat: two repetitions, two paws).

Electrophysiology and CBF

The first group of rats (n = 12) were mounted on a stereotaxic frame and small burr holes were drilled for insertion of adjacent electrical and laser-Doppler flowmetry (LDF) probes to simultaneously measure neural and CBF signals (Schridde et al. 2008). Although arterial spin labeling (ASL) MRI is used to provide quantitative CBF measurements at steady-state, we used LDF for dynamic CBF measurements because ASL techniques loose perfusion sensitivity at higher temporal resolution (Kida et al. 2004). Recordings were localized to middle cortical layers (4.4 mm lateral, 1.0 mm anterior to bregma, 0.9±0.1 mm depth from cortical surface) and confirmed histologically (Englot et al. 2008; Schridde et al. 2008) for comparison with MRI signals at the same depth. The scalp was used as the reference and ground. Local field potential (LFP) and multi unit activity (MUA) were obtained by splitting into low (<150 Hz) and high (0.4–10 kHz) bands. Magnitude of the LDF data was calibrated to CBF collected with ASL MRI (3 Hz, 2 mA, 0.3 ms, >90 pulses) (Kida et al. 2004). Electrical and optical signals were digitized with CED µ-1401 using Spike 2 software (Cambridge Electronic Design, Cambridge, UK) at 20 kHz and 50 Hz, respectively. To compare with lower temporal resolution BOLD and CBV data, we averaged the neural raw data by running 0.02s bins.

Multi-modal fMRI

In the second group of rats (n = 14) all fMRI data were obtained on a modified 11.7T Bruker horizontal-bore spectrometer (Bruker, Billerica, MA) using a 1H surface coil radio-frequency probe (1.4 cm diameter) with conventional methods for BOLD and CBV contrasts (Herman et al. 2008; Sanganahalli et al. 2008). We used echo-planar imaging with repetition and gradient echo times of 1000 and 15 ms, respectively.

Estimating parameters of gamma-based transfer functions

The transfer function, h(t), can be achieved by deconvolution between the input signal, i(t), and the output signal, r(t). The LFP was used as the input signal, i(t), whereas the BOLD, CBV, and CBF responses each was used as an independent response, r(t). It can be shown that

i(t)⊗h(t)=r(t) (2)

where t is time. The gamma variate function is widely used for transfer function modeling (Supplementary Text A).

To calculate a transfer function, a least-square mean (Gauss-Newton) fitting method (Matlab, Natick, MA) was used with iterative steps (Supplementary Fig. 2): a transfer function was created with initial parameters; it was convolved on the input function; a difference between the modeled and the measured response was calculated to create a residual signal. This method is a modification of Newton's method for detecting a function minimum without using second derivatives, thereby minimizing computational load and time. If the modeled response was significantly different from the measured response, then parameters of the transfer function were changed and the process was repeated.

The fitting process was usually completed within several hundred iterations. We assumed the residuals to be acceptable if all of their values were within the range of uncertainty of the measured response, given by ± standard deviation (SD) of the raw signal.

RESULTS

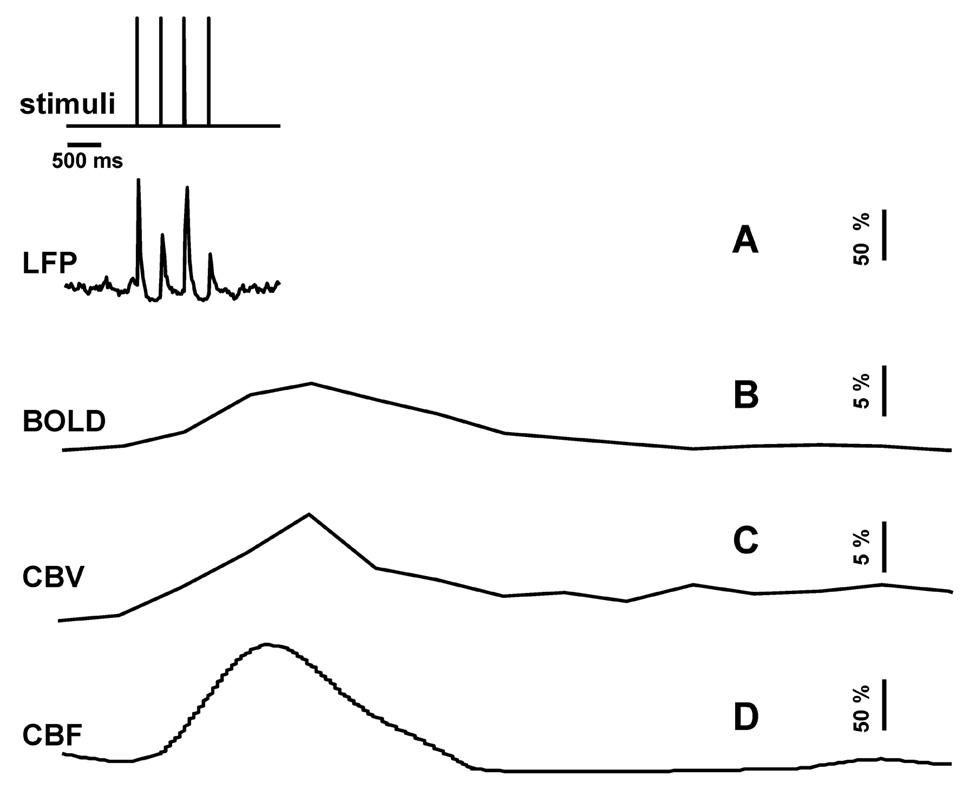
We simultaneously measured LFP and CBF signals from the somatosensory cortex using a dual-sensor probe and compared these signals with BOLD and CBV signals (at 11.7T) in the same cortical location. The neural (LFP) and imaging signals (BOLD, CBV, CBF) were measured with short and long forepaw stimuli to assess whether the hyperemic responses were linearly associated with neural activity. Fig. 1 shows a representative single-trial data set with 4 stimulus pulses. Briefly, the evoked neural response was immediate and short lived in comparison to the imaging signals which lasted about 4s.

Fig 1.

Fig 1

Open in a new tab

Single trial multi-modal data. Representative neural (A; LFP) and imaging (B–D; BOLD, CBV, CBF) signals for short forepaw stimuli. While there was an evoked LFP for each stimulus pulse, alternate LFP’s were not identical. A similar trend was observed for MUA (data not shown).

The neural response had two phases (Fig. 1A). A positive phase was initiated immediately after each stimulus pulse which lasted about 150ms. After the positive peak was a negative phase which lasted about 200ms, but its amplitude was less than 5% of the initial positive peak which was below the SD of the measurement. These positive peaks were used as input signals for the convolution analysis (Supplementary Fig. 2). Evoked neural responses to multiple stimulus pulses demonstrated a unique pattern (Fig. 1A) which have been noted by others (Matsuura and Kanno 2001) where the alternate responses were attenuated most likely due to inhibitory mechanisms (Hellweg et al. 1977). Therefore all subsequent evoked responses were normalized to the first positive component (Fig. 2A). For long lasting stimuli (90 pulses), in addition to the alternating stronger and weaker responses for consecutive stimulus pulses, the magnitude of responses generally decreased during the initial 5–6s to subsequently reach a new plateau (e.g., see Fig. 2A, extreme right). These observations are in good agreement with prior results (Ances et al. 2000; Sheth et al. 2004).

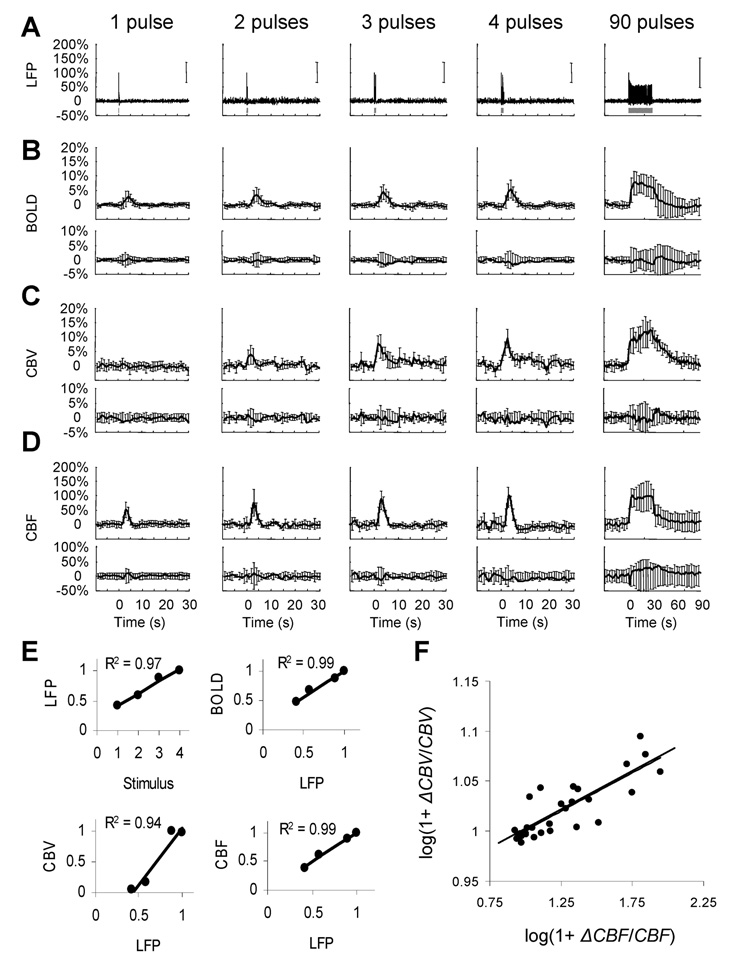
Fig 2.

Fig 2

Open in a new tab

Multi-modal data for brief and long-lasting events. Measured neural (A; LFP) and imaging (B–D; BOLD, CBV, CBF, upper rows) signals were used to generate transfer functions. Transfer functions were used to generate modeled signals. The residual signal, created by subtracting the modeled signal from the measured signal, was lower than ±SD of the measured signal (B–D; BOLD, CBV, CBF, lower rows). (E) Relationship between strength (i.e., both intensity and width) of evoked signals. The LFP responses were normalized to the response with 4 stimulus pulses. The BOLD, CBV and CBF data were calculated as normalized by area under the curves. (F) The so-called Grubb’s law (i.e., CBV = CBFΦ) given by the slope of the log-log plot of change in CBF and CBV. The data points are from the hyperemic portion for all stimuli with Φ of ∼0.08 where the peak values averaged to ∼0.15.

Amplitudes and time-to-peak of the imaging signals (Figs. 2 B–D) are in good agreement with prior observations (Kida et al. 2007; Shen et al. 2008). The mean time-to-peak of the BOLD response was 3.9±0.3s. The response intensity (and width) gradually increased from 1 to 4 pulses and reached a plateau for 90 pulses (2.9±1.8%, 3.4±1.2%, 4.4±2.1%, 8.02±1.3%, and 7.8±4.2%, respectively). The CBF signals showed similar tendencies. The mean time-to-peak of the CBF response was 3.2±0.2s, whereas the intensities were 51.8±28.2%, 75.1±23.3%, 87.7±23.2%, 100.9±31.1%, and 100.1±37.8%, respectively. The mean time-to-peak in CBV response was 3.3±0.7s and the response intensities gradually increased from 1 to 4 pulses (0.8±1.8%, 3.8±1.2%, 7.6±2.1%, and 9.5±1.4%, respectively). The CBV response for 90 pulses of stimulation after a first initial rise (10.8±3.6%) showed a secondary slow increase (15±5%) lasting more than 15s. These temporal characteristics of CBV are typical of red blood cell and plasma volume changes (Herman et al. 2008). Using the strength (i.e., both intensity and width) of each evoked signal, the neural responses were correlated with the strength of each imaging signal. Increasing number of stimulus pulses augmented responses in each of the signals (Fig. 2E). The so-called Grubbs law (Grubb et al. 1974), i.e., CBV = CBFϕ, is critical for calculating dynamic CMRO2 from calibrated fMRI (Kida et al. 2007). The value of Φ was ∼0.15 at the peak of the hyperemic response (Fig. 2F), which is in agreement with prior animal studies (Jin and Kim 2008; Shen et al. 2008).

Difference between linear and non-linear relationships can be elucidated with a transformation between neural and imaging signals, using a transfer function. We applied convolution and fitting methods in an iterative way to find a transfer function relating the neural and imaging signals. The effectiveness of this process was characterized by the residual signal given by the difference between the raw and modeled signals (Supplementary Fig. 2). In all cases examined, the residual signal was lower than ±SD in measurement of each imaging signal (Fig. 2B–D, bottom traces). For a more thorough inspection for goodness of fit, we averaged the root mean square (RMS) of the residual signal for an entire data set and compared that with the average of measurement SD. In all cases examined, the average value of RMS residual signal was significantly lower than the average values of measurement SD. These results suggest a linear relationship between neural and imaging signals to provide universal transfer functions (Supplementary Fig. 3) applicable for both brief- and long-lasting stimuli. Results of linearity from the convolution analysis, therefore, provides a strong basis for applying Eq. 1 to calculate CMRO2 changes (using A = 0.5 (Englot et al. 2008; Schridde et al. 2008)), not only for steady-state stimuli but also for transient events. The calculated CMRO2 dynamics in Fig. 3 show experimental evidence of a linear dependency of oxidative energy demanded by neural events and its relationship with CBF. A detailed description of the SD calculation for CMRO2 (Supplementary Text B) shows that CBF has the most dominant influence and thus the larger SD of CBV has minimal effect on CMRO2 uncertainties.

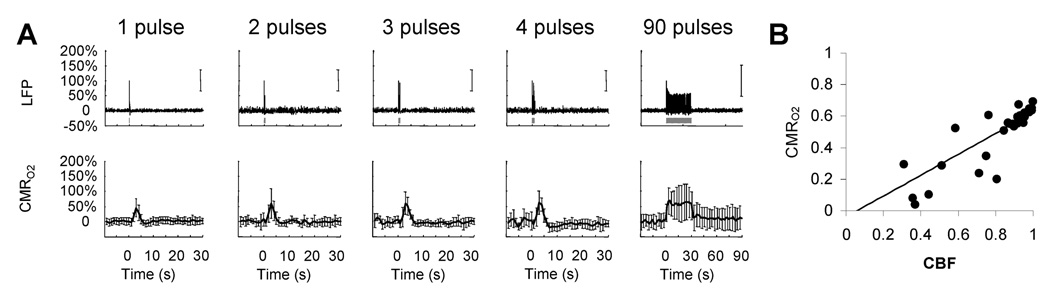
Fig 3.

Fig 3

Open in a new tab

(A) Measured LFP and calculated CMRO2 signals for transient to steady-state stimuli. Convolution analysis of the universal transfer functions (Supplementary Fig. 3) suggests linearity of the imaging signals with neural activity (Fig. 2E). (B) Coupling between changes in CBF and CMRO2 with a linear fit (slope=0.661, interception= −0.039, r2=0.81).

DISCUSSION

The goal here was to calculate CMRO2 transients using dynamic calibrated fMRI. We used a systematic convolution analysis to find a transfer function between neural activity and each imaging signal. Effectiveness of the impulse response function was portrayed by the residual signal. If fluctuations of the residual signal were smaller than the uncertainty or SD of the raw signal, the convolution process could produce a universal impulse response function that may be used to model each BOLD-related component successfully for all stimulus parameters (Supplementary Fig. 3). Then linearity between each imaging signal and neural activity will be demonstrated to render the respective transfer functions to be time invariant. While we did not discuss the MUA data (data not shown), the general trends were quite similar to the LFP data.

In α-chloralose anesthetized rats, multi-modal fMRI and electrophysiology data (Fig. 1) were evaluated to show that the respective transfer functions (of BOLD, CBV, CBF) generated by convolution with neural activity (LFP) are indeed linear and time invariant, for both brief- and long-lasting events (Fig. 2). It was possible, therefore, to extract a considerable part of the BOLD signal and assign it to dynamic CMRO2 changes, for stimuli ranging from milliseconds to minutes (Fig. 3). Because CMRO2 predicted at steady-state by calibrated fMRI had been validated in the past by independent measurements (Hyder et al. 2001), the CMRO2 data calculated here for 90 stimulus pulses withstands the same corroboration because ΔCMRO2 predicted in our prior and present studies are in good agreement. Given that the exact same transfer functions (of BOLD, CBV, CBF) can be used for modeling signals with few or many stimulus pulses, the CMRO2 data validation for longer stimuli can be extended to shorter stimuli, pending independent measurements. The characteristics of CMRO2 responses were similar to CBF changes, but were impacted by CBV dynamics. However because the Φ value (prescribed by Grubb’s law: CBV = CBFϕ) varied throughout the hyperemic response, we did not use a fixed Φ value for the CMRO2 calculation (Kida et al. 2007).

Results of a convolution are contingent on the choice of the input signal. The stimulus itself is often used as the input when neural activity measures are lacking. However the evoked neural response is preferred because the imaging signals are mechanistically linked to both pre- and post-synaptic events at the nerve terminal (Hyder 2008), but not the stimuli. Neural activity can be measured invasively (i.e., directly with microelectrodes) or non-invasively (i.e., indirectly with surface EEG). Extracellular recordings (LFP, MUA) typically represent activity from neuronal-glial ensembles in the microelectrode’s vicinity, integrating a wide bandwidth of signals spanning short distances in the cortex (µm to mm). Surface EEG covers a much larger area (mm to cm) and noninvasively represents slower rhythmic activities of post-synaptic currents. Because of the higher spatiotemporal resolution of extracellular recordings, LFP (or MUA) is an obvious candidate for the input signal because each evoked signal in response to a stimulus pulse can be incorporated into the convolution analysis, thereby sensitizing the subtle nuances of neural activities onto the modeled imaging signals. While evoked signals captured by EEG may appear to be similar in shape and form to LFP, there is greater chance of signal contamination due to noise injection from a variety of sources (e.g., limb movements, breathing, heart beat, etc.).

Because of technical limitations, it is difficult to measure neural and imaging signals from the same exact tissue volume. Therefore our convolution analysis of the multi-modal data acquired within a single (0.1–0.5 µL) compartment could be termed as a heuristic approach. However multi-compartment oxygen delivery models, which have detailed descriptions of the microvascular bed, take account of different sampling volumes (Buxton et al. 1998; Friston and Price 2001; Herman et al. 2006; Huppert et al. 2007) but lack multi-modal experimental data. Therefore future renditions of these oxygen transport models can make use of the multi-modal data availed from our study.

Consistent, yet peculiar, practices in convolution analysis are smoothing and integration of neural signals. The smoothing (or box-car) approach stems from lumping consecutive stimuli prior to convolution (e.g., (Glover 1999; Birn et al. 2001). This means that difference between one and two pulses would be double, one and three pulses would be triple, and so on, and it overlooks attenuation of early vs. late responses during long stimuli (90 pulses). The integration approach is related to interpolating between separate neural events to create the impression of a more robust neural signal (Ances et al. 2000; Norup Nielsen and Lauritzen 2001; Martin et al. 2006). This means that if there were four evoked responses to four stimulus pulses, by integrating between the signals there would be one pseudo box-car to represent the neural signal. For long stimulus durations, the smoothing/integration processes will have minimal impacts on the convolution analysis compared to the case if actual neural signals were used. However for shorter stimuli, where the goal is to include subtleties of the neural response variations from moment-to-moment, these practices could generate apparent non-linearity trends.

The same universal transfer function is applicable for event related paradigms and steady-state conditions (Fig. 1–Fig. 3) but also for stimuli with higher (6Hz) and lower (1.5Hz) frequencies (data not shown), which is in agreement with prior studies where linearity has been observed with variation of stimulation frequencies using different anesthetics (Matsuura and Kanno 2001; Nemoto et al. 2004). Although different anesthetized (or baseline) states produce different sensory-induced magnitude of responses (Smith et al. 2002; Maandag et al. 2007; Masamoto et al. 2007; Huttunen et al. 2008), coupling between changes in neural and imaging signals are well correlated. In agreement with our findings, prior studies using a similar stimulation paradigm but different anesthetized conditions have shown that neural activity is coupled with imaging signals using a variety of stimulus durations (Nemoto et al. 2004; Ureshi et al. 2004).

Prior studies demonstrate non-linearity trends with stimulus amplitude variations (Norup Nielsen and Lauritzen 2001; Devor et al. 2003; Jones et al. 2004; Nemoto et al. 2004; Sheth et al. 2004; Franceschini et al. 2008). Therefore our approach excluded amplitude variations given the narrow dynamic range for testing linearity relationships. Since the transfer functions are dependent on measured neural responses and each of the measured imaging signals, we expect that the predictions could be applied to other baseline situations, but limited to the somatosensory region.

In summary, we collected multi-modal data consisting of neural and imaging signals and applied convolution analysis to demonstrate linear relationships between neural and imaging signals to verify the time invariance of their transfer functions. Because these transfer functions could produce modeled signals for brief (1–4 pulses) and long (90 pulses) stimuli successfully, we extended calibrated fMRI for CMRO2 calculation, from transient events to steady-state. Preliminary results from our laboratory (data not shown) suggest that this approach may be extended for stimuli of varying frequencies and across the somatosensory cortex. However further studies are required to understand differences between cortical and subcortical regions where neural activity patterns and microvasculature are known to be significantly different (Ebner and Armstrong-James 1990).

Factors that affect the BOLD signal include hematocrit (Hyder et al. 2001). At steady-state, CMRO2 calculation by calibrated fMRI assumes that volume (or discharge) hematocrit is unchanged. Under steady-state conditions, this assumption has been partly confirmed by comparing kinetics of red blood cell and plasma volumes (Herman et al. 2008). However dynamically different velocities of red blood cell and plasma compartments may become exaggerated in capillaries which in turn could affect the flow (or tube) hematocrit (Pries et al. 1986). Therefore an important consideration for future studies is the involvement of transient hematocrit changes (Fahraeus 1929) on the dynamic BOLD contrast, which may account for some of the observed small imperfections in the residual signals.

Supplementary Material

Supp Fig S2
Supp Fig S3
Supp Mat
01

ACKNOWLEDGEMENTS

This work was supported by NIH grants (R01 MH-067528, R01 DC-003710, R01 NS-049307, P30 NS-52519).

REFERENCES

  1. Ances BM, Zarahn E, Greenberg JH, Detre JA. Coupling of neural activation to blood flow in the somatosensory cortex of rats is time-intensity separable, but not linear. J Cereb Blood Flow Metab. 2000;20:921–930. doi: 10.1097/00004647-200006000-00004. [DOI] [PubMed] [Google Scholar]
  2. Birn RM, Saad ZS, Bandettini PA. Spatial heterogeneity of the nonlinear dynamics in the FMRI BOLD response. Neuroimage. 2001;14:817–826. doi: 10.1006/nimg.2001.0873. [DOI] [PubMed] [Google Scholar]
  3. Buxton RB, Wong EC, Frank LR. Dynamics of blood flow and oxygenation changes during brain activation: the balloon model. Magn Reson Med. 1998;39:855–864. doi: 10.1002/mrm.1910390602. [DOI] [PubMed] [Google Scholar]
  4. Devor A, Dunn AK, Andermann ML, Ulbert I, Boas DA, Dale AM. Coupling of total hemoglobin concentration, oxygenation, and neural activity in rat somatosensory cortex. Neuron. 2003;39:353–359. doi: 10.1016/s0896-6273(03)00403-3. [DOI] [PubMed] [Google Scholar]
  5. Ebner FF, Armstrong-James MA. Intracortical processes regulating the integration of sensory information. Prog Brain Res. 1990;86:129–141. doi: 10.1016/s0079-6123(08)63172-6. [DOI] [PubMed] [Google Scholar]
  6. Englot DJ, Mishra AM, Mansuripur PK, Herman P, Hyder F, Blumenfeld H. Remote effects of focal hippocampal seizures on the rat neocortex. J Neurosci. 2008;28:9066–9081. doi: 10.1523/JNEUROSCI.2014-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Fahraeus R. The suspension stability of the blood. Physiol Rev. 1929;9:241–274. [Google Scholar]
  8. Franceschini MA, Nissila I, Wu W, Diamond SG, Bonmassar G, Boas DA. Coupling between somatosensory evoked potentials and hemodynamic response in the rat. Neuroimage. 2008;41:189–203. doi: 10.1016/j.neuroimage.2008.02.061. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Friston KJ, Price CJ. Dynamic representations and generative models of brain function. Brain Res Bull. 2001;54:275–285. doi: 10.1016/s0361-9230(00)00436-6. [DOI] [PubMed] [Google Scholar]
  10. Glover GH. Deconvolution of impulse response in event-related BOLD fMRI. Neuroimage. 1999;9:416–429. doi: 10.1006/nimg.1998.0419. [DOI] [PubMed] [Google Scholar]
  11. Grubb RL, Jr, Raichle ME, Eichling JO, Ter-Pogossian MM. The effects of changes in PaCO2 on cerebral blood volume, blood flow, and vascular mean transit time. Stroke. 1974;5:630–639. doi: 10.1161/01.str.5.5.630. [DOI] [PubMed] [Google Scholar]
  12. Hellweg FC, Schultz W, Creutzfeldt OD. Extracellular and intracellular recordings from cat's cortical whisker projection area: thalamocortical response transformation. J Neurophysiol. 1977;40:463–479. doi: 10.1152/jn.1977.40.3.463. [DOI] [PubMed] [Google Scholar]
  13. Herman P, Trubel HK, Hyder F. A multiparametric assessment of oxygen efflux from the brain. J Cereb Blood Flow Metab. 2006;26:79–91. doi: 10.1038/sj.jcbfm.9600165. [DOI] [PubMed] [Google Scholar]
  14. Herman P, Sanganahalli BG, Hyder F. Multimodal measurements of blood plasma and red blood cell volumes during functional brain activation. J Cereb Blood Flow Metab. 2008 doi: 10.1038/jcbfm.2008.100. [2008. Sep 3. Epub, ahead of print.]. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Huppert TJ, Allen MS, Benav H, Jones PB, Boas DA. A multicompartment vascular model for inferring baseline and functional changes in cerebral oxygen metabolism and arterial dilation. J Cereb Blood Flow Metab. 2007;27:1262–1279. doi: 10.1038/sj.jcbfm.9600435. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Huttunen JK, Grohn O, Penttonen M. Coupling between simultaneously recorded BOLD response and neuronal activity in the rat somatosensory cortex. Neuroimage. 2008;39:775–785. doi: 10.1016/j.neuroimage.2007.06.042. [DOI] [PubMed] [Google Scholar]
  17. Hyder F. Dynamic imaging of brain function. Methods Mol Biol. 2008;489:3–22. doi: 10.1007/978-1-59745-543-5_1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Hyder F, Rothman DL, Shulman RG. Total neuroenergetics support localized brain activity: implications for the interpretation of fMRI. Proc Natl Acad Sci U S A. 2002;99:10771–10776. doi: 10.1073/pnas.132272299. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Hyder F, Kida I, Behar KL, Kennan RP, Maciejewski PK, Rothman DL. Quantitative functional imaging of the brain: towards mapping neuronal activity by BOLD fMRI. NMR Biomed. 2001;14:413–431. doi: 10.1002/nbm.733. [DOI] [PubMed] [Google Scholar]
  20. Hyder F, Patel AB, Gjedde A, Rothman DL, Behar KL, Shulman RG. Neuronal-glial glucose oxidation and glutamatergic-GABAergic function. J Cereb Blood Flow Metab. 2006;26:865–877. doi: 10.1038/sj.jcbfm.9600263. [DOI] [PubMed] [Google Scholar]
  21. Ito H, Ibaraki M, Kanno I, Fukuda H, Miura S. Changes in cerebral blood flow and cerebral oxygen metabolism during neural activation measured by positron emission tomography: comparison with blood oxygenation level-dependent contrast measured by functional magnetic resonance imaging. J Cereb Blood Flow Metab. 2005;25:371–377. doi: 10.1038/sj.jcbfm.9600030. [DOI] [PubMed] [Google Scholar]
  22. Jin T, Kim SG. Cortical layer-dependent dynamic blood oxygenation, cerebral blood flow and cerebral blood volume responses during visual stimulation. Neuroimage. 2008 doi: 10.1016/j.neuroimage.2008.06.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Jones M, Hewson-Stoate N, Martindale J, Redgrave P, Mayhew J. Nonlinear coupling of neural activity and CBF in rodent barrel cortex. Neuroimage. 2004;22:956–965. doi: 10.1016/j.neuroimage.2004.02.007. [DOI] [PubMed] [Google Scholar]
  24. Kennan RP, Zhong J, Gore JC. Intravascular susceptibility contrast mechanisms in tissues. Magn Reson Med. 1994;31:9–21. doi: 10.1002/mrm.1910310103. [DOI] [PubMed] [Google Scholar]
  25. Kety SS, Schmidt CF. The nitrous oxide method for the quantitative determination of cerebral blood flow in man; theory, procedure and normal values. J Clin Invest. 1948;27:476–483. doi: 10.1172/JCI101994. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Kida I, Maciejewski PK, Hyder F. Dynamic imaging of perfusion and oxygenation by functional magnetic resonance imaging. J Cereb Blood Flow Metab. 2004;24:1369–1381. doi: 10.1097/01.WCB.0000141501.12558.9B. [DOI] [PubMed] [Google Scholar]
  27. Kida I, Rothman DL, Hyder F. Dynamics of changes in blood flow, volume, and oxygenation: implications for dynamic functional magnetic resonance imaging calibration. J Cereb Blood Flow Metab. 2007;27:690–696. doi: 10.1038/sj.jcbfm.9600409. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Kida I, Kennan RP, Rothman DL, Behar KL, Hyder F. High-resolution CMR(O2). mapping in rat cortex: a multiparametric approach to calibration of BOLD image contrast at 7 Tesla. J Cereb Blood Flow Metab. 2000;20:847–860. doi: 10.1097/00004647-200005000-00012. [DOI] [PubMed] [Google Scholar]
  29. Kudomi N, Hayashi T, Teramoto N, Watabe H, Kawachi N, Ohta Y, Kim KM, Iida H. Rapid quantitative measurement of CMRO(2) and CBF by dual administration of (15)O-labeled oxygen and water during a single PET scan-a validation study and error analysis in anesthetized monkeys. J Cereb Blood Flow Metab. 2005;25:1209–1224. doi: 10.1038/sj.jcbfm.9600118. [DOI] [PubMed] [Google Scholar]
  30. Maandag NJ, Coman D, Sanganahalli BG, Herman P, Smith AJ, Blumenfeld H, Shulman RG, Hyder F. Energetics of neuronal signaling and fMRI activity. Proc Natl Acad Sci U S A. 2007;104:20546–20551. doi: 10.1073/pnas.0709515104. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Martin C, Martindale J, Berwick J, Mayhew J. Investigating neural-hemodynamic coupling and the hemodynamic response function in the awake rat. Neuroimage. 2006;32:33–48. doi: 10.1016/j.neuroimage.2006.02.021. [DOI] [PubMed] [Google Scholar]
  32. Masamoto K, Kim T, Fukuda M, Wang P, Kim SG. Relationship between neural, vascular, and BOLD signals in isoflurane-anesthetized rat somatosensory cortex. Cereb Cortex. 2007;17:942–950. doi: 10.1093/cercor/bhl005. [DOI] [PubMed] [Google Scholar]
  33. Matsuura T, Kanno I. Quantitative and temporal relationship between local cerebral blood flow and neuronal activation induced by somatosensory stimulation in rats. Neurosci Res. 2001;40:281–290. doi: 10.1016/s0168-0102(01)00236-x. [DOI] [PubMed] [Google Scholar]
  34. Nemoto M, Sheth S, Guiou M, Pouratian N, Chen JW, Toga AW. Functional signal- and paradigm-dependent linear relationships between synaptic activity and hemodynamic responses in rat somatosensory cortex. J Neurosci. 2004;24:3850–3861. doi: 10.1523/JNEUROSCI.4870-03.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Norup Nielsen A, Lauritzen M. Coupling and uncoupling of activity-dependent increases of neuronal activity and blood flow in rat somatosensory cortex. J Physiol. 2001;533:773–785. doi: 10.1111/j.1469-7793.2001.00773.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Ogawa S, Lee TM, Barrere B. The sensitivity of magnetic resonance image signals of a rat brain to changes in the cerebral venous blood oxygenation. Magn Reson Med. 1993;29:205–210. doi: 10.1002/mrm.1910290208. [DOI] [PubMed] [Google Scholar]
  37. Pries AR, Ley K, Gaehtgens P. Generalization of the Fahraeus principle for microvessel networks. Am J Physiol. 1986;251:H1324–H1332. doi: 10.1152/ajpheart.1986.251.6.H1324. [DOI] [PubMed] [Google Scholar]
  38. Riera JJ, Schousboe A, Waagepetersen HS, Howarth C, Hyder F. The micro-architecture of the cerebral cortex: functional neuroimaging models and metabolism. Neuroimage. 2008;40:1436–1459. doi: 10.1016/j.neuroimage.2007.12.051. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Sanganahalli BG, Herman P, Hyder F. Frequency-dependent tactile responses in rat brain measured by functional MRI. NMR Biomed. 2008;21:410–416. doi: 10.1002/nbm.1259. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Schridde U, Khubchandani M, Motelow JE, Sanganahalli BG, Hyder F, Blumenfeld H. Negative BOLD with large increases in neuronal activity. Cereb Cortex. 2008;18:1814–1827. doi: 10.1093/cercor/bhm208. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Shen Q, Ren H, Duong TQ. CBF, BOLD, CBV, and CMRO(2) fMRI signal temporal dynamics at 500-msec resolution. J Magn Reson Imaging. 2008;27:599–606. doi: 10.1002/jmri.21203. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Sheth SA, Nemoto M, Guiou M, Walker M, Pouratian N, Toga AW. Linear and nonlinear relationships between neuronal activity, oxygen metabolism, and hemodynamic responses. Neuron. 2004;42:347–355. doi: 10.1016/s0896-6273(04)00221-1. [DOI] [PubMed] [Google Scholar]
  43. Smith AJ, Blumenfeld H, Behar KL, Rothman DL, Shulman RG, Hyder F. Cerebral energetics and spiking frequency: the neurophysiological basis of fMRI. Proc Natl Acad Sci U S A. 2002;99:10765–10770. doi: 10.1073/pnas.132272199. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Srinivasan R, Winter WR, Nunez PL. Source analysis of EEG oscillations using high-resolution EEG and MEG. Prog Brain Res. 2006;159:29–42. doi: 10.1016/S0079-6123(06)59003-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Ureshi M, Matsuura T, Kanno I. Stimulus frequency dependence of the linear relationship between local cerebral blood flow and field potential evoked by activation of rat somatosensory cortex. Neurosci Res. 2004;48:147–153. doi: 10.1016/j.neures.2003.10.014. [DOI] [PubMed] [Google Scholar]
  46. Vafaee MS, Gjedde A. Model of blood-brain transfer of oxygen explains nonlinear flow-metabolism coupling during stimulation of visual cortex. J Cereb Blood Flow Metab. 2000;20:747–754. doi: 10.1097/00004647-200004000-00012. [DOI] [PubMed] [Google Scholar]
  47. Zhang N, Zhu XH, Lei H, Ugurbil K, Chen W. Simplified methods for calculating cerebral metabolic rate of oxygen based on 17O magnetic resonance spectroscopic imaging measurement during a short 17O2 inhalation. J Cereb Blood Flow Metab. 2004;24:840–848. doi: 10.1097/01.WCB.0000125885.54676.82. [DOI] [PubMed] [Google Scholar]
  48. Zhu XH, Du F, Zhang N, Zhang Y, Lei H, Zhang X, Qiao H, Ugurbil K, Chen W. Advanced in vivo heteronuclear MRS approaches for studying brain bioenergetics driven by mitochondria. Methods Mol Biol. 2008;489:317–357. doi: 10.1007/978-1-59745-543-5_15. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supp Fig S2
NIHMS106247-supplement-Supp_Fig_S2.eps (2.3MB, eps)
Supp Fig S3
NIHMS106247-supplement-Supp_Fig_S3.eps (2.1MB, eps)
Supp Mat
NIHMS106247-supplement-Supp_Mat.doc (181.5KB, doc)
01
NIHMS106247-supplement-01.pdf (38.5KB, pdf)

RESOURCES