Rational Optimization and Imaging In Vivo of a Genetically Encoded Optical Voltage Reporter

Abstract

The hybrid voltage sensor (hVOS) combines membrane-targeted green fluorescent protein and the hydrophobic anion dipicrylamine (DPA) to provide a promising tool for optical recording of electrical activity from genetically defined populations of neurons. However, large fluorescence signals are obtained only at high DPA concentrations (>3 μm) that increase membrane capacitance to a level that suppresses neural activity. Here, we develop a quantitative model of the sensor to guide its optimization and achieved an approximate threefold increase in fractional fluorescence change at a lower DPA concentration of 2 μm. Using this optimized voltage reporter, we perform optical recordings of evoked activity in the Drosophila antennal lobe with millisecond temporal resolution but fail to detect action potentials, presumably because spike initiation and/or propagation are inhibited by the capacitive load added even at reduced DPA membrane densities. We evaluate strategies for potential further improvement of hVOS quantitatively and derive theoretical performance limits for optical voltage reporters in general.

Introduction

Understanding the organization and function of neural circuits would benefit greatly from experimental tools that permit detailed characterization of local circuit dynamics. The ideal technique would detect electrical signals in single cells with millisecond temporal resolution and sample densely a significant fraction of identified neurons in a given spatial region. Multielectrode arrays are generally capable of high spatial and temporal resolution (Kralik et al., 2001) but not high-density sampling, although progress is being made on this front (Buzsaki, 2004). Calcium imaging has high spatial resolution and can sample at very high densities (Ohki et al., 2005) but fundamentally suffers from low temporal resolution (Smetters et al., 1999), which can be partially ameliorated through deconvolution (Yaksi and Friedrich, 2006). Voltage-sensitive dye imaging meets all of these requirements in some tissue preparations (Salzberg et al., 1973; Obaid et al., 1999), but nonspecific labeling and phototoxicity are significant obstacles in most mammalian systems.

Genetically encoded optical voltage reporters provide a particularly elegant approach to this problem (Siegel and Isacoff, 1997; Miesenböck and Kevrekidis, 2005; Sjulson and Miesenböck, 2007). Most of these reporters combine nonconducting mutants of voltage-gated cation channels with derivatives of the green fluorescent protein (GFP). For example, FlaSh and its variants (Siegel and Isacoff, 1997; Guerrero et al., 2002) are based on the Shaker potassium channel, whereas SPARC (sodium channel protein-based activity reporting construct) (Ataka and Pieribone, 2002) is a mutant Na_v1.4 sodium channel, and VSFP1 (voltage-sensitive fluorescent protein 1) (Sakai et al., 2001) uses an isolated voltage sensor domain of the Kv2.1 potassium channel.

More recently, Chanda et al. (2005b) introduced a different type of genetically encoded optical voltage reporter. This design, termed hybrid voltage sensor (hVOS), combines a membrane targeted GFP, which serves as a fluorescence resonance energy transfer (FRET) donor, with a voltage-sensitive FRET acceptor dye, dipicrylamine (DPA), that quenches GFP fluorescence. DPA is a hydrophobic anion that partitions into the lipid bilayer and distributes between the inner and outer membrane leaflets according to membrane potential, thus quenching GFP fluorescence in a voltage-dependent manner. hVOS exhibits a high fractional fluorescence change (ΔF/F) of up to 34% per 100 mV, responds with submillisecond kinetics, and is the only genetically encoded optical voltage reporter that has been used to record neuronal action potentials evoked by current injection without averaging (Chanda et al., 2005b). However, like all voltage reporters that sense membrane potential with mobile probe charges, hVOS increases membrane capacitance significantly. In fact, hVOS only produces a substantial ΔF/F at high DPA concentrations (≥3 μm) that increase membrane capacitance to a level where synaptically evoked action potentials are inhibited.

In this paper, we develop a quantitative model of the GFP-DPA interaction. This model is used to guide the optimization of hVOS, yielding a ∼3-fold increase in ΔF/F at low DPA concentrations. The optimized hVOS is expressed in the Drosophila olfactory system, where optical recordings of electrical activity are performed with high temporal resolution. The model is then used to evaluate potential strategies for further improvements of hVOS and derive theoretical performance limits for optical voltage reporters in general.

Materials and Methods

Chemicals and solutions.

All reagents were obtained from Sigma-Aldrich, with the exception of DPA, which was obtained from LaboTest and was stored as a 20 mm stock solution in DMSO at −80°C. For whole-cell voltage-clamp experiments in HeLa and human embryonic kidney 293 (HEK293) cells, solutions were used that block most ionic conductances. The intracellular solution was composed of 130 mm N-methyl-d-glucamine (NMDG) gluconate, 10 mm NMDG chloride, 1 mm EGTA, and 10 mm HEPES, pH 7.4, raised to ∼340 mOsm with sucrose. The extracellular solution was composed of 130 mm NMDG gluconate, 10 mm NMDG chloride, 2 mm MgCl₂, and 10 mm HEPES, pH 7.2, raised to ∼320 mOsm with sucrose. Odor and suction electrode stimulation experiments in flies were performed using adult hemolymph with 2 mm Ca²⁺ (Wong et al., 2005).

Molecular biology.

Experiments in mammalian cells were performed using the pCI-neo expression vector (Promega), which contains the neomycin phosphotransferase gene, allowing selection of stable cell lines. All GFP variants were PCR amplified and inserted into pCI-neo using EcoRI and NotI restriction sites, verified by sequencing, and subcloned into the pUAST vector used for the generation of transgenic flies. PCR templates were either codon-optimized enhanced GFP (EGFP) (Clontech), codon-optimized EGFP-F [generously provided by B. Chanda (University of Wisconsin, Madison, WI) and F. Bezanilla (University of Chicago, Chicago, IL)], or Cerulean (generously provided by D. Piston, Vanderbilt University Medical Center, Nashville, TN) (for full sequences and details of plasmid construction, see supplemental material, available at www.jneurosci.org).

Cell culture and transfection.

HeLa and HEK293 cells were maintained in Advanced DMEM (Invitrogen) supplemented with 2.5% fetal bovine serum, 2 mm GlutaMAX (Invitrogen), 100 U/ml penicillin, and 100 μg/ml streptomycin at 37°C in 5% CO₂. For stable transfection, cells were grown to 50–70% confluency in six-well plates, transfected using FuGene 6 transfection reagent (Roche Diagnostics) according to the manufacturer instructions, and selected in 600 μg/ml G418. Stable transfectants were further screened for adequate GFP expression using epifluorescence microscopy.

Transgenic Drosophila.

EGFP constructs in the pUAST vector (Brand and Perrimon, 1993) were injected by BestGene, and transgenic flies were isolated using standard techniques. For antennal lobe expression, two copies of UAS-EGFP-ΔCAAX, UAS-PS-EGFP-ΔCAAX, or UAS-synapto-pHluorin (Miesenböck et al., 1998; Ng et al., 2002) were used with either one or two copies of OR83b-GAL4 (Ng et al., 2002).

Wide-field fluorometry.

Wide-field fluorometry was performed on a Carl Zeiss Axioskop microscope with a 40× water immersion objective [numerical aperture (NA), 0.8] using a Hamamatsu R1527P photomultiplier tube in a D-104 microscope photometer with a model 804 photomultiplier detection system (Photon Technology International). The output of the photometer was lowpass filtered at 1 kHz and sampled at 20 kHz, the same sampling rate as the electrophysiology channels. For voltage-clamp fluorometry, cells were illuminated by a Carl Zeiss HBO100 arc lamp, using either an EGFP or enhanced cyan fluorescent protein (ECFP) filter set (Chroma Technology). For suction electrode stimulation experiments, the sample was illuminated by a Carl Zeiss HBO100 W/2 arc lamp powered by a Carl Zeiss high-stability power supply, attenuated by a 50% neutral density filter. Despite the high stability power supply, power spectral estimates showed clear peaks at 120 and 240 Hz. These were subtracted off-line in Matlab 7 (Mathworks) using multitaper estimation of a spectral line in a colored noise background (Thomson, 1982).

Two-photon line scan fluorometry.

A previously described high-speed two-photon laser scanning microscope (Roorda et al., 2004) was modified to enable line scanning. Briefly, an analog circuit was created to provide a command signal to the mirror galvanometer controlling the beam position in the Y dimension, enabling rapid computer-controlled switching between frame scan and line scan modes. In either mode, the beam was scanned in the X dimension at a rate of 15.8 kHz, with 600 pixels in each scan line. Data were analyzed off-line with Matlab. For additional details, see the study by Sjulson (2007).

Voltage-clamp electrophysiology.

Voltage clamp was performed in the whole-cell patch configuration using an AxoClamp 2B amplifier with an HS-2A headstage (Molecular Devices). Amplifier outputs were lowpass filtered at 6–8 kHz and sampled at 20 kHz. Electrodes were pulled from 1.5 mm outer diameter (OD) patch pipette glass (World Precision Instruments) and fire-polished to an average tip resistance of 5–7 MΩ. Series resistance and capacitance compensation were not used, because currents were negligible at holding potentials. Data were acquired using pClamp 8.0 (Molecular Devices) and analyzed using Matlab 7 (Mathworks). Cells were held at −40 mV for 50 ms, stepped to the test potential for 50 ms, and then brought back to −40 mV for 50 ms. The test potential ranged from −100 to +50 mV in 10 mV increments.

Suction electrode stimulation.

The fly brain was removed from the head capsule, leaving the antennal nerve intact (Wong et al., 2005). Antennal nerve stimulation was performed using a suction electrode pulled from 1 mm OD borosilicate glass (A-M Systems). The pipette glass was pulled to a large-diameter opening (∼60 μm) and fire-polished to 30–36 μm. A suction electrode holder (A-M Systems) was used with Ag/AgCl wires, and electrical pulses were administered using an A365 constant current stimulation isolator (World Precision Instruments). For hVOS experiments, the stimulus consisted of 150 pulses of 1 ms duration and 100 μA amplitude with alternating polarity, whereas for synapto-pHluorin experiments, the stimulus consisted of trains of 10 1-ms pulses of alternating polarity at 3 ms intervals. The PH1 heated recording chamber (Warner Instruments) was heated to 25°C using a modified Series 800 thermoelectric cooler controller (Alpha Omega Instrument).

Results

Model of hVOS

A simple model (Fig. 1A) forms the basis for our rational optimization of hVOS. We assume that GFP and DPA molecules are uniformly randomly distributed along a planar lipid membrane. The distance DPA translocates between the two membrane leaflets is 30 Å, and each GFP chromophore is assumed to be held at a fixed distance y of 30 Å from the inner membrane leaflet (see below for a discussion of this assumption). At any given time, only a small fraction of GFP molecules is in the excited state; as a result, saturation of DPA-mediated quenching is negligible, and the statistical behavior of one GFP molecule over many trials is equivalent to that of many GFP molecules in one trial (for discussion, see supplemental material, available at www.jneurosci.org). Other parameters of the model include the calculated Förster distance R₀ of 37 Å for the GFP-DPA pair (Chanda et al., 2005b); at this distance, the efficiency of energy transfer is 50%. Effects of transition dipole orientation are neglected, including effects of rotational diffusion. Lateral diffusion is assumed to be negligible during the fluorescence lifetime of GFP, which is ∼2.9 ns (Swaminathan et al., 1997). An action potential is treated as a square pulse from V_m = −70 mV to V_m = +30 mV, and the proportion of DPA molecules in the inner versus outer membrane leaflets follows a Boltzmann distribution with parameters z ≈ −1 and V₀ ≈ −55 mV as follows:

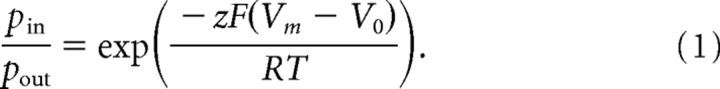In practice, z and V₀ vary between different cells and cell types, with reported values of z ranging from −0.63 in squid axon (Fernandez et al., 1983) to approximately −1 in Xenopus oocytes (Chanda et al., 2005a); in mouse myocytes, z is between −0.6 and −1 (DiFranco et al., 2007). The effect of this variation is discussed below (see Fig. 5).

Figure 1.

GFP fluorescence quenching at physiological DPA concentrations is mediated predominantly by interaction with the single closest DPA molecule. A, Diagram of GFP-DPA interaction model. B, Quenching of GFP is inefficient at physiologically tolerated DPA concentrations (gray background). At all concentrations tested, the majority of quenching is mediated by interaction with the single closest DPA molecule in the inner leaflet (green line), and almost all of these interactions occur at a distance of <1.5 R₀ (blue line). C, Quenching by the single closest DPA molecule accurately approximates ΔQ/Q over physiologically tolerated DPA concentrations (gray background). Almost all of these interactions occur at a distance of <1.5 R₀. D, The proportion of GFP molecules sufficiently close to a single DPA molecule to be eligible for quenching is low at physiological DPA concentrations. At +30 mV, less than half of the GFP molecules are within 1.5 R₀ of a DPA molecule (magenta line), whereas <14% have a DPA molecule inside R₀ (cyan line).

Figure 5.

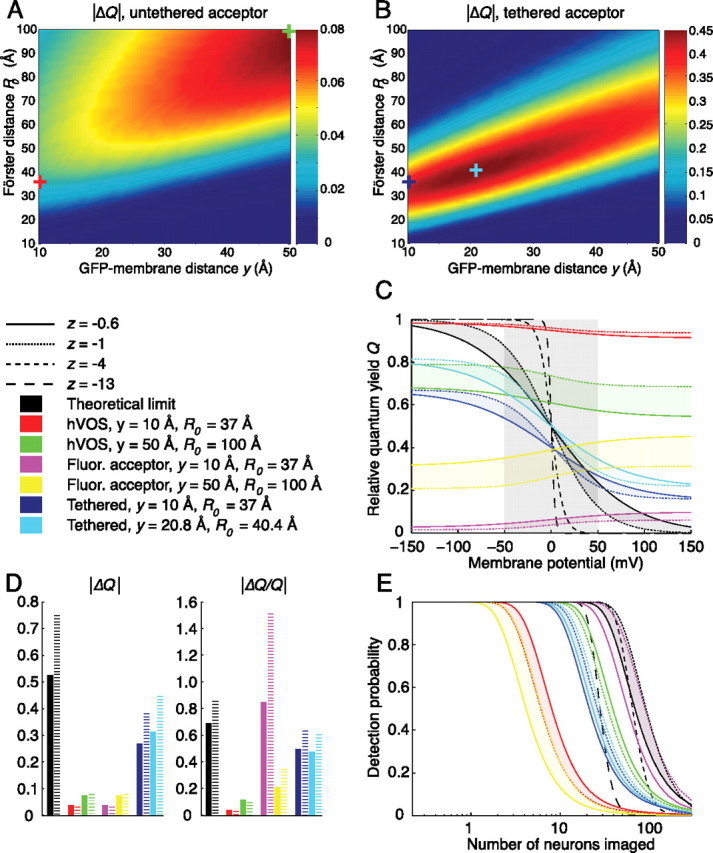
Theoretical performance limits and future optimization of hVOS. A, Predicted |ΔQ| per 100 mV for hVOS at an acceptor density of 1300 molecules/μm², |z| = 1. The DPA/EGFP-ΔCAAX pair (y = 10 Å; R₀ = 37 Å) yields a |ΔQ| of 0.03 (red cross), whereas the optimal values tested (y = 50 Å; R₀ = 100 Å) yield a |ΔQ| of 0.08 (green cross). Note that low values of y are optimal for realistic values of R₀, whereas large y is optimal for very large values of R₀. B, Predicted |ΔQ| per 100 mV for the tethered acceptor configuration, in which the FRET acceptor is covalently linked to the GFP, at a density of 1300 molecules/μm², |z| = 1. For tethered-DPA/EGFP-ΔCAAX (y = 10 Å; R₀ = 37 Å), the |ΔQ| is 0.38 (blue cross), whereas the optimal values tested (y = 20.8 Å; R₀ = 40.4 Å) yield a |ΔQ| of 0.48 (cyan cross). Note that optimal |ΔQ| is attained near experimentally realistic values of y and R₀. C, Relative quantum yield Q, as a function of V_m − V₀, at a maximum induced capacitance of 0.2 μF/cm². The shaded gray box denotes the 100 mV window producing maximum |ΔQ|. The theoretical limit of |ΔQ| increases significantly with increasing |z| (black lines). Values of Q calculated at |z| = 0.6 (solid line) and |z| = 1 (dotted line) represent bounds on optimal values of Q for monovalent anions such as DPA, whereas larger values of |z| (dashed lines) represent upper bounds on |ΔQ| for reporters with cooperative charge movement, such as GFP-ion channel fusions. The ideal hVOS (y = 50 Å; R₀ = 100 Å) yields a modestly increased |ΔQ| (green vs red), whereas the tethered acceptor configuration produces much larger increases in |ΔQ| (blue and cyan). The use of fluorescent FRET acceptor molecules does not change |ΔQ| (magenta and yellow). D, |ΔQ| and |ΔQ/Q| for the three configurations are compared with theoretical limits with |z| = 0.6 (solid black bars) or |z| = 1 (dashed black bars). The tethered acceptor configuration (blue and cyan bars) produces much larger |ΔQ| and |ΔQ/Q| than hVOS (green and red bars), whereas the fluorescent acceptor configuration (magenta and yellow bars) produces identical |ΔQ| with much larger |ΔQ/Q|. The |ΔQ/Q| for the fluorescent acceptor model is able to surpass the theoretical limit, because its fluorescence increases, rather than decreases, with depolarization (see Results for discussion). E, Probability of action potential detection as a function of number of neurons imaged. Performance of the theoretically optimal voltage reporter improves as |z| increases from 0.6 (solid black line) to 1 (dotted black line) and then deteriorates as |z| increases further (dashed black lines). Despite substantially lower |ΔQ| and |ΔQ/Q|, the ideal hVOS (y = 50 Å; R₀ = 100 Å) has better performance than the tethered acceptor model (green vs blue/cyan), caused by greater density of fluorophores, whereas the fluorescent acceptor model (y = 10 Å; R₀ = 37 Å) performs near the theoretical limit (magenta vs black).

Previous studies have determined the membrane density of DPA from capacitance measurements (Fernandez et al., 1983) and found that the relationship between nominal DPA concentration in the bath and DPA density in the membrane is complex, depending on the lipid composition of the bilayer, tissue penetration, and saturation effects at higher concentrations (Wang and Bruner, 1978). For our purposes, we assume that the DPA membrane density A_T is linearly proportional to the DPA bath concentration, with 8300 DPA molecules/μm² corresponding to 2 μm DPA in the bath, as calculated by Chanda et al. (2005b).

Efficiency of FRET between GFP (donor) and DPA (acceptor) is equal to 1 − Q, where Q is the relative quantum yield, or the ratio of donor fluorescence with acceptors present to donor fluorescence in the absence of acceptors. Q is a sixth-order nonlinear function of the distance, r, between GFP and DPA as follows:

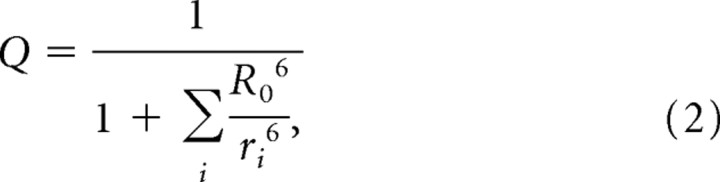where r_i denotes the distance between GFP and the ith DPA molecule, and R₀ denotes the Förster radius, the distance at which one DPA molecule will quench 50% of GFP fluorescence (i.e., Q = 0.5). Qualitatively, Q decreases rapidly as a DPA molecule moves inside of the Förster radius R₀, to a value of 0 (no fluorescence) when r ≪ R₀. Likewise, Q increases rapidly as a DPA molecule moves outside of the Förster radius, to a value of Q = 1 (full fluorescence) when r ≫ R₀, meaning that interactions with DPA molecules far beyond R₀ are not significant. Over realistic ranges of fluorophore excitation, Q is related to F, the total fluorescence collected, as follows:

where F_PM represents GFP fluorescence from the plasma membrane, and F_NS represents nonspecific background fluorescence, resulting from autofluorescence and intracellular GFP not associated with the plasma membrane. ΔQ/Q thus represents an upper bound on ΔF/F but becomes a valid estimate of ΔF/F when background fluorescence F_NS is small. Equations 2 and 3 together suggest that ΔF/F will be highest when ΔQ is large, namely, when the DPA molecules can be brought from a distance further than R₀ at hyperpolarized potentials to a distance closer than R₀ at depolarized potentials.

The primary drawback of hVOS is that ΔF/F is high only when the density of DPA in the membrane is higher than neurons will tolerate. To understand the requirement for high DPA densities, we compare two models: the “full model,” based on the study by Fung and Stryer (1978), takes all DPA molecules in both membrane leaflets into account, whereas the “reduced model” considers only the nearest DPA molecule in the inner membrane leaflet, provided that molecule is closer than a given distance R_max (supplemental material, available at www.jneurosci.org). The models yield similar values of Q for physiologically tolerated DPA concentrations, suggesting that the majority of GFP quenching is mediated by interactions with the single nearest DPA molecule, and the contribution of the nearest DPA molecule is very small if it is outside a radius of 1.5 R₀ (Fig. 1B).

We next examine ΔQ/Q for a 100 mV (−70 to +30 mV) step as a function of DPA membrane density (Fig. 1C). At tolerable DPA concentrations, estimates based on the closest DPA molecule approximate the full model well. At higher concentrations, however, the approximation becomes less accurate, suggesting that interactions with multiple DPA molecules in both membrane leaflets become significant. These predictions match experimental observations (Fig. 2D) relatively well, keeping in mind that ΔQ/Q represents an upper bound on ΔF/F.

Figure 2.

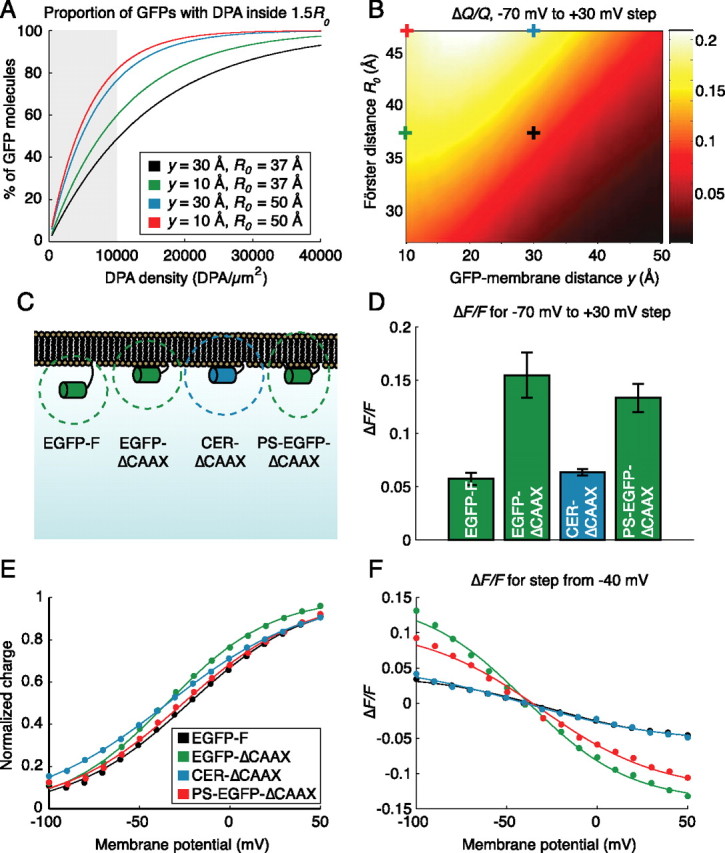
Model-based optimization of hVOS. A, Increasing the Förster distance, R₀, or decreasing the GFP-membrane distance, y, substantially increases the proportion of GFP molecules that encounter a DPA molecule inside a radius of 1.5 R₀ and are therefore eligible for quenching. B, Calculated values of ΔQ/Q for a 100 mV step from −70 to +30 mV at a density of 8300 DPA molecules/μm² (∼2 μm in bath). Modifying either R₀ or y can lead to significant changes in ΔQ/Q. C, Constructs tested. EGFP-F is the original hVOS construct, whereas EGFP-ΔCAAX is designed to minimize y. CER-ΔCAAX has a slightly increased R₀ (42 Å) relative to EGFP-ΔCAAX (37 Å), and PS-EGFP-ΔCAAX contains a palmitoylation site designed to orient the transition dipole moment toward the membrane. D, ΔF/F per 100 mV (−70 to +30 mV step) as measured by wide-field voltage-clamp fluorometry in 2 μm DPA. EGFP-ΔCAAX and PS-EGFP-ΔCAAX showed significant increases in ΔF/F (p < 0.01; two-tailed t test), whereas CER-ΔCAAX was not statistically different from EGFP-F (p = 0.24). E, Experimental measurements of charge translocation in four representative cells (solid dots) are well fit by Equation 1 (solid lines) with z = −0.80, V₀ = −23 mV (EGFP-F); z = −0.90, V₀ = −35 mV (EGFP-ΔCAAX); z = −0.68, V₀ = −34 mV (CER-ΔCAAX); and z = −0.78, V₀ = −26 mV (PS-EGFP-ΔCAAX). F, ΔF/F for voltage steps from a holding potential of −40 mV in 2 μm DPA. Experimental measurements (solid dots) are well fit by Equation 3 (solid lines) with values of z and V₀ determined by fitting Equation 1 (E).

Because the majority of quenching is mediated by interactions with DPA molecules inside a radius of 1.5 R₀, we determined the probability of a GFP having a DPA molecule inside a given distance R_max as follows:

where A_T is the density of DPA in the membrane, and y is the GFP-membrane distance (Fig. 1A). At +30 mV and DPA densities of <10,000 DPA/μm² (∼2.4 μm), less than half of the GFP molecules have a DPA molecule inside the “effective distance” of R_max = 1.5 R₀, and only 14% have a DPA molecule inside the Förster distance (Fig. 1D, magenta and cyan dashed lines). In other words, at depolarized potentials, when the GFP should be maximally quenched, only approximately half of the GFP molecules are close enough to a DPA molecule to be “eligible” for quenching, and only ∼10% of the GFP molecules have DPA molecules inside the Förster radius, where the probability of quenching is >50%. DPA labeling of the membrane at physiologically tolerated concentrations is thus so sparse that most GFP molecules are unlikely to interact with even a single DPA molecule.

Optimization of hVOS: model predictions

The main strategy for increasing ΔF/F at low DPA concentrations is to modify the GFP component of the sensor to enhance its interaction with DPA. This could be accomplished by decreasing the GFP-membrane distance to bring the GFP closer to the DPA molecules and by increasing the Förster distance so that more distant DPA molecules can quench the GFP more effectively.

The GFP-membrane distance, y, is determined by the length of the linker sequence between the C-terminal end of the GFP β-barrel and the prenylated cysteine residue in the CAAX box. Based on the crystal structure of GFP, the last six residues of GFP are unstructured, suggesting that the last residue of the β-barrel is glycine 232 (Ormö et al., 1996). Counting from this residue, the length of the linker in the EGFP-F construct used by Chanda et al. (2005b) is 27 residues. Estimating the average distance of the EGFP from the membrane is a surprisingly complex matter: detailed simulations and analytical calculations indicate that volume exclusion effects exert an entropic “stretching force,” which pulls the GFP further from the membrane than would be expected (Segall et al., 2006; Windisch et al., 2006). Windisch et al. (2006) performed a simulation of a 32 amino acid linker tethered between an infinite wall and a spherical bead of variable diameter. In their simulations, a ball of 30 Å diameter [reasonably close to GFP, which is ∼30 by 40 Å (Ormö et al., 1996; Yang et al., 1996)] leads to an average distance of ∼58 Å from the attachment point to the center of the ball. We thus estimate the mean distance from the GFP chromophore to the membrane (not the attachment point) to be ∼30 Å. If it were possible to place the GFP in direct contact with the membrane, shortening this length to ∼10 Å, the probability of at least one DPA molecule being closer than R_max = 1.5 R₀ (V_m = +30 mV; A_T = 10,000 DPA/μm²) increases from 0.49 to 0.60 (Fig. 2A), and the predicted ΔF/F from the full model also increases significantly (Fig. 2B).

Lengthening the Förster distance, R₀, is the second potential strategy for enhancing GFP-DPA interactions. Increasing R₀ from 37 to 50 Å has an effect similar to decreasing the GFP-membrane distance to ∼10 Å: the probability of a DPA molecule being closer than R_max = 1.5 R₀ increases to 0.76 (Fig. 2A), and the ΔF/F predicted from the full model increases substantially (Fig. 2B).

Optimization of hVOS: experimental results

Several EGFP constructs were used to test these predictions experimentally (Fig. 2C). In one construct, which we term EGFP-ΔCAAX (Roorda et al., 2004), the 31 C-terminal residues of EGFP-F (which include residues 233–238 of EGFP) were replaced with the last 10 C-terminal residues of h-ras, shortening the membrane linker from 27 residues to six. As shown in Figure 2D, the ΔF/F per 100 mV for EGFP-ΔCAAX is approximately threefold larger than that of the original EGFP-F at 2 μm DPA, a concentration that is sufficiently low for cultured rat hippocampal neurons to fire action potentials.

Increasing the Förster distance R₀, however, is less straightforward. R₀ is proportional to the sixth root of four parameters as follows:

These are φ_d, the fluorescence quantum yield of GFP; n, the refractive index of the medium; J, the overlap of the GFP emission spectrum with the DPA absorption spectrum; and κ², the relative orientation parameter. The fluorescence quantum yield of GFP and the refractive index of the medium are difficult, if not impossible, to change, leaving the spectral overlap J and the relative orientation κ².

Spectral overlap can be targeted by using GFP mutants with altered emission spectra. One such mutant, Cerulean, contains the ECFP mutations F64L/S65T/Y66W plus additional mutations S72A/Y145A/H148D, which shift the emission peak of the protein to 475 nm (Rizzo et al., 2004). Factoring in the changes in spectral overlap and slightly increased quantum yield of Cerulean (φ_d = 0.62) relative to EGFP (φ_d = 0.60), the estimated Förster distance is ∼42 Å rather than 37 Å. As shown in Figure 2B, this slight increase in R₀ is not predicted to yield a significant increase in ΔF/F. In fact, Cer-ΔCAAX, which contains Cerulean instead of EGFP in an otherwise identical construct, displayed significantly reduced voltage sensitivity relative to EGFP-ΔCAAX (Fig. 2D). The decreased ΔF/F likely reflects increased background signal and cellular autofluorescence in the ECFP emission band.

κ² depends on the relative orientations of the transition dipole moments of GFP and DPA. Under conditions of unconstrained rotational diffusion that is rapid relative to the fluorescence lifetime of GFP, κ² = 2/3. However, the membrane anchor of the GFP and the association of DPA with the polar phospholipid head groups most likely place constraints on the rotational mobility of these molecules, restricting the transition dipole moments to a preferred distribution of orientations. However, this distribution is unknown. As a result, the calculated value of 37 Å for the Förster distance is likely not correct, and it is not clear how much the performance of EGFP-ΔCAAX could be improved (or worsened) by manipulating the orientation of the transition dipole moment of GFP. Because κ² theoretically can range from 0 (orthogonal) to 4 (collinear), significant improvement may be possible.

Our attempt to force a change in relative orientation relied on Palmitoylation Site-EGFP-ΔCAAX [PS-EGFP-ΔCAAX, formerly known as dual-EGFP (Roorda et al., 2004)], which contains a C-terminal CAAX box identical to that of EGFP-ΔCAAX and, in addition, a palmitoylation site in an internal loop on the opposite end of the GFP β-barrel. Dual lipidation likely orients the transition dipole of PS-EGFP-ΔCAAX toward the membrane (Fig. 2C). As shown in Figure 2D, PS-EGFP-ΔCAAX exhibited a trend toward decreased ΔF/F compared with EGFP-ΔCAAX (p = 0.15; two-sided t test). Because absolute fluorescence intensity was also reduced (data not shown), the decreased ΔF/F may reflect poor folding or chromophore maturation of PS-EGFP-ΔCAAX at 37°C. Transition dipole orientation effects may be significant but difficult to isolate, because altering linker length alone has been shown to influence the distribution of dipole orientations (Windisch et al., 2006). It is therefore possible that transition dipole orientation effects play a role even in the increased voltage sensitivity of EGFP-ΔCAAX over EGFP-F.

How well do our experimental measurements fit the predictions of our model? In agreement with previous reports (Fernandez et al., 1983), measurements of charge translocation follow the Boltzmann distribution (Eq. 1) with values of z ranging from −0.6 to −0.9 and V₀ ranging from −25 to −35 mV (Fig. 2E). To model experimental measurements of ΔF/F, we first obtained values of z and V₀ for each cell and then predicted relative quantum yield Q using the full model (Eq. S7, available at www.jneurosci.org as supplemental material) with y = 30 Å for EGFP-F and y = 10 Å for all other constructs, and R₀ = 42 Å for CER-ΔCAAX and R₀ = 37 Å for all EGFP constructs. The agreement between model predictions of Q and experimental measurements of F, which are related via Equation 3, was good (Fig. 2F).

Photon flux and two-photon shot noise of EGFP-ΔCAAX

ΔF/F is not the only relevant parameter for assessing the performance of an optical voltage reporter (Sjulson and Miesenböck, 2007). The number of photons each cell can generate under realistic experimental conditions is equally important, because thick tissue imaging generally requires confocal or two-photon laser scanning microscopy for single-cell resolution, and measurements of fast events such as action potentials are often shot noise limited. To measure the photon flux generated by single cells expressing EGFP-ΔCAAX, two-photon voltage-clamp fluorometry was performed.

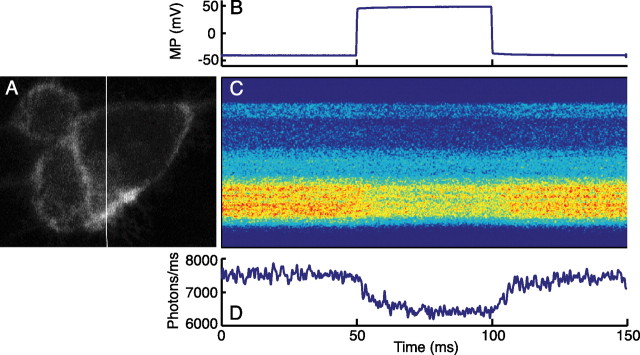
A representative cell shown in Figure 3 generates ∼7.5 × 10³ photons/ms, with a ΔF/F of ∼16%/100 mV in 2 μm DPA. If we approximate an action potential as a square pulse of 1 ms duration from −70 to +30 mV, we can calculate the probability of detecting an action potential at a given false positive probability (Sjulson and Miesenböck, 2007). Choosing a false positive probability P_FP of 10⁻⁵ ms, or one false positive action potential every 100 s, the probability of detecting a 16% drop in amplitude lasting 1 ms is essentially 100%.

Figure 3.

Two-photon voltage-clamp fluorometry yields a large signal with fast kinetics in 2 μm DPA. A, Single focal plane image of HEK293 cells. The white line shows the location of the line scan. B, Command potential for HEK293 cell in voltage-clamp experiment. C, Single trial line scan data show decreased fluorescence at depolarized potentials. D, Photon count estimate from line scan data. With photon counts in this range, shot noise would not be limiting for action potential recording. The slow on/off kinetics of the signal reflect a voltage-clamp artifact, because membrane capacitance was not compensated.

Optical imaging of electrical activity in vivo

To test the ability of optimized hVOS to report electrical activity in vivo, we generated transgenic Drosophila expressing EGFP-ΔCAAX and PS-EGFP-ΔCAAX under control of the UAS promoter (Brand and Perrimon, 1993). These flies were crossed with the OR83b-GAL4 line, which drives expression in ∼70% of all olfactory receptor neurons (ORNs) (Ng et al., 2002). Both EGFP constructs produced bright EGFP fluorescence in the antennal lobe that quenched after addition of DPA, consistent with membrane localization of the EGFP (data not shown). We then attempted two-photon imaging of ORN responses to odor stimulation in the antennal lobe but failed.

The failure to detect odor-evoked electrical activity in this setting could simply reflect the high temporal resolution of hVOS. Unlike synapto-pHluorin (spH) or calcium indicators, the fluorescence responses of which decay over hundreds of milliseconds (Ng et al., 2002; Reiff et al., 2005), the response of hVOS terminates approximately three orders of magnitude faster, making imaging difficult. Because processes from ∼30 individual ORNs are intertwined in each glomerulus at a subresolution scale, glomerular imaging necessarily records activity averaged across multiple neurons (Ng et al., 2002; Shang et al., 2007). If each neuron were firing at 100 Hz, and each action potential is 1 ms in duration, then each neuron would be maximally depolarized, at most, 10% of the time. Signal strength would be decreased by more than a factor of 10, from ∼15 to ∼1.5% ΔF/F, which is less than instrumentation noise.

To rectify this problem, we reasoned that activity could be imaged if action potentials were synchronized across ORNs. Accordingly, we combined wide-field fluorometry with direct electrical stimulation of the antennal nerve, which consists of ORN axons projecting to the antennal lobe, via a suction electrode. As shown in Figure 4A, voltage responses to depolarizing current pulses are detectable under these conditions. The response amplitudes, however, are <1% ΔF/F, which is small compared with what would be expected if action potentials were initiated in every ORN axon. To test whether the optical signal was caused by action potentials or passive spread of depolarization, flies were tested in the presence and absence of 10 μm tetrodotoxin (TTX), a voltage-gated sodium channel blocker. Although a significant passive response remained in the presence of TTX, the peak amplitude of the response to depolarizing pulses was significantly decreased in all flies tested (p < 0.01 in each fly; two-sided t test). The response to hyperpolarizing pulses interleaved with the depolarizing pulses was increased slightly (p < 0.05), as would be expected if TTX increased input resistance (Fig. 4B). Consistent with this interpretation, the response amplitudes of both depolarizing and hyperpolarizing pulses remained constant over the duration of control experiments performed in the absence of TTX (p = 0.30; two-sided t test).

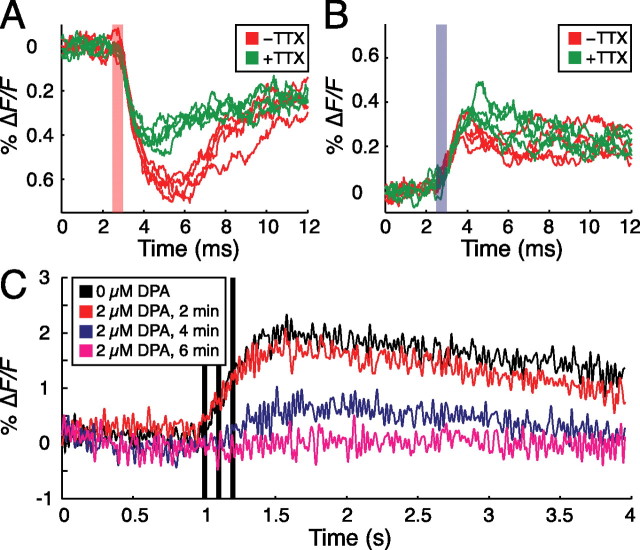
Figure 4.

Imaging fast electrical activity in the Drosophila antennal lobe in vivo. A, Fluorescence responses to depolarizing current pulse (red bar) in 2 μm DPA. Peak response amplitudes are significantly attenuated by 10 μm tetrodotoxin (green trace; p < 0.01). B, Fluorescence responses to hyperpolarizing current pulse (blue bar) in 2 μm DPA. Tetrodotoxin induces a small, but statistically significant, increase in response amplitude (p < 0.05). C, DPA (2 μm) eliminates the spH response to electrical stimulation (black bars), consistent with inhibition of action potentials.

Although the responses are clearly TTX responsive, they are inconsistent with synchronous action potential generation in a large fraction of ORN axons: the ΔF/F of the response is <10% of that expected for synchronized, full-scale action potentials, and the signal outlasts the duration of a single spike by several ms. Together, these characteristics suggest that antennal nerve stimulation caused subthreshold depolarizations rather than propagating action potentials in ORNs. The likely factor limiting action potential initiation or propagation is the increased capacitive load caused by the presence of 2 μm DPA. To test this notion, we performed wide-field fluorometry experiments with suction electrode stimulation of the antennal nerve, but using spH rather than the optimized hVOS as a read-out of ORN activity (Miesenböck et al., 1998; Ng et al., 2002; Shang et al., 2007). In the absence of DPA, spH responses were readily evoked (Fig. 4C, black line). After addition of 2 μm DPA to the bath, however, these responses gradually faded as the density of DPA in axonal membranes increased (Fig. 4C, colored lines). In the steady state, which was reached after several minutes in 2 μm DPA, all electrical excitability was suppressed. Because the off-rate of DPA is so low that DPA incorporation into membranes is practically irreversible (Fernandez et al., 1983; DiFranco et al., 2007), removal of DPA from the extracellular solution did not restore spH signals.

To determine whether DPA concentrations below 2 μm could yield a sufficient ΔF/F without inhibiting action potentials, we repeated the suction electrode stimulation experiments at several lower DPA concentrations. Concentrations below 750 nm DPA did not yield detectable signals, whereas signals recorded at 750 nm and 1 μm DPA exhibited amplitudes smaller than 0.5% and waveforms consistent with subthreshold depolarizations (data not shown).

Model predictions for further optimization of optical voltage reporters

To examine the plausibility of future strategies for optimization of optical voltage reporters, we first determined theoretical upper bounds for ΔQ and ΔQ/Q and compared them to predicted values for hVOS and other candidate voltage reporters. We then applied signal detection theory in a model of realistic photon shot noise to determine how these values translate to performance in optical detection of action potentials.

Theoretical limits on ΔQ and ΔQ/Q are based on constraints that are common to all genetically encoded optical voltage reporters. The first, and most fundamental, of these is thermal noise, which limits the voltage sensitivity of mobile probe charges, as described by the Boltzmann distribution (Eq. 1). For a DPA molecule, where |z| = 0.6–1 (Fernandez et al., 1983; Chanda et al., 2005a; DiFranco et al., 2007), the two voltage-dependent states of Equation 1 correspond to the molecule inhabiting the inner or outer membrane leaflet. At 25°C, a 100 mV change in membrane potential cannot drive all DPA molecules across the membrane; rather, at most, 53% (|z| = 0.6) (Fig. 5C, solid black line) to 75% (|z| = 1) (Fig. 5C, dotted black line) of all DPA molecules will translocate. Mobile probes with more than one elementary charge, such as gating charges in voltage-gated ion channels, have higher voltage sensitivity: with |z| = 4, over 99.9% of molecules switch states per 100 mV, whereas |z| = 13, the approximate value for the Shaker channel (Aggarwal and MacKinnon, 1996) leads to near-total charge translocation over 100 mV (Fig. 5C, dashed black lines).

The second element of our analysis is the efficiency of coupling between voltage-dependent state and fluorescence. The theoretically optimal voltage-sensitive fluorophore has perfect coupling between voltage-dependent state and fluorescence; in other words, there is full fluorescence in one voltage-dependent state and zero fluorescence in the other. Under these conditions, the relative quantum yield Q is the same as the probability of inhabiting the outer leaflet (Fig. 5C, black lines), with a maximum ΔQ per 100 mV ranging from 0.53 for |z| = 0.6 to 0.75 for |z| = 1 (Fig. 5D, black bars); this results in a ΔQ/Q per 100 mV ranging from 0.69 (|z| = 0.6) to 0.86 (|z| = 1) at maximal ΔQ (Fig. 5D, black bars) (for a discussion of maximizing ΔQ/Q, see supplemental material, available at www.jneurosci.org). There are parameter regimes in which these theoretical limits do not apply to the hVOS model, for example, at extremely high DPA densities where each GFP interacts with multiple DPA molecules. At physiologically tolerated DPA densities, however, the approximation is adequate.

In addition to being smaller than the theoretical limit, the maximal ΔQ for hVOS also depends on the density of FRET acceptors in the membrane. As a starting point, we therefore examined the maximum ΔQ per 100 mV when membrane capacitance is increased by 0.2 μF/cm², or ∼20%, which corresponds to a range from ∼1300 molecules/μm² (|z| = 1) to ∼2200 molecules/μm² (|z| = 0.6) (for details, see supplemental material, available at www.jneurosci.org as supplemental material). Using the full model of hVOS discussed above, we first analyzed the impact of varying the Förster distance R₀ and GFP-membrane distance y over wide ranges with |z| = 1 (Fig. 5A). Consistent with our experimental findings, ΔQ is larger at shorter GFP-membrane distances when R₀ = 37 Å. But, surprisingly, the model predicts, in the (hypothetical) regime of large Förster distances (i.e., for R₀ > ∼50 Å), an increase in ΔQ as the GFP moves further from the membrane (Fig. 5A). At first sight, this result seems counterintuitive, because the fractional change in distance resulting from DPA translocation is reduced as the GFP-membrane distance increases. However, this reduction is offset by decreased quenching from DPA molecules in the outer leaflet. Compared with the predicted ΔQ of the DPA/EGFP-ΔCAAX pair (R₀ = 37 Å; y = 10 Å), increasing R₀ and y in the optimal “long-range” hVOS analyzed in our model (R₀ = 100 Å; y = 50 Å) more than doubles the maximum ΔQ per 100 mV from 0.03 to 0.08 (Fig. 5A,D, red and green crosses), representing 4 and 10% of the theoretical limit, respectively. Unfortunately, experimental avenues for increasing the Förster distance into the long-range regime are not immediately apparent, at least for the DPA/EGFP pair studied here. Repeating these calculations for |z| = 0.6 yields surprisingly similar results (Fig. 5C,D), suggesting that characteristics of hVOS are relatively stable across the physiologic range of |z|, with increased DPA surface density and quenching efficiency offsetting the decreased voltage sensitivity resulting from decreasing |z|.

A second potential strategy for improving the performance of hVOS is the “fluorescent acceptor” configuration, in which fluorescent hydrophobic anions are used instead of DPA (Gonzalez and Tsien, 1995, 1997; Cacciatore et al., 1999; Tsien and Gonzalez, 2002; DiFranco et al., 2007), and the fluorescence signal is recorded from the acceptor instead of the donor. In analogy to Q, the relative quantum yield of the donor, we defined a quantity Q_A as follows:

where φ_a and φ_d are the fluorescence quantum yields of the acceptor and donor, respectively. Q_A represents the ratio of two probabilities: the probability of donor excitation leading to photon emission by an acceptor divided by the probability of that donor emitting a photon if no acceptors were present. Assuming φ_a and φ_d to be equal, we used the full hVOS model to calculate Q, with ΔQ_A equal to −ΔQ (Fig. 5A,D). Although the amplitudes of ΔQ_A and ΔQ are the same, Q_A is significantly decreased relative to Q, substantially increasing ΔQ_A/Q_A. With parameters of y = 10 Å and R₀ = 37 Å, the ΔQ_A/Q_A is increased to a range of 0.85–1.51 from a ΔQ/Q of 0.03–0.04 (Fig. 5D, magenta vs red bars). The acceptor fluorescence signal is capable of exceeding the theoretical ΔQ/Q limit of 0.86, because this limit holds only when fluorescence decreases with depolarization. Because acceptor fluorescence increases with depolarization, the thermal noise-limited ΔQ_A/Q_A for a 100 mV depolarizing pulse at maximal ΔQ_A is 6.0; the large ΔQ_A/Q_A of 1.51 (|z| = 1) attains ∼25% of this theoretical maximum (supplemental material, available at www.jneurosci.org). Consistent with these predictions, DiFranco et al. (2007) recently reported that combining EGFP-F with DiBAC₄(5), a fluorescent dye, rather than DPA, leads to a significant increase in ΔF/F. Although DiBAC₄(5) translocation is likely too slow to record neuronal action potentials, it may be sufficient for following slower phenomena such as muscle action potentials or rhythmic subthreshold activity.

Another benefit of fluorescent acceptor molecules is that a potentially significant fraction of any membrane-targeted GFP will be either cytoplasmic or associated with intracellular membranes, thereby contributing to background fluorescence. With fluorescent acceptors, only GFP molecules in close proximity to the acceptors (i.e., at the plasma membrane) contribute to the signal. The downsides of fluorescent acceptors include increased phototoxicity resulting from fluorescence excitation within the membrane bilayer and, for all fluorescent dyes reported to date (Cacciatore et al., 1999), membrane translocation speeds much slower than DPA.

A third potential strategy for increasing ΔQ is the “tethered acceptor” configuration, in which the local DPA concentration at each GFP is increased by covalently linking the FRET acceptor molecule to the GFP via a flexible “leash,” the length of which exceeds the thickness of the membrane. Several technologies for selective covalent attachment of exogenous molecules to specific proteins have been demonstrated (Griffin et al., 1998; Chen et al., 2005; Marks and Nolan, 2006), suggesting that this approach is feasible, at least in principle, although covalent association with the linker would likely slow translocation of the FRET acceptor. It is important to stress that the tethered acceptor model represents a special case of the general class of optical voltage reporters in which the fluorophore and mobile charges are physically associated in a single complex; this class also includes GFP-channel fusions. The tethered acceptor configuration represents the most direct analog of hVOS incorporating physical association; to evaluate the effects of this association, we extended our model to include a tethered acceptor using mathematical methods adapted from the study by Wolber and Hudson (1979) (supplemental Methods, available at www.jneurosci.org as supplemental material) and estimated the maximum ΔQ per 100 mV (Fig. 5B). The maximum ΔQ for the tethered-DPA/EGFP-ΔCAAX pair (R₀ = 37 Å; y = 10 Å) is increased to a range of 0.27–0.38, representing ∼51% of the theoretical limit; this is ∼10-fold greater than the untethered hVOS DPA/EGFP-ΔCAAX pair (Fig. 5D, blue vs red bars). The parameters yielding the largest ΔQ per 100 mV are R₀ = 40.4 Å, y = 20.8 Å, |z| = 1: ΔQ then increases to 0.31–0.45, or ∼60% of the theoretical limit (Fig. 5D, cyan bar). ΔQ/Q is similarly increased relative to optimized hVOS, but less so than for the fluorescent acceptor configuration (Fig. 5D).

Implications for optical detection of action potentials

Because the relationship between ΔQ, ΔQ/Q, and the ability to detect action potentials is complex, we calculated the effects of photon shot noise on the probability of action potential detection using realistic experimental values for excitation power and collection efficiency in high-speed two-photon microscopy. We modeled an action potential as a 100 mV step of 1 ms duration and, approximating Poisson photon statistics using the incomplete Gamma function, calculated the detection probability using the Neyman–Pearson criterion (Whalen, 1971) with a false detection probability of 10⁻³/ms, or one false spike per second, a less stringent criterion than used for our previous signal detection calculation (Fig. 3). A key factor in this analysis is the tolerated density of fluorophores at the membrane, which in turn depends on |z|, the number of mobile probe charges associated with each fluorophore. For example, a maximum tolerated membrane capacitance increase of ∼20% (0.2 μF/cm²) corresponds to ∼2200 fluorophores/μm² when |z| = 0.6, or ∼1300 fluorophores/μm² for |z| = 1. Because the maximum induced capacitance is linearly proportional to |z| (supplemental material, available at www.jneurosci.org), additional increases in |z| require proportional decreases in fluorophore density to maintain the same additional capacitive load. For example, |z| ≈ 13 for most fusions of GFP with voltage-gated cation channels (Aggarwal and MacKinnon, 1996), meaning that the sensor surface density would have to be further decreased 13-fold to ∼100 molecules/μm² to maintain a 20% capacitance increase. Therefore, increasing values of |z| require a tradeoff between decreased fluorophore density and increased voltage sensitivity.

We first examined the performance of the ideal voltage-sensitive fluorophore, that is, a fluorophore switched completely on and off by changes in voltage-dependent state, at densities causing a capacitance increase of 20%. Under typical imaging conditions (λ = 910 nm; NA = 0.8), with |z| ranging from 0.6 to 1, the number of fluorophore molecules inside the two-photon excitation volume ranges from ∼68 (|z| = 1) to ∼115 (|z| = 0.6) (Zipfel et al., 2003). Assuming pulsed excitation at a rate of 82 MHz, a pulse intensity capable of exciting 1% of all fluorophores in the excitation volume per pulse (a realistic value when limited by photobleaching), a quantum yield of 0.6, and a collection efficiency of 2%, ∼660–1100 photons/ms will be collected. It is therefore possible to collect ∼660–1100 photons/ms from one cell, ∼330–550 photons/ms per cell from two cells, and so forth, depending on the value of |z| in the range of 0.6–1. We thus plotted the probability of detecting an action potential as a function of the number of neurons sampled, noting that the differences between various values of |z| reflect a tradeoff between more photons collected at lower |z| and higher voltage sensitivity at higher |z|. Interestingly, the number of neurons that can be imaged is largest at |z| = 1 and decreases as |z| decreases to 0.6 (Fig. 5E, black interval); calculations performed at intermediate values of |z| indicate that this decrease is monotonic (data not shown), suggesting that the positive effect of increasing voltage sensitivity is dominant in the regime of |z| < 1. However, increasing |z| to 2 leads to performance nearly identical to |z| = 1, whereas additional increases of |z| to values of 4 or 13, in the range of voltage-gated cation channels, lead to significant decreases in performance (Fig. 5E, dashed black lines). The negative effects of decreasing photon counts thus dominate in the range of |z| > 2.

We next examined the performance of nonideal fluorophores, which yield a smaller ΔQ than the theoretical limit. The simplest of these is the tethered model, which represents the general class of reporters in which the fluorophore is physically associated with mobile probe charges. This class includes both the tethered acceptor configuration and GFP fusions with voltage-gated cation channels (Siegel and Isacoff, 1997; Sakai et al., 2001; Ataka and Pieribone, 2002; Guerrero et al., 2002). The tethered-DPA/EGFP-ΔCAAX pair (y = 10 Å; R₀ = 37 Å) and optimal tethered pair (y = 20.8 Å; R₀ = 40.4 Å) yield a ΔQ of 51 and 60% of the theoretical limit, respectively (Fig. 5D, blue and cyan bars). Although this ΔQ amounts to more than half of the theoretical limit in both cases, the number of neurons that can be recorded with a detection probability of 50% for the tethered-DPA/EGFP-ΔCAAX pair is only 29–31% of the number in the ideal case (Fig. 5E, blue vs black), or 31–34% of the ideal for the optimal tethered pair (Fig. 5E, cyan vs black). It is difficult to make precise predictions for GFP fusions with voltage-gated cation channels, because the mechanisms of fluorescence modulation are generally unclear. However, performance is likely to be poor given that the ΔF/F of all existing channel-based probes is at least one order of magnitude lower than the predicted ΔQ/Q of the tethered acceptor configuration (Siegel and Isacoff, 1997; Sakai et al., 2001; Ataka and Pieribone, 2002; Guerrero et al., 2002). This problem is compounded by the large number of gating charges associated with each fluorophore (Aggarwal and MacKinnon, 1996), which compromises performance even in the ideal case (Fig. 5E, dashed black lines). In practice, however, the performance of these probes may be improved by attaching several GFP molecules per channel tetramer or by exploiting the hysteretic dynamics of channel inactivation to generate fluorescence responses that outlast the duration of the action potential itself (Siegel and Isacoff, 1997). Neither of these strategies are considered in our analysis.

The analogous calculation for hVOS and the fluorescent acceptor configuration is more complex, because the ratio of fluorophores to probe charges is not fixed. For hVOS, if the inner membrane leaflet was filled to capacity with GFP molecules, there would be ∼10⁵ GFP molecules/μm², compared with 1300–2200 DPA molecules/μm². If 1% of these GFP molecules is excited by each laser pulse, there are ∼1000 excited GFP molecules/μm², rather than 13–22 in the tethered acceptor configuration. As a result, small changes in the signal are much easier to detect; despite exhibiting a ΔQ and ΔQ/Q several-fold lower than the tethered acceptor configuration (Fig. 5D), the performance of the ideal hVOS (R₀ = 100 Å; y = 50 Å) is better than that of the optimal tethered acceptor configuration (Fig. 5E, green vs cyan). Using realistic parameters for optimized hVOS (R₀ = 37 Å; y = 10 Å), however, enables observation of approximately fivefold fewer neurons than in the tethered acceptor configuration (Fig. 5E, red vs blue).

To evaluate the performance of the fluorescent acceptor configuration, we applied the additional constraint that the excitation probabilities of both the donor and acceptor are <1% with each laser pulse. Limiting excitation to low levels is particularly important with small molecule fluorophores residing in the membrane, because both photobleaching and phototoxicity are more severe than with membrane-peripheral GFP. The proportion of acceptors excited with each pulse is determined by the following equation:

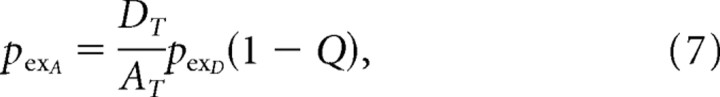where A_T and D_T represent the membrane density of acceptor and donor, respectively, whereas p_exA and p_exD represent excitation probabilities. For realistic values of A_T, D_T, and Q, p_exA is several-fold larger than p_exD, requiring that illumination intensity be decreased for p_exA to equal 0.01 in the resting membrane potential state. The fluorescent FRET acceptor configuration is therefore unable to take full advantage of the higher photon counts associated with hVOS; however, the much smaller background fluorescence at resting potentials more than compensates for this, producing performance nearly identical to the theoretical limit (Fig. 5E, magenta vs black).

Discussion

Increased membrane capacitance as fundamental limitation

Increased membrane capacitance is a significant underappreciated drawback of genetically encoded optical voltage reporters (Chanda et al., 2005b; Sjulson and Miesenböck, 2007). By using a rational model-based approach, we were able to optimize hVOS for lower DPA concentrations, thus enabling recordings of electrical activity in vivo. Nevertheless, increased membrane capacitance remains a limiting factor: our results demonstrate that even low concentrations of DPA in the bath are more poorly tolerated than previous studies suggest (Chanda et al., 2005b).

This apparent discrepancy is likely caused by large differences in the effective DPA concentrations in different preparations; these differences are only poorly reflected in the nominal DPA concentrations in the bath. In addition, different methods are used to elicit and detect action potentials, making direct comparisons difficult. For instance, Chanda et al. (2005b) reported that cultured neurons fire action potentials in 3 μm DPA, but this result was obtained by measurement at the site of current injection. The absence of detectable spH responses at ORN terminals, which lie at considerable distance from the site of antennal nerve stimulation, may thus reflect a failure of action potential propagation rather than initiation. Chanda et al. (2005b) also reported that population spikes in the hippocampal CA1 region have a normal waveform in 4 μm DPA; however, their preparation was a 350-μm-thick tissue slice containing a significant amount of myelin, which is expected to act as a sink for hydrophobic DPA molecules and/or slow their penetration into the slice. The fly brain, in contrast, contains no myelin and is only ∼250 μm wide, with the antennal nerve lying entirely superficial. As a result, the effective concentration of DPA at the membranes of neurons in the hippocampal slice is likely much lower than in the fly antennal nerve, although the bath concentration is higher.

It is worth noting that it has not been conclusively demonstrated that the deleterious effects of DPA are mediated solely by increased membrane capacitance. Adsorption and desorption of DPA carries some current across the membrane and would be expected to influence membrane potential, although Chanda et al. (2005b) estimate the effect to be <2 mV at 5 μm DPA, consistent with the extremely low off rate of DPA (Fernandez et al., 1983; DiFranco et al., 2007). DPA is also protonatable, meaning that it can act as a protonophore with some ability to deplete mitochondrial pH gradients, but this effect is likely negligible at the concentrations used here, because of the low pK_a of 2.66 (Gaboriaud, 1966). Finally, it is possible that DPA exhibits additional unrelated pharmacologic effects that are more severe in flies. These issues could be addressed by future studies examining the effects of other hydrophobic anions, such as tetraphenylborate (Szabo, 1977), on excitability.

More importantly, any source of increased membrane capacitance will necessarily influence important physiological parameters, and the mere fact that action potentials are not inhibited does not guarantee the presence of normal physiological function. For example, it is well known that membrane capacitance is a primary factor limiting axonal propagation speed, and mammalian brain evolution has devoted significant resources to minimizing conduction delays within the brain, including both myelination and scaling relationships dictating disproportionately large axonal diameters with increasing brain size (Harrison et al., 2002). Additionally, increasing membrane capacitance increases the membrane time constant proportionally, and the relationship between the membrane time constant and mean interspike interval is what determines whether a neuron acts as an “integrator” or “coincidence detector” (König et al., 1996). Intact neural circuits encode information and exhibit correlated activity on a timescale of 10–30 ms (Victor and Purpura, 1996; Harris et al., 2003), which matches the membrane time constant, presumed EPSP width (Spruston and Johnston, 1992), and period of the gamma oscillation, leading some authors to speculate that the membrane time constant and EPSP width are the rate-limiting factors in cognitive processing (Harris, 2005). Future studies are needed to explore the effects of increasing conduction delays and membrane time constants, however subtly; in our view, it would be optimistic to assume that large increases would be well tolerated.

Capacitive silencing of neuronal activity

On the flip side, our demonstration that even modest capacitance increases inhibit action potential generation and/or propagation suggests a new general strategy for reversible genetically targeted silencing of neuronal activity. Although most existing approaches rely on the cell type-specific expression of potassium conductances that clamp the neuronal membrane potential at hyperpolarized levels (Baines et al., 2001; Nitabach et al., 2002), these manipulations can alter intracellular ion concentrations, leading to cell death (Nadeau et al., 2000). The expression of nonconducting channels (Perozo et al., 1993) or isolated voltage-sensing modules (Murata et al., 2005) that suppress excitation by virtue of their gating charges promises to circumvent this problem. However, it is possible that increasing membrane capacitance on gene regulation timescales would enable homeostatic upregulation of endogenous conductances to partially offset the silencing effect.

Imaging technology as a limiting factor

Imaging fast events such as action potentials in intact tissue is challenging for two reasons (Sjulson and Miesenböck, 2007). First, single-cell resolution in thick, scattering tissue typically requires laser scanning microscopy. Because the laser is scanned across the sample, it is technically difficult to achieve sufficiently high sampling rates, although progress has recently been made with optical random access in two (Iyer et al., 2006; Salome et al., 2006) and three (Reddy and Saggau, 2005) dimensions. Depth-resolved wide-field multiphoton microscopy may also become a reality (Oron et al., 2005).

A more serious limitation of laser scanning microscopy is that the number of photons collected is low, further compounding the capacitance-limited low membrane density of fluorophores. Fortunately, collection efficiency can be improved significantly through the use of high NA objectives, mirror-based objectives (Vucinic et al., 2006), or collection of light through the condenser (Mainen et al., 1999; Roorda et al., 2004). The use of fluorophores with higher two-photon cross sections, such as quantum dots (Pu et al., 2006), would also significantly improve the situation. The results in Figure 5E are not fundamental but based on collection efficiency and fluorophore characteristics: increases in imaging efficiency will proportionally increase the number of neurons that can be imaged. Likewise, using potentiometric dyes that do not increase membrane capacitance enables higher fluorophore membrane densities and signal-to-noise ratios (Fisher et al., 2008). Nevertheless, imaging technology currently remains a significant limiting factor in detecting action potentials and other fast electrical activity in the intact brain.

Limitations of our modeling approach

Our models make two major simplifications: first, we ignore orientational effects of the molecules, including the fact that relative orientation, and therefore R₀, varies as a function of lateral distance along the membrane. However, one modeling study has shown that this may not be too serious an issue, because orientational effects are generally small in FRET between planes of a bilayer (Domanov and Gorbenko, 2002). A more significant assumption is that the GFP and DPA molecules are uniformly distributed in the membrane. This is almost certainly not true; biological membranes possess significant lateral heterogeneity, and both DPA molecules and GFP prenyl anchors likely partition preferentially into certain sections of the membrane (Zacharias et al., 2002). Our experimental measurements of ΔF/F also necessarily include contributions from GFP not localized to the plasma membrane. The application of total internal reflection fluorescence microscopy in future studies could allow selective measurement of plasma membrane fluorescence (Thompson et al., 1981), enabling direct experimental measurement of relative quantum yield Q. Despite these qualifications, our model produced predictions that allowed us to optimize hVOS and image fast electrical activity in the fly olfactory system. In addition, it has generated testable predictions regarding possible strategies for the future improvement of hVOS.

Our signal detection analysis in Figure 5 addresses only the specific problem of multisite recording of action potentials from the intact brain. This is not necessarily the only, or even the most important, potential application of genetically encoded optical voltage reporters. For example, the ability to target expression to specific cell classes may provide a powerful tool for studying the origins, mechanisms, and modulation of rhythmic activity in the cortex of intact animals, not unlike a local field potential recording, but with genetic resolution. Additionally, FRET acceptor dyes can be chosen with slower translocation time constants that match the time scales of the phenomena being studied, effectively reducing the capacitive load for fast electrical activity. Alternatively, the low phototoxicity relative to voltage-sensitive dyes may be advantageous in studies of dendritic integration where averaging across many trials is possible. These represent areas in which this or other optimized versions of hVOS are likely to make significant contributions in the near future.