Skip to main content
PMC home page
Proceedings of the National Academy of Sciences of the United States of America logoLink to Proceedings of the National Academy of Sciences of the United States of America
. 2000 Sep 12;97(20):11050–11055. doi: 10.1073/pnas.200033797

Measuring the thickness of the human cerebral cortex from magnetic resonance images

Bruce Fischl 1, Anders M Dale 1,*
PMCID: PMC27146  PMID: 10984517

Abstract

Accurate and automated methods for measuring the thickness of human cerebral cortex could provide powerful tools for diagnosing and studying a variety of neurodegenerative and psychiatric disorders. Manual methods for estimating cortical thickness from neuroimaging data are labor intensive, requiring several days of effort by a trained anatomist. Furthermore, the highly folded nature of the cortex is problematic for manual techniques, frequently resulting in measurement errors in regions in which the cortical surface is not perpendicular to any of the cardinal axes. As a consequence, it has been impractical to obtain accurate thickness estimates for the entire cortex in individual subjects, or group statistics for patient or control populations. Here, we present an automated method for accurately measuring the thickness of the cerebral cortex across the entire brain and for generating cross-subject statistics in a coordinate system based on cortical anatomy. The intersubject standard deviation of the thickness measures is shown to be less than 0.5 mm, implying the ability to detect focal atrophy in small populations or even individual subjects. The reliability and accuracy of this new method are assessed by within-subject test–retest studies, as well as by comparison of cross-subject regional thickness measures with published values.

Keywords: atrophy, morphometry, Huntington's, Alzheimer's, schizophrenia

The human cerebral cortex is a highly folded sheet of neurons the thickness of which varies between 1 and 4.5 mm, with an overall average of approximately 2.5 mm (1–3). Regional variations in the cortical thickness can be quite large. For example, Brodmann's area 3 on the posterior bank of the central sulcus is among the thinnest of cortical regions, with an average thickness of less than 2 mm, whereas Brodmann's area 4 on the anterior bank is one of the thickest regions, frequently exceeding 4 mm. Interestingly, the distribution of the thickness is not uniform by layer, nor is the variation in the thickness of the cortical layers proportional to the variation in the total thickness.

The thickness of the cortex is of great interest in both normal development as well as a wide variety of neurodegenerative and psychiatric disorders. Changes in the gray matter that makes up the cortical sheet are manifested in normal aging (4, 5), Alzheimer's disease (4–10) and other dementias (11), Huntington's disease (12, 13), corticobasal degeneration (14), amyotrophic lateral sclerosis (15), as well as schizophrenia (16–19). The cortical thinning is frequently regionally specific, and the progress of the atrophy can therefore reveal much about the evolution and causative factors of a disease. Moreover, longitudinal studies of cortical atrophy are potentially of great use in assessing the efficacy of a wide variety of treatments.

To date, few studies have been completed comparing the thickness of the cortical ribbon in large patient- and age-matched, normal subject populations. In large part, the dearth of studies has been because of the complexity of the process of accurately measuring the cortical thickness on the submillimeter scale. For example, a complete labeling of a human brain from a high-resolution T1-weighted MRI scan can take a trained anatomist days to complete, and even this labor-intensive procedure allows only the measurement of cortical volume, not cortical thickness. This difficulty arises because the thickness of the cortex is a property that can only be properly measured if the location and orientation of the gray/white and pial surfaces both are known. In spatially localized cases in which the image plane is orthogonal to the cortical surface throughout a region of interest, the measurement of thickness can be accomplished from slice data (20). More typically, however, cortical thickness measurements are obtained for spatially localized regions during postmortem studies.

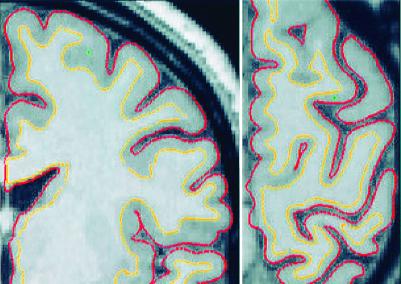
The difficulty of properly measuring the thickness of the cortex without explicit representations of both the gray/white and pial surfaces is illustrated in Fig. 1, which shows coronal and axial slices through a T1-weighted MRI volume. Measuring the thickness from the coronal slice at the point indicated by the green cross would result in an estimate in excess of 1 cm. Examining the other view reveals that this measurement is a dramatic overestimation, resulting from the fact that the surface is locally parallel to the coronal slice. The use of multiple orthogonal views in this fashion can reduce the degree of inaccuracy, as one can choose the slice plane that is closest to being perpendicular to the surface. Nevertheless, measuring the thickness of the cortex from slice data will always result in overestimates, unless the cortical surface happens to be orthogonal to one of the viewing planes. In general, the true value of the thickness over the entire cortex cannot accurately be determined in this way, as the cortex contains many folds that are not aligned with any of the cardinal axes along which slice data are typically viewed. Thus, although thickness and/or volume measurements derived from slice data may suffice to detect gross changes in the cortex, they do not provide the submillimeter precision necessary to characterize the location and progression of subtle cortical atrophy. This level of accuracy is of particular importance, as detecting regionally specific cortical atrophy associated with the early stages of diseases such as Alzheimer's or Huntington's requires this type of precision, and accurately characterizing the early stages of degeneration may be critical to a deeper understanding of the causative factors in the disorders.

Figure 1.

Figure 1

Open in a new tab

Coronal (Left) and horizontal (Right) slices of the left hemisphere with gray/white (yellow) and pial (red) surfaces overlaid. The green crosses indicate a point at which using the coronal view only would result in a dramatic overestimation of the thickness of the cortex.

To address this need, we have developed a technique for automatically measuring the thickness of the gray matter of the human cerebral cortex. The measurement of the thickness is enabled by a procedure for generating highly accurate models of both the gray/white and pial surfaces. The distance between these two surfaces then gives the thickness of the cortical gray matter at any point. In conjunction with automated surface reconstruction (21–24) and high-resolution surface-averaging techniques (25), the measurement of cortical thickness with submillimeter accuracy facilitates the use of powerful statistical methods in the investigation of neurodegeneration and recovery.

Methods

Because of limitations on the resolution of MRI, it is difficult to directly compute the location of the pial surface (21). Instead, we construct an estimate of the gray/white boundary by classifying all white matter voxels in an MRI volume. The surface of the connected white matter voxels then is refined to obtain subvoxel accuracy in the representation of the gray/white boundary, and subsequently deformed outward to find the pial surface, as described in ref. 22.

The basic technique described has been extended in a number of ways and is similar in spirit to many deformable template algorithms in the computer vision and medical image processing literature (26–33). First, we use a multiscale analysis, similar to the type described in ref. 34, to make the detection of the gray/white and pial boundaries less sensitive to noise. In addition, because the cortex itself is smooth at the spatial scale of a few millimeters (except in rare pathologies), we constrain the surface representation to be smooth in a similar manner. The machine vision and image processing research communities have developed many techniques for constraining an evolving curve or surface to be smooth, typically involving some form of minimization of the mean or the Gaussian curvature (27, 35, 36). This type of smoothness constraint is problematic for generating a surface that faithfully reflects the gray/white or pial surface, as there are highly curved regions at the fundi of sulci and the crowns of gyri. A smoothness constraint that seeks to minimize curvature will therefore result in surfaces that are inaccurate in these regions.

To reduce this source of error, we compute the curvature of patches of the surface, then alter the surface representation so that the local surface has this curvature at the finest (i.e., millimeter) scale as well. This technique produces a surface that is second-order smooth (i.e., has a continuous second derivative), in contrast to the curvature-reduction techniques, which attempt to generate a surface whose second derivative is zero. In localized regions in which the pial surface cannot be directly resolved, the smoothness constraint allows the surface to be accurately extended into ambiguous areas. In more extensive such regions, a self-intersection constraint placed on the evolving surface causes it to settle at approximately the midpoint of the sulcus.†

It is important to note that, given a smooth underlying (true) cortical surface, the accuracy of this procedure is not directly limited by the voxel dimensions of the MRI data used to generate the cortical model. Assuming that the radius of curvature of the surface as well as the thickness of the tissue classes is greater than the size of the voxels, and assuming sufficient contrast-to-noise exists between the tissue classes, interpolation can be used to achieve subvoxel accuracy.‡

The surface deformation is implemented by using gradient descent with momentum (37). To prevent the surface from intersecting itself, a spatial lookup table in conjunction with fast triangle-triangle intersection code (38) is used, resulting in computational complexity that is linear in the number of vertices in the surface representation. Specifically, if the movement of the kth vertex results in an intersection, the size of the movement of that vertex is reduced until the self-intersection no longer occurs. The entire procedure is carried out in a multiscale manner, with the target intensity calculation by using derivative information computed from images smoothed with a Gaussian kernel of a given standard deviation. The numerical integration continues until the error functional asymptotes. The standard deviation of the smoothing kernel then is decreased, the target intensities are recomputed, and the integration is repeated until a predefined minimum scale is reached.

The numerical integration was carried out at four decreasing scales for the smoothing kernel (σ = 2 mm, σ = 1 mm, σ = 0.5 mm, and σ = 0.25 mm), with the integration proceeding at each scale until the error functional decreased by less than 1%. The resulting procedure required approximately 5 h to generate the gray/white and pial surfaces and thickness measurements on a 550 MHz Pentium III processor, with the majority of the computational complexity attributable to the self-intersection checking. Both the self-intersection code and the actual measurement of the cortical thickness use a spatial lookup table to obtain O(n) computational complexity, as opposed to the O(n2) that would be required to search the entire surface for self-intersection, or to find the point on one surface that is closest to a given point on the other. The thickness is computed as the average of this distance measured from each surface to the other.

Results

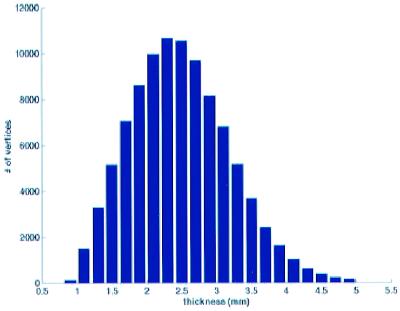
To validate the thickness measurements, we computed the thickness of the cortical gray matter for the left hemisphere of 30 subjects (17 male and 13 female, ages 20–37 years old). Two- and three-dimensional examples of the results of the deformation process are given in Figs. 1 and 2, respectively, whereas Fig. 3 gives a histogram of the distribution of thicknesses across the cortical surface of a representative subject. Note that the vast majority of the thickness measurements (>99%) fall within the known bounds of 1 and 4.5 mm.

Figure 2.

Figure 2

Open in a new tab

Lateral views of the gray/white (Left), pial (Center), and inflated (Right) surface representations with cortical thickness measurements overlaid in a red/green color scale.

Figure 3.

Figure 3

Open in a new tab

Histogram of thickness values in cortical regions of the subject shown in Fig. 2. More than 99% of the surface is between 1- and 4.5-mm thick.

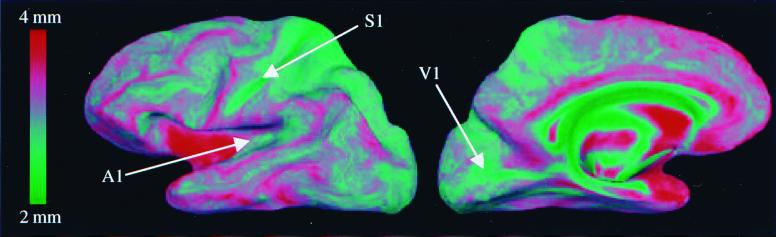
The individual thickness estimates from the results of this analysis then were combined across the 30 subjects by using a high-resolution, surface-based averaging technique that aligns cortical folding patterns (25). The results of this procedure, shown in Fig. 4, reveal that, consistent with published findings (2), the crowns of gyri are thicker than the fundi of sulci, and that sensory areas are among the thinnest in the cortex. More specifically, we find that gyral regions have an average thickness of 2.7 ± 0.3 mm, versus 2.2 ± 0.3 mm for sulcal regions.§

Figure 4.

Figure 4

Open in a new tab

Average cortical thickness across 30 subjects, with primary auditory (A1), somatosensory (S1), and visual (V1) cortices indicated by the white arrows.

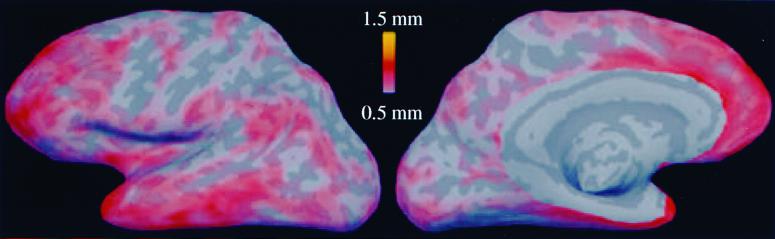
An illustration of the variability of these results across the cortex is given in Fig. 5, which shows the spatial distribution of the cross-subject standard deviations of the thickness measurements. As can be seen, the measurements are quite consistent across subjects, with a standard deviation of less than 0.5 mm over much of the cortex, with a mean of 0.54 mm. Applying a small surface-based Gaussian blurring kernel (σ = 7 mm) reduced the standard deviation to 0.32 mm, indicating that the autocorrelation of the noise falls off quite sharply with distance. One further point to note is that the majority of the variance is localized in association areas: anterior, ventral, temporal, and prefrontal cortices, which are among the thickest of cortical regions.

Figure 5.

Figure 5

Open in a new tab

Map of the standard deviations of the thickness measurements across 30 subjects. Noncortical regions have been excluded on the medial aspect of the surface.

To assess the portion of this variability attributable to measurement noise as opposed to true intersubject differences, we performed two test–retest experiments. In the first, we scanned the same subject in two different sessions and reconstructed surface models for each, aligning them with the group average. The mean intersession standard deviation of these thickness measures was found to be 0.25 mm. Applying the surface-based blurring kernel reduced the variability to 0.1 mm. Next, to assess the robustness of the technique to the varying contrast properties of different pulse sequences, we scanned the same subject on two different scanner types and MRI protocols (3D-SPGR, General Electric and MP-RAGE, Siemens, Iselin, NJ). Reconstructing and aligning as before, we found the mean cross-scanner standard deviation in the thickness measures increased slightly over the within-platform case to 0.31 mm (0.23 mm with the same blurring kernel as before), suggesting that the measurements are relatively robust to differences in MRI protocols and scanners. These results indicate that much of the variability in the cross-subject thickness measurements reflects true intersubject differences, and that even focal abnormalities in cortical thickness may be detectable with these techniques.

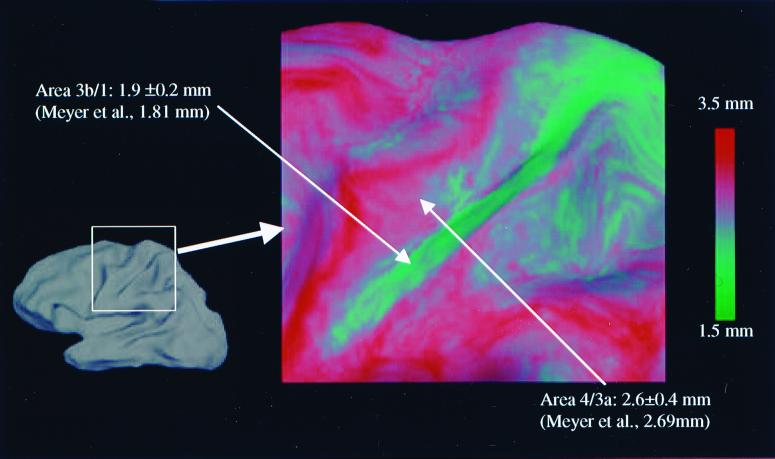
Further validation was obtained by comparing the automated thickness measurements with manual measurements of cortical thickness from MRI data. A recent study, in which a trained anatomist used a jeweler's eyepiece to estimate the thickness in 0.1 mm-gradations from slices oriented perpendicular to the central sulcus, found that the thickness of the anterior and posterior banks of the sulcus differed substantially (20), in agreement with earlier postmortem results (2). Specifically, the average thickness of the anterior bank of the central sulcus was found to be 2.69 mm, whereas the average thickness of the posterior bank was substantially less, averaging 1.81 mm, allowing the banks to be distinguished based solely on thickness. Fig. 6 illustrates these manually measured findings and compares them with the average thickness measured with our technique across the left hemispheres of the same 30 subjects. As can be seen, our measurements are in close agreement with the MRI results, as well as earlier postmortem work that found the mean thickness of the anterior and posterior banks to be 2.7 mm and 1.7 mm, respectively (39). It is important to note here that these results validate both the accuracy of the thickness measurements and the precision of the intersubject alignment in this region. That is, if the alignment procedure did not map anterior banks to anterior banks and posterior banks to posterior banks, the thick cortex on the anterior bank would be averaged with the thin cortex on the posterior bank, yielding no distinction between the two banks in the average.

Figure 6.

Figure 6

Open in a new tab

Average thickness of posterior (area 3b/1) and anterior (area 4/3a) banks of the central sulcus together with a comparison of manually measured published values [Meyer et al. (20)].

Finally, a more quantitative and regionally specific comparison with postmortem findings was performed, the results of which are summarized in Table 1. Note the excellent agreement between the overall average measured by using the current procedure and the postmortem results. Further, the agreement in the regional measurements generated by using the two techniques is quite good, with a maximum discrepancy of slightly more than 0.5 mm. These differences may be accounted for by a number of factors such as individual variability, fixation effects, the precise location of the measurements, as well as MRI artifacts.

Table 1.

Comparison of reported postmortem thickness with the automated methods outlined in this paper, averaged across 30 subjects

Methods Postmortem thickness, mm Average of 30 subjects, mm
Overall average 2.5* 2.5  ± 0.7
Lateral cortex 3.5* 2.9  ± 0.3
Medial cortex 2.7* 2.4  ± 0.3
Inferior cortex 3.0* 2.7  ± 0.3
Open in a new tab

All ranges are standard deviations. 

*

See ref. 2. 

Conclusions

The methods presented here provide highly accurate models of both the gray/white and the pial surfaces of the human cerebral cortex as a precursor to measuring the thickness of the cortical ribbon. The procedure for positioning these surfaces ensures smoothness without sacrificing accuracy in highly folded regions, resulting in a pair of surfaces with submillimeter accuracy. The thickness of the gray matter can then be easily computed at any point in the cortex as the shortest distance between the two surfaces. The comparison with published values indicates that the thickness measurements can accurately reflect submillimeter variations in the gray matter. This level of accuracy, in conjunction with the small standard deviations of the measurements across most of the cortex, implies the ability to distinguish focal atrophy in small patient populations or even individuals. In addition, given the high within-subject test–retest reliability it should be possible to detect subtle localized changes in thickness over time in individual subjects, a capability that may prove important in studying the progression of a disease, as well as for assessing the efficacy of treatments.

The precision of the thickness measurements, of course, is constrained by the contrast-to-noise ratio and fidelity of the underlying MRI data. Although our studies indicate that the methods are relatively insensitive to the specifics of the MRI protocol and scanner, it should be noted that gray/white matter contrast varies across the cortex. In particular, primary sensory areas tend to have a high degree of myelination, resulting in reduced contrast in these regions. To obtain accurate measurements throughout the cortex, including these regions, sequences must be used that provide sufficient spatial resolution and T1 contrast.

In most morphological studies, one wishes to compare average measures across groups (e.g., patients and controls). To carry out this type of comparison, some procedure must be used to relate the points in one cortical hemisphere with those in another. This registration procedure is of importance as the ability to meaningfully assess the early progress of a number of diseases is limited by both the accuracy of the thickness measurements and the precision of the point correspondence across brains. The standard method of averaging human neuroimaging data (40) does not afford the anatomical specificity required to make this type of subtle comparison. In contrast, by using a high-resolution, surface-based averaging technique that aligns cortical folding patterns (25), we have shown the ability to distinguish the opposing banks of the central sulcus based on variations in mean cortical thickness across a large number of individuals. This level of accuracy is critical for diagnostic purposes, as well as for furthering the understanding of intracortical and afferent functional connectivity patterns, as atrophy is frequently associated with a substantial decrease in a previously active set of connections.

The results presented in this study were achieved by combining a number of techniques. These techniques include methods for constructing (22, 24) and transforming (23) models of the human cerebral cortex, as well as a means for using the pattern of cortical folding derived from these models to drive a high-resolution, intersubject alignment procedure (25). These tools, as well as those for measuring cortical thickness and visualizing morphometric and functional properties of the cortex, are part of a freely available software package.‖ Furthermore, the pattern of cortical folds, in the form of mean curvature, Gaussian curvature, or average convexity, can be used to characterize geometric differences between populations in much the same manner as cortical thickness, a capability that may be useful in studying disorders associated with abnormalities in cortical folding patterns, such as polymicrogyria. The combination of these tools yields a set of powerful techniques for analyzing morphometric properties of the human cerebral cortex, with important applications in the study of the patterns of geometric changes associated with specific diseases, as well normal brain development and aging.

Acknowledgments

We thank David Van Essen, Eric Halgren, Christophe Destrieux, David Salat, and Arthur Liu for useful discussions about measuring cortical thickness, as well as for extensive work validating the proposed technique. We also thank Randy Buckner for providing data for testing the thickness measurement procedure, Kevin Teich for providing many useful graphical tools, and Diana Rosas and Eduard Kraft for helpful discussions regarding neurodegenerative disorders. This Human Brain Project/Neuroinformatics research is funded jointly by the National Institute of Neurological Disorders and Stroke, the National Institute of Mental Health, and the National Cancer Institute (R01-NS39581). Further support was provided by the National Center for Research Resources (P41-RR14075 and R01-RR13609).

Footnotes

This paper was submitted directly (Track II) to the PNAS office.

Article published online before print: Proc. Natl. Acad. Sci. USA, 10.1073/pnas.200033797.

Article and publication date are at www.pnas.org/cgi/doi/10.1073/pnas.200033797

†

Regions in which the border between opposing banks cannot be resolved and whose thickness is asymmetric will, of course, then be inaccurate.

‡

All intensity values and intensity gradients are sampled from the volume by using trilinear interpolation.

§

Across the 30 subjects, we find that approximately 90% of the cortex consistently maps gyral/sulcal patterns across individuals. That is, a patch of cortex that is clearly gyral (sulcal) in one individual has a 90% chance of mapping to a gyral (or sulcal) patch in any other individual. Note that 100% alignment is not possible because of the fact that the topology of the folding patterns varies substantially across individuals, and thus no continuous bijection exists.

The measurements summarized in Table 1 (both ours and the published values) all were taken at the crowns of the gyri.

‖

The software can be downloaded from http://www.nmr.mgh.harvard.edu/freesurfer.

References

  • 1.Zilles K. In: The Human Nervous System. Paxinos G, editor. San Diego: Academic; 1990. pp. 757–802. [Google Scholar]
  • 2.von Economo C. The Cytoarchitectonics of the Human Cerebral Cortex. London: Oxford Univ. Press; 1929. [Google Scholar]
  • 3.Brodmann K. Vergleichende Lokalisationslehre der Großhirnrinde in ihren Prinzipien dargestellt auf Grund des Zellenbaues. Leipzig, Germany: Barth; 1909. [Google Scholar]
  • 4.De Leon M J, George A E, Golomb J, Tarshish C, Convit A, Kluger A, De Santi S, McRae T, Ferris S H, Reisberg B, et al. Neurobiol Aging. 1997;18:1–11. doi: 10.1016/s0197-4580(96)00213-8. [DOI] [PubMed] [Google Scholar]
  • 5.Jack C R, Jr, Petersen R C, Xu Y C, Waring S C, O'Brien P C, Tangalos E G, Smith G E, Ivnik R J, Kokmen E. Neurology. 1997;49:786–790. doi: 10.1212/wnl.49.3.786. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 6.Albert M S. Proc Natl Acad Sci USA. 1996;93:13547–13551. doi: 10.1073/pnas.93.24.13547. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 7.Frisoni G B, Beltramello A, Weiss C, Geroldi C, Bianchetti A, Trabucchi M. Am J Neuroradiol. 1996;17:913–923. [PMC free article] [PubMed] [Google Scholar]
  • 8.Grignon Y, Duyckaerts C, Bennecib C, Hauw J J. Acta Neuropathol. 1998;4:395–406. doi: 10.1007/s004010050816. [DOI] [PubMed] [Google Scholar]
  • 9.Double K L, Halliday G M, Kril J J, Harasty J A, Cullen K, Brooks W S, Creasey H, Broe G A. Neurobiol Aging. 1996;17:513–521. doi: 10.1016/0197-4580(96)00005-x. [DOI] [PubMed] [Google Scholar]
  • 10.Rusinek H, de Leon M J, George A E, Stylopoulos L A, Chandra R, Smith G, Rand T, Mourino M, Kowalski H. Radiology (Easton, Pa) 1991;178:109–114. doi: 10.1148/radiology.178.1.1984287. [DOI] [PubMed] [Google Scholar]
  • 11.Kaye J A, Swihart T, Howieson D, Dame A, Moore M M, Karnos T, Camicioli R, Ball M, Oken B, Sexton G. Neurology. 1997;48:1297–1304. doi: 10.1212/wnl.48.5.1297. [DOI] [PubMed] [Google Scholar]
  • 12.Vonsattel J P, DiFiglia M. J Neuropathol Exp Neurol. 1998;57:369–384. doi: 10.1097/00005072-199805000-00001. [DOI] [PubMed] [Google Scholar]
  • 13.Halliday G M, McRitchie D A, Macdonald V, Double K L, Trent R J, McCusker E. Exp Neurol. 1998;154:663–672. doi: 10.1006/exnr.1998.6919. [DOI] [PubMed] [Google Scholar]
  • 14.Boeve B, Maraganore D, Parisi J, Ahlskog J, Graff-Radford N, Caselli R, Dickson D, Kokmen E, Peterson R. Neurology. 1999;52:795–800. doi: 10.1212/wnl.53.4.795. [DOI] [PubMed] [Google Scholar]
  • 15.Kiernan J, Hudson A. Brain. 1994;117:747–757. doi: 10.1093/brain/117.4.747. [DOI] [PubMed] [Google Scholar]
  • 16.Zipursky R B, Lim K O, Sullivan E V, Brown B W, Pfefferbaum A. Arch Gen Psychiatry. 1992;49:195–205. doi: 10.1001/archpsyc.1992.01820030027004. [DOI] [PubMed] [Google Scholar]
  • 17.Zipursky R B, Lambe E K, Kapur S, Mikulis D J. Arch Gen Psychiatry. 1997;55:540–546. doi: 10.1001/archpsyc.55.6.540. [DOI] [PubMed] [Google Scholar]
  • 18.Pfefferbaum A, Marsh L. Clin Neurosci. 1995;3:105–111. [PubMed] [Google Scholar]
  • 19.Kwon J, McMarley R, Hirayasu Y, Anderson J, Fischer I, Kikinis R, Jolesz F, Shenton M. Arch Gen Psychiatry. 1999;56:142–148. doi: 10.1001/archpsyc.56.2.142. [DOI] [PubMed] [Google Scholar]
  • 20.Meyer J R, Roychowdhury S, Russell E J, Callahan C, Gitelman D, Mesulam M M. Am J Neuroradiol. 1996;17:1699–1706. [PMC free article] [PubMed] [Google Scholar]
  • 21.Dale A M, Sereno M I. J Cognit Neurosci. 1993;5:162–176. doi: 10.1162/jocn.1993.5.2.162. [DOI] [PubMed] [Google Scholar]
  • 22.Dale A M, Fischl B, Sereno M I. Neuroimage. 1999;9:179–194. doi: 10.1006/nimg.1998.0395. [DOI] [PubMed] [Google Scholar]
  • 23.Fischl B, Sereno M I, Dale A M. Neuroimage. 1999;9:195–207. doi: 10.1006/nimg.1998.0396. [DOI] [PubMed] [Google Scholar]
  • 24.Fischl, B., Liu, A. & Dale, A. M. (1999) IEEE Trans. Med. Imaging, in press. [DOI] [PubMed]
  • 25.Fischl B, Sereno M I, Tootell R B H, Dale A M. Hum Brain Mapp. 1999;8:272–284. doi: 10.1002/(SICI)1097-0193(1999)8:4<272::AID-HBM10>3.0.CO;2-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 26.Terzopoulos D, Fleischer K. Visual Comput. 1988;4:306–331. [Google Scholar]
  • 27.MacDonald D. Ph.D. thesis. Montreal: McGill University; 1998. [Google Scholar]
  • 28.Davatzikos C, Bryan R N. IEEE Trans Med Imaging. 1996;15:785–795. doi: 10.1109/42.544496. [DOI] [PubMed] [Google Scholar]
  • 29.Kaas M, Witkin A, Terzopoulos D. Int J Comput Vision. 1988;1:321–331. [Google Scholar]
  • 30.Yuille A L. J Cognit Neurosci. 1991;3:59–70. doi: 10.1162/jocn.1991.3.1.59. [DOI] [PubMed] [Google Scholar]
  • 31.Christensen G E, Rabbitt R D, Miller M I. IEEE Trans Image Processing. 1996;5:1435–1447. doi: 10.1109/83.536892. [DOI] [PubMed] [Google Scholar]
  • 32.Thompson P M, Toga A W. IEEE Trans Med Imaging. 1996;15:1–16. doi: 10.1109/42.511745. [DOI] [PubMed] [Google Scholar]
  • 33.McInerney T, Terzopoulos D. Med Image Anal. 1996;1:91–108. doi: 10.1016/s1361-8415(96)80007-7. [DOI] [PubMed] [Google Scholar]
  • 34.Burt P J, Adelson E H. IEEE Trans Commun. 1983;9:532–540. [Google Scholar]
  • 35.Sethian J A. Level Set Methods. Evolving Interfaces in Geometry, Fluid Mechanics, Computer Vision, and Materials Science. Cambridge, U.K.: Cambridge Univ. Press; 1996. [Google Scholar]
  • 36.Sethian J A. J Differ Geom. 1990;31:131–161. [Google Scholar]
  • 37.Press W H, Teukolsky S A, Vetterling W T, Flannery B P. Numerical Recipes inc. 2nd. Ed. Cambridge, U.K.: Cambridge Univ. Press; 1994. [Google Scholar]
  • 38.Möller T. J Graphics Tools. 1997;2:25–30. [Google Scholar]
  • 39.Sholl D A. The Organization of the Cerebral Cortex. New York: Wiley; 1956. [Google Scholar]
  • 40.Talairach J, Tournoux P. Co-Planar Stereotaxic Atlas of the Human Brain. New York: Thieme; 1988. [Google Scholar]

Articles from Proceedings of the National Academy of Sciences of the United States of America are provided here courtesy of National Academy of Sciences

RESOURCES