CHARACTERIZATION OF ANISOTROPIC DIFFUSION TENSOR OF SOLUTE IN TISSUE BY VIDEO-FRAP IMAGING TECHNIQUE

Abstract

In this study, a new method for determination of an anisotropic diffusion tensor by a single fluorescence recovery after photobleaching (FRAP) experiment was developed. The method was based on two independent analyses of video-FRAP images: the fast Fourier Transform (FFT) and the Karhunen-Loève Transform (KLT).

Computer simulated FRAP tests were used to evaluate the sensitivity of the method to experimental parameters, such as the initial size of the bleached spot, the choice of the frequencies used in the Fourier analysis, the orientation of the diffusion tensor, and experimental noise.

The new method was also experimentally validated by determining the anisotropic diffusion tensor of fluorescein (332 Da) in bovine annulus fibrosus. The results obtained were in agreement with those reported in a previous study. Finally, the method was used to characterize fluorescein diffusion in bovine meniscus. Our findings indicate that fluorescein diffusion in bovine meniscus is anisotropic.

This study provides a new tool for the determination of anisotropic diffusion tensor that could be used to investigate the correlation between the structure of biological tissues and their transport properties.

INTRODUCTION

Diffusion is an important transport mechanism for nutrient supply to cells through the dense extracellular matrix in avascular tissues, such as cartilage,¹² ligaments,¹⁵ and intervertebral disc.²⁰ Due to the structures of these tissues, the diffusion of solutes in such media may be anisotropic.^3,5,6,10,18 The determination of the diffusion coefficients of solutes in avascular tissues is important for understanding the physiology and pathology of these systems. However, the methods for characterizing anisotropic diffusivity of solute in tissues are very limited.

Recently, fluorescence photobleaching methods have been extensively adopted for determining solute diffusivity in soft hydrated tissues.^9,10,17,18 One of the advantages of this approach is its high spatial resolution for determining diffusivity (e.g., ~500×500 µm²),¹⁸ compared to the traditional one-dimensional diffusion experiments (e.g., ~5×5 mm²).⁶ Based on different fluorescence photobleaching protocols, several investigators developed various techniques for the determination of anisotropic behavior of solute diffusivity in tissue. Leddy et al. developed continuous point photobleaching method to determine the ratio between the two principal components of the diffusion tensor of large molecules in porcine ligament.¹⁰ Tsay and Jacobson,¹⁹ using spatial Fourier analysis of the images of fluorescence recovery after photobleaching (FRAP), developed a method for the determination of the components of two-dimensional (2D) diffusion tensor along the fixed reference coordinate system. Travascio and Gu reported an alternative method for determining the principal components of a three-dimensional (3D) anisotropic diffusion tensor using three independent FRAP tests in three orthogonal sections of bovine coccygeal disc tissue.¹⁸ However, none of these studies completely determined the diffusion tensor of a solute in biological tissues in a single experiment. Thus, the primary objective of this study was to develop a new method for quantitatively characterizing the 2D anisotropic diffusion tensor by one FRAP test. The other objectives of this study were to investigate the accuracy and robustness of the new method and to apply this new approach to the characterization of the diffusion tensor of a fluorescent probe in a structurally anisotropic biological tissue.

THEORY

In this study a 2D anisotropic diffusion case is considered. It is assumed that the diffusion tensor (D) is symmetric at any point within the system. The components of diffusion tensor (D) depend upon the choice of the coordinate system. Let (x, y) stand for a Cartesian coordinate system which is fixed with respect to a microscope imaging system (i.e., fixed coordinate system). The components of D in (x,y) are D_xx, D_xy, and D_yy. Let (x’,y’) stand for a Cartesian coordinate system in which the matrix of the diffusion tensor is diagonal with components D’_xx and D’_yy. Hereby, the (x’, y’) coordinate system will be denoted as “material coordinate system” as it is oriented in the principal directions of the diffusion tensor. Defining θ as the angle representing the orientation of the material coordinate system with respect to the fixed coordinate system, there always exists a rotation matrix, R, defined as:

$$\mathit{R}=\left[\begin{array}{ll}\text{cos}\theta \hfill & -\text{sin}\theta \hfill \\ \text{sin}\theta \hfill & \text{cos}\theta \hfill \end{array}\right],$$ (1)

such that:

$$\left[\begin{array}{ll}{D}_{\mathit{\text{xx}}}\hfill & D_{\mathit{\text{xy}}}\hfill \\ D_{\mathit{\text{xy}}}\hfill & D_{\mathit{\text{yy}}}\hfill \end{array}\right]=\left[\begin{array}{ll}\text{cos}\theta \hfill & -\text{sin}\theta \hfill \\ \text{sin}\theta \hfill & \text{cos}\theta \hfill \end{array}\right]\left[\begin{array}{cc}\hfill D_{\mathit{\text{xx}}}^{\mathrm{\text{'}}}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill D_{\mathit{\text{yy}}}^{\mathrm{\text{'}}}\hfill \end{array}\right]\left[\begin{array}{cc}\hfill \text{cos}\theta \hfill & \hfill \text{sin}\theta \hfill \\ \hfill -\text{sin}\theta \hfill & \hfill \text{cos}\theta \hfill \end{array}\right],$$ (2)

see Fig. 1(a). From Eq. 2, it follows that:

$$D_{\mathit{\text{xx}}}^{\text{'}}+D_{\mathit{\text{yy}}}^{\text{'}}=D_{\mathit{\text{xx}}}+D_{\mathit{\text{yy}}}=\mathit{\text{tr}}(\mathit{D}),$$ (3)

$$D_{\mathit{\text{xx}}}^{\text{'}}-D_{\mathit{\text{yy}}}^{\text{'}}=\frac{D_{\mathit{\text{xy}}}}{\text{sin}\theta \text{cos}\theta }.$$ (4)

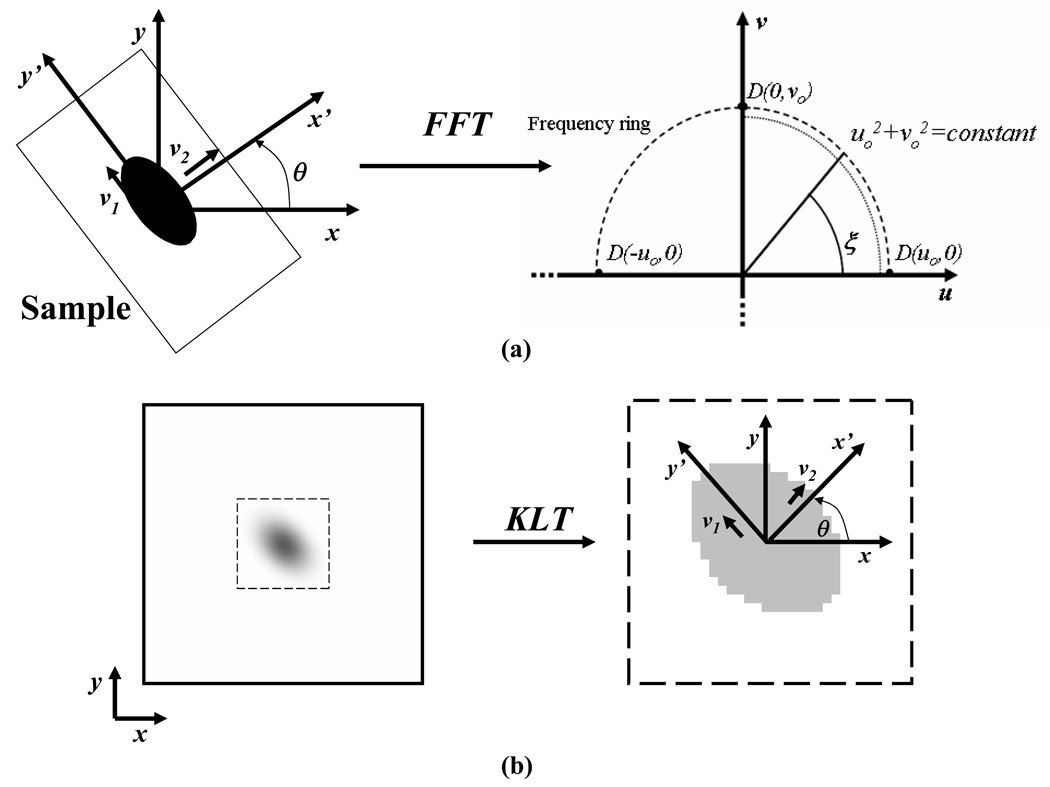
Figure 1.

(a) Transformation of a video-FRAP image into the Fourier space using FFT. The orientation of the principal directions of the sample with respect to the fixed coordinate system is θ The eigenvectors (v₁, v₂) of the covariance matrix C, and the frequency ring used for the determination of D_av (--) and D⁺ _av (…), are shown; (b) Determination of the orientation (θ) of D by KLT analysis of the bleached spot.

The principal values (D’_xx, D’_yy) can be calculated by Eq. (3) and (4) if the values of tr(D), D_xy, and θ are known.

By solving the diffusion equation using spatial Fourier transform, one can obtain the solute concentration,C(u,v,t), in the Fourier space (with frequencies u and v), by ^16,18,19

$$\frac{C(u,v,t)}{C(u,v,\mathit{0})}=e^{-[4{\pi }^{\mathit{2}}(u^{\mathit{2}}+v^{\mathit{2}})D(\xi )t]},$$ (5)

where C(u,v0) is the initial solute concentration. The information on the diffusion tensor (D_xx, D_yy, and D_xy) is embedded in the function, D(ξ), defined as:^18,19

$$D(\xi )=D_{\mathit{\text{xx}}}{\text{cos}}^2\xi +D_{\mathit{\text{yy}}}{\text{sin}}^2\xi +2D_{\mathit{\text{xy}}}\text{sin}\xi \text{cos}\xi ,$$ (6)

where D_xx, D_xy and D_yy are the components of D in the fixed coordinate system and the auxiliary variable ξ is a function of the frequencies u and v:^18,19

$$\xi ={\text{tan}}^{-1}\frac{v}{u}.$$ (7)

In a FRAP experiment the ratio C(u,v,t)/C(u,v,0) is equal, at any time, to the normalized light intensity of the fluorescence recovery image.¹ The function D(ξ) can be determined by curve-fitting the light intensity of a time series of fluorescence recovery images (in the Fourier space) to Eq.5.

By averaging D(ξ) over the arc of an circumference (with u²+v² = constant) spanning from 0 to π, see Fig. 1(b), one can obtain the value of tr(D):¹⁸

$$D_{\mathit{\text{av}}}={\pi }^{-1}{\displaystyle {\int }_{\mathit{0}}^{\pi }D(\xi )d\xi }=\frac{\mathit{\text{tr}}(\mathit{D})}{\mathit{2}}.$$ (8)

The value of D_xy can be found by limiting the average of D(ξ) from 0 to π/2:

$$D_{\mathit{\text{av}}}^{+}={(\frac{\pi }{\mathit{2}})}^{-1}{\displaystyle {\int }_{\mathit{0}}^{\frac{\pi }{\mathit{2}}}D(\xi )d\xi =\frac{\mathit{\text{tr}}(\mathit{D})}{\mathit{2}}+\frac{\mathit{2}{D}_{\mathit{\text{xy}}}}{\pi }.}$$ (9)

The orientation of the diffusion tensor, θ, (i.e., the orientation of the material coordinate system) is related to the shape of the bleached spot during the recovery phase. For the case of isotropic diffusion, the initially bleached circular spot keeps a circular shape during recovery. On the other hand, if diffusion is anisotropic, the shape of the bleached spot will change, from a circle to an ellipse.⁸ Thus, the orientation of the tensor can be determined by Karhunen-Loève Transform (KLT) analysis of the bleached spot during the recovery phase. Karhunen-Loève Transform is an imaging technique for determining the orientation of the principal axes of an image (e.g., ellipse).¹⁴ Briefly, let P_i stand for the position vector (x_i,y_i) of each pixel within the bleached spot. The covariance matrix (C of order 2×2) of the vector population {P_i, i=1,2,…n} is symmetric. The eigenvectors of C are the principal directions of the image, i.e., the major axes of the (elliptical) bleached spot. Note that the second principal vector (v₂) of C corresponds to the shortest axis of the ellipse (denoted as x’-direction in Figure 1), which is the direction of the largest principal value of the diffusion tensor. After tr(D), D_xy and θ are determined, the principal values of tensor D can be calculated by Eq (3) and Eq (4).

METHODS

In this study, numerically simulated FRAP experiments were used to validate the method proposed and to evaluate its sensitivity to experimental parameters, such as the initial size of the bleached spot, the choice of the set of the frequencies (u,v), the orientation of the tensor D, and experimental noise. The method was also validated by analyzing the images from the real FRAP experiments on bovine annulus fibrous (AF),¹⁸ and comparing the results obtained to those reported in the literature.¹⁸ Finally, the approach was applied to the characterization of D of fluorescein in bovine meniscus.

Computer simulation of FRAP test

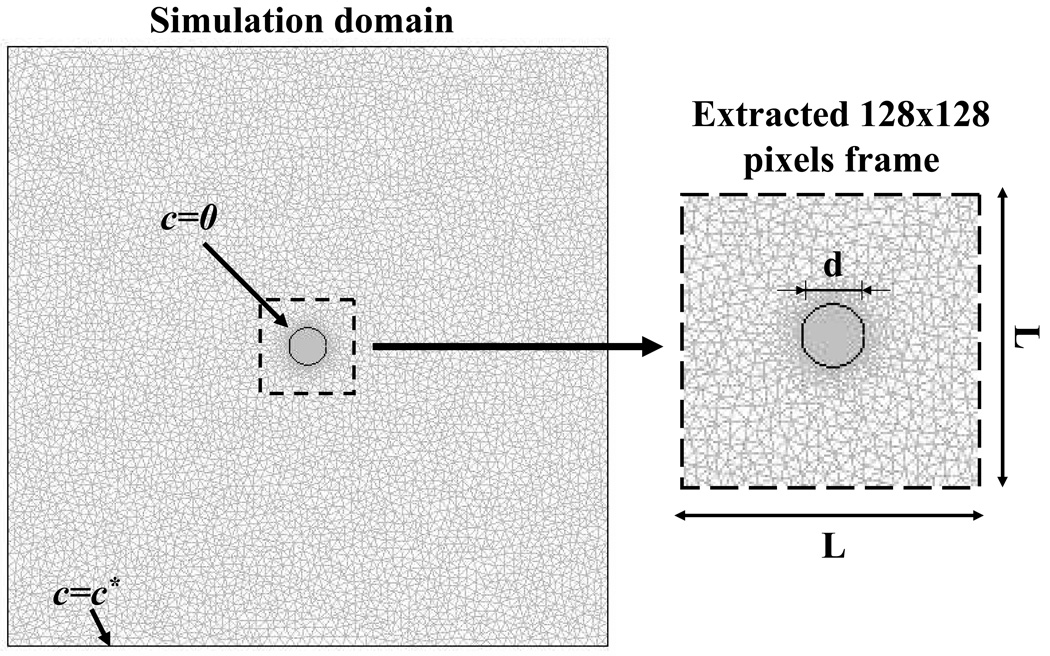
A finite element method package (COMSOL® 3.2, COMSOL Inc., Burlington, MA) was used to simulate 2D anisotropic diffusive recovery of a fluorescent probe after photobleaching. Initially, the fluorescent probe concentration was assumed to be uniform (c=c*) within the sample and zero within the bleached spot. At the boundaries of the simulation domain (4×4 mm²), the concentration of the fluorescent probe was assumed to be constant (c=c*). A mesh of approximately 13000 quadratic Lagrange triangular elements was used in the simulations. The implicit solver of COMSOL® (based on the implicit Euler backward scheme) was used for the simulations. The convergence criterion for the solution was the relative error tolerance of less than 0.001. In each simulation fluorescence recovery was almost complete (>95% of the initial concentration value in the sample c*). For data analysis purposes, a time series of 200 images (8-bit grey scale) of 500×500 µm² (128×128 pixel²) representing the fluorescence recovery on the focal plane of the microscope objective, was extracted from the simulation domain, see Figure 2.

Figure 2.

Mesh and size of the computational domain. The initial and boundary conditions are shown.

Three different anisotropic cases were considered in the simulations: D’_xx = 1.5x, 2x and 3x of D’_yy. The values of D’_xx ranged from 10⁻⁸ to 10⁻⁶ cm²s⁻¹. The orientation of the tensor (θ) varied from 0° to 90° for each of the anisotropic cases studied.

The sensitivity of the method to the ratio of the frame size (L) to the initial diameter (d) of the bleached spot was investigated. For each anisotropic case studied, different values of d were investigated, so that the ratio L/d varied from 1 to 16.

The sensitivity of the method to the choice of the set of frequencies used in Eq. 8 and Eq 9 was studied. The accuracy of the method was evaluated for frequency rings¹⁹ ranging from ‘Ring 2’ to ‘Ring 10’. The “frequency ring” refers to a set of frequency couples (u,v) in the Fourier space, see Figure 1a for an illustration. Note that, because the data are discrete in FFT analysis, the frequency ring is not a continuous arc. Table 1 lists the sets of frequency couples (u,v) composing the rings (up to ‘Ring 6’) in the first quadrant (0≤ξ≤π/2) of the Fourier space The components of higher frequency rings can be easily derived.

Table 1.

List of the frequency couples (u,v) for different frequency rings (0≤ξ≤π/2).

	Frequency couples (u,v)
Ring 2	(2,0)	(2,1)	(1,2)	(0,2)
Ring 3	(3,0)	(3,1)	(2,2)	(1,3)	(0,3)
Ring 4	(4,0)	(4,1)	(4,2)	(3,2)	(3,3)	(2,3)	(2,4)	(1,4)	(0,4)
Ring 5	(5,0)	(5,1)	(5,2)	(5,3)	(4,3)	(4,4)	(3,4)	(3,5)	(2,5)	(1,5)	(0,5)
Ring 6	(6,0)	(6,1)	(6,2)	(6,3)	(6,4)	(5,4)	(5,5)	(4,5)	(4,6)	(3,6)	(2,6)	(2,6)	(1,6)	(0,6)

The effect of the experimental noise on the accuracy of the data analysis was investigated by adding photon noise to the simulated FRAP images. Photon noise is characterized by a Poisson distribution. When photon emission is large (for instance, in a FRAP experiment) Gaussian noise can approximate Poisson noise.^2,19 Therefore, similarly to previous studies,^19,21 Gaussian noise was added to computer-generated FRAP images in order to simulate photon noise. The magnitude of the Gaussian noise was characterized by its standard deviation, σ. Two magnitudes of spatial Gaussian noise, generated by ImageJ software (Version 1.39f, by Wayne Rasband, National Institutes of Health, USA), were added to the simulated sequences of images, namely σ = 5 and 10. For each level of σ investigated, ten FRAP experiments (n=10) were simulated.

FRAP test on bovine AF

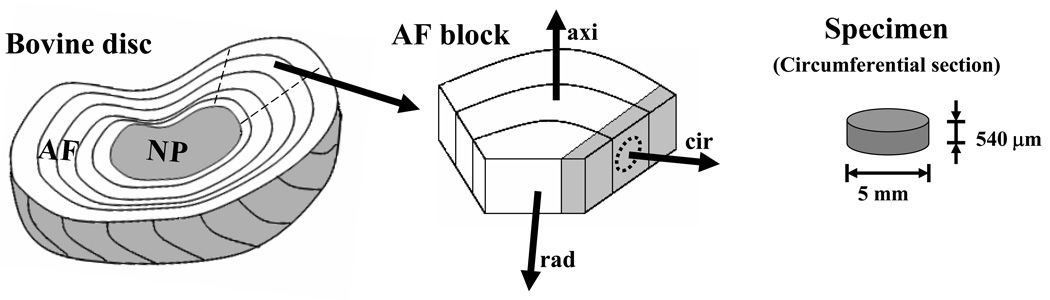
In this study, the experimental data were obtained from FRAP tests (n=48) on bovine coccygeal AF performed in our previous study.¹⁸ Briefly, twelve AF specimens (5 mm diameter and 540 µm thickness) were harvested circumferentially from nine bovine discs (S2–3 and S3–4) belonging to 6–12 months old calves, see Figure 3a. The specimens were equilibrated in a 0.1 mol/m³ fluorescein (332 Da, λ_ex 490 nm; λ_em 514 nm, Fluka-Sigma-Aldrich®, St. Louis, Mo, USA) water solution. In order to prevent swelling, AF specimens were confined between two sinterized stainless steel plates (20 µm porosity) and an impermeable spacer. The experiments were conducted at room temperature (22°C) using a confocal laser scanning microscope (LSM 510 Zeiss, Jena, Germany). The samples were placed on the microscope stage held by a cover glass and moistened after each test. Specimens were photobleached using a 25mW argon laser (488nm wave length) at 70% laser power and 100% transmission. A Plan-Neofluar 20X/0.50 WD 2.0 objective (Zeiss, Jena, Germany) and 86 µm pinhole were used to generate images of 128×128 pixels (460.7×460.7 m²). For each test 200 frames, five of them before multi-layer bleaching (MLB) the sample, were collected at 70% laser power and 2% transmission. The time delay between two consecutive frames was 0.1 seconds.

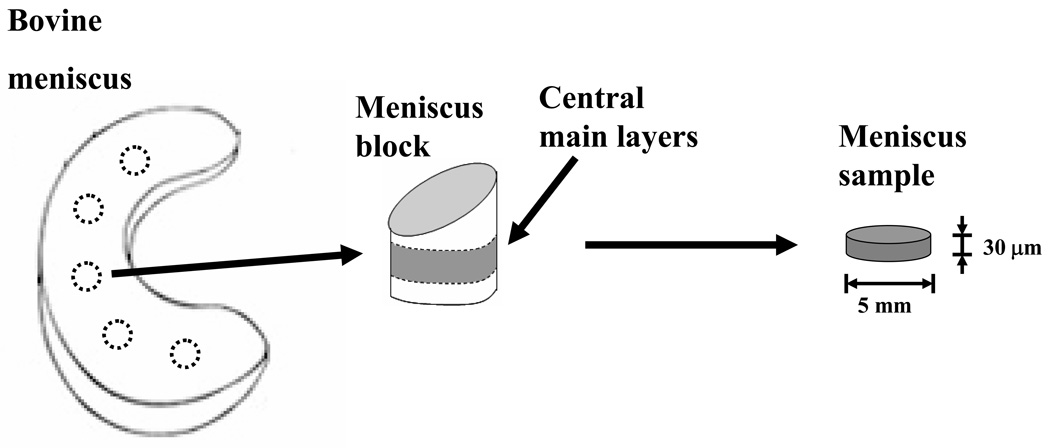
Figure 3.

Schematic of specimen preparation for bovine AF (a) and bovine meniscus (b). The size and orientation of the specimens are shown.

FRAP tests on bovine meniscus

Three bovine menisci, from 6–12 months old calves, were harvested and cylindrical blocks, from all the regions of the tissue, were excised along the transverse direction of the tissue. Menisci blocks were equilibrated in a fluorescein water solution (0.1 mol/m³) for 24 hours. From the central main layers¹³ of each excised block, cylindrical specimens (5 mm diameter and 30 µm thickness) were prepared, see Figure 3b. Twenty cylindrical specimens were used in the experiments to perform a total of 48 FRAP tests (n=48).

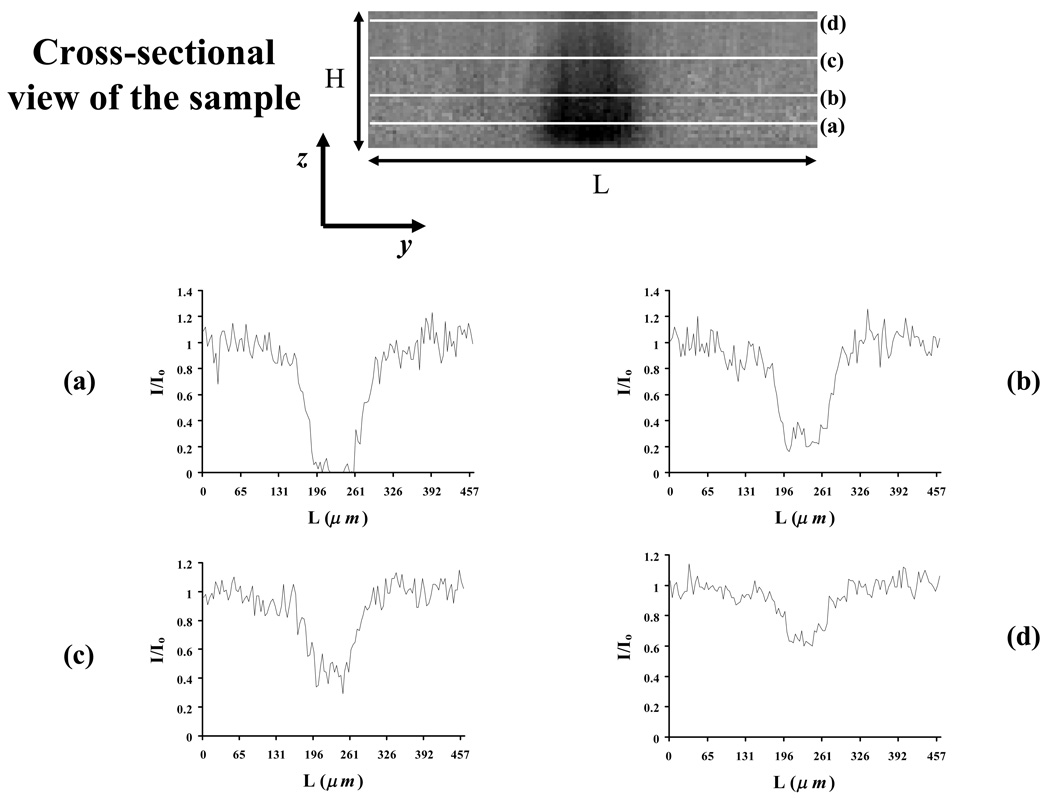
Similar to our previous study,¹⁸ a protocol of MLB was used by the same experimental apparatus for bovine AF (see above). Due to its thickness, two layers of the cylindrical specimen were sequentially bleached; the radii of the circular bleached spots produced were 28.75 µm and their distances from the surface of the cover glass were 7µm and 17µm, respectively. Fluorescence recovery was observed on the focal plane of the lower bleached spot (at 7µm). The magnitude of the bleached volume generated after MLB was observed by acquiring a stack of images of the sample in the z-direction immediately after bleaching. Figure 4 shows a cross-sectional view of the meniscus sample together with the profiles of the normalized fluorescent light intensity within the sample after MLB. Given this light intensity distribution, numerical simulations of three-dimensional (3D) fluorescent recovery were performed using COMSOL software. The results indicated that the value of tr(D) determined by analyzing 2D images (at the focal plane) was affected by a relative error below 10%.

Figure 4.

Cross-sectional view of meniscus sample after multi-layer bleaching. The distributions of normalized light intensity (i.e., normalized fluorescent probe concentration C/C_o) at several layers within the sample are shown (a–d).

Data analysis

Both computer-simulated and experimental FRAP images were analyzed by a custom-made, MATLAB-based algorithm (MATLAB® 6.5, The MathWorks Inc., Natick, MA) performing fast Fourier transform (FFT) and KLT to yield tr(D), D_xy, and θ used in Eq. (3 and Eq 4). The value of the angle θ was determined by KLT analysis of the bleached spot in the recovered images. For computer-simulated FRAP experiments (i.e., ideal cases), only one image showing a fully developed elliptical (bleached) spot was used for determining θ. Around the bleached spot, any pixels with light intensity of 10% lower than the average intensity of image background were considered belonging to the bleached spot and chosen as data points P_i for the KLT analysis. For experimental images and for computer-generated images contaminated by noise, θ was determined by averaging its values determined by KLT over five post-bleaching images, namely the 10^th, 20^th, 30^th, 40^th, and 50^th frames after bleaching.

Statistical analysis

A paired t-test was performed using Excel Spreadsheet software (Microsoft® Office Excel 2003, Microsoft Corp., Seattle, WA) in order to determine if a statistically significant difference existed between the two principal components of the diffusion tensors of fluorescein in both bovine AF and meniscus. For all tests, the significance level was set at P<0.05. All data are given in mean ± standard deviation.

RESULTS

Validation using computer-simulated FRAP images

FRAP images were numerically simulated by inputting the components of D, and subsequently analyzed by FFT and KLT to output the values of the same quantities, see Eq (2–Eq 9). The accuracy of the method was assessed by the relative error (ε), defined as:

$$\epsilon =100\cdot \frac{\left|\mathit{\text{Input}}-\mathit{\text{Output}}\right|}{\mathit{\text{Input}}}(\%).$$ (10)

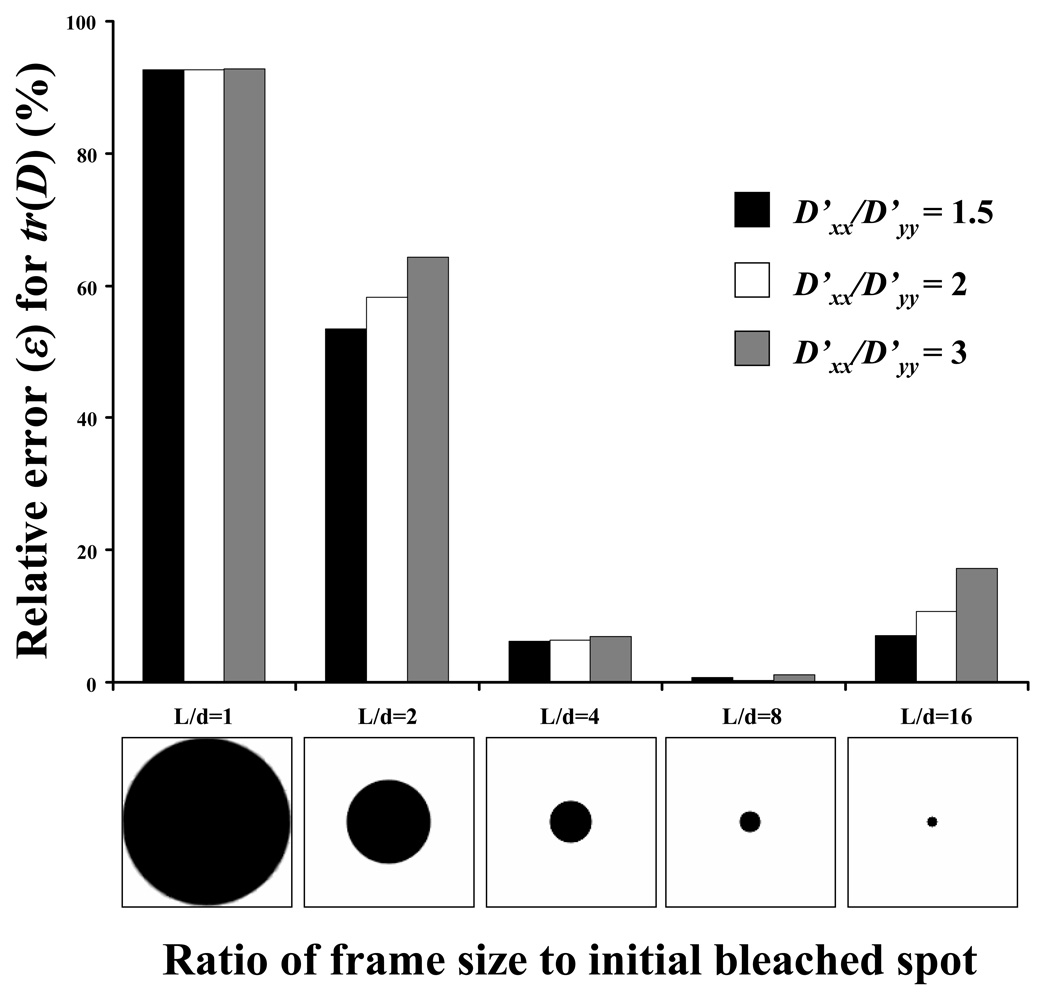
The ratio of the frame size (L) to the initial diameter (d) of the bleached spot significantly affected the accuracy in determining the value of tr(D), see Figure 5. In this case, Eq. 8 was integrated over a special set of frequencies (frequency ring), namely ‘Ring 4’. It was found that, for all the anisotropic cases investigated and for the magnitude of diffusion coefficients used in the analysis, the highest accuracy in the determination of tr(D) was obtained when L/d=8. Similar results were also found when Eq. 8 was integrated over other frequency rings ranged from ‘Ring 3’ to ‘Ring 10’ (data not shown). Therefore, this spot size (i.e., L/d=8) was used in the following numerical and experimental investigations.

Figure 5.

Effect of the ratio of frame size (L) to bleached spot diameter (d) on the relative error (ε) for the determination of tr(D). Data were analyzed at frequency ‘Ring 4’. For all the cases reported in this figure, D’_xx = 10⁻⁷ cm²s⁻¹, and θ=45°.

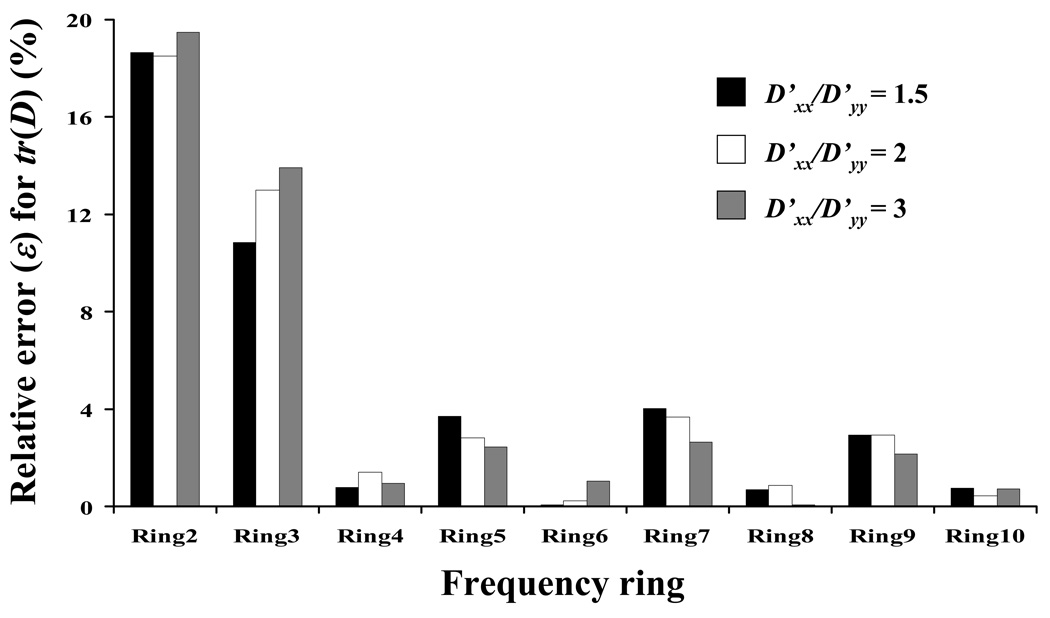
The choice of the frequencies rings used for the integration of Eq. 8 and Eq 9 affected the accuracy for the calculation of D. For all the frequency rings investigated, it appeared that ‘Ring 6’ was the best choice in the determination of tr(D), see Figure 6. However, ‘Ring 6’ might not be optimal for analyzing non-ideal images from real experiments (See ‘Discussion and Conclusions’ below). Note that ‘Ring 4’ was the second best choice, providing a relative error (ε) below 2% (Figure 5). Therefore, ‘Ring 4’ was used in the all following analyses.

Figure 6.

Effect of the frequency ring on the relative error (ε) for the determination of tr(D). For all the cases reported in this figure, L/d=8, D’_xx = 10⁻⁷ cm²s⁻¹, and θ=45°.

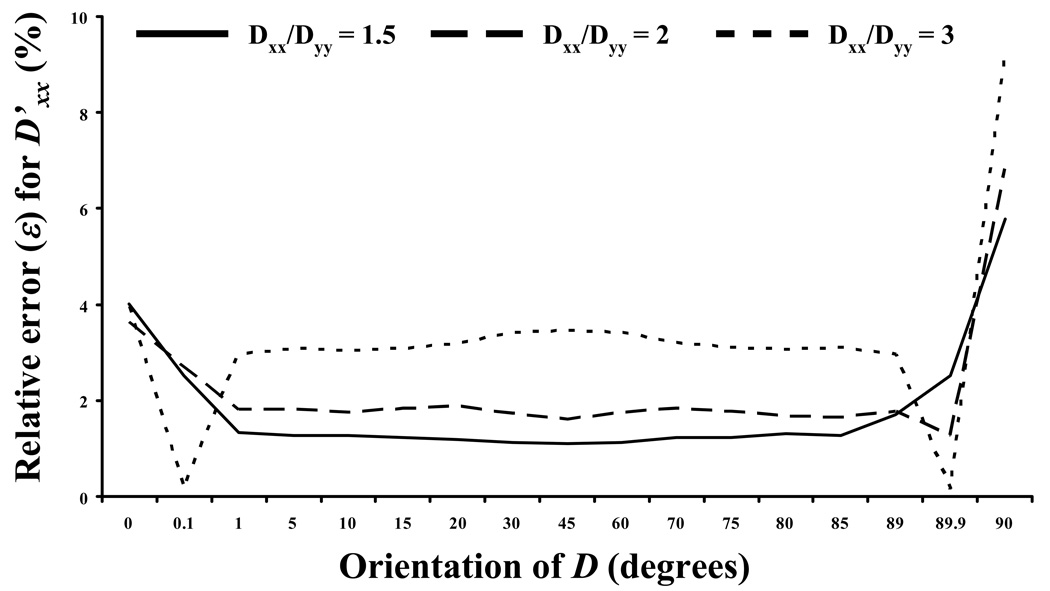
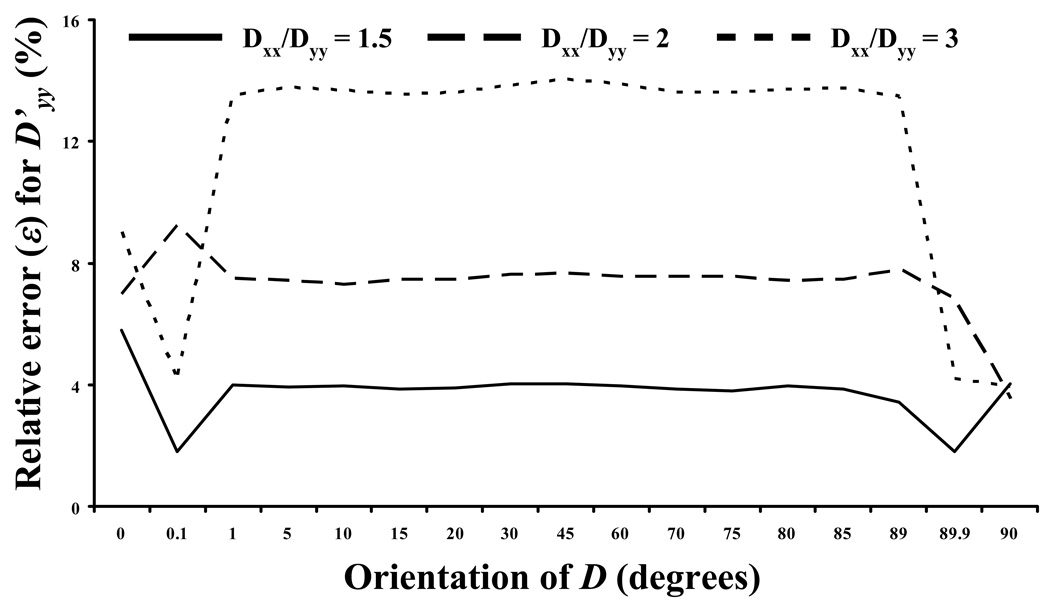
The accuracy in determining the components of D at different orientations (θ) was investigated. Figure 7a-b reports ε for the determination of D’_xx and D’_yy for three different anisotropic ratios: D’_xx/D’_yy = 1.5, 2, and 3, respectively (with D’_xx = 10⁻⁷ cm²s⁻¹). The accuracy of this method is not sensitive to θ, and increases when the anisotropic ratio D’_xx/D’_yy reduces (for most θs investigated). Note that for θ=0° and =90° Eq. (4) is not applicable. For these two special cases the components D’_xx and D’_yy were extracted directly from Eq. (6) by choosing special couples of frequencies at (u=4, v=0; i.e.,ξ=0 ) and (u=0, v=4; i.e.ξ=π/2, ), respectively, as proposed by Tsay and Jacobson.¹⁹

Figure 7.

Effect of the orientation of the diffusion tensor on the relative error (ε) in the determination of D’_xx (a) and D’_yy(b). In all the cases reported in this figure D’_xx = 10⁻⁷ cm²s⁻¹.

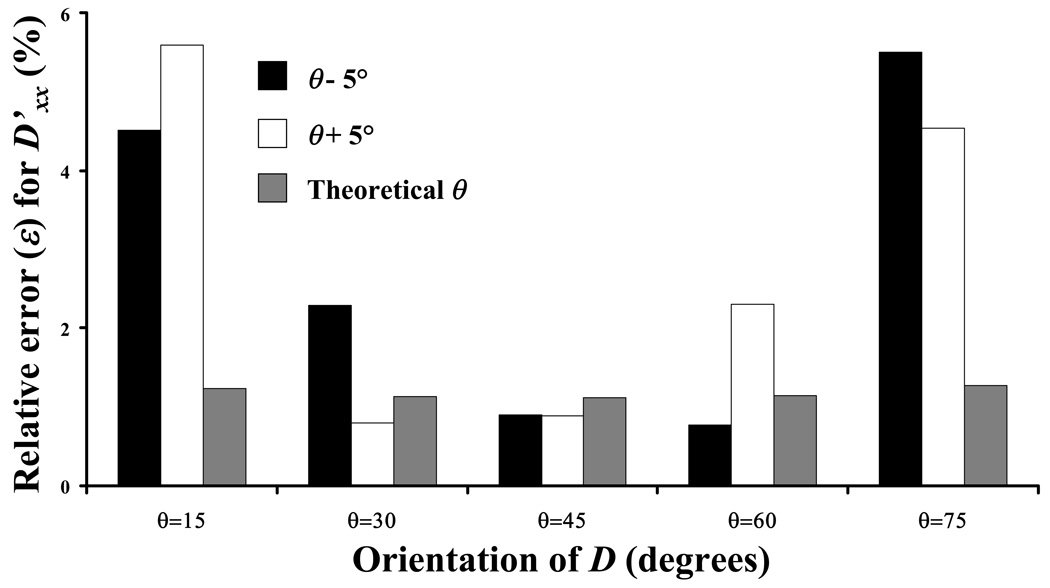
In real FRAP experiments the estimation of θ by KLT may be affected by the quality of the image obtained (see ‘Discussion and Conclusions’). The sensitivity of the precision of the method to the error in the determination of θ was numerically investigated for a representative case where D’_xx/D’_yy = 1.5 (with D’_xx = 10⁻⁷ cm²s⁻¹). Figure 8 reports in determining D’_xx if the estimation of θ by KLT is affected by an error of ±5°. The value of ε is less than 6% for the worst cases considered (for θ= 15° or 75°).

Figure 8.

Effect of the precision (±5°) in determining the tensor orientation (θ)by KLT on the relative error (ε) for the determination of D’_xx. In this case, D’_xx/D’_yy = 1.5 with D’_xx = 10⁻⁷ cm²s⁻¹.

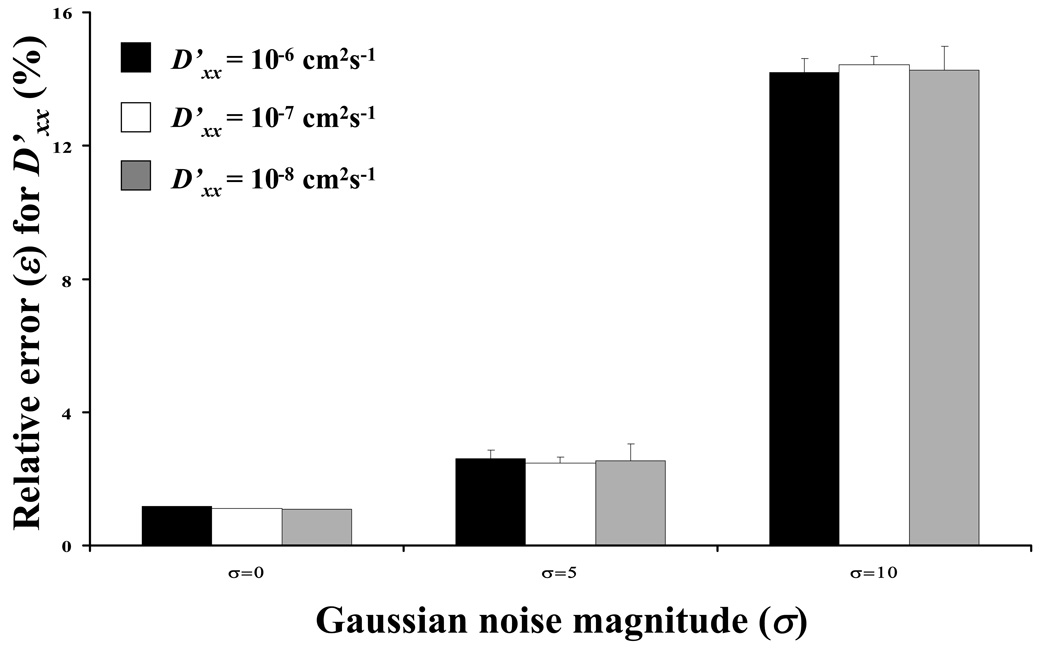
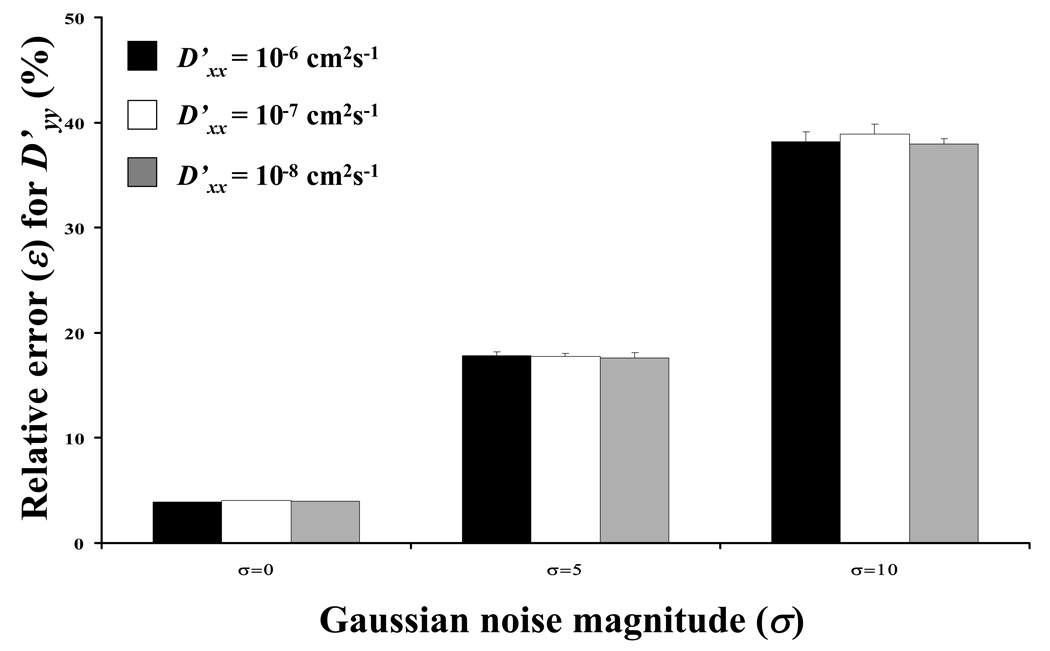
The precision of the method in the presence of spatial Gaussian noise was also investigated for the special case of D’_xx/D’_yy = 1.5 and θ= 45° , with D’_xx ranging from 10⁻⁸ to 10⁻⁶ cm²s⁻¹. Figure 9a-b compares ε in the determination of D’_xx and D’_yy for an ideal case (σ = 0) and for the cases with noise (σ = 5 and 10). The value of ε increased with increasing σ.

Figure 9.

Sensitivity of the results to Gaussian noise magnitude (σ) at different magnitude of diffusivity: (a) relative error (ε) for D’_xx and (b) relative error for D’_yy. For all the cases reported in this figure, D’_xx/D’_yy = 1.5 and θ=45°.

Validation using experimental data

The principal components of fluorescein diffusion tensor in circumferential sections of bovine AF were determined using the current method by analyzing the images of FRAP tests performed in our previous study.¹⁸ The measured diffusion coefficients were statistically different (P<0.05). In particular, it was found that the values of D’_xx and D’_yy were 1.24±0.383×10⁻⁶ cm²s⁻¹ and 0.964±0.283×10⁻⁶ cm²s⁻¹ (mean±SD, n=48), respectively. It is believed that the directions of D’_xx and D’_yy coincide with the axial and radial directions of the disc, respectively (see ‘Discussion and Conclusions’). Furthermore, the values of D’_xx and D’_yy were consistent to those in the axial direction (D_axi=1.26×10⁻⁶ cm²s⁻¹) and in the radial direction (D_rad=0.814×10⁻⁶ cm²s⁻¹) determined by a different approach reported in our previous study.¹⁸

Diffusion coefficients in bovine meniscus

The principal diffusion coefficients of fluorescein in the tissue were: D’_xx = 1.59±0.56×10⁻⁶ cm²s⁻¹ and D’_yy = 0.44±0.28 ×10⁻⁶ cm²s⁻¹ (mean±SD, n=48). The difference between the two principal components of D was significant (t-test, P<0.05). The variability of repeated measurements on the same sample was also investigated. For instance, on sample #1, six repeated measurements (n=6) were performed, and the values of D’_xx and D’_yy were 1.93•10⁻⁶±5.78•10⁻⁷ cm²s⁻¹ and 4.85•10⁻⁷±2.34•10⁻⁷ cm²s⁻¹ (mean ± standard deviation), respectively; on sample #2, five repeated measurements (n=5) were performed, and the values of D’_xx and D’_yy were 1.19•10⁻⁶±1.21•10⁻⁷ cm²s⁻¹ and 3.07•10⁻⁷±8.25•10⁻⁸ cm²s⁻¹ (mean ± standard deviation), respectively; on sample #3, five repeated measurements (n=5) were performed, and the values of D’_xx and D’_yy were 1.88•10⁻⁶±7.17•10⁻⁷ cm²s⁻¹ and 4.48•10⁻⁷±1.89•10⁻⁷ cm²s⁻¹ (mean ± standard deviation), respectively.

DISCUSSION AND CONCLUSIONS

In this new method, two independent analyses of video-FRAP images are used to characterize the anisotropic diffusion tensor: one is the KLT analysis of the shape of the bleached sport to yield the orientation (θ) of D, and the other is the Fourier analysis of light intensity decay of the images to yield tr(D) and D_xy.

The new method presented in this study was validated by both computer simulated and experimental FRAP tests. The experimental validation was performed by determining the principal components of D of fluorescein in bovine AF. The results were compared with the values of the diffusion coefficients reported in our previous study.¹⁸ The values of D’_xx and D’_yy estimated by the current method are consistent with those determined by Travascio and Gu (2007),¹⁸ see Results. Note that in the approach presented by Travascio and Gu (2007), only the principal components of a diffusion tensor were determined. This was achieved by the Fourier analysis of the FRAP images from each of the orthogonal sections of a tissue sample.¹⁸ In the current method, however, the orientation of bleached spot was also analyzed to yield the orientation of a diffusion tensor. This allowed us to completely determine an anisotropic (2D) tensor using a single FRAP test. The new method was also applied for FRAP experiments on bovine meniscus. The results indicate that fluorescein diffusion in meniscus is anisotropic. In particular, the component D’_xx was found to be 3x of D’_yy. Similar findings have been reported for anisotropic diffusion in ligaments.¹⁰

Results from KLT analysis on both AF and meniscus samples suggested that the orientation (θ) of the largest principal component of D is parallel to the direction of the bundles of collagen fibers within the tissues, see Figure 10a-b. Since in the circumferential section of bovine AF sample the collagen fibers are oriented in the axial direction, these findings indicate that the directions of D’_xx and D’_yy coincide with the axial and radial directions of the disc, respectively. Similarly, in bovine meniscus, the orientations of D’_xx and D’_yy are parallel and perpendicular to the collagen fibers in the tissue, respectively.

Figure 10.

Confocal laser scanning images (128×128 pixel², 460.7×460.7 µm²) of FRAP experiments on bovine AF (a) and bovine meniscus (b). The orientations of the bleached spots coincide with the direction of collagen bundles.

Numerical simulations showed that, for all the anisotropic cases reported, the accuracy of the new method was not sensitive to the orientation of D, see Figure 7a-b. This is because the value of D_xy diminishes when θ approaches 0° or 90° (i.e., in the principal directions, see Eq. 4). Note that in the current method, the values of D_xy and are determined by two independent analyses, so the error in determining D_xy would not affect the accuracy in determining θ, and vice versa However, our method is not applicable when the orientation of D coincides with the fixed coordinate system (for θ= 0° or 90°). For these two special cases, the method proposed by Tsay and Jacobson¹⁹ can be used. Alternatively, one could rotate the specimen and repeat the FRAP experiment in order to avoid these special cases.

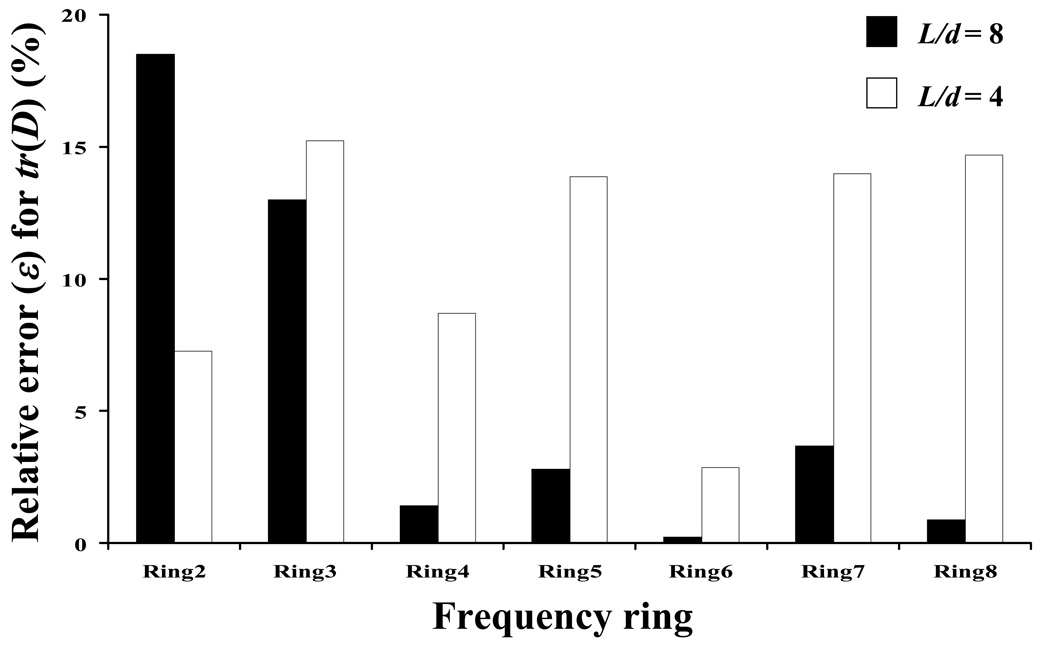
Numerical simulations also showed that the relative size of the bleached spot (L/d) as well as the ‘frequency ring’ significantly affected the accuracy of the method for the determination of D. For the magnitude of the diffusion coefficients used in this analysis, there existed an optimal size for the initially bleached spot relative to the size of the image frame (i.e., at L/d = 8), see Figure 5. For the choice of frequency rings in the FFT analysis, although ‘Ring 6’ is the best choice for numerically simulated (i.e., ideal) FRAP images (Figure 6), ‘Ring 4’ was used in our study. In general, the higher the frequency ring, the more data points of D(ξ) could be used to evaluate D_av and D⁺ _av in Eq. 8 and Eq 9,¹⁹ see Table 1. However, the use of higher frequency rings would increase the cost of data analysis and may not necessarily improve the accuracy of the results for ideal images (Figure 6) or images from real experiments. This is because the values of D(ξ) are determined by the curve-fitting of light intensity (i.e., fluorescent probe concentration) decay in the Fourier space (Eq. 5). Theoretically, the values of D(ξ) should not depend on the choice of the frequency ring, see Eq. 6. In reality, however, the values of D(ξ) determined at higher frequency couples (u, v) may not be accurate since the light intensity decays much faster at higher frequencies due to the exponential term in Eq. 5. A similar observation was also reported by Jönsson et al.⁷ Note that, in a previous study, Tsay and Jacobson investigated the effect of both the spot size and the frequency rings (up to ‘Ring 3’) on the accuracy of FFT analysis of numerically simulated FRAP images (64×64 pixel²). It was found that the ‘Ring 2’ was the optimal frequency ring for the images with spot size of L/d=4.¹⁹ Figure 11 compares the effect of spot size (L/d= 4 vs. L/d=8) on the accuracy in determining tr(D) at different frequency rings. The ratio L/d=8 provided the highest accuracy for all cases investigated, except at ‘Ring 2’. For the case of L/d= 4, frequency ‘Ring 2’ is better than ‘Ring 3’ or ‘Ring 4’. This result is consistent with the finding by Tsay and Jacobson.¹⁹

Figure 11.

Comparison of the relative error (ε) in determining tr(D) using different frequency rings for two different spot sizes: L/d=8 (black) and L/d=4 (white). For all the cases reported in this figure D’_xx/D’_yy = 2 (with D’_xx = 10⁻⁷ cm²s⁻¹), and θ=45°.

The determination of θ is based on the analysis of the shape of the bleached spot during the recovery phase. In a real FRAP experiment, because of the quality of the images acquired, the contour of the bleached spot may not be well defined. Thus, the calculated orientation of the spot may vary from one image frame to another, see Table 2. Numerical simulations performed in this study showed that, when the estimation of θ by KLT is affected by an error of ±5°, the relative error for the determination of D’_xx is less than 6%, see Figure 8. In order to reduce the artifacts produced by noise, the image series could be post-processed by using a multi-scale active shape model for the contour detection of the bleached spot.¹¹

Table 2.

Determination of θ at different time points for fluorescein diffusion in bovine meniscus. Five randomly chosen samples were analyzed and reported.

	Frame 10	Frame 20	Frame 30	Frame 40	Frame 50	Average±SD
Sample 1	80.7°	80.44°	79.95°	82.24°	87.63°	82.19°±3.16°
Sample 2	74.71°	74.64°	72.03°	70.06°	72.09°	72.71°±1.97°
Sample 3	82.64°	85.62°	87.02°	87.88°	83.54°	85.34°±2.23°
Sample 4	55.79°	52.53°	51.41°	50.91°	52.96°	52.72°±1.9°
Sample 5	18.75°	14.24°	15.55°	18.24°	19.94°	17.34°±2.37°

The light intensity of images acquired by a laser scanning microscope tends to decrease with time, due to photobleaching of the background fluorescence. In addition, because of the presence of noise, temporal fluctuations of light intensity can occur. The method presented in this study does not include compensations for these two sources of error. Nonetheless, the main objective of this study was to present a novel approach for determining an anisotropic diffusion tensor by the analysis of FRAP images. We recognize the need to reduce the sources of experimental error for improving the accuracy of the results. Techniques of image post processing could be used in order to compensate the background decay and the temporal fluctuation of the light intensity.^4,7 This will be accomplished in a future study.

In this study, the sensitivity of the new method to the level of Gaussian noise was presented, see Figure 9a-b. The results indicate that an increase in noise level reduces the accuracy of the method. It would be desirable to determine the actual noise level in real FRAP experiments in order to provide a precise estimate of the accuracy in the determination of the diffusion coefficients. This aspect was not investigated in this work and will be subject of a future study.

In summary, this study provides a new tool for the determination of solute diffusivity in structurally anisotropic biological tissues. Using numerically simulated FRAP images, the accuracy of the method was investigated for different sizes of bleached spots and for different frequency rings. The effect of noise level on the data analysis was also investigated. The new method was also validated using real FRAP experiments on bovine AF. Finally, the new technique was applied to the characterization of fluorescein diffusivity in bovine meniscus. Since the diffusion tensor was related to the structure of the tissue, this study is important for understanding the correlation of tissue morphology to its transport properties.