Tuning transport properties of nanofluidic devices with local charge inversion

Abstract

Nanotubes can selectively conduct ions across membranes to make ionic devices with transport characteristics similar to biological ion channels and semiconductor electron devices. Depending on the surface charge profile of the nanopore, ohmic resistors, rectifiers, and diodes can be made. Here we show that a uniformly charged conical nanopore can have all these transport properties by changing the ion species and their concentrations on each side of the membrane. Moreover, the cation vs. anion selectivity of the pores can be changed. We find that polyvalent cations like Ca²⁺ and the trivalent cobalt sepulchrate produce localized charge inversion to change the effective pore surface charge profile from negative to positive. These effects are reversible so that the transport and selectivity characteristics of ionic devices can be tuned, much as the gate voltage tunes the properties of a semiconductor.

Introduction

Ionic devices are systems that control transport of ions and molecules in solutions.^1–10 Recently, there has been renewed interest in these devices for possible applications in biophysics, biosensor, lab-on-a-chip, and artificial cells.^11,12,13 Ionic devices are typically based on biomimetic nanopores embedded in membranes, because ion channels and pores in biological cells control movement of ions in and out of the cell with precision similar to that achieved in solid-state devices for electrons and holes.^10,14 From the physical and chemical point of view, the high surface to volume ratio of nanopores also makes them an ideal template for these ionic systems; transported ions passing through a pore cannot avoid interacting with the pore walls. When the pore walls are charged, their surface charge pattern determines the pore transport characteristics.^{1,2,3,15–20}

Ionic filters—systems that preferentially transport one type of ion species—are an example of ionic nanoporous devices.^21–24 A negatively charged nanopore with a diameter comparable to the thickness of the electrical double-layer is filled predominantly with cations, and under applied electric field, the transmembrane current is carried mainly by cations. Ionic transport and ionic selectivity with polyvalent ions has, however, posed new challenges to experimentalists and modelers. When polyvalent cations are in contact with a negatively charged surface, charge inversion can occur: the total positive charge brought by the cations close to the surface becomes larger than the total negative surface charge on the walls.^25–28 In a pore, charge inversion may switch the pore selectivity from cationic to anionic.^27,29,30,31 The effect of charge inversion is typically explained via the concept of a strongly correlated liquid formed by the multivalent ions at the charged surface,^32,33,34 and have been modeled with molecular dynamics^35,36 and Monte Carlo simulations,³⁷ as well as in analytical models of biological calcium channels.³¹ In the strongly correlated liquid model, positions of cations at the surface are laterally correlated creating a structure that resembles a Wigner crystal of electrons.^32,33 The analogy with ionic liquids might also be of interest.^38,39,40

In this article we describe a method to experimentally study charge inversion in conically shaped nanopores, and demonstrate how a locally induced charge inversion can lead to ionic diode junctions with rectification properties determined by the surrounding electrolyte. Previously, only chemical patterning of the pore surface charge had produced a diode.^4,5,18,19 We find that the charge inversion leads to the two kinds of diodes previously created by chemical patterning, bipolar and unipolar. A bipolar diode has a junction between a positively charged zone of the pore walls and a zone that is negatively charged. A unipolar diode has a junction between a charged zone of the pore walls and a neutral zone. Both types of diodes produce current-voltage curves with a clear distinction between “on” and “off” states (that is, with high rectification measured as a ratio of currents recorded for the same absolute value of voltage, but of opposite polarity).^4,5,41

We also show that this charge inversion can reverse the cation vs. anion selectivity of these pores. The observations are explained by Monte Carlo simulations of ions in nanopores. Because the charge inversion depends on ion type and concentration, the properties of the nanopore can be changed in seconds by washing with a different electrolyte solution. In this way, an ionic device can have flexibility similar to that of a field-effect transistor whose transport characteristics can be tuned with a gate voltage; the ionic device’s transport characteristics can be tuned in response to user input or environmental stimuli.

Experimental Methods

Preparation of nanopores

The single conical nanopores studied in this article were prepared in 12 micrometers thick polyethylene terephthalate (PET) foils by the track-etching technique described previously.^42,43 Briefly, PET films were irradiated with single swift gold ions, which were accelerated to the total kinetic energy of ~2.2 GeV (UNILAC, GSI Darmstadt, Germany). This irradiation process caused the formation of a single damage track through the films, which after chemical etching resulted in single nanopores. Conical nanopores were obtained by etching the irradiated foils only from one side, while the other side of the membrane was in contact with an acidic solution that neutralized the etchant.⁴⁴ The etching process was performed in a conductivity cell and was monitored by measuring the transmembrane current. Details of the fabrication process and diameter measurements are summarized in the Supplementary Materials.⁴⁵

Ion current measurements

Ion current measurements were performed in the same conductivity cell in which the foils were etched. Two Ag/AgCl electrodes were used for applying the transmembrane potential and measuring the ion current. Since Ag/AgCl electrodes are to a large degree non-polarizable and very stable, we could build a two-electrode set-up in which one electrode placed at the tip (the narrow end) of a conical nanopore was grounded. The other electrode, placed at the base (the big opening) of a pore, was used to apply a given potential difference with respect to the ground electrode. The experiments were performed with two types of commercially available reference Ag/AgCl electrodes that were filled with (i) 3 M NaCl (MF-2052, BASi), Fig. 2–Fig. 8, and (ii) 1 M KCl (CH Instruments, CHI111P), Fig. 1, Fig. 10. Since the volume of our conductivity cell was large (1.5 ml), these electrodes were more convenient for the measurements than the agar salt bridges and agar electrodes typically used in electrophysiology.⁴⁶ The current-voltage curves were recorded using Keithley 6487 picoammeter/voltage source controlled by the ExceLINX software (Keithley Instrument, Cleveland, OH). Offsets were small compared to the large voltages (typically 1 volt) we studied (see below and Supplementary Material). The voltage was ramped from −2V to +2V and from +2 V to −2V with 50 mV steps. At least two voltage sweeps were performed. A given voltage step was applied for 2 seconds and a current measurement was performed. The currents through studied conical nanopores were stable and the recordings obtained at subsequent voltage sweeps would typically differ by less than several percent. Recordings for which significantly larger current fluctuations were observed are described in corresponding figure captions.

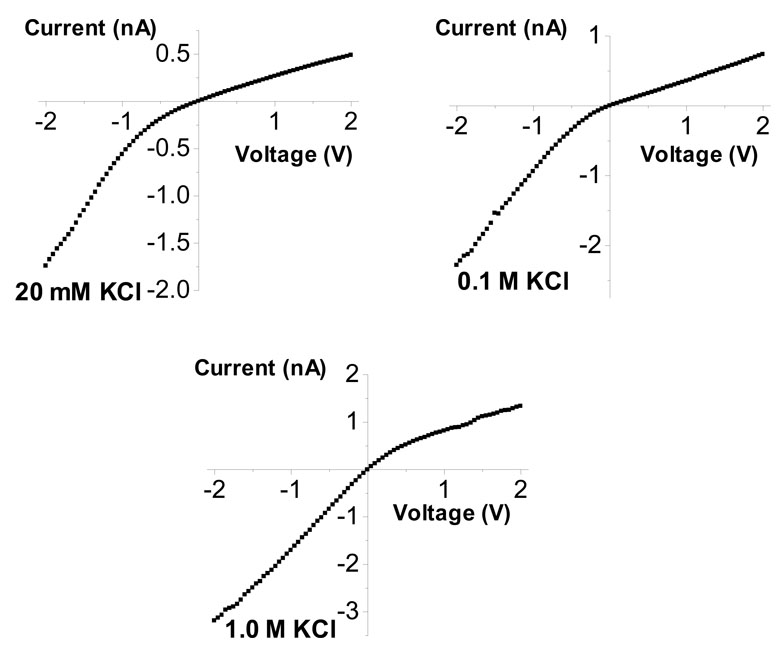
Figure 2.

Current-voltage curves of a single conical nanopore with the tip opening of 3 nm recorded in various KCl concentrations as indicated in the figure. At higher KCl concentrations, the surface charges are more screened, and the rectification becomes weaker (the current-voltage curves become more linear). The ion current rectification effect in a nanopore is determined by the effective surface charge and the pore geometry.²,⁴,¹⁸,⁴⁷,⁴⁹,⁵³,⁵⁶ The wide opening of this pore was 800 nm.

Figure 8.

Current-voltage curves of a single conical nanopore with a tip diameter of 5 nm. The curves were recorded in asymmetric electrolyte conditions: with 10 mM CoSepCl₃ on the base side (shown as black squares, see the left inset for the electrolyte arrangement) and with 10 mM CoSepCl₃ on the tip side (shown as magenta open circles, see the right inset). The other side of the membrane was in contact with 10⁻⁵ M CoSepCl₃. Recordings were performed at pH 8. Data for the same pore recorded in symmetric CoSepCl₃ concentrations are shown in Fig. 4.

Figure 1.

Current-voltage curves of a single conical nanopore with negative surface charges due to carboxyls (black squares), and with positive surface charges due to amines on the pore walls (red ×). The currents were recorded in 0.1 M KCl, pH 6. The narrow opening of this pore was 2 nm, and the big opening was 620 nm. The insets show electrode arrangements that correspond to negative and positive applied voltages, respectively.

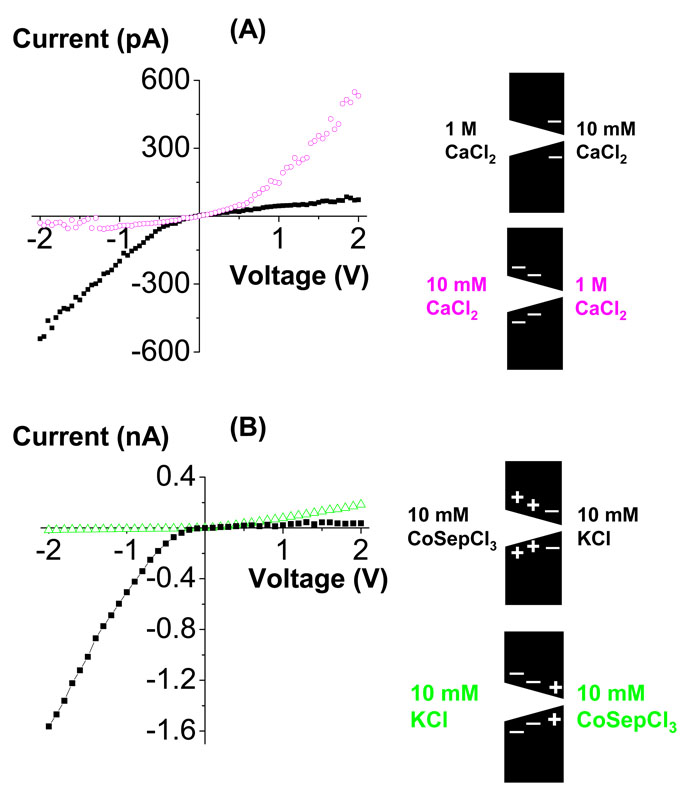
Figure 10.

Current-voltage curves of ionic diodes with local charge inversion. (A) Current-voltage curves recorded in asymmetric Ca²⁺ concentrations. 1 M CaCl₂ caused neutralization of the surface charge, while the side of the pore in contact with 10 mM CaCl₂ remained negatively charged. (B) Current-voltage curves recorded with 10 mM CoSepCl₃ placed on one side of the membrane and 10 mM KCl on the other side of the membrane. The side with CoSep underwent charge inversion and the surface charge became effectively positively charged. The color of the insets corresponds to the colors for the recordings. The tip opening of this pore was 5 nm; the wide opening was 400 nm. For the recordings with 1 M CaCl₂ at the tip, and voltages between −2V and −1 V, the currents were very low and unstable as shown by the current fluctuations.

As we mentioned above, the volume of our conductivity cell was rather large (1.5 ml) thus within the course of a given measurement series (~0.5 hour), no significant leakage from the reference electrodes was observed, and the currents remained stable.

The ion current measurements were performed in symmetric electrolyte conditions (when the electrolyte concentration on both sides of the membrane was the same) as well as in the presence of concentration gradients. In the symmetric conditions, the junction potential created between the electrode and the solution was identical on both sides of the membrane.³⁰ Thus it canceled out and did not contribute to the externally applied voltage. In the asymmetric electrolyte cases, the junction potentials, as calculated from the Henderson equation, did not exceed 28 mV.⁴⁵ Since the current-voltage curves were studied at a wide range of voltages between −2V and +2V, the recordings were not corrected for junction potentials.

Results and Discussion

Current-voltage curves through single conical nanopores in symmetric electrolyte conditions

A single conical pore exhibits a number of interesting transport properties. For example, a conical pore with homogeneous negative (positive) surface charge rectifies the current with the preferential direction of the cation (anion) flow from the narrow entrance towards the wide opening of the pore.⁴⁷ The effect of ion current rectification with asymmetric structures was observed for the first time with glass nanopipettes.⁴⁸ When the ground electrode is placed at the narrow entrance of a conical pore, a negatively charged pore exhibits larger currents at negative voltages, while a positively charged nanopore is characterized by larger currents at positive voltages (Fig. 1).^49,50,51 Conical nanopores with neutral walls produce linear current-voltage curves.

Nanopores in PET contain on their walls carboxyl groups (~1 group per nm²) created during the irradiation and etching processes. At neutral and basic pH, these pores are then negatively charged. Moreover, the surface chemistry of PET pores can be conveniently changed by attaching various groups to the carboxyls.

Figure 1 shows current-voltage curves of a nanopore modified with diamines using a standard organic chemistry procedure.⁴ Amines render the pore walls positively charged, and as a result, a reversed current-voltage curve was observed.^4,49,50 We use this flip in the current-voltage curve as a probe for the cation vs. anion selectivity and, by inference, the effective surface charge on the pore walls (negative for cation selective pores and positive for anion selective pores). We should emphasize that the current-voltage curves have this simple relation to ionic selectivity and surface charge only when the pore is homogeneously charged and the pore is surrounded by the same solution on both sides. We will show later that different bath compositions change the effective surface charge pattern of the pore. The new surface charge can be negative, neutral, or even positive in different regions of the pore, which will obviously change the pore’s selectivity properties.

The surface charge dependent rectification of conically shaped nanopores with homogeneous surface charges makes them ideal for studying charge inversion: a negatively charged pore that undergoes charge inversion should show a reversed current-voltage curve compared to the recordings performed in KCl (where charge inversion has not been reported). Sensitivity of the current-voltage characteristics to the properties of the pore walls also allows one to conveniently study the effect of polyvalent cations over a wide range of concentrations. At low concentrations of polyvalent cations, the net surface charge remains negative.²⁷ Increasing the concentration leads to the effective neutralization of the surface charges and for even larger polyvalent ions concentrations, the effective surface charge switches sign,²⁷ as we will show below.

We recorded current-voltage curves of single conical nanopores in solutions of divalent and trivalent cations, and compared the recordings with current-voltage curves in KCl. All measurements were done at pH 8 so that the pores had a surface charge of ~−1 e/nm². The solutions with salt concentrations of 1.0 M, 0.1 M and 20 mM contained 2 mM Tris buffer, pH 8.0. Solutions of lower concentrations were prepared by the serial dilution of buffered 20 mM solutions with de-ionized water. The pH of all solutions was confirmed with a pH-meter. The narrow opening of the pores used here had diameters between 2 and 6 nm. The wide opening was between 400 nm and 800 nm, thus the cone opening angle was less than 4 degrees.

We started with recordings in KCl since behavior of single conical nanopores in solutions of monovalent cations is best understood. As shown previously,^52,53 changing KCl concentration does not reverse the current-voltage curves of conical pores, suggesting that the pores remain cation selective. This is also shown in Fig. 2.

It is important to note that the measured currents are less dependent on the bulk ionic concentrations than it is expected from ionic conductivity of bulk solutions. This is because the currents through a conical nanopore are limited by the charged region at the narrow opening, where the majority of the pore resistance drops, and where the ionic selectivity of the pore is determined. This region extends several tens of nanometers from the pore opening. Ionic concentrations in this region are strongly influenced by the surface charges. A back-of-envelope calculation based on the necessity of electroneutrality shows that the difference in the concentration of counterions (e.g., potassium ions in case of our negatively charged pores) and the concentration of co-ions (Cl⁻) is given by: $\mathrm{\Delta }c=\frac{2\sigma }{er{N}_A}$ where σ is the surface charge density, e is the elementary charge, r is the pore radius, and N_A is the Avogadro number.⁵⁴ For r = 2 nm, thus at the tip of the cone, Δc is ~1.7 M, and further away from the cone opening, the concentration decreases. This average concentration difference is comparable to our Monte Carlo simulations (as shown later in Fig. 11). Moreover, for all electrolyte conditions examined in this article, the current-voltage curves did not indicate formation of any precipitates, which we studied in previous work.⁵⁵ Although local concentrations of K⁺ at the pore walls can be several molar, since there is almost no Cl⁻ at the walls, precipitation is unlikely (see our Monte Carlo simulations).

Figure 11.

Monte Carlo simulations of ions in a cylindrical nanopore of diameter 5.1 nm. The cation concentration was 10 mM. (A) The radial concentration profiles of all ions in the pore are shown as a function of the distance r from the pore center. Each ion profile has been scaled by its bath concentration thus the actual concentrations can be obtained by multiplying the presented values by the corresponding bulk concentration (e.g. for cations by 10 mM). With this scaling, if the normalized concentration is <1, then its concentration is lower than in the bath. The cation concentration profiles have dashed lines or open symbols and the corresponding Cl⁻ profiles have solid lines or solid symbols. Black: KCl. Red: CaCl₂. Green: CoSepCl₃. (B) The Cl⁻ concentrations from panel A are replotted on a linear scale. The concentrations in the actual nanotube will, of course, be different because it does not have a smooth, hard wall that produces a very sharp concentration peak at the pore wall; we only use this simple model to illustrate that charge inversion is quite likely. In these Monte Carlo simulations, ions are charged, hard spheres with Pauling diameters of 0.266 nm for K⁺, 0.198 nm for Ca²⁺, 0.890 nm for CoSep,²⁶, and 0.362 nm for Cl⁻. The dielectric constant of the entire system is 80. For the simulations we used the grand canonical ensemble. Using this ensemble is crucial in this situation because the concentration of the bulk system with which the electrolyte in the pore is in equilibrium can be established unambiguously. In this procedure, the simulation cell is connected to an external bath with fixed chemical potential of the salt through particle insertion/deletions. Neutral groups of ions (1 Ca²⁺ and 2 Cl⁻, for example) were used to maintain charge neutrality in the simulation cell in every moment of the simulation. The chemical potentials of the bulk electrolytes that corresponded to the prescribed concentrations were determined with the iterative method of Malasics et al.⁶⁶

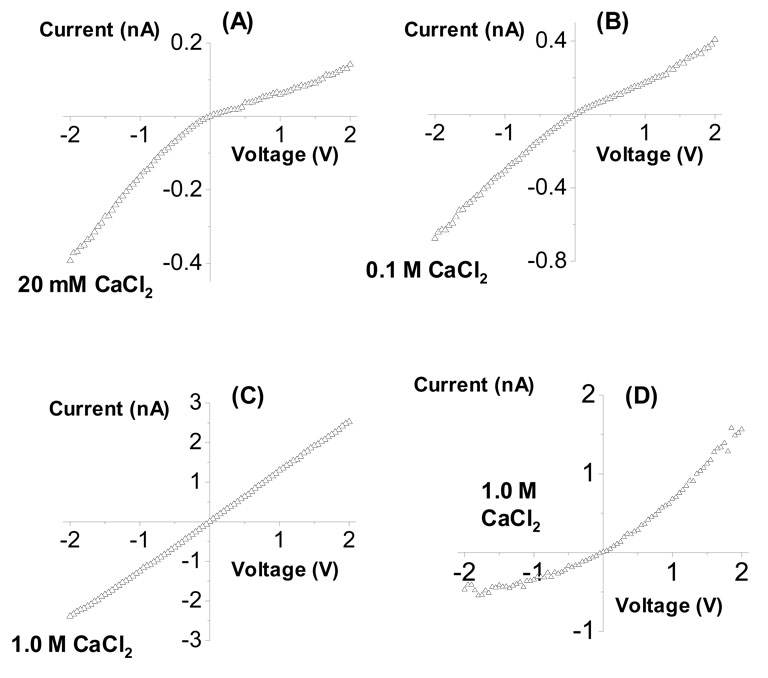
Figure 3 shows current-voltage curves of the same conical nanopore as in Fig. 2 at various concentrations of Ca²⁺. At 20 mM CaCl₂, we observed the same rectification behavior as recorded in KCl (Fig. 3A). Thus, Ca²⁺ at low concentrations does not reverse the surface charge. Increasing the Ca²⁺ concentration to 0.1 M, caused the current-voltage curve to become more linear compared to the recordings in 20 mM CaCl₂ (Fig. 3B). In 1 M CaCl₂, the current-voltage curve for some pores reversed suggesting an effective positive surface charge on the pore walls due to charge inversion (Fig. 3D).

Figure 3.

Current-voltage curves of a single conical nanopore as a function of CaCl₂ concentration: (A) 20 mM, (B) 0.1 M, (C) and (D) 1.0 M. Recordings in (A) – (C) were performed on one nanopore with the tip diameter of 3 nm (the same nanopore was studied with KCl in Fig. 2); recordings shown in (D) were performed on a different nanopore having a tip of 5 nm. The curves were recorded in symmetric CaCl₂ conditions and at pH 8.

However, some of the studied conical nanopores showed a linear current-voltage curve in 1 M CaCl₂, indicating a lack of ionic selectivity of these pores and no charge inversion (i.e., the switch of the effective surface charge sign was not observed, Fig. 3C). In these pores, the divalent ions seem to have only caused the effective neutralization of the surface charge. We believe that these differences in the pores’ behavior in 1 M CaCl₂ stem from differences in the local surface charge distribution in the narrow opening (the tip) of various conical nanopores produced by uncontrolled variations in the process that makes the pores. Sensitivity of transport properties to the local surface charge at the narrow opening was previously identified as a reason for different degrees of ion current rectification obtained with pores of similar opening diameters also in KCl solutions.^53,56 The concentration of polyvalent cations at which the surface charge switches sign is known to be directly related to the surface charge density of the pores walls,^32,33 in our case to the surface charge density at the pore tip.

For surfaces with lower surface charge densities, larger polyvalent cation concentrations are necessary to observe switching of the surface charge sign. Therefore, we believe that the two conical pores shown in Fig. 3C,D differed in local surface charge density, either because there were fewer carboxyl groups or because the tip diameter was larger than we estimated. It is important to note that pores, which did not reverse the current-voltage curves in 1 M CaCl₂, did not reveal the charge inversion at higher concentrations either. This is because, in our case, we detect the charge inversion via the effect of ion current rectification, which is related to the thickness of the electrical double-layer.^41,47,49 In highly concentrated solutions (e.g., 3 M CaCl₂), the electrical double-layer becomes too thin for the ion current rectification to occur. An additional effect that might hinder the observation of charge inversion at higher concentrations of polyvalent ions is the so-called surface charge regulation that diminishes the surface charge density with the increase of ionic strength.⁵⁷

We also studied the behavior of conical nanopores in the presence of trivalent cations, recording current-voltage curves in solutions of trivalent cobalt(III) sepulchrate (CoSep) chloride.^26,27 CoSep is a clathrochelate complex of cobalt that is approximately 0.89 nm in diameter.^26,58 The chemical structure is shown in the Supplementary Materials.⁴⁵ The CoSep cation has been used in studies of charge inversion in silica nanochannels.²⁷ Therefore, we chose this chemical (Sigma-Aldrich, product nr. 260991) as a test compound for charge inversion in our PET pores.

Figure 4 shows current-voltage curves of a single conical nanopore recorded in 1 mM and 10 mM CoSepCl₃. As reported previously for silicon dioxide nanochannels, 1 mM CoSep is close to the concentration at which the surface charge switches its sign, while 10 mM is already sufficient to switch the effective surface charge from negative to positive.²⁷ Our modeling (see below) is consistent with this. Our recordings also confirm these measurements: 1 mM CoSep induced ohmic behavior of the pore, while 10 mM CoSep reversed the current-voltage curves compared to KCl in negatively charged pores (Fig. 2). We believe that with 10 mM CoSep the pore effectively became positively charged and anion selective, because the current-voltage curve has the same shape as the recordings obtained with KCl for pores modified with amines (Fig. 1). It seems that, trivalent ions indeed induce charge inversion at much lower concentrations than divalent ions.

Figure 4.

Current-voltage curves of a single conical nanopore with the tip opening of 5 nm recorded in 1 mM CoSepCl₃ and 10 mM CoSepCl₃ present on both sides of the membrane. The recordings were performed at pH 8. The wide opening of this pore was 400 nm.

To confirm that it is the charge of the ion (and not its chemical character) that plays a dominant role in charge inversion we also studied the behavior of pores in CoCl₂. Current-voltage curves recorded in CoCl₂ were qualitatively very similar to the recordings in CaCl₂ (data not shown). This indicates that charge inversion depends most strongly on the ions’ valence.

Our hypothesis is that charge inversion in our system is due to the interactions of polyvalent cations (as well as anions) with the highly charged surface of the pore walls. To provide evidence for this, we modified the pore walls with amine groups, which resulted in a positively charged (and thus an anion selective) pore (Fig. 1). We expect that in a positively charged pore, Ca²⁺ and CoSep cations would be electrostatically repelled from the pore walls and the electrical double layer would be created with chloride ions. These amine modified pores are not expected to be affected by the polyvalent cations. Transport should not be changed. This is indeed what we observed experimentally (data not shown); the pores remained Cl⁻ selective in KCl, CaCl₂, and CoSepCl₃ solutions.

Studying charge inversion and ion selectivity in asymmetric electrolyte conditions

As the next step we probed in more detail the interactions of polyvalent cations with the carboxyl groups on the pore walls. We did that by measuring the transport properties of conical nanopores that were in contact with an electrolyte present in a final concentration between 20 mM and 1 M only on one side, either tip or base. The other side of the membrane was in contact with 10⁻⁶ M (or 10⁻⁵ M for CoSep) solution of a given salt, which we believe was low enough not to contribute significantly to the measured ion current. This approach allowed us to compare the currents carried separately by cations and anions. For example, with 20 mM KCl at the wide opening of a pore, positive voltages in our electrode configuration cause K⁺ to move across the membrane (Fig. 5). Since the other side of the membrane did not contain any significant concentration of ions, to a good approximation only K⁺ current was measured. For negative voltages, only Cl⁻ current was measured.

Figure 5.

Current-voltage curve of a single conical nanopore with the tip of 3 nm in diameter. The pore is in contact with 20 mM KCl on the base side, and with 10⁻⁶ M KCl on the tip side. For negative voltages the recorded current is due to Cl⁻, while for positive voltages K⁺ current is measured. The wide opening of this pore was 800 nm.

Since the electrolyte conditions on both sides of the membrane were different, finite junction potentials were created at the interface between an electrode and a solution in each half of the conductivity cell. The calculated junction potentials for all our experiments are given in the Supplementary Materials.⁴⁵

Our membranes contained only one nanopore and the volume of each half of the cell was ~1.5 ml. Diffusion of ions across the membrane was thus insignificant making the imposed concentration gradients very stable.

It is also important to mention that the resistance of the reservoir filled with 10⁻⁶ M solution of a given electrolyte is negligible compared to the resistance of the pore itself, as well as the resistance of the pore entrance. Only ~1 cm² of a polymer foil is exposed to solutions, thus the resistance of the reservoir with low concentration is several MΩ, which is three orders of magnitude lower than the resistance of studied single pores. The resistance at the pore entrance, typically referred to as access resistance, can under certain conditions become comparable to the resistance of the pore, as calculated from the pore geometry.⁴⁵ However, as discussed in,^45,59 even with a large voltage drop at the pore entrance, the measured current reflects the ion selectivity properties of the pore.

Figure 6 shows the results obtained with KCl in a single conical nanopore with the tip diameter of 3 nm. In both cases, with KCl placed on the tip or on the base side, the currents carried by K⁺ are larger than the currents carried by Cl⁻. This property does not change qualitatively with increasing KCl concentration, but the cation selectivity in higher KCl concentrations becomes weaker, in agreement with previous results.^16,52,53,60

Figure 6.

Current-voltage curves of a single conical nanopore with the tip of 3 nm in diameter. For the black curves, the base is in contact with KCl, while the tip side is in contact with 10⁻⁶ M KCl (see the upper inset). For the magenta curves, KCl is on the tip side with 10⁻⁶ M KCl on the base side (see the lower inset). (A), (B), and (C) show recordings with 20 mM, 0.1 M, and 1.0 M KCl, respectively. The wide opening of this pore was 800 nm.

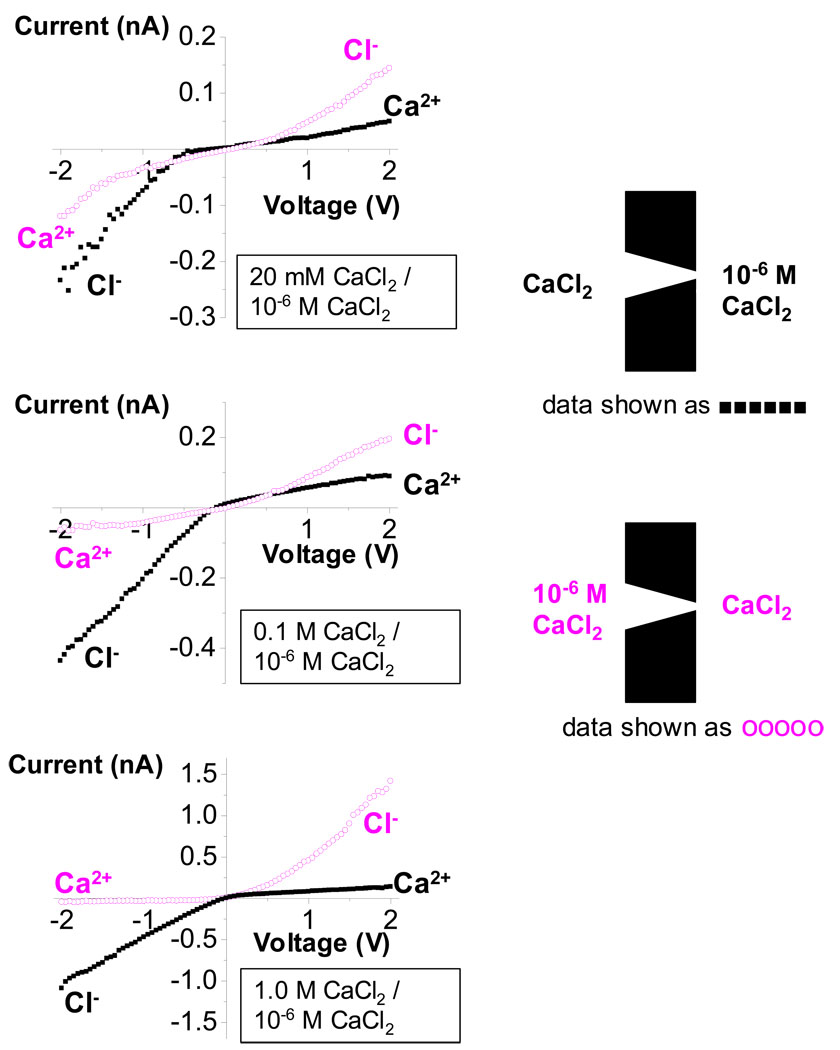
When CaCl₂ is substituted for KCl in the same pore, the rectification properties are reversed: with CaCl₂ at the tip, the currents at negative voltages—carried by Ca²⁺—became very small, while the currents at positive voltages—carried by Cl⁻—became significantly larger (Fig. 7B,C). Before, the K⁺ current was larger than the Cl⁻ current (Fig. 6). The pore is the same thus at high Ca²⁺ concentrations the selectivity properties of the pore have become more anion selective.

Figure 7.

Current-voltage curves of a single conical nanopore with the tip of 3 nm in diameter. For the black curves, the base is in contact with CaCl₂, while the tip side is in contact with 10⁻⁶ M CaCl₂ (see the upper inset). For the magenta curves, CaCl₂ is on the tip side, and 10⁻⁶ M CaCl₂ is on the base side (see the lower inset). (A), (B), and (C) show recordings with 20 mM, 0.1 M, and 1.0 M CaCl₂, respectively. With CaCl₂ at the tip, the ion current fluctuations for the voltages above 1V and −1V were large and reached ~ 30% of the signal that was averaged over three voltage sweeps. All recordings were performed in pH 8. The wide opening of this pore was 800 nm.

Moreover, at even higher Ca²⁺ concentrations, the behavior seems to change from just rectifying to diode behavior in which currents for one polarity of external voltage are essentially zero (Fig. 7B,C). This part of the current-voltage curve with very small currents is called the “off” state of a diode (see, for example, the magenta recordings for negative voltages in Fig. 7C). On the other hand, the other current-voltage branch with higher conductance represents the “on” state of the device (see, for example, the magenta recordings for positive voltages in Fig. 7C). Diode-like current-voltage curves in this system are surprising because diode behavior has not been observed before in nanotubes without specific chemical patterning of the pore walls.^4,5

Similar recordings were observed with CoSep, except that the diode-like behavior is even more pronounced than with Ca²⁺. Because of the lower concentrations of CoSep, the observed currents were significantly lower than the recordings with KCl and CaCl₂ (Fig. 8).

Below we discuss the diode behavior at high polyvalent ion concentrations in more detail. After that, we discuss the low concentration behavior. In the interpretation of the experimental data, the effect of electroosmosis has been neglected, because as shown before.^23,41 in sub-10 nm nanopores electrophoresis is the dominant effect. In future experiments we plan to evaluate the effect of electroosmosis in more detail.

Behavior of nanopores at high polyvalent cation concentrations placed on one side of single conical nanopores

To interpret the results above, we start with the recordings performed in 10 mM CoSep when these cations are at the tip of the pore. The base of the pore is in contact with 10⁻⁵ M solution of CoSep, thus the concentration is too low to significantly contribute to the measured ion current. According to our Monte Carlo simulations (see below) and our experiments, this concentration of CoSep is enough to switch the effective surface charge from negative to positive. One can estimate the distance over which these cations can affect the surface charge by considering CoSep as uncharged particles diffusing into an uncharged pore (described in detail in ref. 4). This is an approximation, but gives insight into the order of magnitude of the length scales over which charge neutralization and charge inversion can take place.

To compute this, we consider a situation with the following boundary conditions: 10 mM CoSep at the tip and 10⁻⁵ M CoSep at the base of a cone. The concentration decay of CoSep from 10 mM at the tip towards the base along the pore axis is very nonlinear because of the conical shape of the pores as well as the surface charges of the pore walls (described in detail in ref. 4). In a pore with 4 nm and 800 nm openings, the concentration decreases by ten times at a distance ~470 nm away from the tip (4% of the 12 µm long pore). Thus, only within ~500 nm of the tip is charge inversion possible. After the region of charge inversion, the effective surface charge becomes zero and then continuously becomes the original negative surface charge as the CoSep concentration drops to almost zero. This analysis suggests that we can indeed have junctions inside conical nanopores with positive surface charges induced by the polyvalent ions, and a zone that remains negatively charged. Moreover, the positively charged zone due to overcharging is a relatively short part of the pore.

Thus, the surface pattern obtained with 10 mM CoSep on one side of a conical nanopore resembles the surface pattern of a bipolar diode.^4,5,15 We illustrate this for 10 mM CoSep at the tip in Fig. 9. With the positively biased electrode on the base side, the Cl⁻ ions pass through the positively charged tip while CoSep is forced away from the tip; enough Cl⁻ current is conducted to make the “on” state of the diode. Conversely, at negative voltages Cl⁻ is forced away from the tip and CoSep into it. CoSep does not conduct easily because of the positive tip charge; very little CoSep is conducted to make the “off” state of the diode seen in Fig. 8B (magenta). These properties are stable at large voltages (up to ± 2V), which indicates that CoSep ions are tightly “bound” to the surface, possibly in the Stern layer.²⁷ The charge inversion is robust.

Figure 9.

Schematic of an ionic diode with local charge inversion induced by the addition of CoSepCl₃ at the tip of a conical nanopore. The other opening of the pore is in contact with 10⁻⁵ M CoSepCl₃, so the remaining parts of the pore walls are still negatively charged.

Charge inversion to switch the effective surface charge from negative to positive is possible only at high enough polyvalent concentrations (e.g., 10 mM CoSep or 1 M Ca²⁺). At lower concentrations or at lower surface charge, charge neutralization can occur. This is characterized by current-voltage curves that became linear, for example in 1 mM CoSep shown in Fig. 4 or some pores in 1 M CaCl₂ shown in Fig. 3C. When neutralization occurs, instead of a local positive surface charge there is a local region of effectively zero surface charge. This junction is the basis of a unipolar diode,^5,41 which also produces ion current rectification.^5,41

Therefore, the systems described here have the potential to create a chemically induced ionic diode whose properties may be qualitatively changed by washing with a different electrolyte solution or polyvalent cation concentration (Fig. 3 and Fig. 4). The system with high Ca²⁺ or CoSep concentrations can be used to create a bipolar ionic diode, while low concentrations of the ions form a unipolar diode. In general, specific ion concentrations used in both baths will make an effective surface charge profile that can change continuously from negative to zero, and even to positive. In other words, depending on the bath composition, these pores can have a wide range of effective surface charge profiles.

Preparation of bipolar and unipolar chemical diodes

In order to check the performance of the ionic diodes that are formed when charge inversion or neutralization occurs on one side of conical pores, we placed the pores between solutions of 10 mM CoSep and 10 mM KCl, as well as between 1 M CaCl₂ and 10 mM CaCl₂ (Fig. 10). In both cases with CoSep and Ca²⁺, very strong current rectification was observed, providing evidence that the diode junctions were indeed obtained in these systems. Insets to Fig. 10 illustrate the effective surface charge distributions formed on the pore walls. These ionic diodes are chemically induced and reversible. When the pores were washed and studied in symmetric electrolyte conditions, the current-voltage curves came back to the previous behavior, as shown in Fig. 2 and Fig. 3.

We were surprised by the asymmetric magnitude of ion currents in the “on” state in the diode system with CoSep (Fig. 10B); the negative currents recorded with KCl at the tip of the pore (black squares) were significantly larger than the positive currents recorded with KCl at the base of the pore (green triangles). We attribute this difference to the conical shape of the studied pores and the direction of the K⁺ flow. With KCl on the tip side, K⁺ is transported from the tip to the base, which is also a direction of the preferential transport of K⁺ in a homogeneously charged conical nanopore (see Fig. 1). On the other hand, when KCl is placed on the base side, K⁺ is transported in the direction that for a homogeneously charged pore is the low conductance state. Moreover, if the surface charge density induced by CoSep is smaller than the intrinsic negative surface charge density of PET, placing CoSep on the tip side means that the tip is filled with a lower concentration of ions, compared to the situation with KCl at the tip. The difference in the ion concentrations at the narrow opening of a pore when this opening is in contact with KCl or CoSepCl₃ can also contribute to the difference in the currents magnitude observed in Fig. 10 A.

Behavior of pores at low Ca²⁺ concentrations

We also compared the behavior of conical nanopores at low concentrations of CaCl₂ when it was present on both sides of the membrane and when it was placed only on one side. The I-V curves recorded in symmetric conditions with 20 mM and 0.1 M Ca²⁺ indicate cation selectivity and net negative surface charge of the pore walls (Fig. 3A,B). On the other hand, the I-V curves in asymmetric conditions did not confirm the cation selectivity; the anion currents were larger than or comparable to the cation currents (Fig. 7 A,B). This observation can be explained by assuming that Ca²⁺, even at low concentrations, strongly screens the negative charge on the pore walls in the narrow tip, decreasing the effective tip surface charge. In this case we obtained a junction between two negatively charged regions of the pore walls with different effective surface charge densities. This junction can also produce a rectification effect,⁴¹ seen strongly in the case with 0.1 M CaCl₂ (Fig. 7 A,B).

Studying current-voltage curves in conical nanopores with symmetric and asymmetric electrolyte conditions therefore gives unique insight into the screening of surface charges of the pore walls by transported ions. These recordings also show how the screening affects transport properties of these pores.

Modeling of charge inversion

To study the feasibility of charge inversion in these nanotubes, we performed standard Metropolis Monte Carlo simulations of hard-sphere ions in an infinite cylinder with diameter ~5 nm to approximate the small opening of the cone. We focused only on charge inversion and the cation vs. anion selectivity of the pores with different cations to illustrate how different regions of the pore can have different selectivity depending on the ions present in that region. Quantitatively reproducing the experimental data was not possible because of the approximate nature of the model and the natural limitations of the Monte Carlo simulations (e.g., identical baths on both sides of the membrane). Indeed, Monte Carlo simulations cannot predict current and calculations that extend Monte Carlo results to predict conductance are only valid under highly idealized linearizing conditions.

The infinite cylinder was modeled using periodic boundary conditions with standard Metropolis Monte Carlo techniques in the grand canonical ensemble.⁶¹ The hard walls of this cylinder had one discrete negative point charge in every 1 nm² square patch to approximate the carboxyl group surface charges; the exact pore diameter (5.1 nm) was chosen to fit an integer number of these tiles. The ions were hard spheres with Pauling radii and a charge at the center. Water was a background dielectric of 80. This is the simplest model that includes all correlations among the ions, but is simple enough to allow simulations to be performed in just a few hours.

Electrostatic correlations are necessary for charge inversion, and they are difficult to model. Monte Carlo simulations automatically include all such correlations (in equilibrium), that is why we use Monte Carlo here. Electrostatic correlations cannot be convincingly included in typical models, e.g. Poisson-Boltzmann (PB) theory.⁶² The PB theory (linearized or not) indeed does not produce charge inversion.³⁷ In PB, ion concentration profiles (namely, the one-particle distribution functions) depend only on the mean electrostatic potential (through the Boltzmann equation), which in turn depends only on the one-particle distribution functions (through the Poisson equation). However, ion concentration profiles also depend on the second- and higher-order correlation functions that describe the effects of two or more ions in different positions. The dependence is strong when ion concentrations are large, as they are likely to be in tiny nanopores. Charge inversion is the result of such second-order correlations, which in fact can produce the largest contribution to the electrochemical potential in such conditions.^28,63 Charge inversion cannot be produced by PB, but it can be produced by theories that include such correlations (density functional theory of fluids, integral equations, various modifications of PB). The Monte Carlo simulations we use here naturally include all these correlations.

Fig. 11 shows the results of Monte Carlo simulations for 10 mM KCl, CaCl₂, and CoSepCl₃. The figure shows normalized concentrations (not relative concentrations) of all the ions that have been scaled by their bath concentration. This explicitly shows if the concentration is less than in the bath and also allows direct comparison of the Cl⁻ concentrations which differ from 10 mM when K⁺ is the cation to 30 mM when CoSep is the cation.

In Fig. 11A all the ion concentrations are shown. With both KCl and CaCl₂, the pore is cation selective; throughout the pore the cation concentration is higher than in the bath (black and red dashed lines) and the Cl⁻ concentrations are lower than in the bath (black and red solid lines). With CoSepCl₃, the center of the pore becomes anion selective; the Cl⁻ concentration is higher than in the bath and the CoSep concentration is less than in the bath (green symbols).

At the edge of the pore, the CoSep concentration (Fig. 11A, green open symbols) is large enough to produce charge inversion, even with only 10 mM CoSep in the baths. This is shown in Fig. 11B. For CoSepCl₃, the Cl⁻ concentration profile (Fig. 11B, green solid symbols) has the “bump” near the wall that is characteristic of charge inversion;³⁷ a large anion concentration is needed to screen the effective positive surface charge created by overcharging negative wall with cations. CaCl₂ has a small bump, but any net Cl⁻ selectivity of the pore does not become significant until the Ca²⁺ bath concentration is ~1 M (data not shown). KCl never showed charge inversion. All these findings are consistent with our experiments.

These simulations then explain our experimental findings:

1. The screening of the wall carboxyl groups by the cations can reduce the effective charge of the pore from fully negative to zero and even to positive.

2. Charge inversion can occur for polyvalent cations in these nanopores at high enough concentrations, changing the selectivity properties of the pores.

Conclusions

In this article we showed how local charge inversion in conical nanopores can lead to the formation of diode junctions and ion current rectification. Our experiments with asymmetric electrolyte conditions gave insight into interactions of ions with chemical groups on the pore walls. They also allowed us to study separately currents carried by positive and negative ions.

The chemical ionic diodes based on conically shaped nanopores may be applied to lab-on-the-chip and biosensing systems. We have shown that the elements can work as ohmic resistors or diodes when divalent or trivalent ions are introduced, and as rectifiers in monovalent ions solutions—and that these properties can be quickly changed by washing with different electrolyte solutions. Ionic concentration dependent rectification of our nanoporous system also resembles the behavior of some biological channels, in which current rectification is induced by the presence of divalent ions.^64,65 It is also possible that the “off” state created by local charge inversion may be related to the shut states of biological channels.

Our experiments have significant implications for studying ionic selectivity of anopores. We have shown that the effective surface charge profile changes with ion species, their absolute concentrations, and their gradients. Depending on the ionic conditions, various diode junctions are created. Therefore, it does not make sense to discuss the selectivity properties of “the pore.” A given pore will have distinct classes of selectivities—not just one kind of selectivity—because unipolar and bipolar junctions have very different selectivities. Rather, the entire system must be considered, the pore and the bathing solutions together.

Supplementary Material

1_si_001

Supporting Information Available: Details on nanopore preparation and sizing, values of junction potentials in all electrolyte combinations used in the article, as well as Poisson-Nernst Planck calculations of ion current through a single conical nanopore in contact with KCl concentration gradients.