High phosphorylation efficiency and depression of uncoupled respiration in mitochondria under hypoxia

Abstract

Mitochondria are confronted with low oxygen levels in the microenvironment within tissues; yet, isolated mitochondria are routinely studied under air-saturated conditions that are effectively hyperoxic, increase oxidative stress, and may impair mitochondrial function. Under hypoxia, on the other hand, respiration and ATP supply are restricted. Under these conditions of oxygen limitation, any compromise in the coupling of oxidative phosphorylation to oxygen consumption could accentuate ATP depletion, leading to metabolic failure. To address this issue, we have developed the approach of oxygen-injection microcalorimetry and ADP-injection respirometry for evaluating mitochondrial function at limiting oxygen supply. Whereas phosphorylation efficiency drops during ADP limitation at high oxygen levels, we show here that oxidative phosphorylation is more efficient at low oxygen than at air saturation, as indicated by higher ratios of ADP flux to total oxygen flux at identical submaximal rates of ATP synthesis. At low oxygen, the proton leak and uncoupled respiration are depressed, thus reducing maintenance energy expenditure. This indicates the importance of low intracellular oxygen levels in avoiding oxidative stress and protecting bioenergetic efficiency.

Atmospheric oxygen levels were probably 0.1% of the present when mitochondria became associated with cells early during evolution (1–4). Such low-oxygen conditions persist in extreme environments (5–8), and oxygen pressures as low as 0.3–0.4 kPa (2–3 mmHg) are observed in the intracellular microenvironment of mitochondria in tissues under normoxia (9–13). Even so, in typical studies with isolated mitochondria, these organelles are artificially exposed to the high partial pressure of oxygen at air saturation (≈20 kPa), despite the fact that this condition is effectively hyperoxic, is rarely physiological, and increases oxidative stress (14, 15). The aim of this paper is to quantify the efficiency of oxidative phosphorylation under oxygen limitation. When a tissue experiences hypoxia, small amounts of oxygen can exert a vitally important influence on cellular energetics (16–18). The key question is whether or not mitochondrial coupling is maintained under conditions when oxygen supply to the mitochondria exerts control over cellular respiration (19–21). To investigate this paradigm of bioenergetics at low intracellular oxygen, we chose as relevant models mitochondria from rat liver and the anoxia-tolerant embryo of the brine shrimp, Artemia franciscana. The latter is the quintessential example of an animal capable of extreme metabolic depression in response to oxygen limitation (22). The absence of energy expenditure on transepithelial ion pumping, coupled with global reductions in gene expression, allow this encysted embryo to reduce metabolic rates to values approaching ametabolic under anoxia (23) and survive in this state for years (24). Consequently, mitochondria from this source provide an ideal reference for studies aimed at evaluating phosphorylation efficiency at low oxygen.

Materials and Methods

Preparation of Mitochondria.

Mitochondria were isolated from livers of Sprague–Dawley rats (25) and gastrula-stage embryos of Artemia franciscana (26). For respirometry and microcalorimetry, mitochondrial protein concentrations were 0.21–0.58 mg/ml for rat liver and 0.26 mg/ml for Artemia. Incubation media for rat liver (in brackets for A. franciscana) mitochondria were: 3 [20] mM K-Hepes/230 mM sucrose [500 mM trehalose/150 mM KCl]/10 [10] mM KH₂ PO₄/0.5 [1.0] mM EGTA/11 [3] mM MgCl₂/1.5 [0.5] mg/ml fatty acid-free BSA/2 [1] mM ATP/5 [5] mM K⁺ succinate/5 [5] μM rotenone, pH 7.35 [7.5]. Oxygen solubilities for these media were 10.5 [11.4] μM O₂/kPa at 25°C. The concentration of ADP in stock solutions was verified by spectrophotometry. Contamination by AMP was undetectable by HPLC. Dinitrophenol stocks were prepared in DMSO and rotenone in ethanol; the final concentration of organic solvent in the incubation media did not exceed 0.5%.

Microcalorimetry and High-Resolution Respirometry.

Heat flux was measured at 25°C with a 2277 Thermal Activity Monitor (Thermometric, Järfälla, Sweden) in the titration configuration (27) at a stirring rate of 110 rpm. The calorimetric signal was corrected for an exponential time constant of 240–280 s determined from electrical calibrations and for nonlinear baseline drift by using datlab software.

An electronically controlled titration-injection micropump (Oroboros Instruments, Innsbruck, Austria) was used for steady-state injection or pulse-titration of air-saturated or anoxic medium through stainless steel cannulae. To minimize disturbances of the injection on the heat and oxygen signals, the injection flow was ≤0.3 μl/s. Mitochondrial protein concentrations were corrected for dilution effects that were <4%.

High-resolution respirometry (Fig. 1) was performed at 25°C with Oroboros Instruments oxygraph and datlab software (18, 28). Data were averaged over 1-s intervals, digitally recorded each second as oxygen concentration, c_raw(t), and corrected for the response time of the oxygen sensor (18),

1

c_O2(t) is the corrected oxygen concentration, and the exponential time constant, τ, was 5 s at a stirring rate of 500 rpm by using a glass-coated magnetic stirrer. The data were smoothed by using a 5-point moving polynomial fit, which reduces noise but retains the time resolution during rapid changes of oxygen flux. Oxygen flux was calculated as the negative time derivative of c_O2(t), by using a symmetric fit through 10 data points. The effect of time correction is particularly important during the first 10 s after a pulse injection of ADP (Fig. 1D). Standard corrections were performed for instrumental background oxygen flux arising from oxygen consumption of the oxygen sensor and minimum back-diffusion into the chamber (18). In addition, corrections were applied for oxygen in the injected and ejected volume during ADP-pulse titrations and steady-state injections. Because oxygen concentration in the respirometer changes with time, the corrections were calculated continuously over the entire oxygen range (J_O2^pump in Fig. 1E) by using algorithms supported by datlab software. The dependence of mitochondrial respiration on oxygen pressure was determined up to 1.1 kPa, as described (18, 21, 28).

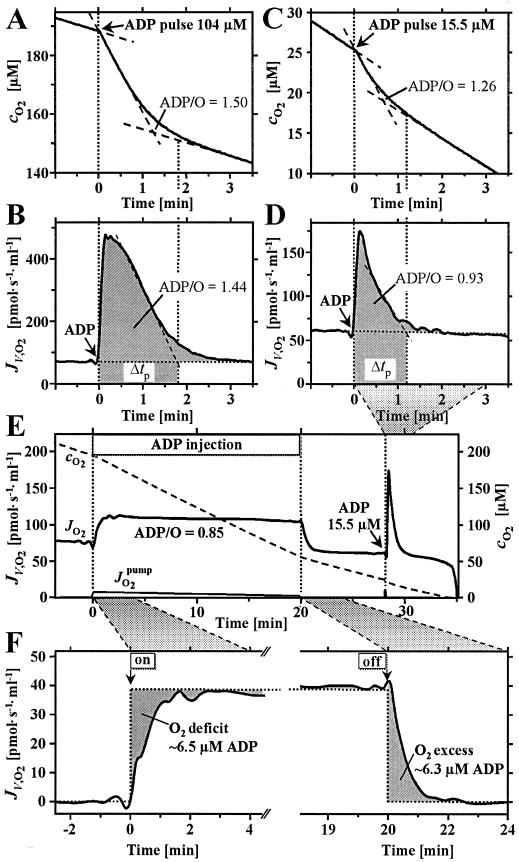
Figure 1.

High-resolution respirometry for determination of ADP/O flux ratios at various levels of ADP stimulation (rat liver mitochondria, 0.21 mg protein/ml). In the conventional analysis of oxygen concentration, c_O2 (A; solid line), linear extrapolations (dashed lines) are made during respiration at state 3 after ADP titration, and at state 4 after ADP depletion. The difference of oxygen concentrations at the intercepts is the total oxygen uptake (29–31). Lower ADP/O ratios were obtained in analyses based on oxygen flux, J_V,O2 (pmol/s/ml) (B) rather than oxygen concentration (A). When initial ADP concentrations are limiting, the ADP/O flux ratio is overestimated by 35% in the conventional analysis (C), owing to the lack of a linear decline in oxygen concentration after ADP stimulation and a sharp peak of oxygen flux (D). At 104 and 15.5 μM initial ADP concentrations, maximum oxygen flux was 6.9- and 2.9-fold above state 4 (ADP regulation ratio; compared with the respiratory control ratio of 7.6 at saturating ADP levels). Evaluation of this integration method was performed by the novel approach of ADP steady-state injection, where the ADP flux set by the pump is divided by the observed steady-state oxygen flux, yielding the total ADP/O flux ratio directly (E; ADP regulation ratio 1.6). After stopping the injection pump, flux returned to state 4, and an ADP titration was performed in the same experiment. The transition periods after switching ADP supply on and off provide the basis for calculating the steady-state ADP level (F).

Microcalorimetric Determination of the Ratio of ADP Flux to Total Oxygen Flux (ADP/O Ratios).

During microcalorimetric measurements, a constant respiratory flux was set by steady-state oxygen injection by using air-saturated medium at a flow of 0.3 μl/s over 20-min periods. Mitochondria (1.32 and 0.66 mg protein) were suspended in a volume that increased from 2.2 to 2.9 and from 2.7 to 3.4 ml during injections for experiments with rat and A. franciscana mitochondria, respectively. The injection medium was identical to the incubation medium but was air saturated and contained 600 μM instead of 100 μM MgADP, to maintain ADP levels constant during oxidative phosphorylation. The heat effect of continuous injections was measured in the absence of mitochondria (−1.0 μW) and subtracted from the experimental heat flow measured above the anoxic baseline. Anoxic conditions before and after oxygen injections were achieved with an argon atmosphere above the stirred solution and were confirmed by measuring an unchanged heat flow from uncoupled mitochondria (140 μM dinitrophenol) on addition of 1.5 mM KCN. Heat flux of coupled and uncoupled mitochondria was measured sequentially in each experiment at an identical oxygen flux maintained for 20-min periods. As presented in Results, ADP/O ratios were derived from the heat/O₂ flux ratios and the molar enthalpy of phosphorylation of ADP to ATP.

Respirometric Determination of ADP/O Flux Ratios.

Analogous to steady-state oxygen-injection microcalorimetry, we developed the approach of steady-state ADP-injection respirometry for the determination of ADP/O flux ratios corresponding to defined states of ADP limitation at saturating oxygen levels. For comparison, conventional ADP-pulse titration (29–31) entails nonsteady-state transitions (Fig. 1A). The corresponding recorder traces of the oxygen signal appear to be linear (Fig. 1A), yet the computed instantaneous time derivatives reveal a gradual decline in oxygen flux over the activation period (Fig. 1B). The lack of linearity of the oxygen slope is particularly apparent at high ATP concentration (32) and at small ADP pulses below saturation levels (Fig. 1 C and D). Because the initial ATP concentration was 2 mM in our experiments, the relative change of ATP was small even after pulses of 300 μM ADP. Owing to the fact that the ATP/ADP concentration ratio is identical before and after the pulse, the added ADP is completely converted to ATP under these conditions (compare ref. 31). Analysis of ADP pulses was improved by integration of oxygen flux over the empirically defined duration of the oxygen peak, Δt_p (Fig. 1 B and D; hatched areas, including the tail end of oxygen flux elevated above state 4 respiration). Compared with conventional calculations of oxygen concentration differences, lower ADP/O flux ratios were obtained by the analysis based on integration of flux (Fig. 1 A–D). This integration method was evaluated by the novel approach of steady-state ADP injection.

Steady-state injection of ADP into the oxygraph chamber sets the flux of mitochondrial ADP consumption and thus activates oxygen flux (Fig. 1E). Division of the rate of ADP injection by the oxygen flux measured at steady-state yields the total ADP/O flux ratio directly. As opposed to steady-state approaches with hexokinase or creatine kinase as ADP-regenerating enzyme systems (25, 33, 34), physiologically relevant high ATP concentrations can be used and no rapid termination of the reaction is required for chemical analyses. The transition periods after switching ADP supply on and off provide the basis for calculating the ADP level established during steady-state injection (Fig. 1F). Integration of oxygen consumption relative to the ideal square wave yields a symmetrical apparent oxygen “deficit” and “excess” after switching ADP injection on and off. Multiplication by the experimental ADP/O ratio (×2) yields the steady-state ADP level. Results obtained by this approach were verified by HPLC analysis of samples obtained during steady-state ADP injection.

Results

Oxygen-Injection Microcalorimetry.

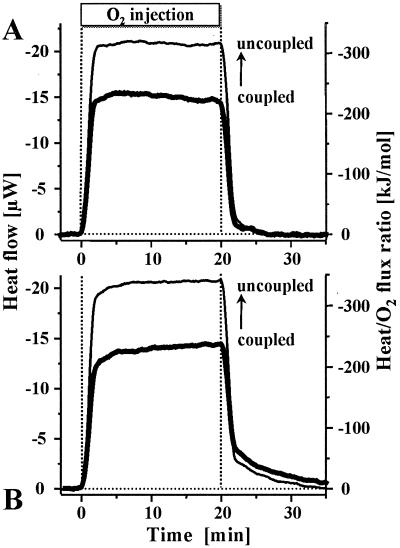
Under nonlimiting oxygen conditions, mitochondrial respiration in the absence of ADP proceeds at a resting rate that maintains a high mitochondrial membrane potential under nonphosphorylating conditions (35–37). To test whether or not ATP production is even possible at oxygen fluxes below this maintenance level, oxygen supply was set at 20–30% of the minimum aerobic rate by continuous injection of air-saturated medium into a suspension of anoxic mitochondria. At steady state, this rate-limiting oxygen supply served as a direct measure of respiration rate at a constant low oxygen level. Simultaneously, the phosphorylation rate was evaluated by microcalorimetry. Fig. 2 depicts the heat flow of hypoxic mitochondria measured during oxygen injection before and after chemical uncoupling. Chemical uncoupling provides the reference state of maximum proton conductance, prevents any conservation of energy in the form of ATP, and thus reduces the chemical process to simply the oxidation of succinate. The corresponding molar enthalpy change for oxidation to fumarate and malate is −297 and −312 kJ/mol O₂ (38), and the equilibrium ratio of malate to fumarate is 4.1 in a mitochondrial incubation medium (39). These values allow one to calculate a theoretical oxycaloric equivalent of −309 kJ/mol O₂. In complete agreement, our measured heat/O₂ flux ratio was −320 ± 14 kJ/mol (mean ± SEM, n = 8). Similarly, −303 kJ/mol O₂ is reported for uncoupled submitochondrial particles (40). In the absence of uncoupler, substantially less heat was dissipated at the same respiration rate, thus demonstrating that coupled oxidative phosphorylation and the conservation of energy in ATP are maintained under oxygen limitation at efficiencies of 31–34% (Fig. 2).

Figure 2.

Oxygen-injection microcalorimetry with mitochondria isolated from rat liver (A) and A. franciscana embryos (B) at limiting oxygen supply (0.050 and 0.092 nmol O₂/s/mg protein, respectively). In the first section of each experiment, respiration was coupled to oxidative phosphorylation, whereas the mitochondria were chemically uncoupled in the second section (superimposed). Because oxygen flux was identical for both treatments, the measured heat flux (μW = μJ/s; left ordinate) is directly proportional to the heat/O₂ flux ratio (right ordinate). In the coupled state, the heat/O₂ flux ratios were (A) 31% (±3.9 SEM; n = 4) and (B) 34% (±3.7 SEM; n = 4) below the uncoupled value, indicating the thermodynamic (enthalpic) efficiency of oxidative phosphorylation.

Oxygen Dependence of Mitochondrial Respiration.

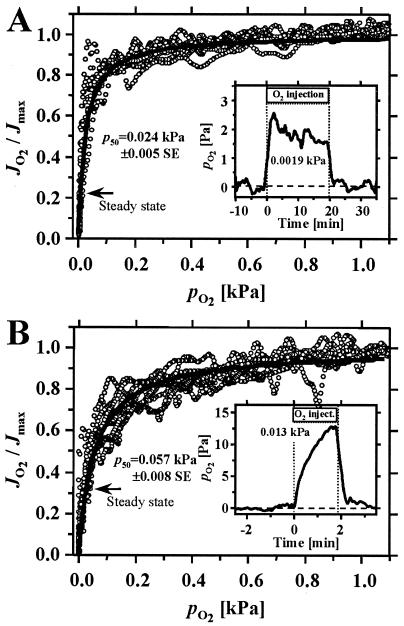
Because of the high oxygen affinity of mitochondrial respiration (Fig. 3), steady-state oxygen pressure was maintained low during oxygen-injection experiments (Fig. 3 Insets). In fact, the steady-state oxygen pressures were well below the p₅₀, the partial pressure of oxygen at which respiration is half maximal (Fig. 3). Surprisingly, the oxygen affinity of the Artemia embryo mitochondria was lower (i.e., the p₅₀ was higher) than that of rat liver mitochondria. No comparison is available for mitochondria from any other invertebrate species (for a bacterial respiratory heme-copper oxidase, see ref. 41). In rat liver mitochondria, the p₅₀ at 25°C (0.024 kPa or 0.18 mmHg; Fig. 3A) was comparable to the value of 0.020 kPa obtained at 30°C in the absence of ADP (refs. 21 and 28; cf. ref. 16). Similarly, the p₅₀ for resting rat heart mitochondria is as low as 0.016 kPa (refs. 21 and 28; cf. refs. 42 and 43), but the p₅₀ generally increases 2- to 3-fold on stimulation of respiration by ADP (21, 28, 44).

Figure 3.

Dependence of respiration on oxygen partial pressure, p_O2, in the absence of ADP at high ATP (state 4) in mitochondria isolated from rat liver (A) and A. franciscana embryos (B). Individual data points of all recordings are shown by symbols (○); the average hyperbolic fits are shown by full lines. The p₅₀ (±SEM; n = 6 preparations; 1–3 replicas each), calculated from hyperbolic fits for individual traces, was significantly different between the rat liver and Artemia mitochondria (P < 0.05; two-tailed t test). (Insets) Hypoxic oxygen regimes were measured in the respirometer during O₂ steady-state injection under conditions identical to those in the microcalorimeter (Fig. 2). (Inset A) The average p_O2 is given at steady state (n = 3). (Inset B) The average p_O2 represents the maximum obtained after 2 min (n = 2). The extent of oxygen limitation during calorimetry experiments is illustrated by transposing these p_O2 values onto the profiles for oxygen kinetics (arrows, labeled steady state); (1 kPa is equivalent to 7.501 mmHg.)

ADP/O Flux Ratios.

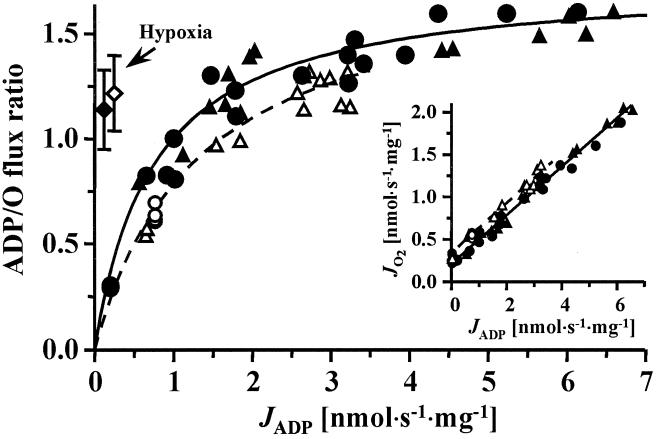
From the reduction in the heat flow of coupled relative to uncoupled mitochondria at constant oxygen consumption (Fig. 2), one can calculate the phosphorylation of ADP to ATP per unit of oxygen consumed, i.e., the total ADP/O flux ratio. The difference in heat/O₂ flux ratios between coupled and uncoupled states was divided by 2 to convert molecular heat/O₂ flux ratios to atomic heat/O ratios. The latter were then divided by 44 kJ/mol ATP, i.e., the enthalpy conserved per mol ATP synthesized under the experimental conditions used in our studies (45). The resulting ADP/O ratios were 1.14 ± 0.19 (SEM; n = 4) for rat liver mitochondria and 1.22 ± 0.18 (SEM; n = 4) for Artemia mitochondria.

To establish an appropriate perspective from which to interpret these phosphorylation efficiencies obtained during hypoxia, we studied ADP/O ratios under conventional conditions of air saturation, where respiration was limited by ADP rather than oxygen availability. At such elevated oxygen pressures, the total ADP/O flux ratios [in contrast to the mechanistic P/O stoichiometry; 46§] fall markedly as ADP flux is lowered to the values of the hypoxia experiments (Fig. 4). The hyperbolic decline in the ADP/O flux ratio with increasing ADP limitation (Fig. 4) is a direct consequence of the linear relation between oxygen flux and ADP flux, and results from the increasing proportion of nonphosphorylating respiration as the resting state is approached (Fig. 4 Inset). A similar pattern is seen when respiration is limited by low hexokinase or ATPase activity (33, 49–53), inhibition of ATP/ADP translocation by carboxyatractyloside (47, 54) or of ATP synthesis by oligomycin (33). In contrast, when the electron transport chain is inhibited by malonate (31, 33, 47), ADP/O flux ratios remain high, comparable to our results based on oxygen limitation. However, severe inhibition of electron transport by antimycin A fails to protect high ADP/O flux ratios (ref. 47; but see ref. 53). Thus, at comparable loads (i.e., ADP fluxes), our data show that mitochondria under hypoxic conditions maintain substantially higher ADP/O ratios than do mitochondria under nonphysiologically high oxygen tensions (Fig. 4). This is a demonstration that phosphorylation efficiencies of mitochondria are high during oxygen limitation, when compared with those under air saturation at the same rate of phosphorylation. That this phenomenon is quantitatively identical in rat liver and Artemia mitochondria suggest that minimization of uncoupled respiration may be a general response to hypoxia.

Figure 4.

Total ADP/O flux ratio as a function of ADP flux, J_ADP, under aerobic conditions compared with the hypoxic conditions (diamonds with SEM bars). Closed symbols, rat liver mitochondria; and open symbols, A. franciscana mitochondria. Aerobic ADP/O ratios fall markedly as ADP fluxes are lowered to the values observed during the hypoxic experiments. Analysis of 95% confidence limits for hypoxic ADP/O ratios, compared with those for hyperbolic fits of the aerobic data, indicate the differences are statistically significant (P < 0.05). (Inset) Linear slopes of oxygen flux as a function of ADP flux were calculated without the data points at zero ADP flux (state 4) and were identical for rat liver (0.283 ± 0.006 SEM) and A. franciscana mitochondria (0.283 ± 0.014 SEM). Full agreement was established between the steady-state fluxes obtained by ADP-injection respirometry (circles) and average fluxes in ADP-pulse respirometry (triangles). The latter were calculated by dividing the initial ADP concentration and the integrated oxygen concentration by the time interval of the oxygen peak (Fig. 1 C and D).

Discussion

Two mechanisms may explain our observation that oxidative phosphorylation at low flux is a more efficient process under hypoxia compared with air saturation. Both mechanisms involve depression of uncoupled respiration, and they are not mutually exclusive. First, because the redox span of the electron transport chain is reduced under oxygen limitation (18), Δp is prevented from increasing into the range of exponential acceleration of the proton leak or slip at low ADP load (36, 55, 56). Interestingly, the first measurements of the mitochondrial proton leak were conducted under severe hypoxia, yielding a low proton leak without artificial elevation of Δp (35).

A second mechanism for maintaining high ADP/O ratios under hypoxia involves reduced ion permeability of the mitochondrial membrane (57). Under conditions of metabolic down-regulation in anoxic tissues, reduction of plasma membrane conductivity for ions is well recognized as a primary adaptive mechanism (58–60). Until now, however, the energetic advantage of reducing ion leaks through the mitochondrial inner membrane under hypoxia has not been addressed. Our observation of high ADP/O ratios at low oxygen suggests an expanded role for the regulation of membrane leaks as an adaptive mechanism in resting states and environmentally imposed hypometabolic states. Reduced production of reactive oxygen species at low p_O2 and low Δp¶ (14, 15, 61, 62) may be critical in controlling leaks, for example, by lowering oxidative damage to membranes, reducing calcium cycling, or closing the mitochondrial permeability transition pore (62–65). The importance of oxidative stress and mitochondrial function is recognized in the context of aging, apoptosis, and ischemia-reperfusion injury (66–71). From the present study, it can be inferred that air saturation as a reference condition is questionable for evaluating mitochondrial efficiency. If representative measures of performance are to be obtained for mitochondria and even cultured cells (42, 44), then oxygen tension should be shifted away from these nonphysiological levels to minimize the risk of oxidative stress. Considering that the oxygen dependence of mitochondrial respiration (Fig. 3) extends well into the physiological range (9, 16, 28) and may be accentuated by competition with nitric oxide (72, 73), our findings underscore the importance of evaluating the efficiency of mitochondrial energy transformation under physiological levels of oxygen. Furthermore, the high efficiency of oxidative phosphorylation at low oxygen emphasizes that even trace amounts of oxygen can make a vital energetic contribution when ATP limitation threatens cellular survival under severe hypoxia encountered at high altitude, in aquatic habitats, and during pathological states of ischemia.

Abbreviation

ADP/O ratio

ratio of ADP flux to total oxygen flux