A thermodynamic approach to PCR primer design

Abstract

We developed a primer design method, Pythia, in which state of the art DNA binding affinity computations are directly integrated into the primer design process. We use chemical reaction equilibrium analysis to integrate multiple binding energy calculations into a conservative measure of polymerase chain reaction (PCR) efficiency, and a precomputed index on genomic sequences to evaluate primer specificity. We show that Pythia can design primers with success rates comparable with those of current methods, but yields much higher coverage in difficult genomic regions. For example, in RepeatMasked sequences in the human genome, Pythia achieved a median coverage of 89% as compared with a median coverage of 51% for Primer3. For parameter settings yielding sensitivities of 81%, our method has a recall of 97%, compared with the Primer3 recall of 48%. Because our primer design approach is based on the chemistry of DNA interactions, it has fewer and more physically meaningful parameters than current methods, and is therefore easier to adjust to specific experimental requirements. Our software is freely available at http://pythia.sourceforge.net.

INTRODUCTION

The polymerase chain reaction (PCR) (1), a method for making many copies of a specific DNA fragment, is one of the most widely applied tools in modern molecular biology (2). Crucial to the success of a PCR is the choice of the primers that flank the template to be copied. These primers must fulfill a number of criteria, and research into primer selection has been ongoing since the advent of PCR (3–7). Primer design is an unsolved problem, especially in studies where regions must be comprehensively analyzed by PCR assays. We focus especially on PCR primer design for regions in repeated sequences, because repeated sequences are not amenable to standard primer design approaches and yet comprise a significant fraction of mammalian genomes.

Our motivation is to develop theoretically guided methods for predicting primer quality. The primary difficulty that we seek to address in PCR primer design is how to predict primer quality—defined here as the ability to efficiently and specifically amplify the desired template fragment—on the basis of the primer sequences, template and the background genome sequence. Our theoretically motivated methods have two significant benefits compared with commonly used ad hoc primer scoring schemes. First, they take advantage of accurate methods for assessing DNA binding (8,9) and folding stability (10); these accurate assessments are critical because PCR relies fundamentally on DNA binding reactions. Second, a physically motivated approach reduces the number of parameters that must be chosen, and shifts the emphasis of primer selection from choosing arbitrary thresholds for quality scoring metrics to specifying physically meaningful reaction conditions and primer quality criteria.

Standard methods for primer design compute a variety of quality metrics in order to evaluate various aspects of primer quality and then combine these individual metrics into a final score using a weighted sum (3–5). These quality scores account for considerations such as primer melting temperature, thermodynamic stability of a primer at the 3′-end, and a variety of other criteria motivated by practical experience with PCR. In this approach, many metrics contribute to the final prediction of primer quality, and a weight for each individual quality metric must be specified in order to obtain the final primer pair score.

However, selecting these quality metric weights presents two significant difficulties. First, these metrics are not always physically interpretable, and second, they can be redundant. For example, good PCR primers should not stably bind to other primers (forming so called primer dimers); if they bind stably to other primers, then they are much less likely to participate in the desired priming reaction. The widely used program Primer3 (6) uses two Smith–Waterman alignment-based metrics to assess the likelihood of a primer binding to itself or the other primer: the max-complementarity metric and the max-3′-complementarity metric. The difference between these two metrics is that one considers overall similarity between two primer sequences, and the other considers similarity anchored at the 3′-ends, as computed by Smith–Waterman alignment scores. These metrics are redundant because high 3′-anchored similarity implies high overall similarity, and these metrics are thermodynamically inaccurate because they do not account for known effects in DNA binding interactions such as the sequence specificity of single internal mismatches (11). Consequently, selecting appropriate weights for these two metrics for the final quality evaluation presents significant difficulties. These difficulties are compounded by the large number of quality metrics that must be weighted for the final primer quality metric. For example, Primer3 has more than 25 weights that must be specified in the primer design process.

We address the problem of choosing acceptable and specific PCR primers for a locus given a genomic DNA sequence, a set of user supplied parameters and constraints, and the coordinates of the locus. Pythia calculates binding and folding energies for a variety of relevant chemical species, and then integrates these calculations into a final measure of PCR efficiency. Below, we describe how these energies are computed and then integrated into our final quality metric. Because computing the final primer efficiency measure is a bottleneck in the screening of primer candidates, we then describe a machine learning approach to predict primer acceptability on the basis of free energy calculations; this classification approach allows us to quickly eliminate infeasible candidates.

In addition to predicting whether the primers will amplify a given locus, we also evaluate the primer specificity. Specific primers will amplify only the desired locus, whereas nonspecific primers have binding sites in the background DNA that lead to undesired copying of background fragments in addition to the target locus. In order to predict primer specificity, we use a precomputed index, in conjunction with a thermodynamic heuristic for predicting primer specificity. Following Miura et al. (12), we identify the shortest sequence at the 3′-end of each primer that could bind stably, and then we identify exact occurrences of this sequence in the background genomic DNA using our precomputed index.

In order to test Pythia, we compared our method with a highly optimized primer selection strategy used for several high-throughput studies (13–15). This method used Primer3 for designing primers and a method focused on the 16 bases at the 3′-end of each primer for predicting specificity. We focused on the problem of tiling genomic regions, in which primers are placed to cover as much of a selected genomic region as possible, with minimal overlap between adjacent PCR products. We show in this work that our approach to evaluating primer quality and specificity is more accurate than current approaches. Furthermore, Pythia has fewer adjustable parameters than current approaches, and these parameters are more physically meaningful. Thus, Pythia is easier to tailor to specific reaction requirements.

MATERIALS AND METHODS

DNA binding and folding energy calculations

We use statistical mechanical models of DNA to compute the binding affinity between the relevant DNA dimers in a PCR reaction (8,9). These models use dynamic programming to evaluate the stability of many configurations in which one molecule is bound to the other via at least 1 bp, and they integrate the stabilities of all of these conformations into a final stability prediction. We use a set of thermodynamic parameters (11) that specify the energetic contributions of base pairing and stacking, as well as internal and hairpin loops, to the thermodynamic stability of DNA duplex molecules.

A different statistical mechanical approach has been developed to predict the folding energy of a nucleic acid molecule (10). There are several dynamic programming algorithms available to derive final folded stabilities. We do not consider folding conformations with pseudoknots, so that we can employ a dynamic programming algorithm with a computational complexity of O(n⁴) in the length of the folded sequence rather than O(n⁷) (16) when pseudo-knots are considered. We use the same thermodynamic parameters as for the binding energy computations.

Chemical reaction equilibrium analysis

The objective of chemical reaction equilibrium analysis is to identify the equilibrium concentrations of all chemical species in a system of simultaneous reactions. This analysis is done by gradient descent optimization, where the quantity being minimized is the Gibbs energy G (17), expressed as

1

where n_i is the amount of each species, in units of moles per liter, and μ_i is the chemical potential of the species.

For DNA dimerization reactions, we use (9)

2

for the chemical potential, where ΔG is the free energy of binding, R is the molar gas constant, T is the temperature in degrees kelvin, n^A is the initial amount of one strand participating in the binding reaction and n^B is the initial amount of the other strand participating in the reaction. For DNA folding chemical potentials, we use

3

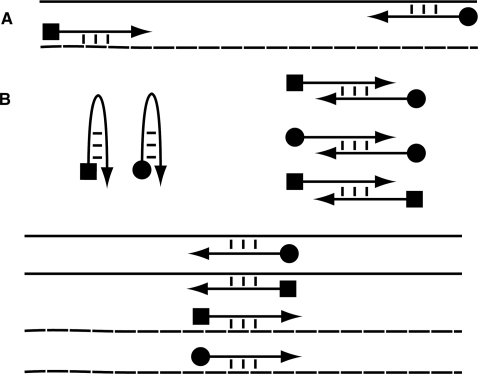
In a PCR, many reactions simultaneously compete for single unbound target fragments. We consider 11 reactions that compete for single unbound strands; these reactions are depicted in Figure 1. In particular, we consider primer folding, primer dimerization, primers binding to template outside of the priming region and primers binding to template in the priming region. Of these reactions, only the last type is desired; the rest should be minimized. However, PCR can work in the presence of some primer folding and dimerization, provided the primers bind well to the priming regions. In order to balance these considerations, we use chemical reaction equilibrium analysis (17).

Figure 1.

Species accounted for in primer feasibility analysis. The solid line is the top strand of the template;the dashed line is the bottom strand of the template; the arrow with the square end is the left primer; the arrow with the round end is the right primer; three dashed lines indicate binding (or folding) via hydrogen bonding. (A) Desired binding interactions. High rates of binding are desired between the primers and the template priming regions. (B) Undesired binding and folding reactions. Primers should not fold, dimerize or bind to the target outside of the priming regions.

Chemical reaction equilibrium analysis determines the concentration of each chemical species at thermodynamic equilibrium; in this context, we obtain the concentration of each DNA folded, unfolded and dimer species. In order to evaluate the feasibility of a primer pair, we compute the free energy of all of the duplex and folded forms at a late stage in an idealized PCR and then compute the equilibrium concentration of all of these species as described above. We perform this analysis at a late stage of an idealized PCR in order to screen for problematic interactions between a primer and template molecule that might not occur when the templates are at extremely low concentrations at the beginning of a PCR. In order to characterize the quality of the primer pair, we use a quantity that characterizes the efficiency of PCR assuming equilibrium binding conditions. In particular, we determine the equilibrium efficiency as the minimum of the fraction of left primers binding to the left primer binding site and the fraction of the right primers binding to the right primer binding site. We choose the minimum of these fractions because a PCR can only be as efficient as its least efficient priming reaction.

Of course, PCR is manifestly not an equilibrium reaction. Our use of equilibrium analysis is designed to detect potential problems by identifying binding and folding reactions that are significant enough to disrupt priming. We assume that if a primer pair works under our equilibrium model, then it will work in PCR conditions. The converse is not true; because some dimerization reactions may be kinetically slow, some binding interactions that are problematic at thermodynamic equilibrium may not be relevant under PCR conditions. Nevertheless, Pythia rejects primer pairs in which equilibrium binding conditions result in insufficient binding of primers to their priming sites in the template molecules.

Primer specificity assessment

We employ a heuristic to determine primer specificity (12) that focuses on the 3′-end of the primer. This heuristic determines the shortest suffix of the primer that has sufficient stability such that, at equilibrium, a prespecified fraction of molecules in the background DNA with exact complementarity to the suffix would be bound, and then searches for exact occurrences of this suffix using a precomputed index.

We use a modified suffix array (18–21) and a hash table on that suffix array as our precomputed index. In our suffix array, pointers to each suffix in a sequence are sorted lexicographically, based on the first k positions. We then build a hash table, so that the suffixes in the sequence beginning with any particular k-mer can be quickly identified. This data structure can be used to retrieve sequences of arbitrary length l in ⌈l/k⌉ queries.

If two occurrences are close (within 1000 bases of one another) and oriented appropriately to generate an amplifiable product, then the PCR primer pair is rejected as nonspecific.

Support vector machine prediction of feasibility

In typical primer design problems, on the order of 10 000 primer pairs satisfy the user-supplied constraints (such as melting temperature and length restrictions). Because the gradient descent procedure for chemical reaction equilibrium analysis requires many relatively slow O(n³) matrix inversion steps for each update to the solution, we developed a filtering procedure to quickly reject infeasible candidates.

Our approach is to use a support vector machine classifier (22) to predict whether a primer pair would meet an efficiency threshold if the full equilibrium analysis were run, on the basis of the free energies of the various species that we consider. A support vector machine uses a hyperplane to classify a sample on the basis of a vector of features in a feature space. Support vector machines are widely used in computational biology (23) and have been applied to many bioinformatics problems such as translation site initiation recognition (24), microarray analysis (25) and genome annotation (26).

A critical component of a support vector machine classifier is the design of feature vectors associated with the samples. We designed our feature vectors to account for the intuition that in a system with many competing reactions, it is not the absolute free energy of any particular reaction that is important, but rather the relative free energy of a reaction as compared with its competitors. We therefore used a quadratic kernel (22) on vectors consisting of the 11 free energy values that we compute for each primer pair; this quadratic kernel provides information on all pairs of free energy values to the classifier. For further speed improvement, we explicitly compute the weight vector so that we can compute the classifier decision function as an inner product rather than a kernel expansion. We trained the support vector machine using the LibSVM program.

Pythia algorithm

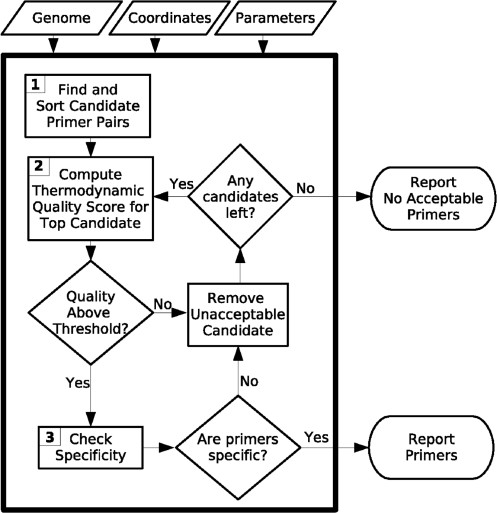
Our method, Pythia, takes as input the genomic sequence, locus coordinates to be amplified and user specified parameters. Figure 2 illustrates our method. In Step 1, Pythia identifies all pairs of sequences that satisfy the user constraints, such as primer melting temperature, primer length and amplicon length. Pythia then sorts these primers by the discrepancy between the desired melting temperature and the average of the computed primer melting temperatures. Pythia then examines the candidates on the list. In Step 2, the support vector machine classifier evaluates the candidate primer pair. If the primer pair is predicted to be feasible, then the full equilibrium analysis is performed and the quality metric for the primer pair is computed. If that metric is above a user-specified threshold, then Pythia computes a specificity check as Step 3. If the primers meet the specificity criterion, then Pythia outputs the primer pair. If the equilibrium efficiency is not above the user-specified threshold or the primers are not specific, Pythia examines the next candidate. Pythia proceeds in this way until a feasible candidate is found, or until no candidates are left.

Figure 2.

Flowchart of the Pythia algorithm. Inputs are the genomic sequence, locus coordinates and user-specified parameters. In Step 1, Pythia identifies all primer pairs meeting the user-specified requirements and sorts these primer pairs by the sum of the differences between the computed and target primer melting temperatures. In Step 2, Pythia computes the thermodynamic quality metric for the top ranked candidate. If this candidate meets a user-specified metric threshold, then Pythia proceeds to Step 3. If not, the top ranked candidate is removed from the list and Pythia returns to Step 2. In Step 3, Pythia performs a specificity check. If the primer passes the specificity check, it is given to the user, and the program terminates. If not, the top ranked candidate is removed from the list and Pythia returns to Step 2.

Comparison to other methods

In order to evaluate Pythia, we compare it to a highly optimized primer selection strategy used for several high-throughput studies (13–15). This approach uses carefully chosen parameters for Primer3 and a method for assessing primer specificity based on the 16 bases at the primer 3′-end. In this approach, exact occurrences of the sequence formed by the 16 bases at the 3′-end of each candidate primer are located in the genome, and if there are too many occurrences of either sequence, the primer pair is rejected. We refer to this combination of Primer3 and the 3′-end-based specificity evaluation as P316. The full set of parameters for each method are supplied in the Supplementary Data.

We first evaluated Pythia before developing the support vector machine classifier to predict primer feasibility based on free energies. For this test, we selected three regions of the human genome for which tiling primers had already been designed by the P316 method. Because computing the solution to our coupled equilibrium problem requires about 0.7 s of computation, and a typical region has on the order of 10 000 primer candidates (100 candidates for the left primer and 100 for the right), we limited the amount of time our program was allowed to attempt to design primers for any particular interval to 10 min, thus allowing Pythia to consider at most ∼900 candidates per interval.

Motivated by the bottleneck induced by the coupled equilibrium analysis, we then developed the support vector machine classifier, which was fast enough so that Pythia could evaluate all of the candidates in a region if necessary. We then chose to tile short regions near transcription start sites annotated as interspersed repeats, because these regions were challenging for the methods employed by the P316 approach.

We evaluate each method by the fraction of successful PCRs. Because we use melting curve analysis to assess each PCR, we must infer the success rates of each method and the coverage based on the success rates of a selected group of PCRs that were analyzed both by melting curve analysis and by running the PCR products on an agarose gel.

PCR conditions

Quantitative PCRs (qPCRs) were run using the Immomix master mix, with 35 ng human genomic DNA from the GM cell line, and 0.6 μM primers with SYBR green I used as a fluorescent reporter dye. qPCRs were run according to the following thermal cycling program: 95°C, 7 min, followed by 35 cycles of 98°C, 15 s; 60°C, 15 s; 68°C, 45 s on an ABI 7900 HT. Each PCR was run twice.

After thermal cycling, a melting curve was taken by slowly increasing the temperature from 68°C to 98°C and measuring SYBR green I fluorescence. The negative derivative of this fluorescence profile was taken and manually scored according to morphology. All reactions with inconsistent labels among replicates were eliminated from further analysis.

RESULTS

Evaluation of primer feasibility classifier

We evaluated the accuracy of our primer feasibility classifier as follows. First, we collected candidate primer pair examples for seven human genomic loci, and computed the equilibrium efficiency metric for each example. We then trained a support vector machine to predict whether the equilibrium efficiency was above a threshold for several threshold choices, and we evaluated classifier performance using 5-fold cross-validation. For each choice of threshold, we selected all of the negative examples and an equal number of positive examples. Support vector machines require a parameter to specify the trade-off between training set model accuracy and complexity; we set this cost parameter to 0.1.

We used receiver operating characteristic (ROC) analysis (27) to evaluate the performance of our classifier. An ROC curve plots the true positive fraction against the false positive fraction for a range of decision function values. The area under this curve, the ROC score, is a measure of how well the classifier is able to distinguish between the two classes: an area of 0.5 is the expected area under the ROC curve for a random classifier, and an area of 1.0 is the area under the ROC curve for a perfectly accurate classifier.

We used 5-fold cross-validation to evaluate the ability of the support vector machine (SVM) to predict the results of equilibrium analysis on data which was not used in training. We split each dataset randomly into five parts, and trained the classifier on data from four of the parts. We evaluated its performance using ROC analysis on the fifth part. For our final classifier evaluation, we computed the average ROC score over all five portions of the data.

Our results show that the classifiers are able to learn to distinguish between acceptable primer pairs and unacceptable primer pairs with high accuracy, and thus predict, given a set of free energies, whether the minimum equilibrium binding fractions are above the specified thresholds. Table 1 shows the training set sizes and the mean ROC score over all cross-validation folds. For each choice of threshold, the ROC scores were above 0.99. Thus, the classifier can accurately filter primer candidates at low computational cost.

Table 1.

Training set sizes

Threshold	Dataset	ROC score
	size
0.8	642	0.9995
0.85	1474	0.9986
0.9	3056	0.9951
0.95	10 498	0.9937

The number of training points for each acceptability threshold. For each threshold, we show the number of examples used to train the SVM, and the ROC and ROC50 scores. We assessed SVM performance using 5-fold cross-validation

The computational savings are due to the nature of the rule that the support vector machine uses to classify data. This rule associates a weight with each of the input features, and the classifier decision is made by computing the sum of the input features multiplied by the corresponding weights. If this sum is greater than zero, then the SVM classifies a datapoint as acceptable according to equilibrium analysis, and unacceptable otherwise. Because we use a quadratic kernel on a vector with 11 features, we can screen primers pairs on the basis of the free energies with just 264 multiplications and 131 additions by explicitly using the weight vector; this is a substantial efficiency improvement over applying the equilibrium analysis to each primer candidate.

Calibration of melting curve analysis

We chose a set of PCRs not used in the primer design comparison to run on a gel in order to evaluate the melting curve analysis of PCR success. In melting curve analysis, the reaction mixture is slowly heated after thermal cycling to a temperature high enough to denature the PCR amplicons. Because amplicon denaturation typically occurs in a narrow temperature interval (28,29), the fluorescence used in qPCR to detect double-stranded DNA will decrease sharply in the temperature range in which the PCR amplicon denatures. A plot of the negative first derivative of this fluorescence will yield a single prominent peak for PCRs in which the amplicon molecules denature in a narrow range of temperatures. Melting curves were scored manually as valid if they had a single prominent peak, and invalid if they had multiple prominent peaks or other unusual morphology.

In order to calibrate melting curve scores and determine reaction success rates, we ran 259 PCR products on agarose gels stained with the dye SYBR Green I. We manually examined the lanes and marked them as clean or not according to the two levels of stringency. Under a permissive scoring system, lanes were marked as not clean if there was significant smearing, missing bands or prominent additional bands in addition to the band of the expected size. Under a stringent scoring system, all bands marked not clean under the permissive system were also marked not clean, as well as all bands with faint additional bands or faint smearing. Table 2 shows the results of the melting curve analysis.

Table 2.

Concordance between gel and melting curves

Gel label	Valid melting curve		Invalid melting curve
	Stringent	Permissive	Stringent	Permissive
Clean	172	199	33	41
Not clean	38	11	16	8

For a selected set of PCR primers, we compared the results of melting curve analysis to agarose gel analysis of PCR amplicon. Melting curves were classified as valid or invalid based on melting curve morphology, and gel lanes were classified as clean or not clean at two levels of stringency. In each table entry, the numbers correspond to the number of reactions with the corresponding gel and melting curve label at stringent and permissive levels of gel scoring stringency

Based on this data, we compute the success rates by extrapolating from the stringent success rates and the permissive success rates. Under the extrapolation from the stringent success rates, the overall success rate is calculated as

4

where V is the number of PCRs labeled ‘valid’ and I is the number of PCRs labeled ‘invalid’. Similarly, under extrapolation from the permissive success rates, the overall success rate is calculated as

5

Application to genomic tiling

We chose three regions for which primers had already been designed for the first evaluation of Pythia. Table 3 summarizes the three regions that we tiled in the first test of our method. We attempted to tile these regions as densely as possible with PCR products whose size ranged from 225 bases to 275 bases, and whose primers had melting temperatures ranging from 60°C to 64°C, with a target of 62°C. Primers were constrained in length to lie between 18 bases and 30 bases.

Table 3.

Genomic characteristics of selected human genome regions

Region	Chromosome	Interval	Interval	Length	Description
		start	stop	(Kb)
1	16	147 000	164 000	17	High GC
					content
2	16	181 000	215 000	34	Repetitive
3	11	5 252 000	5 277 000	25	Typical

We compared the ability of Pythia to the ability of the P316 algorithm to tile these regions. We show the location, size and a brief description of each locus

We attempted to design a PCR primer for the first 275 bp window in the region. If Pythia was able to choose a primer pair in the allotted time, we then attempted to design primers for the 275 bp window starting at the end of the last successful design. If Pythia was not able to design primers for the window, then we moved the window by 25 bases and tried again. We stopped this iterative process when the design window reached the end of the region. We then attempted to fill gaps by attempting to tile the gaps, increasing the time allowed per interval to 20 min.

Even when constrained in the time allowed to design primers, Pythia achieves comparable performance with P316 on human genomic intervals. Table 4 shows that Pythia achieves comparable success rates and attempts to place slightly fewer primers in two of the three regions. Examination of this data revealed that for some regions, Pythia must consider on the order of 10 000 primer pairs. However, due to the time required for equilibrium analysis, Pythia could only evaluate ∼900 candidates in the allotted 10 min. In order to increase the number of candidates that Pythia could examine in a fixed amount of time, we developed an SVM approach to screening primer candidates. Using the SVM approach, we were able to reduce the total time per primer design attempt to approximately ∼20 s on a standard linux workstation, as compared with ∼1.5 s using the P316 method.

Table 4.

Primer design performance for selected human regions

Region	P316	P316		Pythia	Pythia
	PCRs	success rate		PCRs	success rate
		Permissive (%)	Stringent (%)		Permissive (%)	Stringent (%)
1	49	94	80	41	94	81
2	93	94	81	102	94	81
3	63	92	78	43	94	81

Shown are the number of PCRs and the extrapolated success rates for permissive and stringent criteria

Application to repetitive elements

After developing the SVM classifier to screen primer candidates, we applied our method to tile a set of regions near transcription start sites that were annotated as interspersed repeats by the RepeatMasker program by Smit, Hubley and Green (http://www.repeatmasker.org). We designed primers to tile each region along with 125 bases flanking each end. Because the PCR products were between 225 and 275 bases in length, each primer pair had at least one primer in a repeat-annotated region. We designed primers to tile 38 such intervals with a mean length of 1.5 kb (where the minimum interval length was 751 bases and the maximum interval length was 6198 bases).

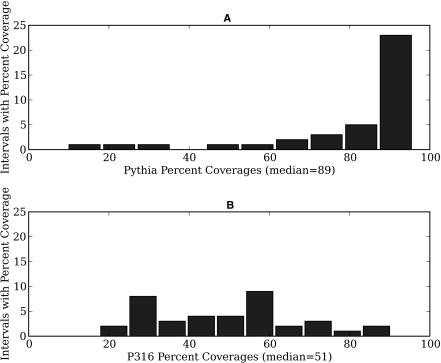
For these regions, Pythia was able to design primers for much greater coverage. Figure 3 shows a histogram of the percentages of each region that were covered by primer pairs designed by Pythia or the P316 approach. Pythia designed 195 primer pairs to tile these regions, whereas the P316 method designed 106 primer pairs to tile these regions. Based on melting curve analysis, Pythia achieved a 94% success rate under the permissive criteria and an 80% success rate under the stringent criteria; similarly, the P316 approach achieved a 95% success rate under the permissive criteria and an 82% success rate under the stringent criteria. Of the 38 regions, Pythia was able to design primers to cover at least 80% of 27 regions, whereas the P316 approach was able to design primers to cover at least 80% of only two regions. In contrast, Pythia was able to design primers to cover <50% of only three regions, compared with 18 regions with <50% coverage for the P316 approach.

Figure 3.

Primer pair design coverages for interspersed repeat regions. Design coverage is defined as the fraction of an interval covered by PCR product sequences. (A) Histogram of coverages for Pythia (mean 80%). (B) Histogram of coverages for P316 (mean 50%).

Primer quality prediction

Crucial to the success of a primer design method is how well it can assess the quality of a primer pair. We therefore sought to compare the primer pair scoring functions in order to assess how well they can assess the likelihood that a primer pair will produce a product in a PCR. To assess the accuracy of these functions, we used Primer3 to assess the primers designed by Pythia, and we used the Pythia primer scoring function to assess the primers designed by the P316 approach.

The majority (94%) of the P316 primers were acceptable by the standards of the Pythia scoring function. Table 5 shows the results of Pythia analysis of the P316 primers. Pythia's primer design approach is conservative: most of the primers which Pythia scored as unacceptable (85%) resulted in acceptable amplicons.

Table 5.

Primer design method acceptability assessments

Pythia/P316 evaluation	Melting curve
	Valid	Invalid
Acceptable	276/17	15/3
Unacceptable	17/322	3/39

We show Pythia acceptability assessment of P316 primers and P316 acceptability assessment of Pythia primers. We assessed the ability of the Pythia primer pair quality metric to predict the quality of the P316 primers and vice versa. The first number in each cell shows the Pythia assessment of P316 primers, and the second number shows the P316 assessment of the Pythia primers. For example, 276 primer pairs designed by P316 were acceptable to Pythia and had a valid melting curve, whereas only 17 of the primer pairs designed by Pythia were acceptable to the P316 program and had a valid melting curve

Interestingly, the Primer3 primer metric rejected almost all of Pythia's primers. Table 5 also shows the results of Primer3 analysis of the Pythia primers. About 95% of the Pythia primers were scored as unacceptable by the Primer3 scoring function, with only three of the unacceptable primer pairs resulting in failed PCR as judged by melting curve analysis. An informal examination of the Primer3 output revealed that no single property of Pythia's primers led to their rejection by Primer3. Rather, Pythia's primers collectively violated a variety of Primer3′s primer evaluation rules.

We computed the precision and recall of both methods using the pooled set of primers, and our stringent success extrapolation of PCR success based on melting curve data. We found that both methods had a precision of 81%, but Pythia had a recall of 97%, as compared with P316 with a recall of 48%.

DISCUSSION

We propose our measure of equilibrium efficiency as a physically motivated criteria for predicting primer quality based on DNA thermodynamics. We have shown that Pythia compares favorably with the P316 primer design approach, which is based on Primer3, and thus Pythia has significant advantages when attempting PCR in RepeatMasked regions. Repeat sequences are important genomic features, comprising significant fractions of mammalian genomes, and thus it is important to extend PCR-based assays to cover these regions.

Pythia differs from existing approaches primarily in the evaluation of primer feasibility. Rather than designing an ad hoc primer quality metric, we use a single thermodynamic measure of primer pair quality to identify an acceptable primer pair and a thermodynamically motivated heuristic to ensure that the primers will amplify only the desired locus. In Pythia, the user must specify constraints that primers must satisfy (such as a specified range of melting temperatures and lengths), and then we enumerate the acceptable primer pairs that flank a locus, outputting the first acceptable pair according to our primer quality and specificity metrics.

In addition to performance considerations, Pythia has several advantages compared to current approaches. First, our assessment of primer pair feasibility is based on thermodynamics; this is in contrast to methods such as Primer3, where primer feasibility is predicted using an ad hoc scoring function. Second, our method requires relatively few free parameters; these parameters are physically meaningful, and thus our method is easier to use. Although the set of primers designed by Pythia will be strongly influenced by parameters that take the form of thresholds, as will Primer3 and other primer design methods, these threshold parameters more closely correspond to experimental variables than more abstract threshold parameters such as minimum acceptable alignment scores, and thus the choice of appropriate values can be guided by the experimental system.

While the Primer3 primers have a high success rate, our results show that the Primer3 primer assessments are overly conservative, and rejected most of Pythia's primers. The conservative approach does well in most genomic regions but is unable to densely tile challenging regions such as the interspersed repeats in the human genome.

When Primer3 is unable to choose primers for a particular region, users are advised to relax the various quality thresholds (6). However, it is often unclear how to carry out this relaxation in a principled way. In contrast, Pythia uses the minimum equilibrium efficiency, with only one parameter that can be adjusted independently of reaction conditions. We have shown that Pythia to assessing primer quality is more accurate than Primer3.

Many of the limitations of Pythia stem from an incomplete understanding of DNA stability in PCR mixtures. Many PCR formulations, such as the one used in this study, rely on DNA denaturants that preferentially destabilize GC base pairs. These denaturants improve the success of PCR, especially when amplifying GC rich templates; however, they also significantly distort DNA stability parameters. A better understanding of DNA thermodynamics in the presence of these solvent additives would improve both Pythia's primer acceptability scoring method and Pythia's primer specificity assessments. Another limitation of Pythia is that the dynamic programming algorithm that computes nucleic acid interaction energies is computationally intensive. One direction for future work is evaluation of approximations to the free energy computation, such as (30), which could yield substantial algorithmic acceleration with little loss in accuracy.

In summary, Pythia can tile difficult regions more densely than Primer3, and is simpler to tailor to reaction conditions. In addition, the Pythia algorithm will naturally incorporate improvements in thermodynamic parameters and methods for computing DNA binding. Finally, Pythia can efficiently design primers for large primer design problems by using our efficient filters to quickly eliminate infeasible primers from consideration.

FUNDING

National Institutes of Health (grant R01 GM071923); National Human Genome Research Institute (grant T32 HG00035). Funding for open access charge: National Institutes of Health.

Conflict of interest statement. None declared.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.