Effects of Condylar Elastic Properties to Temporomandibular Joint Stress

Abstract

Mandibular condyle plays an important role in the growth and reconstruction of the temporomandibular joint (TMJ). We aimed to obtain orthotropic elastic parameters of the condyle using a continuous-wave ultrasonic technique and to observe the effects of condylar elastic parameters on stress distribution of the TMJ using finite element analysis (FEA). Using the ultrasonic technique, all nine elastic parameters were obtained, which showed that the mandibular condyle was orthotropic. With the condyle defined as orthotropic, the occlusal stress was transferred fluently and uniformly from the mandible to the TMJ. The stress distribution in the isotropic model showed stepped variation among different anatomical structures with higher stress values in the cartilage and condyle than in the orthotropic model. We conclude that anisotropy has subtle yet significant effects on stress distribution of the TMJ and could improve the reality of simulations.

1. Introduction

Stresses in the temporomandibular joint (TMJ) are important for maintaining normal structure and function [1]. Finite element analysis (FEA) is often used in stress analysis of the TMJ. Two-dimensional FEA of the mandible was developed by Haskell et al. [2] and Maeda et al. [3] to investigate stress distribution in the TMJ. Three-dimensional models were subsequently developed to simulate the human mandible, including the TMJ, more accurately [4–8]. Some of these models were used to investigate the influences of craniofacial discrepancy [9] and the relationship between disc displacement and TMJ stress distribution [10–12]. Although FEA is a promising tool in the study of functional morphology of craniofacial structures, its reliability depends greatly on the accuracy of the input, that is, parameters such as load, geometrical form, and elastic properties.

A series of studies have shown that if bone properties are regarded as isotropic, it may result in misinterpretations of strain data, for bony structures of identical shape will resist loads differently if their elastic properties differ [13, 14]. However, in FEA of the TMJ, the condyle is usually assumed to be isotropic and defined with the same elastic properties as the mandible. Mechanical testing, however, has shown that the cancellous bone of the condyle is anisotropic [15, 16] and consists of parallel plate-like trabeculae primarily oriented in the vertical direction, perpendicular to the mediolateral condylar axis. In the horizontal direction, the plate-like trabeculae are interconnected with rods [17]. To our knowledge, no studies have determined all isotropic elastic parameters of the mandibular condyle.

Many researchers use mechanical testing to obtain elastic parameters of biological tissues [18, 19]. However, mechanical testing can lead to nonuniform loading at the specimen ends due to surface irregularities, induced bending, and difficulties associated with measuring accurately. Comparatively, ultrasonic techniques offer advantages over mechanical techniques [20, 21]. Smaller specimens can be used, and anisotropic properties can be determined from a smaller region of the whole bone. Until now, ultrasonic techniques have been used to determine elastic properties of human and canine cortical femora [22], mandible [23], cancellous bone [24], cortical bone [21], dentate mandible [18], enamel and dentin [25], and craniofacial skeletons of primates [26]. However, there are no reports on the application of ultrasonic techniques to the mandibular condyle.

We investigated the orthotropic elastic properties of the condyle with continuous-wave ultrasonography and then applied findings to the FEA model. Our objective was to determine the orthotropic parameters of the condyle and further to prove the effects of the condylar anisotropy to the level and distribution of the TMJ stress.

2. Materials and Methods

2.1. Ultrasonic Measurement of Condylar Elastic Properties

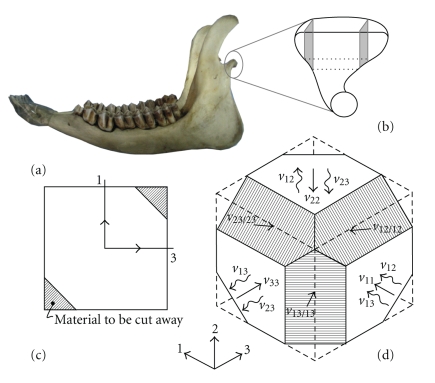
The freshness of samples is important for elastic properties measurement [27]. Because of the limitations of obtaining fresh human condyles, this study used sheep joints. Compared with other animals, the size, anatomy, function, and joint accessibility of sheep are similar to humans [28] (Figure 1(a)). Six fresh condyles from sheep (aged 10 ± 2 months) were dissected and measured. Care was taken throughout the procedure to maintain the specimens in a moist state. The specimens were frozen in saline for preparation. Before measurement, the condyles were taken out and cut into 4 × 6 × 10-mm standard samples (Figure 1(b)). After the specimens were prepared, they were stored in a solution of 50% ethyl alcohol and 50% normal saline to maintain the elastic properties of the tissue [22]. The density of each specimen was calculated based on Archimedes' principle of buoyancy. On the samples, the sides were marked to denote the orientation with respect to the three-dimensional coordinate system, in which x1 was the antero-posterior direction, x2 was the vertical direction, and x3 was the mesio-lateral direction.

Figure 1.

An illustration of the ultrasonic measurement process of sheep condyle. (a) Anatomic sketch of sheep mandible and condyle. (b) Condyle sample prepared for ultrasonic measurement. (c) Two-dimensional illustration of the bone material cut away so that v_13/13 can be measured. (d) A three-dimensional sketch of the bone sample after all the cuts have been made (shown as hatched parts) as well as the measurement direction for each v. 1 was the antero-posterior direction, 2 was the vertical direction, and 3 was the mesio-lateral direction. indicates longitudinal wave speed, which was measured with the generation and sensing transducer in line. 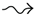indicates the transverse wave speed measured with the generation and sensing transducer at a right angle.

We used an ultrasonic pulse transmission to measure the elastic properties [14, 23]. Ultrasonic waves were generated with a pulse generator, and two sets of mounted piezoelectric transducers were used (1.25 MHz longitudinal; 2.5 MHz transverse, Valpey-Fischer, Hopkinton, MA). Both longitudinal and transverse ultrasonic waves were passed through various axes (Figures 1(c) and 1(d)). Time delays were measured using a digital storage oscilloscope (54601-A, Hewlett-Packard, Austin, Texas) to make a phase comparison of the signal before and after its transmission through a specimen. Ultrasonic velocities were calculated by dividing the specimen thickness by the apparent time delay minus the system time delay. Organic glass with known ultrasonic velocity was used for system verification. The absolute error of the system was 0.11 m/s. Five measurements were performed for each specimen. Thus, 9 ultrasound velocities transmitted in the condyle were obtained, in which v₁₁, v₂₂, v₃₃, v_12/12, v_23/23, and v_13/13 were longitudinal wave speed measured with the generation and sensing transducer in line, and v₁₂,v₂₃, and v₁₃ were the transverse wave speed measured with the generation and sensing transducer at a right angle. Here, 1 indicated the antero-posterior direction, 2 indicated the vertical direction, and 3 indicated the mesio-lateral direction. Linear elastic wave theory yields relationships between various velocities through the specimen, and its elastic properties was as follows: c₁₁ = ρv₁₁², c₂₂ = ρv₂₂², c₃₃ = ρv₃₃², c₄₄ = ρv₃₂² = ρν₂₃², c₅₅ = ρv₃₁² = ρv₁₃², c₆₆ = ρv₁₂² = ρv₂², c₁₂ = (c₁₁ + c₆₆ − 2ρv_12/12²)(c₂₂ + c₆₆ − 2ρv_12/12²) − c₆₆, c₁₃ = (c₁₁ + c₅₅ − 2ρv_13/13²)(c₃₃ + c₅₅ − 2ρv_13/13²) − c₅₅, c₂₃ = (c₂₂ + c₄₄ − 2ρv_23/23²)(c₃₃ + c₄₄ − 2ρv_23/23²) − c₄₄ [29], from which all the 9 independent elastic coefficients of the condyle were calculated. Further, according to the matrix relationship between elastic coefficients and technical constants expressed as follows [22], Young's modulus E, shear modulus G, and Poisson's ratio ν in each direction were obtained, which were further applied to FEA for defining the orthotropic material parameters of the condyle:

$$\left(\begin{array}{cccccc}{C}_{11}& C_{12}& C_{13}& 0& 0& 0\\ C_{12}& C_{22}& C_{23}& 0& 0& 0\\ C_{13}& C_{23}& C_{33}& 0& 0& 0\\ 0& 0& 0& C_{44}& 0& 0\\ 0& 0& 0& 0& C_{55}& 0\\ 0& 0& 0& 0& 0& C_{66}\end{array}\right)={\left(\begin{array}{cccccc}\frac{1}{E_1}& -\frac{{\nu }_{21}}{E_2}& -\frac{{\nu }_{31}}{E_3}& 0& 0& 0\\ -\frac{{\nu }_{12}}{E_1}& \frac{1}{E_2}& -\frac{{\nu }_{32}}{E_3}& 0& 0& 0\\ -\frac{{\nu }_{13}}{E_1}& -\frac{{\nu }_{23}}{E_2}& \frac{1}{E_3}& 0& 0& 0\\ 0& 0& 0& \frac{1}{G_{23}}& 0& 0\\ 0& 0& 0& 0& \frac{1}{G_{13}}& 0\\ 0& 0& 0& 0& 0& \frac{1}{G_{12}}\end{array}\right)}^{-1}.$$ (1)

2.2. Construction of the FEA Model

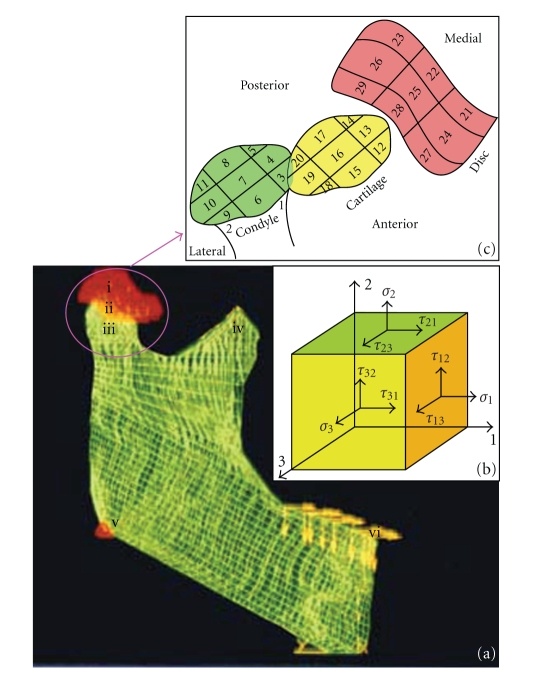
A young male adult cadaver with normal interjaw relationship and natural dentition was used to construct the FEA model. The use of a cadaver conforms to a written protocol that was reviewed and approved by the Department of Anatomy of the Fourth Military Medical University. Multiplanar computerized tomography scan (Tomoscan SR 7000, Philip, Eindhoven, the Netherlands) images of the bone structure with 1.0 mm sections were obtained for hard tissue reconstruction. One-millimeter manually sliced and digitalized images of bilateral discs of the same cadaver were used for soft tissue reconstruction. A layer of 2 mm elements was established to simulate articular cartilage. Then, the tetrahedral elements with three degrees of freedom per node were adopted to build superficial and internal structure meshes for the model. During that process, the meshes in mandible were relatively sparse and those of condyle were densely plotted for it was one of the pivots in this research. Thus, a three-dimensional FEA model was established by ALGOR (Super Sap) software (ALGOR Inc., Plano, Texas. At the end of this process, the FEA model presented a mesh comprising 8292 elements and 10936 nodes (Figure 2(a)).

Figure 2.

Finite element analysis model of temporomandibular joint (TMJ) stress. (a) Three-dimensional finite element mesh of the TMJ, including the mandible, disc (i), cartilage (ii), condyle (iii), and coracoid process (iv), with the mandible angle fixed (v) and alveolar ridge loaded by two-dimensional occlusal force vectors (vi). (b) State of stress in an orthotropic element. Each of the three material axes was assigned a value for the elastic modulus (E), and each of the three planes defined by those axes received values for the shear modulus (G) and Poisson's ratio (ν). Thus, one principle stress (σ) and two shear stress (τ) values could be calculated from each plane of the element. 1, 2, and 3 indicate the same corresponding directions as in Figure 1. (c) Twenty-nine observation points map the TMJ for stress value collection.

Superior disc surface and the mandibular angle area were restricted. Two different models with the same geometry, mesh, boundary, and loading conditions but different condylar material properties, one with isotropic and the other with orthotropic elastic parameters, were established. Isotropic material properties were homogeneous in all directions of the element. Orthotropic material had three material axes, which corresponded to those in ultrasonic measurements. The orientations of each axis in the orthotropic element are shown in Figure 2(b). Each of the three material axes was assigned a value for the elastic module, and each of the three planes defined by those axes received values for the shear modulus and Poisson's ratio. The elastic parameters of the mandible, disc, and cartilage were determined by referring to previous studies [5, 10, 30]. For the load condition, stress vectors previously measured by us with a photoelastic method [31] were applied to each mandibular tooth position.

During observation of stress values, each of the three functional parts was divided into nine parts from the medial to the lateral part and from the anterior to the posterior part. Twenty-nine observation points were located (Figure 2(c)), in which point number 1 and number 2 were in the medial and lateral part of the condylar neck, number 3 to number 11 were in the condyle, number 12 to number 20 were in the cartilage, and number 21 to number 29 were in the disc. Maximal principal stress and minimal principal stress were considered to quantitatively compare the effect of anisotropy of the condyle.

2.3. Statistical Analysis

Elastic coefficients obtained were analyzed by analysis of variance. Dunnett's post hoc test was used to test for significant differences between directions for the elastic moduli, shear moduli, and Poisson's ratios. TMJ stress values of a group of observation points in the condyle, cartilage, or disc between the isotropic and orthotropic models were compared by the between-subjects effects test of univariate analysis of variance with significance set at 0.05 using SPSS 11.5 software (SPSS Inc., Chicago, Illinois).

3. Results

3.1. Elastic Parameters of Condyle

Ultrasound velocities transmitted in the condyle (v), the elastic coefficients (c), and the technical constants (E, G and ν) that were applied to the FEA are shown in Table 1. All 9 orthotropic elastic coefficients of the condyle were successfully obtained from each small condyle sample. The results showed significant differences of elastic coefficients between directions, such as c₂₂ > c₁₁ > c₃₃ > c₄₄ > c₆₆ > c₅₅ (P < .05) and c₁₂ > c₂₃ > c₁₃ (P < .01), which indicated that the mandibular condyle was orthotropic material. The values of condylar elastic parameters (see Table 1) were different from that of cortical bone (E = 1.37 × 10⁴ MPa, ν = 0.30) and cancellous bone (E = 7.93 × 10³ MPa, ν = 0.30) [9]. Young's modulus of condyle in x₂ (vertical to transverse axis) direction, in which the condyle endures the primary force in functional movement, showed the highest value For the shear modulus, and G₂₃ had the highest value, which meant that the condyle has high endurance for shearing or twisting loads along the direction parallel to the transverse ridge.

Table 1.

Ultrasound velocity and elastic property of the condyle (mean ± SD, n = 6).

Ultrasound velocity		Elastic coefficients		Technical constants (GPa)
(×103 m/s)		(GPa)		Young's modulus		Shear modulus		Poisson's ratio
v11	1.73 ± 0.04	c11	4.19 ± 0.12	E1	3.05 ± 0.16	G12	0.88 ± 0.03	ν21	0.42 ± 0.03
v22	1.79 ± 0.08	c22	4.60 ± 0.21	E2	3.58 ± 0.19	G23	0.95 ± 0.05	ν12	0.36 ± 0.01
v33	1.53 ± 0.01	c33	3.25 ± 0.18	E3	2.73 ± 0.19	G13	0.68 ± 0.04	ν31	0.28 ± 0.02
v12/12	0.90 ± 0.02	c44	0.95 ± 0.05					ν13	0.31 ± 0.02
v23/23	0.93 ± 0.01	c55	0.68 ± 0.04					ν23	0.17 ± 0.03
v13/13	0.97 ± 0.03	c66	0.86 ± 0.03					ν32	0.13 ± 0.02
v12	0.79 ± 0.01	c12	1.99 ± 0.05
v23	0.83 ± 0.02	c23	1.39 ± 0.02
v13	0.70 ± 0.03	c13	1.12 ± 0.05

v: ultrasound velocities that were measured directly by ultrasonic method; v₁₁, v₂₂, v₃₃, v_12/12, v_23/2X, v_13/13 were longitudinal wave speed measured with the generation and sensing transducer in line, and v₁₂, v₂₃, v₁₃ were the transverse wave speed measured with the generation and sensing transducer at a right angle. c: elastic coefficients that were calculated from v. E (Young's modulus), G (Shear modulus), and ν (Poisson's ratio) were calculated from c and would be further applied into the finite element analysis for material definition of the condyle. For subscript numbers of v, E, G, and ν. 1 was in the antero-posterior direction, 2 was in the vertical direction, and 3 was in the mesio-lateral direction, while the subscript numbers of c did not the indicate directions, which were just the calculation results from vij and further for calculating the technical constants.

3.2. Stress Distribution of TMJ

A three-dimensional FEA model, including the mandible, condyle, disc, and cartilage, was established in this study. The distributions of the maximal and minimal principal stress in the model with the orthotropic condyle are shown in Figures 3(a) and 3(b). After loading of occlusal force, the stress was transferred fluently and uniformly from the mandible to the TMJ. Stress of the anterior part of the TMJ was mainly compressive and that of posterior part was mainly tensile in the intercuspal position. The maximal and minimal principle stress in the condyle and cartilage of the TMJ model with the orthotropic condyle was lower than that of the model with the isotropic condyle (observation points 1–20, P < .05), especially in the condylar neck and condyle area (observation points 1–11, P < .01), whereas the stress level in the disc of both models was not significantly different (observation points 20–29, P > .05, Figures 3(c) and 3(d)). Thus, the stress distribution in the isotropic model showed stepped variation in different anatomic structures.

Figure 3.

Distribution map of the maximal principal stress (a) and the minimal principal stress (b) in the TMJ with orthotropic properties. The pictures show us that the stress uniformly transferred from the surface to the central part of the orthotropic condyle. Stress of the anterior part of the TMJ was mainly compressive and that of posterior part was mainly tensile (the cartilage could not be seen clearly from this direction). Comparisons of the maximal principle stress and the minimal principle stress in TMJ between the finite element analysis model with an orthotropic condyle and isotropic condyle were marked in (c) and (d), in which black curve corresponded with data based on the orthotropic model and the multicolored curve with data based on the isotropic model. It showed that stress values in the condylar neck (point 1, 2), condyle (points 3–11), and cartilage (points 12–20) of the isotropic model were higher than those of the orthotropic model (with ∗∗ indicating P < .01 and ∗ indicating P < .05), whereas values in the disc of the both models showed no differences (points 20–29).

4. Discussion

4.1. Elastic Property of the Condyle

The anatomy for sheep condyle in our research showed several characteristics that resembles to those of human, including diameter in mesial-lateral direction being longer than that in anterior-posterior direction, the long axis of bilateral condyle directing backwards, and bigger anterior condylar slope. Architecturally, the condyle also had a thin external cortex that envelops a central medullary component that is made up of trabecular bone and soft tissue marrow. The only difference was that the fossa and condyle of the sheep were flat, much like an adapted edentulous human TMJ. The condyles of 1-year-old sheep adopted in this research almost had the same size with that of adult human being. There were also thin layer of fibrocartilage covered on the condylar surface. Before the ultrasonic measurement, fibrocartilage layer had been carefully divested to ensure that elastic parameters obtained were indeed from the bone tissue of condyle. In a much detailed report on comparative anatomy research on TMJ of the goat and sheep [32], it was ponited out that the TMJ of goat and sheep showed many charicteristics just as those of human, such as a distinct absence of protection against anteroposterior forces, a medial and lateral ligament attaching the disc to the condyle, and the translatory capacity of the condyle. As a result, it was concluded that the goat and sheep should be strongly considered as the prime models for TMJ research and procedural training [32, 33]. Besides, it was also reported that the mean trabecular thickness in young sheep (10 ± 2 months) was 0.28 mm, which corresponded well with that of human (age 30–49, 0.27–0.34 mm) [28]. Whereas, we also noticed that strains in the mandible are caused by muscle contraction and occlusal force. The conditions of isognathy versus anisognathy are expected to produce different patterns of mandibular strain during mastication. In sheep, the TMJ affords greater lateral movement of the mandible, because only one tooth row can occlude at a time, and the bite point acts as a fulcrum, which would inevitably lead to larger and differently oriented strains on the working side compared to the balancing side. The impacts of this different strain distribution character on the elastic parameters of the condyle still need further investigation.

The ultrasonic technique for measuring elastic parameters offers particular advantages over mechanical techniques, including application to small specimens and independence from friction and damage due to gripping specimens, making repetitive measurements on a single specimen possible. Thus, it has the potential to characterize three-dimensional elastic anisotropy from a single sample, which effectively reduces individual errors in measurements [21]. Using this technique, the values of condylar elastic parameters were shown to be different from those of cortical bone and cancellous bone of the mandible [23]. This finding could probably be explained by the different functional and remodeling characteristics of different bones [34]. Our results showed that the highest Young's modulus of condyle was in x₂ direction (vertical to its transverse axis). Young's modulus in the axial direction was also shown to be higher than that of the transverse direction using mechanical tests of the human condyle [16].

4.2. Effects of Condylar Elastic Properties to TMJ Stress

Anisotropy of the mandible has been shown to affect interface stresses and peri-implant strain [35]. In addition, FEA can be adversely affected when elastic properties are modeled imprecisely, and modelers should attempt to obtain elastic properties data about the species and skeletal elements that are the subject of their analyses [36]. Our finite element calculations appeared to be the first to include regional anisotropy in TMJ stress analysis. We found that anisotropy of the condyle caused stress levels of the TMJ to decrease in the cartilage and condyle area. The stress in the TMJ, with the characteristic elastic parameters in the present study, was distributed uniformly in the condyle and transferred smoothly from the condyle to other parts of the TMJ. When the condyle was defined with the same parameters as the mandible, the stress values of the condyle were close to that of the condylar neck but much higher than those of the disc and cartilage. Thus, it seemed that the stress was not transferred continuously and gradually from the mandible to the condyle and further to the cartilage and disc, but rather descended in a step fashion.

5. Conclusions

It was approved by the present study that the mandibular condyle was orthotropic, with all nine elastic parameters having been obtained by the continuous-wave ultrasonic technique. The anisotropy character of the condyle has subtle yet significant effects on stress distribution of the TMJ, which could improve the simulation reality of finite element modeling.