Inference for current leukemia free survival

Abstract

Donor lymphocyte infusion (DLI) for patients who relapse following an allogeneic stem cell transplant has proved remarkably durable. Because of the potential for second remissions with DLI, the current leukemia free survival (CLFS), which is the probability that a patient has not failed the entire course of the treatment, is becoming of interest to clinical investigators. Based on either a multistate Markov model or a linear combination of Kaplan–Meier estimators, we explore regression models for the CLFS. We focus on the two sample problem and we develop confidence bands for the CLFS or for differences in CLFS as well as a Kolmogorov type hypothesis test using a re-sampling technique. We also examine the use of pseudo-values to make inference on the direct effects of covariates on the CLFS function and we develop a score test for the equality of two CLFS. We illustrate these inference methods on a bone marrow transplant dataset.

1 Introduction

Allogeneic bone marrow transplantation has in recent years become standard therapy for patients with acute and chronic leukemia as well as other hematological malignancies. Here a patient receives high doses of radiotherapy and/or chemotherapy to ablate the disease in the marrow. The normal function of the bone marrow is restored by transfusion to the patient of hematopoietic stem cells collected from a normal donor.

Most often studies have focused on the chance a patient is cured of his or her disease, the chance a patient may die as a consequence of complications of the transplant procedure and/or the chance that the leukemia may relapse and eventually be the cause of the patient’s death.

In recent years, particularly for leukemia patients, post-relapse therapies have been developed that will induce a second remission. One such therapy was based on the anti-leukemic effect of lymphocytes (The graft-versus-leukemia or GVL effect) derived from the donor’s marrow when transfused to the patient (cf. Horowitz et al. 1990). The recognition of this so-called GVL effect led to the development of a new approach to managing patients who relapse after hematopoietic stem cell transplant (HSCT), namely collection of lymphocytes from the donor and infusion to the patient without further radiotherapy or chemotherapy (cf. Kolb et al. 1990; Collins et al. 1997; Craddock et al. 2000). The intention of this donor lymphocyte infusion (DLI) therapy is to reinforce the GVL effect in the patient and restore complete remission. In practice, this therapy has been remarkably successful in patients who relapse after allografting for chronic myeloid leukemia (CML) and effective also in patients with acute leukemia, myeloma and lymphoma.

With the advent of DLI and other post-transplant therapy, it is clear that patients who relapse after transplantation are no longer considered as failures for the transplant. Traditional statistical measures such as the relapse or treatment-related mortality cumulative incidence functions or the leukemia free survival curve are not appropriate measures of the success of the transplant. The current leukemia free survival function has been used to describe the success of transplants with post-relapse therapy. This function is the probability that a patient is alive and in remission (first or second) at a time after transplant.

In this report, we examine inference for the current leukemia free survival (CLFS) function. In the next section we briefly review estimation for the CLFS function. In Sect. 3, we extend the results of Lin (1997) to develop confidence bands for the CLFS function, an omnibus test comparing two CLFS functions and a confidence band for the difference of two CLFS functions. In Sect. 4, we show how the pseudo-value approach of Andersen et al. (2003) can be used to make inference on the CLFS function. We develop a new score test to compare two cumulative incidence functions. In the final section, we illustrate these techniques on a data set of 614 CML patients treated at the Hammersmith hospital in London first reported in Craddock et al. (2000).

2 Estimation of the current leukemia free survival

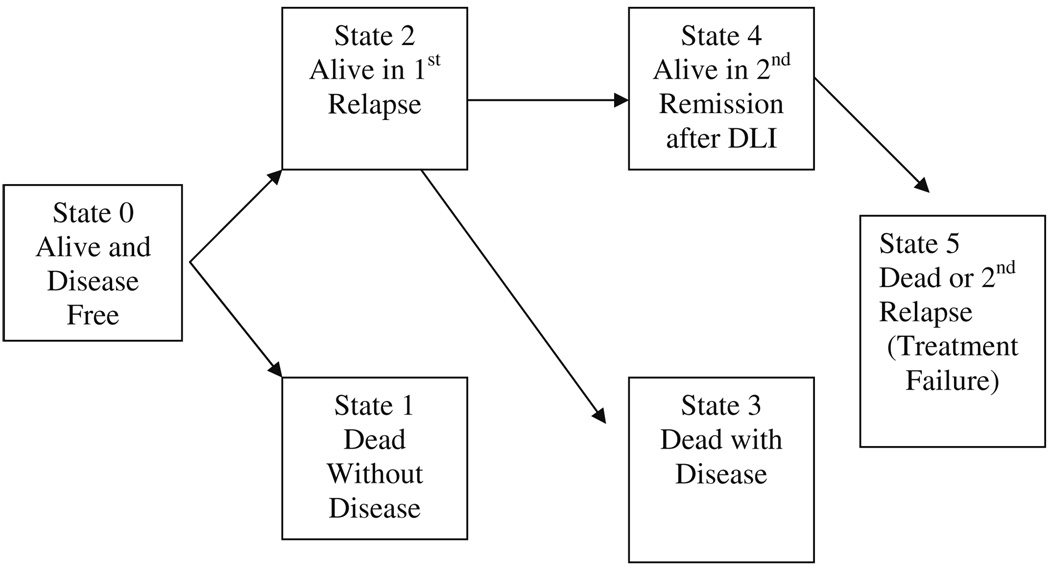
The Current leukemia Free Survival function can be estimated using either a multistate modeling approach (cf. Klein et al. 2000b) or by using a representation as a linear combination of survival functions (cf. Klein et al. 2000a). The multistate process on which the CLFS function is based can be illustrated as in Fig. 1. In the HSCT process, patients at time t can be in one of three transient states: Alive in remission after transplant (State 0), alive and relapsed (State 2) or alive and in second remission (State 4) or in one of three possible absorbing states: dead without disease (State 1), dead with disease (State 3) or dead or in second remission (State 5). The CLFS function is the probability a patient is alive in first remission (State 0) or alive in second remission (State 4).

Fig. 1.

Multistate model for donor leukocyte infusion

Based on Fig. 1, we define N_i(t) be the indicator that the patient has visited state i prior to time t and λ_i() the rate of transition into state i = 1, …, 5. Define the set of orthogonal martingales

$$M_i(t)=N_i(t)-{\displaystyle \underset{0}{\overset{t}{\int }}{\stackrel{⌢}{Y}}_i(u){\lambda }_i(u)du}$$

where ${\stackrel{⌢}{Y}}_i(t)$ is the number at risk for a transition into state i at time t. Note that ${\stackrel{⌢}{Y}}_1(t)$ and ${\stackrel{⌢}{Y}}_2(t)$ are both equal to Y₀(t), the number in State 0 at time t; ${\stackrel{⌢}{Y}}_3(t)$ and ${\stackrel{⌢}{Y}}_4(t)$ are both equal to Y₂(t), the number in State 2 at time t; and ${\stackrel{⌢}{Y}}_5(t)$ is equal to Y₄(t), the number in State 4 at time t. Using basic results (cf. Andersen et al. 1993) on multistate modeling the state probabilities can be estimated using the product-integral of the Nelson-Aalen estimators of the transition intensities (See Klein et al. 2000b) as follows:

$$\widehat{C}(t)={\widehat{P}}_0(t)+{\widehat{P}}_4(t)$$

where

$$\begin{array}{cc}{\widehat{P}}_0(t)=\hfill & {\displaystyle \prod _{u\le t}\left[1-\frac{d{N}_1(u)+d{N}_2(u)}{Y_0(u)}\right]}\hfill \\ {\widehat{P}}_4(t)=\hfill & {\displaystyle \sum _{u\le \upsilon \le t}{\widehat{P}}_0(u-)\left(\frac{d{N}_2(u)}{Y_0(u)}\right)}\hfill \\ \hfill & \times {\displaystyle \prod _{u\le s<\upsilon }\left[1-\frac{d{N}_3(s)+d{N}_4(s)}{Y_2(s)}\right]}\left(\frac{d{N}_4(\upsilon )}{Y_2(\upsilon )}\right){\displaystyle \prod _{\upsilon \le w\le t}\left[1-\frac{d{N}_5(w)}{Y_4(u)}\right]}.\hfill \end{array}$$ (1)

An alternative estimator suggested by Klein et al. (2000a) is based on using the difference of two Kaplan–Meier estimators to estimate P₄(t). For this estimator, define N˜₁(t) = N₁(t) + N₂(t) to be the number of patients who have visited States 1 or 2; N˜₂(t) = N₁(t) + N₃(t) + N₅(t) be the number of patients who have died or had a second relapse; and N˜₃(t) = N₁(t) + N₃(t) + N₄(t) be the number of patient who have died prior to a second remission or who have experienced a second remission. Let Y˜₁(t) = Y₀(t), Y˜₂(t) = Y₀(t)+Y₂(t)+Y₄(t) and Y˜₃(t) = Y₀(t)+Y₂(t) and λ̃_k(t) be the intensity function for N˜_k(t), k =1, 2, 3. One can show that

$${\tilde{M}}_k(t)={\tilde{N}}_k(t)-{\displaystyle \underset{0}{\overset{t}{\int }}{\tilde{Y}}_k(u)}{\tilde{\lambda }}_k(u)du,k=1,2,3$$

are martingales, but they are not orthogonal to each other since N₁(t) at least is common to each martingale. We define the three Kaplan–Meier estimators by

$${\tilde{S}}_k(t)={\displaystyle \prod _{s\le t}\left[1-\frac{d{\tilde{N}}_k(s)}{{\tilde{Y}}_k(s)}\right]},k=1,2,3.$$

Note that S˜₁(t) is the chance a patient is in State 0, S˜₂(t) the chance the patient is in States 0, 2, or 4 and S˜₃(t) the chance the patient is State 0 or 2. Hence the current leukemia free survival function can be estimated as

$$\tilde{C}(t)=\text{Pr}\left[\text{State}0\text{or}4\text{at time}t\right]={\tilde{S}}_1(t)+\left[{\tilde{S}}_2(t)-{\tilde{S}}_3(t)\right]$$ (2)

This estimator, which can be computed using standard statistical software, is used in the sequel.

To make inference about the current leukemia free survival function, we use the fact (cf. Andersen et al. 1993) that for large samples

$${\tilde{S}}_k(t)-S_k(t)\approx -{\tilde{S}}_k(t){\displaystyle \underset{0}{\overset{t}{\int }}\frac{d{\tilde{M}}_k(u)}{{\tilde{Y}}_k(u)},k=1,2,3}$$ (3)

The martingales M˜_k(t) are not independent since they depend on common counting processes. However, we can represent these martingales as functions of the basic martingales for the individual transitions. Routine algebraic manipulation yields the following result.

Lemma 1

1. $$\begin{array}{ll}d{\tilde{M}}_1(t)=d{M}_1(t)+d{M}_2(t)+Y_0(t)\left[{\lambda }_1(t)+{\lambda }_2(t)-{\tilde{\lambda }}_1(t)\right]dt\hfill & \hfill \end{array}$$
2. $$\begin{array}{ll}d{\tilde{M}}_2(t)=\hfill & d{M}_1(t)+d{M}_3(t)+d{M}_5(t)+Y_0(t)\left[{\lambda }_1(t)-{\tilde{\lambda }}_2(t)\right]dt\hfill \\ & +Y_2(t)\left[{\lambda }_3(t)-{\tilde{\lambda }}_2(t)\right]dt+Y_4(t)\left[{\lambda }_5(t)-{\tilde{\lambda }}_2(t)\right]dt\hfill \end{array}$$
3. $$\begin{array}{ll}d{\tilde{M}}_3(t)=\hfill & d{M}_1(t)+d{M}_3(t)+d{M}_4(t)+Y_0(t)\left[{\lambda }_1(t)-{\tilde{\lambda }}_3(t)\right]dt\hfill \\ \hfill & +Y_2(t)\left[{\lambda }_3(t)+{\lambda }_4(t)-{\tilde{\lambda }}_3(t)\right]dt\hfill \end{array}$$
4. $$d\langle {\tilde{M}}_k\rangle ={\tilde{Y}}_k(t){\tilde{\lambda }}_k(t)dt,k=1,2,3$$
5. $$\begin{array}{c}d\langle {\tilde{M}}_1,{\tilde{M}}_3\rangle =Y_o(t){\lambda }_1(t)dt,d\langle {\tilde{M}}_1,{\tilde{M}}_3\rangle =Y_o(t){\lambda }_1(t),\hfill \\ d\langle {\tilde{M}}_2,{\tilde{M}}_3\rangle =Y_o(t){\lambda }_1(t)dt+Y_2(t){\lambda }_3(t)dt\hfill \end{array}$$

Using (4) and (5) after some simplification we can show that the variance of $\widehat{CLFS}(t)$ can be estimated consistently by

$$\begin{array}{ll}{\sigma }^2(t)=& {\displaystyle \sum _{k=1}^3{\tilde{S}}_k^2(t){\displaystyle \underset{0}{\overset{t}{\int }}\frac{d{\tilde{N}}_k(u)}{{\tilde{Y}}_k(u)}+2{\tilde{S}}_1(t){\tilde{S}}_2(t){\displaystyle \underset{0}{\overset{t}{\int }}\frac{d{N}_1(u)}{{\tilde{Y}}_1(u){\tilde{Y}}_2(u)}}}}\\ \\ & -2{\tilde{S}}_1(t){\tilde{S}}_3(t){\displaystyle \underset{0}{\overset{t}{\int }}\frac{d{N}_1(u)}{{\tilde{Y}}_1(u){\tilde{Y}}_3(u)}}-2{\tilde{S}}_2(t){\tilde{S}}_3(t){\displaystyle \underset{0}{\overset{t}{\int }}\frac{d{N}_1(u)+d{N}_3(t)}{{\tilde{Y}}_2(u){\tilde{Y}}_3(u)}}\end{array}$$

3 Inference for the CLFS based on Lin’s approach

To make inference about the distribution of the estimated CLFS function, we can use a modification of the sampling technique proposed by Lin (1997). To apply this approach, first substitute the martingale representation S˜_k(t) − S_k(t), k = 1, 2, 3 in (3) into (2) to obtain a representation for W(t) = [C˜(t) − C(t)]. In this representation, the three terms are based on non-orthogonal martingales, M˜_k(t), k = 1, 2, 3. We next use (1–3) in Lemma 1 to replace M˜_k(t) by sums of the orthogonal martingales, M_j(t). After this replacement, we then approximate the distribution of Ŵ(t) by replacing M_j(t) with $M_j={\displaystyle {\sum }_{i=1}^n{G}_{ji}{N}_{ji}(t),(j=1,\dots ,5)}$ where the G_ji’s are independent standard Normal variables and all other unknown quantities are replaced by their sample estimates. After some simplification, we have

$$\begin{array}{ll}\widehat{W}(t)=& \{-{\tilde{S}}_1(t){\displaystyle \underset{0}{\overset{t}{\int }}\frac{{\displaystyle {\sum }_{i=1}^n[G_{1i}d{N}_{1i}(u)+G_{2i}d{N}_{2i}(u)]}}{Y_0(u)}}\\ & -{\tilde{S}}_2(t){\displaystyle \underset{0}{\overset{t}{\int }}\frac{{\displaystyle {\sum }_{i=1}^n[G_{1i}d{N}_{1i}(u)+G_{3i}d{N}_{3i}(u)+G_{5i}d{N}_{5i}(u)]}}{Y_0(u)+Y_2(u)+Y_4(u)}}\\ & +{\tilde{S}}_3(t){\displaystyle \int \frac{{\displaystyle {\sum }_{i=1}^n[G_{1i}d{N}_{1i}(u)+G_{3i}d{N}_{3i}(u)+G_{4i}d{N}_{4i}(u)]}}{Y_0(u)+Y_2(u)}\}}\end{array}$$ (4)

Given the data, Ŵ(t) is asymptotically equivalent to the distribution of W(t) and the large sample distribution of W(t) can be approximated by a large number of realizations from Ŵ based on repeated sampling of the G_ji’s. This approximation can be used in a number of applications.

3.1 Confidence bands for the CLFS function

Confidence bands for the current leukemia free survival function can be constructed as suggested by Lin (1997). Consider the transformed process

$$Q(t)=g(t)\{\varphi (\widehat{C}(t))-\varphi (C(t))\}$$

where ϕ(t) is a known function with a non-zero continuous first derivative ϕ′ and g is a known weight function which has a non-negative bounded limiting function. Note that we can use either the Markov estimator (1) or the linear combination of Kaplan– Meier (2) estimators here. Now using the functional delta method, we have that Q(t) is asymptotically equivalent to $g(t)\varphi \prime ((\widehat{C}(t))W(t))$ whose large sample distribution we can approximate by $g(t)\varphi \prime ((\widehat{C}(t))\widehat{W}(t))$. If we let q_α be the critical value with the property that

$$\text{Pr}\left[\underset{{\tau }_1\le t\le {\tau }_2}{\text{sup}}|Q(t)|>q_{\alpha }\right]=\alpha$$

then an approximate (1 − α) confidence band for ϕ(C(t)) is

$$\varphi (\widehat{C}(t))\pm q_{\alpha }/g(t)\text{for}{\tau }_1\le t\le {\tau }_2$$

which can be readily converted to a confidence band for the current leukemia free survival function. As noted by Borgan and Liestøl (1990) confidence bands based on a log transform seem to work well for small to moderate samples. Thus, we take ϕ(x) = ln[− ln[x]]. For g(t), we use either $g_1(t)=\text{ln}[\widehat{C}(t)]/\widehat{\sigma }(t)$ or $g_2(t)=\text{ln}[\widehat{C}(t)]/[1+{\widehat{\sigma }}^2(t)]$. The two resulting confidence bands are of the form $(\widehat{C}{(t)}^{1/\theta (t)},\widehat{C}{(t)}^{\theta (t)})$ where for g₁ we have ${\theta }_1(t)=\text{exp}\{q_{\alpha }\widehat{\sigma }(t)/\text{ln}[\widehat{C}(t)]\}$ and for g₂ we have ${\theta }_2(t)=\text{exp}\{q_{\alpha }[1+{\widehat{\sigma }}^2(t)]/\text{ln}[\widehat{C}(t)]$. When there are no transitions out of State 2, then the CLFS function reduces to the usual leukemia free survival with death or relapse as an event and the interval based on g₁ is the (log-transformed) equal probability (EP) confidence band of Nair (1984) and the interval based on g₂ is the Hall and Wellner (1980) version of band for the survival function. Following the recommendation of Nair (1984), we suggest using τ₁ and τ₂ so that t is restricted to those values with σ̂ (t)/[1 + σ̂²(t)] ∈ [0.01, 0.99].

3.2 Confidence bands and test for the difference of two CLFS functions

The above approach can be extended to the comparison of two CLFS functions. Suppose that we have two independent samples of size n₁ and n₂, respectively. Let $\widehat{C_i}(t)$, i = 1, 2 be the estimated CLFS function for sample i. Using (4), we can approximate the distribution of $D(t)=[\widehat{C_1}(t)-C_1(t)]-[\widehat{C_2}(t)-C_2(t)]$ by D^(t) = Ŵ₁(t) − Ŵ₂(t). Using this representation, we can generate samples from the process D() using independent normal deviates for each sample.

An omnibus test of the null hypothesis that the two current leukemia free survival functions are equal can be based on U = Sup|C^₁(t) − C^₂(t)|. Under the null hypothesis, the distribution of U can be found by repeated sampling from D(·), so that based on M samples from D(), the p-value of the test is the proportion of samples for which sup |D^(t)| ≥ U.

This approach can also be used to find confidence bands for the difference of two CLFS functions. These bands are useful for assessing where the CLFS functions differ and what part of the therapy is driving the difference. To construct the intervals, we find a confidence coefficient d_α, based on repeated sampling from D^(t), as $\text{Pr}[{\text{sup}}_{{\tau }_1\le t\le {\tau }_2}|\widehat{D}(t)|>d_{\alpha }]=\alpha$. This leads to the confidence band C^₁(t) − C^₂(t) ± d_α for τ₁ < t < τ₂.

Both the confidence band and the hypothesis test could be easily modified to look at weighted differences between the two CLFS functions.

4 Inference based on pseudo-values

An alternative approach to inference for the CLFS function is to use the methods for pseudo values presented for CLFS functions in Andersen et al. (2003) and Andersen and Klein (2007). This approach has been used in a general regression model approach in Andersen and Klein (2007) to directly model the CLFS function. In this section, we will focus on the two sample problem and present an approach to comparing two CLFS functions based on a score test constructed using the pseudo-values at all the jump points of the estimated pooled sample CLFS function. In this simple case, the score test has a simple closed form solution.

To construct the test let τ₁,…,τ_D be the distinct times at which the estimated CLFS function changes values. Note that these are the set of times where a transition to State 1, 2, 3, 4 or 5 occurs and that a single individual may contribute anywhere from zero to three times to this set. Let

$${\widehat{\theta }}_{ij}=n\widehat{C}({\tau }_j)-(n-1){\widehat{C}}^{(i)}({\tau }_j),i=1,\dots ,n,j=1,\dots ,D,$$

where C^(·) is the estimated CLFS function using the pooled sample of size n and C^⁽ⁱ⁾ (·) is based on the sample of size n − 1 obtained by deleting the ith observation. Either the Markov estimator or the linear combination of Kaplan-Meier estimators can be used to estimate the CLFS.

Once we have obtained the pseudo-values, we define a covariate Z_i = 1 if the patient was in group 1 and 0 if they were in the other group. We model the CLFS at time τ_j for the ith patient, θ_ij as g(θ_ij) = α_j+γ Z_i. Here g() is a link function. Let µ_i(α_j + γ Z_i) = g⁻¹ (α_j + γ Z_i), j = 1,…,D and µ(β|Z_i) = (µ_i(α₁ + γ Z_i), …, µ_i(α_D + γ Z_i)), where β = (γ, α₁,…, α_D). Estimates of model parameters can be based on the unbiased estimating equations

$${\displaystyle \sum _i{\left(\frac{\partial \mu (\mathbf{\beta }|Z_i)}{\partial \mathbf{\beta }}\right)}^{\mathrm{T}}{V}_i^{-1}}\left({\widehat{\mathbf{\theta }}}_i-\mu (\mathbf{\beta }|Z_i)\right)={\displaystyle \sum _i{U}_i(\mathbf{\beta })}=U(\mathbf{\beta })=0.$$ (5)

Here V_i is a working covariance matrix which we will for simplicity take to be the identity matrix and θ̂_i = (θ̂_i1,…, θ̂_iD)^t. A sandwich estimator can used to estimate the variance of β̂ = (γ̂, α̂₁,…, α̂_D). Let

$$\begin{array}{l}I(\beta )={\displaystyle \sum _i{\left(\frac{\partial \mu (\mathbf{\beta }|Z_i)}{\partial \mathbf{\beta }}\right)}^{\mathrm{T}}{V}_i^{-1}\left(\frac{\partial \mu (\mathbf{\beta }|Z_i)}{\partial \mathbf{\beta }}\right)},\\ \widehat{\text{Var}}(U(\mathbf{\beta }))={\displaystyle \sum _i{U}_i{\widehat{(\mathbf{\beta })}}^{\mathrm{T}}{U}_i}\widehat{(\mathbf{\beta })},\text{then}\\ \widehat{\text{Var}}\widehat{(\mathbf{\beta })}\approx I{\widehat{(\mathbf{\beta })}}^{-1}\widehat{\text{Var}}(U(\widehat{\mathbf{\beta }}))I{\widehat{(\mathbf{\beta })}}^{-1}.\end{array}$$

Alternative estimators of the variance of β̂ can be found by using a bootstrap technique.

When there is a limited number of time points, estimates of the α’s and γ can be obtained by standard generalized estimating equation software such as PROC GENMOD in SAS or the package GEESE in R.

An alternative use of the pseudo values is a score test of the hypothesis of no group effect (i.e., γ = 0). Note that for the two sample problem with no covariates we have that

$${\left(\frac{\partial \mu (\mathbf{\beta }|Z_i)}{\partial \mathbf{\beta }}\right)}^{\mathrm{T}}=\left(\begin{array}{ccc}{Z}_i\dot{g}({\alpha }_1+\gamma Z_i)& \cdots & Z_i\dot{g}({\alpha }_D+\gamma Z_i)\\ \dot{g}({\alpha }_1+\gamma Z_i)& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & \dot{g}({\alpha }_D+\gamma Z_i)\end{array}\right)$$

where g¨(x) = ∂g⁻¹ (x)/∂x. This leads to a set of score equation given by

$$U=\left(\begin{array}{c}{U}_{\beta }(\alpha ,\gamma )\\ U_{{\alpha }_1}(\alpha ,\gamma )\\ ⋮\\ U_{\alpha D}(\alpha ,\gamma )\end{array}\right)=\left(\begin{array}{c}{\displaystyle \sum _i{Z}_i{\displaystyle \sum _j\dot{g}({\alpha }_j+\gamma Z_i)({\widehat{\theta }}_{ij}-\mu ({\alpha }_j+\gamma Z_i))}}\\ {\displaystyle \sum _i\dot{g}({\alpha }_1+\gamma Z_i)({\widehat{\theta }}_{i1}-\mu ({\alpha }_1+\gamma Z_i))}\\ ⋮\\ {\displaystyle \sum _i\dot{g}({\alpha }_D+\gamma Z_i)({\widehat{\theta }}_{iD}-\mu ({\alpha }_D+\gamma Z_i))}\end{array}\right).$$

Under the null hypothesis that γ = 0 one can solve the score equations explicitly for α so that ${\widehat{\alpha }}_k=g({\overline{\widehat{\theta }}}_k)$ where ${\overline{\widehat{\theta }}}_k={\displaystyle {\sum }_{i=1}^n{\widehat{\theta }}_{ik}/n}$ for k=1,…, D.

To construct the score statistics we need an estimator, under H₀, of the model, ∑_M, and empirical, ∑_E, based variance estimates. The model based variance is given by ${\Sigma }_{\mathrm{M}}=I_{\mathrm{o}}^{-1}$. Here we have that I_o is the partitioned matrix given by

$$I_{\mathrm{o}}={\displaystyle \sum _{i=1}^n\left(\frac{\partial \mu (\mathbf{\alpha },\gamma |Z_i)}{\partial \mathbf{\beta }}\right)}{\left(\frac{\partial \mu (\mathbf{\alpha },\gamma |Z_i)}{\partial \mathbf{\beta }}\right)}^t{|}_{\widehat{\mathbf{\alpha }},\gamma =0}=\left(\begin{array}{cc}{A}_{11}& \\ A_{12}^t\end{array}\begin{array}{c}{A}_{12}\\ A_{22}\end{array}\right)$$

where A₁₁ is the scalar $n_1{\displaystyle {\sum }_{j=1}^D}{({\dot{g}}_j^0)}^2$; $A_{12}=(n_1{({\dot{g}}_1^0)}^2,\dots ,n_1{({\dot{g}}_D^0)}^2)$ and A₂₂ is the D × D diagonal matrix with (j, j) element $n{({\dot{g}}_j^0)}^2$, ${\dot{g}}_j^0=\dot{g}\left[g\left({\overline{\widehat{\theta }}}_j\right)\right]$, and n₁ is the number in sample 1. The inverse of this partitioned matrix is also a partitioned matrix with

$$I_{\mathrm{o}}^{-1}=\left(\begin{array}{cc}{A}^{11}& \\ A^{{12}^t}\end{array}\begin{array}{c}{A}^{12}\\ A^{22}\end{array}\right).$$

Here $A^{11}=n{\left[n_1{n}_2{\displaystyle \sum _{j=1}^D{({\dot{g}}_j^0)}^2}\right]}^{-1},A^{12}=-{\left[n_2{\displaystyle \sum _{j=1}^D{({\dot{g}}_j^0)}^2}\right]}^{-1}(\mathrm{1\dots 1})$ and

$$A^{22}=\left(\begin{array}{cccc}\frac{1}{n_1{({\dot{g}}_j^0)}^2}+\frac{n_1}{n{n}_2{\displaystyle \sum _{j=1}^D{({\dot{g}}_j^0)}^2}}& \frac{n_1}{n{n}_2{\displaystyle \sum _{j=1}^D{({\dot{g}}_j^0)}^2}}& \cdots & \frac{n_1}{n{n}_2{\displaystyle \sum _{j=1}^D{({\dot{g}}_j^0)}^2}}\\ \frac{n_1}{n{n}_2{\displaystyle \sum _{j=1}^D{({\dot{g}}_j^0)}^2}}& \frac{1}{n_1{({\dot{g}}_2^0)}^2}+\frac{n_1}{n{n}_2{\displaystyle \sum _{j=1}^D{({\dot{g}}_j^0)}^2}}& \cdots & \frac{n_1}{n{n}_2{\displaystyle \sum _{j=1}^D{({\dot{g}}_j^0)}^2}}\\ ⋮& ⋮& \ddots & \ddots \\ \frac{n_1}{n{n}_2{\displaystyle \sum _{j=1}^D{({\dot{g}}_j^0)}^2}}& \frac{n_1}{n{n}_2{\displaystyle \sum _{j=1}^D{({\dot{g}}_j^0)}^2}}& \cdots & \frac{1}{n_1{({\dot{g}}_D^0)}^2}+\frac{n_1}{n{n}_2{\displaystyle \sum _{j=1}^D{({\dot{g}}_j^0)}^2}}\end{array}\right).$$

The empirical based variance is given by ${\Sigma }_{\mathrm{E}}=I_{\mathrm{o}}^{-1}{I}_1{I}_{\mathrm{o}}^{-1}$ where $I_1={\sum }_{i=1}^n{U}_i{U}_i^T$. Here we have

$$I_1=\left[\begin{array}{cccc}{\displaystyle \sum _{i=1}^n{Z}_i^2}{\left[{\displaystyle \sum _{k=1}^D{\dot{g}}_j^0}\left({\widehat{\theta }}_{ij}-{\overline{\widehat{\theta }}}_j\right)\right]}^2& {\displaystyle \sum _{i=1}^n{Z}_i}\left[{\displaystyle \sum _{k=1}^D{\dot{g}}_j^0}\left({\widehat{\theta }}_{ij}-{\overline{\widehat{\theta }}}_j\right)\right]& \cdots & {\displaystyle \sum _{i=1}^n{Z}_i}\left[{\displaystyle \sum _{k=1}^D{\dot{g}}_j^0}\left({\widehat{\theta }}_{ij}-{\overline{\widehat{\theta }}}_j\right)\right]\\ & {\dot{g}}_1^0\left({\widehat{\theta }}_{i1}-{\overline{\widehat{\theta }}}_1\right)& & {\dot{g}}_D^0\left({\widehat{\theta }}_{iD}-{\overline{\widehat{\theta }}}_D\right)\\ {\displaystyle \sum _{i=1}^n{Z}_i}\left[{\displaystyle \sum _{k=1}^D{\dot{g}}_j^0}\left({\widehat{\theta }}_{ij}-{\overline{\widehat{\theta }}}_j\right)\right]& {\displaystyle \sum _{i=1}^n{\left({\dot{g}}_1^0\right)}^2}{\left({\widehat{\theta }}_{i1}-{\overline{\widehat{\theta }}}_1\right)}^2& \cdots & {\displaystyle \sum _{i=1}^n{\dot{g}}_1^0{\dot{g}}_D^0}\left({\widehat{\theta }}_{i1}-{\overline{\widehat{\theta }}}_1\right)({\widehat{\theta }}_{iD}-{\overline{\widehat{\theta }}}_D)\\ {\dot{g}}_1^0\left({\widehat{\theta }}_{i1}-{\overline{\widehat{\theta }}}_1\right)& & & \\ ⋮& ⋮& \ddots & ⋮\\ {\displaystyle \sum _{i=1}^n{Z}_i}\left[{\displaystyle \sum _{k=1}^D{\dot{g}}_j^0}\left({\widehat{\theta }}_{ij}-{\overline{\widehat{\theta }}}_j\right)\right]& {\displaystyle \sum _{i=1}^n{\dot{g}}_1^0{\dot{g}}_D^0({\widehat{\theta }}_{i1}-{\overline{\widehat{\theta }}}_1)({\widehat{\theta }}_{iD}-{\overline{\widehat{\theta }}}_D)}& \cdots & {\displaystyle \sum _{i=1}^n{({\dot{g}}_D^0)}^2{({\widehat{\theta }}_{iD}-{\overline{\widehat{\theta }}}_D)}^2}\\ {\dot{g}}_D^0({\widehat{\theta }}_{iD}-{\overline{\widehat{\theta }}}_D)& & & \end{array}\right]$$

The generalized score statistic for testing the hypothesis of no treatment effect, γ = 0 (Boos 1992; Rotnitzky and Jewell 1990) is ${\chi }^2={[I_0^{-1}{I}_1{I}_0^{-1}]}_{(11)}^{-1}{[I_0^{-1}]}^2{[U_{\beta }(\stackrel{⌢}{\alpha },0)]}^2$ where (11) implies the (1,1) term of the matrix. This statistic reduces to

$${\chi }^2={\left(\frac{n}{n_1{n}_2}\right)}^2\frac{{\left[{\displaystyle {\sum }_{Z_i=1}{\displaystyle {\sum }_{j=1}^D{({\dot{g}}_j^0)}^2({\widehat{\theta }}_{ij}-{\overline{\widehat{\theta }}}_j)}}\right]}^2}{\left\{\frac{{\displaystyle {\sum }_{Z_i=1}{\left[{\displaystyle {\sum }_{j=1}^D{({\dot{g}}_j^0)}^2({\widehat{\theta }}_{ij}-{\overline{\widehat{\theta }}}_j)}\right]}^2}}{n_1^2}+\frac{{\displaystyle {\sum }_{Z_i=2}{\left[{\displaystyle {\sum }_{j=1}^D{({\dot{g}}_j^0)}^2({\widehat{\theta }}_{ij}-{\overline{\widehat{\theta }}}_j)}\right]}^2}}{n_2^2}\right\}}$$

which has a chi-square 1 distribution under H_o.

For some standard models, the weights are easy to compute. That is ${\dot{g}}_j^0$ reduce to 1 for the identity link function; to ${\overline{\widehat{\theta }}}_j\text{log}[{\overline{\widehat{\theta }}}_j]$ for the complimentary log–log link function and to ${\overline{\widehat{\theta }}}_j(1-{\overline{\widehat{\theta }}}_j)$ for the logit link function.

5 Application

To illustrate the techniques, we use a set of 614 CML patients treated at the Hammersmith hospital in London. The data were reported in Craddock et al. (2000). In the study, there were 202 patients who died in first remission and 245 patients who relapsed. Of the 245 relapse patients, 118 died without achieving a second remission and 77 achieved a second remission. Thirteen of the 77 second remission patients either died or experienced a second relapse at which time they were considered as treatment failures. The mean follow-up of all patients was 5.2 years (range 0.02–21.1 years). We will focus on comparing the current leukemia free survival between patients with a HLA matched sibling donor (n₁ =371) and those with a HLA-matched unrelated donor (n₂ = 243).

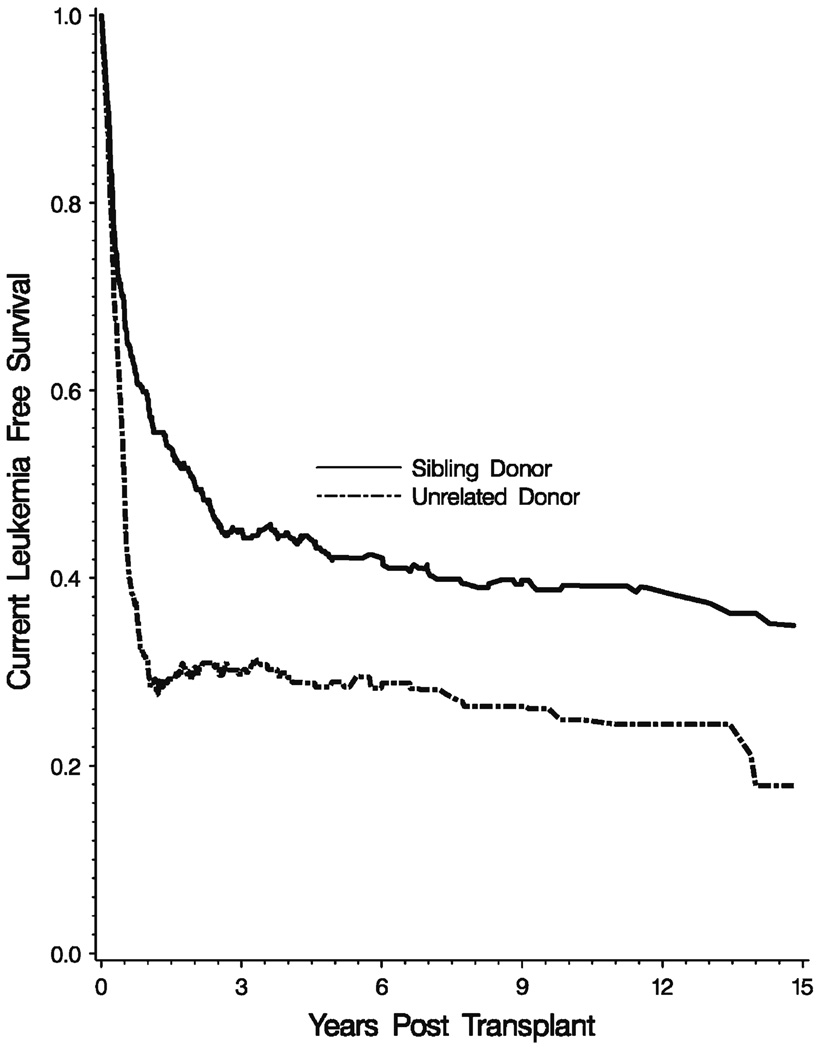
In Fig. 2, we present a plot of the two current leukemia free survival functions. Note that the CLFS function is not a monotone function of time reflecting that a patient may relapse, recover and then fail again.

Fig. 2.

Current leukemia free survival

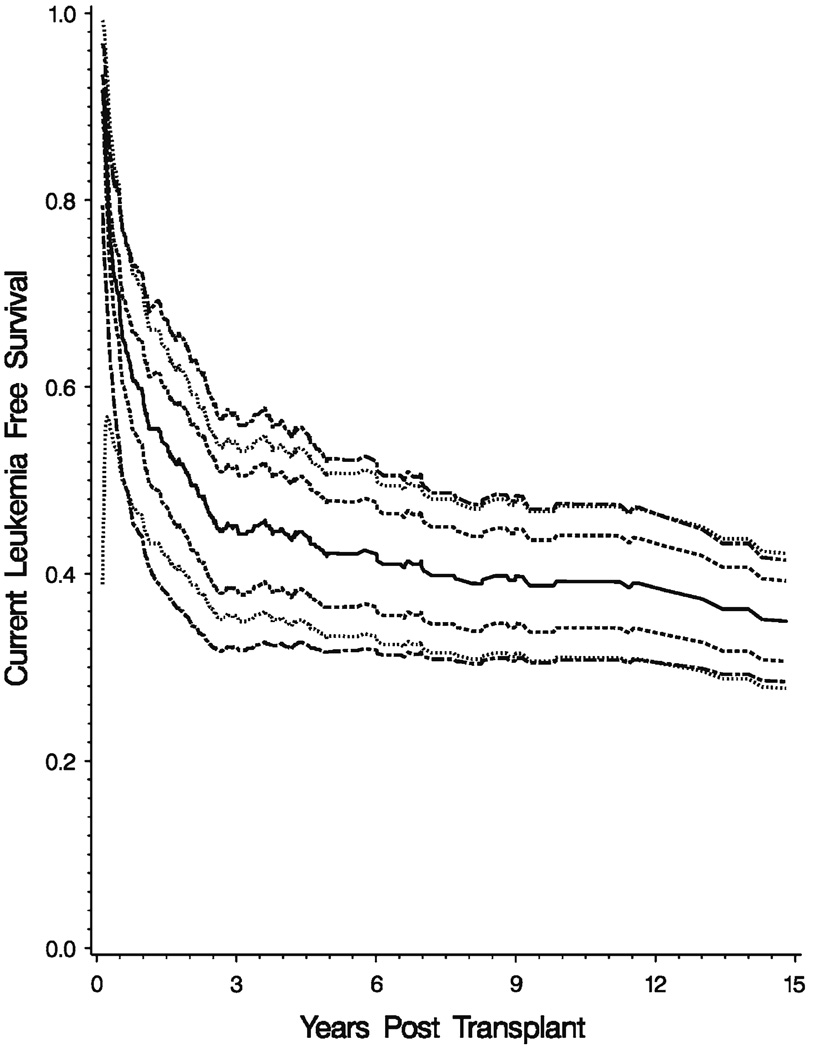
Figure 3 shows the CLFS function for the HLA-matched sibling donor group. The solid line is the estimate of the CLFS, the dashed line the 95% pointwise confidence interval, the dotted line is the 95% EP like confidence band and the dot-dash lines the 95% Wellner type confidence bands. The confidence bands are based on a log transformation of the CLFS and 1000 Monte Carlo replicates. They are both over the range 30 days–15 years. Note that there is little difference between the two bands.

Fig. 3.

Estimated CLFS for HLA identical sibling donors. Solid line estimated CLFS; dashed line is the 95% pointwise confidence interval; dotted line is 95% EP like confidence band and the dot-dash lines are the 95% Wellner type confidence bands

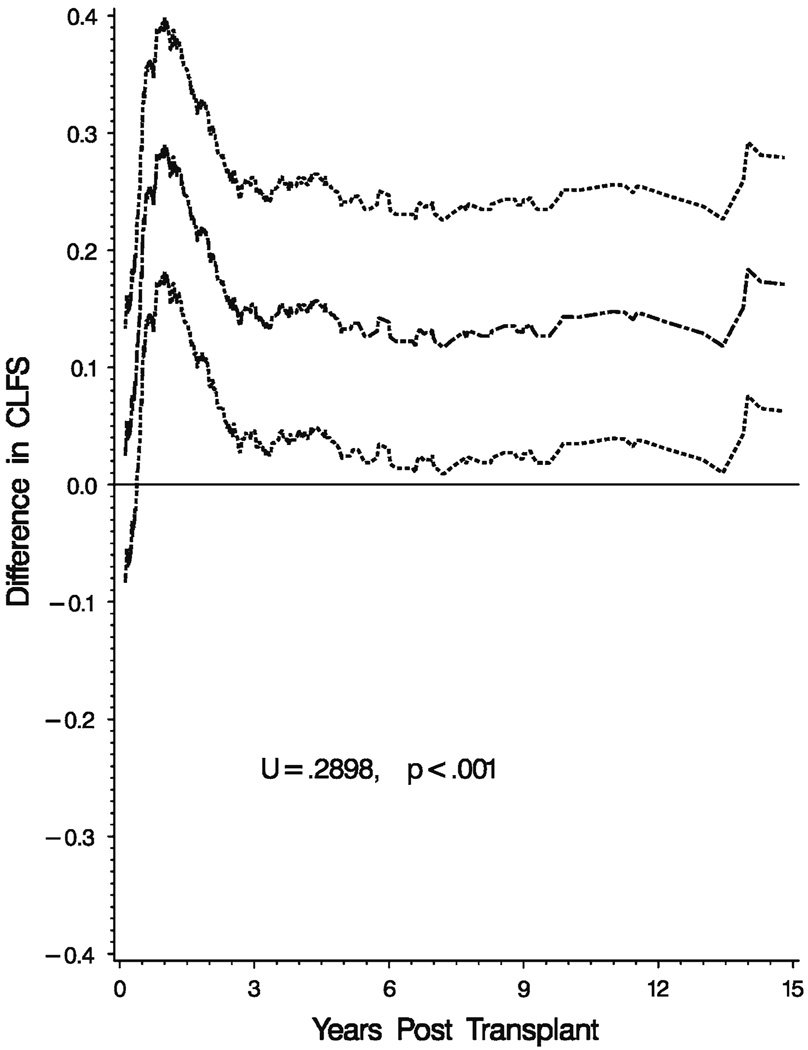
Figure 4 shows the estimate (solid line) and a 95% confidence band (dashed lines) for the difference in the two CLFS functions. Again the confidence bands are based on 1000 replicates. The maximum difference between the two CLFS function was 0.2898 and the p-value for testing the hypothesis that the two curves are different, based on 1000 independent replicates, was less than 1/1000. Note the figure clearly shows the advantage of using a sibling donor for this procedure.

Fig. 4.

95% Confidence band for the difference in CLFS

Using the pseudo-value approach the score statistics using the identity, the log-log and the logit link and all time points gave chi-squares of 24.56, 25.60 and 26.34, respectively. All tests are highly significant when compared to a chi-square with one degree of freedom. This is again strong evidence that the CLFS functions are different between the sibling and unrelated donor transplant recipients.

Some additional modeling/testing is available if we restrict the number of time points at which the pseudo-values are computed. Below we base estimation on nine pseudo values computed at approximately 100 days, 6 months and 1, 2, 3, 4, 5, 6, and 9 years. Using the complementary log–log (CLL) and logistic models, we can estimate the relative risk or the odds ratio, respectively, of the effect of donor type on the CLFS, as e^γ. For the CLL model, we have that γ̂ = 0.49 and the relative risk of an unrelated donor as compared to a sibling donor is 1.6 (95% confidence interval [1.3,2.0]), while for logistic model we have that γ̂ = .74 and the odds ratio is 2.1 [1.6,2.8]. Both have p < 0.0001. We can also adjust our estimates for other effects. Here we adjust for the effect of stage of disease (early 73.8%, intermediate 22.5%, and advanced 3.7%) and patient age. Table 1 shows the results of a model with donor type and the other two factors. Note that the effect of donor is more pronounced in the adjusted model. We can also examine the effect of donor by looking at a model with an interaction between time and donor type. This model is shown in Table 2. As the confidence band in Fig.4 showed there is an advantage for sibling donors for most time points and that this advantage is the highest at about one year.

Table 1.

Models adjusted for age and stage of disease

Effect	CLL model			Logit model
	β̂	SE	p-Value	β̂	SE	p-Value
Unrelated donor	0.5307	0.1020	<0.0001	0.8072	0.1541	<0.0001
Age	0.0136	0.0051	0.0081	0.0199	0.0075	0.0079
Intermediate disease	0.6154	0.1133	<0.0001	0.9458	0.1801	<0.0001
Advanced disease	1.8831	0.2607	<0.0001	3.1821	0.4949	<0.0001

Table 2.

Effect of donor type over time

Time	CLL model		Logit model
	Relative risk	95% Confidence interval	Odds ratio	95% Confidence interval
100 days	1.44	1.06–1.97	1.53	1.06–2.20
6 months	1.82	1.41–2.36	2.16	1.55–3.02
1 year	2.35	1.87–2.95	3.51	2.48–4.95
2 years	1.77	1.42–2.21	2.40	1.70–3.38
3 years	1.57	1.26–1.95	2.03	1.43–2.89
4 years	1.52	1.22–1.89	1.93	1.36–2.76
5 years	1.45	1.16–1.81	1.81	1.27–2.60
6 years	1.44	1.15–1.80	1.79	1.25–2.58
9 years	1.45	1.16–1.83	1.86	1.26–2.74

6 Discussion

The analysis of multistate models in general and inference for the current leukemia free survival function in particular provides a challenge to statisticians, especially when interest is the direct modeling of the effect of treatment on outcome. These problems are of particular interest in HSCT studies where post-transplant events or therapy may influence the patient’s health state. In the case of the CLFS function, it is of interest to compare how various treatment therapies may affect the chance a patient is in the healthy state of remission.

These techniques provide a way to estimate the CLFS and to provide an idea of the statistical uncertainty associated with that estimate. As seen in the example and Fig. 2 for HLA identical siblings we can say with 95% confidence that between 3 and 15 years after transplant that between 30% and 50% of the patients will be in either first or second remission.

More useful, perhaps, than the estimates of CLFS is the tests and associated confidence bands for comparing treatment effects. The test and methods based on the approach in Sect.3 provide an omnibus test to compare the two treatments. The test simply asks the question are the treatments different at some point in time while the confidence band for the difference in survival curves tells us where they are different and by how much. In the example, we see that patients with an HLA sibling donor do significantly better than patients given an unrelated donor transplant. Figure 4 shows that the improvement in CLFS is highest at about 9 months where the difference is between about 20% and 40% and that in the long run after about 3 years there is between 3% and 27% increase in CLFS on an absolute scale.

The pseudo-observation approach provides an alternative approach to inference for the CLFS. The score test provides a relatively simple, closed form test which does not require extensive Monte Carlo work to obtain the p-value. The pseudo-observation approach allows direct regression modeling of the CLFS function. In this example, the tests based on the pseudo-observation method tell the same story as the omnibus test, namely, that patients given a sibling donor transplant are more likely to be in remission then those with an unrelated donor transplant. Here the magnitude of the difference is expressed by an odds ratio or relative risk as opposed to a figure such as Fig. 4.

An obvious question is which method is better. Clearly the power of these tests depends on the type of differences one expects to see. For crossing CLFS functions, the omnibus test in Sect.4 has higher power while the tests based on pseudo-observations may have limited power. The tests based on the pseudo-observations will depend on the structure of the alternative hypothesis and the selection of the link function. This question is currently being investigated.

While these methods were developed for inference for the CLFS function they can be extended and applied to other multistate models that explain the HSCT recovery process. The pseudo-observation approach is particularly adaptable as shown in Andersen and Klein (2007).