Inter-Subunit Coordination in a Homomeric Ring-ATPase

Abstract

Homomeric ring-ATPases perform many vital and varied tasks in the cell, ranging from chromosome segregation to protein degradation. Here we report the first direct observation of the inter-subunit coordination and the step size of such a ring-ATPase, the dsDNA packaging motor in the bacteriophage φ29. Using high-resolution optical tweezers, we find that packaging occurs in increments of 10 bp. Statistical analysis of the preceding dwell times reveals that multiple ATPs bind during each dwell, and application of high force reveals that these 10-bp increments are composed of four 2.5-bp steps. These results indicate that the hydrolysis cycles of the individual subunits are highly coordinated via a mechanism novel for ring-ATPases. In addition, a step size that is a non-integer number of base pairs demands new models for motor-DNA interactions.

Introduction

Multimeric ring-ATPases of the ASCE (Additional Strand, Conserved E) superfamily represent a structurally homologous yet functionally diverse group of proteins involved in such varied tasks as ATP synthesis, protein unfolding and degradation, and DNA translocation^1-5. Despite their importance, the coordination mechanism between the hydrolysis cycles of the individual and often identical subunits that compose these ringed-proteins is poorly understood. Recent crystallographic and bulk biochemical studies^{2, 4} suggest various models of coordination in which subunits act sequentially and in order^6-14, simultaneously and in concert¹⁵, or independently and at random¹⁶. Unfortunately, direct observation of subunit dynamics has only been reported for a heteromeric system, the F1 ring of ATP synthase⁸, whose heterodimers function in a sequential manner.

The DNA packaging motor in the Bacillus subtilis bacteriophage φ29 provides a model system to investigate the inter-subunit coordination in homomeric ring-ATPases because it can be fully reconstituted in vitro¹⁷, it has a relatively slow translocation rate^{18, 19}, and it has been extensively characterized by bulk²⁰ and single-molecule^{18, 19, 21-23} methods. Packaging of the double-stranded DNA genome of φ29 into its proteinaceous precursor capsid (prohead) is driven by a powerful molecular machine¹⁸ which consists of three multimeric rings organized coaxially around the point of DNA entry²⁰: a dodecameric²⁴ ring of gene product 10 (gp10) known as the head-tail connector, a pentameric^24-26 ring of RNA molecules known as the prohead-RNA (pRNA), and a pentameric^{24, 26} ring of the ATPase gp16 (see Figure 1a). Sequence homology²⁷ places gp16 in the FtsK/HerA family of dsDNA translocases²⁸. This family is itself a member of the large ASCE superfamily, thus relating the packaging motor to the ubiquitous AAA+ and RecA-like proteins^{3, 5}.

Figure 1. Bacteriophage φ29 Packages DNA in Bursts of 10 bp.

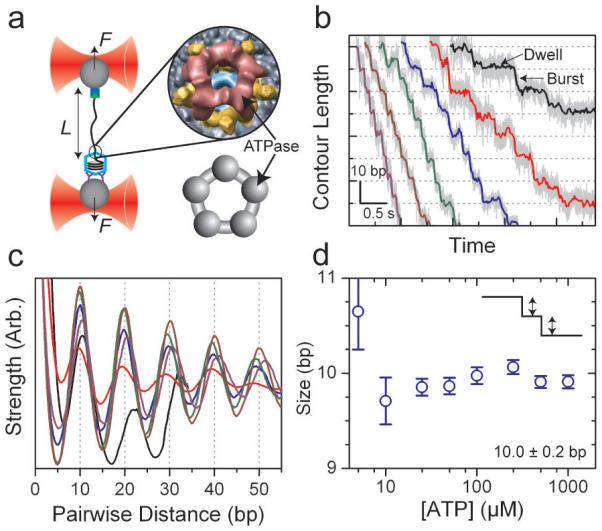
(a) A single packaging bacteriophage prohead-motor complex and its dsDNA substrate are tethered between two beads each held in an optical trap. Inset: cryo-EM reconstruction of the full motor complex²⁶ (Courtesy of M. Morais), ATPase in red, pRNA in yellow, connector in cyan, and capsid in gray with a top view cartoon of the ATPase ring alone (below, gray). (b) Representative packaging traces collected under low external load, ∼8 pN, and different [ATP]: 250 μM, 100 μM, 50 μM, 25 μM, 10 μM, and 5 μM in purple, brown, green, blue, red, and black, respectively, all boxcar-filtered and decimated to 50 Hz. Data at 1.25 kHz are plotted in light gray. (c) Average pairwise distributions of packaging traces selected for low noise levels (50% of all packaging data; see Supplementary Figures 2 and 3). Color scheme as in (b). (d) The average size of the packaging burst versus [ATP] determined from the periodicity in (c). Error bars are the error in the slope from a linear fit to the peak position. Data collected at 500 μM and 1 mM [ATP] are not shown in (b) and (c) for clarity.

Recent studies of the packaging motor have suggested a mechanism in which the subunits operate sequentially¹⁹, each binding ATP, hydrolyzing it, and translocating the DNA by 2 bp^{19, 29}, before the next subunit repeats this cycle. While this scheme is consistent with the observed data^{19, 24, 30} and with sequential models proposed for other ring-ATPases^{2, 4, 6-14}, direct observation of the coordination of the mechanochemical cycles of the individual subunits in the packaging motor is still lacking. In this article, we report the first measurements of the individual packaging steps of the φ29 motor, which reveal both its step size and the novel coordination between its subunits. Because of its relation to the ASCE superfamily²⁷, the mechanism for the packaging motor we propose here may have implications for the function of a diverse set of ring-ATPases.

DNA is Packaged in 10-bp Increments

To probe the dynamics of the packaging motor of φ29, single prohead-motor-DNA complexes are tethered between two 860-nm diameter polystyrene beads held in two optical traps as in Figure 1a. Packaging is initiated in situ^{22, 23} or by restarting stalled complexes^{18, 19} in an ATP packaging buffer and monitored in a semi-passive mode in which the tension applied to the motor is kept within a narrow range by periodically changing the distance between the two traps (Supplementary Figure 1). Motor translocation is determined from the decrease in the contour length of the DNA tether and is followed with base-pair-scale resolution^31-33.

In our first experiments we probe packaging at an average low external tension of ∼ 8 pN, and at ATP concentrations ([ATP]) above and below the K_M of the motor, ∼30 μM¹⁹. Figure 1b shows representative packaging traces collected under these conditions. Across the full range of [ATP], packaging of DNA occurs in a stepwise manner consisting of “dwells,” in which the DNA length remains constant, followed by “bursts,” in which DNA is translocated in ∼10-bp increments. We determine the average length of DNA encapsidated in these packaging bursts for each [ATP] from the periodicity in the average pairwise distance distribution (PWD) as seen in Figure 1c. No statistically significant trend is observed in the size of these bursts as a function of [ATP] (see Figure 1d); thus, the average of these values, 10.0 ± 0.2 bp (s.d.), is the best estimate for the burst size.

To elucidate the mechanism by which the motor translocates in 10-bp increments, we analyze the time the motor spends in the dwell before each burst and the time it takes to complete each burst as a function of [ATP]. Figure 2a shows the distribution of dwell times before the packaging bursts. The mean dwell time, seen in Figure 2b, shows a strong dependence on [ATP] that follows an inverse hyperbolic expression, 〈τ〉 = (K_1/2 + [T])/(k_cat [T]), with a K_1/2 of 23 ± 7 μM (s.d.) and a k_max of 8.7 ± 0.7 s⁻¹ (s.d.). In contrast, Figure 2b shows that the average duration of the packaging burst has little or no dependence on [ATP], suggesting that ATP binding occurs only in the dwells and not in the bursts. Taken together these observations produce a packaging velocity with a Michaelis-Menten [ATP] dependence consistent with previous measurements¹⁹.

Figure 2. Dwells Before 10-bp Bursts Contain Multiple Kinetic Events.

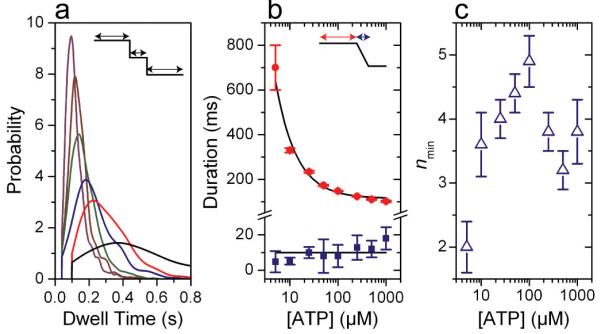
(a) Probability distributions for the dwell times preceding a 10-bp burst under low external load, ∼8 pN, and different [ATP]: color scheme as in Figure 1. Distributions were estimated using kernel density estimation with a Gaussian kernel and the optimum bandwidth⁴⁶ and are truncated at the lowest detectable dwell time. Supplementary Figure 2 contains the number of observed bursts for each [ATP]. Distributions for 500 μM and 1 mM [ATP] are not shown for clarity. (b) The mean dwell time before the 10-bp bursts (red circles) for all [ATP] with an inverse hyperbolic fit (black) and the mean duration of all bursts (blue squares, average denoted by black line). (c) The minimum number of rate-limiting kinetic events during the dwell before the 10-bp bursts, n_min, for all [ATP]. Error bars are the standard error.

The specific shape of the dwell time distributions seen in Figure 2a provides further information on the kinetic transitions within a single dwell. In particular, the more sharply peaked the distribution, the larger the number of rate-limiting kinetic transitions that compose the dwell³⁴. We quantify the degree to which these distributions are peaked with the ratio of the squared mean of the dwell times to their variance, the inverse of the randomness parameter³⁴ (Figure 2c). It can be shown that this parameter, n_min, provides a strict lower bound³⁵ on the number of rate-limiting transitions under each [ATP] that occur during the dwell.

At limiting [ATP], 5 μM << K_M, we measure an n_min of 2.0 ± 0.4 (s.e.m), indicating that there are at least two rate-limiting transitions in each dwell. Since ATP binding must be rate-limiting under these conditions, we conclude that no less than 2 ATP molecules bind to the motor before each 10-bp burst. (In contrast, if a single ATP were to bind during each dwell, one would expect the dwell time distribution to be a single exponential and n_min to be 1)^{34, 36}. At saturating [ATP], 1 mM >> K_M, we measure an n_min of 3.8 ± 0.5 (s.e.m.). Since binding is no longer rate-limiting, this indicates that at least 4 additional non-binding transitions must occur in each dwell. For intermediate [ATP], both binding and non-binding transitions can be rate-limiting; thus, we expect n_min to peak to a value greater than either of the extreme values, exactly as is observed. Thus, Figure 2c indicates that in total no less than 6 kinetic transitions must occur in the dwell before each 10-bp burst—at least 2 ATP binding events and at least 4 non-binding transitions.

Packaging Occurs in Four 2.5-bp Steps

The findings that packaging occurs in 10-bp increments—five times larger than the 2-bp value proposed from bulk measurements^{19, 29} —and that the preceding dwells contain multiple ATP binding transitions suggest that the 10-bp bursts may be composed of multiple smaller steps that in general may be too fast to resolve under the above conditions. This inference is supported by the observation that many bursts have durations larger than the measurement bandwidth (Figure 1b and Figure 2b), indicative of intermediate kinetic transitions. Supplementary Figure 4 shows that occasionally these intermediate transitions can be resolved, appearing as short micro-dwells that split the 10-bp burst into smaller steps. A correlation analysis³⁶ confirms that these smaller steps occur in groups that add to 10 bp, ruling out the possibility that these events represent a variable burst size (Supplementary Discussion).

As a direct demonstration of the composition of the 10-bp bursts, we follow packaging against high external loads at near-saturating [ATP] (250 μM). Since translocation steps correspond to force-generating kinetic transitions, we expect that the duration of the micro-dwells preceding these steps will increase with increasing external force³⁷. Figure 3a shows that, under 40 pN of average load, smaller steps of ∼2.5 bp and integer multiples thereof can be clearly and frequently observed. The PWD for this data, shown in Figure 3b, reveals a periodicity of 2.4 ± 0.1 bp (s.d.) and the step size distribution, shown in Supplementary Figure 6, has a peak at 2.48 ± 0.03 bp (s.e.m.). The inset to Figure 3b shows that the periodicity in the PWD is independent of force, indicating that the 2.5-bp step size is a constant feature of the motor and that the 10-bp bursts observed at low force are composed of four 2.5-bp steps. This conclusion is further supported by the prominent fourth peak observed in the PWD which is consistent with the corresponding 10-bp periodicity observed at low force.

Figure 3. The 10-bp Bursts are Composed of Four 2.5-bp Steps.

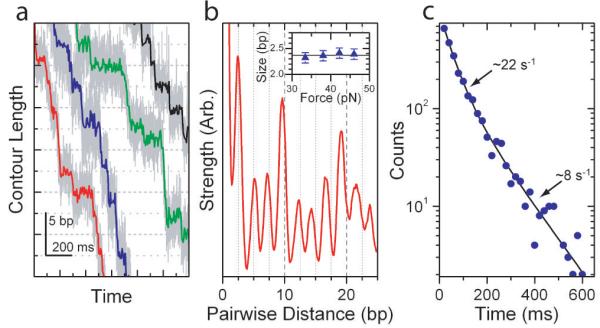
(a) Representative packaging traces collected with external loads of ∼40 pN and 250 μM [ATP]. Data in light gray are plotted at 1.25 kHz while data in color are boxcar-filtered and decimated to 100 Hz. (b) Average pairwise distribution of packaging traces selected for low noise levels (50% of all packaging data; see Supplementary Figures 2 and 3). Inset: Force dependence of the observed spatial periodicity. The solid line is the mean for all forces 2.4±0.1 bp (s.e.m.). (c) Dwell time histogram for the 2.5-bp steps observed under the packaging conditions seen in (a) plotted in blue circles with a bi-exponential fit in black (N=2,662).

The dwell time distribution associated with the 2.5-bp steps (Figure 3c) is well described by a weighted sum of two exponential decays, with a fast rate of 22 ± 2 s⁻¹ (s.d.) and a slow rate of 8 ± 1 s⁻¹ (s.d.). The fast rate rationalizes the fraction of 2.5-bp steps that are missed in our analysis and the slow rate is consistent with one out of every four dwells coming from the same peaked dwell time distribution observed at low force (Supplementary Figures 5 and 6). Finally, our data do not support alternative interpretations of the 2.5-bp periodicity, such as distortions from B-form or alternating integer steps, as discussed in Supplementary Figures 7 and 8 and in the Supplementary Discussion, though some variability in the step size on the ∼0.1-bp scale cannot be ruled out.

Inter-Subunit Coordination

Taken together these results indicate that the mechanochemical cycles of the identical subunits of the packaging motor of φ29 are highly coordinated, with the loading of ATP and the translocation of DNA segregated into two distinct phases that comprise the mechanochemical cycle of the entire ring (Figure 4a). During the initial, “dwell,” phase the DNA is held at constant length while multiple ATPs are loaded, giving this dwell its observed [ATP] dependence (Figure 2). This process is followed by the “burst” phase in which DNA is packaged in four increments of 2.5 bp, totaling 10 bp of DNA translocated per cycle (Figures 1d and 3b). Thus, this phase has an average duration that is independent of [ATP] but dependent on force (Figures 2b and 3c).

Figure 4. Inter-Subunit Coordination in the Ring-ATPase of φ29.

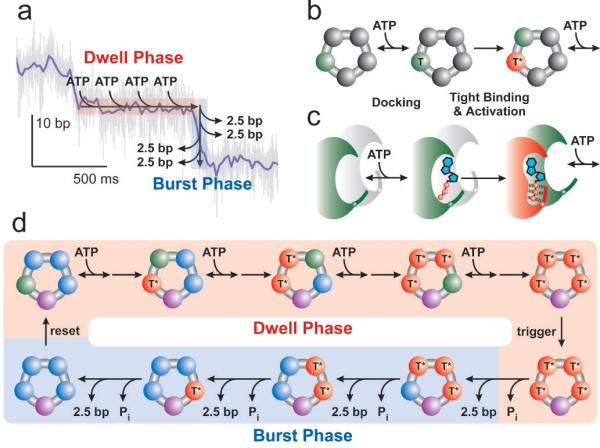
(a) Schematic diagram of the two-phase mechanochemical cycle of φ29 overlaid on a sample packaging trace. (b) Detailed kinetics of ATP binding. Binding occurs in two steps, ATP docking (green, T) followed by tight-binding (red, T*). (c) Schematic diagram of the communication between subunits during ATP binding. Upon tight-binding of an ATP, the binding pocket of the next subunit, formerly inactive (gray), is activated for docking (green). (d) Schematic depiction of the full mechanochemical cycle of φ29. During the burst phase, ADP may remain on the ring (blue) to be released in the dwell phase. One subunit must be distinct from the others (purple) in order to break the symmetry of the motor and generate only 4 steps per cycle. The identity of this subunit may change each cycle.

The observation of four translocation steps per burst strongly suggests that four ATPs bind to the ring each dwell, one for each of the subsequent steps in the burst phase. This inference is consistent with the measured value of n_min at limiting [ATP] since reversibility in binding or differences in binding rates will decrease the observed value of n_min from the actual number of binding events³⁴. It is also consistent with the 10-bp burst size since a single ATP provides insufficient free energy to package 10-bp against the high forces tested previously^{18, 19, 37}. Moreover, the binding of four ATPs predicts a coupling constant between ATP consumption and packaging of 2.5 bp/ATP, in reasonable agreement with the ∼2 bp/ATP value estimated from bulk measurements^{19, 29}. The ∼25% discrepancy may be explained by additional processes that consume ATP in bulk measurements, such as the repackaging of DNA that slips from the capsid^{18, 19}. However, it is also possible that a regulatory fifth ATP is bound each cycle and hydrolyzed futilely.

Our data also restrict the possible mechanisms by which these ATPs bind to the ring. The requirement that multiple substrate molecules bind per cycle typically results in a sigmoidal dependence on [ATP]³⁸—the hallmark of binding cooperativity. Yet previous velocity measurements¹⁹ and the mean dwell times measured here (Figure 2b) are well described by a simple, non-sigmoidal ATP dependence. Since a sigmoidal [ATP] dependence arises whenever two or more binding events are connected reversibly³⁸, these two observations can be reconciled if and only if the binding of each ATP is separated from the other binding events by a largely irreversible transition. In this case the mean dwell time will display a non-sigmoidal [ATP] dependence despite the cooperative binding of ATP (Supplementary Discussion). This requirement is consistent with previous observations for φ29¹⁹ and related ring-ATPases³⁹ which indicate that binding occurs in at least two kinetic steps – (1) a reversible “docking” transition in which the molecule comes in weak contact with the catalytic pocket followed by (2) a largely irreversible “tight-binding” transition³⁹ in which ATP makes a stronger contact to the binding site and is committed to the hydrolysis cycle (Figure 4b). More intermediate kinetic states in ATP binding are also possible, but are not required to explain our observations.

In addition, the non-sigmoidal [ATP] dependence of the mean dwell times also restricts the temporal order in which the subunits can dock ATP. Kinetic schemes in which multiple subunits are capable of reversibly docking ATP simultaneously will necessarily have a sigmoidal [ATP] dependence because such schemes have binding events that are reversibly connected³⁸ (Supplementary Discussion.) Thus, it is not sufficient to require that each loose docking of ATP be followed by a tight-binding transition; we must also require that only one subunit at a time can be involved in ATP docking. The simplest model that produces this time-ordered docking is one in which the tight-binding transition of one subunit allosterically activates the binding pocket of another subunit, making it competent to dock ATP, a process depicted in Figure 4c (Supplementary Discussion). While our data cannot uniquely determine the actual sequence in which the subunits bind ATP, this required allosteric activation in combination with the known interfacial interactions of adjacent subunits in related ring-ATPases^{3, 5} strongly favors a mechanism in which successive ATP binding occurs in a sequential and ordinal fashion around the ring as depicted in Figure 4.

Figure 4d summarizes the kinetic transitions that occur during a complete mechanochemical cycle of the packaging motor. During the binding phase, four ATPs bind to the ring in the two-step process depicted in Figure 4b and c. Previous work has shown that the release of phosphate precedes or coincides with translocation¹⁹. Thus, after the ring has bound four ATPs, the burst phase is triggered, the first phosphate is released, and the first 2.5-bp step is taken. The burst phase then proceeds with three additional 2.5-bp steps preceded by three force dependent micro-dwells. The number of rate-limiting steps, n_min, at saturating ATP (Figure 2c) indicates that multiple kinetic transitions besides ATP binding must occur during the dwell phase. These transitions may correspond to the hydrolysis of the bound ATPs or the release of multiple ADPs from the previous cycle or, perhaps, both. Moreover, these transitions may occur together either as trigger or reset processes (Figure 4d) or interspersed between ATP binding events. It is also possible that these additional events correspond to the tight-binding transitions, though this is unlikely given that tight-binding is believed to occur quite rapidly¹⁹.

The two-phase model we propose here is also consistent with previous measurements of the packaging motor^{18, 19}. For example, it has been shown that the binding of a single non-hydrolyzable ATP analog is sufficient to pause the entire motor¹⁹—a result consistent with the high degree of inter-subunit coordination observed here. Furthermore, a biphasic sedimentation profile observed in sucrose gradient experiments suggests the ability of the ring to load multiple nucleotides¹⁹, consistent with our model. Finally, the two-phase model predicts the same dependence of the packaging velocity with force and [ATP] as observed previously^{18, 19}.

Non-Integer Step Size Models

Our finding that packaging occurs in four 2.5-bp translocation steps raises two notable questions on the motor mechanism. First, how does a dsDNA translocase move in a non-integer number of base pairs? And, second, how is the pentameric symmetry^24-26 of the motor broken, generating only four steps per cycle? A step size that is a non-integer number of base pairs prohibits any mechanism in which every motor subunit within a closed ring makes specific and identical chemical contacts with one strand of the DNA. Under this constraint, we can speculate on several alternative mechanisms that would produce a 2.5-bp step size and the implications these models have for a pentameric motor.

A non-integer step size could be generated if each subunit is capable of binding two or more alternating chemical moieties, which may or may not be on the same strand. Alternatively, the motor may make no specific contacts, but rather drive translocation via steric interactions, in which case the step size would be set not by the chemical periodicity of the DNA but by the size of the internal conformational changes that generate the power stroke. One example of such a mechanism is depicted in Figure 5a where each subunit makes non-specific contacts with the major groove of the DNA. In such a model, generation of four translocation steps requires that one of the five subunits is not equivalent to the other four, breaking the symmetry of the pentameric ring. Since the nucleotide-free state is disengaged from the DNA¹⁹, one subunit may be required to retain nucleotide at the end of the previous cycle, ensuring that a strong contact with the DNA is maintained while the remaining subunits load ATP during the subsequent dwell phase.

Figure 5. Packaging Models that Produce a Non-Integer Step Size.

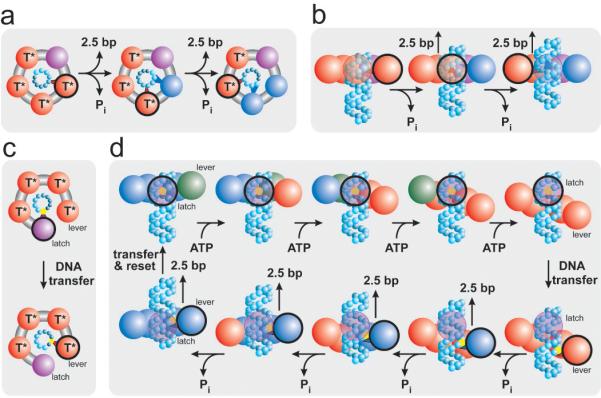
(a) Depiction of a translocation model in which all subunits eventually contact the DNA (cyan spheres.) The contacting subunit is outlined in black. (b) In such a model the size of internal conformational changes set the step size (side view.) (c) Depiction of a translocation model in which only two subunits contact the DNA (black outline.) (d) In such a model, one subunit maintains contact with the DNA (the latch) while the loading of each ATP introduces relative subunit-subunit rotations which distort the ring. This distortion extends one subunit (the lever) along the DNA by ∼10-bp. The DNA contact point is then transferred from the latch to the lever, and the release of hydrolysis products relaxes the ring, retracting the lever and the DNA. The DNA contact is then transferred back to the latch, the ring resets, and the cycle begins again. Because there are four subunits, the ring is retracted in four steps, dividing a 10-bp step into four ∼2.5-bp substeps. The subunit color scheme is the same as in Figure 4.

Alternatively, a single specific chemical contact may be made with the DNA but not with every subunit. In this class of models, only a subset of the subunits interact with the DNA and relative motion between these subunits is what drives translocation. Figure 5b depicts an example of such a mechanism in which only two subunits make specific contact with the DNA. Translocation is achieved via an “inchworm-like” movement of these two subunits driven by distortions in the ring. One appeal of this mechanism is that because a single specific contact is made with the DNA, it produces an integer burst size, yet because the DNA-binding subunits are retracted by conformational changes induced into the ring by the other subunits, this burst can be divided into non-integer steps. Moreover, this model also explains naturally the observation of four steps by a pentameric motor since one subunit interface must bear the accumulated distortion of the other four subunits, perhaps inactivating one of the five binding pockets. The relative motion between adjacent subunits needed to accommodate such a mechanism has been observed in the crystal structures of other ring-ATPases^{6, 40} but has not been implicated as part of the translocation mechanism⁴¹. Future measurements will be aimed at testing the spectrum of models discussed here.

Conclusions

We have presented here the first high-resolution measurements of the stepping dynamics of the ring-ATPase of the packaging motor of bacteriophage φ29. Our results indicate a highly coordinated two-phase mechanism in which the binding of ATP and the translocation of DNA by multiple subunits are organized into two distinct and temporally segregated portions of the mechanochemical cycle of the ring. Our observation of a 2.5-bp step size challenges the long-held view that DNA translocation must occur in integer base pair increments, making it necessary to devise new and more complex models for motor-DNA interactions. In addition, while the inter-subunit coordination we observe is reminiscent of aspects of both the concerted-action model of the large tumor antigen of SV40¹⁵ and the sequential models proposed for the translocases BPV E1, T7 gp4, ϕ12 P4, E. coli rho, and FtsK^{6, 7, 9-14}, our mechanism represents a novel type of coordination not previously proposed for ring-ATPases. Provocatively, while a two-phase mechanisms contrasts with these other models, it appears to be consistent with many of the biochemical^11-14 and structural^{6, 7, 9, 10, 13} observations made on these related systems. One notable exception is the ClpX protease for which biochemical data clearly suggest a limited degree of subunit coordination¹⁶. However, recent work on a related system, the archaeal MCM, suggests that coordinated systems can take alternative pathways when overcoming functional barriers such as catalytically inactive subunits⁴². Ring-ATPases of the ASCE superfamily support a large and remarkably diverse set of cellular functions by drawing upon a comparatively small set of common structural features. Direct measurements of the inter-subunit dynamics in these systems, such as those presented here, promise to reveal if these diverse cellular functions arise from a similarly small set of common structural dynamics.

Methods Summary

Complexes of prohead, gp16, and biotinylated DNA were prepared and attached to 860-nm polystyrene beads (Spherotech, Libertyville, IL) coated with antibodies to φ29 or streptavidin using methods that have been described previously^{18, 19}. Tethers were assembled and packaging was restarted in a packaging buffer (50 mM TrisHCl, 50 mM NaCl, 5 mM MgCl₂, 10 μg/mL BSA, 0.1% NaN₃, pH 7.8) supplemented with various amounts of ATP (Sigma-Aldrich, St. Louis, MO)^{18, 19}. Experiments were conducted in two separate dual-trap instruments, built around two different trapping lasers^{32, 33}, and calibrated using standard techniques^{32, 33, 43}. The contour length of the DNA tether was calculated from the measured force and extension using the extensible worm-like-chain model as described previously^{18, 19}. Pairwise distributions were calculated from data filtered with a sliding 20 ms box-car window as described previously⁴⁴. The location and duration of stepping transitions were found with a t-test analysis similar to previous methods⁴⁵. Dwell times were calculated directly from the time between transitions, and burst durations were calculated from the number of points within transitions. The mean and variance were calculated directly from these dwell times, and the errors were estimated using a bootstrap method. n_min was calculated directly from these moments^{34, 36}.

Methods

Sample Preparation

Prohead, gp16, and genomic DNA were isolated as described previously⁴⁷. For a stalled complex method of initiation^{18, 19}, a ClaI (New England Biolabs, Ipswich, MA) digest of genomic DNA was biotinylated using Klenow exo- (New England Biolabs, Ipswich, MA) to fill in the overhang with biotinylated nucleotides (Sigma-Aldrich, St. Louis, MO) ^{18, 19}. Preferential packaging of the left end of the genome²⁰ favors the formation of prohead-motor-DNA complexes with the 6,149 bp fragment of the ClaI digest. Stalled complexes were then bound to antibody beads, made as described previously¹⁸, and introduced into the tweezers with streptavidin coated beads. For the in situ method of initiation^{22, 23}, a 4,277 bp tether PCR amplified from lambda DNA with a biotinylated primer was bound to streptavidin coated beads, and stalled prohead-motor complexes^{22, 23} were bound to antibody beads. In both initiation methods, tethers were formed in the tweezers by physically bumping the two beads. The in situ initiation method was used for all [ATP] ≥ 25 μM since data were in general less noisy and easier to collect; however, a severe drop in tether formation efficiency below 25 μM required the use of the stalled complex method for low [ATP]. All tether lengths were selected to reduce the effect of packaged DNA on motor dynamics^{18, 23}.

Optical Trapping Instruments

Two different optical trapping instruments were used in these studies^{32, 33}. All low force data for 25 μM ≤ [ATP] ≤ 250 μM were collected using a instrument built around a 845-nm, 200 mW diode laser³². All other data were collected using an instrument built around a high-power, diode-pumped, solid-state 1064-nm laser³³. Both instruments exploit the correlations in the motion of the two trapped beads with a differential detection technique³² to achieve base-pair-resolution on the second time scale^31-33. Due to increased laser absorption at 1064-nm⁴⁸, the high force data were collected in an 80% Deuterium-oxide (D2O) buffer to avoid heating effects caused by the high laser power needed to provide the large opposing forces. Supplementary Figure 5 shows that while D2O alters the kinetics of packaging, it does not change the size of the packaging bursts. In addition, when working with the 1064-nm trapping laser, an oxygen scavenging system was added (100 μg/mL glucose oxidase, 20 μg/mL catalase, 5 mg/mL dextrose; Sigma-Aldrich, St. Louis, MO) to prevent the formation of the reactive species singlet oxygen.

Calibration

Traps were calibrated using the thermal fluctuations of the trapped beads⁴³. The contour length was calculated from the measured extension and force with the extensible worm-like-chain model using a persistence length of 53 nm, a stretch modulus of 1200 pN^{19, 49}, and an average B-form DNA rise of 3.4 Å/bp⁵⁰. Distance calibrations were corroborated with video microscopy³³, which was calibrated to 0.3% with two different distance standards (Nikon, Mellville, NY; Graticules, London) and confirmed to 1% by measuring the extension of DNA of different lengths, ∼1, 2, 3, and 5.6 kb. All packaging experiments were conducted in a semi-passive mode (Supplementary Figure 1), in which the trap separation was kept constant as packaging proceeded and was changed discretely to keep the tension within a set range, ∼6-10 pN for low force experiments and ∼33-46 pN for high force experiments. All reported data have been corrected for small systematic errors, ∼4% (Supplementary Figures 1 and 2), determined from the discrete changes in the trap separation as described in the Supplementary Discussion.

Analysis

The one-sided autocorrelation of a positional histogram of each semi-passive mode segment was used to calculate the pairwise distributions⁴⁴. 0.25-bp bins and 0.1-bp bins were used for the histograms for the low force and high force distributions respectively. Data were selected for low noise and clarity of steps as described in the Supplementary Discussion. The pairwise distributions of the selected data were averaged together to produce the reported distributions. The average spatial periodicity was quantified from the position of the peaks. Subsets of the high force data were analyzed to produce the step size measurement as a function of force.

Stepping transitions were identified using a t-test analysis⁴⁵ and a probability threshold of observing a given t-value of 10⁻⁴. Dwell times were calculated from the time between transitions and step sizes were calculated from the difference in mean position between transitions. The reported dwell time distributions in Figure 2a and 3c were selected based on the size of the subsequent step, 8-12 bp and 1.5-4 bp respectively. Burst durations were estimated from the exponential decay rate of the distribution of the number of contiguous points for which the t-value probability was below the 10⁻⁴ threshold. Because of our limited time resolution, we could not observe the expected peak in this distribution; thus, we report the observed exponential decay, a value less biased by the time resolution than the mean. The effective bandwidth of the t-test algorithm was varied to maximize the number of observed steps while minimizing the systematic errors introduced into the moments of the distribution from a finite dead-time. By assuming a Poisson distribution, it was determined that this dead-time algorithm introduces negligible systematic errors in the calculated moments for all reported distributions.