Abstract
PURPOSE
To compare the Swedish interactive thresholding algorithm (SITA) with the full-threshold (FT) strategy for short-wavelength automated perimetry (SWAP).
METHODS
One eye of 286 patients with glaucomatous optic neuropathy (GON) and 289 age-matched participants without GON from the Diagnostic Innovations in Glaucoma Study (DIGS) and the African Descent and Glaucoma Evaluation Study (ADAGES) were classified with optic disc stereophotographs taken within 6 months of visual field testing, conducted within a 3-month period. Six parameters were derived per test, including pattern standard deviation (PSD) and the number of pattern deviation plot (PDP) points triggered at <1%. Receiver-operating characteristic (ROC) analysis equated the tests for specificity (80%, 90%, and 95%). Sensitivities of parameters with the highest area under the curve (AUC) and STATPAC (Carl Zeiss Meditec, Inc., Dublin, CA) PSD were compared. Agreement, severity, and test duration between algorithms were assessed.
RESULTS
Sensitivities were not different between algorithms using PSD. With PDP <1%, SWAP-FT was more sensitive (35%) than SWAP-SITA (29%) at 95% specificity (P < 0.05). Sensitivity and specificity using the STATPAC PSD at 95% (P < 5%) and 99.5% (P < 0.05%) was similar between algorithms. Severity correlated significantly between algorithms (P < 0.001), although there was bias for SWAP-SITA to suggest more severe loss. SWAP-SITA required significantly less test time than did SWAP-FT (P < 0.001). Mean differences in PSD, PDP < 1%, and MD between algorithms were not clinically significant.
CONCLUSIONS
Both algorithms performed similarly when equated for specificity. The reduced test duration makes SWAP-SITA the better choice. Testing with both algorithms within a short period is recommended for confirmation of results when switching from FT to SITA.
Short-wavelength automated perimetry (SWAP) is a visual function–specific field test that is processed preferentially by short-wavelength–sensitive cones through their connections to the small bistratifed ganglion cells1; these make up 8% to 10% of the retinal ganglion cells. SWAP has been very useful for detecting glaucoma.2–8 However, an important clinical drawback of SWAP using the full-threshold (FT) algorithm has been the lengthy test time.9 To decrease the test duration of SWAP, Bengtsson10 implemented a Bayesian-based algorithm, the Swedish interactive thresholding algorithm (SITA), in a method similar to the one she had used for standard automated perimetry (SAP).
Previous reports have observed that the test time for SWAP with SITA was reduced by 65% compared with the time necessary to conduct SWAP-FT.10,11 SWAP-SITA has also demonstrated higher mean sensitivities in normal eyes and lower intersubject variability than SWAP-FT.12,13 Despite these apparent advantages, the sensitivity and specificity of SWAP-SITA have not been evaluated systematically against the original SWAP-FT. Such a comparison is essential for understanding what similarities or differences might have been introduced with the SITA strategy. We compared the performance of SWAP with both algorithms on the same group of participants tested within a short time on specificity-equated and machinederived (STATPAC; Carl Zeiss Meditec, Inc., Dublin, CA) parameters.
METHODS
All participants were selected from the ongoing longitudinal Diagnostic Innovations in Glaucoma Study (DIGS), conducted at the Hamilton Glaucoma Center at the University of California at San Diego (UCSD) and the African Descent and Glaucoma Evaluation Study (ADAGES), a multicenter study conducted at UCSD, the University of Alabama at Birmingham, and the New York Eye and Ear Infirmary. These ongoing studies are prospectively designed to assess structure and function in glaucoma. The methods, inclusion and exclusion criteria for participation in DIGS and ADAGES are the same. Healthy participants were recruited from the general population through advertisement, from referring practices and from the staff and employees at each of the study institutions. Informed consent was received from all participants and the Institutional Review Board of each pertinent institute approved the study, which adhered to the tenets of the Declaration of Helsinki and to the Health Insurance Portability and Accountability Act (HIPAA) for research involving human subjects.
Inclusion Criteria for DIGS/ADAGES
Participants underwent complete ophthalmic examinations, including slit lamp biomicroscopy, intraocular pressure (IOP) measurement, and dilated stereoscopic fundus examination. Simultaneous stereoscopic photographs with good clarity and stereopsis were obtained for all participants. At study entry, all participants had open angles, a best corrected acuity of 20/40 or better, a spherical refraction within ±5.0 D, and cylinder correction within ±3.0 D. Participants with a family history of glaucoma was allowed.
Exclusion Criteria for DIGS/ADAGES
Participants were excluded if they had (1) a history of intraocular surgery, except for uncomplicated cataract or glaucoma surgery; (2) nonglaucomatous secondary causes of elevated IOP (e.g., iridocyclitis, trauma); (3) other intraocular diseases affecting the visual field (e.g., pituitary lesions, demyelinating diseases, HIV + or AIDS, or diabetic retinopathy), or (4) a history of taking medications known to affect visual field sensitivity, and/or deficiencies other than glaucoma affecting color vision (screened with the Farnsworth-Munsell D15 test).
For the present study, all participants were evaluated on SWAP-SITA, SWAP-FT, and standard automated perimetry (SAP-SITA). SAP-SITA was performed for descriptive purposes, as it is the clinical standard (Table 1). (Previous results comparing SWAP-SITA and SWAP-FT with SAP-SITA are summarized in the Discussion section.) SWAP is described in greater detail later. Test order was randomized, and all visual field tests were performed within a 3-month period. Participants who were new to perimetry were given practice tests before those visual fields that were included in the analysis. Only reliable visual fields (<33% fixation losses and <15% false-positive responses) were included. One eye from each subject was selected at random, except in cases in which only one eye was tested. For participants who performed reliably more than once on a given test within the required 3-month period, one of the reliable tests was chosen randomly. All visual field tests from DIGS and ADAGES were reviewed for artifacts and suspected learning effects by the Visual Field Assessment Center (VisFACT). The first visual field test of each patient available to us was considered to show a learning effect if the difference score between the first and second tests was greater than or equal to the 99.5th percentile of a large subset of the DIGS cohort (nSWAP-SITA = 2805; nSWAP-FT = 2102) on either the MD or PSD measurement. Reviewers were masked to all other information about the participant.
TABLE 1.
Descriptive Measures of Study Participants with or without GON
| GON (n = 286) |
Non-GON (n = 289) |
|
|---|---|---|
| Mean age ± SD (y) | 65.6 ± 12.9 | 63.5 ± 12.2 |
| Median age (y) | 67.2 | 64.8 |
| Age range (y) | 20.5–92.7 | 21.4–88.6 |
| Sex (% male) | 44.1 | 38.1 |
| Eye (% OD) | 53.8 | 53.6 |
| SAP-SITA MD (mean ± SD) | −4.49 ± 6.31 | −1.01 ± 1.87 |
| SAP-SITA MD range | −31.46–2.44 | −12.41–2.04 |
| SAP-SITA PSD (mean ± SD) | 4.35 ± 3.73 | 2.06 ± 1.05 |
| SAP-SITA PSD range | 1.08–17.00 | 1.05–6.72 |
Participants
Five hundred seventy-five participants met the study criteria. Optic disc stereophotographs were used to classify all participants as having glaucomatous optic neuropathy (GON) or not. Classification depended on the assessment of simultaneous stereophotographs (TRC-SS; Topcon, Paramus, NJ, or 3-DX; Nidek, Fremont, CA) taken within 6 months of the visual field tests. Classification required agreement between the independent assessments of two trained graders, who were masked to the identity of the participant as well as to other grader determinations. A third trained grader, also masked to the identity of the other graders, adjudicated disagreements. The ages of the study groups were then matched by age distribution. The number of patients classified as having GON was 286; the number of participants classified as not having GON was 289. Descriptive measures are shown in Table 1.
GON Group
Participants included in this group had abnormal glaucomatous appearance of the optic disc on simultaneous stereophotographs. Abnormal appearance of the optic disc was defined as having more than a 0.2 cup-to-disc ratio asymmetry between the two eyes, evidence of excavation, neuroretinal rim thinning, rim notching, or nerve fiber layer defects. Visual fields were not used to classify participants into study groups.
Control Group (Non-GON)
Participants included in this group had normal appearance of the optic disc on stereophotographs. They also had IOP levels ≤22 mm Hg and no history of ocular hypertension. Visual fields results were not used to classify participants into study groups.
Visual Field Tests
SWAP-SITA, SWAP-FT, and SAP-SITA were all performed on the Humphrey Visual Field Analyzer HFAIIi (Carl Zeiss Meditec, Inc., Dublin, CA) using program 24-2. The two locations just above and below the blind spot were not included in the analysis, leaving 52 test locations for each. Adequate refraction was provided for each device according to the manufacturer’s specifications, and the pupils had a diameter of at least 3 mm. The pupils were dilated when this requirement was not met. The HFAIIi provides a STATPAC analysis for each visual field examination that includes the global indices: mean deviation (MD), PSD, and Glaucoma Hemifield Test (GHT). It also indicates which location on the pattern deviation plot (PDP) and total deviation plot (TDP) are triggered at <0.5%, <1%, <2%, and <5%.
Short-Wavelength Automated Perimetry
A blue (440-nm narrow-band), 1.8° target (Goldmann size V) was presented at 200-ms duration on a 100-cd/m2 bright yellow background to selectively test the short-wavelength–sensitive cones by decreasing the sensitivity of the long- and medium-wavelength–sensitive cones.
SWAP using the Full-Threshold Method
The SWAP-FT method presents target stimuli at test locations in a pseudorandom order. Target intensities vary in 0.1-log-unit steps (in decibels) using a 4-2-2 staircase at each location.14
SWAP using the Swedish Interactive Thresholding Algorithm
The SITA algorithm, developed by Bengtsson, is similar to the full-threshold algorithm except that it (1) uses a Bayesian approach to potentially terminate the staircase earlier than in the full-threshold algorithm, given the precision of the threshold estimate; (2) determines the false-positive and -negative responses without catch trials; and (3) applies a proprietary postprocessing algorithm to the obtained threshold values.10 After each response, the threshold is updated and recalculated to determine the intensity of the next target. In the 52 locations, 4-dB steps are applied until the first reversal, and then an additional 2-dB step is applied after the first reversal at points within 12° of eccentricity.
Analyses
Statistical analyses were performed with two commercial software programs (JMP ver. 5.1.2; SAS Institute, Inc., Cary, NC, and MATLAB, ver. 7.6, The Mathworks, Inc., Natick, MA).
Sensitivity and Specificity Comparisons
For each visual field test, receiver-operating characteristics (ROC) curves were generated for the following six parameters: MD, PSD, TDP points triggered at less than 1% and 5%, and PDP points triggered at less than 1% and 5%. ROC curves plotted the “hits” (i.e., sensitivity for those with GON) by the “false alarms“ (i.e., 1 – specificity for those that were non-GON). This method is useful for comparisons across procedures. Next, the AUC, a recommended index of accuracy with an ROC curve,15 was determined. Perfect classification is defined by an AUC of 1, which indicates that the outcome of the visual field test matches exactly with the stereophotograph classification. Chance discriminability is an AUC of 0.5. The AUC for the two best parameters was compared with the nonparametric Mann-Whitney U test according to the method of De-Long et al.16 Since a test’s sensitivity varies as the criteria of specificity changes, ROC curves were used to estimate the sensitivity of each test and parameter combination at three levels of specificity: 80%, 90%, and 95%. McNemar’s test was used to compare the sensitivities of the two best parameters for each test at each specificity level. Sensitivities and specificities using machine-derived PSD at probability levels of <0.5% and <5% were also examined.
Severity of Visual Field Defects
PSD, PDP <1%, and MD were compared across algorithms using a correlation analysis to determine the strength of the relationship between measurements (Spearman’s nonparametric correlation). The dynamic range has expanded with SWAP-SITA,10 which is advantageous for testing patients with more severe to end-stage visual field defects. Although the participants in this study did not include many advanced patients, we looked for any within-subject differences between algorithms across all levels of severity by using a nonparametric matched-pair comparison (two-sided Wilcoxon signed-rank test).
Agreement between SWAP-FT and SWAP-SITA Abnormality by Study Group
To assess agreement of the visual field measures (PSD and PDP <1%), we used Bland-Altman plots, correlation analyses, and matched-pair comparisons and looked for any systematic trends between the algorithm measurements.17 If the mean difference of two measurements is different from 0, there is a fixed bias such that one test measurement is typically higher or lower than the second test. If the difference between the two test results expands or contracts through the range of measurements, there is a proportional bias. Because SWAP-SITA has been reported to have an increased dynamic range compared with SWAP-FT in visual fields with greater damage,9 we expected to see a proportional bias. For example, we expected PSD values with SWAP-SITA to be higher than with SWAP-FT at greater PSD measurements. To formally evaluate this relationship, we regressed the difference between two test measurements on their average.18 The Spearman’s nonparametric correlation test was then used to assess the strength of the relationship between algorithm measurements. Both parameter measurements were also compared with the two-tailed Wilcoxon signed-rank, matched-pairs test.
To assess agreement of visual field outcomes, we used ROC-derived PSD at 95% specificity and machine-derived PSD at 95% (P < 5%) and 99.5% (P < 0.5%) to define abnormality. We looked at sensitivity and specificity for GON classification between ROC-derived and machine-derived PSD and the overlap in GON visual field outcomes across algorithms using Venn diagrams, and then evaluated the agreement between SWAP-FT and SWAP-SITA by using the κ statistic,19 which rated the strength of agreement as poor (κ = 0.00), slight (κ = 0.01–0.20), fair (κ = 0.21–0.40), moderate (κ = 0.41–0.60), substantial (κ = 0.61–0.80), or almost perfect (κ = 0.81–1.00).
Test Duration
Bengtsson10 found a significant reduction in test time with the implementation of SITA in SWAP. Using our relatively large data set, we compared the test duration in two ways: (1) GON versus non-GON within test type, and (2) SWAP-FT versus SWAP-SITA, using dependent t-tests assuming unequal variance.
RESULTS
Sensitivity and Specificity Comparisons
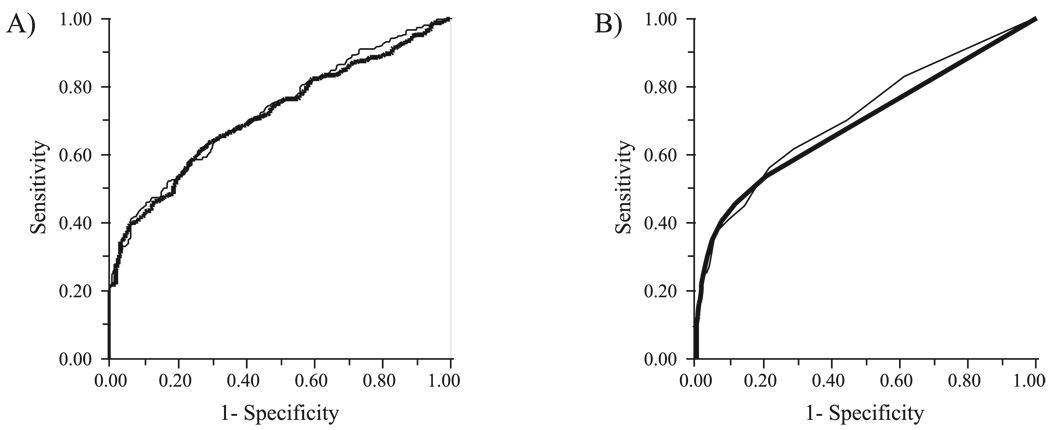
Table 2 shows the AUC. The parameter yielding the highest AUC was PSD for both SWAP-FT (0.715) and SWAP-SITA (0.722). The second highest AUC was PDP <5% for SWAP-FT and PDP <1% for SWAP-SITA. There was no significant difference between these AUCs (P > 0.05). The similarity in ROC curve shape between algorithms is seen in Figure 1. Since PDP <1% offers greater stringency than PDP <5%, it was used in addition to PSD in subsequent analyses.
TABLE 2.
AUC for SWAP Using FT and SITA and Six Parameters
| Parameter | SWAP-FT (95% Confidence Interval) |
SWAP-SITA (95% Confidence Interval) |
P-value |
|---|---|---|---|
| PSD | 0.715 (0.673–0.758) | 0.722 (0.681–0.767) | 0.323 |
| Points triggered on PDP <1% | 0.695 (0.654–0.735) | 0.712 (0.670–0.753) | 0.180 |
| Points triggered on PDP <5% | 0.709 (0.667–0.752) | 0.689 (0.646–0.731) | 0.115 |
| Points triggered on TDP <1% | 0.691 (0.649–0.733) | 0.680 (0.637–0.723) | 0.196 |
| Points triggered on TDP <5% | 0.640 (0.596–0.685) | 0.645 (0.601–0.690) | 0.335 |
| MD | 0.634 (0.589–0.680) | 0.658 (0.614–0.703) | 0.012 |
FIGURE 1.
ROC curves using (A) PSD and (B) PDP points triggered at P < 1% for SWAP with the FT strategy (thick line) and the SITA (thin line).
The sensitivity and criterion values of these comparisons are shown at three different specificity levels (80%, 90%, and 95%) for all visual field tests and parameters in Table 3. At all specificity levels examined, there was no significant difference in the sensitivities between algorithms when the ROC-derived PSD was used (P > 0.05, McNemar test). There was no significant difference using the PDP <1% parameter at 80% or 90% specificity (P > 0.05); however, at 95% specificity, SWAP-FT was more sensitive than SWAP-SITA (P = 0.032).
TABLE 3.
Sensitivities and Criterion Values for SWAP Using FT and SITA and Six Parameters at Approximately 80%, 90%, and 95% Specificity
| 80% Specificity |
90% Specificity |
95% Specificity |
|||||
|---|---|---|---|---|---|---|---|
| Parameter | Test | Sensitivity | Criterion | Sensitivity | Criterion | Sensitivity | Criterion |
| PSD | SWAP-FT | 53.2 (80.3) | 3.83 | 41.6 (90.3) | 4.31 | 36.7 (95.2) | 4.79 |
| SWAP-SITA | 52.8 (80.3) | 3.91 | 44.1 (90.3) | 4.37 | 32.9 (95.2) | 5.24 | |
| Points triggered on | |||||||
| PDP <1% | SWAP-FT | 53.5 (79.58) | 2 | 45.45 (88.6) | 3 | 34.6 (95.5) | 5 |
| SWAP-SITA | 55.9 (78.2) | 4 | 40.9 (90.0) | 7 | 28.7 (95.5) | 10 | |
| Points triggered on | |||||||
| PDP < 5% | SWAP-FT | 56.3 (78.9) | 6 | 42.3 (90.0) | 9 | 32.9 (95.2) | 12 |
| SWAP-SITA | 45.8 (78.6) | 12 | 36.36 (88.9) | 15 | 28.0 (94.8) | 19 | |
| Points triggered on | |||||||
| TDP < 1% | SWAP-FT | 50.7 (78.6) | 7 | 38.8 (89.3) | 13 | 21.0 (95.2) | 25 |
| SWAP-SITA | 48.6 (78.2) | 9 | 32.2 (90.0) | 19 | 20.6 (95.2) | 31 | |
| Points triggered on | |||||||
| TDP <5% | SWAP-FT | 42.0 (79.6) | 25 | 28.3 (90.0) | 35 | 17.5 (95.2) | 43 |
| SWAP-SITA | 40.2 (78.2) | 31 | 27.6 (90.0) | 41 | 13.6 (95.5) | 48 | |
| MD | SWAP-FT | 43.7 (80.3) | −7.36 | 32.5 (90.3) | −9.02 | 24.5 (95.2) | −10.84 |
| SWAP-SITA | 45.8 (80.3) | −7.08 | 33.9 (90.3) | −8.82 | 25.9 (95.2) | −10.66 | |
Exact specificity is in parentheses adjacent to the sensitivity.
Table 4 presents contingency tables of the optic disc stereophotograph classification of GON with SWAP-FT and SWAP-SITA using different PSD criteria to determine visual field abnormality. For SWAP-FT, the ROC-derived PSD set at 95% specificity and machine-derived PSD at 95% (P < 5%) produced comparable results: 36.7% and 39.9% sensitivity, and 95.2% and 93.4% specificity, respectively. Abnormality set by machine-derived PSD at 99.5% (P < 0.5%) for SWAP-FT produced a sensitivity of 21.0% and a specificity of 100%. For SWAP-SITA, the ROC-derived PSD set at 95% specificity produced results comparable to those of the machine-derived PSD at 99.5% (P < 0.5%): 32.9% and 36.7% sensitivity, and 95.5% and 91.3% specificity, respectively. Abnormality set by machine-derived PSD at 95% (P < 5%) for SWAP-SITA produced a sensitivity of 60.5% and a specificity of 70.2%.
TABLE 4.
Contingency Tables of Visual Field Outcomes for SWAP Using FT and SITA and Optic Disc Stereophotograph Classification of Participants with or without GON
| ROC PSD 95% Specificity |
Machine PSD 95% (P < 5%) |
Machine PSD 99.5% (P < 0.5%) |
|||||||
|---|---|---|---|---|---|---|---|---|---|
| Classification | Abnormal | Normal | Abnormal | Normal | Abnormal | Normal | |||
| SWAP-FT | |||||||||
| GON | 105 | 181 | 286 | 114 | 172 | 286 | 60 | 226 | 286 |
| 36.7* | 63.3 | 39.9* | 60.1 | 21.0* | 79.0 | ||||
| Non-GON | 14 | 275 | 289 | 19 | 270 | 289 | 0 | 289 | 289 |
| 4.8 | 95.2† | 6.6 | 93.4† | 0.0 | 100.0† | ||||
| SWAP-SITA | |||||||||
| GON | 94 | 192 | 286 | 173 | 113 | 286 | 105 | 181 | 286 |
| 32.9* | 67.1 | 60.5* | 39.5 | 36.7* | 63.3 | ||||
| Non-GON | 13 | 276 | 289 | 86 | 203 | 289 | 25 | 264 | 289 |
| 4.5 | 95.2† | 29.8 | 70.2† | 8.7 | 91.3† | ||||
Visual field abnormality is determined by the PSD derived by the ROC curve at 95% specificity, the machine PSD at 95% (P < 5%), and the machine PSD at 99.5% (P < 0.5%).
Sensitivity.
Specificity.
Visual Field Severity
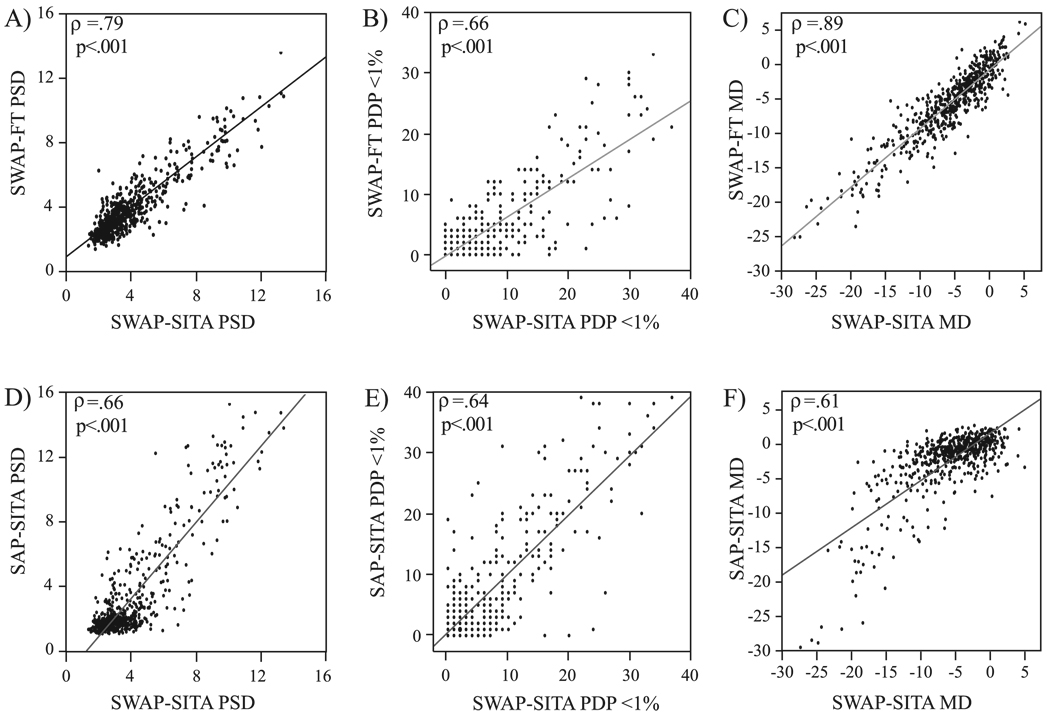
Figure 2 shows the strength of the relationship between SWAP-FT and SWAP-SITA for PSD (Fig. 2A), PDP <1% (Fig. 2B), and MD (Fig. 2C) parameter values across all participants (n = 575). All global indices (mean ± SD) of visual field severity correlated significantly (PSD: ρ = 0.79; PDP <1%: ρ = 0.66; MD: ρ = 0.89, all P < 0.001). SWAP-SITA PSD (4.01 ± 2.20) was significantly higher (P = 0.011) than the SWAP-FT PSD (3.85 ± 1.85; Table 5). SWAP-SITA PDP <1% (5.06 ± 7.17) was also significantly higher (P < 0.001) than SWAP-FT (2.96 ± 5.50; Table 5). There was no significant difference (P = 0.209) in average MD between SWAP-FT (−5.72 ± 5.44) and SWAP-SITA (−5.83 ± 5.10) visual fields test (Table 5).
FIGURE 2.
Correlation of all participants, SWAP results with the FT strategy and SITA visual fields (n = 575) using (A, D) PSD, (B, E) number of points in the PDP triggered at P < 1%, and (C, F) MD. ρ, Spearman’s nonparametric correlation.
TABLE 5.
Visual Field Parameter Data for SWAP with the FT Strategy and SITA
| Range | Median | Mean ± SD | P-value | |
|---|---|---|---|---|
| All participants (n = 575) | ||||
| PSD | ||||
| SWAP-FT | 1.35–13.56 | 3.28 | 3.85 ± 1.85 | 0.011 |
| SWAP-SITA | 1.41–13.42 | 3.23 | 4.01 ± 2.20 | |
| PDP <1% | ||||
| SWAP-FT | 0–33 | 1 | 2.96 ± 5.50 | <0.001 |
| SWAP-SITA | 0–37 | 2 | 5.06 ± 7.17 | |
| MD | ||||
| SWAP-FT | −25.22–6.10 | −5.20 | −5.83 ± 5.10 | 0.209 |
| SWAP-SITA | −28.04–5.25 | −4.87 | −5.72 ± 5.44 | |
| GON (n = 286) | ||||
| PSD | ||||
| SWAP-FT | 1.35–13.56 | 3.92 | 4.61 ± 2.22 | <0.001 |
| SWAP-SITA | 1.48–13.42 | 4.03 | 4.91 ± 2.67 | |
| PDP <1% | ||||
| SWAP-FT | 0–33 | 2 | 4.99 ± 7.01 | <0.001 |
| SWAP-SITA | 0–37 | 4 | 7.80 ± 8.73 | |
| MD | ||||
| SWAP-FT | −25.22–5.80 | −6.48 | −7.17 ± 5.80 | 0.161 |
| SWAP-SITA | −28.04–5.25 | −6.21 | −7.40 ± 6.28 | |
| Non-GON (n = 289) | ||||
| PSD | ||||
| SWAP-FT | 1.55–6.37 | 2.98 | 3.11 ± 0.91 | 0.7567 |
| SWAP-SITA | 1.41–7.20 | 2.89 | 3.11 ± 1.01 | |
| PDP <1% | ||||
| SWAP-FT | 0–14 | 0 | 0.95 ± 1.88 | <0.001 |
| SWAP-SITA | 0–24 | 1 | 2.36 ± 3.50 | |
| MD | ||||
| SWAP-FT | −21.52–6.10 | −4.31 | −4.510 ± 3.889 | 0.002 |
| SWAP-SITA | −18.92–4.43 | −3.66 | −4.072 ± 3.801 | |
P for the comparison of parameter averages between algorithms is shown.
Agreement between SWAP-FT and SWAP-SITA Abnormality within a Study Group
Bland-Altman Plots
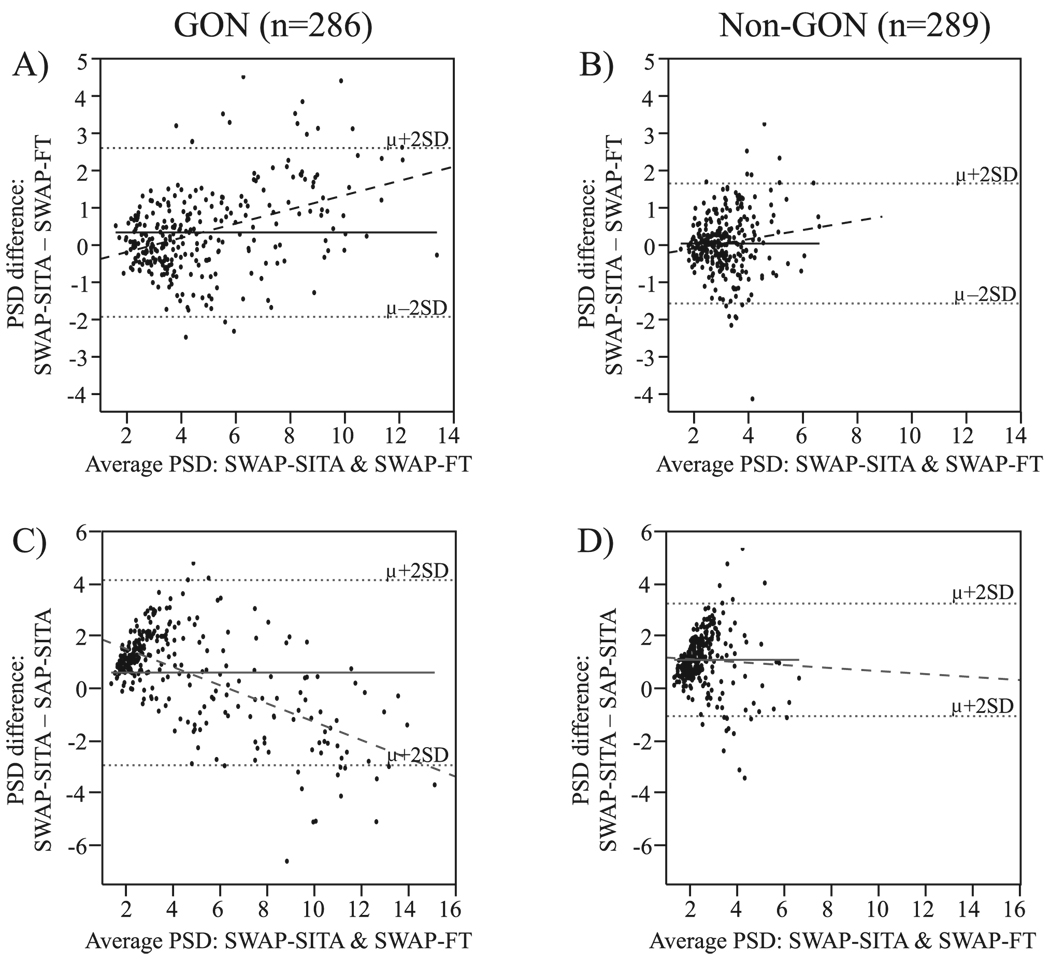
Figures 3A and 3B show Bland-Altman plots of the PSD measurements for the participants with GON and those without, respectively. The mean PSD difference (SWAP-SITA minus SWAP-FT: μdiff = 0.30; 95% confidence interval [CI]: 0.17–0.43) was significantly different from 0 (P < 0.001), indicating the presence of a fixed bias such that SWAP-SITA PSD measures are consistently worse than SWAP-FT PSD measures in the GON participants (Fig. 3A). A regression to the Bland-Altman plot was also significant (P < 0.001) and indicated the presence of a proportional bias: PSD tended to be worse with SWAP-SITA than SWAP-FT at higher PSD measures in the GON participants.
FIGURE 3.
Bland-Altman plots of the PSD (A, B) and correlations (C, D) of SWAP using the FT strategy and the SITA among participants with GON and those without GON, respectively. μ, mean; solid black line, mean difference; dashed line, regression; gray shading, 95% CI; ρ, Spearman’s rank correlation.
The mean PSD difference for the non-GON group was not significantly different from 0 (SWAP-SITA minus SWAP-FT: μdiff = 0.00; 95% CI: −0.09–0.10; P = 0.757), indicating that no fixed bias was present (Fig. 3B). However, a regression to the Bland-Altman plot was significant (P = 0.030), indicating the existence of a proportional bias; PSD tended to be worse with SWAP-SITA than SWAP-FT at higher PSD measures in participants without GON.
Bland-Altman analyses performed using PDP <1% had similar results with one exception: A fixed bias was present among the non-GON participants. More points were triggered with SWAP-SITA than with SWAP-FT as the number of points triggered increased (μdiff = 1.41; 95% CI: 1.05–1.76; P < 0.001).
Correlations and Matched-Pair Comparisons
Figures 3C and 3D show correlations of the PSD measurements for SWAP-FT and SWAP-SITA in the GON and non-GON groups, respectively. The strength of the relationship between measurements for participants with GON was significant (ρ = 0.87, P < 0.001), as well as in those without GON (ρ = 0.63, P < 0.001). The PDP <1% parameter was also significantly correlated in the GON (ρ = 0.80, P < 0.001) and non-GON (ρ = 0.38, P < 0.001) participants (correlation plots not shown).
The GON group had a significantly larger SWAP-SITA PSD and PDP <1% than SWAP-FT (P < 0.001); no significant difference in MD was found (P = 0.161; Table 5). The non-GON group had a significantly larger PDP <1% with SWAP-SITA than with SWAP-FT (P < 0.001) and a significantly larger MD with SWAP-FT than SWAP-SITA (P = 0.002); no significant difference was found in PSD (P = 0.757; Table 5).
Venn Diagram and κ Statistic
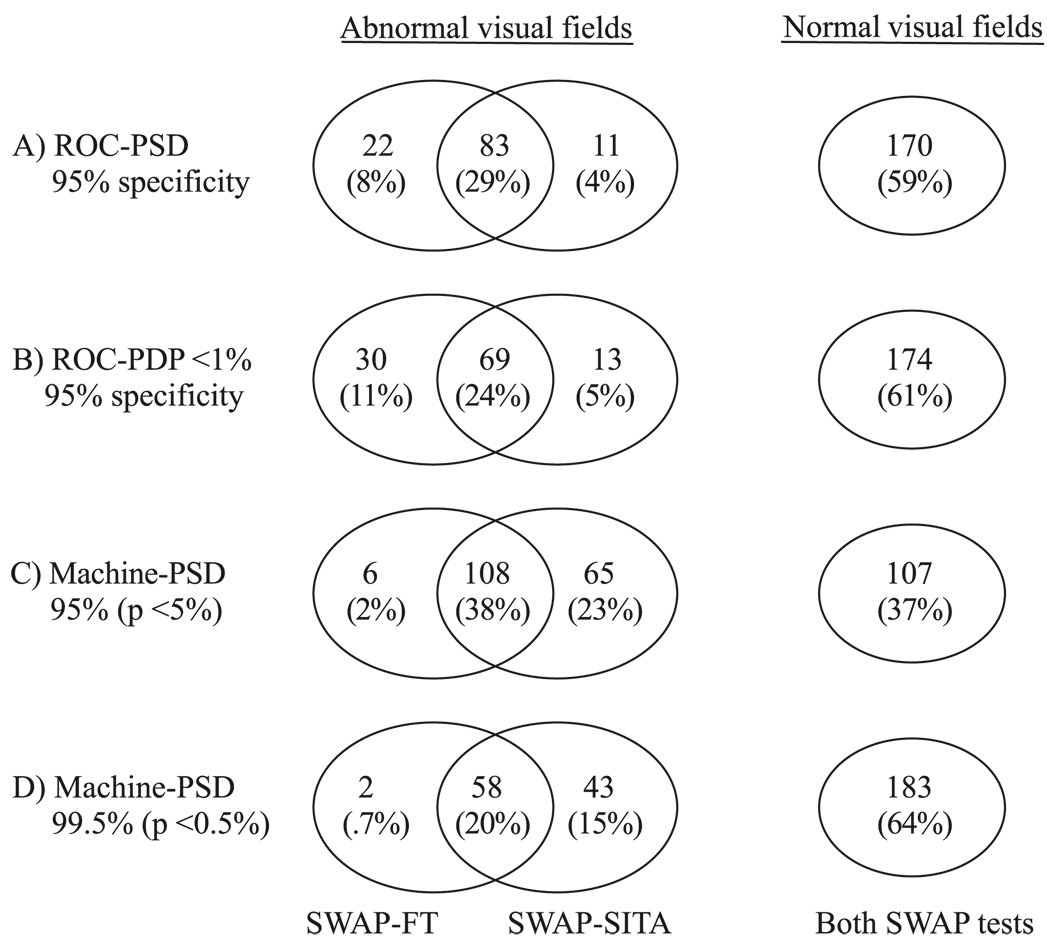
Figure 4 shows Venn diagrams of the algorithms’ overlap of normality and abnormality outcomes among the GON participants (n = 286). The ROC-derived PSD and PDP <1% parameters set at 95% specificity produced similar patterns of overlap (Fig. 4A, 4B). Abnormality overlap was 29% (PSD) and 24% (PDP <1%), and normality overlap was 59% (PSD) and 61% (PDP <1%). The overall normal and abnormal overlap in visual field outcome of the GON fields was 88% using ROC-derived PSD and 85% ROC-derived PDP <1%. Agreement was substantial using both parameters (ROC-PSD: κ = 0.75 ± 0.04; ROC-PDP <1%: κ = 0.65 ± 0.05).
FIGURE 4.
Venn diagrams of SWAP using the FT strategy and the SITA outcomes among the patients with GON (n = 286). Visual field abnormality is determined by: (A) ROC curve-derived PSD at 95% specificity, (B) ROC-derived PDP points triggered at <1% at 95% specificity, (C) machine-derived PSD at 95% (P < 5%), and (D) machine-derived PSD at 99.5% (P < 0.5%).
Also shown in Figure 4 is the overlap when the machine-derived PSD is used. With the machine-derived PSD at 95% (P < 5%), agreement was moderate (κ = 0.52 ± 0.05): there were 38% overlapping abnormal fields and 37% overlapping normal fields for a 75% total overlap in the outcome of GON fields between algorithms; for the nonoverlapping GON fields, there were 23% that were abnormal by SWAP-SITA only, and 2% that were abnormal by SWAP-FT only (Fig. 3C). With the machine-derived ROC at 99.5% (P < 0.5%), agreement was substantial (κ = 0.62 ± 0.05). There were 20% overlapping abnormal fields and 64% overlapping normal fields for a total 84% overlap in GON field outcome between both algorithms. For the nonoverlapping GON fields, there were 15% that were abnormal by SWAP-SITA only and less than 1% abnormal by SWAP-FT only (Fig. 4D).
Test Duration
Two sets of pair-wise comparisons were made using dependent t-tests assuming unequal variance: (1) test duration between the GON and non-GON study groups within SWAP-FT or SWAP-SITA and (2) test duration between algorithms. For the first set of comparisons within algorithm type, we found that the GON group required more time than the non-GON group did when tested with SWAP-SITA (GON: 4:15 ± 00:52 [min:sec] versus non-GON: 3:50 ± 0:41, P < 0.001). No difference was found with SWAP-FT (GON: 11:39 ± 1:53 versus non-GON: 11:44 ± 1:25, P = 0.481). In the second set of comparisons within study group, we found that all participants needed significantly more time to perform SWAP-FT than SWAP-SITA (P < 0.001).
DISCUSSION
In this study, we compared SWAP visual field results with the FT strategy and SITA in eyes with and without GON.
Sensitivity to GON using PSD was similar with both algorithms when equated for specificity at 80%, 90%, and 95%. Using the number of points triggered on the PDP at <1%, SWAP-FT was significantly more sensitive than SWAP-SITA only at 95% specificity. The machine-derived PSD at 95% (P < 5%), a more clinically relevant parameter, had a sensitivity similar to the ROC-derived PSD at 95% specificity for SWAP-FT; whereas the sensitivity for SWAP-SITA was lower. Using the machine-derived PSD at 95%, however, SWAP-SITA had a higher sensitivity (61%) than did SWAP-FT (40%). The sensitivity of the machine-derived PSD at 95% (P < 5%) for SWAP-FT was similar to what SWAP-SITA would provide at a machine-derived PSD of 99.5% (P < 0.5%). These variations are probably due in part to differences in the normative databases for the two SWAP tests, even though similar criteria were used to select participants for each respective normative database. This is a limitation in the study, but is an important comparison, as clinically relevant parameters for each test were derived with different normative databases.
Another possible source of differences is our use of optic disc stereophotographs as the gold standard. It provides independence from visual field measures and high correlation with disease progression.20–22 However, some misclassification is likely to occur, so that some of the GON classifications may be false-negatives or -positives, not necessarily indicative of glaucomatous damage.23 These factors contributed to the relatively low sensitivities reported herein. It is important to note that the main purpose of this widely used gold standard is to equate visual field tests for specificity to allow a fair comparison and not to draw conclusions about the individual test’s efficacy, since the true state of the eye may not be known without longitudinal validation.
Similar methods have been used to compare SWAP-SITA to SAP-SITA24 and to compare SWAP-FT to SAP-SITA.25 These studies found no significant differences in using SWAP over SAP-SITA for separating groups of eyes with GON from those without. Specifically, in a study by Tafreshi et al.24 of 174 GON and 164 non-GON eyes, the diagnostic accuracy of SAP-SITA was similar to that of SWAP-SITA (AUROC 0.692 for SAP-SITA; 0.693 for SWAP-SITA). In a study by Sample et al.25 of 111 GON and 51 non-GON participants, the diagnostic accuracy of SAP-SITA was similar to that of SWAP-FT (AUROC 0.713 for SAP-SITA; 0.733 for SWAP-SITA).25 Similarly, in the present study of 286 GON and 289 non-GON participants, no difference was found between the diagnostic accuracy of SAP SITA and SWAP SITA (data not shown). However, because SWAP tests an aspect of visual function that SAP does not, it provides additional information about the status of the visual system for a given individual. In addition, when a defect is present on both tests, it falls within the same retinal area. Tafreshi et al.24 found that confirmation of a SAP-SITA defect with either another SAP-SITA or with a SWAP-SITA offers a similar combination of sensitivity and specificity.
SWAP-SITA parameter measures (PSD and PDP <1%) had a tendency to be slightly more severe than SWAP-FT. However, the less than 1 dB difference in PSD is probably not clinically significant. Bengtsson and Heijl26 examined the number of points triggered at <5% on the pattern deviation plot and found no significant difference. In our study, a statistically significant difference was found in the number of points triggered at <1% on the PDP; but again, the 3-point difference may not be clinically significant.
In summary, in this study SWAP-SITA performed similarly to SWAP-FT. The high correlation between the two algorithms lends confidence to clinicians and researchers that similar results can be expected when switching to the more rapid SWAP-SITA technique. Although the agreement and sensitivities of both algorithms were similar when equated for specificity, some differences were observed when comparisons were based on the STATPAC (machine-derived) PSD. Since SWAP-SITA identifies more abnormal points, clinicians should be careful interpreting the results. A change in the number of abnormal points, even if repeated, may be due to a change in the test algorithm and not to the progression of glaucoma. Therefore, it is recommended that longitudinally observed patients formerly tested on SWAP-FT be tested on both SWAP-FT and SWAP-SITA within a short period to confirm agreement of the visual field results and to determine whether a new baseline is needed before switching solely to SWAP-SITA for continued longitudinal evaluation.
Acknowledgments
The authors thank Madhusudhanan Balasubramanian, PhD, for his assistance with statistical analyses using MatLab.
Supported by Grants EY08208 and EY U1014267 (PAS), EY11008 (LMZ), EY13959 (CAG), and EY U1014267 (PAS) from the National Eye Institute and by the Eyesight Foundation of Alabama (CAG). Participant incentive grants in the form of glaucoma medication at no cost from Alcon Laboratories, Inc., Allergan, Inc., Pfizer, Inc., Merck, Inc., and Santen, Inc.
Footnotes
Disclosure: M. Ng, None; L. Racette, None; J.P. Pascual, None; J.M. Liebmann, Carl Zeiss Meditec, Inc. (F); C.A. Girkin, Carl Zeiss Meditec, Inc. (F), Heidelberg Engineering (F), OptoVue (F); S.L. Lovell, None; L.M. Zangwill, Allergan, Inc. (F), Carl Zeiss Meditec, Inc. (F), Heidelberg Engineering (F), OptoVue (F); R.N. Weinreb, Carl Zeiss Meditec, Inc. (F, C), Heidelberg Engineering (F); P.A. Sample, Carl Zeiss Meditec, Inc. (F), Haag-Streit (F), Welch-Allyn (F)
References
- 1.Dacey DM, Lee BB. The ‘blue-on’ opponent pathway in primate retina originates from a distinct bistratified ganglion cell type. Nature. 1994;367:731–735. doi: 10.1038/367731a0. [DOI] [PubMed] [Google Scholar]
- 2.Sample PA, Weinreb RN. Color perimetry for assessment of primary open-angle glaucoma. Invest Ophthalmol Vis Sci. 1990;31:1869–1875. [PubMed] [Google Scholar]
- 3.Sample PA, Taylor JD, Martinez GA, Lusky M, Weinreb RN. Short-wavelength color visual fields in glaucoma suspects at risk. Am J Ophthalmol. 1993;115:225–233. doi: 10.1016/s0002-9394(14)73928-5. [DOI] [PubMed] [Google Scholar]
- 4.Johnson CA. Diagnostic value of short-wavelength automated perimetry. Curr Opin Ophthalmol. 1996;7:54–58. doi: 10.1097/00055735-199604000-00010. [DOI] [PubMed] [Google Scholar]
- 5.Johnson CA, Adams AJ, Casson EJ, Brandt JD. Blue-on-yellow perimetry can predict the development of glaucomatous visual field loss. Arch Ophthalmol. 1993;111:645–650. doi: 10.1001/archopht.1993.01090050079034. [DOI] [PubMed] [Google Scholar]
- 6.Johnson CA, Brandt JD, Khong AM, Adams AJ. Short-wavelength automated perimetry in low-, medium-, and high-risk ocular hypertensive eyes: initial baseline results. Arch Ophthalmol. 1995;113:70–76. doi: 10.1001/archopht.1995.01100010072023. [DOI] [PubMed] [Google Scholar]
- 7.Sample PA, Bosworth CF, Weinreb RN. Short-wavelength automated perimetry and motion automated perimetry in patients with glaucoma. Arch Ophthalmol. 1997;115:1129–1133. doi: 10.1001/archopht.1997.01100160299006. [DOI] [PubMed] [Google Scholar]
- 8.Sample PA. Short-wavelength automated perimetry: its role in the clinic and for understanding ganglion cell function. Prog Retin Eye Res. 2000;19:369–383. doi: 10.1016/s1350-9462(00)00001-x. [DOI] [PubMed] [Google Scholar]
- 9.Racette L, Sample PA. Short-wavelength automated perimetry. Ophthalmol Clin North Am. 2003;16:227–237. doi: 10.1016/s0896-1549(03)00010-5. [DOI] [PubMed] [Google Scholar]
- 10.Bengtsson B. A new rapid threshold algorithm for short-wavelength automated perimetry. Invest Ophthalmol Vis Sci. 2003;44:1388–1394. doi: 10.1167/iovs.02-0169. [DOI] [PubMed] [Google Scholar]
- 11.Bengtsson B, Heijl A. Inter-subject variability and normal limits of the SITA Standard, SITA Fast, and the Humphrey Full Threshold computerized perimetry strategies, SITA STATPAC. Acta Ophthalmol Scand. 1999;77:125–129. doi: 10.1034/j.1600-0420.1999.770201.x. [DOI] [PubMed] [Google Scholar]
- 12.Bengtsson B, Olsson J, Heijl A, Rootzen H. A new generation of algorithms for computerized threshold perimetry, SITA. Acta Ophthalmol Scand. 1997;75:368–375. doi: 10.1111/j.1600-0420.1997.tb00392.x. [DOI] [PubMed] [Google Scholar]
- 13.Bengtsson B, Heijl A. Normal intersubject threshold variability and normal limits of the SITA SWAP and full threshold SWAP perimetric programs. Invest Ophthalmol Vis Sci. 2003;44:5029–5034. doi: 10.1167/iovs.02-1220. [DOI] [PubMed] [Google Scholar]
- 14.Sample PA, Johnson CA, Haegerstrom-Portnoy G, Adams AJ. Optimum parameters for short-wavelength automated perimetry. J Glaucoma. 1996;5:375–383. [PubMed] [Google Scholar]
- 15.Swets D, Green J. Signal Detection Theory and Psychophysics. New York: John Wiley & Sons; 1966. [Google Scholar]
- 16.DeLong ER, DeLong DM, Clarke-Pearson DL. Comparing the areas under two or more correlated receiver operating characteristic curves: a nonparametric approach. Biometrics. 1988;44:837–845. [PubMed] [Google Scholar]
- 17.Bland JM, Altman DG. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet. 1986;1:307–310. [PubMed] [Google Scholar]
- 18.Altman DG, Bland JM. Measurement in medicine: the analysis of method comparison studies. Statistician. 1983;32:307–317. [Google Scholar]
- 19.Landis JR, Koch GG. The measurement of observer agreement for categorical data. Biometrics. 1977;33:159–174. [PubMed] [Google Scholar]
- 20.Johnson CA, Sample PA, Zangwill LM, et al. Structure and function evaluation (SAFE): II. Comparison of optic disk and visual field characteristics. Am J Ophthalmol. 2003;135:148–154. doi: 10.1016/s0002-9394(02)01930-x. [DOI] [PubMed] [Google Scholar]
- 21.Mansberger SL, Zangwill LM, Sample PA, Choi D, Weinreb RN. Relationship of optic disk topography and visual function in patients with large cup-to-disk ratios. Am J Ophthalmol. 2003;136:888–894. doi: 10.1016/s0002-9394(03)00570-1. [DOI] [PubMed] [Google Scholar]
- 22.Medeiros FA, Zangwill LM, Bowd C, Sample PA, Weinreb RN. Use of progressive glaucomatous optic disk change as the reference standard for evaluation of diagnostic tests in glaucoma. Am J Ophthalmol. 2005;139:1010–1018. doi: 10.1016/j.ajo.2005.01.003. [DOI] [PubMed] [Google Scholar]
- 23.Girkin CA. Relationship between structure of optic nerve/nerve fiber layer and functional measurements in glaucoma. Curr Opin Ophthalmol. 2004;15:96–101. doi: 10.1097/00055735-200404000-00007. [DOI] [PubMed] [Google Scholar]
- 24.Tafreshi A, Sample PA, Liebmann JM, et al. Visual function specific perimetry to identify glaucomatous visual loss using three definitions of visual field abnormality. Invest Ophthalmol Vis Sci. 2008 October 31; doi: 10.1167/iovs.08-2535. Published online. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Sample PA, Medeiros FA, Racette L, et al. Identifying glaucomatous vision loss with visual-function-specific perimetry in the diagnostic innovations in glaucoma study. Invest Ophthalmol Vis Sci. 2006;47:3381–3389. doi: 10.1167/iovs.05-1546. [DOI] [PubMed] [Google Scholar]
- 26.Bengtsson B, Heijl A. Diagnostic sensitivity of fast blue-yellow and standard automated perimetry in early glaucoma. Ophthalmology. 2006;113:1092–1097. doi: 10.1016/j.ophtha.2005.12.028. [DOI] [PubMed] [Google Scholar]