A Scaling Law of Vascular Volume

Abstract

Vascular volume is of fundamental significance to the function of the cardiovascular system. An accurate prediction of blood volume in patients is physiologically and clinically significant. This study proposes what we believe is a novel volume scaling relation of the form: $V_c=K_v{D}_s^{2/3}{L}_c$, where $V_c$ and $L_c$ are cumulative vessel volume and length, respectively, in the tree, and $D_s$ is the diameter of the vessel segment. The scaling relation is validated in vascular trees of various organs including the heart, lung, mesentery, muscle, and eye of different species. Based on the minimum energy hypothesis and volume scaling relation, four structure-function scaling relations are predicted, including the diameter-length, volume-length, flow-diameter, and volume-diameter relations, with exponent values of 3/7, $1\frac{2}{7}$, 2⅓, and 3, respectively. These four relations are validated in the various vascular trees, which further confirm the volume scaling relation. This scaling relation may serve as a control reference to estimate the blood volume in various organs and species. The deviation from the scaling relation may indicate hypovolemia or hypervolemia and aid diagnosis.

Introduction

Blood pressure and perfusion of an organ depend on a complex interplay between cardiac output, intravascular volume, and vasomotor tone among others. The vascular system provides the basic architecture to transport the fluids while other physical, physiological, and chemical factors affect the intravascular volume to regulate the blood pressure and flow in the body. Although intravascular volume can adapt to normal physical training (1,2), many diagnostic and treatment options depend on the estimation of the volume status of patients (3–10). For example, a recent study classified the blood volume status as hypovolemic, normovolemic, and hypervolemic (3). Heart failure results in an increase of intravascular volume (hypervolemia) in response to decreased cardiac output and renal hypoperfusion (4–7). Conversely, myocardial ischemia (8) and postural tachycardia syndrome lead to hypovolemia (9). Furthermore, patients of edematous disorders have been found to have abnormal blood volume (10). Currently, there is no noninvasive method to determine the blood volume in suborgans, organs, organ system, or organism. The objective of this study is to propose a scaling law that provides the basis for determination of blood volume throughout the vasculature.

A novel, to our knowledge, volume scaling law is proposed in a vessel segment and its corresponding distal tree of normal organs and in various species as: $V_c=K_v{D}_s^{2/3}{L}_c$, where $V_c$ and $L_c$ are the vascular volume and length, respectively, $D_s$ is the diameter of the vessel segment, and $K_v$ is a constant. The scaling relation is validated with available vascular morphometric tree data (11). The validated volume scaling law may serve as a control reference to examine the change of blood volume in various organs under different states using conventional imaging (e.g., CT scan). The scaling law is further validated through diameter-length, volume-length, flow-diameter, and volume-diameter scaling relations (11), which were previously derived based on a minimum energy hypothesis (12). Hence, the proposed volume scaling law is consistent with an (minimum energy) efficient state of vascular system.

Theory

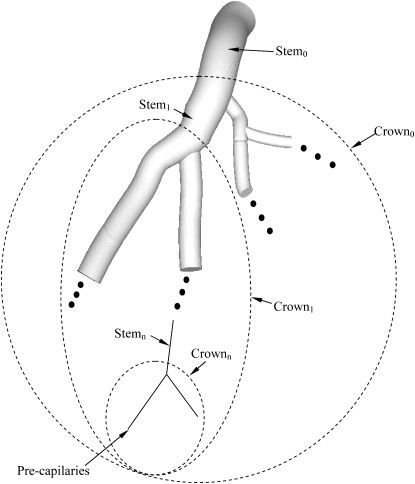
A vessel segment is defined as a stem and the tree distal to the stem is defined as a crown, as shown in Fig. 1. An entire tree consists of many stem-crown units down to the capillary vessels. The capillary network (13) is excluded from the present analysis because it is not a treelike structure.

Figure 1.

Schematic illustration of the definition of the stem-crown unit. Three stem-crown units are shown successively (1, 2, and n), with the smallest unit corresponding to an arteriole-capillary or venule-capillary unit.

It is known that $V_c\propto M$ (M is the mass perfused by the stem-crown unit) from the 3/4 allometric scaling law (14,15), where $V_c$ is the crown volume (i.e., the sum of all vessel volumes in the crown). Therefore, $V_c$ can be represented as

$$V_c=C_v{M}^{1/4}{M}^{3/4},$$ (1)

where $C_v$ is a volume-mass constant. There are two scaling relations: stem diameter-mass relation, $D_s\propto M^{3/8}$ ($D_s$ is the diameter of the stem vessel) (14,15), and crown length-mass relation, $L_c\propto M^{3/4}$ ($L_c$ is the crown length, defined as the sum of the lengths of all vessels in the crown) (15). From $D_s=C_d{M}^{3/8}$, $L_c=C_l{M}^{3/4}$, and Eq. 1, we obtain

$$V_c=C_v{M}^{1/4}{M}^{3/4}=C_v{\left(\frac{D_s}{C_d}\right)}^{2/3}\frac{L_c}{C_l}=K_v{D}_s^{2/3}{L}_c,$$ (2a)

where $K_v=C_v/\left(C_d^{2/3}{C}_l\right)$ is a constant. Since Eq. 2a is applicable to any stem-crown unit, we obtain $V_{\max }=K_v{D}_{\max }^{2/3}{L}_{\max }$ such that $K_v=V_{\max }/\left(D_{\max }^{2/3}{L}_{\max }\right)$, where $D_{\max }$, $L_{\max }$, and $V_{\max }$ correspond to the most proximal stem diameter, the cumulative vascular length of the entire tree, and the cumulative vascular volume of the entire tree, respectively. Equation 2a can be made nondimensional as

$$\left(\frac{V_c}{V_{\max }}\right)={\left(\frac{D_s}{D_{\max }}\right)}^{\frac{2}{3}}\left(\frac{L_c}{L_{\max }}\right).$$ (2b)

An additional validation for volume scaling law in relation to minimum energy hypothesis is described in the Appendix.

Methods

Morphometry of vascular trees

The volume scaling law is validated in the asymmetric entire coronary arterial tree reconstructed in pig hearts through a growth algorithm (16) based on measured morphometric data (17). Furthermore, the asymmetric epicardial coronary arterial trees with vessel diameter >1 mm were used to validate the scaling laws in partial vascular trees to mimic the resolution of medical imaging.

Symmetric vascular trees of many organs down to the smallest arterioles, constructed in the Strahler system, based on available literature, were used to verify the proposed structure-function scaling law. The pulmonary arterial tree of rats was obtained from the study of Jiang et al. (18), the pulmonary arterial/venous trees of cats from Yen et al. (19,20), the pulmonary arterial trees of humans from Singhal et al. (21,22) and Huang et al. (23), the pulmonary venous trees of humans from Horsfield et al. (24) and Huang et al. (23), the skin muscle arterial tree of hamsters from Bertuglia et al. (25), the retractor muscle arterial tree of hamsters from Ellsworth et al (26), the mesentery arterial tree of rats from Ley et al. (27), the sartorius muscle arterial tree of cats from Koller et al. (28), and the bulbular conjunctiva arterial/venous trees of humans and the omentum arterial tree of rabbits from Fenton et al. (29).

Data analysis

All scaling relations (i.e., Eqs. 2b and A8–A11) can be represented by a form of the type

$$Y=A\mathrm{\times }{X}^B,$$ (3)

where X and Y are defined such that A and B should have theoretical values of unity (Eq. 2b). X and Y are defined as ${\left(D_s/D_{\max }\right)}^{2/3}\left(L_c/L_{\max }\right)$ and $\left(V_c/V_{\max }\right)$, respectively. For Eqs. A8–A11, X and Y are defined as $\left(L_c/L_{\max }\right)$ and $\left(D_s/D_{\max }\right)$, $\left(L_c/L_{\max }\right)$ and $\left(V_c/V_{\max }\right)$, $\left(D_s/D_{\max }\right)$ and $\left(Q_s/Q_{\max }\right)$, and $\left(D_s/D_{\max }\right)$ and $\left(V_c/V_{\max }\right)$, respectively. A nonlinear regression was used to calculate A, with B constrained to $3/7$, $1\frac{2}{7}$, 2⅓, and 3 for Eqs. A8–A11, respectively. The nonlinear regression uses the Marquardt-Levenberg algorithm to find the parameter A for the variables X and Y to provide the “best fit” between the equation and the data. In Eqs. 2b and A8–A11, the parameter A should have a theoretical value of 1.

Results

Asymmetric tree model

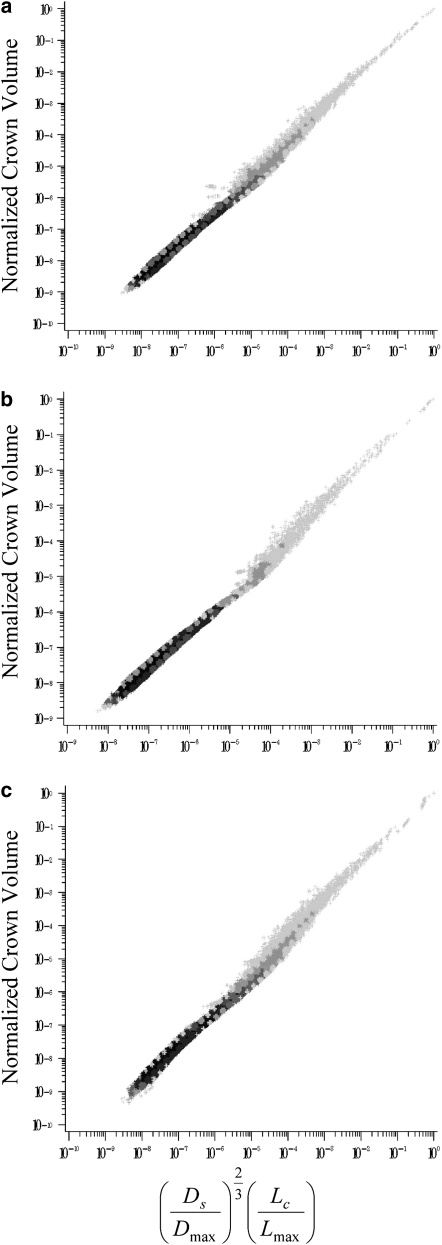
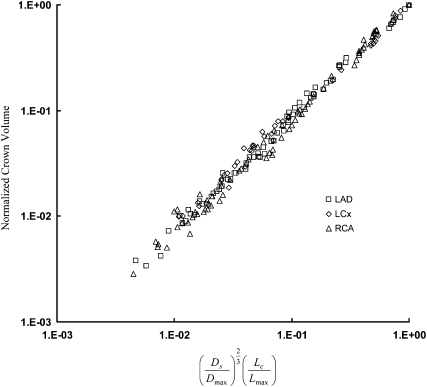
This study proposes what we believe is a novel volume scaling law that relates the crown volume to the stem diameter and crown length (Eq. 2). The validity of Eq. 2 was examined in the entire asymmetric (down to the precapillary vessel segments) and epicardial (vessel diameter ≥1 mm) left anterior descending artery (LAD), left circumflex artery (LCx), and right coronary artery (RCA) trees of pig, as shown in Figs. 2 and 3, respectively. In Table 1, exponent B is determined from a least-square fit and parameter A is calculated by nonlinear regression with the exponent B constrained to 1. For the entire asymmetric and partial trees, both B and A show agreement with the theoretical value of 1.

Figure 2.

Relation between ${\left(D_s/D_{\max }\right)}^{2/3}\left(L_c/L_{\max }\right)$ and normalized crown volume in the entire asymmetric LAD (a), LCx (b), and RCA (c) trees of pig, which include 946,937; 571,383; and 836,712 vessel segments, respectively. The entire tree data are presented as log-log density plots showing the frequency of data because of the enormity of data points, i.e., the darkest shade reflects the highest frequency or density and the lightest shade the lowest frequency (45).

Figure 3.

Relation between ${\left(D_s/D_{\max }\right)}^{\frac{2}{3}}\left(L_c/L_{\max }\right)$ and normalized crown volume in the asymmetric LAD, LCx, and RCA epicardial trees of pig with vessel diameter >1 mm, which include 66, 42, and 71 vessel segments, respectively.

Table 1.

Parameters B and A in the asymmetric entire coronary trees and in the corresponding epicardial trees with vessel diameter >1 mm

Entire trees	Least-square fit		Marquardt-Levenberg method
	B	R2	A	SE	R2
Pig LAD	1.07	1	1.02	0.006	0.998
Pig LCx0	1.08	1	0.99	0.008	0.997
Pig RCA	1.08	1	0.99	0.014	0.989
	Least-square fit		Marquardt-Levenberg method
Epicardial trees	B	R2	A	SE	R2
Pig LAD	1.07	0.995	0.95	0.008	0.996
Pig LCx	1.03	0.994	0.97	0.013	0.994
Pig RCA	1.08	0.990	1.02	0.019	0.986

Parameter B was obtained from least-square fits and parameter A from nonlinear regression with B constrained to 1 when Eq. 2b is represented by Eq. 3, where independent variables $X={\left(D_s/D_{\max }\right)}^{2/3}\left(L_c/L_{\max }\right)$ and $Y=\left(V_c/V_{\max }\right)$, as shown in Figs. 2 and 3. SE, standard error; R², correlation coefficient.

Symmetric tree model

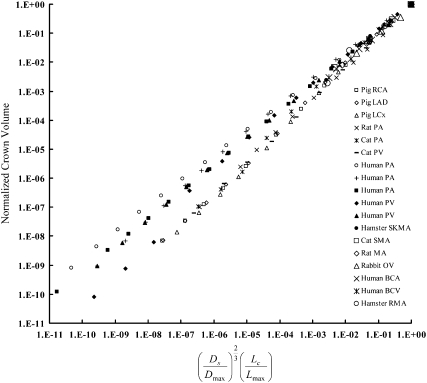
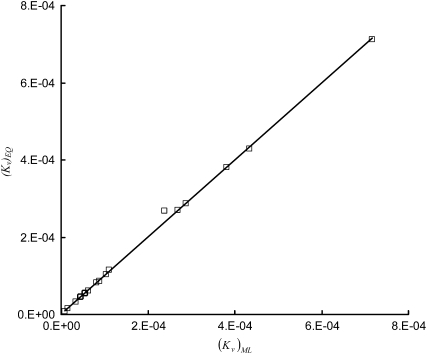
Equation 2b is also validated in symmetric trees for various organs and species, as shown in Fig. 4. Parameters B and A, listed in Table 2, have mean ± SD values of 1.02 ± 0.02 and 1.00 ± 0.01, respectively, by averaging over various organs and species. These parameters are in agreement with the theoretical value of 1. Furthermore, Eq. 2a implies that $K_v=V_{\max }/D_{\max }^{2/3}{L}_{\max }$, which can be compared with the regression-derived value. Fig. 5 shows a comparison of ${\left(K_v\right)}_{\text{ML}}$ obtained from the nonlinear regression of anatomical data and ${\left(K_v\right)}_{\text{EQ}}$ calculated from Eq. 2a. A least-square fit results in a relation of the form ${\left(K_v\right)}_{\text{EQ}}=0.998{\left(K_v\right)}_{\text{ML}}$ (R² = 0.999).

Figure 4.

Relation between${\left(D_s/D_{\max }\right)}^{\frac{2}{3}}\left(L_c/L_{\max }\right)$ and normalized crown volume in the symmetric vascular tree for various organs and species (18–29), corresponding to Table 2.

Table 2.

Parameters B and A in various organs

Species (N)	Least-square fit		Marquardt-Levenberg method
	B	R2	A	SE	R2
Pig RCA (11)	1.09	0.999	1	0.003	1
Pig LAD (11)	1.10	0.999	1	0	1
Pig LCx (10)	1.13	0.999	1	0.001	1
Rat PA (11)	1.06	0.999	0.99	0.017	0.997
Cat PA (10)	1.11	0.996	1.01	0.013	0.999
Cat PV (10)	1.09	1	0.99	0.018	0.997
Human PA (17)	0.88	1	1	0.004	1
Human PA (15)	0.95	0.998	1.02	0.025	0.991
Human PA (17)	0.92	1	0.997	0.006	0.999
Human PV (15)	1.05	0.995	1.02	0.019	0.996
Human PV (15)	0.94	1	1.01	0.014	0.997
Hamster SKMA (4)	1.02	0.995	1.01	0.031	0.997
Rat MA (4)	1	1	1	0.007	1
Rabbit OV (4)	0.98	0.994	0.96	0.073	0.981
Human BCA (5)	0.98	1	1.01	0.015	0.999
Human BCV (4)	1.02	1	1	0.004	1
Hamster RMA (4)	1.03	0.977	1	0.014	0.999
Cat SMA (4)	0.95	1	1	0.012	1

Parameter B was obtained from least-square fits and parameter A from nonlinear regression with B constrained to 1 when Eq. 2b is represented by Eq. 3, where independent variables $X={\left(D_s/D_{\max }\right)}^{2/3}\left(L_c/L_{\max }\right)$ and $Y=\left(V_c/V_{\max }\right)$, as shown in Fig. 4. SE, standard error; R², correlation coefficient.

Figure 5.

Comparison of ${\left(K_v\right)}_{\text{ML}}$ from the nonlinear regression of anatomical data and ${\left(K_v\right)}_{\text{EQ}}$ based on the equation $K_v=V_{\max }/D_{\max }^{2/3}{L}_{\max }$. Through a least-square fit, the comparison can be represented as ${\left(K_v\right)}_{\text{EQ}}=0.998{\left(K_v\right)}_{\text{ML}}$ (R² = 0.999).

Scaling relations

To further validate the volume scaling law, a number of scaling relations between morphological and hemodynamic parameters are proposed in the Appendix. For these relations, parameter A has the theoretical value of 1 as exponent 3/7, $1\frac{2}{7}$, 2⅓, and 3 for the diameter-length relation, volume-length relation, flow-diameter relation, and volume-diameter relation represented in Eqs. A8–A11, respectively. The values for A, as determined from nonlinear regression, are listed in Table 3. These values, averaged over various organs and species, have mean ± SD values of 1.01 ± 0.07, 1.00 ± 0.02, 0.99 ± 0.05, and 0.99 ± 0.03 for Eqs. A8–A11, respectively. The agreement of data with theoretical predictions is excellent.

Table 3.

Parameter A obtained from nonlinear regression in various organs

Species	Diameter-length			Volume-length			Flow-diameter			Volume-diameter
	A	SE	R2	A	SE	R2	A	SE	R2	A	SE	R2
Pig RCA	1.01	0.010	0.999	1	0.002	1	1	0.007	1	1	0.007	0.999
Pig LAD	1.02	0.019	0.996	1	0.003	1	0.99	0.017	0.997	1	0.01	0.999
Pig LCx	1	0.007	1	1	0.001	1	1	0.001	1	1	0.001	1
Rat PA	1.02	0.021	0.995	0.99	0.014	0.998	0.98	0.021	0.995	0.98	0.032	0.99
Cat PA	1	0.014	0.998	1.01	0.011	0.999	1.01	0.006	1	1.01	0.017	0.998
Cat PV	0.99	0.017	0.997	0.99	0.020	0.996	1.01	0.012	0.999	0.99	0.01	0.999
Human PA	0.92	0.037	0.977	1	0.006	0.999	1.02	0.034	0.982	1.01	0.022	0.993
Human PA	0.97	0.025	0.991	1.01	0.020	0.995	1.02	0.025	0.992	1.02	0.041	0.977
Human PA	0.90	0.041	0.973	0.99	0.014	0.997	1.03	0.041	0.974	1.01	0.021	0.993
Human PV	0.96	0.016	0.996	1.02	0.013	0.998	1.04	0.029	0.990	1.04	0.041	0.979
Human PV	0.88	0.054	0.955	1	0.001	1	1.02	0.053	0.963	1.01	0.041	0.976
Hamster SKMA	0.96	0.096	0.942	1	0.015	0.999	1.03	0.087	0.974	1.02	0.079	0.98
Rat MA	1.13	0.203	0.592	1.01	0.034	0.996	0.89	0.156	0.914	0.92	0.132	0.944
Rabbit OV	1.02	0.107	0.849	0.95	0.081	0.977	1.06	0.107	0.954	0.97	0.062	0.987
Human BCA	1.14	0.190	0.447	1.02	0.038	0.994	0.88	0.133	0.912	0.92	0.099	0.955
Human BCV	1.06	0.068	0.964	1	0.009	1	0.96	0.061	0.983	0.97	0.056	0.987
Hamster RMA	1.03	0.078	0.965	1	0.017	0.999	1.01	0.029	0.997	1	0.006	1
Cat SMA	1.11	0.193	0.633	1.01	0.034	0.996	0.92	0.133	0.938	0.95	0.103	0.966

Values from regression when Eqs. A8–A11 (diameter-length, volume-length, flow-diameter, and volume-diameter relations, respectively) are represented by Eq. 3. Exponent B is constrained to $\frac{3}{7}$, $1\frac{2}{7}$, $2\frac{1}{3}$, and 3 for Eqs. A8–A11, respectively. SE, standard error; R², correlation coefficient.

Discussion

The major finding of this study is what we believe is a novel scaling law that relates the vascular blood volume of an organ to the segment diameter and crown length. The scaling law was validated based on morphometric data of several organs and species. Further validation was made through several structure-structure and structure-function relations.

Volume scaling law

Many structural and functional features are found to have a power-law (scaling) relation to body size, metabolic rates, etc. (30–34). Previous studies from our group (11) showed several scaling relations connecting structure and function. Here, we add what we believe is a novel volume scaling relation (Eq. 2) to the list.

Clinical techniques (e.g., indicator and dye-dilution method) have been used to predict blood volume for decades (35). The blood volume varies significantly with body size such that it is difficult to evaluate the change of blood volume in patients because of lack of reference. Although Feldschuh and Enson (36) used the metropolitan life height and weight tables to determine an ideal weight as an approximate reference, this approach lacks a physical or physiological basis for calculating normal blood volume. The proposed volume scaling law may establish the “normality” of blood volume, and deviation thereof may be indicative of pathology.

The remodeling of intravascular volume may be physiologic during normal growth, exercise, or pregnancy. It may also be pathological, however, in hypertension, tumor, or diffuse vascular diseases (37–39). Diffuse vascular disease is difficult to quantify because the normal reference does not exist. This study shows that the volume scaling law holds in the coronary epicardial trees (vessel diameter >1 mm), as shown in Fig. 3 and Table 1. Such data on coronaries or other vascular tree are available by angiography, CT, or MRI. Hence, the proposed volume scaling law can serve to quantify diffuse vascular disease in various organs clinically. Future studies will focus on the clinical utility of the proposed scaling model.

Comparison with the ZKM model

Vascular trees provide the channels to transport fluid to different organs. An optimal design of vascular tree is required to minimize energy losses. Although many theoretical approaches (40,41) are proposed to explain the design of vascular tree, the minimum energy hypothesis (42) may be the most validated hypothesis. The ZKM model (11,12), based on the minimum energy hypothesis, predicted the exponents $\chi =3(\varepsilon \prime -2)/4(\varepsilon \prime +1)$, $\beta =5/(\varepsilon \prime +1)$, and $\delta =4(\varepsilon \prime +1)/3(\varepsilon \prime -2)$ for diameter-length, volume-length, and flow-diameter relations, respectively, where the parameter ${\varepsilon }^{\text{'}}$ in the exponents is the ratio of maximum metabolic to viscous power dissipation for a given tree. Based on the newly proposed Eq. 2, this study shows the corresponding exponents χ = 3/7, β = $1\frac{2}{7}$, and δ = 2⅓. With the respective $\varepsilon \prime$ (see Table 1 of Kassab (11)), the mean values over all organs and species are 0.43 ± 0.02, 1.28 ± 0.09, and 2.33 ± 0.11 for exponents χ, β, and δ, respectively, which agrees well with the predictions presented here, i.e., 3/7 ≈ 0.43, $1\frac{2}{7}$ ≈ 1.29, and 2⅓ ≈ 2.33. Furthermore, the ZKM model shows the mean ± SD value of 2.98 ± 0.34 for the volume-diameter relation with the respective $\varepsilon \prime$, which is consistent with the exponent value of 3 in Eq. A11. This provides further validation for the proposed volume scaling law, as demonstrated in the Appendix.

Optimal cost function

From Eqs. A5 and A7, the nondimensional cost function can be written as

$$f_c=\frac{1}{6}\frac{{(L_c/L_{\max })}^3}{{(D_s/D_{\max })}^4}+{\left(\frac{D_s}{D_{\max }}\right)}^{2/3}\left(\frac{L_c}{L_{\max }}\right).$$ (7)

This is the minimum cost of maintaining an optimal design of a vascular tree under homeostasis. From the structure-function scaling relations (Eq. A8), ${(L_c/L_{\max })}^3/{(D_s/D_{\max })}^4={\left(L_c/L_{\max }\right)}^{1\frac{2}{7}}$ and ${\left(D_s/D_{\max }\right)}^{2/3}\left(L_c/L_{\max }\right)={\left(L_c/L_{\max }\right)}^{1\frac{2}{7}}$, we obtain ${(L_c/L_{\max })}^3/{(D_s/D_{\max })}^4={\left(D_s/D_{\max }\right)}^{2/3}\left(L_c/L_{\max }\right)$. The power required to overcome the viscous drag of blood flow (second term in Eq. 7) is one-sixth of the power required to maintain the volume of blood (third term in Eq. 7). This expression implies that most of the energy dissipated is for maintaining the metabolic cost of blood, which is proportional to the metabolic dissipation (43).

Critique of the volume scaling law

Although our scaling law is based on measured anatomical data of vascular vessels, there are still a number of assumptions made. For example, 1), all vessels in this model are assumed to be in a vasodilated state in the absence of vascular tone; 2), a vessel is assumed to be a cylindrical tube, with no consideration of more complex geometry; 3), pulsatility and compliance are neglected. In future studies, to mimic the in vivo state, this scaling law should be extended to include the dynamic changes of crown length and volume and vessel diameter. This analysis provides a theoretical basis for considering thesis higher-order effects.

Significance of the volume scaling law

The novel, to our knowledge, volume scaling law (Eq. 2) predicts the relation between crown volume, stem diameter, and crown length in normal vessels. Furthermore, the volume-diameter relation (Eq. A11) is proposed based on the volume scaling law. From the volume-diameter relation, the crown volume distal to a stem vessel can be estimated when the total intravascular volume and inlet diameter (e.g., aorta) are known. At this time, a new use of computed tomography, whole-body CT scanning, is promoted, which is effective in measuring the whole-body blood volume. A comparison of theoretically predicted and experimentally measured blood volume can assess hypovolemia and hypervolemia in the organ of a patient. This may improve the benefit of whole-body CT scanning.

The volume scaling law can be used to determine appropriate boundary conditions for the computational software that have both basic and clinical significance. The computational software, coupled with the noninvasive imaging techniques, can provide quantitative information (e.g., 3-D visualization of pressure and velocity fields at any points inside the lumen), which may help clinicians select appropriate treatment.

Appendix: Additional Validation of Volume Scaling Law

From Eq. 2, we propose the cost function for a crown, $F_c$, consistent with a previous formulation (11,12):

$$F_c=Q_s\mathrm{\times }\Delta P_c+K_m{V}_c=Q_s^2\mathrm{\times }{R}_c+K_m{K}_v{D}_s^{2/3}{L}_c,$$ (A1)

where $Q_s$ and $\Delta P_c=Q_s\mathrm{\times }{R}_c$ are the flow rate through the stem and the pressure drop in the distal crown, respectively, and $K_m$ is a metabolic constant of blood in a crown. We have recently shown the resistance of a crown as $R_c=K_c\frac{L_c}{D_s^4}$, where $K_c$ is a constant (44). The cost function of a crown tree in Eq. A1 can be written as

$$F_c=Q_s^2\mathrm{\times }{R}_c+K_m{K}_v{D}_s^{2/3}{L}_c=K_c{Q}_s^2\frac{L_c}{D_s^4}+K_m{K}_v{D}_s^{2/3}{L}_c.$$ (A2)

Equation A2 can be normalized by the metabolic power requirements of the entire tree of interest, $K_m{V}_{\max }=K_m{K}_v{D}_{\max }^{2/3}{L}_{\max }$, to obtain

$$\begin{array}{l}{f}_c=\frac{F_c}{K_m{K}_v{D}_{\max }^{2/3}{L}_{\max }}\\ =\frac{Q_{\max }^2{R}_{\max }}{K_m{K}_v{D}_{\max }^{2/3}{L}_{\max }}{\left(\frac{Q_s}{Q_{\max }}\right)}^2\mathrm{\times }\frac{(L_c/L_{\max })}{{(D_s/D_{\max })}^4}+{\left(\frac{D_s}{D_{\max }}\right)}^{2/3}\left(\frac{L_c}{L_{\max }}\right),\end{array}$$ (A3)

where $f_c$ is the nondimensional cost function. A previous analysis (11) shows

$$Q_s=K_Q{L}_c\Rightarrow \frac{Q_s}{Q_{\max }}=\frac{L_c}{L_{\max },}$$ (A4)

where $K_Q$ is a flow-crown length constant. When Eq. A4 is applied to Eq. A3, the dimensionless cost function can be written as

$$f_c=\frac{Q_{\max }^2{R}_{\max }}{K_m{K}_v{D}_{\max }^{2/3}{L}_{\max }}\times \frac{{(L_c/L_{\max })}^3}{{(D_s/D_{\max })}^4}+{\left(\frac{D_s}{D_{\max }}\right)}^{2/3}\left(\frac{L_c}{L_{\max }}\right).$$ (A5)

Similar to Murray's law (42), we minimize the cost function with respect to diameter at a fixed $L_c/L_{\max }$ to obtain

$$\begin{array}{l}\frac{\partial f_c}{\partial \left(\frac{D_s}{D_{\max }}\right)}=0\Rightarrow \frac{(-4)Q_{\max }^2{R}_{\max }}{K_m{K}_v{D}_{\max }^{2/3}{L}_{\max }}\mathrm{\times }\frac{{(L_c/L_{\max })}^3}{{(D_s/D_{\max })}^5}=-\left(\frac{2}{3}\right){\left(\frac{D_s}{D_{\max }}\right)}^{\frac{2}{3}-1}\left(\frac{L_c}{L_{\max }}\right)\\ \Rightarrow \frac{6Q_{\max }^2{R}_{\max }}{K_m{K}_v{D}_{\max }^{2/3}{L}_{\max }}\mathrm{\times }{\left(\frac{L_c}{L_{\max }}\right)}^2={\left(\frac{D_s}{D_{\max }}\right)}^{4+\frac{2}{3}}.\end{array}$$ (A6)

Equation A6 applies to any stem-crown unit. When $L_c=L_{\max }$ and $D_s=D_{\max }$ in Eq. A6, we obtain

$$\frac{6Q_{\max }^2{R}_{\max }}{K_m{K}_v{D}_{\max }^{2/3}{L}_{\max }}=1\Rightarrow \frac{Q_{\max }^2{R}_{\max }}{K_m{K}_v{D}_{\max }^{2/3}{L}_{\max }}=\frac{1}{6}.$$ (A7)

Therefore, Eq. A6 can be written as

$$\left(\frac{D_s}{D_{\max }}\right)={\left(\frac{L_c}{L_{\max }}\right)}^{\frac{3}{7}}.$$ (A8)

From Eqs. 2b and A8, we obtain

$$\left(\frac{V_c}{V_{\max }}\right)={\left(\frac{L_c}{L_{\max }}\right)}^{1\frac{2}{7}}.$$ (A9)

From Eqs. A4 and A8, we find that

$$\left(\frac{Q_s}{Q_{\max }}\right)={\left(\frac{D_s}{D_{\max }}\right)}^{2\frac{1}{3}},$$ (A10)

where $Q_{\max }$ is the flow rate through the most proximal stem. From Eqs. A8 and A9, we obtain

$$\left(\frac{V_c}{V_{\max }}\right)={\left(\frac{D_s}{D_{\max }}\right)}^3.$$ (A11)

Equations A8–A11 are the structure-function scaling relations in the vascular tree, based on the minimum energy hypothesis. Equations A8, A9, and A11 represent the diameter-length, volume-length, and volume-diameter relations, respectively, and Eq. A10 represents the general Murray's law in the entire tree.