Abstract
We present a polarizable force field based on the charge-equilibration formalism for molecular dynamics simulations of phospholipid bilayers. We discuss refinement of headgroup dihedral potential parameters to reproduce ab initio conformational energies of dimethylphosphate calculated at the MP2/cc-pVTZ level of theory. We also address the refinement of electrostatic and Lennard-Jones (van der Waals) parameters to reproduce ab initio polarizabilities and water interaction energies of dimethylphosphate and tetramethylammonium. We present results of molecular dynamics simulations of a solvated dimyristoylphosphatidylcholine bilayer using this polarizable force field as well as the nonpolarizable, fixed-charge CHARMM27 and CHARMM27r force fields for comparison. Calculated atomic and electron-density profiles, deuterium order parameters, and headgroup orientations are found to be consistent with previous simulations and with experiment. Polarizable interaction models for solvent and lipid exhibit greater water penetration into the lipid interior; this is due to the variation of water molecular dipole moment from a bulk value of 2.6 Debye to a value of 1.9 Debye in the membrane interior. The reduction in the electrostatic component of the desolvation free-energy penalty allows for greater water density. The surface dipole potential predicted by the polarizable model is 0.95 V compared to the value of 0.8 V based on nonpolarizable force-field calculations. Effects of inclusion of explicit polarization are discussed in relation to water dipole moment and varying charge distributions. Dielectric permittivity profiles for polarizable and nonpolarizable interactions exhibit subtle differences arising from the nature of the individual component parameterizations; for the polarizable force field, we obtain a bulk dielectric permittivity of 79, whereas the nonpolarizable force field plateaus at 97 (the value for pure TIP3P water). In the membrane interior, both models predict unit permittivities, with the polarizable models contributing from one to two more units due to the optical dielectric (high-frequency dipole fluctuations). This contribution is a step toward the continuing development of a CHARMM (Chemistry at Harvard Molecular Mechanics) polarizable force field for simulations of biomacromolecular systems.
Introduction
Integral membrane proteins have become a focus of intense effort of fundamental research due to the ubiquitous nature of these macromolecules. Comprising roughly one-third of the human genome, they are implicated in myriad physiological functions and, unfortunately, dysfunctions. For instance, for normal physiological functioning, integral membrane proteins are involved in signaling processes, passive and active transport, and interfacial enzymatic processes (1). Of course, one cannot speak about integral membrane proteins independent of the lipidic context in which they function. Lipid membranes in their own right have garnered much attention as well, with particular focus on membrane properties and behaviors, including structural deformation (in the presence of small molecules as well as integral membrane proteins), and electrostatic properties such as the interfacial dipole (or total) potential (2) and dielectric constant variation with location in a bilayer (3). Of particular recent interest are protein-lipid interactions, and specifically the interactions of charged and/or polar amino acid residues as they pertain to an understanding of the thermodynamics of structural and energetic stability of integral membrane proteins upon desolvation of such systems.
Complementing the enormous volume of experimental effort to understand lipid bilayers and integral membrane proteins, computational approaches based on the analytics of statistical mechanics (molecular dynamics and Monte Carlo simulations) have been indispensable to understanding properties and processes in these systems at the atomic and molecular levels, and providing insights at a resolution inaccessible to current state-of-the-art experimental methods (1,4–16). These methods require information about the forces between interacting species; ideally, the necessary information would be contained in a quantum mechanical potential energy surface, which could then be directly applied to generate forces. However, simplifying assumptions must be made to arrive at tractable functional forms of a classical nature. Thus, current state-of-the-art modeling approaches employ empirical potentials, or force fields, to model interspecies interactions. Though initially developed with a fully atomistic perspective, with secondary efforts pursuing more “coarse-grained” potentials (17,18), development and application of coarse-grained models continues at a rigorous pace today (19–24). Nevertheless, under the current paradigmatic approach to development, such models are generally referenced to results from fully atomistic simulations. Thus, the need for accurate all-atom potentials still persists. Toward this end, effort continues to refine today's fixed-charge models to incorporate explicit electrostatic polarization effects to dynamically model the response to varying electric fields at the molecular to atomic level. We mention that complementing the fully atomistic models for solvent and lipid (to be discussed below) are implicit solvent/membrane models that are fast providing an efficient alternative for modeling of large assemblies over timescales approaching microseconds (25–28).
All-atom simulation methods invariably employ fixed-charge representations of electrostatic interactions based on a Coulomb model. The shortcomings of such models, and the plausible importance of explicitly accounting for nonadditive electrostatic and charge-transfer effects, have been widely discussed in the literature (29–32). The past decade has witnessed an increasing pace of development and application of polarizable force fields for a range of applications, though such models have not yet realized the popularity enjoyed by fixed-charge models. To begin to explore the effects of polarization in biological systems, the first step undoubtedly has to be the development of self-consistently parameterized models. Though several models have appeared in which application to proteins and nucleic acids is discussed, polarizable models for membrane systems have not yet been reported.
Polarizable interaction models that incorporate dipole induction effects have already proven an indispensable tool for obtaining an accurate theoretical estimation of solution structure and thermodynamics in interfacial systems such as aqueous solutions of inorganic salts. The development of nonadditive, or polarizable, force fields for small molecular and larger biologically relevant macromolecules (33–43) has attracted considerable interest and has resulted in the development of several conventional approaches for modeling atomic and molecular polarization. These approaches include point-dipole (and higher-order multipole) polarizable models (34,44–46), Drude oscillator models (37,47,48), and charge-equilibration/fluctuating-charge models (35,36,49–54) in addition to fully ab initio based approaches such as Car-Parrinello molecular dynamics techniques.
Thus, the goals of this contribution are as follows. First, in the Methods section, we discuss the charge-equilibration formalism to explicitly account for nonadditive electrostatic effects. In the section “Force field refinement”, we discuss the parameterization of our model, and in the Results and Discussion section, we talk about various properties of a model dimyristoylphosphatidylcholine (DMPC) bilayer predicted using molecular dynamics simulations. We conclude our contribution with a discussion of continuing work in our laboratory.
Methods
Charge equilibration model
The simulations presented here employ polarizable force fields based on the charge-equilibration model for the entire lipid molecule and the solvent. The formalism employed to explicitly treat nonadditive electrostatic effects is the charge-equilibration model. In the following text, we discuss the specifics of the formalism. The development of charge-equilibration models for DMPC will be discussed further.
The nonpolarizable CHARMM (55) force field partitions the quantum mechanical energy surface into classical terms representing bond-stretching, bond-angle bending, dihedral/torsional motion, out-of-plane distortion, dispersion interactions (Lennard-Jones), and electrostatic interactions of the pairwise Coulomb type. The polarizable model is based on the charge-equilibration scheme (53) as applied to classical molecular dynamics. Although applied here in a classical potential, the formalism derives rigorously from the density functional theory of atoms in molecules (56) based on Sanderson's idea of electronegativity equalization (57,58); polarization is effected via the migration of charge density (in the classical sense, this is condensed to a partial charge) between atomic species within a given molecule. The electronic density adjusts within the molecule to equalize the electrochemical potential (or, equivalently, the electronegativity) at each point in the molecule. The direction and ease of flow are determined by physical properties of individual atoms, as will be discussed. The reader is referred to the literature for more details (35,36,49–53,56,59–61).
The electrostatic energy of a system of M molecules containing N atoms/molecule is
| (1) |
where χ represents atom electronegativity and η is the atomic hardness. The former quantity gives rise to a directionality of electron flow, whereas the latter represents a resistance, or hardness, to electron flow to or from the atom. The third term in Eq. 1 is a standard Coulomb interaction between sites not involved in dihedral, angle, and bonded interactions with each other (the primed notation indicates a summation only over such sites). The second term represents the local charge transfer interaction, generally restricted to within a molecule (no charge transfer) or some appropriate charge normalization unit. The last term is a Lagrange-multiplier-based constraint on total charge on a given normalization unit; this constraint helps to restrict charge equilibration (hence charge redistribution) over chemically relevant and distinct units (62). We note that although the electronegativity and hardness follow exactly from the definitions of electron affinity and ionization potential, they are considered here as empirical parameters to be determined as described below. Homogeneous hardness values (for each atom type) are parameterized as discussed in Patel and Brooks (52). Heterogeneous elements (interaction elements between different atom types) are derived from the individual atom type values based on the combining rule (51):
| (2) |
where Rij is the separation between atoms (or, more generally, sites) i and j. This local screened Coulomb potential has the correct limiting behavior as 1/r for separations >∼2.5 Å. This interaction is computed for sites 1–2, 1–3, and 1–4 (sites included in bonds, angles, and dihedrals, respectively). Sites in a molecule separated by five or more sites interact via a Coulomb interaction; in the case of interacting molecules, the interaction between sites on different molecules is again of the Coulomb form.
Regarding polarizability, the charge-equilibration model is indeed a polarizable model, as the molecular polarizability can be derived as follows:
| (3) |
where denotes the molecular hardness matrix, and and are the β and γ Cartesian components, respectively, of the atomic position vector. A more detailed derivation can be found elsewhere (62). The hardness matrix can be augmented to enforce charge constraints within a molecule (62) for explicit calculations of polarizability such as those carried out in this study for the refinement of electrostatic parameters. In addition, the charge-equilibration model, which is an all-atom representation with partial charges assigned to all atomic species, contains all higher-order electrostatic multipole moments, in contrast to point-dipole polarizable models (63–65) and Drude oscillator models (38,66,67). As such, the charge-equilibration model incorporates higher-order electrostatic interactions explicitly.
The charge degrees of freedom are propagated via an extended Lagrangian formulation that imposes a molecular charge neutrality constraint, thus strictly enforcing electronegativity equalization at each dynamics step. The system Lagrangian is
| (4) |
where the first two terms represent the nuclear and charge kinetic energies, the third term is the total potential energy, and the fourth term is the molecular charge neutrality constraint with λi the Lagrange multiplier for each molecule i. The fictitious charge dynamics, analogous to the fictitious wavefunction dynamics in Car-Parinello (CP) type methods (68), are determined with a fictitious charge “mass” (adiabaticity parameter in CP dynamics). The units for this mass are (energy time2/charge2). The charges are propagated based on forces arising from the difference between the average electronegativity of the molecule and the instantaneous electronegativity at an atomic site.
We will discuss the charge-equilibration model for DMPC in further detail below. We comment here that the polarizable TIP4P-FQ water model is used to model solvent-solvent and solvent-solute interactions. The TIP4P-FQ water model is a four-site model, based on the original TIP4P water model of Jorgensen et al. (69). The charges reside on the hydrogen atoms and a virtual site situated along the perpendicular bisector of the HOH angle 0.15 Å from the oxygen atom. The model has been characterized in previous studies, and the reader is referred to the relevant literature for further details.
Molecular dynamics simulations: protocol
Simulations were carried out in the constant pressure, surface area, and temperature (NPAT) ensemble using the CHARMM molecular modeling package (12,55). The polarizable hydrated DMPC bilayer system consisted of 72 lipid molecules and 2836 molecules of TIP4P-FQ (36) water. The total system size was initially 46.8 × 46.8 × 76.0 Å; the starting geometry was obtained from a simulation using the CHARMM27 nonpolarizable force field. Dynamics were propagated using a Verlet leapfrog integrator (70) with time steps of 0.5 fs. The system temperature was maintained at 303 K using the Nosé-Hoover (70,71) method with a thermal piston mass of 3000 kcal/mol ps2. Pressure was maintained at 1 atm using the Langevin piston method with a piston mass of 750 amu in the z direction only (bilayer normal) (70), resulting in constant surface area. Particle mesh Ewald (72,73) summation with screening parameter κ = 0.320 was used in all simulations to account for the conditionally convergent long-range electrostatic interactions; a grid spacing of 1 Å was used for the Fast Fourier transform grid. Several replicate simulations of varying lengths were run, for a total simulation time of ∼40 ns. In addition, several replicate simulations (a total of ∼45 ns) were run on this system using the nonpolarizable CHARMM27 (C27) force field for lipids and TIP3P water (69); furthermore, to compare the results of the CHEQ force field with the latest CHARMM lipid force field, simulations were also performed using the recently revised C27r force field (74). Simulation parameters were the same as described above, except that a 1 fs timestep was used. Atomic charge degrees of freedom (the partial atomic charges) are propagated within an extended Lagrangian formulation. Since the Nosé-Hoover charge dynamics does not inherently enforce strict charge neutrality (or charge conservation in general), during each Nosé-Hoover iteration, we enforce charge neutrality for individual normalization units by subtracting out the average excess charge (excess relative to the required total charge constraint) from each atom. This approach, which serves as an efficient means to ensure strict charge neutrality during the course of the simulation, has been applied and validated previously (75).
Regarding computational cost, the charge-equilibration approach for molecular dynamics incurs ∼10% (serial) to 13% (parallel) overhead on a per-integration-step basis (the value for parallel calculations is due to communication latency); these performance numbers are similar to those quoted by Patel et al. (52) and Rick et al. (36). Due to the propagation of light charge variables (small masses), the time steps required are smaller by a factor of 2–4 for simulations of polarizable models relative to fixed-charge models, though multiple-time-step methods can be implemented; hence, the CPU time is roughly on the order of 2–4 times more at this time.
Control of lipid molecular polarizability
Charge equilibration models are known to treat molecular systems as conductors, where charge is allowed to flow through space based on the relative electronegativities of the constituent atomic species. Consequently, superlinear scaling of the molecular polarizability has been observed in previous studies of extended molecules in vacuum (76). As such, care must be taken to control the polarizability scaling in such systems. Unlike point-dipole or Drude oscillator models, charge-equilibration models do not possess intrinsic length scales governing the polarizable volume associated with fundamental units (i.e., methylene units in an alkyl chain). We note, however, that unlike Drude oscillator or point-dipole models, charge-equilibration models can both effectively capture higher-order electrostatic multipole moments and allow extension to charge-transfer models in a rigorous manner. In this case, to modulate the lipid molecular polarizability, the charge is normalized (constrained to a constant overall charge for the unit) over smaller regions of the molecule. It is important to note that these regions correspond to the molecular model compounds employed to parameterize the electrostatic, bonded, and nonbonded (van der Waals) interactions. Fig. 1 a is a schematic of the molecular groups over which charge is constrained for the current polarizable force field. Within this framework, the electrostatic energy expression is modified slightly to incorporate the charge constraints over groups within a molecule:
| (5) |
Insofar as the charge conservation units are intimately associated with the molecular dimensions of the model compounds used to parameterize the various energy terms comprising the total interaction potential, we believe that the current approach offers a consistent, straightforward, and natural means to integrate charge-equilibration force fields developed based on parameterization to properties of smaller model compounds to larger biomacromolecular assemblies.
Figure 1.
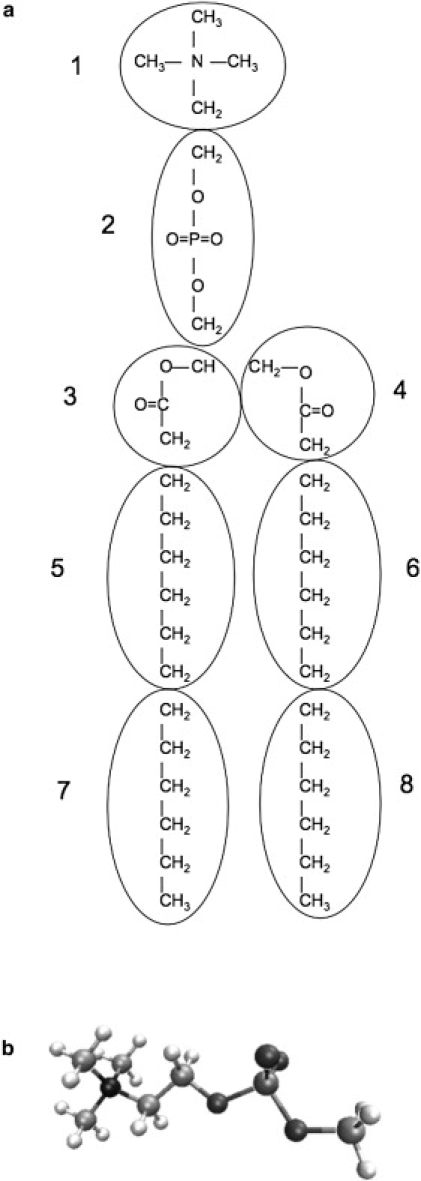
(a) Diagram of the units over which charge is constrained in the charge-equilibration model for DMPC. Units 1 and 2 are analogous to the model compounds TMA and DMP, respectively. Units 3 and 4, the acyl parts, were previously parameterized (52) and were not included in this parameterization. Units 5–8 are analogous to hexane, which was previously parameterized (75). (b) The model compound o-phosphorylcholine, used to fit the N-C-C-O and C-C-O-P torsional parameters of DMPC.
For the headgroup regions, the molecular ions tetramethylammonium (TMA) and dimethylphosphate (DMP) are employed as the model compounds. We will discuss the parameterization of these regions below. The alkane force fields developed originally by Patel et al. (39) and recently refined by Davis et al. (75) are taken as the basis for the aliphatic chains. For this work, we split the aliphatic chain, for normalization purposes, into two groups, each six carbon units long. Davis et al. have demonstrated that such a normalization scheme for larger alkanes leads to an effective scaling of molecular polarizability in larger alkanes that follows an effectively linear trend as predicted by ab initio methods and confirmed by experimental measurements.
Force-field refinement
Parameterization approach
For the charge-equilibration model currently developed for DMPC (and related saturated phospholipid molecules), we follow an approach to force field development that constructs a biomacromolecular force field based on smaller model compound systems. Based on Fig. 1, plausible choices for the headgroup regions are the tetramethylammonium and dimethylphosphate ions. The ester groups are modeled by methyl acetate, and the alkyl tails by linear alkanes. As classical force fields attempt to model inter- and intramolecular interactions, we consider interaction energetics and geometries of the model compounds with water as a means to incorporate necessary information into the force field description. We consider vacuum water-model compound systems as efficient proxies for developing necessary interaction models; moreover, since water is the solvent of choice, it is necessary to arrive at a reasonably accurate description of this interaction. For this work, we focus on the phosphorylcholine group atoms (the headgroup regions) of DMPC while transferring force field parameters for the glycerol group (ester linkage) and associated atoms from earlier work by Patel and Brooks as part of the CHARMM protein polarizable force field (52). The torsion angles for the o-phosphorylcholine model compound are adjusted in this work to reproduce more “global” structural properties of the headgroup region, with particular attention to the distribution of the P-N dipole vector. For the acyl chains, we transfer the force field of Davis et al. (75), which was recently revised and tuned to more accurately reproduce a wide range of properties of liquid alkanes including bulk structural and thermodynamic properties as well as single-molecule torsional energetics. The transfer of this force field to the DMPC system is in the spirit of CHARMM force field development. We note that ideally, one would like to employ larger systems for model building; however, due to limitations in current state-of-the-art resources (hardware and software), one must still invoke one of the strongest assumptions associated with the construction and application of empirical (classical) force fields, namely, that atom type parameters are transferable from smaller model compounds to larger systems. Finally, intramolecular components of the DMPC force field, including bond and angle stretching and bending, respectively, are transferred from the CHARMM27 nonpolarizable model and work of Patel et al. (52). The adequacy of this approach has been verified in previous studies (38,75).
Electrostatic parameter refinement
The electrostatic parameters of the atoms in the phospholipid headgroup have been refined to better reproduce the atomic charges and molecular polarizability of model compounds TMA and DMP. The target data was obtained from optimized geometries of TMA and the gg conformer of DMP calculated at the MP2/cc-pVTZ level of theory using Gaussian 03 (77). Atomic charges were calculated in Gaussian using the CHelpG method for fitting of electrostatic potentials (78). An initial set of atomic hardnesses and electronegativities was determined using the protocol of Patel et al. (52). Briefly, the approach involves perturbing a single molecular species (in this case, DMP or TMA) with a dipolar probe situated at various locations on and beyond the molecular surface. The difference in charges in the presence and absence of the external electric field generated by the dipolar probes (linear response regime) provides a relation for determining the atomic hardnesses as
| (6) |
where is a perturbing external potential introduced by the dipolar probe. The electronegativities are then determined independently to reproduce the atomic charges and dipole moments from the ab initio calculations. For the initial parameter set, density functional theory calculations were employed to generate the zero-field and perturbing field charges for DMP and TMA. This initial parameter set is shown in Table 1.
Table 1.
Electrostatic parameters for the original and refined polarizable DMPC models
| Atom Type | Original |
Refined |
||
|---|---|---|---|---|
| χ (kcal/mol e) | η/2 (kcal/mol e2) | χ (kcal/mol e) | η/2 (kcal/mol e2) | |
| NTL | 19.844 | 83.270 | 49.709 | 112.415 |
| CTL5 | 22.471 | 120.662 | 59.462 | 162.894 |
| HL | 0.000 | 268.105 | 0.000 | 361.942 |
| PL | 51.925 | 92.305 | 42.909 | 156.919 |
| O2L | 131.555 | 162.540 | 389.763 | 276.318 |
| OSL | 47.435 | 133.633 | 209.849 | 227.176 |
| CTL2 | 0.132 | 120.533 | 42.690 | 204.906 |
| HAL2 | 0.000 | 221.902 | 41.562 | 377.233 |
The atomic charges and polarizabilities resulting from the original CHEQ polarizable force field and from the ab initio calculations are shown in Tables 2 and 3. It is evident that the polarizability for DMP is nontrivially higher than consensus ab initio values (37). We note that in applying this set of charge-equilibration parameters for simulations of solvated DMPC, severe overpolarization was encountered; this is not surprising in light of the fact that the molecular polarizability of the initial models systematically overestimated ab initio values for the corresponding molecular polarizabilities. Consequently, for the charge-equilibration (CHEQ) force field for DMP, the molecular polarizability was reduced below the ab initio value in an attempt to correct this. This was accomplished by scaling the atomic hardnesses (η) of all atom types in DMP by a factor of 1.7. For TMA, the ab initio polarizability was reproduced in the CHEQ model by scaling the atomic hardnesses by 1.35. Atomic electronegativities (χ) are obtained by making use of the electrostatic energy expression for a single molecule:
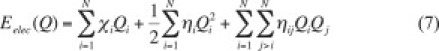 |
(7) |
The terms ηij represent Coulomb integrals and in the CHEQ force field are approximated as a function of the hardness by the atomic combination rule (51), so these terms are implicitly parameterized along with the atomic hardnesses. As described elsewhere (62), minimizing the energy with respect to the atomic charges and casting the resulting system of equations in matrix form yields
| (8) |
Using the scaled hardnesses and ab initio atomic charges, an appropriate set of electronegativites can be obtained by evaluating this expression. For DMP, the resulting values were then modified to ensure that the methyl hydrogens were less electronegative than the methyl carbons and to increase the positive charge on the phosphorus. The original and refined electrostatic parameters are shown in Table 1. The CHEQ minimized charges and the polarizability are shown in Tables 2 and 3. We note that the final polarizability for dimethylphosphate, 8.057 Å3 is reduced from the gas-phase ab initio value of 8.786 Å3, a scaling that is also reflected in the value of 6.63 Å3 determined by MacKerell and co-workers for their Drude oscillator models of nucleic acids (37). The extent of condensed-phase polarizability scaling remains an empirical matter in the context of polarizable force field development.
Table 2.
Atomic charges and polarizability for DMP calculated using the original and refined CHEQ force fields compared to ab initio computed MP2/cc-pVTZ values
| Atomic charge | CHARMM (fixed-charge) | CHEQ (original) | CHEQ (refined) | MP2/cc-pVTZ |
|---|---|---|---|---|
| P1 | 1.500 | 1.278 | 1.315 | 1.339 |
| O3 | −0.780 | −0.783 | −0.864 | −0.834 |
| O4 | −0.780 | −0.783 | −0.864 | −0.834 |
| O1 | −0.570 | −0.389 | −0.563 | −0.500 |
| O2 | −0.570 | −0.389 | −0.563 | −0.500 |
| C1 | −0.170 | −0.033 | 0.207 | 0.210 |
| H11 | 0.090 | 0.022 | 0.019 | −0.030 |
| H12 | 0.090 | 0.011 | 0.041 | −0.020 |
| H13 | 0.090 | 0.033 | 0.002 | 0.005 |
| C2 | −0.170 | −0.033 | 0.207 | 0.210 |
| H21 | 0.090 | 0.033 | 0.002 | 0.005 |
| H22 | 0.090 | 0.022 | 0.019 | −0.030 |
| H23 | 0.090 | 0.011 | 0.041 | −0.020 |
| Polarizability (Å3) | n/a | 13.587 | 8.057 | 8.786 |
Ab initio values were computed at the MP2/cc-pVTZ level of theory using Gaussian 03. The fixed charges used in the nonpolarizable CHARMM force field are also shown.
Table 3.
Atomic charges and polarizability for TMA calculated using the original and refined CHEQ force fields compared to ab initio computed MP2/cc-pVTZ values
| Atomic charge | CHARMM (fixed-charge) | CHEQ (original) | CHEQ (refined) | MP2/cc-pVTZ |
|---|---|---|---|---|
| N | −0.600 | 0.194 | 0.185 | 0.187 |
| C1 | −0.350 | −0.284 | −0.294 | −0.271 |
| C2 | −0.350 | −0.284 | −0.294 | −0.294 |
| C3 | −0.350 | −0.284 | −0.294 | −0.291 |
| C4 | −0.350 | −0.284 | −0.294 | −0.279 |
| H11 | 0.250 | 0.162 | 0.166 | 0.159 |
| H12 | 0.250 | 0.162 | 0.166 | 0.159 |
| H13 | 0.250 | 0.162 | 0.166 | 0.159 |
| H21 | 0.250 | 0.162 | 0.166 | 0.165 |
| H22 | 0.250 | 0.162 | 0.166 | 0.165 |
| H23 | 0.250 | 0.162 | 0.166 | 0.165 |
| H31 | 0.250 | 0.162 | 0.166 | 0.164 |
| H32 | 0.250 | 0.162 | 0.166 | 0.164 |
| H33 | 0.250 | 0.162 | 0.166 | 0.164 |
| H41 | 0.250 | 0.162 | 0.166 | 0.162 |
| H42 | 0.250 | 0.162 | 0.166 | 0.161 |
| H43 | 0.250 | 0.162 | 0.166 | 0.161 |
| Polarizability (Å3) | n/a | 10.05 | 7.53 | 7.58 |
Ab initio values were computed at the MP2/cc-pVTZ level of theory using Gaussian 03. The fixed charges used in the nonpolarizable CHARMM force field are also shown.
Refinement of van der Waals parameters
The van der Waals (Lennard-Jones) contribution to the total potential energy is given by the following expression.
| (9) |
The adjustable atomic parameters are the potential well depth, ɛ, and the van der Waals radius, σ. The parameters of the PL, OSL, and O2L atom types were fit to ab initio interaction energies and hydrogen bond distances of DMP with water. The target data was obtained from calculations performed at the MP2/cc-pVTZ level of theory on two configurations of the DMP-water complex, one in which the water forms hydrogen bonds with both double-bonded oxygens (type O2L) of the phosphate and one in which the water hydrogen-bonds with one bridging oxygen (type OSL) and one double-bonded oxygen. In addition, specific nonbonded interaction terms (NBFIX) were added for interactions of OSL and O2L atoms of DMP with the HT atoms of TIP4P water to better reproduce the ab initio energies and geometries. This is in the spirit of the Drude oscillator models for alcohols recently presented by Anisimov et al. (48), whose study revealed the need for special unique interaction parameters between certain atom types to match more closely the relevant experimental data. Together, these separate results seem to suggest that in certain cases, polarizable models may require addition of further specific combinations of interactions, or at least further atom types. Nonbond interaction parameters are determined by iterating through several values of each parameter. The set of values that resulted in the smallest sum of squared errors was taken to be the final result, which was then modified manually to further increase agreement with the target data. Table 4 shows the original and refined van der Waals parameters and Table 5 shows the calculated dimer energies compared to ab initio values.
Table 4.
van der Waals parameters for the original and refined polarizable DMPC models
| Original |
Refined |
|||
|---|---|---|---|---|
|
ɛ |
Rmin |
ɛ |
Rmin |
|
| (kcal/mol) | (Å) | (kcal/mol) | (Å) | |
| PL | −0.5500 | 2.50 | −0.5000 | 2.15 |
| O2L | −0.2500 | 2.00 | −0.0650 | 1.80 |
| OSL | −0.0500 | 2.25 | −0.0500 | 1.80 |
| HT/O2L (NBFIX) | n/a | n/a | −0.2975 | 2.75 |
| HT/OSL (NBFIX) | n/a | n/a | −0.3000 | 2.60 |
Table 5.
Interaction energies for complexes of DMP with water
| Interaction energy (kcal/mol) |
|||
|---|---|---|---|
| Original CHEQ | Refined CHEQ | MP2/cc−pVTZ | |
| Complex 1 | −13.04 | −14.34 | −15.01 |
| Complex 2 | −12.65 | −15.72 | −15.62 |
Energies computed at the MP2/cc-PVTZ level of theory using Gaussian 03 are compared to those calculated using the original and revised CHEQ models in CHARMM. Complex 1 has the water hydrogen-bonded to one bridging oxygen and one double-bonded oxygen of the phosphate, and complex 2 has the water hydrogen bonded to both double-bonded oxygens of the phosphate.
Torsion potential refinement
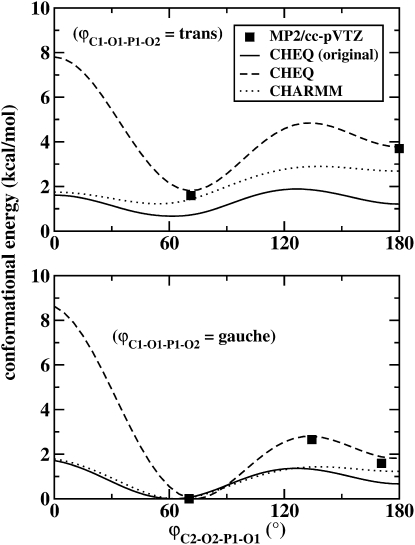
The refinement of the phospholipid headgroup torsional potential involved optimizing torsional parameters of the N-C-C-O, C-C-O-P, and C-O-P-O dihedrals. The C-O-P-O torsion was parameterized against ab initio conformational energies of DMP. DMP has two C-O-P-O torsions that define its conformation; by convention, we refer to the orientation of the two P-O bonds involved in the torsion (ϕ1, ϕ2) as either trans (t), ∼180°, or gauche (g), ∼60°. The global energy minimum occurs at gg, which may not seem reasonable based on steric considerations, but can be explained by the anomeric or gauche effect (79).
In the CHARMM27 force field, the torsional potential energy of a molecule is represented as a sum of contributions from each dihedral angle in the molecule:
| (10) |
The sum is carried out over all parameter sets j and all relevant dihedral angles ϕ for each dihedral type. The parameterization approach used here is described in more detail elsewhere (74,75). A weighed sum of squared energy differences is used as the fitting function:
| (11) |
A given reference point i has a weight W, a reference (in this case ab initio) energy Eref, and the energy, E, calculated using the empirical model being optimized. Only the amplitude parameters, Kj, are optimized; the n and δ values associated with each K were obtained from the revised CHARMM27 force field, C27r (74). Minimizing the fitting function χ with respect to Kj results in a set of equations:
| (12) |
where
| (13) |
Here, K has been factored out, so the problem is reduced to a set of linear equations. In addition, the energy terms, E, have been replaced with ΔE terms taken relative to the global minimum (gg form). The term ΔE0 accounts for the remaining energy terms, excluding the torsional potential being optimized and ϕg is the dihedral angle in the gg form, which must be accounted for, since the reference energies are taken relative to the gg form. To obtain the reference energies for the fit, ab initio optimizations of four conformations of DMP were carried out at the MP2/cc-pVTZ level of theory using the Gaussian 03 software suite (77). The geometries and relative energies of these conformers are summarized in Table 6. The values for ΔE0 were obtained by performing a constrained minimization and energy calculation on each conformer using a modified set of parameters in which the K (amplitude) values for the relevant torsions were set to zero, making the total dihedral potential for that dihedral type zero; the resulting parameters were validated via constrained optimizations starting with the MP2/cc-pVTZ geometries. The relative energies are shown in Table 6, and a torsional profile is shown in Fig. 2. Both illustrate the significantly improved agreement with ab initio conformational energies. Also worth noting is the cis barrier, which appears to be overestimated by the refined force field. We performed constrained geometry optimizations of DMP with one dihedral constrained in the cis conformation, minimizing all other coordinates. These results suggest an energy barrier of 8 kcal/mol for even the lowest-energy cis conformer at the MP2/cc-pVTZ level of theory. Further calculations at the HF/6-31G∗ and MP2/6-31G∗ levels of theory suggest a barrier of 6 kcal/mol. Thus, our refined model is in good agreement with the MP2 energy barrier despite not having been explicitly fit to it.
Table 6.
Comparison of optimized geometries and conformational energies of dimethylphosphate using different calculation methods
| ϕ1 | ϕ2 | ΔEgg (MP2) | ΔEgg (original) | ΔEgg (refined) | |
|---|---|---|---|---|---|
| gg | 70.3° | 70.3° | 0.00 | 0.00 | 0.00 |
| tg | −170.7° | 71.3° | 1.59 | 0.39 | 1.90 |
| tg/gg | 134.4° | 70.7° | 2.65 | 0.92 | 2.74 |
| tt | 180.0° | 180.0° | 3.70 | 0.61 | 3.70 |
Values are given in kcal/mol. Those calculated at the MP2/cc-pVTZ level of theory (MP2) using Gaussian 03 are compared to CHARMM energies using the original and refined polarizable force fields (ϕ1 = C1-O1-P1-O2; ϕ1 = C2-O2-P1-O1).
Figure 2.
Torsional profile of the C-O-P-O dihedral angle of dimethylphosphate computed using the nonpolarizable CHARMM force field and the original and revised charge-equilibration (CHEQ) models. The ab initio energies computed at the MP2/cc-pVTZ level of theory using Gaussian 03 are also shown.
The N-C-C-O and C-C-O-P torsional potentials were fit simultaneously to the torsional energy surface of o-phosphorylcholine, shown in Fig. 1, a compound that has been used previously to model phospholipids (80). The fit was carried out using the CMAP (81,82) function in CHARMM, which allows a reference energy surface of two dihedrals to be reproduced almost exactly. The torsional energy surface generated by the nonpolarizable C27r force field (74) was used as the reference. To generate this surface, the two relevant dihedrals were set to range from −180° to 180° in steps of 10° and energies were calculated relative to (−70°, −60°), a low-energy conformer most likely close to the global minimum. The other dihedrals, analogous to the C-O-P-O torsions in DMP, were constrained in the trans conformation. Since the energies are relative, contributions from the C-O-P-O torsion cancel out, meaning that this fit is independent of the C-O-P-O torsional parameters. Likewise, the C-O-P-O torsional fitting is independent of the N-C-C-O and C-C-O-P torsional fitting, since DMP does not involve the latter two dihedral types.
Results and Discussion
Lipid headgroup surface area
Time profiles of the predicted surface area per headgroup are shown in Fig. 3. Simulations for assessing this system property were performed on smaller systems to minimize computational requirements during the parameterization process. Systems of 24 lipid molecules (12 molecules per leaflet) in a hexagonally periodic simulation box were hydrated with 1079 water molecules (TIP4P-FQ in the polarizable case, and TIP3P for the fixed-charge case). Molecular dynamics simulations under constant pressure (1 atm) and temperature (303 K) conditions maintained using a Nosé-Hoover thermostat and Langevin piston barostat were performed using a Verlet leap-frog integrator; three independent trajectories were generated for sampling for the polarizable CHEQ model. The average headgroup area is predicted to be 55.8 ± 1.1 Å2, lower than the most recent experimental value of 60.5 Å2 and the fixed-charge prediction of 58.3 ± 1.6Å2. We observe, for one of the trajectories, rather large fluctuations of the surface area, an effect of small system size observed in earlier simulations (83). Moreover, consistent with earlier studies comparing the system-size dependence of zero surface tension molecular dynamics simulations of DPPC bilayers (83), we find that the average surface area based on smaller systems is systematically reduced; based on previous studies (83), the increase in surface area per headgroup of DPPC bilayers for increases in system size (number of lipids) of factors of 4 or 20 (from a smallest system of 32 lipids per leaflet) leads to increases in surface area of ∼2–3 Å2. Nevertheless, quite satisfyingly, the final equilibrium values of the surface area converge for all three simulations. For this work, we adopt the approach to implement fixed surface area simulations to study actual problems. Ongoing refinement, as is currently pursued for most major force fields (84) will improve this system property.
Figure 3.
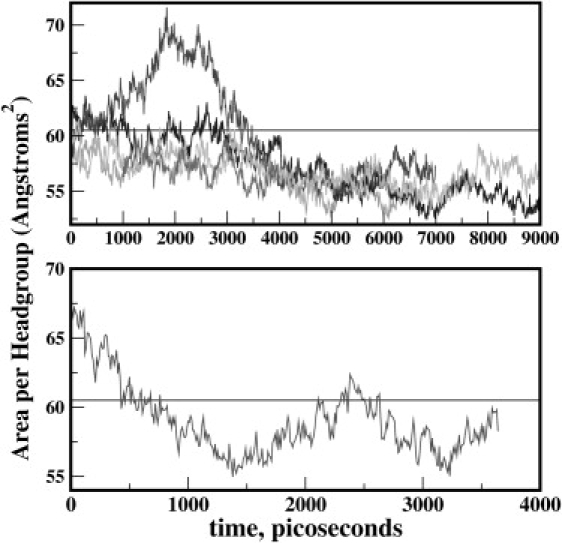
Time profiles of the surface area per lipid headgroup from constant pressure simulations. Horizontal lines represent the experimental value. (Upper) Revised CHEQ model, with several trajectories shown. (Lower) Nonpolarizable CHARMM27 (C27) model.
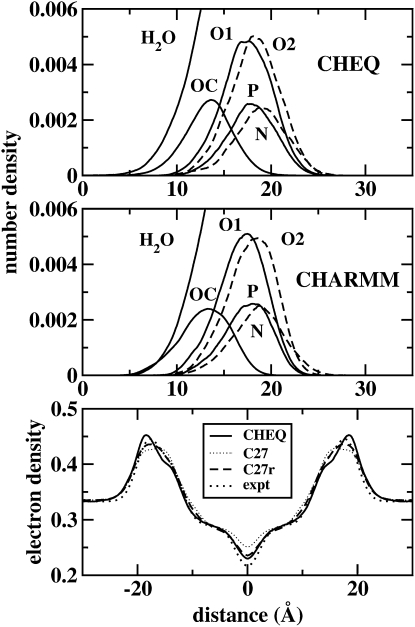
Component atomic and electron density profiles
One measure of the stability of the bilayer is the number density of various atomic species as a function of distance along the bilayer normal. Fig. 4 shows the component density profiles for water and atomic species of the lipid (headgroup phosphorus, oxygens, and nitrogen). These are consistent with previous studies (85–87) as well as the nonpolarizable CHARMM27 model. We note the subtle difference in the extent of water penetration into the membrane interior between the polarizable and nonpolarizable force fields. Polarizability of both solvent and lipid tends to accommodate, in a free-energetic manner, the presence of waters in the low-dielectric environment of the lipid interior. The potential of mean force for the water molecules derived from the computed density profiles shows a “slight” stabilizing effect introduced by the polarizability of the lipid and water as compared to the simulations without polarizability. This behavior has direct bearing on the thermodynamics associated with integral membrane proteins. Specifically, there has been recent effort to understand the free energetics of integral membrane protein structure and stability associated with desolvation of amino acid side chains of varying degrees of hydrophilicity/hydrophobicity and polarity. This attention has arisen based on the observation of lipid-exposed arginine residues in two recent crystal structures of voltage-gated potassium channels. Based on long-timescale molecular dynamics simulations, McCallum et al. demonstrated the role of water defects, which form local “solvation cages” around the lipid-exposed arginine, in determining the relative costs for burying charged residues in lipidic environments. The results presented here, though far from definitive, suggest the role of nonadditive electrostatic effects (polarization) in contributing to the stability of lipid-exposed residues of integral membrane proteins. Continuing work in our laboratory will address the free energetics associated with transfer of polarizable amino acids into such systems, much in the spirit of recent studies (7).
Figure 4.
Densities of various components as a function of distance along the bilayer normal (z axis). O1 and O2 refer to phosphate oxygens, with O1 the bridging oxygens. (Upper) Refined polarizable model. (Middle) Nonpolarizable CHARMM force field. (Lower) Electron density for both polarizable and nonpolarizable models (both C27 and the revised C27r (74)), and for experiment.
The bottom panel of Fig. 4 shows the electron density profile for both polarizable and nonpolarizable models. Both are consistent with previous simulations of DMPC (84) and DPPC (12), as well as with experiment (88). Relative to C27, the C27r nonpolarizable force field (refined based on alkane properties) (74) shows improved performance with respect to predicting electron density profiles. To better compare these simulation results to experiment, the functional form of the experimental data was generated using models determined by Klauda et al. (89). The authors fit electron density profiles to match experimental form factors using the equation
| (14) |
The individual density terms correspond to contributions from the phosphate, methyl, carbonyl/glycerol, methylene, and water/choline, as described in Klauda et al. The first three terms are fit to simple Gaussians of the form
| (15) |
where the parameters C, σ, and z0 represent the integrated size, width, and position, respectively. The second to last term has the form
| (16) |
where erf(z) is the error function. The parameters , DC, , and r represent the methylene electron density, the boundaries of the hydrocarbon interfaces, the width, and the ratio of the methyl volume to the methylene volume, respectively. Finally, the last term in Eq. 14 has the form
| (17) |
where ρw represents the known electron density of pure water, 0.333 e/Å3 (88). The parameters DBC and σBC are fit to reproduce the sum of the water and choline group electron densities as described in Klauda et al. (89). The fitted values for all of these parameters can be found in that work.
The bottom panel of Fig. 4 shows that the polarizable and nonpolarizable C27r models perform equally well in matching the experimental data (88,89). However, the CHARMM nonpolarizable force field for DMPC has been recently refined to better reproduce electron density profiles. Thus, though the results presented here suggest that this polarizable model is equally faithful in terms of representing the electron density along the membrane normal, existing nonpolarizable models continue to be modified to improve such representations. We emphasize that the electron density profile was not used as a fitting criterion for the polarizable force field presented here (nor were the deuterium order parameters discussed below). In this sense, it is quite satisfying that the model is in such good agreement with experiment. The differences in electron density profiles between the two force fields studied here have implications related to water penetration effects/energetics (as well as NMR order parameters, to be discussed further below), to which we now turn.
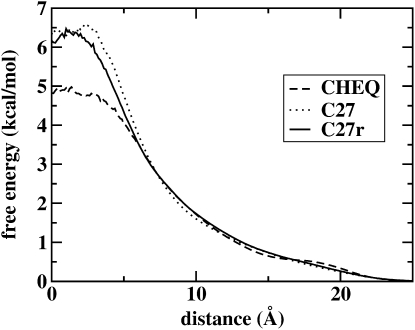
An estimate of the free-energy cost for water transfer across the membrane is obtained through the potential of mean force (PMF). Taking the water density profile in Fig. 4 as an estimate of the probability of finding a water molecule at a given z-coordinate, the PMF relative to bulk solution is determined as
| (18) |
where ρ0 is the bulk density. The calculated PMF profiles for the CHEQ and nonpolarizable CHARMM27 force fields are shown in Fig. 5. Due to mutual polarization induction effects, the polarizable models are more able to accommodate water density in the center of the lipid bilayer. Since the polarizable solvent model exhibits a lower dipole moment in the bilayer center (not identically matching the gas-phase value due to the dielectric effect from membrane polarizability) compared to the nonpolarizable model, the electrostatic free energy cost to desolvate a polarizable solvent molecule appears to be less than the penalty for a molecule with a higher dipole interaction as afforded by fixed-charge force fields (which is attributed to a condensed-phase dipole moment that cannot vary with local environment). This effect is nontrivial and subtle. Moreover, as noted above, the differences in electron density in the bilayer center between the two force fields would also suggest that the reduction in free volume at the center of the bilayer, as predicted by the nonpolarizable model, supporting a slightly higher density (i.e., denser packing) in the bilayer center, would contribute to a higher barrier to water penetration into the bilayer center.
Figure 5.
Potential of mean force for the movement of water across the membrane, calculated from the water density profile for both the revised polarizable model and the nonpolarizable CHARMM model (both C27 and the revised C27r (74)).
For the moment, the estimated potential of mean force shows a free-energy barrier of ∼5 kcal/mol using the polarizable force field; the nonpolarizable force field allows many fewer water molecules into the membrane (within the timescale of the simulations), resulting in a less precise estimate of the free-energy cost (∼6 kcal/mol). It is interesting to note that an early study by Marrink and Berendsen of DPPC at a higher temperature suggests a free-energy barrier on the order of 6 kcal/mol (90). Furthermore, the shape of the water PMF using the nonpolarizable force field demonstrates a qualitatively similar profile, which recent studies (91) have decomposed into a four-region kinetic model. The nonpolarizable PMF exhibits a shallow minimum at the bilayer center, much like the profile computed by Marrink and Berendsen (90). Both nonpolarizable models give rise to similar free-energy profiles in contrast to the polarizable model that exhibits a monotonic profile throughout the bilayer. We conclude by acknowledging that further, more rigorous calculations of free-energy profiles of solutes will be of particular interest, and current work in our laboratory continues to probe such effects.
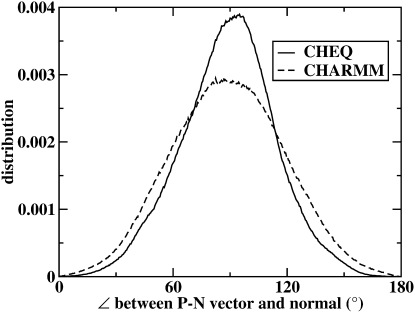
Lipid orientation and dynamics
The orientation of the lipid headgroups in the bilayer can be analyzed by computing the angle between the phosphorus-nitrogen vector () and the bilayer normal (z axis). This distribution is shown in Fig. 6. It is evident that the headgroups prefer an orientation of ∼90° relative to the normal. This is consistent with previous studies of DPPC in which the headgroups favored an orientation of ∼80–90° relative to the normal (85,92), as well as earlier molecular dynamics studies of solvated pure DMPC bilayers using the GROMOS force field (93). Furthermore, these distributions are as broad as those computed using the GAFF (generalized amber force field) and Berger (94,95) force fields in a recent study by Siu et al. (16). Though not discussed in this study, there have been indications recently that the orientation of the PN dipole may be implicated in the hydration of the interfacial region in lipid bilayer systems (16). Finally, we note that the probability distribution obtained from the CHEQ model is narrower than that of the nonpolarizable C27. This seems to suggest a more restricted range of rotation for the phosphate and/or choline groups. In the case of the phosphate group, this effect could be attributed to the higher cis energy mentioned above; with a high barrier to overcome, the range of likely orientations of the phosphate group is more restricted.
Figure 6.
Distribution of the angle between the P-N vector and the bilayer normal (z axis) from simulations using the revised polarizable model and the nonpolarizable CHARMM force field.
The dynamics of the phospholipid tailgroups are probed by the variation of deuterium order parameters with respect to the position along the alkyl chain. The deuterium order parameter, SCD, is obtained by
| (19) |
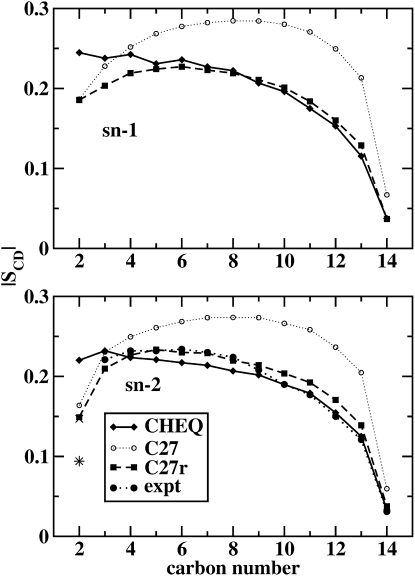
where θ is the angle between a particular CH vector and the bilayer normal, and , the second Legendre polynomial. This is equivalent to the SZZ component of the NMR quadrupolar splitting tensor (16). Fig. 7 shows the magnitude of the calculated order parameters as a function of position along the alkyl chain. Also included for comparison are values from the nonpolarizable C27 force field, the revised C27r force field for alkanes (74), and experimental values for the sn-2 chain (60). Both polarizable and nonpolarizable models reproduce experimental trends (60,96,97), with the revised C27r model performing much better than the original C27 model, as it was refined to improve agreement with alkyl chain relative torsional energetics, which have significant bearing on lipid chain order and dynamics. The polarizable model displays less order in the bilayer center (more closely in agreement with experiment). As discussed earlier, this difference would also contribute to the enhanced water penetration into the bilayer core. We note that the current polarizable model is not able to discern between the two C2 hydrogen atoms that are stereoscopically different (see Table 7). The differences between the 2R and 2S order parameters are indistinguishable compared to experiment, and consistent with previous estimates of this property using force-field-based methods (16). This general behavior is attributable more to a fundamental flaw in a classical representation of the local valence interactions than to electrostatic or polarization effects. It appears to be a general deficiency of classical force fields (16), and further work continues to address this issue.
Figure 7.
Deuterium order parameters for the tail groups as a function of position on the sn-1 (upper) and sn-2 (lower) hydrocarbon chain. Values are shown for the polarizable (CHEQ) and nonpolarizable (C27) models, as well as for the revised CHARMM force field for alkanes (C27r) (74). Experimental data (60) for the asymmetric sn-2 chain (lower) are also shown, with the star and X symbols marking the values for the 2R and 2S hydrogens, respectively.
Table 7.
Deuterium order parameters for the tail groups as a function of position on the hydrocarbon chain
| sn-1 (CHEQ) | sn-1 (CHARMM27) | sn-2 (CHEQ) | sn-2 (CHARMM27) | sn-2 (Experiment) | |
|---|---|---|---|---|---|
| 2R | −0.251 ± 0.024 | −0.193 ± 0.033 | −0.227 ± 0.021 | −0.177 ± 0.032 | 0.094 |
| 2S | −0.237 ± 0.021 | −0.181 ± 0.029 | −0.214 ± 0.026 | −0.150 ± 0.030 | −0.147 |
| 3 | −0.237 ± 0.017 | −0.228 ± 0.021 | −0.232 ± 0.017 | −0.231 ± 0.022 | −0.221 |
| 4 | −0.242 ± 0.017 | −0.252 ± 0.023 | −0.224 ± 0.018 | −0.249 ± 0.021 | −0.232 |
| 5 | −0.231 ± 0.017 | −0.269 ± 0.025 | −0.221 ± 0.018 | −0.261 ± 0.022 | −0.232 |
| 6 | −0.236 ± 0.017 | −0.277 ± 0.027 | −0.217 ± 0.018 | −0.269 ± 0.023 | −0.234 |
| 7 | −0.227 ± 0.018 | −0.282 ± 0.028 | −0.214 ± 0.017 | −0.273 ± 0.025 | −0.230 |
| 8 | −0.222 ± 0.016 | −0.285 ± 0.030 | −0.207 ± 0.019 | −0.274 ± 0.024 | −0.224 |
| 9 | −0.207 ± 0.018 | −0.284 ± 0.030 | −0.202 ± 0.020 | −0.274 ± 0.024 | −0.208 |
| 10 | −0.196 ± 0.020 | −0.280 ± 0.031 | −0.190 ± 0.020 | −0.266 ± 0.026 | −0.190 |
| 11 | −0.175 ± 0.023 | −0.271 ± 0.031 | −0.179 ± 0.020 | −0.258 ± 0.026 | −0.177 |
| 12 | −0.153 ± 0.022 | −0.249 ± 0.033 | −0.155 ± 0.019 | −0.237 ± 0.027 | −0.150 |
| 13 | −0.115 ± 0.020 | −0.213 ± 0.030 | −0.125 ± 0.016 | −0.205 ± 0.025 | −0.121 |
| 14 | −0.037 ± 0.007 | −0.067 ± 0.013 | −0.033 ± 0.007 | −0.060 ± 0.011 | −0.031 |
Stereoscopically different hydrogens on C2 are listed separately. Values are shown for both sn-1 and sn-2 chains and both the refined CHEQ and nonpolarizable CHARMM27 force fields. Experimental data (60) for the sn-2 chain is also shown.
Water-lipid interactions
To investigate the nature of water-lipid interactions we first consider radial distribution functions (RDF), g(r), between relevant water and lipid atom pairs. We compute the RDF for two particular atom types by counting all atom pairs separated by a distance r over all frames in a trajectory. The resulting distribution is normalized by dividing by the number of frames and the average density of the integration shell, leaving a function approaching unity at large separations. In addition, the volume of the integration shell is truncated at the dimensions of the bilayer system, so that the integration volume does not contain empty space. Finally, pairs on opposite sides of the bilayer are excluded to ensure that the peaks represent interacting pairs that are not separated by the lipid bilayer.
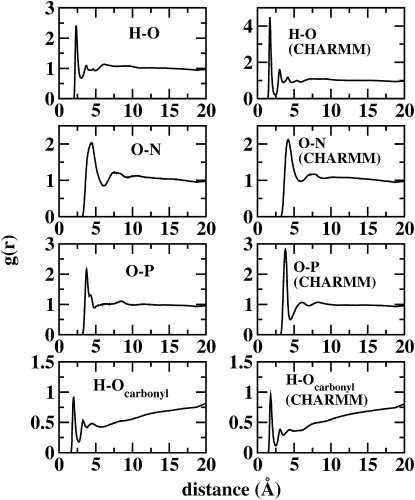
Fig. 8 shows RDFs of water hydrogen to lipid phosphate oxygen, water oxygen to lipid nitrogen, water hydrogen to lipid carbonyl oxygen, and water oxygen to lipid phosphorus. Both polarizable and nonpolarizable models demonstrate a significant interaction. The first peak around 4.5–5 Å in the choline nitrogen to water oxygen RDFs indicates a significant solvation structure surrounding the choline group (as the water oxygen does not directly interact with the nitrogen atom per se). The second peak near 7.5 Å defines a second solvation shell surrounding this group. These results are in striking agreement with the all-atom molecular dynamics calculations of Lopez et al. (86) using the AMBER force field with SPC/E water as solvent. The water oxygen to phosphate atom RDFs indicate differences between the polarizable and nonpolarizable models. The nonpolarizable model shows slightly more structure of water around the phosphate group; this structural feature is similar to that observed by Lopez et al. (86) and is indicative of bridging interactions between waters solvating the headgroup. The polarizable force field RDF exhibits a broader second peak, suggesting a less specific interaction; this is further demonstrated by the water hydrogen to phosphate oxygen atom RDFs in Fig. 8 (upper left). The location of the peaks provides information about the distances between interacting lipids and waters, which is used to examine the difference in polarization between interacting and noninteracting lipids, discussed below.
Figure 8.
Radial distribution functions for water hydrogens with lipid phosphate oxygens, water oxygens with lipid nitrogens, water oxygens with lipid phosphorus atoms, and water hydrogens with carbonyl oxygens. Results from the revised polarizable model and the nonpolarizable CHARMM model are shown.
Electrostatic properties
Charge distributions
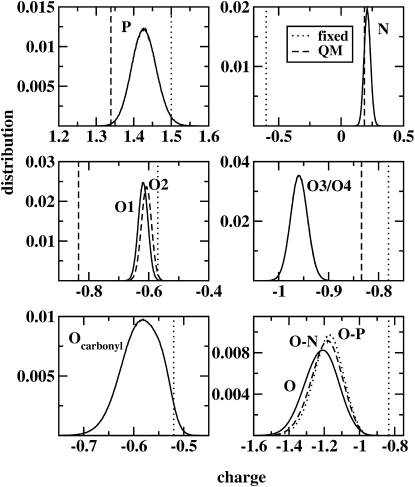
The charge-equilibration models allow molecular charge distributions to fluctuate over time in response to changing chemical environments. It is therefore informative to examine the range of charge values for a particular atom type during the simulation. Fig. 9 shows charge distributions for phosphorus, oxygen, and nitrogen atoms of the lipid headgroups. It is worth noting that the two bridging phosphate oxygens (O1 and O2) are both of type OSL, but have different charge distributions. This is a result of differing chemical environments; fixed-charge representations (as in the CHARMM nonpolarizable case) ascribe equivalent charges to “like” oxygen atoms (in an average sense, based on gas-phase quantum mechanical calculations of single or dimer complexes for instance). To further quantify this effect, the peak values of each distribution were compared to the average gas-phase minimized charges of all lipid molecules in a snapshot. These values were obtained from a single snapshot in the trajectory by deleting all atoms except for one lipid molecule, allowing the charges to equilibrate without minimizing the atomic coordinates, and averaging the charges over all 72 lipid molecules in the snapshot. This procedure was then repeated using a full coordinate minimization. Table 8 shows these charges as well as the peak values of the charge distributions from the trajectories. Comparing these values to the ab initio charges of the model compounds used in the parameterization, it is clear that the polarizable model allows the charges to shift in response to the condensed-phase environment. The magnitude of the shift in charge distributions varies with atomic species but in general is on the order of 0.05e to 0.1e. Furthermore, the lower right panel of Fig. 9 demonstrates the effect of lipid association on water oxygen atoms. Oxygen atoms on water molecules directly associated with the phosphate groups show the largest shift toward higher values relative to the pure water distribution; this is directly related to the polarization effect on the water hydrogen atoms interacting with the phosphate oxygen atoms. In the case of water associating with the choline moiety, there is a lesser effect due to the lower polarizability of this group; nevertheless, there is a shift in oxygen charges due to the larger interaction between the permanent, total choline charge of +1e and the water molecular dipole.
Figure 9.
Charge distributions of headgroup atoms and water oxygens over the trajectory. O1 and O2, refer to the bridging phosphate oxygens; O3 and O4 refer to the equivalent double-bonded phosphate oxygens; O-N refers to water oxygens associated with headgroup nitrogen atoms; and O-P refers to water oxygens associated with headgroup phosphorus atoms. The corresponding charges in the fixed-charge CHARMM force field (dotted lines), as well as the MP2/cc-pVTZ charges for the headgroup atoms included in the parameterization (dashed lines), are also shown.
Table 8.
Comparison of peak values of charge distributions over the simulation trajectory with average gas phase minimized charges of all 72 DMPC molecules
| Peak | Gas phase∗ | Gas phase† | |
|---|---|---|---|
| N | 0.210 | 0.151 | 0.171 |
| P1 | 1.430 | 1.514 | 1.484 |
| O1 | −0.619 | −0.598 | −0.599 |
| O2 | −0.608 | −0.612 | −0.597 |
| O3 | −0.960 | −0.863 | −0.904 |
| O4 | −0.960 | −0.865 | −0.894 |
Molecules without minimization.
Models with minimization.
Dipole moment variation
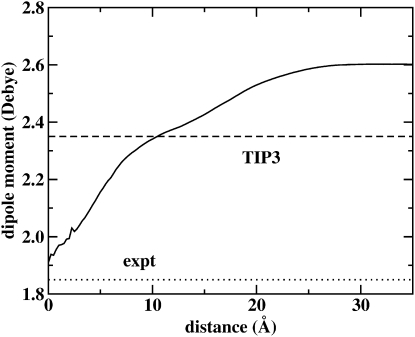
Polarizable force fields allow for a response to local electrostatic environment. As such, one anticipates a variation in the average dipole moment of water molecules when moving along the interface normal from bulk solution to membrane interior. Fig. 10 shows the water molecular dipole moment distributions obtained by averaging the dipole moment of water molecules found in slabs of width 0.25 Å along the interface normal. In bulk solution, the water dipole moment plateaus at a value of 2.60 Debye, 0.8 Debye above the gas-phase value of 1.85 Debye; this is consistent with the bulk TIP4P-FQ dipole moment. The profile exhibits a monotonic decrease to a value of ∼1.9 Debye within the membrane interior. There are two items of note. First, the polarizable water model captures the condensed-phase environment effect on the local water molecular electrostatics via an enhanced dipole moment; we note that there still is no single consensus value of the liquid-phase dipole moment of water, with values ranging from 2.5 to 3.0 Debye (98–102). Second, we observe that the dipole moment does not fall exactly to the gas-phase value at the center of the membrane. Moving toward the interface from the center, the average molecular dipole moment increases monotonically; thus, there is a significant interior region over which the water dipole moment, though not at the gas-phase value, exhibits an enhanced electrostatic moment in the lipidic environment. This suggests a nontrivial dielectric effect exerted by the polarizable membrane, i.e., the membrane possesses a dielectric constant different from unity. This arises from the local lipid-chain polarizability, as well as longer-ranged electric field effects from the polar headgroup region. For the polarizable lipid model presented here, the alkyl segment contributes ∼36.3 Å3 to the overall DMPC molecular polarizability. This is based on the polarizability of tetradecane calculated using two charge constraint units consisting of seven carbons each (75). Applying the Clausius-Mosotti relation, an estimate of the infinite frequency contribution to the “isotropic” dielectric in the membrane is found to be 1.004, giving a total interior dielectric constant of ∼2, consistent with calculations of the dielectric permittivity profile discussed below. This demonstrates that lipid polarization effects can modulate water electrostatics in the lipid interior more than fixed-charge force fields would allow. We note the significant differences in the behavior of the properties of individual water molecules and stress that these differences will ultimately lead to differences in the properties observed using fixed-charge force fields and next-generation polarizable models, as we have shown here. Finally, it is important to keep in mind that the water dipole moment, moving away from the center of the bilayer, begins to interact with the stronger electrostatic fields generated by the phosphate, ester, and ammonium moieties.
Figure 10.
Profile of the average molecular dipole moment of water from the center of the bilayer to the bulk solution as a function of distance along the bilayer normal (z axis). The dashed line represents the static dipole moment of nonpolarizable TIP3 water (2.35 Debye) and the dotted line the experimental dipole moment of water in the gas phase (1.85 Debye).
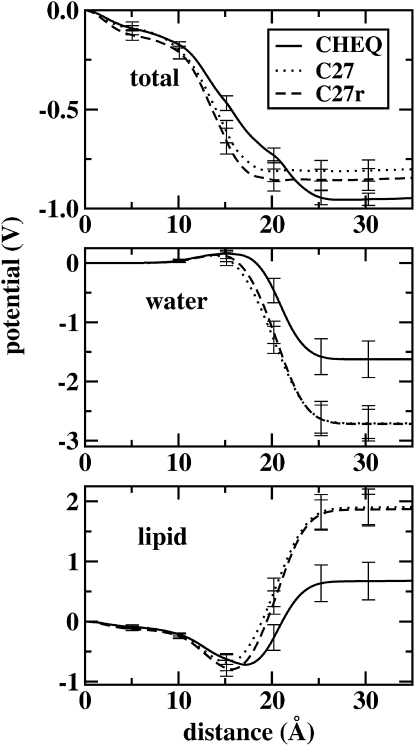
Interfacial potential
The membrane dipole potential remains an elusive physical quantity to reproduce based on atomistic simulations. In part, the difficulty is based on the still rather ambiguous definitions of the interfacial potential as it is experimentally measured; this is a particularly sinister effect for assessing the accuracy of predicted liquid water contributions to the neat water and lipid system interfacial regions. For phosphatidylcholine-based lipid bilayers, such as DMPC, experimental values range from 220 to 280 mV; these are determined indirectly using ion permeability measurements (103–105), the lipid monolayer method (2), and voltage-sensitive dyes (2). More recently, novel cryo-EM approaches have been used to estimate membrane electrostatics with electrons as probes (2), measuring values on the order of 510 mV (0.51V) for ester-DPhPc (diphytanoylphosphatidylcholine) systems and 260 mV for ether-DPhPc systems.
The surface potential is calculated from simulations by twice integrating the charge density as a function of distance from the center of the bilayer:
| (20) |
where z = 0 is at the center of the bilayer, ɛ0 is the permittivity of vacuum, and ρ(z) is the charge density obtained by dividing the system into slabs along the bilayer normal (z axis) and summing the charges in each slab. Individual molecular species charge densities are twice integrated to obtain component electrostatic potential contributions. Fig. 11 shows the total and component contributions to the interfacial potential for both polarizable and nonpolarizable models. There is a slightly deeper potential drop for the polarizable model, on the order of 0.1 V, with both models overestimating the magnitude of the experimental range of values, 220–500 mV (2). We note here that the difference is within the range of fluctuations observed based on all-atom simulations using a variety of force fields.
Figure 11.
Profiles of the electrostatic potential from the center of the bilayer to the bulk solution as a function of distance along the bilayer normal (z axis). The total electrostatic potential (upper) and the contributions from the water (middle) and lipid components (lower) are shown, with results from the refined polarizable model (solid line) and the nonpolarizable CHARMM force field (both C27 (dotted line) and the revised C27r (74) (dashed line)).
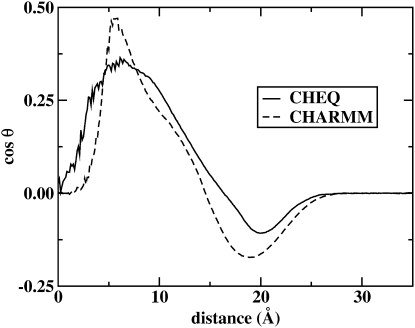
Regarding the contributions from lipid and water, Fig. 11 shows that the polarizable models predict lower individual absolute potential changes across the interface (though the directions must be the same). However, the total potential drops are rather similar for both models, differing by only 0.1 V. A major difference between the two profiles is the rate of change of the potential across the interfacial region. The polarizable force field generates a broader potential profile (on the order of 7 Å broader). This is due to the more orientationally structured water generated by the nonpolarizable model; this is captured by the angle between the bilayer normal (z axis) and the water molecular dipole moment vector as shown in the upper panel of Fig. 12. Since the dipole potential is a direct measure of the orientation of dipoles, Fig. 12 indicates a rather precipitous change in water molecule orientation that begins ∼5 Å from the bilayer center (for the nonpolarizable force field) and reaches a minimum 19 Å away. In contrast, the polarizable solvent model shows a less severe variation of water orientation from bilayer center to bulk, though both models predict a transition from parallel to antiparallel alignment of the water dipole along the bilayer normal. Finally, Fig. 12 again illustrates the subtle differences in the nature of water penetration into the bilayer center predicted by the two force fields.
Figure 12.
Profile of cos θ, where θ is the angle between the water molecular dipole moment vector and the bilayer normal, as a function of distance along the bilayer normal for both polarizable and nonpolarizable models.
Finally, we note that the undulations in the total electrostatic potential profile within the midbilayer region arise from the fluctuations in the lipid contribution. For the polarizable and nonpolarizable force fields, there is a maximum at the center of the bilayer resulting from the nonzero charge density. This is in contrast to united-atom models, which, due to the null charge attributed to midbilayer segments, exhibit a minimum in the electrostatic potential profile.
Dielectric permittivity profiles
Electrostatic properties at the solution-water interface play an integral role in mediating transfer processes, interfacial binding and catalysis, and association of small molecules at the solution-bilayer interface. One can ask about the nature of the variation in dielectric constant across this interface; we next consider the application of the approach developed by Stern and Feller (3) for computing the longitudinal profile of the parallel component of the z-dependent dielectric permittivity. We acknowledge a recent approach developed by Nymeyer et al. (106), but consider the former approach for the present. A comparison of the two methods is beyond the scope of this work.
We compute profiles of the parallel (in-plane) component of the dielectric permittivity using Eqs. 71 and 26 of Stern and Feller (3) for tin-foil boundary conditions:
| (21) |
| (22) |
P‖(z) is the local polarization density and M‖ is the total system dipole moment. In their formulation, Stern and Feller decompose the total fluctuation into contributions from fixed charges and/or dipole and explicit polarization (point-dipole polarizabilities); however, in the approach presented here, the polarization component is self-consistently included in the first term of Eq. 22. We briefly expand on this in the discussion below. The polarization density is computed using a bond-charge approach similar to that outlined in Stern and Feller (3). Briefly, the charge on a particular atom, i, is determined from a set of bond-charge increments (bcis), bjk. The bcis are defined so that each atom (j or k) associated with a particular bci, bjk, receives an amount of charge ±bjk. The total charge on an atom is then a sum over all the contributions from the bond charge increments to which the atom belongs, as represented by the mapping
| (23) |
with
| (24) |
Given a set of charges, we obtain the bond charge increments, bjk, by inverting the C matrix via singular value decomposition (3), or for well conditioned matrices via straightforward inversion. The inverse is computed once for a given molecule (using the minimal topology-based description of bond charge increments) and reused for analysis of trajectory snapshots.
The polarization density, P‖(z) is computed as a sum of the local bond charge dipole moments in a bin of width dz at a position z. As in Stern and Feller, we use
| (25) |
The bond dipole is determined simply as
| (26) |
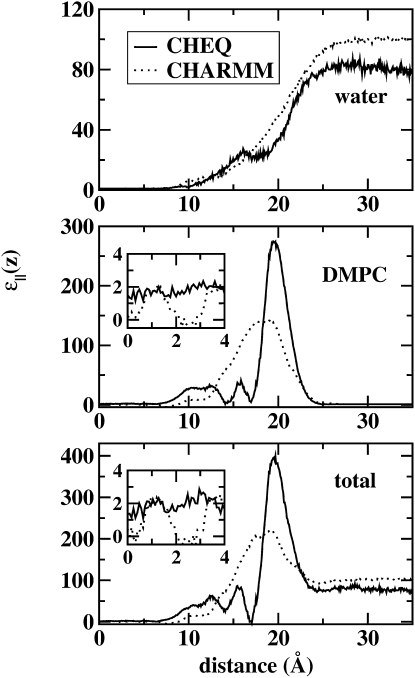
Fig. 13 shows the z-dependent parallel component of the dielectric constant for the polarizable and nonpolarizable models. The bulk water values reflect the properties of the pure solvent models, with the polarizable TIP4P-FQ possessing a value much closer to experiment (80 versus 97 for TIP3P). Within the bilayer interior, both models approach a value of 1 (the polarizable model slightly higher due to contributions from polarization), which is the expected value for alkyl-type species via the Kirkwood-Frölich formalism. Furthermore, we have neglected to include the infinite-frequency dielectric for the polarizable model, though the contributions from this are on the order of 2 for the membrane interior, and 1.6–1.9 for more polar regions (headgroups and bulk solvent). Results are presented as averages of two or three individual trajectories, each of length 10–12 ns. It has been shown previously (3) that for this approach, 10 ns is sufficient to achieve convergence, though more sampling is certain to improve the prediction of fluctuation properties.
Figure 13.
Profile of the water, lipid, and total contributions to the parallel component of the dielectric permittivity as a function of distance along the bilayer normal. Results from both polarizable (solid line) and nonpolarizable models (dotted line) are shown.
The DMPC headgroup regions display relatively larger dielectric constants; this has been attributed to the large magnitude of the headgroup dipoles, which experimentally are in the range of 19–25 Debye (in-plane component) (3). The qualitative behavior has been observed previously via molecular dynamics simulations of DPPC (3)and POPC (106). The polarizable force field predicts a larger interfacial dielectric arising from the additional fluctuations in the induced dipoles (toward the water phase of the interfacial region). The water dielectric for the polarizable model displays a monotonic decay from a bulk value of 79 to ∼1 in the membrane interior (again, these limiting values neglect minor contributions from the infinite-frequency dielectric). The nonpolarizable TIP3P model similarly displays a monotonic decay, but its bulk value is slightly higher (97); this is a well-accepted property of the TIP3P model (107). The polarizable model exhibits more fluctuations in the dielectric permittivity in the polar regions of the lipid; we attribute this to stronger correlations between static and induced dipoles that are not present in the nonpolarizble case.
Conclusions
We have presented an initial study on the applicability and properties predicted by the use of nonadditive electrostatic models for solvated lipid membrane systems in all-atom molecular dynamics simulations. We have demonstrated that incorporation of explicit electronic polarization effects through the charge-equilibration formalism is a viable means of allowing for induction effects in such systems. The lack of polarization in current state-of-the-art force fields has been implicated as a possibly nontrivial deficiency in such treatments of bilayer systems.
For the solvated DMPC bilayer system, the polarizable force field is able to reasonably reproduce standard benchmark properties of such model systems, including surface area/headgroup, NMR deuterium order parameter profiles along the lipid tails, component number and electron density profiles, and electrostatic properties. Density profiles show that in comparison to the CHARMM27 and C27r nonpolarizable force fields, the combination of the TIP4P-FQ polarizable water model and equilibration force field allows for greater water probability in the bilayer center. This is consistent with the attenuation of water molecular dipole moment moving toward the bilayer center. Unlike fixed-charge water models, since the electrostatic component of the water-lipid interaction diminishes with a smaller water dipole moment (approaching, but not reaching, the gas-phase value), there is reduction in the free-energy penalty for “desolvating” a water molecule relative to a fixed-charge (dipole moment) water model. An estimate of the free-energy profile along the bilayer normal suggests a barrier to water penetration of ∼5 kcal/mol, slightly lower than the 6-kcal/mol barrier predicted using fixed-charge models. This is a significant effect, having implications for recent questions regarding the role of water in mediating the desolvation of charged and polar amino acid residues comprising integral membrane proteins. We acknowledge that further work in this area is needed, and ongoing work in our laboratory is focusing on probing the free energetics of transfer processes using such models.
Finally, both polarizable and nonpolarizable models predict surface dipole potentials on the order of 0.8–0.95 V, overestimating a range of experimental values, even with vastly different charge distributions for the constituent species. The use of all-atom force fields for predicting this property still remains an outstanding question, from both the theoretical/simulation and experimental perspectives.
Acknowledgments
The authors thank Dr. G. Lee Warren for helpful discussions and comments.
The authors gratefully acknowledge support from the Center of Biomedical Research, sponsored by the National Institutes of Health, grants P20-RR017716 (Department of Chemistry and Biochemistry) and P20-RR015588 (Department of Chemical Engineering) at the University of Delaware.
References
- 1.Roux B., Allen T.W., Berneche S., Im S.W. Theoretical and computational models of ion channels. Q. Rev. Biophys. 2004;37:15–103. doi: 10.1017/s0033583504003968. [DOI] [PubMed] [Google Scholar]
- 2.Wang L., Bose P.S., Sigworth F.J. Using cryo-EM to measure the dipole potential of a lipid membrane. Proc. Natl. Acad. Sci. USA. 2006;103:18528–18533. doi: 10.1073/pnas.0608714103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Stern H., Feller S.E. Calculation of the dielectric permitivity profile for a nonuniform system: application to a lipid bilayer simulation. J. Chem. Phys. 2003;118:3401–3412. [Google Scholar]
- 4.Allen T.W., Bastug T., Kuyucak S., Chung S.H. Gramicidin A channel as a test ground for molecular dynamics force fields. Biophys. J. 2003;84:2159–2168. doi: 10.1016/S0006-3495(03)75022-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Berneche S., Roux B. The ionization state and the conformation of Glu-71 in the KcsA K+ channel. Biophys. J. 2002;82:772–780. doi: 10.1016/S0006-3495(02)75439-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Allen T.W., Andersen O.S., Roux B. Energetics of ion conduction through the gramicidin channel. Proc. Natl. Acad. Sci. USA. 2004;101:117–122. doi: 10.1073/pnas.2635314100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.MacCallum J.L., Bennett W.F.D., Tieleman D.P. Distribution of amino acids in lipid bilayer from computer simulations. Biophys. J. 2008;94:3393–3404. doi: 10.1529/biophysj.107.112805. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Dorairaj S., Allen T.W. On the thermodynamic stability of a charged arginine sidechain in a transmembrane helix. Proc. Natl. Acad. Sci. USA. 2007;104:4943–4948. doi: 10.1073/pnas.0610470104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Aliste M.P., Tieleman D.P. Computer simulation of partitioning of ten pentapeptides Ace-WLXLL at the cyclohexane/water and phospholipid/water interfaces. BMC Biochem. 2005;6:30. doi: 10.1186/1471-2091-6-30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Tieleman D.P., MacCallum J.L., Ash W.L., Kandt C., Xu Z. Membane protein simulations with a united atom lipid and all atom protein model: side chain transfer free energies and model proteins. J. Phys. Condens. Matter. 2006;18:S1221–S1234. doi: 10.1088/0953-8984/18/28/S07. [DOI] [PubMed] [Google Scholar]
- 11.Xu Z., Luo H.H., Tieleman D.P. Modifying the OPLS-AA force field to improve hydration free energies for several amino acid side chains using new atomic charge and an off-plane charge model for aromatic residues. J. Comput. Chem. 2007;28:689–697. doi: 10.1002/jcc.20560. [DOI] [PubMed] [Google Scholar]
- 12.Feller S.E. Molecular dynamics simulations of lipid bilayers. Curr. Opin. Colloid Interface Sci. 2000;5:217–223. [Google Scholar]
- 13.MacCallum J.L., Tieleman D.P. Computer Simulation of the distribution of hexane in a lipid bilayer: spatially resolved free energy, entropy, and enthalpy profiles. J. Am. Chem. Soc. 2006;128:125–130. doi: 10.1021/ja0535099. [DOI] [PubMed] [Google Scholar]
- 14.Pandit S.A., Bostick D., Berkowitz M.L. Complexation of phosphatidylcholine lipids with cholesterol. Biophys. J. 2004;86:1345–1356. doi: 10.1016/S0006-3495(04)74206-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Berkowitz M.L., Bostick D.L., Pandit S.A. Aqueous solutions next to phospholipid membrane surfaces: insights from simulations. Chem. Rev. 2006;106:1527–1539. doi: 10.1021/cr0403638. [DOI] [PubMed] [Google Scholar]
- 16.Siu S.W.I., Vacha R., Jungwirth P., Bockmann R.A. Molecular simulations of membranes: physical properties from different force fields. J. Chem. Phys. 2008;128:125103. doi: 10.1063/1.2897760. [DOI] [PubMed] [Google Scholar]
- 17.Holcomb C.D., Clancy P., Thompson S.M., Zollweg J.A. A critical study of simulations of the Lennard-Jones liquid-vapor interface. Fluid Phase Equil. 1992;75:185–196. [Google Scholar]
- 18.Schuler L.D., Daura X., van Gunsteren W.F. An improved GROMOS96 force field for aliphatic hydrocarbons in the condensed phase. J. Comput. Chem. 1996;22:1205–1218. [Google Scholar]
- 19.Marrink S.J., de Vries A.H., Mark A.E. Coarse grained model for semiquantitative lipid simulations. J. Phys. Chem. B. 2004;108:750–760. [Google Scholar]
- 20.Marrink S.J., Risselada H.J., Yefimov S., Tieleman D.P., Vries de A.H. The MARTINI forcefield: coarse grained model for biomolecular simulations. J. Phys. Chem. B. 2007;111:7812–7824. doi: 10.1021/jp071097f. [DOI] [PubMed] [Google Scholar]
- 21.Monticelli L., Kandasamy S.K., Periole X., Larson R.G., Tieleman D.P. The MARTINI coarse grained force field: extension to proteins. J. Chem. Theory Comput. 2008;4:819–834. doi: 10.1021/ct700324x. [DOI] [PubMed] [Google Scholar]
- 22.Srinivas G., Klein M.L. Molecular dynamics simulations of self-assembly and nanotube formation by amphiphilic molecules in aqueous solution: a coarse-grain approach. Nanotechnology. 2007;18:205703. [Google Scholar]
- 23.Ensing B., Nielsen S.O., Moore P.B., Klein M.L., Parrinello M. Energy conservation in adaptive hybrid atomistic/coarse-grain molecular dynamics. J. Chem. Theory Comput. 2007;3:1100–1105. doi: 10.1021/ct600323n. [DOI] [PubMed] [Google Scholar]
- 24.Lopez C.F., Nielsen S.O., Srinivas G., DeGrado W.F., Klein M.L. Probing membrane insertion activity of antimocrobial polymers via coarse-grain molecular dynamics. J. Chem. Theory Comput. 2006;2:649–655. doi: 10.1021/ct050298p. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Im W., Feig M., Brooks C.L. An implicit embrane generalized born theory for the study of structure, stability, and interactinos of membrane proteins. Biophys. J. 2003;85:2900–2918. doi: 10.1016/S0006-3495(03)74712-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Tanizaki S., Feig M. Molecular dynamics simulations of large integral membrane proteins with an implicit membrane model. J. Phys. Chem. B. 2006;110:548–556. doi: 10.1021/jp054694f. [DOI] [PubMed] [Google Scholar]
- 27.Tanizaki S., Feig M. A generalized Born formalism for heterogeneous dielectric environments: application to the implicit modeling of biological membranes. J. Chem. Phys. 2005;122:124706. doi: 10.1063/1.1865992. [DOI] [PubMed] [Google Scholar]
- 28.Lazaridis T. Effective energy function for proteins in lipid membranes. Proteins. 2003;52:176–192. doi: 10.1002/prot.10410. [DOI] [PubMed] [Google Scholar]
- 29.Bucher D., Raugei S., Guidoni L., Dal Peraro M., Rothlisberger U. Polarization effects and charge transfer in the KcsA potassium channel. Biophys. Chem. 2006;124:292–301. doi: 10.1016/j.bpc.2006.04.008. [DOI] [PubMed] [Google Scholar]
- 30.Halgren T.A., Damm W. Polarizable force fields. Curr. Opin. Struct. Biol. 2001;11:236–242. doi: 10.1016/s0959-440x(00)00196-2. [DOI] [PubMed] [Google Scholar]
- 31.Patel S., Brooks C.L. Fluctuating charge force fields: recent developments and applications from small molecules to macromolecular biological systems. Mol. Simul. 2006;32:231–249. [Google Scholar]
- 32.Koch D.M., Peslherbe G.H. Importance of polarization in quantum mechanics/molecular mechanics descriptions of electronic excited states: NaI(H2O)n photodissociation dynamics as a case study. J. Phys. Chem. B. 2008;112:636–649. doi: 10.1021/jp709656z. [DOI] [PubMed] [Google Scholar]
- 33.Dang L.X., Chang T.-M. Many-body interactions in liquid methanol and its liquid/vapor interface: a molecular dynamics study. J. Chem. Phys. 2003;119:9851–9857. [Google Scholar]
- 34.Ren P., Ponder J.W. Consistent treatment of inter- and intramolecular polarization in molecular mechanics calculations. J. Comput. Chem. 2002;23:1497–1506. doi: 10.1002/jcc.10127. [DOI] [PubMed] [Google Scholar]
- 35.Rick S.W., Berne B.J. Dynamical fluctuating charge force fields: the aqueous solvation of amides. J. Am. Chem. Soc. 1996;118:672–679. [Google Scholar]
- 36.Rick S.W., Stuart S.J., Berne B.J. Dynamical fluctuating charge force fields: application to liquid water. J. Chem. Phys. 1994;101:6141–6156. [Google Scholar]
- 37.Anisimov V.M., Lamoureux G., Vorobyov I.V., Huang N., Roux B. Determination of electrostatic parameters for a polarizable force field based on the classical Drude oscillator. J. Chem. Theory Comput. 2005;1:153–168. doi: 10.1021/ct049930p. [DOI] [PubMed] [Google Scholar]
- 38.Vorobyov I.V., Anisimov V.M., MacKerell A.D. Polarizable empirical force field for alkanes based on the classical Drude oscillator model. J. Phys. Chem. B. 2005;109:18988–18999. doi: 10.1021/jp053182y. [DOI] [PubMed] [Google Scholar]
- 39.Patel S., Brooks C.L. Revisiting the hexane-water interface via molecular dynamics simulations using non-additive alkane-water potentials. J. Chem. Phys. 2006;124:204706. doi: 10.1063/1.2198538. [DOI] [PubMed] [Google Scholar]
- 40.Banks J.L., Kaminski G.A., Zhou R., Mainz D.T., Berne B.J. Parametrizing a polarizable force field from ab initio data. I. The fluctuating point charge model. J. Chem. Phys. 1999;110:741–754. [Google Scholar]
- 41.Stern H.A., Kaminski G.A., Banks J.L., Zhou R.H., Berne B.J. Fluctuating charge, polarizable dipole, and combined models: parameterization from ab initio quantum chemistry. J. Phys. Chem. B. 1999;103:4730–4737. [Google Scholar]
- 42.Kaminski G.A., Stern H.A., Berne B.J., Friesner R.A. Development of an accurate and robust polarizable molecular mechanics force field from ab initio quantum chemistry. J. Phys. Chem. A. 2004;108:621–627. [Google Scholar]
- 43.Gresh N., Garmer D.R. Comparative binding energetics of Mg2+, Ca2+, Zn2+, and Cd2+ to biologically relevant ligands: combined ab initio SCF supermolecule and molecular mechanics investigation. J. Comput. Chem. 1996;17:1481–1495. [Google Scholar]
- 44.Caldwell J.W., Kollman P.A. Structure and properties of neat liquids using nonadditive molecular dynamics: water, methanol, and N-methylacetamide. J. Phys. Chem. 1995;99:6208–6219. [Google Scholar]
- 45.Ren P., Ponder J.W. Polarizable atomic multipole water model for molecular mechanics simulation. J. Phys. Chem. B. 2003;107:5933–5947. [Google Scholar]
- 46.Jiao D., Golubkov P.A., Darden T.A., Ren P. Calculation of protein-ligand binding free energy by using a polarizable potential. Proc. Natl. Acad. Sci. USA. 2008;105:6290–6295. doi: 10.1073/pnas.0711686105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Lamoureux G., Roux B. Absolute hydrogen free energy scale for alkali and halide ions established from simulations with a polarizable force field. J. Phys. Chem. B. 2006;110:3308–3322. doi: 10.1021/jp056043p. [DOI] [PubMed] [Google Scholar]
- 48.Vorobyov I.V., Anisimov V.M., Greene S., Venable R.M., Moser A. Additive and classical drude polarizable force fields for linear and cyclic ethers. J. Chem. Theory Comput. 2007;3:1120–1133. doi: 10.1021/ct600350s. [DOI] [PubMed] [Google Scholar]
- 49.Mortier W.J., Genechten K.V., Gasteiger J. Electronegativity equalization. Application and Parametrization. J. Am. Chem. Soc. 1985;107:829–835. [Google Scholar]
- 50.Mortier W.J., Ghosh S.K., Shankar S. Electronegativity equalization method for the calculation of atomic charges in molecules. J. Am. Chem. Soc. 1986;108:4315–4320. [Google Scholar]
- 51.Nalewajski R.F., Korchowiec J., Zhou Z. Molecular hardness and softness parameters and their use in chemistry. Int. J. Quantum Chem. 1988;22:349–366. [Google Scholar]
- 52.Patel S., Brooks C.L. CHARMM fluctuating charge force field for proteins: I. Parameterization and application to bulk organic liquid simulations. J. Comput. Chem. 2004;25:1–15. doi: 10.1002/jcc.10355. [DOI] [PubMed] [Google Scholar]
- 53.Rappe A.K., Goddard W.A. Charge equilibration for molecular dynamics simulations. J. Phys. Chem. 1991;95:3358–3363. [Google Scholar]
- 54.Rick S.W. Simulations of ice and liquid water over a range of temperatures using the fluctuating charge model. J. Chem. Phys. 2001;114:2276–2283. [Google Scholar]
- 55.Brooks B.R., Bruccoleri R.E., Olafson B.D., States D.J., Swaminathan S. CHARMM: a program for macromolecular energy, minimization, and dynamics calculations. J. Comput. Chem. 1983;4:187–217. [Google Scholar]
- 56.Parr R.G., Yang W. Oxford University Press; Oxford, United Kingdom: 1989. Density-Functional Theory of Atoms and Molecules. [Google Scholar]
- 57.Sanderson R.T. 2nd ed. Academic Press; New York: 1976. Chemical Bonds and Bond Energy. [Google Scholar]
- 58.Sanderson R.T. An interpretation of bond lengths and a classification of bonds. Science. 1951;114:670–672. doi: 10.1126/science.114.2973.670. [DOI] [PubMed] [Google Scholar]
- 59.Rick S.W., Stuart S.J. Potentials and algorithms for incorporating polarizability in computer simulations. In: Lipkowitz K.B., Boyd D.B., editors. Reviews in Computational Chemistry. John Wiley and Sons; New York: 2002. p. 89. [Google Scholar]
- 60.Douliez J.-P., Leonard A., Duforc E.J. Restatement of order parameters in biomembranes: calculation of C–C bond order parameters from C-D quadrupolar splitting. Biophys. J. 1995;68:1727–1739. doi: 10.1016/S0006-3495(95)80350-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Chelli R., Procacci P. A transferable polarizable electrostatic force field for molecular mechanics based on the chemical potential equalization principle. J. Chem. Phys. 2002;117:9175–9189. [Google Scholar]
- 62.Warren G.L., Davis J.E., Patel S. Origin and control of super-linear polarizability scaling in chemical potential equalizatioin methods. J. Chem. Phys. 2007;128:144110. doi: 10.1063/1.2872603. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Jiao D., King C., Grossfield A., Darden T.A., Ren P. Simulation of Mg2+ and Ca2+ using polarizable atomic multipole model. J. Phys. Chem. B. 2006;110:18553–18559. doi: 10.1021/jp062230r. [DOI] [PubMed] [Google Scholar]
- 64.Rasmussen T.D., Ren P., Ponder J.W., Jensen F. Force field modeling of conformational energies. The importance of multipole moments and intramolecular polarization. Int. J. Quantum Chem. 2006;107:1390–1395. [Google Scholar]
- 65.Schnieders M.J., Baker N.A., Ren P., Ponder J.W. Polarizable atomic multipole solutes in a Poisson-Boltzmann continuum. J. Chem. Phys. 2007;126:124114–124134. doi: 10.1063/1.2714528. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Harder E., Anisimov V.M., Vorobyov I.V., Lopes P.E.M., Noskov S.Y. Atomic level anisotropy in the electrostatic modeling of lone pairs for a polarizable force field based on the classical Drude oscillator. J. Chem. Theory Comput. 2006;2:1587–1597. doi: 10.1021/ct600180x. [DOI] [PubMed] [Google Scholar]
- 67.Lopes P.E.M., Lamoureux G., Roux B., MacKerell A.D. Polarizable empirical force field for aromatic compounds based on the classical Drude oscillator. J. Phys. Chem. B. 2007;111:2873–2885. doi: 10.1021/jp0663614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Car R., Parrinello M. Unified approach for molecular dynamics and density-functional theory. Phys. Rev. Lett. 1985;55:2471–2474. doi: 10.1103/PhysRevLett.55.2471. [DOI] [PubMed] [Google Scholar]
- 69.Jorgensen W.L., Chandrasekhar J., Madura J.D., Impey R.W., Klein M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983;79:926–935. [Google Scholar]
- 70.Allen M.P., Tildesley D.J. Clarendon Press; Oxford, United Kingdom: 1987. Computer Simulation of Liquids. [Google Scholar]
- 71.Nose S. A molecular dynamics method for simulations in the canonical ensemble. Mol. Phys. 1984;52:255–268. [Google Scholar]
- 72.Darden T., York D., Pederson L. Particle mesh Ewald: an N log(N) method for Ewald sums in large systems. J. Chem. Phys. 1993;98:10089–10092. [Google Scholar]
- 73.Essman U., Perera L., Berkowitz M.L., Darden T., Lee H. A smooth particle mesh Ewald method. J. Chem. Phys. 1995;103:8577–8593. [Google Scholar]
- 74.Klauda J.B., Brooks B.R., MacKerell A.D., Venable R.M., Pastor R.W. An ab initio study of the torsional surface of alkanes and its effect on molecular simulations of alkanes and a DPPC bilayer. J. Phys. Chem. B. 2005;109:5300–5311. doi: 10.1021/jp0468096. [DOI] [PubMed] [Google Scholar]
- 75.Davis J.E., Warren G.L., Patel S. A revised charge equilibration potential for liquid alkanes. J. Phys. Chem. B. 2008;118:8298–8310. doi: 10.1021/jp8003129. [DOI] [PubMed] [Google Scholar]
- 76.Chelli R., Procacci P., Righini R., Califano S. Electrical response in chemical potential equalization schemes. J. Chem. Phys. 1999;111:8569–8575. [Google Scholar]
- 77.Frisch M.J., Trucks G.W., Schlegel H.B., Scuseria G.E., Robb M.A. Gaussian; Wallingford, CT: 2004. Gaussian 03. [Google Scholar]
- 78.Breneman C.M., Wiberg K.B. Determining atom-centered monopoles from molecular electrostatic potentials. The need for high sampling density in formamide conformational analysis. J. Comput. Chem. 1990;11:361–373. [Google Scholar]
- 79.Newton M.D. A model conformational study of nucleic acid phosphate ester bonds: the torsional potential of dimethyl phosphate monoanion. J. Am. Chem. Soc. 1973;95:256–258. doi: 10.1021/ja00782a055. [DOI] [PubMed] [Google Scholar]
- 80.Woolf T.B., Roux B. Conformational flexibility of o-phosphorylcholine and o-phosphorylethanolamine: a molecular dynamics study of solvation effects. J. Am. Chem. Soc. 1994;116:5916–5926. [Google Scholar]
- 81.MacKerell A.D., Feig M., Brooks C.L. Extending the treatment of backbone energetics in protein force fields: limitations of gas-phase quantum mechanics in reproducing protein conformational distributions in molecular dynamics simulations. J. Comput. Chem. 2004;25:1400–1415. doi: 10.1002/jcc.20065. [DOI] [PubMed] [Google Scholar]
- 82.Feig M., Alexander J., MacKerell D., Brooks C.L. Force field influence on the observation of π-helical protein structures in molecular dynamics simulations. J. Phys. Chem. B. 2003;107:2831–2836. [Google Scholar]
- 83.Lindahl E., Edholm O. Mesocopic undulations and thickness fluctuations in lipid bilayers from molecular dynamics simulations. Biophys. J. 2000;79:426–433. doi: 10.1016/S0006-3495(00)76304-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Hogberg C.-J., Nikitin A.M., Lyubartsev A.P. Modification of the CHARMM force field for DMPC lipid bilayer. J. Comput. Chem. 2008;29:2359–2369. doi: 10.1002/jcc.20974. [DOI] [PubMed] [Google Scholar]
- 85.Pandit S.A., Bostick D., Berkowitz M.L. Molecular dynamics simulation of a dipalmitoylphosphatidylcholine bilayer with NaCl. Biophys. J. 2003;84:3743–3750. doi: 10.1016/S0006-3495(03)75102-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Lopez C.F., Nielsen S.O., Klein M.L., Moore P.B. Hydrogen bonding structure and dynamics of water at the dimyristoylphosphatidylcholine lipid bilayer surface from a molecular dynamics simulation. J. Phys. Chem. B. 2004;108:6603–6610. [Google Scholar]
- 87.Moore P.B., Lopez C.F., Klein M.L. Dynamical properties of a hydrated lipid bilayer from a multinanosecond molecular dynamics simulation. Biophys. J. 2001;81:2484–2494. doi: 10.1016/S0006-3495(01)75894-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Kucerka N., Liu Y.F., Chu N.J., Petrache H.I., Tristram-Nagle S.T. Structure of fully hydrated fluid phase DMPC and DLPC lipid bilayers using x-ray scattering from oriented multilamellar arrays and from unilamellar vesicles. Biophys. J. 2005;88:2626–2637. doi: 10.1529/biophysj.104.056606. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Klauda J.B., Kucerka N., Brooks B.R., Pastor R.W., Nagle J.F. Simulation-based methods for interpreting x-ray data from lipid bilayers. Biophys. J. 2006;90:2796–2807. doi: 10.1529/biophysj.105.075697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.Marrink S.J., Berendsen H.J.C. Simulation of water transport through a lipid membrane. J. Phys. Chem. 1994;98:4155–4168. [Google Scholar]
- 91.Mathai J.C., Tristram-Nagle S., Nagle J.F., Zeidel M.L. Structural determinants of water permeability through the lipid membrane. J. Gen. Physiol. 2008;131:69–76. doi: 10.1085/jgp.200709848. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Pandit S.A., Bostick D., Berkowitz M.L. Mixed bilayer containing dipalmitoylphosphatidylcholine and dipalmitoylphosphatidylserine: lipid complexation, ion binding, and electrostatics. Biophys. J. 2003;85:3120–3131. doi: 10.1016/S0006-3495(03)74730-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Czub J., Baginski M. Comparative molecular dynamics study of lipid membranes containing cholesterol and ergosterol. Biophys. J. 2006;90:2368–2382. doi: 10.1529/biophysj.105.072801. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94.Berger O., Edholm O., Jahnig F. Molecular dynamics simulations of a fluid bilayer of dipalmitoylphosphatidylcholine at full hydration, constant pressure, and constant temperature. Biophys. J. 1997;72:2002–2013. doi: 10.1016/S0006-3495(97)78845-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.Chiu S.W., Clark M., Balaji V., Subramaniam S., Scott H.L. Incorporation of surface tension into molecular dynamics simulation of an interface: a fluid phase lipid bilayer membrane. Biophys. J. 1995;69:1230–1245. doi: 10.1016/S0006-3495(95)80005-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Otten D., Brown M.F., Beyer K. Softening of membrane bilayers by detergents elucidated by deuterium NMR spectroscopy. J. Phys. Chem. B. 2000;104:12119–12129. [Google Scholar]
- 97.Trouard T.P., Nevzorov A.A., Alam T.M., Job C., Zajicek J. Influence of cholesterol on dynamics of dimyristoylphosphatidylcholine bilayers as studied by deuterium NMR relaxation. J. Chem. Phys. 1999;110:8802–8818. [Google Scholar]
- 98.Carnie S.L., Patey G.N. Fluids of polarizable hard-spheres with dipoles and tetrahedral quadrupoles: integral-equation results with application to liquid water. Mol. Phys. 1982;47:1129–1151. [Google Scholar]
- 99.Chen B., Xing J., Siepmann J.I. Development of polarizable water force fields for phase equilibrium calculations. J. Phys. Chem. 2000;104:2391–2401. [Google Scholar]
- 100.Silvestrelli P.L., Parrinello M. Structural, electronic, and bonding properties of liquid water from first principles. J. Chem. Phys. 1999;111:3572–3580. [Google Scholar]
- 101.Silvestrelli P.L., Parrinello M. Water molecule dipole in the gas and in the liquid phase. Phys. Rev. Lett. 1999;82:5415. [Google Scholar]
- 102.Watanabe K., Klein M.L. Effective pair potentials and the properties of water. Chem. Phys. 1989;131:157–167. [Google Scholar]
- 103.Brockman H. Dipole potential of lipid-membranes. Chem. Phys. Lipids. 1994;73:57–79. doi: 10.1016/0009-3084(94)90174-0. [DOI] [PubMed] [Google Scholar]
- 104.Clarke R.J. The dipole potential of phospholipid membranes and methods for its detection. Adv. Colloid Interface Sci. 2001;89:263–281. doi: 10.1016/s0001-8686(00)00061-0. [DOI] [PubMed] [Google Scholar]
- 105.Gawrisch K., Ruston D., Zimmerberg J., Parsegian V.A., Rand R.P. Membrane dipole potentials, hydration forces, and the ordering of water at membrane surfaces. Biophys. J. 1992;61:1213–1223. doi: 10.1016/S0006-3495(92)81931-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 106.Nymeyer H., Zhou H.-X. A method to determine dielectric constants in nonhomogeneous systems: application to biological membranes. Biophys. J. 2008;94:1185–1193. doi: 10.1529/biophysj.107.117770. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 107.Price D.J., Brooks I.C.L. A modified TIP3P water potential for simulation with Ewald summation. J. Chem. Phys. 2004;121:10096–10103. doi: 10.1063/1.1808117. [DOI] [PubMed] [Google Scholar]