Fast Electromechanical Amplification in the Lateral Membrane of the Outer Hair Cell

Abstract

Outer hair cells provide amplification within the mammalian cochlea to enhance audition. The mechanism is believed to reside within the lateral membrane of the cell that houses an expansive array of molecular motors, identified as prestin, which drives somatic electromotility. By measuring nonlinear capacitance, the electrical signature of electromotility, at kilohertz rates we have uncovered new details of the early molecular events that arise from voltage perturbations of prestin. We show that dynamic changes in motor state probability occur within the kilohertz range, and signify an amplificatory event. Additionally, we show a lack of effect of Cl driving force, an absence of cell length effect (indicating that the kinetics does not vary across auditory frequency), and the first demonstration of the time dependence of tension induced amplificatory shifts. The process we have identified, where the stimulus-response function shifts in time along the stimulus axis in a multi-exponential manner, bears similarities to those components of adaptation found in the OHC stereociliar transducer identified recently. As with the forward transducer, the speed of the reverse transducer amplificatory event consequently impacts on high frequency peripheral auditory processing.

Introduction

The hallmark of mammalian cochlear amplification is a mechanical nonlinearity that is thought to arise from the mechanical activity of outer hair cells (OHC). There are two key nonlinear electro-mechanical systems in OHCs, the stereocilia forward transduction apparatus and lateral membrane reverse transduction apparatus. Each is considered a potential powerhouse for cochlear amplification. These systems transduce acoustically derived electrical energy back into mechanical energy that must finally feedback into the organ of Corti to provide an enhanced drive to the inner hair cells (IHC), which predominately control eighth-nerve afferent activity.

The favored mechanism for fast stereocilia feedback corresponds to events underlying a Ca-dependent adaptation of the hair cell's receptor current (1,2). Owing to tension dependence of the stereocilia channel, insight into channel open/closed state probability derives from inspection of the cell's nonlinear receptor current-bundle displacement (I-X) or conductance-displacement (G-X) relationship, which quantifies the activity of the channels' tension sensors. Positive tension increases the probability that the channels will reside in the open state. During a step bundle displacement, fast adaptation apparently results from the influx and binding of Ca ions to a component of the unidentified transduction channel, somehow closing the channel. At the channel population level, the process is observed as a shift of the channels' Boltzmann distribution along the stimulus axis in the same direction (polarity) as the stimulus (bundle displacement). Thus, the process of opening transduction channels tends to close those same channels in a time-dependent manner, and the process has been shown recently to operate at the submillisecond timescale (kHz range) in OHCs (3). The resultant, channel-induced bundle movements may provide feedback into the auditory end organ.

The OHC lateral membrane motor, recently identified as prestin (4), is voltage dependent, and has been known for some time to work effectively in the kilohertz range (5,6). One popular model posits that the integral lateral membrane motors fluctuate in area between two states, contracted and expanded, just as bundle channels fluctuate between closed and open states (7,8). Owing to the motor's voltage dependence, insight into motor state probability derives from inspection of the cell's nonlinear charge-voltage (Q-V) or capacitance-voltage (C-V) relationship, which quantifies the activity of the motors' voltage sensors (9,10). Depolarization favors the contracted state. Prestin presents a behavior somewhat akin to, but notably different from the bundle adaptation process. That is, during a step voltage stimulus there is a shift in the motors' Boltzmann distribution along the stimulus axis, but unlike bundle adaptation, the shift is of opposite polarity (11). A negative voltage step will shift the distribution in the positive direction, and visa versa. This necessarily leads to an amplification of the mechanical response, because, for example, the shift caused by a hyperpolarizing voltage stimulus results in an accompanying, time-dependent augmentation in the number of motors in the expanded state at the new voltage (see Fig. 2). Thus, the voltage-dependent process that causes motors to expand tends to recruit more motors into the expanded state, whereas the process that contracts motors tends to recruit additional motors into the contracted state. Whereas the OHC motor can be driven between states at frequencies in excess of 80 kHz (6), the fastest component of the amplificatory shift was shown previously to be ∼70 ms (11), a timescale well below the kilohertz requirements for an influence on cochlear amplification. We show that just as previous measures of bundle adaptation kinetics were and still may be compromised by the technical problems inherent in studying acoustic rate events (3), our previous measures of amplificatory kinetics were underestimated. We now find components of the amplificatory shift that operate at submillisecond timescales, establishing the significance of this phenomenon in high frequency auditory processing. Additionally, we investigate the influence of Cl⁻ anions, a recently identified key player in OHC motor activity (12,13), and membrane tension on this amplificatory mechanism.

Figure 2.

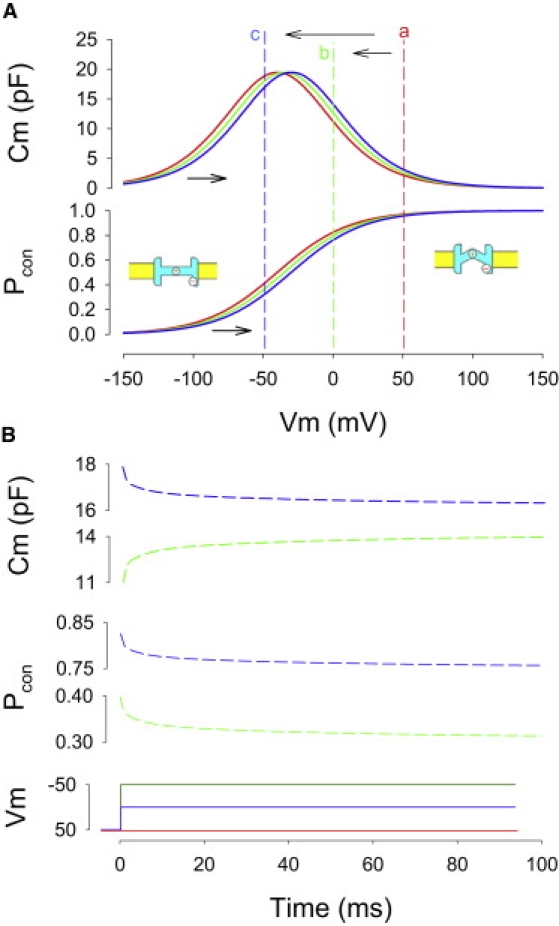
NLC shifts report on the conformational state probability of the OHC motor protein. (A) Model NLC and corresponding probability of the motor being in the compact state (P_con) versus membrane voltage. Cartoons depict motor in expanded state with anion bound and with positive gating charge on cytoplasmic side, and in contracted state with gating charge displaced toward the extracellular side of the membrane. (B) Corresponding time-dependent changes in state probability and NLC (green traces) during voltage steps from +50 mV to 0 mV (a → b) or from +50 mV to −50 mV (a → c; blue traces). Note polarities of relaxations.

Methods

Guinea pigs were decapitated after anesthetic overdose with halothane. Outer hair cells were freshly isolated from the guinea pig cochlea using Dispase (1 mg/ml) followed by trituration, and were whole-cell voltage clamped at room temperature using an Axon 200B amplifier. Membrane voltages were corrected for the effects of residual series resistance, which ranged from 3–5 MΩ. Ionic blocking solutions were used to remove voltage-dependent ionic conductances so that capacitive currents could be analyzed in isolation (10). Extracellular solution included: 100 mM NaCl, 20 mM TEA, 20 mM CsCl, 2 mM CoCl₂, 1.48 mM MgCl₂, 2 mM CaCl₂, 10 mM HEPES, and 5 mM dextrose, adjusted to pH 7.2 with NaOH, and adjusted to 300 mOsm with dextrose. Pipette solution included: 140 mM CsCl, 10 mM EGTA, 2 mM MgCl₂, and 10 mM HEPES, adjusted to pH 7.2 with CsOH, and adjusted to 300 mOsm with dextrose (used in Figs. 1 and 3–5). In some cases, TEA, CsCl, CoCl₂, CaCl₂, and MgCl₂ were omitted (Figs. 6–8). Gluconate was used to replace chloride (Fig. 6). In some experiments, the extracellular solution was used in patch electrodes. In a few experiments, 50 μM GdCl₃ was included in the extracellular solution to decrease residual currents. At this concentration, gadolinium has an insignificant affect on OHC capacitance (14).

Figure 1.

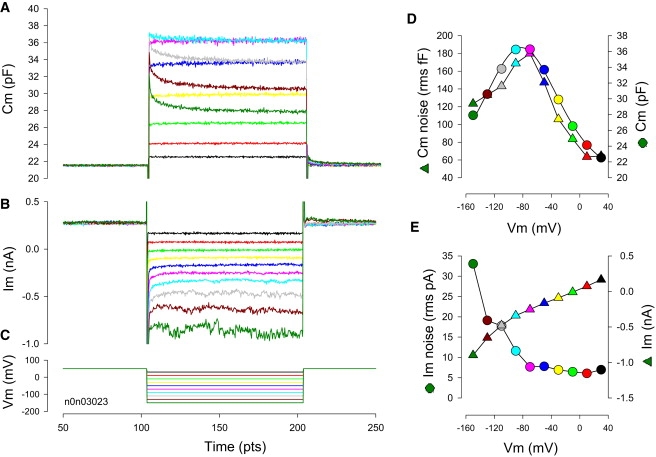
Time-dependent changes in NLC at fixed voltages. Capacitance (A), and current (B) in response to voltage steps (C) from +50 mV to −150 mV of 200 ms duration. C_m noise and magnitude (D) values are from the last 35 ms of the C_m traces. Current noise and magnitude (E) values are from the last 35 ms of the current traces.

Figure 3.

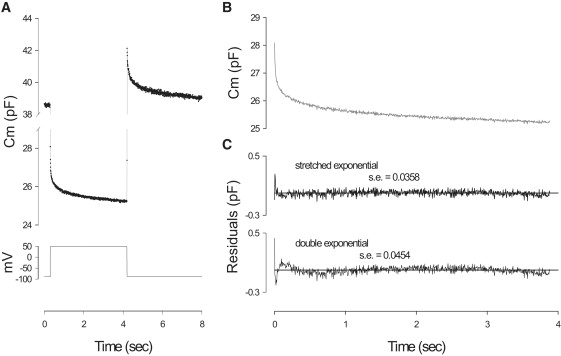
Long duration voltage pulse stimulation shows multi-exponential components in the OHC C_m relaxation. (A) C_m response induced by 4 s voltage step from −87 mV to + 53 mV. (B) C_m trace during pulse fitted with a stretched exponential. Note excellent fit with residuals (C) being greater for the double exponential fit.

Figure 4.

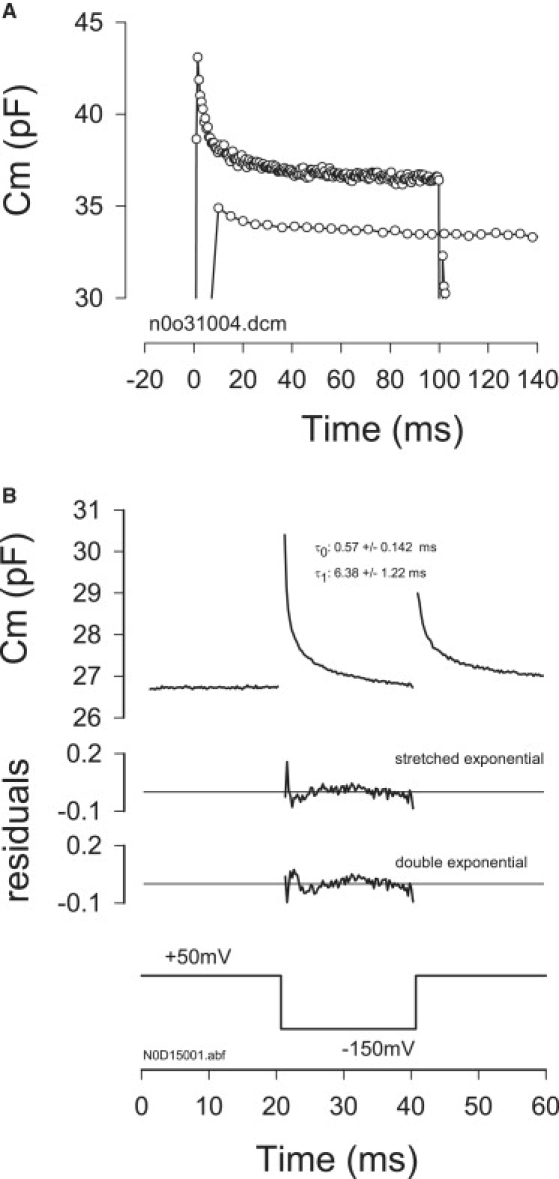
Early components of the amplificatory shift are shown with a faster C_m sampling rate. (A) C_m relaxations measured in the same cell in response to a voltage step from +50 mV to −150 mV. Top trace was sampled at 1.96 kHz and bottom trace (shifted down for visibility) was sampled at 196 Hz. Early components are evident with fast sampling. (B) Example of C_m relaxation (averaged traces, n = 9) in response to 20 ms voltage step from +50 to −150 mV at a C_m sampling frequency of 3.9 kHz. In this case a double exponential fit and stretched fit provide equally good fits as indicated by residuals. For six cells, τ₀: 0.57 ± 0.142 τ₁: 6.38 ± 1.22 ms; A₀: 1.61 ± 0.3, A₁: 1.7 ± 0.41 pF.

Figure 5.

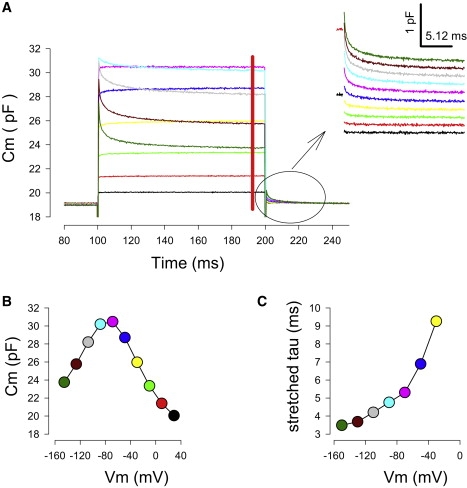
Voltage dependence of amplificatory shift. (A) Averaged C_m traces (n = 9) in response to voltage steps from +50 mV to −150 mV as in Fig. 1. The red bar indicates the region used to plot the C-V curve (B). Tail capacitance (inset) was used to measure voltage dependent time constants (C).

Figure 6.

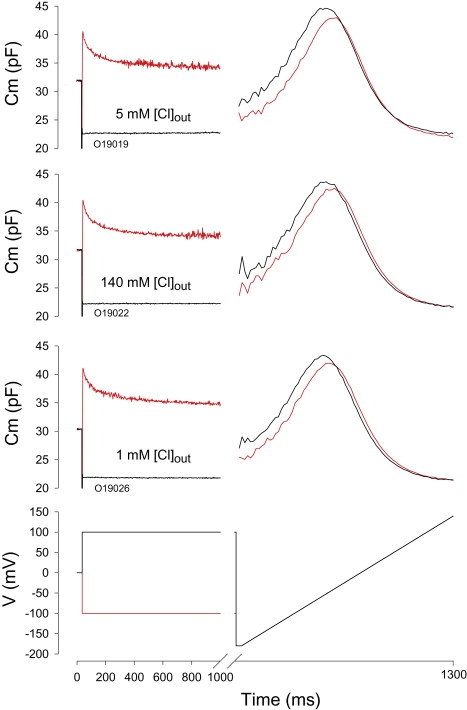
Time course and magnitude of amplificatory shift is not dependent on Cl⁻ driving force. Results from a typical cell clamped with a perforated gramicidin patch to maintain intracellular Cl⁻ levels. Extracellular Cl⁻ was altered to 5 mM (top, C_m traces), 140 mM (middle, C_m traces) and 1 mM (bottom, C_m traces). Voltage protocol is shown at bottom. After step jumps to either 100 or −100 mV from 0 mV, a ramp was voltage delivered to gauge the shift of V_pkcm. Shifts were −47.8 to −40.9, −50 to −41.5, and −54 to −46 for 5, 140, and 1 mM Cl⁻, respectively.

Figure 7.

Whole cell characteristics do not influence time course of the amplificatory shift. Double exponential fits were made. Short OHC labeled trace is averaged C_m response (return to +50 mV from −150 mV) from four short cells (C_lin: 10.3 ± −0.69 pF; τ₀: 0.76; τ₁: 4.09 ms). Long OHC labeled trace is average from five long cells (C_lin: 20.27 ± 0.88; τ₀: 0.76;τ₁: 3.98 ms). Time courses are essentially equal.

Figure 8.

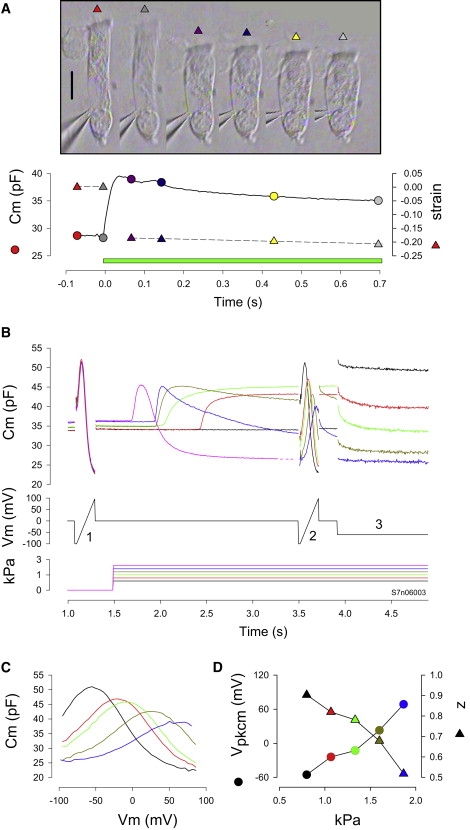
Rapid turgor pressure changes induce membrane tension with accompanying relaxations in C_m. (A) Photos of an OHC at different time points during a 1.8 kPa pressure step. C_m relaxation and longitudinal strain ((L − δL)/L) are plotted beneath. Green bar indicates pressure delivery to the cell. Note the majority of strain occurs before C_m relaxation begins. (B) Another cell. Color coded C_m traces induced by combinations of voltage ramps (1 and 2), voltage steps (3) and pressure steps. Single exponential fits of the C_m relaxations due to 1.4 (dark green), 1.6 (blue), and 1.8 (purple) kPa steps were 1.01, 0.88, and 0.16 s, respectively. (C) C-V plots obtained 2 s after onset of pipette pressure steps. Voltage was corrected for R_s effects that ranged from 1.7–4.5 MΩ during the pressure changes. (D) Boltzmann parameters V_pkcm and z as a function of pressure.

To deliver rapid changes in membrane tension, we used a pressure clamp system from ALA Instruments (Westbury, NY). Pipette tip diameters were increased in size for these experiments (∼1 MΩ).

Outer hair cell capacitance was measured with a continuous high-resolution two-sine voltage stimulus protocol (20 mV peak at both f1 and f2; f2 = 2 × f1; f1 ranging up to 3906.3 Hz), and subsequent FFT based admittance analysis (11,15). These small, high frequency sinusoids were superimposed on voltage steps and sinusoids that spanned up to ±200 mV.

Outer hair cell C-V plots were fitted with the function C_m = C_lin+ C_v, where C_lin is the voltage-independent (linear surface area component) capacitance of the lipid bilayer, and C_v = dQ_nonL/dV is the voltage-dependent component of C_m originating from prestin voltage-sensor activity. The first derivative with respect to V_m of a two-state Boltzmann function Q = Q_max/(1 + exp(−ze(V_m − V_pkCm)/k_BT)) was used to fit the C-V data (10). Q_max is total charge moved. The measured apparent valence of prestin voltage-sensor (z) is defined as z = q × d, where d is a normalized perpendicular projection of distance traveled by the voltage sensor charge (q) within the plasma membrane field. V_pkCm is the membrane potential (V_m) at which prestin molecules are distributed equally between expanded and contracted states. It corresponds to the peak of the C_v function.

All data collection and most analyses were carried out with an in-house developed Window's based whole-cell voltage clamp program, jClamp (www.scisoftco.com), using a Digidata (Axon, CA) 1320 board. MATLAB (The MathWorks, Natick, MA) or SigmaPlot was used for fitting the C_m data.

Results

Voltage steps from a holding potential of +50 mV (Fig. 1 C), a potential chosen because it is in a near-linear region of the OHC Q-V function, induce changes in whole cell current and capacitance (Fig. 1, A and B). The change in steady state current is a monotonic function of voltage (in this case, residual unblocked currents largely representing the activity of G_metL (13) (Fig. 1 E), whereas capacitance is a bell-shaped function of voltage (Fig. 1 D). Membrane current noise increases with hyperpolarization level due to activation of membrane conductances, reaching a maximum at the most hyperpolarized level of −150 mV. On the other hand, membrane capacitance noise peaks near the voltage at peak capacitance (V_pkcm). This likely results from the cresting chatter of prestin transitions between compact and expanded states at that voltage, because for a molecule that fluctuates between two states, variance of activity will be maximal when state probability is 0.5. Both channel current noise and gating shot noise analyses have been used to garner single channel characteristics (16–18). For the OHC, NLC noise, which is analogous to shot noise, should peak when motor state probability is half, i.e., where NLC is maximal. As far as other possible contributors to the generation of OHC capacitive noise, because the mechanical compliance of the lateral membrane (analogous to behavior hair bundle compliance (19)) is maximal at the midpoint voltage (V_pkcm) of the Boltzmann (20), the membrane embedded motors might be more susceptible to mechanical and/or thermal noise influences. It has been shown that motors are quite sensitive to mechanical and thermal perturbations (21–24).

Time-dependent changes in the magnitude of C_m (ΔC_m) at a fixed step occur because the C-V function shifts along the voltage axis as a result of changes from initial voltage conditions (Fig. 1 A). Fig. 2 illustrates a mechanistic account of the observation, and is discussed later. As a methodological control, Dieters' cells, supporting cells from the organ of Corti, were tested. No time-dependent changes in capacitance are observed during step changes in voltage (data not shown).

In our original work on this time-dependent phenomenon, double exponential fits to ΔC_m were made (11)

$$\Delta C_{\mathrm{m}}=C_{\mathrm{m}}\left(t\right)=C_{\mathit{0}}{e}^{-t/{\tau }_{\mathit{0}}}+C_{\mathit{1}}{e}^{-t/{\tau }_{\mathit{1}}}+C_{\text{off}},$$ (1)

where C₀ and C₁ are the magnitudes of each of the components of the exponential time courses τ₀ and τ₁, respectively. C_off is an offset, the cell's linear capacitance, required for fitting purposes. An example is shown in Fig. 3 A, using a C_m sampling rate (f1) of 195 Hz, used previously. However, Fig. 3, B and C, shows that the double exponential is not as accurate as the stretched exponential fitting function (25),

$$\Delta C_{\mathrm{m}}=C_{\mathrm{m}}\left(t\right)=C_{\mathit{0}}·e^{\left[-{\left(t/\tau \right)}^{\mathit{1}/h}\right]}+C_{\text{off}},$$ (2)

where meanings are as above, and h is an indicator of nonhomogeneity in the time course of change, the value of 1 reducing to a single exponential distribution. Residuals of the double exponential fit, especially at early times, are larger than those of the stretched exponential fit. The stretched exponential approach has been used to characterize complex relaxations in proteins where the discrete assumptions of single or multi-exponential processes may not hold (26). It can be useful when component rates of a phenomenon are not stationary in time, or when a phenomenon could present multiple components if looked at over a wider timescale. For example, because the apparent viscosity of a medium may depend on rate, duration and magnitude of deformation, such stimulus dependence could be better assessed by a more dynamic fit. Although this type of fitting procedure may be especially important when an extended time course of ΔC_m is inspected, if we focus our attention on short initial time segments during a step in voltage, a double exponential proves adequate to show the fast kinetics of ΔC_m (Fig. 4). To resolve faster components of ΔC_m, sampling frequency was extended to 1.9–3.9 kHz, and step durations were restricted below 100 ms. By increasing sampling frequency from 0.196 to 1.95–3.9 kHz, a significant enhancement in the resolution of early events is obtained, simply because sampling begins at 256 or 512 μs, rather than 5.12 ms after the onset of the voltage step. Because typically the first few points are discarded because of the transient current response contamination of the FFT, most of our older data (11) were obtained after an initial delay of >10 ms, having clearly biased the analysis toward slower components of ΔC_m. Fig. 4 A illustrates this enhancement in resolution over our previous measurements (11). Fig. 4 B shows the ΔC_m response to a 20-ms step voltage where fits to either a stretched exponential or a double exponential were made and the residuals plotted. Each seems adequate (SE = 0.0326 vs. 0.0337 pF, respectively). The stretched fit gives a time constant of 1.2 ms and h value of 2.2. The first component of the double exponential is well below 1 ms, and the second is an order of magnitude larger (τ₀: 0.57 ± 0.142; τ₁: 6.38 ± 1.22 ms; A₀: 1.61 ± 0.3, A₁: 1.7 ± 0.41 pF, n = 6). These data indicate that early components of the amplificatory shift work in the kilohertz range.

The time course of ΔC_m, and consequently, the shift in V_pkcm, is dependent on voltage step magnitude (Fig. 5). Because the clamp time constant (τ_clamp) will depend on the step potential when recording from OHCS, as it depends on the sum of linear- and voltage-dependent capacitance, C_m (τ_clamp = Rs × Rm/(Rs + Rm) × C_m), the time course of capacitance shift was determined at the termination of the voltage step when the holding voltage was reestablished (tail capacitance; Fig. 5 A, inset). The greater the voltage change the faster was the amplificatory shift. This voltage dependence could be due to a variety of voltage-dependent phenomenon in the OHC that may affect prestin, including membrane tension, membrane stiffness (as it can influence tension effects), or transmembrane chloride movements.

Chloride is a major player in prestin activity (12,13,27), and has been shown to permeate the OHC lateral plasma membrane under the control of membrane voltage and tension (13). Because chloride can shift the voltage dependence of NLC (13,28), it is conceivable that chloride influx during step changes in membrane potential could shift V_pkcm in a time-dependent manner. However, inspection of currents and capacitance simultaneously evoked by voltage steps (Fig. 1) indicates no correspondence of the two in time. Instead, it is possible that the time course of accumulation or removal of subplasmalemmal intracellular chloride may be the important factor. To evaluate this possibility, we varied the chemical driving force for Cl by changing the concentration of extracellular Cl⁻ (1, 10, or 140 mM), while using either normal pipettes with 10 mM intracellular Cl⁻ or perforated patch pipettes to maintain normal low intracellular Cl⁻ concentrations of ∼10 mM (27). These manipulations produced neither significant changes in the magnitude nor the time course of the amplificatory shift (Fig. 6). These data indicate that Cl⁻ in and of itself does not contribute to the timing of the amplificatory process, leaving the possibility that mechanical events, e.g., membrane tension, within the OHC membrane might influence the generation of the shift. We had previously modeled the shift as resulting from relaxations of motor induced membrane tension (11).

The voltage-induced deformations of the lateral membrane must be influenced by the mechanical properties of the cell; for example, the stiffness of the OHC varies with cell length (30) and whole cell stiffness (that is additionally voltage dependent (31)) might feedback into the active mechanics of the lateral membrane. To see if cell stiffness can influence the shift, we tested whether cell length correlates with the time course of the shift. Fig. 7 shows that cell length does not influence the time course of the amplificatory shift.

Finally, we tested whether rapid changes in membrane tension, which are expected to produce rapid changes in motor state probability (21,22,24), can mimic or interact with the voltage induced amplificatory shift. Fig. 8 shows that rapid changes in membrane tension at a fixed voltage shifts V_pkcm in a time-dependent manner, mimicking to some extent the C_m relaxations induced by step voltage changes. The examples shown are two of the best cells obtained in over 30 cells studied. An example of the OHC strain associated with a pressure step (black solid trace) is depicted in Fig. 8 A, and shows that the major strain occurs at the onset of the pressure delivery to the cell. In Fig. 8 B, before step changes in pipette pressure, a voltage ramp (denoted by the numeral 1) was delivered to measure V_pkcm. Subsequently, a step in pressure was delivered and after 2 s another voltage ramp (2) was delivered to gauge the shift in V_pkcm. Finally, a voltage step from 0 to −50 mV was delivered to observe the voltage-induced C_m relaxation at the stepped pressure. The protocol was repeated after a minute wait for recovery. In this manner, pressure steps up to 2 kPa were delivered. The lowest pressure step depicted (Fig. 8 B, black line) produced no response because cellular material in the pipette tip obstructed flow. With increasing pressures it can be seen that the pipette unplugged at decreasingly shorter times after onset of the pressure step (red, green, dark green, blue, and purple). The last pressure pulse (purple) caused the cell to burst at ∼1.75 s after onset. The shift in V_pkcm and changes in z are plotted in Fig. 8, C and D. The reduction in z may correspond to the restricted movements of charge that Adachi and Iwasa (33) found on extreme inflation of the trypsinized OHCs. In general, the effects of rapid pressure changes correspond to analogous step changes in voltage; however, the time course of the shifts (compare relaxations due to pressure alone versus the additional voltage step (3)) is slower for pressure changes. One caveat is that intracellular pressure may not be as constant as membrane voltage because OHC strain changes slightly during the constant pipette pressure pulse.

Discussion

By measuring OHC nonlinear membrane capacitance at submillisecond resolutions, we have examined the early time course of the dynamic response of the OHC motor to preconditioning membrane voltages and tensions. We show for the first time that this time course is multi-exponential, with the earliest detectable components residing in the kilohertz range, thereby establishing the phenomenon's potential significance in peripheral auditory processing of the mammal. These effects actually extend well into the low frequency range, as well; indeed, altering steady state resting potentials can stably set the operating point of electromotility to different points along the voltage axis.

Our data, although measuring whole cell capacitance, actually provide insight into the initial condition-dependent conformational states of the motor protein, prestin. As such, the correspondence between voltage-induced ΔC_m and motor state probability can be extracted from the data of Fig. 1, as schematized in Fig. 2. Thus, for voltage steps to potentials positive to V_pkcm (Fig. 2 A, a → b), the magnitude of C_m increases during the step duration, because the rising side of the C-V function moves to the right and the shift eventually halts at a point where capacitance is now larger at the step potential. For steps to potentials negative to V_pkcm (Fig. 2 A, a → c), the magnitude of C_m decreases during the step duration, because the falling side of the C-V function moves to the right and the shift halts at a point where capacitance is now lower at the step potential. Although capacitance may increase or decrease (Fig. 2 B), both correspond to a unidirectional change in motor state probability, as a conversion of capacitance to gating charge would show. Consequently, depolarizing voltages, in addition to causing a near instantaneous redistribution of motors to the compact state, will foster a supplemental recruitment of additional motors into that state, leading to an amplification of the initial response. The same amplification effect holds for hyperpolarizing voltages, where recruitment of motors will be into the expanded state. To reiterate, when OHC holding potential is stepped to a negative potential and maintained there, there will be a shift in the motor state probability function in the opposite direction to positive potentials. The initial voltage step to a negative potential will immediately cause a set of motors to move to the expanded state. When the motor state probability function moves to positive potentials, at the fixed holding potential more motors will enter the expanded state because the new probability at the fixed holding potential dictates it. From this, it is easy to predict the distortion in the mechanical response that will arise, distortion being the hallmark of mammalian cochlear amplification (34).

It should be emphasized that the amplificatory shift that occurs in the Boltzmann function does not predict a high pass response. In contrast, it is a process that rapidly follows the instantaneous change in motor state probability initiated by a step voltage, and continues over the stretched exponential time course we have described, reaching maximum at steady state. Thus, it is a low pass response where motors are recruited into the same state initially evoked by the onset of the voltage stimulus. We previously modeled the expected response (11), which we and others have observed in OHC mechanical responses. The multi-exponential amplificatory response dictates that the phenomenon will have impact in the acoustic frequency range. To be sure, the most important frequency range for humans is that of the speech frequencies (500–2000 Hz).

Although anions play a major role in NLC generation, our results indicate that modifying the driving force for chloride movement across the OHC lateral membrane through G_metL (13) does not modify the extent or time course of the amplificatory shift. This is in marked contrast with the effects of altering the driving force for Ca²⁺ on stereociliar adaptation (3). Reducing the entry of Ca²⁺ through the stereociliar channels can remove the tension-induced shift in the forward transducer function along the stimulus axis. Thus, parallels between the two mechanisms (apical stereociliar and lateral prestin motor) are not tight. It should be noted that although driving force for chloride did not significantly affect the amplificatory shift of the motor, the interactions of anions with the motor may still play a role. In this regard, we have found recently that the state probability of prestin influences anion binding affinity (L. Song and J. Santos-Sacchi, unpublished), and that even if concentrations remain the same at the intracellular binding sites of prestin, changes in binding site affinity, as can occur with allosteric modulation, could alter energy profiles, resulting in V_pkcm shifts. We are exploring such possibilities currently.

Since the initial observations of Iwasa (21), membrane tension effects on the OHC motor have provided important information on surprisingly efficient piezoelectric activity of this protein (35). Because membrane tension can shift V_pkcm and, indeed, in extreme applications, restrict conformational activity (33), we had modeled the voltage-induced amplificatory shift as resulting from motor induced tension (11). In this study we attempted to directly test this by applying rapid changes in membrane tension and seeking C_m relaxations that mimic those induced by voltage steps. Although there are indications of C_m relaxations after rapid tension changes, the time courses of voltage-induced and tension-induced C_m relaxations differ, tension effects being slower. It is possible that during our attempts to alter membrane tension through global changes in OHC structure we may have been restricted by the viscoelastic properties of the whole cell. For example, Ehrenstein and Iwasa (36) found that mechanical relaxations in the OHC have a time constant on the order of 40 s. However, because the fastest C_m relaxation time constants that we found with pressure steps were ∼2 orders of magnitude faster than their measured time course, our pressure clamp driver seems to have been quite successful in overcoming this mechanical impediment. We suggest that tension induced by the molecular motors themselves can better bypass this viscoelastic constraint, thereby providing more rapid tensions to evoke fast amplificatory shifts. Thus, we still view motor-derived membrane tension, possibly through alterations of anion binding affinity, to underlie voltage-induced amplificatory shifts. Nevertheless, as we have shown previously, the membrane environment of prestin can have profound effects on the magnitude and time course of the amplificatory shift (37).

In summary, we show remarkably fast changes in the Boltzmann distribution of prestin motor states induced by initial voltage conditions. The shifts along the voltage axis represent amplificatory supplementation to the voltage-induced mechanical response of the cell, and it is expected that this phenomenon will impact on high frequency peripheral auditory processing.