Replica Exchange Simulations of the Thermodynamics of Aβ Fibril Growth

Abstract

Replica exchange molecular dynamics and an all-atom implicit solvent model are used to probe the thermodynamics of deposition of Alzheimer's Aβ monomers on preformed amyloid fibrils. Consistent with the experiments, two deposition stages have been identified. The docking stage occurs over a wide temperature range, starting with the formation of the first peptide-fibril interactions at 500 K. Docking is completed when a peptide fully adsorbs on the fibril edge at the temperature of 380 K. The docking transition appears to be continuous, and occurs without free energy barriers or intermediates. During docking, incoming Aβ monomer adopts a disordered structure on the fibril edge. The locking stage occurs at the temperature of ≈360 K and is characterized by the rugged free energy landscape. Locking takes place when incoming Aβ peptide forms a parallel β-sheet structure on the fibril edge. Because the β-sheets formed by locked Aβ peptides are typically off-registry, the structure of the locked phase differs from the structure of the fibril interior. The study also reports that binding affinities of two distinct fibril edges with respect to incoming Aβ peptides are different. The peptides bound to the concave edge have significantly lower free energy compared to those bound on the convex edge. Comparison with the available experimental data is discussed.

Introduction

Amyloid assembly of polypeptide chains is related to a number of diseases, including Alzheimer's, Parkinson's, type II diabetes, and Creutzfeldt-Jakob disease (1). The aggregation pathway represents a complex cascade of structural transitions, which involves oligomerization of individual chains and formation of amyloid fibrils (2). Although oligomers appear to be the primary cytotoxic species (3–5), amyloid fibrils play the important role of reservoirs of monomers, which are in dynamic equilibrium with soluble oligomeric species (6,7). Amyloid internal organization shows remarkable homogeneity due to extensive β-sheet structure (8–14). The network of noncovalent interactions (primarily, backbone hydrogen bonds (HBs) and hydrophobic contacts) renders significant stability to amyloid fibrils against denaturation (15).

Recently, important progress has been made in elucidating detailed molecular organization of amyloid fibrils. In particular, solid-state nuclear magnetic resonance (NMR) experiments have revealed a parallel in-registry arrangement of Aβ peptides in amyloid fibrils (9,12,16,17). A structure of the wild-type Aβ fibril protofilament has been proposed on the basis of experimentally derived constraints (11) (Fig. 1 a). However, the mechanisms of fibril growth are still poorly understood (18,19). Experiments indicate that preformed Aβ fibrils may serve as templates for the deposition of Aβ monomers (18,20,21). Based on the interpretation of experimental observations, Aβ fibril elongation was proposed to proceed via a two-stage, dock-lock mechanism (22). During the first stage, a disordered Aβ monomer docks to the fibril without being integrated into the fibril structure. During the second stage, a monomer locks in the fibril state through activated structural reorganization. Recent experiments revealed additional Aβ locking and, possibly, docking stages that are each distinguished by a deposition rate constant (23,24).

Figure 1.

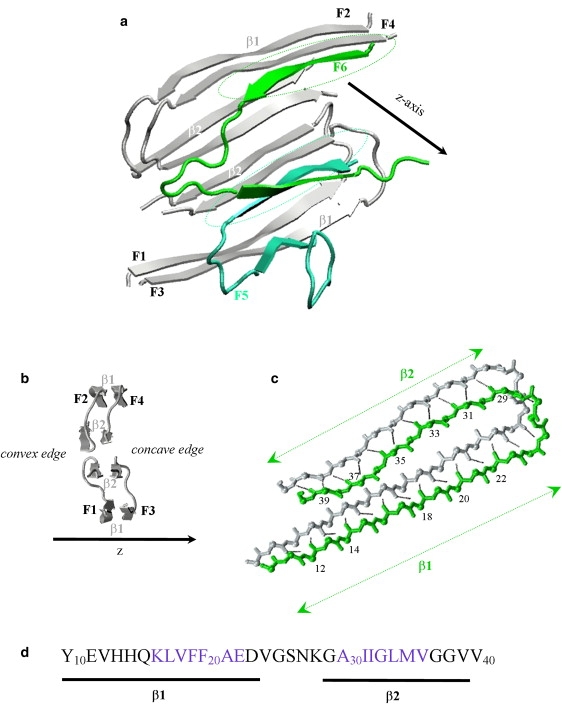
(a) Cartoon backbone representation of Aβ_10–40 hexamer used in this study. Aβ peptides F1-F4 (in gray) represent fibril fragment derived from solid-state NMR measurements (11). Fibril protofilament consists of four laminated β-sheets formed by the β1 and β2 strands in Aβ sequence (see panel d). The incoming peptides F5 and F6 (in aqua and green) are docked to the fibril edge. Two β strands in incoming peptides form parallel off-registry β-sheets with the fibril (marked by dashed stretched circles), which constitute the emerging locked phase. The fibril axis is parallel to the z axis. (b) Lateral view on the Aβ fibril fragment shown in panel a. Due to the stagger of β2 sheets with respect to β1, Aβ fibril has two distinct edges—concave and convex. (c) Parallel in-registry alignment of the fibril peptide (in gray) and the edge peptide (in green) on the concave fibril edge. This structure is typical for the peptides in the fibril interior. Backbone HBs are shown by black dashed lines. The indices of the residues in the edge peptide engaged in HBs and allocation of β1 and β2 strands are shown. Panels a–c are prepared using VMD (73). (d) The sequence of Aβ_10–40 monomer and the allocation of the β1 and β2 segments, which participate in fibril β-sheets (see panel a). The residues in blue have the highest propensity to form β-sheet structure according to NPS consensus prediction tool (74). Central hydrophobic cluster includes the residues 17–21 in β1. The color version of this figure is available online.

Computer simulations of fibril elongation provide important microscopic information complementary to the experiments (25). Employing a coarse-grained peptide model, Nguyen and Hall (26) and Jang et al. (27) reproduced the multistage process of fibril assembly starting with the dissociated state. Pellarin et al. (28) used a simplified peptide model to investigate the growth of amyloidlike aggregates and mapped a deposition pathway reminiscent of the dock-lock mechanism. All-atom molecular dynamics (MD) simulations of short peptides also support the elongation mechanism with multiple dock-lock stages (29–33). The energetics of Aβ_1–40 fibril structures was studied using MD (34,35).

In this article, we investigate the thermodynamics of deposition of Aβ peptides on the edge of the preformed amyloid fibril. The questions posed in this study are as follows:

• Is the dock-lock mechanism applicable to describe equilibrium fibril growth? If so, what is the nature of the structural transitions, which result in docked and locked phases?

• What are the interactions that stabilize binding of Aβ peptides to fibril edges?

• Is it possible to compare the binding affinities of the Aβ fibril edges?

In general, brute-force, all-atom MD simulations of Aβ fibril growth are not computationally feasible. Experiments show that the timescales of Aβ peptide unbinding are in the range from 1 s to 10³ min (22–24). Roughly similar timescales were reported for the growth of amyloid fibrils (36,37). Therefore, to answer the questions posed above, we employ an all-atom implicit solvent protein model and replica exchange molecular dynamics (REMD) (38). Extensive sampling in the wide range of temperatures allowed us to compute the free energy landscapes of fibril elongation as well as temperature dependence of various structural probes. We also investigated the structural properties of Aβ peptides on the surface of the amyloid fibril.

Methods

Molecular dynamics simulations

Simulations of Aβ fibrils were performed using the CHARMM MD program (39) and the all-atom force field CHARMM19 coupled with the SASA implicit solvent model (40). Previous simulations have demonstrated that this force field does not favor particular protein secondary structure. The model has been used to fold polypeptides of the length up to 60 residues, which contained α-helices or β-sheets (41,42). In addition, SASA simulations were employed for studying oligomerization of amyloidogenic peptides (43).

Sampling the conformational space of Aβ peptides interacting with the fibril represents a difficult computational problem even with implicit solvent representation. To achieve converging conformational sampling, we simultaneously utilized two approaches—REMD and application of fibril restraints.

Construction of the fibril sample

Using solid-state NMR, Petkova et al. (11) have derived the positions of residues in Aβ_1–40 fibril except for ∼10 disordered N-terminal amino acids. Consequently, in our study, we use the Aβ_10–40 hexamer (Fig. 1 a). (It is important to note that the solid-state NMR experiments on Aβ_10–40 peptides reveal that their fibril structure is very similar to that of Aβ_1–40 (44)). To emulate the stability of the large fibril sample, the backbone heavy atoms of the peptides F1–F4 (Fig. 1 a) were constrained to their fibril positions using soft harmonic potentials with the constant k_c = 0.6 kcal/(mol Ų) (33). The harmonic constraints permit backbone fluctuations with the amplitude of ∼0.6 Å at 360 K, which are comparable with the fluctuations of atoms on the surface of folded proteins (45). Constraints were not applied to F1–F4 side chains nor to the peptides F5 and F6, which were free to dissociate and reassociate with the fibril. The use of constraints is related to the observations that the dynamics of folded protein cores is solidlike and the extent of structural fluctuations increases toward the protein surface (45). Therefore, the constraints capture the rigidity of fibril interior and eliminate the necessity to simulate large fibril systems to achieve their stability. The precise value of k_c has minor impact on the simulation results. In the test simulations, we varied k_c from 0.06 to 6.0 kcal/(mol Ų) and observed no qualitative change in the interactions between F1–F4 and F5 (F6).

Replica exchange simulations

We used REMD (38) to study the deposition of Aβ peptides onto the fibril. REMD is a computational method, which accelerates sampling of the rugged free energy landscapes. In the past, REMD has been applied to study the thermodynamics of proteins folding and aggregation (43,46–50). Because REMD is well documented elsewhere (38), we present only the details of its specific implementation. We used 24 replicas distributed linearly in the temperature range from 330 to 560 K. The acceptance rate varied from 25 to 49% with the average of 36%. The exchanges were attempted every 20 ps between all neighboring replicas. In all, we produced 10 REMD trajectories of the length 0.2 μs each (per replica). Therefore, each replica was simulated for the total time of 2 μs and the cumulative simulation time of all replicas was 48 μs. The structures were saved every 20 ps. Between replica exchanges, the system was evolved using NVT underdamped Langevin dynamics with the damping coefficient γ = 0.15 ps⁻¹ and the integration step of 2 fs. Small value of γ compared to that of water accelerates sampling without affecting system's thermodynamics. The simulation system was subject to spherical boundary condition with the radius R_s = 90 Å and the force constant k_s = 10 kcal/(mol Ų). The concentration of Aβ peptides is therefore ≈3 mM.

Due to the stagger of the C-terminal β-strand β2 with respect to the N-terminal β-strand β1 (Fig. 1 b), there are concave and convex fibril edges (11). To reduce sampling bias, we used different starting structures for REMD simulations. Out of 10 trajectories, six were started with the peptides F5 and F6 being in random dissociated conformations. We have also used starting structures, in which F5 and F6 adopt fibril conformations on the concave or convex fibril edges (two REMD trajectories per each such initial structure). The REMD equilibration interval τ_eq depended on starting conformation. To determine τ_eq, we monitored the hexamer energy for the onset of equilibrium regime. As a result, the initial parts of REMD trajectories of the lengths from τ_eq = 40 to 80 ns were excluded from the analysis. Consequently, the cumulative equilibrium simulation time was reduced to τ_sim = 34 μs. Note that throughout the article, the term “fibril” refers to the peptides F1–F4 in Fig. 1 a; F5 and F6 are termed “edge” or “incoming” peptides.

Computation of structural probes

To characterize the interactions between the peptide F5 or F6 with the fibril, we computed the number of side-chain hydrophobic contacts as described in Klimov and Thirumalai (51). Backbone hydrogen bonds between NH and CO groups were assigned according to Kabsch and Sander (52). In all, we consider three classes of backbone HBs between the edge peptides and the fibril. The first includes any peptide-fibril HB. The second class is restricted to those peptide-fibril HBs, which have the certain registry offset R. Registry offset is defined as R = i − j, where i and j are the indices of the matching residues in the edge and fibril peptides, respectively. In-registry parallel alignment of peptides in the Aβ fibril displayed in Fig. 1 c corresponds to R = 0. HBs occurring in the conformations with the small registry offsets (R = 0 or |R| = 2) are termed fibrillike (fHB). The third class corresponds to parallel (antiparallel) β-sheet HBs. A parallel HB (pHB) is formed between the residues i and j, if at least one other HB is also present between i + 2 and j or j + 2 (or between i − 2 and j or j − 2). Conversely, an antiparallel HB (aHB) is formed between the residues i and j, if at least one other HB is also formed between either i + 2 and j − 2 or between i − 2 and j + 2. In general, pHBs may occur in the conformations with arbitrary registry offsets R.

Secondary structure in the edge peptides was assigned by evaluating their dihedral angles (ϕ, ψ) (51). The peptide effective energy E_eff^p is defined as the sum of potential energy and the SASA solvation energy. Potential energy includes bonded and nonbonded interactions between peptide atoms and with the fibril. Throughout the article, angular brackets 〈…〉 indicate thermodynamic averages. Because our simulations include two indistinguishable peptides (F5 and F6), all data in the article represent the averages over two peptides. The distributions of states produced by REMD were analyzed using multiple histogram method (53).

To estimate the thickness D of the layer formed by Aβ peptide docked to the fibril edge we apply the following procedure. Using REMD, the probability distribution P(R_cm,z) for the location of the incoming peptide center-of-mass ${\overrightarrow{R}}_{\text{cm}}$ along the z axis was computed. At the temperatures $T\lesssim 500\text{K}$, P(R_cm,z) displays two well-defined peaks associated with the localization of Aβ on the concave and convex fibril edges (Fig. 1 b). The thickness D is defined as a width of the peaks in P(R_cm,z) at the level of one-third of the maximum. The temperature dependence D(T) is not sensitive to the details of the definition.

Convergence of REMD simulations

To evaluate the quality of the REMD sampling, we consider the number N_s of unique states (E_eff, N_hb), which were sampled in the course of simulations at least once. Each state (E_eff, N_hb) is defined by the effective energy of the hexamer E_eff and the number of HBs between the edge peptide and the fibril, N_hb. Fig. 2 shows N_s as a function of the cumulative equilibrium simulation time τ_sim. At ${\tau }_{\text{sim}}\gtrsim 25\mu \text{s}$, N_s approximately levels off, suggesting approximate convergence of REMD simulations. The convergence of REMD data was also checked using the states (E_eff, N_phb). The results were very similar to those shown in Fig. 2. Another indicator of the reliability of REMD sampling is a small difference between N_s(τ_sim) for the two incoming peptides in Fig. 2. All data reported in this article have the errors not exceeding 14%.

Figure 2.

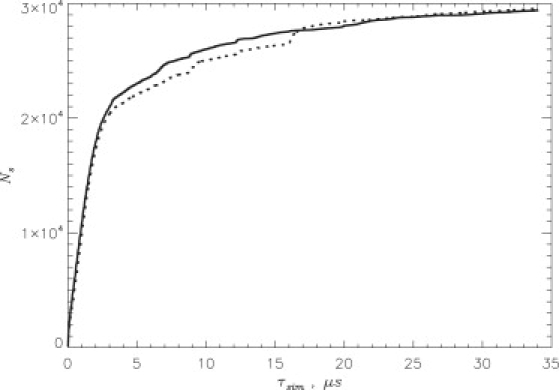
The number N_s of the new states (E_eff, N_hb) not previously sampled in REMD as a function of the cumulative equilibrium simulation time τ_sim. Because N_s approximately levels off at τ_sim > 25 μs, REMD simulations start to exhaust new (E_eff, N_hb) states. Continuous and dotted lines indicate N_s for each of the two incoming peptides.

Results

Docking of peptides to the fibril

Using REMD, the deposition of Aβ peptides on the preformed fibril fragment was investigated as a function of temperature T. To monitor the peptide-fibril interactions we computed the thermal averages of the number of HBs, 〈N_hb(T)〉, and the number of hydrophobic contacts 〈C_hh(T)〉, between the fibril and incoming peptide (see Methods and Fig. 3 a). The figure shows a gradual change in the number of peptide-fibril interactions spanning a wide temperature interval. For example, at T = 500 K there are, on an average, approximately three hydrophobic contacts and one HB linking the peptide to the fibril. According to the inset to Fig. 3 a, at this temperature, the probability to form at least one peptide-fibril HB, P_a, is ≈0.5. This implies that the deposition is initiated at T = 500 K, which is referred to as the association temperature T_a. At T = 360 K, 〈N_hb〉 and 〈C_hh〉 increase up to ≈10.5 and 9.8, respectively, and P_a > 0.99. Even at the low-end of the temperature interval studied ($T\lesssim 360\text{K}$), 〈N_hb〉 and 〈C_hh〉 are still significantly smaller than their values N_hb^fib (≥22) and C_hh^fib (≥23) computed for the edge peptides in the fibril conformation (Fig. 1 c). Fig. 3 a indicates that hydrogen bonding and hydrophobic effect are both important for the deposition of Aβ peptide on the fibril.

Figure 3.

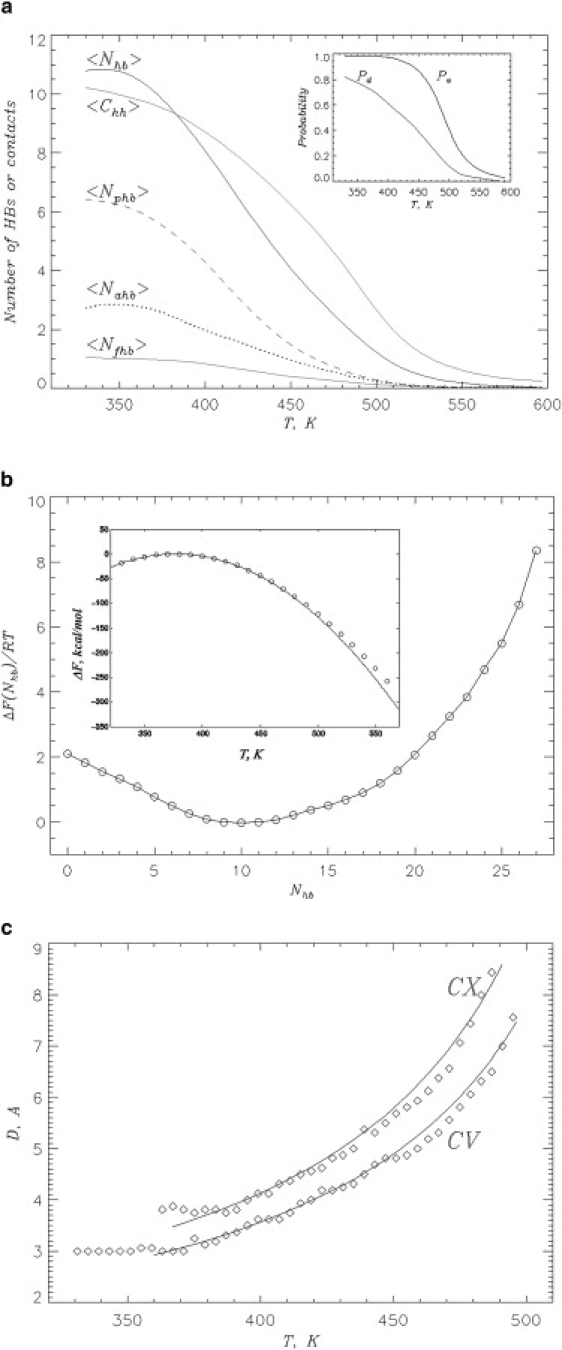
(a) Equilibrium deposition of incoming Aβ peptide on the fibril edge is characterized by the thermal averages of the following peptide-fibril structural probes: number of hydrophobic contacts 〈C_hh〉, number of HBs 〈N_hb〉, number of parallel HBs 〈N_phb〉, number of antiparallel HBs 〈N_ahb〉, and number of fibrillike HBs 〈N_fhb〉. The inset shows the temperature dependence of the probabilities to form peptide-fibril HBs P_a and to form HBs between the incoming peptides P_d. The midpoint of P_a determines the association temperature T_a = 500 K. (b) Free energy of incoming peptide, ΔF(N_hb), as a function of the number of peptide-fibril HBs N_hb at 360 K. The inset shows the temperature dependence of the free energy ΔF of Aβ hexamer. Quadratic fit ΔF(T) = −α(T − T_d)² with T_d ≈ 380 K and α ≈ 0.0085 kcal/(mol K²) is shown by the solid curve. Because the plot of F(N_hb) does not show barriers or metastable states and ΔF(T) is well fit by the quadratic function, docking to the fibril appears to be a continuous transition. Free energies in panel b are shifted to reach zero at minimum (maximum). (c) The thickness D of the layers formed by Aβ peptides bound to the concave (CV) and convex (CX) fibril edges as a function of temperature. The solid curves indicate the fits D(T) = D₀/(T_u − T). The fitting parameters are D₀ = 667 Å K, T_u = 588 K (CV) and D₀ = 736 Å K, T_u = 579 K (CX).

In Fig. 3 a the deposition of Aβ peptides onto the fibril appears as noncooperative transition. To further investigate its nature, we choose the number of peptide-fibril HBs N_hb as a progress variable describing binding of Aβ monomer to the fibril. The free energy profile ΔF(N_hb) for incoming peptide is shown in Fig. 3 b. Consistent with the gradual peptide-fibril association curves in Fig. 3 a, ΔF(N_hb) reveals a single minimum without metastable states separated by barriers. Apart from the location of the free energy minimum, this plot remains qualitatively the same in the entire temperature range 330 K < T < 560 K. The inset to Fig. 3 b displays the temperature dependence of the free energy ΔF(T) of the Aβ hexamer. An important implication is that ΔF(T) is well described by a quadratic function ΔF(T) = −α(T − T_d)². In the statistical mechanics of phase transitions a quadratic dependence of the free energy on the external parameter (in our case, temperature T) (54,55) is associated with continuous phase transition (see Discussion). Following this analogy, we identify T_d ≈ 380 K as a docking temperature for Aβ peptide. At the temperature T_d, the docking of incoming peptides to the fibril edge, which is initiated at T_a, is completed.

To verify the description of the docking transition proposed above we consider the thickness D of the layer formed by Aβ peptide adsorbed on the peptide edge (see Methods). Fig. 3 c demonstrates that at the temperatures $T\lesssim T_d$ the thickness of the adsorbed layer remains approximately constant and is equal to 3 or ≈4 Å, depending on the specific fibril edge. However, at T > T_d the layer dramatically expands indicating gradual peptide dissociation. At $T\gtrsim T_a=500\text{K}$ Aβ peptide is no longer localized on the fibril edges (the probability of forming peptide-fibril interactions P_a < 0.5 in the inset to Fig. 3 a) and the thickness D diverges (more precisely, becomes comparable with the radius of the sphere R_s).

Formation of the ordered locked phase by incoming Aβ peptides

Experimental data suggest that incoming Aβ peptides eventually become locked into fibril structure by adopting ordered conformations. To investigate the formation of ordered (i.e., locked) phase we used several structural probes described in Methods. We first computed the number of fibrillike HBs (fHB) between Aβ peptide and the fibril, 〈N_fhb〉, as a function of T (Fig. 3 a). In general, the number of fHBs is small compared to the total number of peptide-fibril HBs 〈N_hb〉. For example, at T = 360 K 〈N_fhb〉 barely exceeds 1.0 (compare with 〈N_hb〉 ≈ 10.5 at T = 360 K). Computation of the free energy F(N_fhb) as a function of N_fhb indicates that the free energies of the bound peptide states with significant number of fHB (∼10) are higher by ∼5 RT than of the states with N_fhb = 0 (data not shown). (We also note that the effective energy E_eff^p of the bound peptide does not attain global minimum in the fibrillike edge conformation.) Consequently, the thermal probability to form at least one fHB is only 0.23 at T = 360 K. Therefore, fibrillike conformations of Aβ peptides on the fibril edges appear to be thermodynamically unstable.

However, the emergence of partially ordered structure formed by the edge Aβ peptides can be detected by analyzing the distributions of parallel and antiparallel peptide-fibril HBs (pHB and aHB). As explained in Methods, these HBs report the formation of the elements of parallel or antiparallel β-sheets. To map the relevant structural states, we plot the free energy surface ΔF(N_phb, N_ahb) in Fig. 4 as a function of the number of pHBs and aHBs, N_phb and N_ahb. The free energy landscape reveals four basins. The first narrow basin (r) corresponds to the state in which no pHBs or aHBs are formed (ΔF_r = 0). This basin is populated by the states with random peptide-fibril HBs (denoted as rHB), which do not contribute to ordering in the bound Aβ peptides. A wide basin (p) represents Aβ edge states with large N_phb. The minimum of (p) ΔF_p = 0.07 RT is only marginally higher than ΔF_r and contains no aHBs. The basin associated with the large number of aHBs (a) has the minimum free energy of ΔF_a = 0.9 RT. Note that in the basin (a) N_phb = 0. Finally, a shallow wide basin (p + a) corresponds to the states, in which pHBs and aHBs are co-mixed. This basin is unstable as its minimum free energy ΔF_p+a is ≈ 2.9 RT. Fig. 4 shows that the free energy basins (except (p + a)) are surrounded by high free energy barriers. For example, the largest escape free energy barrier is found for (p), ΔΔF_ts1–p = 4.3 RT, whereas the escape barrier for (a) is smaller (ΔΔF_ts2–a = 3.4 RT). In contrast, the escape barrier for the (p + a) basin (along the path to (p)) is only ΔΔF_ts3–(p+a) = 1.0 RT. The escape barrier for (r) is similar to ΔΔF_ts1–p.

Figure 4.

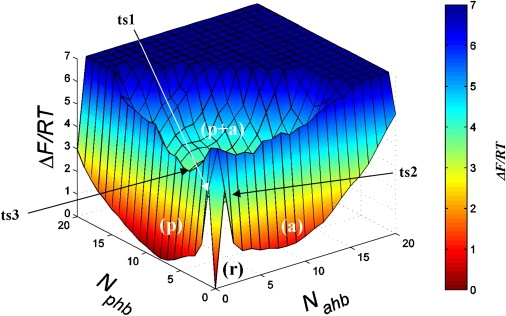
Free energy surface ΔF(N_phb, N_ahb) for Aβ incoming peptide as a function of the number of parallel HBs N_phb and antiparallel HBs N_ahb formed between the peptide and the fibril. ΔF(N_phb, N_ahb) is computed at the locking temperature T_l = 360 K < T_d. Four free energy basins are associated with parallel β-sheet structure (p), antiparallel β-sheet structure (a), formation of random peptide-fibril HBs (r), and the states with mixed parallel and antiparallel β-sheet structure (p + a). Transition states (ts1–ts3) between the basins are indicated. Free energy of the (r) state is set to zero. The contour projection of ΔF(N_phb, N_ahb) is provided in the Supporting Material. The color version of this figure is available online

The analysis of the free energy landscape in Fig. 4 is corroborated by computing the thermal averages of the number of pHBs and aHBs. According to Fig. 3 a, at T = 360 K 〈N_phb〉 ≈ 6.0 and 〈N_ahb〉 ≈ 2.8, whereas the number of rHBs (formed in the state (r)) is only 1.7. Consistent with Fig. 4, the thermal probability for the edge Aβ to form conformations with co-mixed pHBs and aHBs (the state (p + a)) is only 0.16. Due to the existence of metastable states and rugged free energy landscape, the formation of (p) states bears some similarity to the first-order transition (see Discussion). Because the basin (p) is associated with the formation of parallel β-sheet structure by the edge Aβ peptide, we termed the state (p) as locked. The locking temperature T_l was estimated by computing the thermal probability P_l(T) of occupancy of the locked state (operationally defined as N_phb ≥ 4 and N_ahb = 0). Because at T = 360 K P_l ≈ 0.5, the locking temperature is assumed to be T_l = 360 K. Note that T_l is lower than the docking temperature T_d.

Given that experimental structure of Aβ fibril has distinct edges (Fig. 1 b), it is interesting to probe their binding affinities to incoming Aβ peptides. To this end, the free energy profile ΔF(z) is computed along the z axis in Fig. 5. Two minima in ΔF(z) are attributed to Aβ binding to the convex (z ∼ −9 Å, CX) and concave (z ∼ 9 Å, CV) fibril edges. This plot has two important features. First, the two minima are separated by a large free energy barrier. For example, the barriers for the paths CV→CX and CX→CV are ≈ 7.5 RT and ≈ 5.5 RT, respectively. Hence, lateral binding of Aβ peptides to the fibril is rare and binding to the edges is strongly preferred. Second, there is a considerable free energy gap ΔΔF_CX–CV ≈ 2.5 RT between CV and CX states. This result is further supported by the computation of the numbers of peptide-fibril HBs formed by Aβ peptide bound to the concave and convex edges, N_hb^cv and N_hb^cx. At T = 360 K, their thermal averages are 〈N_hb^cv〉 ≈ 9.5 and 〈N_hb^cx〉 ≈ 1.0.

Figure 5.

The free energy of the incoming Aβ peptide ΔF(z) along the z axis coinciding with the fibril axis (Fig. 1a). ΔF(z) is obtained at T_l = 360 K. Two free energy minima reflect Aβ binding to the concave (CV) and convex (CX) fibril edges. Binding to CV is thermodynamically preferred. Free energy of the CV minimum is set to zero.

Analysis of the interactions between Aβ peptides and the fibril

We next probe the distribution of interactions linking edge Aβ peptides and the fibril. Fig. 6 shows the thermal averages of the number of peptide-fibril pHBs 〈N_phb(i)〉 formed by NH and CO groups of the residues i in the edge Aβ peptide. Although none of the backbone groups form strong pHBs, they tend to occur within β1 and β2 strand segments (Fig. 1 d). Specifically, the number of pHBs formed by β1 〈N_phb^β1〉 ≈ 3.0, whereas 〈N_phb^β2〉 ≈ 2.3. There are relatively few pHB in the turn region between β1 and β2 segments. Qualitatively similar conclusions are reached if the computations are extended to include all peptide-fibril HBs formed by individual NH and CO groups (data not shown). Therefore, the β1 strand segment in incoming Aβ peptide forms somewhat larger number of pHBs with the fibril than β2.

Figure 6.

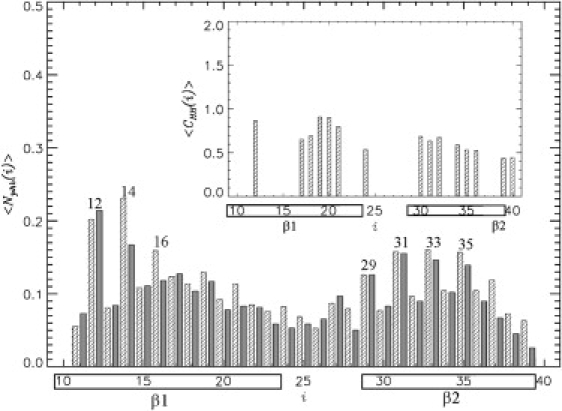
Average number of parallel HBs 〈N_phb(i)〉 formed by the backbone NH and CO groups of the residues i in the Aβ edge peptide. The data in solid and shaded representation are for NH and CO groups, respectively. Numbers mark Aβ residues, which form HBs in the fibril state shown in Fig. 1c. A preference to form pHBs within the β1 and β2 segments is in agreement with the propensity of β1 and β2 residues to form an extended β-structure (Fig. 1d). The inset shows the average number of peptide-fibril hydrophobic contacts 〈C_hh(i)〉 formed by hydrophobic residues i in the edge peptide. The distributions 〈N_phb(i)〉 and 〈C_hh(i)〉 are obtained at the locking temperature T_l = 360 K. The allocations of β1 and β2 segments are shown by boxes.

The distribution 〈N_phb(i)〉 in Fig. 6 shows significant variations between neighboring residues. Because the vast majority (93%) of pHBs in Fig. 6 occur on the CV fibril edge, we can compare the pattern of fHB (shown in Fig. 1 c) with that of pHB in Fig. 6. In the fibril state, fHB are formed by even-numbered residues within the β1 segment and by odd-numbered residues in β2. The peaks in 〈N_phb(i)〉, which comply with the fibril pattern, are observed at i = 12, 14, and 16, and within the entire β2 segment (i = 29, 31, 33, and 35). Therefore, fibrillike pattern of interactions, albeit formed by off-registry pHBs (see Discussion), tends to localize in the Aβ C-terminal and within few first β1 residues.

To investigate the distribution of hydrophobic peptide-fibril interactions, we obtained the thermal averages of the number of hydrophobic contacts 〈C_hh(i)〉 formed by apolar residues i (the inset to Fig. 6). The total numbers of contacts formed by the hydrophobic residues in the β1 and β2 segments are 4.9 and 4.0, respectively. This result reflects a slight preference for the central hydrophobic cluster (i = 17–21) to form more extensive peptide-fibril interactions than elsewhere in Aβ sequence (the inset to Fig. 6).

Finally, it is instructive to consider the distribution of secondary structure in the edge Aβ peptides (see Methods). At T = T_l, the edge peptide reveals a strong preference to form an extended β-structure. The fraction of residues in β conformation 〈S〉 is 0.52, whereas the fraction of α-helical residues 〈H〉 is only 0.11. For most Aβ residues i the fraction of the β-structure 〈S(i)〉 varies between 0.4 and 0.8, except for four Gly residues within and near the β2 segment (their 〈S(i)〉 < 0.3). As a result, the tendency to form the β-structure within the β1 segment is more consistent than in β2. Hence, the N-terminal (β1 segment) of the edge Aβ peptide forms somewhat stronger interactions with the fibril and tends to adopt more extended conformations.

Discussion

Thermodynamics of Aβ fibril growth

Docking of Aβ peptides

In this article, we have studied the equilibrium binding of Aβ monomers to the fibril fragment. Noncooperative binding curves 〈N_hb(T)〉 and 〈C_hh(T)〉 in Fig. 3 a and the existence of the single free energy minimum in Fig. 3 b suggest that docking of Aβ peptides to the fibril is a continuous transition without intermediates. Two other findings support this conclusion.

First, in the statistical mechanics of continuous phase transitions (54), the free energy of the system is expected to scale with temperature T as F ∼ (T − T₀)², where T₀ is the transition point. The inset to Fig. 3 b demonstrates that the free energy of Aβ hexamer indeed obeys quadratic temperature dependence in a wide range and we identify T₀ with the docking temperature T_d = 380 K.

Second, it is known from polymer theory that the adsorption of a polymer on attractive wall is a continuous transition and the thickness of adsorbed layer grows as ∼(T_u − T)⁻¹ in the transition region before unbinding at T_u (55). In Fig. 3 c, the layer thickness D(T) can indeed be reasonably well described by inverse temperature dependence. Note also that docking is stretched over a wide temperature range. It begins at the association temperature T_a = 500 K, when the probability of forming peptide-fibril interactions P_a exceeds 0.5 (Fig. 3 a). It is completed at T_d = 380 K, when the thickness of the peptide bound to the edge levels off (Fig. 3 c). Taken together, these observations are consistent with the continuous (barrierless) docking of Aβ peptides to the preformed amyloid fibril.

Because our simulations include two incoming peptides, they may bind to the fibril as monomers or dimers. The inset to Fig. 3 a shows the probability P_d of forming HBs between incoming peptides. At all temperatures P_d is significantly smaller than P_a. When the probability of forming peptide-fibril interactions P_a exceeds 0.5 at T_a = 500 K, P_d ≈ 0.1. When the edge Aβ peptide locks into an ordered phase at T_l = 360 K, P_d is still ∼0.75. These observations suggest that, although the interactions between incoming peptides do occur, they are less frequent than peptide-fibril interactions. Therefore, consistent with the experimental data, the Aβ peptide deposits to the fibril predominantly as a monomer (20,56).

Formation of ordered locked phase

Our results suggest that at low temperatures $T\lesssim T_l<T_d$ an ordered phase emerges in the Aβ peptides bound to the fibril. Under these conditions, parallel β-sheet structure (p) in the edge Aβ peptides becomes stable (see Results and Fig. 4). Due to the existence of metastable states, which include (a), (r), and (p + a) states in Fig. 4, and the rugged free energy surface, the formation of (p) states bears similarity to the first-order transition. Formation of parallel β-sheet structure by the edge peptide is consistent with the Aβ fibril structure, which is also based on parallel β-sheets (Fig. 1 a). However, it is important to emphasize that the (p) states are distinct from the fibril interior. First, the thermal average of the number of pHBs at T_l, 〈N_phb〉 ≈ 6.0, is much smaller than the total number of interpeptide fHBs in the fibril conformation (N_fhb^fib = 25 in Fig. 1 c). This implies that only a small part of Aβ edge peptide is actually involved in the locked phase. Second, the number of fHBs between incoming peptide and the fibril at T_l, 〈N_fhb〉 ≈ 1.0, is very small. Therefore, most pHBs are off-registry as opposed to a perfect in-registry alignment of fHBs in the fibril state (compare the edge peptides in Fig. 1, a and c). Hence, edge Aβ peptides even in the locked phase differ considerably from those buried in the fibril bulk (33).

Experimental studies support the existence of the edge states, which are neither fully locked in the fibril nor unbound. For example, dissociation kinetics of Aβ monomers from the fibril is typically described by multiple dissociation rate constants implying differing degrees of association between monomers and the fibril (22–24).

Reliability of low dimensional free energy projections

Projections of multidimensional free energy surface on low-dimensional progress variables can be misleading. Consequently, independent evidence is needed to support the conclusions inferred solely from such projections. Continuous nature of docking transition is consistent with two independent observations: 1), the quadratic temperature dependence of hexamer free energy (Fig. 3 b); and 2), the inverse temperature dependence of the thickness of adsorbed layer D (Fig. 3 c). The independent support for the similarity of locking and first-order transitions comes from our previous investigation (33). In that study we used free-energy disconnectivity graphs to analyze partially locked-edge Aβ peptides. Based on this methodology, which does not utilize reaction coordinates, we found that partially locked states are separated by large free energy barriers. This finding is consistent with Fig. 4 and the first-order nature of locking.

Comparing peptide deposition to protein folding

What could be the reason for Aβ peptide to display two transitions, docking and locking, in the course of deposition? To answer this question, we consider the ratio of the number of pHBs and aHBs to the number of all HBs, (〈N_phb〉 + 〈N_ahb〉)/〈N_hb〉. Over the temperature range of docking, this ratio increases from ≈0.4 at T_a to 0.85 at T_d. Therefore, only at low temperatures do ordered HBs dominate the peptide-fibril interactions. This conclusion is also consistent with the analysis of the probability of occupancy of (p) states P_l(T), which is >0.5 only at T ≤ T_l = 360 K. In contrast, in the high end of the docking interval, mostly random HBs link Aβ peptides to the fibril. Indeed, the plot in Fig. 4 recomputed at 450 K shows that the free energy of the (r) state is lower by, at least, 2 RT than that of any other state (data not shown). At this temperature, the probability of forming peptide-fibril interactions P_a is still ≈0.9 (the inset to Fig. 3 a). These findings suggest that docking and locking are distinct transitions occurring within different (albeit partially overlapping) temperature intervals.

Existence of separate disordered (collapsed) and ordered (native) phases is observed in the folding of some proteins (57). Proteins collapse at the temperature T_c and attain native state at the folding transition temperature T_F ≤ T_c. Both transitions are markedly different, because collapse (for flexible chains) occurs through a continuous transition, whereas folding is weakly first-order transition (58–60). Exploiting this analogy, we suggest that docking transition is reminiscent of protein collapse or polymer adsorption on a wall, whereas locking bears some similarity with folding.

Comparison with experiments

From the experiments on fibril thermodynamics, the dissociation temperature for Aβ amyloids appears to be ∼373 K at much smaller (micromolar) concentrations of Aβ monomer (61). Similar results were obtained for insulin fibrils (62), which stop growing at $\gtrsim 400\text{K}$ at micromolar concentration. The experimentally measurable temperatures are likely to correspond to the association temperature in our simulations. To evaluate the impact of Aβ concentration on docking we performed REMD at the concentration of 3 μM (the sphere radius of R_s = 900 Å). These limited simulations were designed only to sample docking stage. The docking interval was found to narrow and shift to lower temperatures, between T_d = 370 K and T_a = 440 K. Similar effect is known experimentally, in which the temperature of fibril dissociation (analog of our T_a) decreases with the polypeptide concentration (61). Thus, our docking temperature interval (T_d = 380 K to T_a = 500 K) appears to be qualitatively consistent with experimental observations and the high value of T_a is a consequence of high concentration of Aβ in our simulations.

Our data indicate that the structure of the edge Aβ peptide even in the locked phase differs from the structure of the peptides in the fibril interior. We expect that further binding of new incoming peptides would force already locked peptides to adopt more fibrillike conformations (31). In this context, our description of the deposition of Aβ monomer should only be applicable on the timescales τ_d ∼ 0.1s, on which binding of a single Aβ monomer occurs (36).

It will be important to test the thermodynamics of fibril growth using explicit solvent models. We cannot rule out that some details in peptide-fibril interactions are solvent-model-dependent, especially related to the hydration of the Lys28-Asp23 interpeptide salt bridge (11). However, an agreement between explicit and implicit solvent models obtained in protein folding simulations (63,64) suggests that implicit models do capture protein interactions fairly accurately.

Structure of Aβ edge peptides

Our simulations suggest that Aβ fibril edges have different binding affinities to incoming peptides. Aβ peptides bound to the concave edge have the free energy lower by ≈2.5 RT than those bound to the convex edge (Fig. 5). The figure also indicate that lateral binding to the fibril is thermodynamically unfavorable, although this observation may be related to a small size of the fibril fragment used by us. Difference in the binding affinities of the edges also finds support in Fig. 3 c. The thickness of the layer formed by the peptide docked to the CV edge, D_cv(T), is always smaller than that of the peptide bound to the CX edge, D_cx(T). Smaller values of D_cv(T) suggest stronger interactions between the peptide and the fibril edge.

To rationalize differing affinities of the edges we computed the average effective energies 〈E_eff^p〉 of the edge peptides (see Methods). For the peptides on the CV and CX edges, 〈E_eff^p〉 values are −92.5 kcal/mol and −70.1 kcal/mol, respectively. A 25% increase in 〈E_eff^p〉 on the CX edge is primarily due to destabilization of peptide-fibril interactions. For example, the sum of van der Waals and electrostatic peptide-fibril energies is −165.5 kcal/mol for the CV edge and only −135.5 kcal/mol for the CX edge. In contrast, solvation energy and the energy of intrapeptide interactions in 〈E_eff^p〉 are similar for both edges. One may speculate that, because CV edge contains a groove, to which edge peptide is partially confined, its 〈E_eff^p〉 is lower and, accordingly, CV binding is thermodynamically preferred. Therefore, Aβ fibril may grow faster on its CV tip compared to the CX. Similar conclusion has been reached in the study, which used a coarse-grained Aβ model (65), and in our previous simulations (33). Polarized growth has also been observed experimentally for the amyloid fibrils formed by Aβ_25–35 peptides (66).

Our analysis of structural propensities in edge Aβ peptides suggests that the N-terminal (β1 segment) forms somewhat stronger interactions with the fibril and tends to adopt more extended conformation. Similar observations were made in our previous study, which used an EEF1 implicit solvent model (33). More importantly, this result is consistent with experimental observations suggesting the importance for amyloid growth of the central hydrophobic cluster located in the β1 strand segment (Fig. 1 d) (67,68). Furthermore, a study of NMR dynamics in the Aβ_1–40 monomer revealed that its C-terminal has higher mobility than the N-terminal (69). Consequently, one may speculate that immobilization of the C-terminal in the fibril results in higher entropic cost than that associated with the N-terminal.

Conclusions

Using all-atom replica exchange molecular dynamics, we explored the thermodynamics of deposition of Aβ monomers on the preformed amyloid fibril. Consistent with the experiments, two deposition stages have been identified. Docking stage spans a wide temperature range, starting from the temperature of forming first peptide-fibril interactions T_a = 500 K and extending down to the docking temperature T_d = 380 K, at which the docking process is completed. Our analysis of the peptide-fibril interactions suggests that the docking transition is continuous and occurs without free energy barriers or intermediates. Furthermore, it does not result in the formation of ordered structures in the edge Aβ peptides. Interestingly, docking bears similarity with protein collapse and adsorption of polymers on attractive walls. Locking stage occurs at the temperature T_l = 360 K < T_d and is characterized by the rugged free energy landscape. Locking transition is associated with the emergence of parallel β-sheets formed by incoming Aβ peptide with the fibril. Locking resembles first-order transition and, in this sense, is similar to folding transition in proteins.

Our results suggest that binding affinities of two distinct fibril edges are different with respect to incoming Aβ peptides. The peptides bound to the concave edge have lower free energy and, therefore, it is conceivable that Aβ fibril exhibits, at least to some degree, an unidirectional growth. Our data further indicate that the β1 strand segment in the Aβ sequence forms more peptide-fibril interactions than the β2 strand segment. One may expect that the mutations at the sequence positions 10–23 would have a stronger impact on fibril growth rather than those occurring elsewhere.

In this study we continued the investigation of Aβ peptides found on the surface of amyloid fibril (33). Although these peptides can form partially ordered locked conformations, their structures differ substantially from the structures of peptides buried in the fibril interior. As in the fibril interior, surface peptides predominantly form parallel β-sheet conformations. However, in contrast to fibril in-registry β-sheets, those on the fibril surface are off-registry. In the process of fibril elongation, the edge peptides are likely to progress gradually toward fibril in-registry conformations due to the deposition of new Aβ peptides.

A potential biomedical implication of our work is that partially ordered surface Aβ monomers represent a target for antiaggregation molecular agents, such as NSAID derivatives (70,71). Structural information about the surface of the Aβ fibril may be useful in improving their antiaggregation propensity. Surface Aβ monomers are also important, because they determine, at least in part, the interactions with the cell membranes and, therefore, fibril cytotoxicity (72).

Supporting Material

A figure is available at www.biophys.org/BPJ/supplemental/S0006-3495(08)00062-3.