Macromolecular Crowding Modulates Folding Mechanism of α/β Protein Apoflavodoxin

Abstract

Protein dynamics in cells may be different from those in dilute solutions in vitro, because the environment in cells is highly concentrated with other macromolecules. This volume exclusion because of macromolecular crowding is predicted to affect both equilibrium and kinetic processes involving protein conformational changes. To quantify macromolecular crowding effects on protein folding mechanisms, we investigated the folding energy landscape of an α/β protein, apoflavodoxin, in the presence of inert macromolecular crowding agents, using in silico and in vitro approaches. By means of coarse-grained molecular simulations and topology-based potential interactions, we probed the effects of increased volume fractions of crowding agents (ϕ_c) as well as of crowding agent geometry (sphere or spherocylinder) at high ϕ_c. Parallel kinetic folding experiments with purified Desulfovibro desulfuricans apoflavodoxin in vitro were performed in the presence of Ficoll (sphere) and Dextran (spherocylinder) synthetic crowding agents. In conclusion, we identified the in silico crowding conditions that best enhance protein stability, and discovered that upon manipulation of the crowding conditions, folding routes experiencing topological frustrations can be either enhanced or relieved. Our test-tube experiments confirmed that apoflavodoxin's time-resolved folding path is modulated by crowding agent geometry. Macromolecular crowding effects may be a tool for the manipulation of protein-folding and function in living cells.

Introduction

Proteins play important roles in the regulation of functions in cells where macromolecules such as nucleic acids, lipids, proteins, and other cytoskeletons can take up to 40% (1–3) of the total cellular volume. In such “crowded” or “concentrated” environments, the dynamics of proteins will likely be different from those in dilute solutions in test tubes. Proteins in cell environments experience volume restrictions because of the surrounding macromolecules; this will restrict the allowed protein conformations. To circumvent difficulties in experimenting on living matter, experimentalists used bovine serum albumin or synthetic polymers (e.g., Ficoll, Dextran, and polyethylglycol, PEG) as “crowding agents” to mimic the crowded conditions of the cell (4). Using this framework, analyses of crowding effects on protein folding (5–7) and stability (8,9), protein association (10–12), and protein aggregation (13) were described.

Such experiments are challenging because proteins often aggregate at highly crowded conditions (∼200–400 mg/mL). In response to the demand for understanding macromolecular crowding effects, theories and computer simulations provide mechanistic explanations for these phenomena (14–19). The most accepted view about crowding effects is that native-state protein stability is enhanced because of the compression of unfolded state conformations, attributed to depletion-induced attractions (18,20,21). This idea assumes that perturbations of the native state of a protein are negligible in the presence of crowding. However, recent theories and in vitro experiments suggest that, as protein sizes increase with respect to crowding agents, structural changes in native states of proteins can occur at high volume fractions of crowding agents (9,22–24). However, how protein transient conformations and folding mechanisms are affected by macromolecular crowding is still unclear.

In an experimental and computational collaboration on the folding dynamics of apoflavodoxin (9), we revealed that in the presence of high volume fractions of crowding agents, stability enhancement of the native protein was in part attributable to mechanistic protein-crowding agent interactions in the folded state. The crowding agent was modeled by inert hard-core spheres in silico, to match in vitro experiments with Ficoll 70 (a cross-linked, spherical, sucrose-based polymer) (25). The native-state effect took place in combination with the generally accepted destabilization of the denatured state in the presence of crowding agents. Desulfovibro desulfuricans apoflavodoxin is a 148-residue protein containing a central β-sheet surrounded by α-helices on both sides (26,27). In vitro far-ultraviolet circular dichroism (CD) measurements indicated that the helical content of folded apoflavodoxin was increased by additions of Ficoll 70 (9).

Here we pursue a quantitative, combined in silico and in vitro analysis of the folding mechanism of apoflavodoxin in different crowding conditions, varied by both volume fraction (ϕ_c) and the geometry of crowding agents. We find that folding routes are sensitive to the space available to protein dynamics, particularly at high ϕ_c. At high ϕ_c, the average void formed by the density fluctuation of (spherical) crowding agents is small. Under this condition, elongated, rod-like, unfolded ensemble structures are favored that lead to topological frustration when diagnosed by folding route analysis. However, upon changing the geometry of a crowding agent from spherical to anisotropic, the elastic deformation of proteins attributable to the crowding agents is relieved. This idea can be rationalized by analyzing the space available to a protein, (1 − ϕ_c)/ρ_c, where ρ_c is N_c/V (V is the total volume, and N_c is the number of crowding agents larger than solvent molecules.) If we thread two spherical crowding agents into an elongated spherocylindrical (dumbbell) one, while keeping ϕ_c the same, the value of (1 − ϕ_c)/ρ_c doubles as N_c is reduced in half within the same V. As a consequence, the average void volume will become larger for nonspherical crowding agents.

With our in silico model of apoflavodoxin, we show that correct contact formation around the third β-strand in the central sheet is crucial to continue folding to the native state, in agreement with previous experimental findings (28). Upon the addition of spherical crowding agents (corresponding to Ficoll 70), we observe an off-pathway folding route that favors early formation of the first terminal β-strand that dominates at high ϕ_c. This causes topological frustration and the protein must unfold, to allow the third β-strand to recruit long-range contacts to complete the central β-sheet. Surprisingly, when the spherical crowding agents are replaced by dumbbell-shaped ones, the topological frustration in apoflavodoxin's folding routes vanishes. In agreement, stopped-flow mixing experiments with purified apoflavodoxin in vitro show that folding in buffer and in Ficoll 70 involves the rapid formation of an intermediate with ∼30% native-like secondary structure, followed by a slow final folding phase. In contrast, in Dextran 70, which is a rod-like crowding agent, apoflavodoxin's intermediate includes ∼70% native-like secondary structure.

Methods

Simulations

Coarse-grained models for proteins and crowding agents

A coarse-grained side chain-C_α model (SCM) (18,29) is used to represent protein structures. Each amino acid (except glycine) is modeled by two beads: a C_α bead from protein backbones, and a side-chain bead derived from the center of mass of a side chain. An all-atomistic (as an illustration) and a coarse-grained SCM representation of apoflavodoxin (using Protein Data Bank file 2fx2, D. vulgaris apoflavodoxin) are shown in Fig. 1, A and B, respectively. Spherical crowding agents are modeled for Ficoll 70, using hard-core spheres with a radius of 55 Å. Spherocylindrical crowding agents (dumbbell-shaped) are modeled for Dextran 70, using two hard-core Ficoll 70 spheres linked by a bond. The distance between two centers of mass is the diameter of a Ficoll 70 (i.e., 110Å). Thus N_c is reduced in half, whereas others remain intact. Another small dumbbell, composed of two smaller spheres, is also used (length of the bond distance, 87Å), and its volume is equivalent to one Ficoll 70. The potential energy of an entire system with a protein and crowding agents is E_p + E_pc + E_cc, where E_p is the potential energy for a protein, and E_pc and E_cc are interactions for protein-crowding agents and crowding agents-crowding agents, respectively. E_p = E_structural + E_nonbonded, where E_structural is the structural Hamiltonian and E_nonbonded is the nonbonded interactions in a protein. The structural energy, E_structural, is the sum of the bond-length potential, the bond-angle potential, the dihedral potential, and the chiral potential. Descriptions of each term are provided elsewhere (30). E_nonbonded includes interactions between a pair of side chains that follows Lennard-Jones potentials ($E_{ij}^{\text{NB}}$), and backbone hydrogen bonding that takes the angular alignment of two interacting backbones into account. Nonbonded interactions $E_{ij}^{\text{NB}}$ between a pair of i and j side-chain beads at a distance r are given as:

$$E_{ij}^{\text{NB}}={\varepsilon }_{ij}[{\left(\frac{{\sigma }_{ij}}{r_{ij}}\right)}^{12}-2{\left(\frac{{\sigma }_{ij}}{r_{ij}}\right)}^6],$$ (1)

where σ_ij = f(σ_i + σ_j). σ_i and σ_j are the van der Waals (VdW) radii of side-chain beads. To avoid a volume clash, f = 0.9, and |i − j| > 2.

Figure 1.

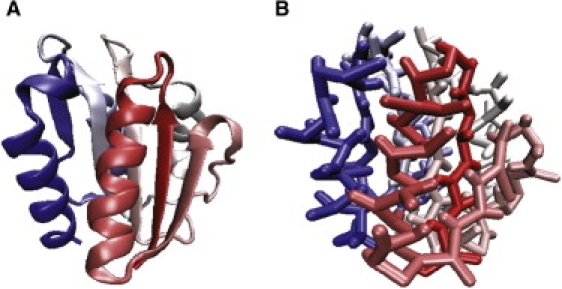
α/β apoflavodoxin protein in (A) an all-atomistic representation and (B) a coarse-grained side chain-C_α model (SCM). Structures are colored according to the sequence index.

A modified Go-like model (31) is used in which only native interactions are retained attractive. Consideration for native contact pairs is determined by the Contacts of Structural Units program (32). The amplitude of Go interactions (ɛ_ij) depends on residue types of i and j, and are dictated by the Betancourt-Thirumalai (33) statistical potential. As for nonnative interactions, only the repulsive term is used, and details of this model are provided elsewhere (30).

For backbone hydrogen bonding interactions, an angular-dependent function that captures the directional properties of backbone hydrogen bonds is used (30):

$$E_{ij}^{\text{HB}}=A\left(\rho \right)E_{ij}^{\text{NB}}$$ (2)

$$A\left(\rho \right)=\frac{1}{{[1+(1-{\text{cos}}^2\rho )(1-\frac{\text{cos}\rho }{\text{cos}{\rho }_a})]}^2},$$ (3)

where $E_{ij}^{\text{NB}}$ shares the same formula as in Eq. 1, except that ɛ_ij for backbone hydrogen bonding is 0.6 kcal/mol, and σ_ij is the hydrogen bond length, 4.6 Å. A(ρ) measures the structural alignment of two interacting strands. ρ is the pseudo-dihedral angle between two interacting strands of backbones, as defined elsewhere (30). A(ρ) = 1 if the alignment points to β-strands or α-helices. ρ_a is the pseudo-dihedral angle of a canonical helical turn, 0.466 (rad). A native pair of backbone hydrogen bonding between C_α and C_α is determined by the DSSP program (34). Details of this model are provided elsewhere (30).

Nonbonded pairwise interactions between C_α and side-chain beads, between a protein and crowding agents (E_pc), and between crowding agents themselves (E_cc) are repulsive. The repulsion, E^rep_ij, between two interacting beads i and j at a distance r, is given as:

$$E_{ij}^{\text{rep}}=\varepsilon {\left(\frac{{\sigma }_{ij}}{r_{ij}}\right)}^{12},$$ (4)

where σ_ij = σ_i + σ_j, σ_i and σ_j are the VdW radii of interacting beads, and ɛ = 0.6 kcal/mol (18).

Simulation details

Apoflavodoxin (using Protein Data Bank file 2fx2) is positioned in a periodic cubic box that includes crowding agents modeled after Ficoll 70 or spherocylindrical crowding agents such as Dextran 70. The box size is twice the length of an extended protein, 300σ, where σ = 3.8 Å is the average distance between two adjacent values of C_α. The volume fraction of crowding agents, ϕ_c, is 4πN_cR_c³/3V, where R_c is the radius of a Ficoll 70 (55Å), N_c is the number of crowding agents, and V is the total volume. ϕ_c= 0% (bulk), 25%, and 40%, and is chosen as it represents a broad range of volume fractions in a cell.

Thermodynamic properties are obtained by molecular simulations where the Langevin equations of motion at a low friction limit are implemented (35).To enhance sampling efficiency in a simulation, a replica exchange method (REM) is used (36) to incorporate high-performance computing resources nationwide. Details of REM simulations can be found in previous studies (9,18). Temperatures for REM simulations range from 250–450 K and more than 40 temperatures (or replicas) within this range are assigned. Starting configurations are randomly taken from high-temperature simulations, and then quenched to starting temperatures. The integration time step is 10⁻⁴τ_L, τ_L = (mσ²/ɛ)^1/2, where m is the mass of a residue (35). At certain steps (40τ_L), configurations with “neighboring” temperatures are exchanged. The exchange rate between each replica is ∼40%. A total number of 40,000 statistically significant data points is collected from each replica for free energy computations. For a bulk case at T = 360 K, there are ∼40 folding/unfolding transition events within 40,000 data points. The weighted histogram analysis is used to extrapolate thermodynamic properties and to compute errors (37).

Clustering analysis of ensemble structures

Ensemble structures are dissected into the folded state, the unfolded state, and the transition state by their locations in a folding energy landscape. A protein folding energy landscape is plotted as a function of Q (the fraction of native contacts where Q ranges from 0 to 1, and Q = 1 is the native state), and it presents with double minima separated by a barrier at Q^∗. The region of the folded state is chosen within ±20% of the minimum near Q = 1. For the unfolded state, configurations within ±20% of the other free energy minimum near Q = 0 are collected. For the transition state (TS), configurations within 20% of the peak of a barrier at Q^∗ are collected.

Configurations in each region are sorted into fewer sets of clusters, using a clustering method (38,39) based on a self-organized neural-net algorithm (40,41) that does not require a prior structural knowledge of an ensemble. A conformation of j is described by a vector x_j. Elements of x_j are the separations between pairwise side-chain beads in j. The Euclidean distance between the jth conformation and the center of mass of the kth cluster is measured and compared to a cutoff. Conformations of j will be individually sorted to the kth cluster if this Euclidean distance is shorter than the cutoff. After all conformations are sorted, the center of mass of the kth cluster will be reevaluated, and the sorting of each conformation will start over again. This process is performed iteratively until the centers of masses of all clusters converge. Details of the procedure are given elsewhere (38). The cutoff in this study is ∼60σ, depending on the number of clusters generated (∼10 clusters).

Shape analysis

The shape of configurations can be characterized by two rotationally invariant quantities, the asphericity (Δ) and shape parameter (S) (42). Asphericity (Δ) ranges from 0 to 1, and Δ = 0 corresponds to a sphere. Deviation of Δ from 0 indicates the extent of anisotropy. The shape parameter (S) ranges from −0.25 to 2: S < 0 corresponds to oblates, and S > 0 to prolates, whereas S = 0 is a sphere.

Experiments

Protein preparation

Apoflavodoxin from D. desulfuricans (ATCC 29577) was expressed in Escherichia coli cells and purified as previously described (43), with some modifications. In brief, the protein was first isolated using a Q-Sepharose column, and further purified using a Superdex-75 gel filtration column using an AKTA FPLC system (Amersham-Amersham Pharmacia, Uppsala, Sweden).

In vitro measurements

Thermal unfolding experiments with apoflavodoxin were performed using CD (Jasco-810) (Jasco, Easton, MD) in 10 mM HEPES (pH 7). The CD was monitored at 222 nm from 20°C to 95°C at a rate of 2.5°C/min. No scan-rate dependence was found between 0.1°C/min and 2.5°C/min. The temperature was controlled with a Jasco PTC 424S peltier. Separate experiments were performed with 100-mg/mL increments of Dextran 70 (Amersham Biosciences) between 0–400 mg/mL. The urea-induced equilibrium unfolding of apoflavodoxin was monitored by CD in the presence of final concentrations of 0, 75, and 150 mg/mL Dextran 70 and Ficoll 70 (Amersham Biosciences, Piscataway, NJ) in 10 mM HEPES (pH 7) at 20°C. High-quality urea (Sigma-Aldrich, St. Louis, MO) was made fresh to a stock of 10 M, and filtered using 0.45-μm syringe filters (Fisher, Austin, TX) before use. Each CD spectrum (260–200 nm) was the result of averaging two successive scans. Samples were made at 0.25-M increments of urea between 0–6 M, and were allowed to equilibrate at room temperature for ∼1.5 h before measurements. The urea-induced kinetic folding/unfolding of apoflavodoxin was monitored using CD at 222 nm with an Applied Photophysics (Leather head, UK) Pi-Star stopped-flow mixer as a function of Dextran 70 and Ficoll 70 (0, 75, and 150 mg/mL). In the case of Ficoll 70, which is assumed to be spherical, calculations suggest that 75 mg/mL should correspond to ∼35% volume occupancy; thus 150 mg/mL Ficoll 70 would represent ∼70% volume occupancy. However, these values are likely overestimates, insofar as it is possible to make Ficoll solutions as concentrated as 400 mg/mL (although the shape may not be spherical at the higher mg/mL:s). Temperature was maintained at 20°C, using a Julabo (Allentown, PA) F30-C peltier. The buffer was 10 mM HEPES, pH 7. Apoflavodoxin was unfolded to proper concentrations of urea using 1:5 mixing, and was refolded by dilution upon 1:10 mixing. Stock protein solutions were equilibrated at room temperature for 1.5 h before measurement. Observed kinetic traces were fit to single exponential decays. The missing amplitude in the mixing step was estimated from the baselines of folded and unfolded protein signals. All experiments were performed with a final protein concentration of 20 μM.

Results

Macromolecular crowding enhances protein stability

We find that folding temperatures (T_f, defined by the temperature for ΔG_fu = 0) for apoflavodoxin unfolding increase with ϕ_c. In the bulk case (i.e., ϕ_c = 0), T_f is 354 K, and ϕ_c (Ficoll 70) = 25%, T_f = 360 K, and ϕ_c (Ficoll 70) = 40%, T_f = 373 K (9). This indicates an enhancement of protein stability in the presence of crowding agents. Interestingly, when dumbbell-like crowding agents are included, despite the same volume fraction, T_f increases (ϕ_c (dumbbell) = 40% and T_f = 388 K) more than in the presence of spherical crowding agents. This is also found experimentally in heating experiments with purified apoflavodoxin detected by far-ultraviolet CD changes. Thermal midpoints for apoflavodoxin in various amounts of Ficoll 70 were reported previously (9). We performed similar experiments in the presence of the same amounts of Dextran 70, and compared the thermal stability of apoflavodoxin in the two crowding agents. We found that the effects of Dextran 70 at each condition were greater than with Ficoll 70 (Table 1).

Table 1.

Thermal midpoints (in degrees Kelvin) for apoflavodoxin unfolding as detected by far-ultraviolet CD in different amounts of Ficoll 70 (9) and Dextran (10 mM HEPES buffer)

Crowding agent (mg/mL)	Ficoll 70	Dextran 70
0	317	317
100	321	321
200	325	327
300	331	337
400	337	344

Error in each value is ±1 K.

Enhancement of protein stability because of crowding can be also observed in free energy profiles plotted as a function of Q under different crowding conditions (Fig. 2). The enhancement of stability can be explained by the density fluctuation of crowding agents. These prompt the protein to reside at low-density regions so that compact unfolded protein conformations are favored on average. (The radius of gyration, R_g, of unfolded proteins, is reduced in the presence of crowding agents. See Table S1 in the Supporting Material.) This depletion-induced attraction is more prominent in the ensemble of unfolded states than in the folded states. Although the destabilization of unfolded states by crowding is well-discussed (20), how crowding agents affect the folded states of large proteins (such as apoflavodoxin) is poorly understood. At ϕ_c = 25%, the free-energy minimum of apoflavodoxin's folded state (Q_f) shifts toward 1 (Q = 1 is the crystal structure) (9). This indicates that the folded state resembles the crystal structure more in the presence of crowding agents than in buffer, whereas native-state shifts in Q have not been observed for small proteins and peptides (18). Mechanistic interactions between a large, malleable apoflavodoxin and the crowding agents result in more tightly formed contacts in frayed loops, floppy termini regions, and between sheets and helices.

Figure 2.

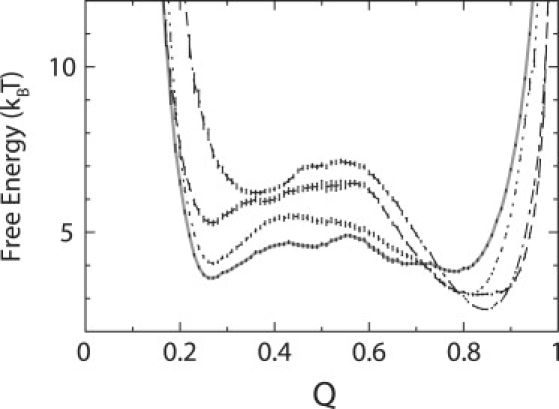
Free energy profiles are plotted as a function of Q (fraction of native contact formation) at different crowding conditions at 354 K. ϕ_c (bulk) = 0, solid line; ϕ_c (Ficoll 70) = 25%, dotted line; ϕ_c (Ficoll 70) = 40%, dashed line; and ϕ_c (dumbbell) = 40%, dot-dashed line. Error bars are included.

Nevertheless, at higher ϕ_c (e.g., ϕ_c (Ficoll 70) ≥25%), mechanistic interactions by crowding agents may cause local deformations of the folded state (the protein is modeled as an elastic object). This may compromise the favorable effects of crowding on protein stability. To dissect such subtle differences, we performed composite analyses of energy and entropy, using the energy landscape theory framework (44–46). Differences in energy (ΔE_fu) and entropy (ΔS_fu) between the folded and unfolded states in the presence of crowding agents are given in Table 2. At low ϕ_c (e.g., ϕ_c <25%), because the crowding agents act on the protein with repulsive forces, there is a slight reduction in energy (ΔE_fu) compared with the bulk case (ϕ_c = 0). Nevertheless, as the effects of crowding produce more compact unfolded states, the difference in entropy between the folded and unfolded states (ΔS_fu) further decreases.

Table 2.

Differences (in units of k_BT) in energy (ΔE_fu) and entropy (ΔS_fu) between folded and unfolded states at 354 K at various crowding conditions

ϕc	ΔEfu	ΔSfu
0% (bulk)	−86.92	−86.97
25% (Ficoll 70)	−83.89	−83.53
40% (Ficoll 70)	−21.86	−20.03
40% (dumbbell)	−23.76	−20.83
40% (small dumbbell∗)	−22.25	−20.46

These values are derived from free energy computation in Fig. 2. Estimated errors are of the same order as free energy (∼0.05 k_BT).

^∗Small dumbbell is a spherocylindrical crowder with the equivalent volume of one Ficoll 70.

At ϕ_c = 40%, nonspecific repulsive interactions between the crowding agent and folded protein play predominant roles in apoflavodoxin stability. Elastic deformation is nonnegligible, and it offsets the energy bias (ΔE_fu). However, the folded state at high ϕ_c is still favored thermodynamically for two entropic reasons. First, the entropy of the unfolded state decreases because of the compaction of the unfolded states. Second, the entropy of the folded state increases because of the large growth of crowding-induced states that are not originally accessible in the bulk case. As a consequence, ΔS_fu between the folded and unfolded states is much lower than ΔE_fu, and therefore the free energy stabilization (ΔG_fu) at ϕ_c = 40% strongly favors the folded state.

We also analyzed the free energy landscape for this condition when spherical crowding agents are replaced by dumbbell crowding agents (Fig. 2). At the same volume fraction (ϕ_c = 40%), the minimum of the unfolded state (Q_u) with dumbbell crowding agents shifts to Q_u = 0.38, compared with Q_u = 0.30 in the presence of spherical crowding agents. This indicates that more native contacts are formed in the unfolded state in the presence of dumbbell crowding agents than in the presence of spherical ones. Moreover, the stability of unfolded states in the presence of dumbbell crowding agents decreases, such that the stability of the folded state (ΔG_fu) is relatively favored.

We speculate that this enhancement in stability at ϕ_c (dumbbell) = 40% is partly attributable to better chances of forming larger voids that are available to the protein as two spherical crowding agents are linked into one in a pool of fluctuating crowding agents. Despite ϕ_c remaining the same, the space available to a protein, (1 − ϕ_c)/ρ_c, doubles under the dumbbell conditions because the number of dumbbell particles, N_c (dumbbell), is half of Ficoll 70, N_c (Ficoll 70). In the larger voids formed upon fluctuations of dumbbell crowding agents, there is less crowding-induced deformation in the folded state at high ϕ_c, and the distribution of structures in the unfolded state may also be altered accordingly. This speculation can be partly supported by the analysis of ΔE_fu and ΔS_fu. The differences in both energy and entropy are larger with dumbbell crowding agents than with Ficoll 70 (Table 2). It is tempting to suggest that this type of adjustment of the space available to a protein at high ϕ_c may result in changes in protein folding mechanisms. Next, we explore the folding mechanism of apoflavodoxin under different crowding conditions.

Crowding effects on the folding mechanism of apoflavodoxin

The folding mechanism of apoflavodoxin was studied during analysis of the behavior of selected groups of native contacts in the evolution of Q on the folding energy landscape. This profile measures the heterogeneity of folding routes by following contact formations from specific regions. For example, if all contacts are formed in a homogeneous fashion, the behavior of the ith group of contacts will be the same as the average behavior of the whole. Such a mean-field like behavior will show that the probability of a contact formation in the ith group (〈Q〉_i) progresses linearly with Q. However, if heterogeneity in a contact formation exists, the rise and fall of route profiles, presented as 〈Q〉_i vs. Q, will be diagnostic of topological frustration in a funnel-like folding energy landscape. Several studies used this and similar parameters (47) to evaluate the folding routes of protein L (48) and β-trefoil proteins (49).

Using this diagnostic tool, we monitored contact formations in the first β-strand (β₁), the first α-helix (α₁), and the third β-strand (β₃) regions. These places are identified as particularly interesting in apoflavodoxin. The 〈Q〉_i for these regions (i: β₁, α₁, and β₃) is plotted as a function of Q in Fig. 3. In the absence of crowding agents (Fig. 3 A), 〈Q〉_α1 rises sharply when Q < 0.2, indicating that contacts in α₁ (Fig. 3 A, red) form early in the unfolded states. In the transition state ensemble (TSE) region (Q ∼ 0.5), 〈Q〉_β3 rises quickly as compared with the rest, as contacts in β₃ (Fig. 3 A, green) form predominantly, and the major core in the central β-strand region is being constructed. Contacts in β₁ (Fig. 3 A, black) are greatly suppressed until the very late stage of folding (Q > 0.7). These folding pathways that involve recruiting contacts in β₃ in the TSE are in accordance with experimental data (50) and simulations (51) on the folding of apoflavodoxin.

Figure 3.

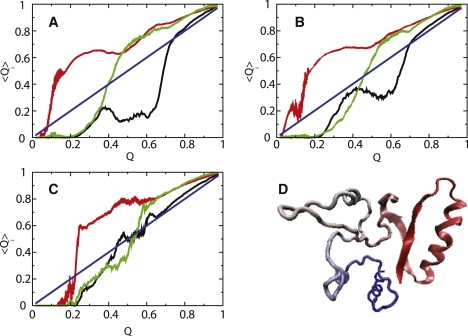
Probability of select native contact formation 〈Q〉_i at the ith region of a protein in the evolution of protein folding. Contact formation of first β-strand (black), first α-helix (red), and third β-strand (green) is plotted as a function of Q in (A) bulk, (B) ϕ_c = 40%, Ficoll 70, and (C) ϕ_c = 40%, dumbbell crowding agent, respectively. (D) Typical conformation in unfolded state, with some contacts formed about β₁ in early Q that cause topological frustrations in folding landscape. Diagonal line (blue) is provided as visual guidance for mean-field-like behavior. Error bars are included.

At the high levels of crowding agents (ϕ_c (Ficoll 70) = 40%) in Fig. 3 B, depletion-induced attraction from the presence of Ficoll 70 results in early contact formation in terminal β₁ before central β₃ as 〈Q〉_β1 rises sharply at Q = 0.4. Surprisingly, to continue folding further to the folded state, contacts in β₁ have to unfold (as 〈Q〉_β1 dramatically drops from ∼0.4 to 0.3) at the TS (Q^∗ = 0.55), to make clear ways for β₃ to recruit other long-range contacts and form the β-sheet core. This situation clearly elucidates topological frustration in the folding of apoflavodoxin because early contact formation in β_1, despite being native contacts, hinders further folding. We analyzed the conformations causing topological frustration, and found that a small loop formed in the terminal β₁ region (Fig. 3 D).

However, when we consider the folding routes for apoflavodoxin with dumbbell crowding agents at ϕ_c (dumbbell) = 40% in Fig. 3 C, the pattern changes dramatically. The profile for 〈Q〉_β1 along Q in Fig. 3 C is significantly more coherent with 〈Q〉_β3 than profiles in Fig. 3, A and B, indicating that contact formations in β₁ and β₃ come together in a homogeneous fashion. We speculate that the distribution of unfolded-state conformations, which depend on crowding agent geometry, dictates partitioning between apoflavodoxin folding routes.

To assess this finding by in vitro experiments, we performed a set of time-resolved mixing experiments with apoflavodoxin in the presence of Ficoll 70 and Dextran 70 at 20°C (pH 7), using urea as the denaturant. Apoflavodoxin unfolds in an apparent two-state reaction upon additions of urea (Fig. 4 A, inset). The presence of 75 and 150 mg/mL Ficoll 70 gradually increases the unfolding midpoint and the unfolding free energy (obtained from two-state fits to the data). The same trends are observed with Dextran, although the effects are somewhat greater (Fig. 4 B, inset). Unfolding and refolding kinetics were probed by urea jumps to conditions favoring unfolded and folded states, respectively in 0, 75, and 150 mg/mL Ficoll 70 and Dextran 70. The semilogarithmic Chevron plots for apoflavodoxin are shown in Fig. 4, A (Ficoll 70) and B (Dextran 70). In buffer, apoflavodoxin folds via a burst-phase intermediate with ∼30% of the total native-state CD signal at 222 nm, which reports on secondary-structure content. This phase is followed by a slow exponential conversion of the intermediate to the native state (27). The same kinetic mechanism is found in the presence of Ficoll 70. As in buffer, there is an initial burst intermediate (< ms) with ∼30% of the native CD signal. In agreement with the predicted crowding effects (18), the subsequent final folding event is 2–3-fold faster in the presence of Ficoll 70 than in buffer. When the same refolding experiments were repeated with apoflavodoxin in the presence of Dextran 70, we found that the burst-phase intermediate now included 70% of the native state's secondary structure content. Thus, after a few milliseconds of folding, the structural content of apoflavodoxin is more than twofold higher in Dextran than in Ficoll. The subsequent final folding step of apoflavodoxin in Dextran was similar in terms of the rate constant to that in Ficoll 70. These experimental results support the in silico findings of different folding routes in different crowding agents. Although there is an intermediate in both cases, the structural content of the intermediate differs dramatically between the two crowding agents (although we cannot assess experimentally whether any of these structures are misfolded or not). Rate constants for unfolding and the final folding step under each condition, extrapolated to zero denaturant concentration, are reported in Table 3.

Figure 4.

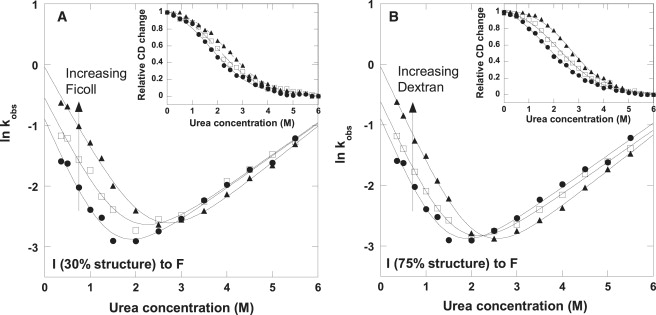
Kinetic semilogarithmic plots of lnk versus [urea] for apoflavodoxin folding/unfolding in buffer (solid circles), 75 mg/mL crowding agent (open squares), and 150 mg/mL crowding agent (solid triangles), using Ficoll 70 (A) and Dextran 70 (B). The kinetic folding mechanism involves a burst phase occurring within the mixing time (i.e., in less than a few milliseconds) that corresponds to 30% of the total CD change in buffer and in Ficoll, but 75% of the total CD change in Dextran. The measurable rate constants for the subsequent folding of the intermediate to the native state are shown. In both crowding agents, the rate constants extrapolated to 0 M urea increase 2–3-fold compared with the rate constants in buffer alone (Table 3). There is no significant effect on unfolding rates extrapolated to 0 M urea in the different conditions (Table 3). (Insets) Equilibrium unfolding curve as a function of [urea] for each condition. Two-state fits to the equilibrium data reveal that the free energy of unfolding increases from 4.4 kJ/mol (buffer) to 8.9 kJ/mol (150 mg/mL Dextran) and to 7.2 kJ/mol (150 mg/mL Ficoll 70).

Table 3.

Rate constants for final folding step (after the burst) and unfolding for each condition (extrapolated to 0 M urea) extracted from data in Fig. 4

Crowding agent (mg/mL)	kf (s−1)	ku (s−1)
0	0.39 ± 0.02	0.016 ± 0.005
75 (Ficoll 70)	0.56 ± 0.02	0.016 ± 0.005
150 (Ficoll 70)	0.95 ± 0.02	0.010 ± 0.005
75 (Dextran 70)	0.53 ± 0.02	0.014 ± 0.005
150 (Dextran 70)	0.95 ± 0.02	0.009 ± 0.005

Clustering analysis of ensemble structures

To explain deviations of folding routes at different crowding conditions, we further dissect the characteristics of each state at T = 360 K, using clustering analysis (see Methods for details).

Unfolded states

In Table 4, the percentage of unfolded conformations in the first dominant cluster under different crowding conditions is given. As ϕ_c (Ficoll 70) increases to 40%, the size of the first dominant cluster increases by 2.6-fold, compared with the bulk. Interestingly, when dumbbell-like crowding agents are considered (ϕ_c (dumbbell) = 40%), the size increases by 3.6-fold.

Table 4.

Clustering analyses of ensemble structures

ϕc	Cluster size of folded state	Cluster size of unfolded states
0% (bulk)	63%	10%
25% (Ficoll 70)	90%	16%
40% (Ficoll 70)	99%	26%
40% (dumbbell)	100%	36%

Cluster size is percentage of conformations in dominant cluster.

Next, we compute the asphericity (Δ) and the shape (S) of conformations in the first dominant cluster (Table 5). In the bulk case, the ensemble structures in unfolded states are mostly prolate (S = 0.448 ± 0.008) and rod-like (Δ = 0.389 ± 0.003). Upon the addition of Ficoll 70, the geometric characteristics in the dominant cluster of unfolded states are still prolate and rod-like (Table 5). Given elongated, rod-like conformations, loop formation at the terminal β1 that causes topological frustration is overwhelmingly favored. This can explain the enhanced topological frustration diagnosed in Ficoll 70 from the folding-route analysis in Fig. 3.

Table 5.

Asphericity (Δ) and shape (S) parameters of structures from dominant cluster at different crowding conditions

Folded state
ϕc	Δ	S
0% (bulk)	0.037 ± 0.000	−0.012 ± 0.000
25% (Ficoll 70)	0.036 ± 0.000	−0.012 ± 0.000
40% (Ficoll 70)	0.036 ± 0.000	−0.012 ± 0.000
40% (dumbbell)	0.036 ± 0.000	−0.011 ± 0.000
Transition state
ϕc	Δ	S
0% (bulk)	0.029 ± 0.000	−0.001 ± 0.000
25% (Ficoll 70)	0.035 ± 0.000	0.001 ± 0.000
40% (Ficoll 70)	0.031 ± 0.000	−0.008 ± 0.000
40% (dumbbell)	0.037 ± 0.000	−0.004 ± 0.000
Unfolded state
ϕc	Δ	S
0% (bulk)	0.389 ± 0.003	0.448 ± 0.008
25% (Ficoll 70)	0.265 ± 0.006	0.212 ± 0.013
40% (Ficoll 70)	0.306 ± 0.009	0.276 ± 0.019
40% (dumbbell)	0.138 ± 0.008	0.078 ± 0.011

Interestingly, with dumbbell crowding agents (ϕ_c (dumbbell) = 40%), the geometric characteristics of the dominant unfolded ensemble become spherical (S = 0.078 ± 0.011). Given more spherical and compact structures, contact formation in the central β₃ can better recruit other long-range contacts to form the core β-sheet, as the chances of contact formation in terminal β₁ diminish. Patterns of folding routes with dumbbell crowding agents are therefore more homogeneous (Fig. 3 C) than with spherical crowding agents (Fig. 3 B).

Folded states

In the presence of crowding agents, depletion-induced attraction produces more compact structures, and the size of the first dominant cluster resembling the native crystal state increases. At high ϕ_c, these ensemble structures are compressed into slightly oblate shapes (S = −0.012 ± 0.000; Table 4). This behavior was discussed further in our previous equilibrium analysis of apoflavodoxin in the presence of Ficoll 70 (9).

Transition states

The probability of contact formation in the transition-state ensemble (the definition of a transition state is in Methods) at different crowding conditions ϕ_c (Ficoll 70) = 0%, 25%, and 40%, and ϕ_c (dumbbell) = 40%, are given in Fig. S1, A–D. Both axes indicate residue indices. Elements in the upper triangles in Fig. S1 show the probability of contact formation between backbone hydrogen bonds, and the lower triangular elements show contact formation between side-chain beads. Even at high volume fractions of the crowding agents, microscopic descriptions of the transition state structures, as measured by native contact formation, are similar to those in the bulk. Short-range, on-diagonal contacts, and contacts in the central β-strands, are mostly formed. Contacts in the TSE in the presence of crowding agents are not greatly affected by crowding agents, except that the overall molecules are more compact, as seen from the increase in the probability of off-diagonal, long-range contacts.

Despite the similarity in microscopic details in TSE, the overall geometry of TSE structures is mildly susceptible to protein-crowding interactions at high ϕ_c. The shape and asphericity of the first dominant clusters are given in Table 4, and the TSE structures are shaped by crowding interactions into spheres. These changes in shapes, however, are not as dramatic as those in the unfolded states at different crowding conditions.

Discussion

Volume interactions and the geometry of crowding agents in protein stability

Volume fractions of crowding agents (ϕ_c) play a major role in the enhancement of protein stability, because (1 − ϕ_c)/ρ_c defines the range of space available to accommodate proteins. To this end, density fluctuations of crowding agents are also important, because they dictate the available ranges for structural fluctuations in protein ensembles, particularly in our case, where the crowder size is much bigger than an apoflavodoxin protein. It was shown in both experiments and simulations that at low ϕ_c (≤25%) or low weight concentrations (≤100 mg/mL), the effect of crowding on protein thermodynamics is minimal. The size effect on biopolymer folding was earlier studied by Minton (52), who suggested that large crowding agents impose less of an effect on conformations of small biopolymers, compared with small crowding agents. However, as ϕ_c increases, the interactions of crowding agents with folded forms of proteins are not negligible, and protein dynamics become sensitive to the geometry of a crowding agent.

Our results show that crowding agents act on the native state at high ϕ_c (ϕ_c = 40%). To investigate the role of crowding agent geometry under these conditions, we consider two extreme cases that deviate from spherical Ficoll 70. The first case involved putting two spherical Ficoll 70 molecules together in an elongated dumbbell. This dumbbell has an effective radius of gyration 25% larger than the Ficoll 70 sphere. Essentially, given the same ϕ_c, the available space (1 − ϕ_c)/ρ_c of a protein is doubled when the number of crowding agents N_c is reduced by half. This gives us a controlled way to address the importance of void size, caused by fluctuations of crowding agents. Despite the small change, we show here that its effect on protein stability and folding mechanism is significant. We find that at high ϕ_c, an increase in (1 − ϕ_c)/ρ_c, by introducing a different crowding-agent geometry that results in larger voids, can relieve mechanistic interactions between crowding agents and proteins.

The other case involved creating a dumbbell with a volume equivalent to that of Ficoll 70 (we term this the “small dumbbell” in Methods). As shown in Table 2, there is still an enhancement of the native state stability, but the effect is not as significant as with the other agents at ϕ_c = 40%. The size of the depletion layer in the protein-crowder radial distribution function is the smallest for the small dumbbell (which is in line with the analysis by Berg (53) of the behavior of dumbbell molecules with an equivalent volume of spheres), indicating significant unfavorable protein-crowder interactions that offset the enhancement of protein stability (data not shown). Together with Ficoll 70, these two dumbbell models provide a framework for discussing the characteristics of shape and size of crowding agents. We argue that the best computer model for Dextran 70 may be a “swelled” dumbbell (and not the small dumbbell), because Dextran 70 has a lower density than Ficoll 70 (25).

Spherocylindrical crowding agents can exclude more volume than spherical crowding agents, and the stability of a protein can be further enhanced. This finding appears to be supported by some experimental studies. In addition to the experimental data reported here for apoflavodoxin (Table 1), an experimental study by Perham et al. showed that Dextran promoted larger effects than Ficoll 70 on the thermal stability of holoflavodoxin and of another unrelated protein, VlsE (23).

Summarizing the results of this numerical analysis, what is the crowding condition that best promotes protein stability? The dominant factor is, no doubt, ϕ_c. However, at high ϕ_c, protein-crowder interactions may also start creating negative impacts. Therefore, there appears to be another competing factor, i.e., the available space to a protein is also important in defining the folding mechanism and protein stability. The space available to proteins is related to the probability of void formation, which increases with (1 − ϕ_c)/ρ_c, as seen in previous studies of fluid models (54,55). The available space can be adjusted by the geometry of the crowding agents. This was also discussed by Minton, who stated that the shape of crowding agents is important to protein stability (56). We suggest that the stability of a native protein, ΔG_fu, in the presence of ρ_c crowding agents is partly proportional to the following equation:

$$\Delta G_{fu}\sim (\alpha {\varphi }_c+\beta {\varphi }_c^2+\gamma {\varphi }_c^3)/{\rho }_c\text{.}$$ (5)

This equation is based on the fact that ΔG_fu is primarily determined by ϕ_c (up to a critical ϕ_c^∗). We propose that a ϕ_c^∗ defines the optimal volume fraction of crowding agents that best enhances protein stability. β is a parameter that defines how crowding-agent geometry influences the available space of a protein. In this study, β is likely a negative value, insofar as protein-crowding interactions at high ϕ_c provide some unfavorable effects on the stability of the native state. Thus at ϕ_c > ϕ_c^∗, a second-order effect is introduced, so that the protein native stability is less enhanced. By changing ρ_c (or equivalently, N_c), we can manipulate this second-order effect. In addition, our results from the small dumbbell with the equivalent volume of Ficoll 70 suggest a third factor that arises from the shapes of crowding agents, and that relates to the extent of packing of a protein and crowders in three-dimensional space. This is a many-body problem that can be included in the third-order term (γ) in Eq. 5 (to be pursued in future studies). Certainly, there are other factors to consider when going beyond the hard-core approximation, such as attractive interactions between constituents (57,58). This relationship, based on the excluded volume, indicates that by manipulating ϕ_c and the geometry of crowding agents, switch-like protein activities (that are triggered by structural changes) may be achieved in a cell.

Crowding effects on folding mechanism of apoflavdoxin

Apoflavodoxin is a large protein with a central β-sheet sandwiched by α-helices at both facets. Recent experiments showed that multiple folding routes exist, and some misfolded structures must unfold to continue their route to the folded state (50). In this process, the formation of the third β-strand is crucial for recruiting long-range contacts, and this behavior was modeled for a nucleation growth (51).

We investigated crowding effects on these folding routes by profiling regional contact formation along with Q on the folding energy landscape. At a high ϕ_c of spherical crowders, available spaces for unfolded states are limited, and unfolded states adopt prolate shapes. As a consequence, local interactions along the chain are favored, and that causes a population of contacts in the terminal β₁. Despite native contacts, the early formation of the β1 causes topological frustration and hinders further contact formation in β₃. “Topological frustration” in the folding mechanism was also seen in other protein families (49,59). However, to our knowledge this is the first study to suggest using crowding-agent geometry to get around topological frustrations in folding pathways.

Conclusions

The effects of macromolecular crowding on the stability, structures, and folding routes of apoflavodoxin were investigated using a combined approach of molecular simulations, energy landscape theory, and in vitro measurements. Our results show that native protein stability is partially proportional to the volume fraction of crowding agents (ϕ_c) and the space available to a protein, i.e., (1 − ϕ_c)/ρ_c. The latter is significant at high ϕ_c, and protein stability can be fine-tuned using different geometries of crowding agents. We found the folding mechanism of apoflavodoxin to be modulated by changes in crowding conditions. Conditions were evident that altered the folding route, so that topological frustration was avoided. We propose that selective crowding conditions may be a useful tool for manipulateing protein-based biological reactions in vitro and in vivo.

Supporting Material

A table and a figure are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(08)00072-6.