Curvature-Driven Pore Growth in Charged Membranes during Charge-Pulse and Voltage-Clamp Experiments

Abstract

We find that curvature-driven growth of pores in electrically charged membranes correctly reproduces charge-pulse experiments. Our model, consisting of a Langevin equation for the time dependence of the pore radius coupled to an ordinary differential equation for the number of pores, captures the statistics of the pore population and its effect on the membrane conductance. The calculated pore radius is a linear, and not an exponential, function of time, as observed experimentally. Two other important features of charge-pulse experiments are recovered: pores reseal for low and high voltages but grow irreversibly for intermediate values of the voltage. Our set of coupled ordinary differential equations is equivalent to the partial differential equation used previously to study pore dynamics, but permits the study of longer timescales necessary for the simulations of voltage-clamp experiments. An effective phase diagram for such experiments is obtained.

Introduction

The formation and kinetics of pores in cell membranes play fundamental roles in the interaction of cells with macromolecules or with other cells. Virus-cell and cell-cell fusion (1,2), exocytosis and endocytosis in neurons (3), and regulation of plant cell growth (4) are some examples of processes that rely crucially on the precise regulation of the opening and closing of holes in cell membranes. A good understanding of this process is necessary for controlled drug delivery (5), somatic hybridization (6), and many other medical and biotechnological applications (7). Simple membrane energetics explains why pores in membranes subjected to small electric fields open and close reversibly. For slightly higher fields, pores grow irreversibly and rupture the membrane (8). What cannot be explained by simple energetics is a phenomenon studied in a series of experiments by Benz and co-workers (9–14), now called electroporation. When a membrane is pulse-charged to a larger value of the transmembrane potential, it will shunt off all excess charge by nucleating many small pores, which will reseal once the field pulse has passed. While an intermediate-valued potential can rupture a membrane, the membrane protects itself against short high-amplitude pulses. This phenomenon is also called reversible electrical breakdown.

An achievement of the past few decades has been the description of this electroporation process by a Smoluchowski equation describing the drift and diffusion of the pore radius distribution (15–21). Even though the Smoluchowski equation, combined with membrane energetics, was successful in explaining how membranes reseal after having been exposed to short pulses of high electric fields, it has limitations. At each time step, the probability distribution must be solved for every possible radius, and so the computational work grows with the maximum radius considered. The direct solution of the Smoluchowski equation is therefore not adequate for the simulation of voltage-clamp experiments that require long times and low voltages (20). In addition, the Smoluchowski equation cannot describe the growth rate of a single pore (1). By exposing small patches of black membrane to small voltages, Wilhelm et al. (1) nucleated single pores or pairs of pores and observed their radii growing linearly in time. The Smoluchowski equation describes the behavior of a probability distribution and thus does not address single pores.

In this work, we will supplement the classic description of electroporation using the Smoluchowski equation by a Langevin equation for the curvature-driven growth of pores in charged membranes. A Langevin equation was used previously to describe the dynamics of the fusion pore (22) but it was derived from a different pore energy and did not account for the contribution of an electric potential. Using a Langevin equation drastically reduces the computational time needed to simulate charge-pulse and voltage-clamp experiments and allows one to tackle the long-time regime unattainable by the direct solution of the Smoluchowski equation. We show that our formalism reproduces the essential behavior of electroporation: pores that reseal for low and high voltages but grow irreversibly for intermediate values of the voltage. Furthermore, we study long-time behavior of individual pores and produce a membrane conductance that grows linearly in time, as seen experimentally (1). Finally, we present an effective phase diagram for voltage-clamp experiments on plasma membranes and predict whether the electrical breakdown is reversible or irreversible.

Our article is organized in the following way: the growth rate of the pores is derived in the subsection Motion of Pore Radius. The dynamics of the number of pores is obtained by an asymptotic solution of a Fokker-Planck-Smoluchowski equation in the Fokker-Planck Equation and in Asymptotic Solution. Finally, the charging and discharging of the membrane in different experimental setups is described in Charge Pulse Experiment.

General Theory

Motion of pore radius

The equation of motion governing the growth of the pore radius is determined using a thermodynamic approach (8,23). The pore dynamics are driven by the free energy E(r) of a membrane containing a circular pore of radius r

$$E\left(r\right)=2\pi \gamma r-(\sigma +a_{\mathrm{p}}{V}_{\mathrm{m}}^2)\pi r^2+{(C_s/r)}^4\text{.}$$ (1)

The first term containing the line tension γ is the free energy cost of the pore edge. The second term containing the surface tension σ and the transmembrane potential V_m is the gain in free energy due to the reduction of surface area of the membrane under mechanical and electrical tension. The constant a_p is related to the conductivity of the bulk electrolyte and the thickness of the membrane (20). The third term of this energy, introduced by Israelachvili (24) and Weaver and Chizmadzhev (25) and including the repulsion constant C_s, is due to the steric repulsion of the monomers in curved membranes. The motion of the pore radius depends on this free energy in the following manner. The simplest model for the pore growth rate is the Langevin equation $\frac{\partial r}{\partial t}=\frac{-D}{k_{\mathrm{B}}T}\frac{\partial E\left(r\right)}{\partial r}+\eta \left(t\right)$ (26,27) where D is the diffusion coefficient and η(t) is a noise term. This Langevin equation is equivalent to the Smoluchowski equation used previously to describe electroporation experiments (15–21). Unfortunately, this Langevin equation predicts that the pore, once it has grown bigger than the critical pore radius $r_{\mathrm{c}}=\frac{\gamma }{\sigma +a_{\mathrm{p}}{V}^2}$, grows exponentially in time. Since this result is contrary to experimental observations (1), the derivation of a correct Langevin equation must be constrained by further physical principles.

Before presenting our model, we discuss the prevalent model for the steady growth rate of a membrane pore (1,28), i.e., the assumption that a membrane pore grows like a pore in a soap film. Assuming that inertial effects dominate viscous effects, the growth rate of a pore in a soap film converges to the Culick-Dupré velocity $v_{\mathrm{c}}=\sqrt{(2\sigma /h\rho )}$ (29) after a short period of exponential growth. This transition from viscous to inertial regimes, and exponential to linear growth, has been observed for polymer films suspended in air at velocities of v = 6.3 m/s (30). For biological membranes with values of the surface tension and membrane thickness given in Table 1 and ρ = 1 g/cm³, the predicted Culick-Dupré velocity is v_c = 24.5 m/s. While such high velocities were observed in soap films (29), the velocities for pores in membranes range between 0.17 and 0.93 m/s (1,28), that is, nearly two orders-of-magnitude below theoretical predictions. We argue that this discrepancy is due to the effects of viscous forces on membrane pore growth. While the inertial regime is appropriate for thick soap films with high velocity fields, the calculation of the Reynolds number suggests that the viscous regime is more appropriate for the calculation of the membrane pore velocity. For biological membranes with v = 0.18 m/s (28) and a dynamic surface viscosity μ_s = 1 × 10⁻⁹ Ns/m (31), the ratio of inertial forces to viscous forces is given by the Reynolds number Re = ρ_svh/μ_s = 4.5 × 10⁻⁶. The surface density is ρ_s = hρ = 5 × 10⁻⁷ g/cm². Using the Culick velocity instead of the experimental velocity raises the Reynolds number to Re = ρ_sv_ch/μ_s = 0.0006.

Table 1.

Explanation, value, and source of different parameters used in the simulations

Parameter	Symbol	Value	Source
Electroporation constant	q	2.46	(46)
Electroporation parameter	α	100.0 cm−2 ms−1	(46)
Equilibrium pore density	N0	1.5e 2 cm−2	(1,46)
Characteristic voltage of electroporation	Ve	285 mV	(46)
Surface tension	σ	1.5e − 7 J·cm−2	(21)
Pore conductance	$\tilde{\rho }$	13 mS·cm−1	(20,46)
Minimum radius of aqueous pore	rm	0.8 nm	(41)
Steric repulsion constant	Cs	9.67e − 13 J1/4·cm	(41,50)
Constant in Eq. 1	ap	6.9e − 6 F·cm−2	(41)
Area of membrane patch	A	0.03 cm2	(1)
Membrane capacitance per area	C	0.95e − 6 F·cm−2	(46)
Membrane thickness	h	5 nm	(50)
Line tension	γ	1.8 e − 11 J·m−1	(21,50)
Membrane rest potential	Vr	0 mV	(1)
Radius of phospholipid molecule	rl	0.45 cm	(51)
Second radius of curvature of pore	re	2.5 nm	(50)
Diffusion constant	D	5e − 14 m2·s−1	(21)
Injection current	I	1–5 A·cm−2	(1)
External resistance	RE	1012 Ω	(1)
Internal resistance	RN	50 Ω	(1)

In the viscous regime, the flow v of molecules in a film must satisfy

$$\sigma -\frac{\gamma }{R}=2{\eta }_{\mathrm{m}}\frac{\partial v}{\partial r}+h{\eta }_{\mathrm{w}}\left(\frac{\partial v}{\partial z}+\frac{\partial u}{\partial r}\right),$$ (2)

where v and u denote the components of the velocity field in the r and z directions. Here h is the membrane thickness and η_m,η_w are the dynamic surface viscosity of the membrane and the dynamic bulk viscosity of water, respectively. The second term on the right-hand side is the rz component of the shear rate tensor accounting for the drag from the medium bathing the film. To model the rupture of soap films in air, the air drag can be neglected since air has a very low viscosity (29). Neglecting air drag, the assumptions of a pressure field independent of r and of a velocity field v = RV/r where V is a constant and R is the pore radius lead to an exponential pore growth (16). The case of membrane motion in a water solution is different from the free film motion since the water viscosity is high and there is a no-slip condition at the membrane-water interface (32). The assumptions that the velocity field is nearly constant in the radial direction as well as $\frac{\partial u}{\partial r}=0$ lead to the radial velocity at the rim of the pore,

$$v=\frac{z}{h{\eta }_{\mathrm{w}}}\left(\sigma -\frac{\gamma }{R}\right),$$ (3)

where z is the distance from an immobile layer of water parallel to the membrane. An estimate of this quantity is given by the minimum radius at which a membrane pore allows water flow, i.e., z = 0.15 nm (33). These quantities yield, for large pores, a rim velocity of v = zσ/hη_w = 0.3 m/s, which is well in the range of rim velocities measured in charge-pulse experiments (28). The assumption that the velocity profile is locally flat is based on the observation that the pore growth rate is linear in time for sufficiently large pore radii (1). A radial velocity field of the form v = RV/r, as proposed by Deryagin and Gutop (16), would produce a short-lived regime of exponential pore growth followed by a regime of steady growth given by Eq. 3. Inserting this circularly divergent velocity field into Eq. 2 shows that the strain rate due to the bulk medium becomes larger that the strain rate due to the membrane viscosity once the rim has grown beyond a certain transition radius, and that Eq. 2 converges to a constant growth rate as the rim radius grows. The transition radius is given by $2{\eta }_{\mathrm{m}}\frac{v}{\mathrm{R}}=h{\eta }_{\mathrm{w}}\frac{v}{\mathrm{z}}$, and yields R = 30 nm for a thickness of 10 nm. However, experiments suggest that the transition to linear growth happens before the rim has reached this length (1).

Using this pore velocity obtained from fluid dynamics, we can now derive the mobility and noise of a Langevin equation describing the pore statistics. From equilibrium thermodynamics and viscous fluid dynamics, the fluid flow j (34–36) is given by

$$\mathbf{j}=-{\Gamma }_{\mathrm{s}}\frac{\nabla \mu }{T}-{\Gamma }_{\mathrm{q}}\frac{\nabla T}{T^2}\text{.}$$ (4)

Here Γ_s and Γ_q are mobility coefficients for the flow due to chemical potential and temperature gradient, respectively. ∇μ is the gradient of the chemical potential or force acting on each molecule and T is the temperature. The chemical potential is defined as the energy per molecule $\mu =\frac{\partial E}{\partial N_{\mathrm{m}}}$ where N_m denotes the number of phospholipid molecules in the perforated membrane. By writing N_m = M – (r/r_l)² where r_l is the average radius of one phospholipid molecule and M is the total number of monomers in the membrane, we obtain the chemical potential $\mu =\frac{-\partial E\left(r\right)}{\partial (r^2/r_l^2)}$ or

$$\mu =\frac{-\pi r_l^2\gamma }{r}+\pi r_l^2(\sigma +a_{\mathrm{p}}{V}_{\mathrm{m}}^2)+\frac{2C^4{r}_l^2}{r^6}\text{.}$$ (5)

The chemical potential is decreased when the lipids rearrange to relax the tensile stress and the electrocompressive stress due to the electric potential. In the vicinity of the pore, this occurs through the formation of pore rim; the lipids tilt until they are perpendicular to the electric field. Far from the pore, the lipids are pulled by the tensile stress τ. From Eq. 3, the tensile stress in a sheet is related to the energy per surface σ by τ = σ/h. For a curved surface, thin shell theory (37) produces τ = σ/2h. Thus, the tensile force f_τ acting on each membrane monomer is related to the energy per monomer μ by f_τ = μ/h. We equate the tensile force f_τ to the thermodynamical force f = −∇μ to obtain – ∇μ = μ/h. We can now relate the velocity of the pore edge $\mathbf{v}=\frac{\mathrm{d}r}{\mathrm{d}t}$ to the flow given by Eq. 4 through j = vρ, where ρ is the membrane density.

We obtain a pore radius growth rate, which is directly proportional to the chemical potential (34)

$$\frac{\partial r}{\partial t}=\frac{{\Gamma }_{\mathrm{s}}\mu }{\rho \text{Th}}=\frac{{\Gamma }_{\mathrm{s}}{r}_l^2}{\rho \text{Th}}\left(\frac{-1}{2r}\frac{\partial E}{\partial r}\right)\text{.}$$ (6)

A similar equation was used previously by Allen and Cahn (38) for the motion of antiphase boundaries, where the growth of droplets is controlled by energetic considerations alone, and conservation laws play no important role. Substituting the energy function into this expression yields

$$\frac{\partial r}{\partial t}=\frac{r_l^2{\Gamma }_{\mathrm{s}}}{\rho Th}\left(\frac{-\pi \gamma }{r}+\pi (\sigma +a_{\mathrm{p}}{V}_{\mathrm{m}}^2)+\frac{2C^4}{r^6}\right),$$ (7)

which produces pore growth driven by curvature and tension. The contribution to the mobility Γ_s due to lipid diffusion is much smaller than the contribution due to the convective flow given by Eq. 3. Therefore, its value cannot readily be obtained from the diffusion constant of the lipids (32). Rather, the mobility must be such that the pore growth rate given by Eq. 7 matches, at zero transmembrane potential, the rim velocity Eq. 3 obtained from the consideration of viscous fluid dynamics. Here 1/r is the curvature of the pore. Curvature-driven growth was predicted for fusion pores (22) and droplets (38). Furthermore, in the regime where the contribution from the electric field is negligible (1), the right-hand side of Eq. 7 converges to a constant as the radius grows.

To obtain a complete description of the pore motion, it is necessary to account for the strong fluctuations in the motion of the lipids forming the bilayer. A standard Langevin equation is obtained by adding a multiplicative noise term

$$\frac{\partial r}{\partial t}=-\Gamma \left(r\right)\frac{\partial E}{\partial r}+g\left(r\right)\eta \left(t\right)\text{.}$$ (8)

Here η(t) is a Gaussian noise with temporal correlation 〈η(t)η′(t)〉 = δ (t – t′). The noise in our model stems from the random collisions between the lipid monomers. As expressed by the Einstein-Smoluchowski relation, the force exerted through random collisions generates the diffusive flux of monomers in the absence of mechanical tension and external electric field. The strength of the noise can therefore be related to the diffusion constant through a generalization of the above principle, the fluctuation-dissipation relation. The fluctuation-dissipation relation is $g\left(r\right)=\sqrt{2k_{\mathrm{B}}T\Gamma \left(r\right)}$ (39). From Eq. 7, the friction coefficient is given by $\Gamma \left(r\right)=\frac{r_l^2{\Gamma }_{\mathrm{s}}}{2r\rho \text{Th}}\text{.}$

Fokker-Planck equation

The Langevin description of the pore radius is equivalent to and can be transformed into a Fokker-Planck equation (FPE) for the probability P(r, t) of the pore to have a radius r. Essentially, it states that the probability distribution drifts and diffuses in time until it reaches a state of equilibrium.

The FPE that corresponds to the Langevin equation above depends on the interpretation of the noise term and the noise integral (26,27)

$$dW(t^{\prime },\Delta t^{\prime })={\int }_{t\text{'}}^{t\text{'}+\Delta t\text{'}}\mathrm{d}\text{tg}\left[r\left(t\right)\right]\eta \left(t\right)\text{.}$$ (9)

Since the temperature of the system is assumed to be uniform and the transport coefficient Γ(r) dependent on r, the isothermal convention is used (40). This convention, prescribing that g[r(t)] is evaluated after the noise occurs, is the only one that guarantees a FPE with an equilibrium probability having a Boltzmann distribution (39). After the derivation of Lau and Lubensky and using the isothermal convention, the Langevin equation can be transformed into the Fokker-Planck equation

$$\frac{\partial P(r,t)}{\partial t}=\frac{\partial }{\partial r}\left(\Gamma \left(r\right)\frac{\partial E}{\partial r}+\frac{g^2\left(r\right)}{2}\frac{\partial }{\partial r}\right)P(r,t),$$ (10)

with equilibrium distribution $P_{\text{eq}}\sim e^{-E/k_{\mathrm{B}}T}\text{.}$

This Fokker-Planck equation can readily be compared to the Smoluchowski equation used to describe electroporation (15–21). The Smoluchowski equation is closely related to the Fokker-Planck equation. Both are driven by an energy function and display drift-diffusion dynamics. However, while the Fokker-Planck equation describes a probability and is normalized such that $\int P\left(r\right)dr=1$, the Smoluchowski equation describes the distribution n(r) of pores of radius r. Since the total number of pores $N=\int n\left(r\right)dr$ changes in time, the Smoluchowski equation contains a source term in addition to the drift-diffusion term. Assuming that the drift-diffusion operator acting on n(r) is identical to the drift-diffusion operator acting on P(r), a Smoluchowski equation can be derived from Eq. 10. Using the relation $D=\frac{{\Gamma }_{\mathrm{s}}{k}_{\mathrm{b}}}{\rho }$, the Smoluchowski equation is written as

$$\frac{\partial n(r,t)}{\partial t}=\frac{\partial }{\partial r}\left(\frac{D{r}_l^2}{2r_{\mathrm{e}}r}\left(\frac{1}{k_{\mathrm{B}}T}\frac{\partial E}{\partial r}+\frac{\partial }{\partial r}\right)\right)n(r,t)+S(r,t)\text{.}$$ (11)

The first term between parentheses on the right-hand side of Eq. 11 drives the pore distribution toward an equilibrium state. The source term S(r, t) (41) describing the fluctuation in the number of pores due to pore creation and pore destruction is

$$S(r,t)=\frac{{\nu }_{\mathrm{c}}h}{k_{\mathrm{B}}T}{U}_r{e}^{\frac{-U}{k_{\mathrm{B}}T}}-{\nu }_{\mathrm{d}}nH(r-r^{\ast })\text{.}$$ (12)

Here U = (r/r_∗)²F_∗ – π a_pr²V² is the energy of nonconducting pores and U_r its derivative with respect to pore radius, F_∗ = 45 kT is the energy of a pore of radius r_∗, and H(r_∗ – r) is the Heaviside step function. The radius r_∗ denotes the radius at a local maxima of the pore energy in the absence of an electric field (41). The values v_c and v_d are the fluctuation rates per unit volume and molecule, respectively, and h is the membrane thickness.

The numerical values for these parameters are given in Table 1. Pores are created at a rate at which fluctuations overcome the nucleation energy barrier, which is dependent on the transmembrane potential. Meanwhile, pores are destroyed at a rate proportional to their number in the state of minimum radius r_∗. The equation given above has the same form as the Smoluchowski equation used previously (15–21,41).

Asymptotic solution

Neu and Krassowska (41) used boundary layer theory to derive a solution of the Smoluchowski equation for the total number of pores in the membrane. Their analysis yields a first-order differential equation with a right-hand side which has essentially the same form as the source term S(t) given above (41). While pores are created at a rate depending on $e^{{\mathrm{V}}^2}$, they are destroyed at a rate proportional to their total number. We will follow the procedure used by Neu and Krassowska (41) and show that the same asymptotic solution is obtained in our case.

The asymptotic analysis starts with a convenient rescaling of the Smoluchowski equation. The energy E will be denoted ϕ and the derivative with respect to r will be denoted by $\frac{\partial }{\partial r}$ or the subscript. The variables r, t, ϕ, U, and n are rescaled in the corresponding units r_∗ = r_l, 2r_∗r_e/D, E_∗, and 1/r³_∗. The rescaled Smoluchowski equation becomes

$$n_t+{\partial }_r\left(\frac{1}{r}\left(-\frac{{\varphi }_r}{\varepsilon }-\frac{\partial }{\partial r}\right)\right)n=\frac{U_r}{\mu \varepsilon }{e}^{-\frac{U}{\varepsilon }}-\frac{\xi }{\mu }nH(1-r)\text{.}$$ (13)

Here ɛ = kT/E_∗, μ = D/v_cr²_∗, and ξ = v_d/v_chr²_∗ are dimensionless parameters. By comparing the order of magnitude in terms of ɛ of the solution n on the 1⁺ and 1⁻ side of the boundary layer, it appears that n⁺ is much greater than n⁻. Hence, one can solve the problem in r > 1 and replace the pore destruction in the source term by an absorbing boundary condition. The reduced boundary value problem is given by

$$n_t+{\partial }_r\left(\frac{1}{r}\left(-\frac{{\varphi }_r}{\varepsilon }-\frac{\partial }{\partial r}\right)\right)n=\frac{U_r}{\mu \varepsilon }{e}^{-\frac{U}{\varepsilon }}$$ (14)

and the absorbing boundary condition n(1, t) = 0.

The Ansatz for the solution of this problem used by Neu and Krassowska (41) has the form

$$n(r,t)=g(r,t)e^{-(\varphi -{\varphi }_{\mathrm{m}})/\varepsilon }$$ (15)

and the reduced Smoluchowski equation in terms of the unknown function g is

$$g_{\mathrm{t}}-\frac{({\varphi }_t-{\dot{\varphi }}_m)}{\varepsilon }g+\frac{1}{r}(-g_{\text{rr}})$$ (16)

$$+(\frac{{\varphi }_r}{\varepsilon }+\frac{1}{r})g_{\mathrm{r}})=\frac{U_r}{\mu \varepsilon }{e}^{-U/\varepsilon }{e}^{(\varphi -{\varphi }_{\mathrm{m}})/\varepsilon }\text{.}$$ (17)

One can find the outer solution to this partial differential equation from the balance of the O(1/ɛ) terms.

However, since the outer solution does not match the boundary condition g(1, t) = 0, we must look for the boundary layer solution. In the boundary layer, g is of order O(ɛ), while g_r and g_rr are of order O(1) and O(1/ɛ), respectively. We therefore drop the smaller terms, keeping the bigger O(1/ɛ) terms from Eq. 17 and obtain

$$\frac{1}{r}(-g_{\text{rr}}+\frac{{\varphi }_r{g}_r}{\varepsilon })\sim \frac{U_r}{\mu \varepsilon }{e}^{-U/\varepsilon }{e}^{(\varphi -{\varphi }_{\mathrm{m}})/\varepsilon }\text{.}$$ (18)

We use the boundary layer coordinate

$$R=\frac{r-1}{\varepsilon },$$ (19)

and taking the limit ɛ → 0 while keeping R > 0 fixed, yields

$$-g_{\text{RR}}-\left|{{\varphi }^{\prime }}_{\ast }\right|g_{\mathrm{R}}\sim \frac{\varepsilon {U^{\prime }}_{\ast }}{\mu }{e}^{-{\varphi }_{\mathrm{m}}/\varepsilon }{e}^{-({U^{\prime }}_{\ast }+|{{\varphi }^{\prime }}_{\ast }\left|\right)R}\text{.}$$ (20)

To obtain the previous expression, the Taylor expansion ϕ = ϕ_∗ – |ϕ′_∗|(r − 1) as well as the relations g_r = g_R/ɛ and g_rr = g_RR/ɛ² were used. In this equation ϕ′_∗ = ϕ_r(1⁺, t) and U′_∗ = U_r(1⁺, t). The boundary condition g = 0 at R = 0 remains and the solution should converge to the outer solution as R → ∞. This result is identical to the intermediate expression obtained by Neu and Krassowska (41). One can see that the 1/r adds only lower-order terms to the differential equation and therefore produces the same end result.

Equation 20 and, thus, the Smoluchowski equation have the boundary layer solution in terms of the electric potential and total number of pores:

$$\frac{dN}{dt}=\alpha e^{{(V_{\mathrm{m}}/V_{\text{ep}})}^2}\left(1-\frac{N{e}^{-q{(V_{\mathrm{m}}/V_{\text{ep}})}^2}}{N_0}\right)\text{.}$$ (21)

Here α, N₀, and q are constants whose values in the following simulations are fitted from experiments. We refer to Neu and Krassowska (41) for the intermediate steps leading from Eq. 20 to the previous equation.

We now have two equivalent descriptions for the pore dynamics in membranes. The Smoluchowski equation, describing the distribution of pore radii, is best suited for a large number of pores and short integration times. The second description is a Langevin equation for the pore radius, Eq. 8, coupled the equation for the number of pores due to Neu and Krassowska (41). These two ordinary differential equations are faster to solve numerically and allow us to simulate the growth rate of single pores. Furthermore, by using these coupled equations we can simulate voltage-clamp systems that involve long integration times unattainable by the solution of the Smoluchowski equation.

Charge pulse experiment

Our description of electroporation must be coupled to an equation for the transmembrane potential. During a pulse-charge experiment, a membrane is charged by a short current injection and then discharged as ions leak through nucleated pores. This experiment (1,21,42) can be modeled by a resistor-capacitor circuit in parallel with a current source I, which is switched on at the beginning of the experiment and switched off after the pulse ends (∼5 μs) (20,21). The first-order differential equation for the transmembrane potential is

$$C\frac{\mathrm{d}{V}_{\mathrm{m}}}{\mathrm{d}t}=\frac{\mathrm{I}{R}_{\mathrm{N}}}{R_{\mathrm{E}}+R_{\mathrm{N}}}-V_{\mathrm{m}}G\left(t\right)-\frac{V_{\mathrm{m}}}{R_{\mathrm{E}}+R_{\mathrm{N}}}$$ (22)

if t < t_pulse and

$$C\frac{\mathrm{d}{V}_{\mathrm{m}}}{\mathrm{d}t}=-V_{\mathrm{m}}G\left(t\right)$$ (23)

if t > t_pulse. While many models have been used for the membrane conductance G(t), we choose a minimalistic model

$$G\left(t\right)=\frac{N\left(t\right)}{R_{\text{ch}}},$$ (24)

where

$$R_{\text{ch}}=\left(h+r\left(t\right)\pi /2\right)\frac{\tilde{\rho }}{r{\left(t\right)}^2\pi }\text{.}$$ (25)

This expression relates the membrane conductance to the number of pores and the average pore radius. The value of the channel resistance R_ch converges, for large radii, to $R_{\text{ch}}=\tilde{\rho }/2r$ (43). This limit is based on the calculation of the field distribution on a plate condenser containing a circular defect of radius r (44) and is the same as the access resistance used previously (43). Here $\tilde{\rho }$ is the pore conductivity. A correction that has not been included in our analysis is the effect of ion diffusion (45,46).

Numerical Results

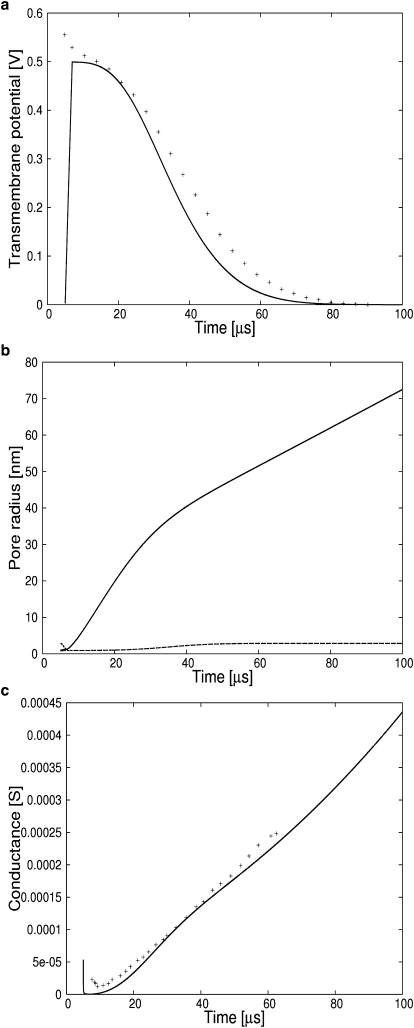
During the charge-pulse experiment conducted by Wilhelm et al. (1), a small patch (0.03 cm²) of membrane was exposed to a low voltage of ∼0.55 V. Under these conditions, a single pore was nucleated in the membrane patch. Its radius was measured indirectly using the membrane conductance. We simulate this experiment by coupling Eqs. 7 and 22–24 and the membrane parameters listed in Table 1. The asymptotic equation for the number of pores, Eq. 21, will not be used since the number of pores is very small and the variation in the number of pores proceeds by discrete jumps. The equation for the number of pores will be necessary for setups with large voltages (0.8–1.4 V), where the number of pores is large (8 × 10³ − 1 × 10⁶) and varies continuously. Such a setup will be discussed below. As seen from the solution of these equations shown in Fig. 1, a–c, a membrane charged to ∼0.5 V will discharge in 100 μm. As seen in Fig. 1 b, the pore radius grows without bounds, showing that this voltage induces membrane rupture. As emphasized on Figs. 1 b, 2 a, 3 b, and 4 b, the pore grows when its radius is greater than the critical radius $r_{\mathrm{c}}\left(t\right)=\frac{\gamma }{\sigma +a_{\mathrm{p}}\mathrm{V}{\left(t\right)}^2}$ and the pore shrinks otherwise. During this time, the membrane conductance is given by the relation $G\left(t\right)=\frac{-\mathrm{d}V}{\mathrm{d}t}\frac{C}{V\left(t\right)}$ (1). The result is shown in Fig. 1 c. The conductance is nearly linear in time if the surface tension σ = 3.5 mJ·m⁻² is used. The conductance from our simulation is compared to a field-induced breakdown experiment conducted on a diphytanoyl phosphatidylcholine/n-decane membrane. These data were recorded in an aqueous phase containing 1 M KCl (1).

Figure 1.

(a) (Dashed line) Numerical results showing how a small membrane patch, charged to 0.53 V, discharges while a single pore grows. The simulations were performed with σ = 3.5e − 7 J·cm⁻². (Crosses) The data recovered from an experiment performed on a diphytanoyl phosphatidylcholine/n-decane membrane in an aqueous phase containing 1 M KCl (1). (b) (Solid line) Single pore radius. (Dashed line) Critical radius. (c) (Dashed line) Numerical membrane conductance. (Crosses) Experimental data.

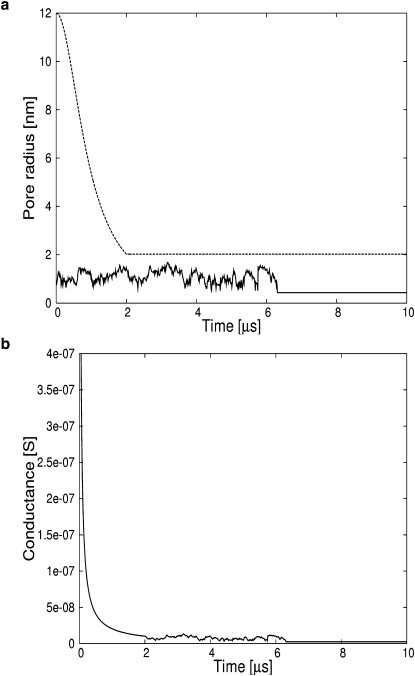
Figure 2.

A small membrane patch charged to 0.32 V reseals as seen from the limited growth of a single pore. (a) (Solid line) Single pore radius. (Dashed line) Critical radius. (b) Membrane conductance.

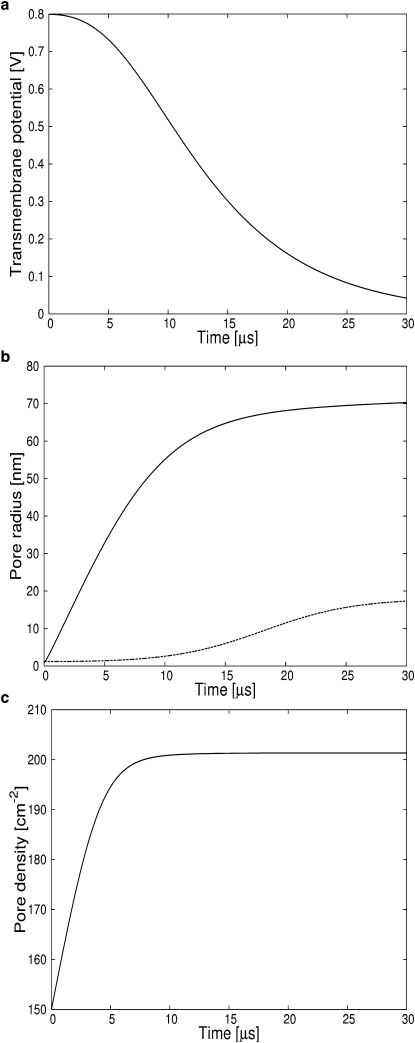
Figure 3.

A membrane patch charged to 0.8 V ruptures as seen from steady increase in the average pore radius. The pore density is insufficient to shunt off excess charge before irreversible membrane breakdown. (a) Transmembrane potential. (b) (Solid line) Single pore radius. (Dashed line) Critical radius. (c) Pore density.

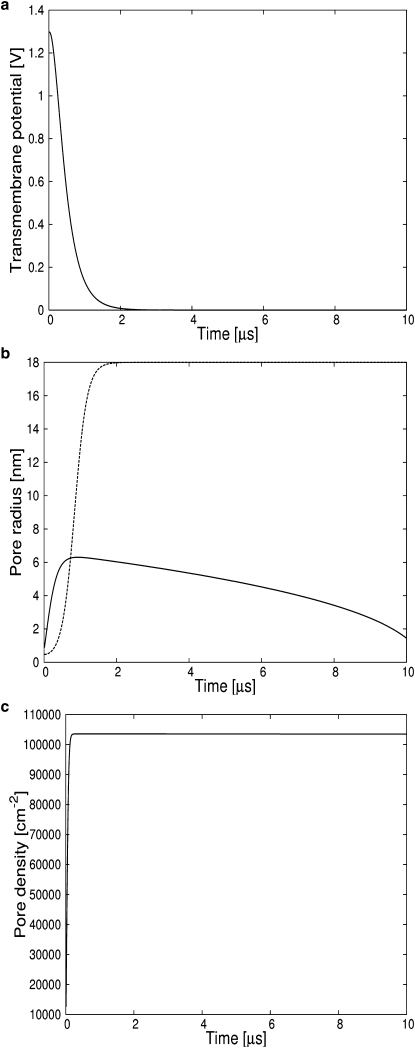
Figure 4.

A membrane patch charged to 1.3 V reseals as seen from the reversible growth and decay of the average pore radius. The very high pore density shunts off excess charge before the average pore radius exceeds the critical radius. (a) Transmembrane potential. (b) (Solid line) Single pore radius. (Dashed line) Critical radius. (c) Pore density.

Generally accepted values(21) for membranes discharge times are >100 μs, 10–100 μs, and 1–10 μs for transmembrane potentials of 0.4 V, 0.4–1.0 V, and >1.0 V, respectively. These values are reproduced by our simulations and shown in Figs. 1–4.

If the current source in the charge-pulse experiment is weaker and the membrane is charged to voltages <0.4 V, the membrane will reseal after the nucleation of a pore. The pore will stop growing because the line tension is stronger than the combination of the mechanical and electric-field-induced surface tensions. The voltage, pore radius, and membrane conductance for a membrane charged to 0.32 V are shown in Fig. 2, a–c. Since the voltage is below the critical value of 0.4 V necessary for pore growth, the pore remains very small, <∼0.8 nm. Due to the fluctuations of the pore radius induced by random collisions between lipid monomers, the radius eventually falls <r_∗ = 0.5 nm, meaning that the pore effectively collapses. Meanwhile, the membrane conductance fluctuates around a value very close to zero. The transmembrane potential rises to 0.33 V and then stays constant. Since the voltage is essentially constant through time, its curve is not shown. This first set of simulations shows that our equation for the time dependence of the pore radius reproduces one important feature of pore dynamics: a pore in a membrane will continue to grow if the transmembrane potential is >0.4 V and will shrink if the voltage is ever lower while its radius is below the critical radius. Consequently, membranes rupture if charged to slightly higher voltages than the critical voltage (8) but reseal for voltages below the critical value.

A second well-documented feature of pore dynamics is electroporation: the nucleation of many pores inducing rapid discharge and resealing of a membrane charged to high (>1.2 V) potentials. This reversible electrical breakdown was modeled previously using the Smoluchowski equation (20,21). While the asymptotic solution due to Neu and Krassowska (41) describes the nucleation and subsequent destruction of many small pores, their solution cannot distinguish between a membrane that reseals and a membrane that ruptures. By coupling Eq. 7 for the pore radius to Eq. 21 for the number of pores and Eqs. 22–24 for the membrane potential, we can distinguish between reversible electrical breakdown and irreversible electrical breakdown (rupture). Membranes rupture when charged to voltages up to 1.2 V (Fig. 3) and reseal for higher voltages (Fig. 4). The average growth rate of radius of a pores is proportional to a_pV² but the equilibrium pore density is proportional to $e^{{\mathrm{V}}^2}$. This dependence explains the high number of pores that are created in membranes charged to higher potentials. Figs. 3 c and 4 c show that the pore density in the membranes shortly after the end of the pulse is >250,000 cm⁻² for the membrane charged to 1.3 V but only ∼220 cm⁻² for a membrane charged to 0.8 V. The large variation in pore density explains why the first membrane discharges in 2–3 μs while the membrane charged to an intermediate potential requires >20 μs to discharge. As can be seen from Fig. 4 c, the membrane initially charged to 0.8 V retains a transmembrane potential higher than the critical 0.4 V for roughly 15 μs. This time span allows the pore that nucleated at 0.8 nm to grow beyond the critical radius of 18 nm (41) thus preventing resealing even when the transmembrane potential is back to zero Volt. Under these conditions, a membrane will rupture. On the other hand, a membrane charged to 1.3 V will discharge so fast that the pore will not have enough time to overcome the second energy barrier necessary for rupture. The average pore radius will grow rapidly while the transmembrane potential is >0.4 V and will shrink slowly once the voltage drops below that value, at a time of 2 μs.

Voltage-clamp experiments

The phenomenon of reversible electrical breakdown is possible due to the very high (10²⁸ s⁻¹ (21)) pore nucleation rate of phospholipid membranes. These pores allow the excess charge to redistribute within microseconds and the transmembrane potential to decay before individual pores grow beyond the critical size. Imposing a constant transmembrane potential by a variable current source (a voltage-clamp experiment) prevents the charge redistribution and the voltage decay, even in the presence of a very high number of aqueous pores. The voltage-clamp setup will allow an individual pore, driven by the constant electric field, to grow beyond the critical size and rupture the membrane. According to our simulations, imposing a high command voltage for a long pulse duration leads to the disappearance of the phenomenon of reversible electrical breakdown.

As before, the pore dynamics were described using Eqs. 7 and 21. Instead of using Eq. 23 for the charging and discharging of the membrane, we use

$$C\frac{\mathrm{d}{V}_{\mathrm{m}}}{\mathrm{d}t}=\frac{V_{\mathrm{c}}-V_{\mathrm{m}}}{R_{\mathrm{E}}+R_{\mathrm{N}}}-V_{\mathrm{m}}G\left(t\right)\text{.}$$ (26)

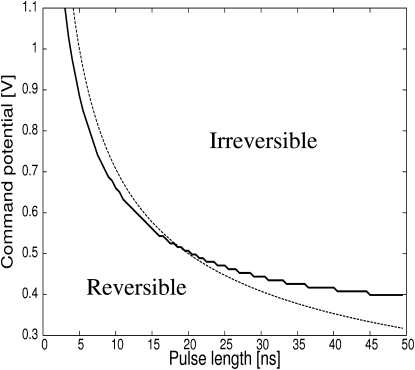
Here V_c is the command voltage imposed by the voltage-clamp amplifier. Its value is a constant and chosen, for each simulation, between 0.3 and 1.1 V until the end of the pulse. After the end of the pulse, it is set to zero. Once the transmembrane potential has reached the command voltage, its value is held constant until the command voltage changes. The result of these simulations for different values of the pulse length and the value of the command voltage during the pulse are shown in Fig. 5 in the form of an effective phase diagram. While the membrane breaks down reversibly for imposed transmembrane potentials <0.4 V, it will break down irreversibly and rupture for high values of the command voltage and pulse duration. The shape of the line separating the parameter space leading to rupture from the parameter space leading to reversible breakdown can be interpreted as follows. Using Eq. 7 and neglecting the contribution of the surface tension, we assume a constant pore growth rate proportional to the square of the transmembrane potential. To rupture the membrane, the duration t of the pulse must be sufficient for the pore to reach the critical radius at zero potential, i.e., r_c(V=0) = γ/σ. Consequently, the command voltage necessary to rupture the membrane for a given pulse length must satisfy to r/t ∝ V_c² > r_c/t. This function is shown by the dashed line in Fig. 5.

Figure 5.

(Solid line) Effective phase diagram for voltage-clamp experiment with pulse length and command voltage during the pulse as parameters. The region labeled “Irreversible” covers the parameter space for which the membrane ruptures, i.e., irreversible electrical breakdown, whereas the region labeled “Reversible” covers the parameter space of reversible electrical breakdown. (Dashed line) $V=\sqrt{5/t}$ where V is the command voltage and t is the pulse length.

Discussion

We have introduced a Langevin-type equation for the pore radius of single pores and for the average pore radius of ensembles of pores. Using this model, we reproduced the known phenomenology of pore dynamics in pulse-charged membranes. Whereas pores grow irreversibly and rupture the membrane for intermediate values of voltage, pores grow and shrink reversibly for low and high voltage values. Growth of single pores was tracked and the membrane conductance was simulated for experiments involving long timescales and low voltages, thus allowing a direct and successful comparison to experiments (1,42). Finally, voltage-clamp experiments were simulated and an irreversible membrane breakdown (rupture) was predicted for high voltage values and sufficiently long pulse times. The value of 0.4 V as a lower limit for irreversible breakdown is due to the free energy of the membrane, Eq. 1, which sets the height of the energy barrier to overcome for membrane rupture. With the current values of surface tension and noise amplitude, pores will never grow beyond the critical radius if the voltage is kept <0.4 V. However, a higher mechanical tension as well as a higher temperature and noise amplitude would allow pores to rupture irreversibly at voltages <0.4 V (8). The choice of 1.2 V for a limiting voltage is arbitrary. The behavior at higher voltages should follow the trend observed in Fig. 5.

The great advantage of our formalism is an ability to model membrane systems that involve single or few pores such as the fusion pore involved in exocytosis. The behavior of this pore is assumed to be entirely determined by lipid interactions following the lipid-stalk model (47–49). While there has been a good first model of this pore using a Langevin formalism by Chizmadzhev et al. (22), many features that may be important to the growth of a fusion pore were not addressed. Anisotropic voltages and tensions in membranes might lead to noncircular pores, rendering the use of a pore energy as a function of the pore radius E(r) inadequate. In such circumstances, the use of a local curvature-dependent energy functional and a chemical potential-dependent pore-edge velocity are necessary.