Tensile Mechanics of Alanine-Based Helical Polypeptide: Force Spectroscopy versus Computer Simulations

Abstract

In nature, an α-helix is commonly used to build thermodynamically stable and mechanically rigid protein conformations. In view of growing interest in the mechanical rigidity of proteins, we measured the tensile profile of an alanine-based α-helical polypeptide on an atomic-force microscope to investigate the basic mechanics of helix extension with minimal interference from side-chain interactions. The peptide was extended to its maximum contour length with much less force than in reported cases of poly-L-Glu or poly-L-Lys, indicating that chain stiffness strongly depended on the physicochemical properties of side chains, such as their bulkiness. The low tensile-force extension originated presumably in locally unfolded parts because of spontaneous structural fluctuations. In 50% trifluoroethanol, the well-known helix-promoting agent, the rigidity of the sample polypeptide was markedly increased. Computer simulations of the peptide-stretching process showed that a majority of constituent residues underwent a transition from an α-helical to an extended conformation by overcoming an energy barrier around ψ ∼0° on the Ramachandran plot. The observed lability of an isolated helix signified the biological importance of the lateral bundling of helices to maintain a rigid protein structure.

Introduction

The α-helix, along with the β-sheet, is one of the two most fundamental secondary structures to comprise the native conformation of protein molecules, and is uniquely determined as the most stable thermodynamic state for a given amino-acid sequence under physiological conditions (1). The periodically hydrogen-bonded α-helical conformation itself was shown to be a thermodynamically stable state for polypeptides such as poly-L-glutamic acid (PGA), poly-L-Lys, and for L-Ala-based polypeptides, without any interchain interactions (2,3). However, its stability within a protein molecule seems to be augmented by side-chain interactions with other polypeptide segments or chains. One notable example is a protein with coiled-coil conformations where two helical rods are intertwined to form a doubly chained superhelix as observed, for example, in the rod section of myosin molecules (4). As a consequence, a certain level of mechanical rigidity is conferred to the protein structure, which might act as a vital foothold during the activation process of muscle contraction (5). Similarly, in the case of an enzyme molecule, a mechanically rigid conformation is required to hold its substrate in an activated form (6). Thus there is growing interest in measuring the mechanical stability or rigidity of proteins and those of polypeptides as the model compounds at the single-molecular level and further, into the distribution of local rigidity within a single molecule (7,8). Efforts to measure the mechanical properties of single-protein and polypeptide molecules used recently developed instruments such as laser tweezers, surface-force apparatus, and atomic-force microscopy, with notable examples revealing tensile strength and force-extension (F-E) profiles of model proteins and polypeptides (9–15). In contrast to bulk thermodynamic measurements, mechanical measurements enable an ascertainment of the material properties of localized structures and their response to anisotropic perturbations, such as a uniaxial pulling of a sample protein or polypeptide. Because the mechanical property of a protein molecule is built mainly upon those inherent to the α-helix and β-sheet structures and to their mutual interactions, it is vital to accumulate knowledge on the corresponding properties of the α-helix and β-sheet in terms of chain stiffness, tensile strength, and elastic (Young's) modulus, i.e., measures of material resistance against externally applied forces (16,17).

Morozov and Morozova reported on their mechanical characterization of macroscopic protein crystals using vibrational analysis, but they did not interpret their data in terms of physical properties of the molecules comprising the crystals (18). Kojima et al. pulled a double-helical actin fiber, using a glass rod as a force sensor, and obtained the tensile strength and Young's modulus of a single actin fiber as 600 pN and 2.5 GPa, respectively (19). Their measurement gave a surprisingly high value for Young's modulus of ∼10 GPa for a bound tropomyosin to an actin fiber. Suda et al. used a surface-force apparatus (SFA) to measure the stiffness and Young's modulus of myosin molecules (20). In an early attempt to use an atomic force microscope as a nanoindenter, Radmacher et al. compressed lysozyme molecules adsorbed on a mica surface and estimated Young's modulus to be ∼0.5 GPa from an analysis based on the Hertz model (21). Afrin et al. (22) improved the atomic force microscopy (AFM)-based method, and obtained Young's modulus for immobilized carbonic anhydrase molecules as 70–80 MPa by applying a newly developed theoretical model of Tatara, which extends the Hertz model to a large deformation regime (23).

Experimental results on the tensile property of α-helical polypeptides were reported by Lantz et al. (24), Idiris et al. (25), and Kageshima et al. (26). Mechanical unfolding of predominantly α-helical proteins such as apo-calmodulin (27) and of the helical domains of spectrin (28) was also reported. The helical portion of these polypeptides and proteins seems to show quite different levels of stiffness against an axially applied tensile force.

Even in the absence of side-chain interactions between neighboring chains, therefore, geometrical or mechanical constraints between side chains on the same helical segment are possible. To know the basic mechanical property of an α-helix with as little influence from such side-chain interactions as possible, it is desirable to perform a mechanical measurement on poly-L-Ala, which is insoluble in aqueous buffer. To circumvent this difficulty, we can adopt the strategy followed in work on the determination of the helical propensity of various amino-acid residues by using L-Ala (A)-based polypeptides with regularly inserted hydrophilic amino-acid residues such as Lys, Glu, or Arg (29–31). For example, a polymer with the repeating sequence of (AAAAK)_n was found to be readily soluble and to form α-helices in aqueous buffers as well as in a mixed solvent of water with trifluoroethanol (TFE). We modified the sequence of (AAAAK)_n, inserting terminal Cys (C) residues, so that the peptide could be covalently immobilized to an AFM probe as well as to a solid substrate. Thus the peptide could be mechanically stretched by using AFM, as was done for α-helical PGA (25). When the polypeptide was stretched on the AFM, the resulting F-E profiles were surprisingly different from those obtained for PGA. We present the experimental results of the mechanical stretching of [C(KAAAA)₁₀KC]_n in neutral buffer, with and without high concentrations of NaCl, in 50% TFE and in 6 M guanidinium chloride (GdmCl), and then compare the results with those for PGA. The general experimental setup is presented in Fig. 1. A general axial stretching of a helical structure imposes a rotation around the helical axis, but in the experimental setup shown in Fig. 1, the twisting stress is alleviated through rotation about any of the single bonds in the nonhelical parts of the system, including those in the cross-linkers. We also present the results of a steered molecular-dynamics (SMD) simulation that indicated possible routes of the conformational change in terms of dihedral angles on a Ramachandran plot. Although controversy continues regarding the precise geometry of the helix of Ala-based polypeptides (32), our experimental results apply to a transition from a “helical” to an “extended” state, based on a conventional circular dichroism (CD) spectrum and AFM-based mechanical pulling.

Figure 1.

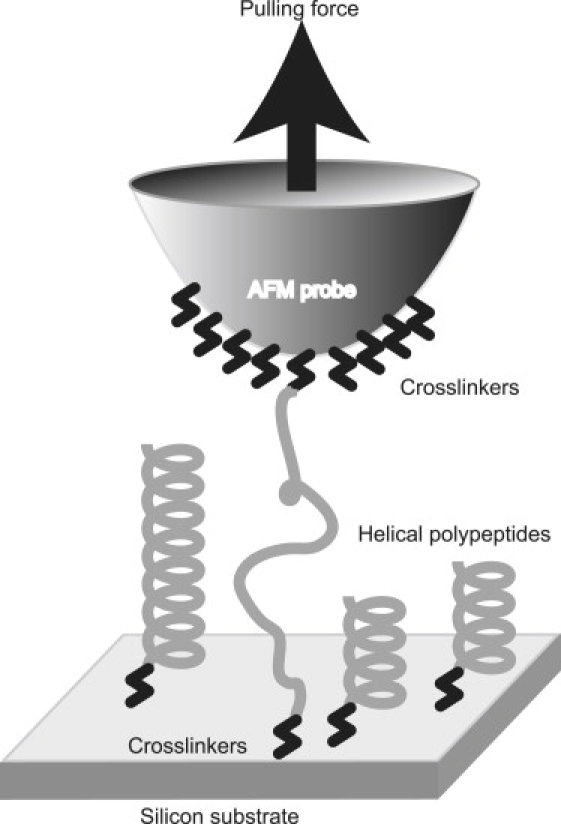
Schematic presentation of experimental setup for measurement of extension profile of [C(KAAAA)₁₀KC]_n. Polypeptide was sandwiched between AFM probe and substrate through covalent cross-linkers, and pulled in vertical direction.

Materials and Methods

Polypeptide

The polypeptide with a sequence of C(KAAAA)₁₀KC was synthesized by the Peptide Institute (Suita, Osaka, Japan). Its purity was confirmed by reverse-phase chromatography, and the molecular weight of the peptide was confirmed using matrix-assisted laser desorption/ionization time of flight mass spectrometry, by the manufacturer. The results of our preliminary gel chromatography using Sephadex G-200 indicated that the peptide was covalently polymerized to various degrees through disulfide linkages, as confirmed by AFM experiments. We used the polymerized sample in subsequent AFM experiments, denoting it as [C(KAAAA)₁₀KC]_n because the original peptide with 53 amino-acid residues was too short for determining F-E profile with confidence.

Chemicals

Succinimidyl 6-(3′-[2-pyridyldithio]-propionamido)hexanoate (LC-SPDP) was purchased from Pierce (Rockford, IL) and stored under highly dehydrated and low-temperature conditions. The silanization reagent, 3-aminopropyltriethoxy silane (APTES), was purchased from Shin-Etsu Chemicals (Tokyo, Japan). The GdmCl and other chemicals were purchased from Sigma Chemical Co. (St. Louis, MO) and Wako (Tokyo, Japan). All reagents were used without further purification.

CD spectroscopy

Circular dichroism spectra were recorded at 25°C on a J-720WI spectropolarimeter (JASCO, Tokyo, Japan), using 1-mm quartz cells for the sample in Tris buffer at pH 7.4, with or without 400 mM NaCl. Spectra in 50% TFE and in 6 M GdmCl, both also in Tris buffer at pH 7.4, were taken at 25°C.

Atomic force microscopy

We used a Nanoscope III multimode scanning probe microscope (Digital Instruments, Santa Barbara, CA) in the force mode to obtain the mechanical response of [C(KAAAA)₁₀KC]_n upon application of a tensile force. Silicon substrates and silicon nitride NP-S AFM probes (Veeco Instruments, Plainview, NY) were chemically modified, first with APTES, and then with LC-SPDP, so that the surfaces of both the substrate and the probe became reactive to sulfhydryl groups of terminal Cys residues of [C(KAAAA)₁₀KC]_n. To prepare the AFM for stretching experiments, an aliquot of aqueous solution of [C(KAAAA)₁₀KC]_n was dropped on the modified silicon substrate and left for 30 min for immobilization. The substrate was then rinsed with buffer several times, and the remaining cross-linkers were deactivated if any remained, and finally the substrate was ready for the AFM operation. The modified probe was mounted on the cantilever holder of the AFM, and then brought into contact with the substrate covered with [C(KAAAA)₁₀KC]_n, so that covalent bonds were formed between the tip and the peptide. The substrate was then lowered, to break the contact and stretch the peptide. To reduce the possibility of multiple-bond formation, the number density of [C(KAAAA)₁₀KC]_n on the substrate was controlled by changing the peptide concentration of the modifying solution, so that covalent-bond formation was kept to less than 40% of the total number of probe-substrate contacts (22,25). The spring constant of cantilevers was determined according to a method proposed elsewere (33). The pulling speed was ∼100–1000 nm/s.

Computer simulation

Computer simulations of peptide-stretching were performed on the Origin 2000 supercomputer (Japan SGI, Tokyo, Japan), maintained at the Computer Center of the Tokyo Institute of Technology. Stretching experiments of C(KAAAA)₅KC peptide were simulated by the SMD method, as initiated by Lu et al. (34) and extensively developed and applied by others (35–37). The molecular model of the C(KAAAA)₅KC peptide of 28 residues (357 atoms) was created by using HyperChem 6 software (Hypercube, Inc., Gainesville, FL), and equilibrated in the presence of 8431 explicit TIP3P water molecules (25,293 atoms) solvating the peptide. Six Cl⁻ counterions against the positive charges of the amino groups on the Lys residues and the N-terminus were also added. A Sander classic module of AMBER 7 (38) was used, with a modification required for SMD simulation. The molecular model of C(KAAAA)₅KC peptide was equilibrated for 120 ps by raising the temperature from 100 K to 300 K in six steps (100 K, 200 K, 300 K, 300K, 300 K, and 300 K, with a 20-ps equilibration time for each step), before the stretching simulation was initiated. The helicity after equilibration was 97.7% according to the criteria of main-chain hydrogen-bond formation. Our criteria of main-chain hydrogen-bond formation included a distance between the O atom on the i-th peptide group and the N atom on the (i + 4)-th peptide group of less than 0.34 nm, and an O-H-N angle of between 0–50°.

In SMD simulations, a virtual spring was assumed to connect the C^α atom of the N-terminus residue to a rigid wall, which was made to recede at three different speeds of 0.1 nm/ps, 0.01 nm/ps, and 0.001 nm/ps, whereas the C-terminus was kept at a fixed position. The time step of integration of the equation of motion in the simulation was set at 1 fs. The cutoff distance for van der Waals force was set at 1.5 nm, with no cutoff for the Coulomb force. The simulation conditions were 300 K and 1 atm. Simulation results were expressed in terms of the length of the stretched peptide against the tensile force, and compared with the experimental results.

Results

CD spectra

Fig. 2 summarizes the CD spectrum of [C(KAAAA)₁₀KC]_n in 50 mM Tris buffer at pH 7.4 (to be abbreviated as 50 mM Tris) (red) and under three other conditions, i.e., in the same buffer with an additional 400 mM NaCl (to be referred to as 400 mM NaCl) (green), with an additional 50% (v/v) TFE (to be referred to as 50% TFE) (brown), and with an additional 6 M GdmCl (to be referred to as 6 M GdmCl) (blue) at 25°C. The spectrum in 6 M GdmCl was cut off at 212 nm, because of increasing noise in the shorter-wavelength region. The helix content of [C(KAAAA)₁₀KC]_n was estimated by a method described elsewhere (39), and the result was ∼70% in 50 mM Tris at 25°C. By repeating a similar procedure, the helical content of [C(KAAAA)₁₀KC]_n was determined at 25°C as ∼72% in 400 mM NaCl, ∼80% in 50% TFE, and ∼5% in 6 M GdmCl. The temperature dependence of the CD spectrum of [C(KAAAA)₁₀KC]_n in aqueous buffer (data not shown), as well as in 50% TFE, confirmed that the helix-coil transition of this peptide was not a sharp but a gradual one, as shown previously (3). A deep trough at ∼205 nm, observed in 50% TFE, was reported (40). As discussed below, the sample polypeptide was an oligomerized version of [C(KAAAA)₁₀KC]_n through disulfide-bond formation between the cysteine residues at its two ends. Although (KAAAA)₁₀ parts have a high propensity to form an α-helix, the disulfide linking parts do not, and consequently, our estimation of the conformation of the sample polypeptide was a small number of helical segments connected by flexible joints.

Figure 2.

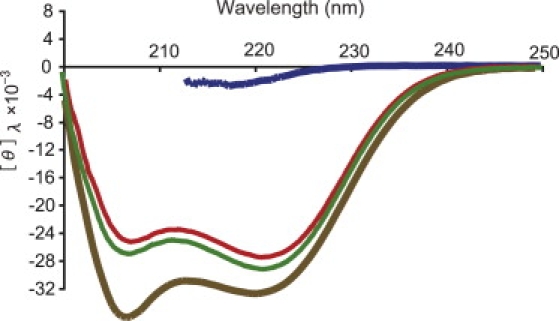
CD spectra of [C(KAAAA)₁₀KC]_n peptide in 50 mM Tris buffer at pH 7.4 (red), with an additional 400 mM NaCl (green), 50% TFE (brown), and 6 M GdmCl (blue), respectively. Ordinate represents molar residue ellipticity, [θ]_λ, in units of [degree·cm²/decimol], as a function of wavelength.

AFM experiment

The raw data from the force mode of AFM involves the relationship between the cantilever deflection (d) versus the distance covered by the sample stage (D) driven by the piezo motor. The curve is converted to a mechanically meaningful one of tensile force versus the chain extension (force-extension, F-E) curve by calculating the tensile force, F = −k × d, where k is the spring constant of the cantilever, and the chain extension is E = D − d (20).

Representative force curves obtained in four different solvent conditions are presented in Fig. 3 A. Curves a, b, and c were obtained in 50 mM Tris, but only curve a has no indication of nonspecific adhesion, either of the AFM probe or of the sample peptide to the substrate, whereas both curves b and c show such adhesive interactions, either as plateaus or as force peaks in the initial part of the retraction curves. We collected only those curves similar to curve a, without any indication of nonspecific adhesion of the sample to the substrate for later analysis. Curves d, e, and f were obtained in 400 mM NaCl, in 50% TFE, and in 6 M GdmCl, respectively. Both the approach and the retraction curves in all cases exhibited gradually changing, reversible slopes extending approximately to 10 nm, signifying that the end-grafted polypeptide chains extended into the bulk solution, without any indication of unwanted adhesive plateaus or peaks. The average final rupture force was greater than 1.2 nN in aqueous buffer systems, which confirmed that the pulling experiment was performed on polypeptide chains covalently fixed to the substrate and to the AFM probe. Only in 50% TFE was the final rupture force slightly less than 1.0 nN, for unknown reasons.

Figure 3.

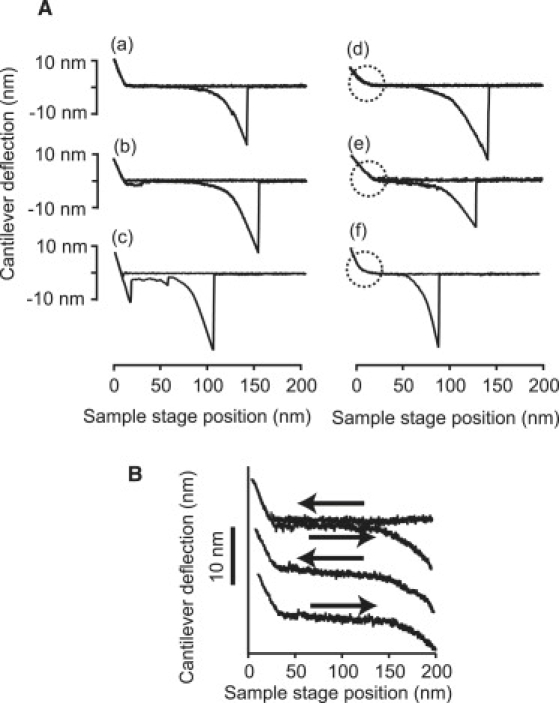
Collection of force curves of [C(KAAAA)₁₀KC]_n obtained under different conditions. (A) Collection of various types of force curves. (a) In 50 mM Tris buffer, pH 7.4: force curve without any indication of adhesion. (b) With a plateau like adhesion. (c) With initial strong adhesion, followed by extension of a plateau. (d) Obtained in 50 mM Tris buffer, pH 7.4, with 400 mM NaCl. (e) 50 mM Tris buffer, pH 7.4, with 50% TFE. (f) 50 mM Tris buffer, pH 7.4, with 6 M GdmCl. Parts of curves marked by dotted circles highlight gradual change of slope, as explained in text. (B) Record of approach and retraction cycles obtained in 50% TFE, showing reversibility of the conformational change of the sample polypeptide.

In Fig. 3 B, an example of the continuous approach and retraction cycles observed in 50% TFE shows completely reversible cyclic mechanics, without any indication of adhesion to the substrate.

Because the extension of [C(KAAAA)₁₀KC]_n from its α-helical state is of major concern here, any modification of helical conformation because of interactions with the solid substrate should be avoided. Such conformational change was implicated for short peptides, either directly adsorbed to the substrate or adjacent to the adsorbed peptides (41–43). Although we did not measure the CD spectra of [C(KAAAA)₁₀KC]_n after immobilization on silicon wafer covered with APTES and subsequently with LC-SPDP, force curves with no adhesion, as collected in 50 mM Tris, in 400 mM NaCl, and in 50% TFE, should represent the stretching events of α-helical polypeptides. In the latter two solvent cases, the absence of adhesion was further substantiated by the fact that the polypeptide was extended into the bulk solvents.

A collection of representative F-E curves is given in Fig. 4 A with substantially different lengths of total extension, reflecting that the original cysteine-containing [C(KAAAA)₁₀KC] was oligomerized through disulfide-bond formation. From the most prevalent values of total extension lengths of 70–80 nm obtained in the present AFM experiments, an average degree of oligomerization was estimated at 4–5 by setting the contour length of a monomeric [C(KAAAA)₁₀KC] to 18 nm. Several factors, such as 1), horizontal and vertical attachment sites of the two ends of the polymer to the substrate and to the probe; and/or 2), nonentropic extension of the chain at a higher tensile force because of, e.g., bond angle opening, would affect this estimation (44). Because the cross-linker LC-SPDP is reactive only to free -SH and not to the disulfides that were responsible for oligomer formation, the above estimate should be reasonably correct.

Figure 4.

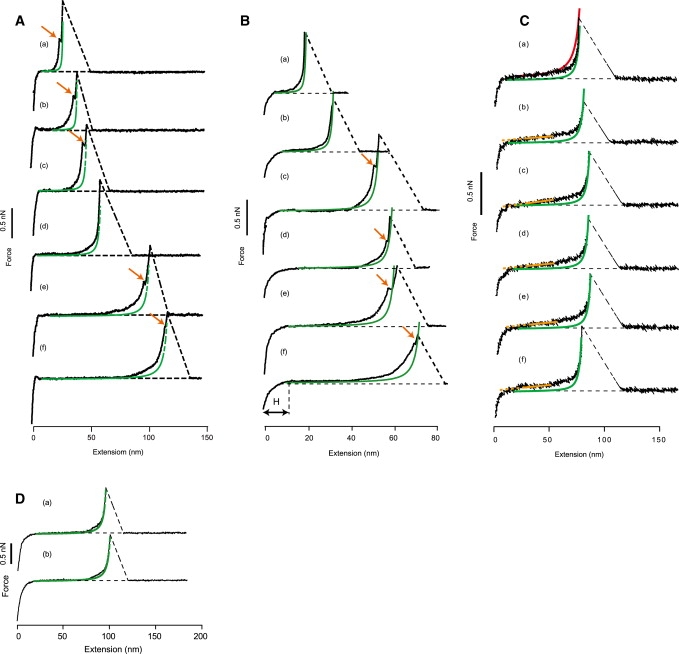
(A) Six representative F-E curves obtained in 50 mM Tris buffer, pH 7.4 (black curves). Green curves indicate WLC curves with p = 0.35 nm and appropriate contour length L, according to Eq. 1. Orange arrows mark inflection points, as described in text. (B) F-E curves obtained in 50 mM Tris buffer, pH 7.4, with 400 mM NaCl (black curves). Black arrow (labeled H) shows approximate height of end-grafted polypeptides on the substrate. (C) F-E curves obtained in 50% TFE in 50 mM Tris buffer, pH 7.4. Red curve is a WLC curve, with p = 0.16 nm and L = 95 nm. Yellow curves represent linear fitting line in the middle of the curve (solid lines) and their extensions (dotted parts) for the “pseudoplateau” test (see text). (D) In 50 mM Tris buffer, pH 7.4, with 6 M GdmCl (black curves).

All curves obtained in 50 mM Tris looked similar to the well-known curve for a worm-like chain (WLC) of structureless polymer according to Eq. 1, with p = 0.35 nm and L = 77 nm (Figs. 4, B–D, green curves), except for a small increase of force in the middle of stretching (45). As a genuinely unique feature, in five cases (a, b, c, e, and f), the curves were characterized by the presence of small inflection points (orange arrows) toward the end of stretching at around 0.5–1 nN in the ordinate; the green curves showed substantial deviations from the experimental ones where such inflections were observed. These inflections may very likely be attributable to transitions from α-helical to an extended conformation going over a high energy barrier (see Discussion). A similar inflection was evident in the extension experiment of polysaccharides, and was attributed to the mechanically induced chair-to-boat transition (46).

The reason for the surprisingly low tensile force obtained may be explained as follows. First, the sample peptide was only partially helical, with ∼70% helicity, so that forced stretching of the chain could always originate from its nonhelical parts. Second, a helix-coil transition could take place spontaneously by unfolding the helical parts to the coils and vice versa at a rapid time scale, allowing any helical part to unfold with much less tensile force expected for the unfolding of a perfect helix. The effect of such spontaneous local denaturation of helices was discussed by Chakrabarti and Levine from a theoretical point of view (47). They pointed out that because mechanical stretching concentrates on such locally unfolded parts of high compliance, the F-E curve is biased toward a lower-force region, resulting in WLC curves. This argument also applies to the case of data obtained in 400 mM NaCl.

The theoretical curve for WLC extension was calculated according to Eq. 1 (48) where F, k_B, T, p, x, and L represent tensile force, Boltzmann constant, temperature (K), persistence length of the chain, extension of the chain, and total contour length of the chain, respectively:

$$F=\frac{k_{B}T}{p}\left[\frac{1}{4{(1-x/L)}^2}-0.25+\frac{x}{L}\right]\text{.}$$ (1)

Effect of high salt concentration

The F-E curves in Fig. 4 B were obtained in 400 mM NaCl, where a gradual release of the polymer chain from a repulsive layer of 5–10 nm in thickness is evident, indicated as H for curve f with a black arrow. We believe that this repulsive layer was, as stated earlier, attributable to extension of end-grafted [C(KAAAA)₁₀KC]_n into the bulk solvent. Among the six curves given in the figure, four (c, d, e, and f) have inflection points similar to those mentioned above.

Effect of organic solvent

As presented in Fig. 4 C, the F-E curves obtained in 50% TFE showed, in general, higher tensile forces compared with those obtained in 50 mM Tris or 400 mM NaCl, reflecting the fact that TFE stabilizes α-helical conformations in polypeptides with appropriate sequences (49). If the free energy of [C(KAAAA)₁₀KC]_n in the α-helical state is lowered without a reduction of activation energy for unfolding by the same magnitude, the kinetics of unfolding would become slower, together with an increase in the force to unravel the helix mechanically. If the stability of a helix is higher, local unfolding from helix to coil would be much less frequent compared with the situation at 50 mM Tris. Thus the F-E curve would represent the mechanical property of a helix much more faithfully than the curves obtained without TFE. The overall appearance of the curves in Fig. 4 C involves a more or less linear increase of the force from the onset of pulling at the crossover point of curves with the baseline up to ∼80% of total stretch length, followed by a steep increase of force because of the chain-length limit. The red curve in curve a in Fig. 4 C represents a WLC model of Eq 1, with p = 0.16 nm and L = 95 nm, which together with the green curve shows the difficulty of fitting the experimental curves by a WLC curve. See Rief et al. (50) for a WLC model with different parameters.

According to Chakrabarti and Levine (47), the F-E curve of a helical polypeptide in the absence of local denaturation should have a “pseudoplateau” over a wide range of chain extension. We tried to find an implication of “pseudoplateau” in the six curves given in Fig. 4 C by fitting a straight line with a slope of 1.5 pN/nm (solid yellow line) in the middle range of chain extension (25–55 nm on the abscissa), and extending the line to the left (dotted yellow line) to see if there was any gap between it and the baseline where the F-E curve crossed the latter line. Only in the case of curve b did there appear to be a small gap, but for other curves, no gaps were noticed. It is therefore likely that the F-E curve in Fig. 4 C still does not represent the F-E curve of a purely α-helical chain, but is biased toward that of an unfolded one.

Effect of denaturant

The F-E curves obtained in 6 M GdmCl (Fig. 4 D) had a curvature in the initial release part similar to that observed in Fig. 4, A and B. In this case, the curvature was attributable to the repulsive force from randomly coiled polypeptides on the substrate. Although the shape of the F-E curves was similar to those given in Fig. 4, A and B, no inflection points were evident in any of the force curves obtained in 6 M GdmCl. A small but consistent deviation from the theoretical WLC curve was noted in the midrange of chain extension.

SMD simulation

We performed SMD simulations of stretching events of C(KAAAA)₅KC surrounded by bulk water, using the AMBER 7 force field according to the method described in Materials and Methods. The result of SMD simulation is given in Fig. 5 in the form of F-E curves. The calculation was performed with three different pulling speeds of 0.1 nm/ps, 0.01 nm/ps, and 0.001 nm/ps, and the results at different pulling speeds showed that the tensile force dropped drastically, confirming that the low values of tensile force experimentally observed at a much slower pulling speed of ∼100 nm/s were not unreasonable. The red arrows in Fig. 5 indicate where the ψ angle constraints are relaxed. It was also revealed that most of the main-chain hydrogen bonds were disrupted at an early stage of chain elongation. Fig. 5 also provides snapshots of helix-unfolding from our SMD simulation at a pulling speed of 0.1 nm/ps with the fractional helicity in each of six snapshots. Upon stretching, α-helical hydrogen bonds from the i-th to the (i + 4)-th amide group were rapidly replaced by the i-th to the (i + 3)-th amide hydrogen bonds, similar to that of a 3₁₀ helix, with a longer axial distance between residues of 0.2 nm (0.15 nm for the α-helix). The helicity given in Fig. 5 involves the percentage of both kinds of amide hydrogen bonds against the initial 19 hydrogen bonds.

Figure 5.

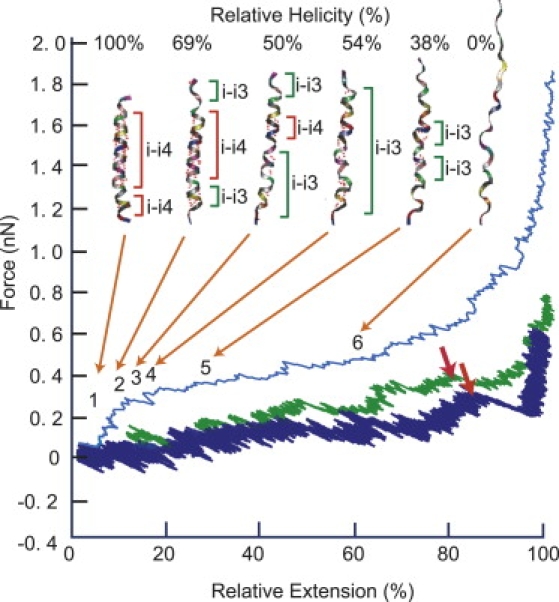
Results of SMD simulation on stretching of the helical part of C(KAAAA)₅KC at three different pulling speeds. Three curves from the top are blue, green, and navy blue, indicating pulling speeds of 0.1 nm/ps, 0.01 nm/ps, and 0.001 nm/ps, respectively. Red arrows indicate positions where transition of ψ angle occurs, and can be considered to correspond to experimentally observed inflection points. Selected snapshots of mechanical unfolding of sample polypeptide from our SMD simulations at pulling speed of 0.1 nm/ps, with values of instantaneous helicity in percentages, and marking of structurally different parts along the chain: red zones for α-helical hydrogen bonds (i-i4 stands for amide hydrogen bonds from i-th to (i + 4)-th residue), and green for 3₁₀-like helical zones (i-i3 stands for hydrogen bonds from i-th to (i + 3)-th residue). Dotted red lines in chains represent amide hydrogen bonds. Helicity (top of the figure) is fraction of residues retaining amide hydrogen bonds against initial α-helical hydrogen bonds. In two cases of a slower pulling rate, transition from α-helix to 3₁₀ helix, and ensuing breakdown of 3₁₀ helix, occurred in earlier parts of extension.

Rohs et al. used molecular mechanics to predict the pulling mechanics of helical poly-L-Ala in several different ways (51). They concluded that the mechanical extension of an α-helix proceeded through 3₁₀ helices. We think our experimental and simulation results are in agreement with their sequential unraveling case.

Discussion

From the experimental results on the mechanical response of the Ala-based helical polypeptide, [C(KAAAA)₁₀KC]_n, we confirmed that, at a slow pulling speed of ∼100–1000 nm/s, the resistance of the peptide against tensile stretching was not much higher than that of the same peptide without an α-helix. The observed mechanical response of the peptide was in surprising contrast to those responses obtained previously for PGA with a similar degree of helix content. We conclude that the mechanical strength of a helical polypeptide, as studied by AFM, is not a simple function of helical content, but depends strongly on the physical properties of side chains, most likely on their bulkiness and possibly on their hydrogen-bonding properties.

As mentioned above, our observations can be explained according to the theoretical argument proposed by Chakrabarti and Levine (47), i.e., that the tensile mechanics of a partially helical chain would be dominated by the preferred stretching of locally denatured parts of the chain. Such local denaturation should be expected to occur spontaneously because of energy fluctuations in the helix-coil transition equilibrium, and such fluctuations, being dependent on local denaturation, would be more readily accessible to polypeptides with less bulky side chains.

The distinctively different results obtained in 50% TFE, showing that the α-helix was more rigid than in aqueous buffer, can be explained along the same line of reasoning. First, a higher helical content of the polypeptide in 50% TFE because of an increased stability of the α-helix in this solvent should have lowered the probability of the spontaneous denaturation of local helices along the polypeptide chain. Thus, the chain was extended not only from the locally unfolded but also from the helically folded parts when a uniaxial tensile force was applied. The F-E curves obtained in 50% TFE should therefore reflect the mechanical properties of an α-helix more faithfully, but not completely. There should still be a bias toward the preferred unfolding of spontaneously formed, more compliant parts of the chain, rendering the experimentally accessible tensile force less than what would be expected from the overall helical content. We did not observe inflection points in F-E curves in 50% TFE for reasons that are not clear. Maybe because the final rupture force was lower in 50% TFE than in 50 mM Tris, the covalent bonds were ruptured before the strain energy was released.

In the case of 50% TFE, experimentally observed F-E curves were well above the WLC curve, and so we calculated the area between the two curves as accumulated strain energy in the chain at the end of stretching. The result was ∼2600–3000 kJ/chain/mol and 13–15 kJ/residue/mol, assuming 200 helical residues per chain. With somewhat larger error ranges, similar estimates of strained energy (or dissipated energy at the inflection point) were obtained for [C(KAAAA)₁₀KC]_n in 50 mM Tris, in 400 mM NaCl, and in 6 M GdmCl, respectively, as ∼5–10 kJ/residue/mol, ∼5–10 kJ/residue/mol, and ∼1 kJ/residue/mol. These values are preliminary and depend specifically on the parameters used for WLC models, but are not unreasonable values, considering the calculated value of a barrier height of ∼17 kJ/residue/mol between right-handed α-helical and extended-chain positions on a Ramachandran plot of alanine residues (52). A more detailed strain-energy analysis of the data will be given in the future.

This line of theoretical argument (47), together with our current observations, has the important biological implication that, when an isolated and incomplete α-helix is to be used as a mechanical element in structural assembly, one must expect that its tensile property is much akin to that of a nonhelical, randomly coiled chain. In addition, the mechanics of large-scale helix deformation are primarily governed by the properties of side chains, such as their bulkiness, and not so much by the properties of amide hydrogen bonding. An example of such a case can be found in the tensile mechanics of apo-calmodulin.

The results of SMD simulations at several different pulling speeds indicated that the main-chain hydrogen bonds were broken at an early stage of peptide stretching. If most of the main-chain hydrogen bonds are lost in an early phase of stretching, what contributed to the different mechanical resistance of the peptide studied in this work and that of PGA? An interesting obsevation on this question was obtained in our SMD simulation by tracing the transition of each Ala and Lys residue from an α-helical to an extended conformation on the Ramachandran plot (53). In Fig. 6 A, we summarize the observed paths of dihedral angles ϕ and ψ, when the peptide was extended from right-handed α-helical (region 1) to an extended (regions 4 and 5) conformation for individual residues in C(KAAAA)₅KC. Out of 26 residues of Ala and Lys in the helical conformation, 18 Ala and 4 Lys residues spent a considerable time in the region where ϕ is ∼−160° and ψ is −20 to +60° (regions 2 and 3 in Fig. 6 A), meaning that the main chain is constrained near the energetically unfavorable cis configuration. Transition pathways were not clearly defined for the remaining four residues. Thus, our simulation results indicate that tensile force is mainly dispensed to overcome this constraint in the dihedral angle, and not to break interamide hydrogen bonds. The energy barrier around regions 2 and 3 is expected to be high for polypeptides with bulky side chains, because the ψ ∼0° configuration involves constraints at least between C^β of the side chains and carbonyl oxygens on the main chain. According to Brant and Schimmel, the pathway through ψ = 0, the cis configuration, has the lowest energy on the Ramachandaran plot for amino-acid residues bearing a side chain at the α-carbon (52).

Figure 6.

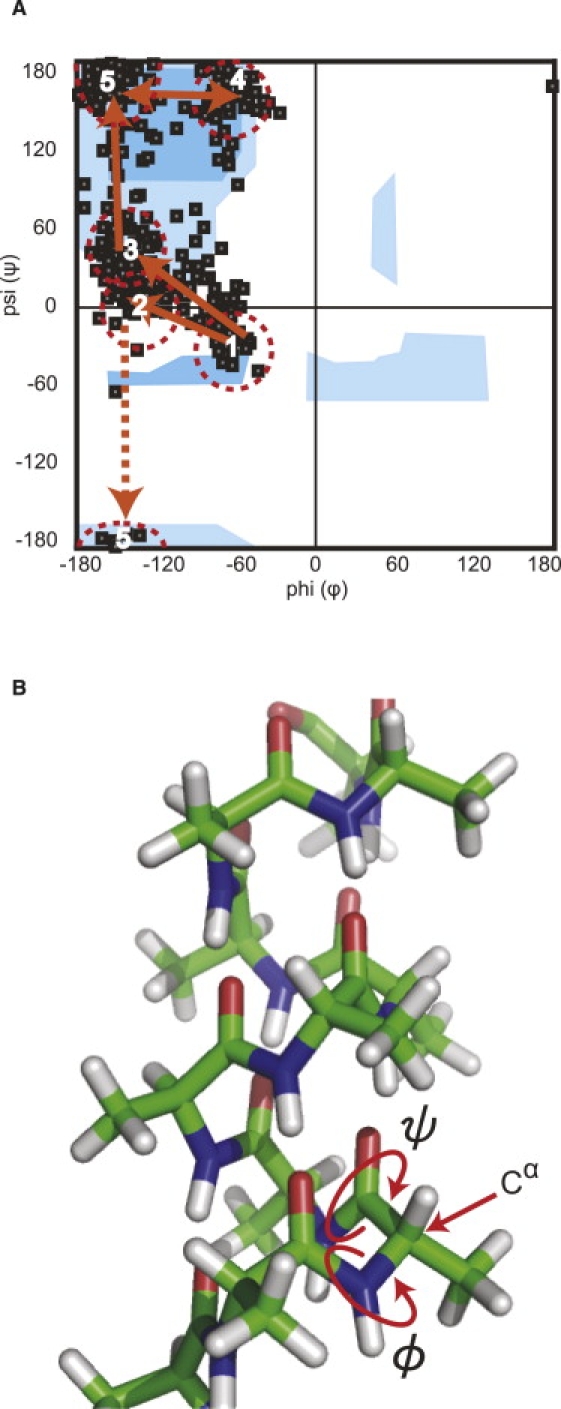
(A) Representative routes of dihedral-angle change in transition from helix to extended conformation on Ramachandran plot. A majority of residues took route from right-handed α-helix (region 1) to extended forms (regions 4 and 5) upon tensile extension, going over energy barriers in regions 2 and 3. Regions 1-5 are marked with dotted circles. A few of them took the route to region 5 through the dotted arrow. Blue regions represent low-energy regions for poly-Ala (52). (B) A model of poly-L-Ala α-helix shows preferred rotation around ϕ and ψ dihedral angles, when viewed from C^α as predicted by our SMD simulations (green, carbon atoms; blue, nitrogen atoms; red, oxygen atoms; white, hydrogen atoms).

Preferred modes of rotation around the dihedral angles, ϕ (N-C-C-N) and ψ (C-C-N-C), according to the results given in Fig. 6 A, are presented in Fig. 6 B. In both cases, when a pulling force is applied vertically parallel to the helix axis, the two dihedral angles prefer to change in the direction marked by the arrowed red circles. In minor cases, different modes of angle rotation are possible, as indicated in Fig. 6 A. The allowed and disallowed regions in the original Ramachandran plot were based on hard-sphere repulsions (53), but recent modifications try to include other noncovalent interactions between the main-chain as well as side-chain atoms (54,55). Contributions of atoms on side chains farther than C^β are not clearly described, but we expect that the energy barrier between the right-handed α-helix region and extended β-sheet region is higher for larger side chains. To cross the energy barrier from region 1 to 4 or 5 in Fig. 6 A, the ψ dihedral angle must go over the cis configuration that accompanies a shortening of the distance between two nitrogens in N-C-C-N from 0.297 to 0.278 nm. The energy required to overcome this and other constraints should be supplied by the externally applied tensile force.

If we accept the above reasoning, it is possible to interpret the stretching curve of apo-calmodulin (27) in terms of the relative bulkiness of the side chains. First, we adopt the molecular weight of individual side chains as their relative bulkiness index, and express the average bulkiness index (B_L) of PGA, apo-calmodulin, and [C(KAAAA)₁₀KC]_n as 73, 57, and 26, respectively. Fig. 7 reproduces the F-E curves of the three polypeptides, and qualitatively confirms that the average rigidity of polypeptides follows the order of the average bulkiness index. When interpreted in terms of stiffness of the chain at a normalized length of 80 nm, the stiffness was 15 pN/nm, 13 pN/nm, 0.5–1 pN/nm, and 0.2–0.5 pN/nm, respectively for PGA (25), poly-L-Lys (26), apo-calmodulin (27), and [C(KAAAA)₁₀KC]_n (this study) at ∼50% of chain extension.

Figure 7.

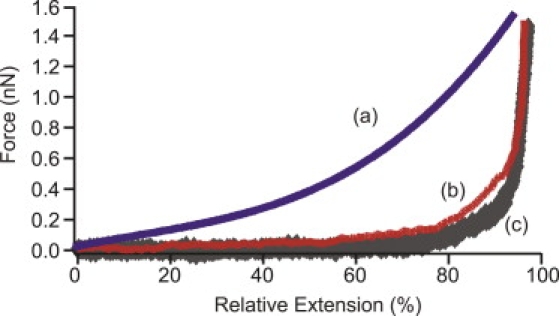
F-E curves of apo-calmodulin (curve b from Hertadi and Ikai (27), with permission), flanked by those of helical PGA (curve a from Idiris et al. (25), with permission) and [C(KAAAA)₁₀KC]_n (curve c).

Calmodulin represents the rare case where a stand-alone helix forms an isolated domain in a protein structure. In many other cases, helices are laterally bundled through side-chain interactions to form doubly or multiply coiled-coil conformations. This must be an important strategy, to confer reasonable rigidity on the native structure of such proteins.