Pulsed EPR Determination of Water Accessibility to Spin-Labeled Amino Acid Residues in LHCIIb

Abstract

Membrane proteins reside in a structured environment in which some of their residues are accessible to water, some are in contact with alkyl chains of lipid molecules, and some are buried in the protein. Water accessibility of residues may change during folding or function-related structural dynamics. Several techniques based on the combination of pulsed electron paramagnetic resonance (EPR) with site-directed spin labeling can be used to quantify such water accessibility. Accessibility parameters for different residues in major plant light-harvesting complex IIb are determined by electron spin echo envelope modulation spectroscopy in the presence of deuterated water, deuterium contrast in transversal relaxation rates, analysis of longitudinal relaxation rates, and line shape analysis of electron-spin-echo-detected EPR spectra as well as by the conventional techniques of measuring the maximum hyperfine splitting and progressive saturation in continuous-wave EPR. Systematic comparison of these parameters allows for a more detailed characterization of the environment of the spin-labeled residues. These techniques are applicable independently of protein size and require ∼10–20 nmol of singly spin-labeled protein per sample. For a residue close to the N-terminus, in a domain unresolved in the existing x-ray structures of light-harvesting complex IIb, all methods indicate high water accessibility.

Introduction

Membrane proteins define the functionality of the interface between living cells and their environment and play an important role in cell energetics. Their function can be understood in detail only if their structure, and in many cases also their structural dynamics, is known. Despite recent progress, structure determination of membrane proteins remains a challenging task (1,2). Membrane proteins do not crystallize easily, and current size limitations of NMR techniques (3), in particular for α-helical species, exclude many proteins of interest. Electron cryomicroscopy provides an interesting alternative technique, but it usually requires at least two-dimensional crystals to obtain highly resolved structures (4). In principle, near-atomic resolution can also be achieved with electron cryomicroscopy based on single-particle reconstruction techniques, as was recently demonstrated on a rotavirus particle (5). The applicability of such a high-resolution approach to membrane proteins remains to be demonstrated. In this situation, alternative techniques for characterizing membrane protein structure are of great interest.

In particular, there are no approaches that we know of that provide reliable information on partially ordered structures and on structural changes in membrane proteins. Such information is required to characterize folding intermediates and flexible domains that are involved in regulatory processes. It cannot easily be obtained with established techniques, because signal assignment to particular sites in the protein molecule fails for lack of resolution in ensembles with a broad conformational diversity. Site-directed spin labeling (SDSL) techniques circumvent this problem, as the signal originates exclusively from the labeled sites (6,7) so that site-specific ensemble-averaged information can be obtained. No crystallization is required and the techniques are applicable to proteins reconstituted into membranes, liposomes, or detergent micelles. The same applies to site-directed fluorescence labeling techniques (8–10), which have the advantage of higher sensitivity and can be applied even to single molecules in vivo (11). However, compared to fluorescence labeling, SDSL offers two advantages. First, nitroxides have a size that is comparable to the size of amino acid side groups, whereas chromophores are often significantly larger. Second, the weak coupling of spins to their environment allows for a separation of interactions by pulsed electron paramagnetic resonance (EPR) experiments (12). Such separation of interactions improves the reliability of signal interpretation and precision of signal quantification. Fluorescence and SDSL EPR techniques thus nicely complement each other.

To date the majority of SDSL studies on membrane proteins has been performed with continuous-wave (CW) EPR approaches (6,7). Pulsed EPR techniques were applied mostly for long-range distance measurements (13–16). In this work, we explore the potential of several pulsed EPR techniques for determination of water accessibility of spin-labeled residues in membrane proteins.

Due to the dependence of the fluorescence spectrum on the polarity of a chromophore's environment, water accessibility can be characterized by fluorescence techniques (8–10). Likewise, EPR spectra are sensitive to the polarity of the environment. In particular, the A_zz principle value of the ¹⁴N hyperfine tensor and the g_xx principal value of the g tensor depend on the dielectric constant of the environment and on hydrogen bonding to the nitroxide (17,18). Accordingly, these parameters correlate with immersion depth in the membrane (19). An alternative way of characterizing water accessibility by CW EPR relies on relaxation enhancement by water-soluble paramagnetic quenchers that can be detected by progressive saturation measurements (20). Both techniques measure parameters that depend strongly on the proximity of water but can also be modified by other influences. Here, we propose electron-spin-echo envelope modulation (ESEEM) spectroscopy as the main new technique for obtaining a reliable water accessibility parameter in a large transmembrane protein by quantification of hyperfine couplings to deuterium nuclei in deuterated water molecules. This technique can provide estimates of the distance and number of nuclear spins in the proximity of an electron spin on length scales in the range ∼3–6 Å (12,21). Thus, ESEEM is suitable to provide a water accessibility parameter, as was demonstrated previously in studies on water penetration in micelles (22) and along the membrane (23–26), localization of peptides in membranes (27,28), and detection of changes in water accessibility of a fatty acid by interaction with a protein binding pocket (29).

Deuterium exchange of water also influences transversal relaxation of electron spins at low temperatures, as such relaxation is mainly driven by proton spin diffusion (30–32). This technique can be applied to the same samples as used for ESEEM, provided that samples with protonated water have also been prepared. It is sensitive to proton concentration on length scales in the range ∼7–20 Å and thus provides access to an intermediate-distance water accessibility parameter.

Longitudinal relaxation is related to spin label dynamics, which is influenced by the local solvation cage around a spin label (33). As water solvation cages are unique with respect to their hydrogen-bond-related rigidity, this parameter may also be correlated to water accessibility, although in a more indirect way. Local dynamics also influences the line shape in echo-detected EPR spectra (33–35). In this work, we compare all these different water-accessibility-related parameters in a model system.

Our model system is the main light-harvesting complex (LHC) IIb of photosystem II of green plants. It consists of a membrane protein and several cofactors, such as chlorophyll a and b, carotenoids, and lipids that are noncovalently bound to it. The protein, in turn, consists of a 232-amino-acid polypeptide chain and features three transmembrane helices (36–38). LHCIIb is involved in a number of regulatory processes that are associated with conformational changes (39–41), and it self-assembles from its components in vitro on a timescale of a few minutes (42,43).

Crystal structures of the complex, except for the first few residues of the N-terminal domain of the protein, are available (37,38). Hence, sites with high, moderate, and low water accessibility can be predicted. With respect to the N-terminal domain, an earlier EPR study suggested that it exists in at least two different conformational states and that at least one of those should be exposed to water (14).

This manuscript is structured as follows. In the Results section we define a water accessibility parameter for each technique. In ideal cases, this parameter is proportional to local water concentration in a certain region around the spin label. This parameter is then determined for several spin-labeled LHCIIb mutants, as well as for two reference samples consisting of free spin labels, one in an aqueous solvent and one in a solution of the detergent-containing buffer used for LHCIIb purification. In the Discussion section, we compare the relative water accessibilities obtained by the various methods and consider the influence of other changes in the spin label environment for each of these parameters. The data are also discussed in terms of the structure of detergent-solubilized, monomeric LHCIIb as compared to trimeric LHCIIb in crystals and in terms of the localization of the N-terminus. We conclude with considerations on applying the entire toolbox to the same protein sample.

Materials and Methods

Mutagenesis, expression, spin labeling, and reconstitution

Several mutant versions of the Lhcb1^∗2 (AB80) gene (44) from pea (Pisum sativum) that contain a single cysteine were constructed by replacing serine or valine at different protein sites. The mutation positions, as well as a schematic picture of the LHCIIb protein, are shown in Fig. 1. In all mutants, the native single cysteine at position 79 was replaced by serine. Protein overexpression in Escherichia coli was performed as described previously (45).

Figure 1.

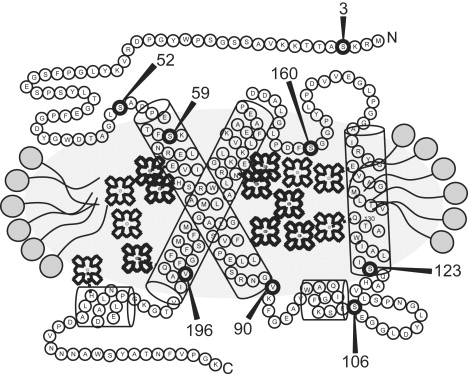
Schematic structure of LHCIIb. Each circle with a letter represents an amino acid residue. Circles labeled with numbers show mutation positions where spin labels were attached in this work. Cylinders represent helices, and chlorophylls are symbolized by schematic porphyrin formulas. Other pigments and lipids are not shown. The gray oval around the protein represents the micelle, as expected from analyzing the crystal structure (36–38). The top corresponds to the stromal side and the bottom to the lumenal side of the thylakoid membrane.

The purified apoproteins were dissolved (1 mg/ml) in an aqueous solution of 0.5% lithium dodecyl sulfate (Applichem, Darmstadt, Germany), 20 mM sodium phosphate (Merck, Darmstadt, Germany) (pH 7), and 2 mM tris-(2-cyanoethyl)phosphine (Alfa Aesar, Waard Hill, MA) (1 M in dimethyl formamide) and were incubated for 2 h at 37°C. The proteins were then spin-labeled on cysteine by adding 3-(2-iodoacetamido)-2,2,5,5-tetramethyl-1-pyrrolidinyloxyl (IAA-PROXYL) (Sigma, St. Louis, MO) (10 mg/ml dimethyl sulfoxide (DMSO) solution, 20-fold molar excess over protein) and incubated overnight at 37°C on a shaker. The labeling efficiency was determined to be at least 90%. In the following, spin-labeled mutants are abbreviated in the form S52r for a serine at position 52 that was mutated to a cysteine and then labeled by IAA-PROXYL.

Spin-labeled proteins were precipitated by adding 5% trichloracetic acid (Merck) at room temperature and immediate centrifugation (12,000 × g for 5 min at 4°C). This step has to be performed quickly, as reduction of the spin label can occur at slower speeds (46). The protein pellet was washed five times with distilled water and dried for 15 min at ambient temperature. The spin-labeled protein was then reconstituted with a pigment extract from pea thylakoids (47) isolated as described in Paulsen et al. (45) to self-assemble in the biologically relevant LHCIIb.

Monomeric LHCIIb was purified by ultracentrifugation on 0.1–1 M sucrose density gradients containing 0.1% (w/w) n-dodecyl-β-D-maltoside (Merck) and 5 mM Tris-HCl (pH 7.8) (Serva). After spinning for 16 h at 230,000 × g at 4°C, the band containing monomeric LHCIIb was collected and concentrated by Centricon centrifugal filter units (30 kDa) (Millipore, Billerica, MA) up to ∼600 μM. The mutants thus prepared were checked by fluorescence- and CD-spectroscopy to detect possible structural changes due to the mutations and spin-labeling. The fluorescence spectra of all the mutants used showed the characteristic peak of chlorophyll a fluorescence at 680 nm when exciting chlorophyll b at 470 nm. The CD spectra were used as a fingerprint and showed characteristic peaks at 491 nm, 649 nm, and 680 nm for all the used mutants.

The concentrated protein was then mixed 1:1 with 80% glycerol (Roth, Karlsruhe, Germany) as a cryoprotectant (14) to a final concentration of ∼300 μM. Samples for saturation measurements were prepared in the same way, with the only difference that tris(oxalato)chromium(III) complex (Cr(ox)₃)³⁻ (Aldrich) was added to some of them to a final concentration of 10 mM.

A solution of IAA-PROXYL in water (300 μM) with 0.8% DMSO was measured as a reference. This sample will be further referred to as Reference 1. Another reference sample is prepared as follows: IAA-PROXYL was dissolved in DMSO (20 mg/ml). The solution was then added to the buffer consisting of 0.275 M saccharose, 0.1% n-dodecyl-β-D-maltoside and 5 mM Tris-HCl (pH 7.8) to obtain a spin-label concentration of 600 μM. This buffer simulates the one after ultracentrifugation on a sucrose gradient. The spin-label solution in buffer is then mixed with an equal volume of 80% glycerol. Such a sample also allows the detection of micellization effects of the unbound spin probe. In the case of deuterated samples, the buffer was prepared with deuterated water. Glycerol d₈ (Isotec, Sigma-Aldrich) was diluted with D₂O (Aldrich) to a concentration of 80%. The reference sample contains some DMSO, which is not the case for the protein sample. This sample will be further referred to as Reference 2.

The concentration of samples for three-pulse ESEEM measurements was kept at 300 μM, as slight concentration effects were observed in the data. Slightly different concentrations were used for V196r (395 μM) and S52r (263 μM), but these are still assumed to be in the range where concentration effects are smaller than other experimental errors.

For CW progressive saturation measurements, the concentration was also kept fixed at 300 μM. The sample concentration for CW EPR and relaxation measurements was not specifically adjusted. After preparation, all samples were in a concentration range between 130 and 400 μM and no significant effects were observed in CW EPR spectra or relaxation data when reproducing experiments for the same mutant at different concentrations in this range. In echo-detected EPR (ESE) experiments, concentration varied from 150 to 300 μM. As the observed effects on line shape are relaxation-induced (33), and no effects on relaxation time were detected in this concentration range, we assume that this variation is not a significant source of error. The sample concentration in W-band measurements was 300 μM.

Deuterium exchange experiments

A 4-ml amount of the reconstituted purified LHCIIb sample prepared, as described above, in buffer consisting of 0.275 M sucrose, 0.1% n-dodecyl-β-D-maltoside, and 5 mM Tris-HCl (pH 7.8), was concentrated at 3000 × g in a 30-kDa Centrikon filter unit at 4°C until the sample volume reached 50 μl. The sample was then diluted to a volume of 250 μl with the same buffer as described above, but this time prepared with deuterated water. After that the sample was again concentrated to 50 μl. This procedure was repeated five times. Concentration was adjusted by dilution with buffer and determined photometrically at 670 nm. The samples were then mixed with glycerol-d₈ (80% solution in D₂O (Aldrich, Milwaukee, WI)) as a cryoprotectant to a final buffer/glycerol ratio of 1:1 (v/v). The CD and fluorescence spectra of the samples after deuteration did not show changes compared to the samples that were not deuterated.

X-band CW measurements

Experimental

CW EPR spectra were measured on a Miniscope 200 spectrometer (Magnettech, Berlin, Germany) with a TE102 rectangular resonator at a temperature of 103 K with liquid nitrogen cooling using a TC HO2 temperature controller (Magnettech). Samples were loaded into 3 mm homemade quartz capillaries (50–100 μL volume), shock frozen in liquid nitrogen, and rapidly inserted into the resonator at 103 K.

We checked that the typical microwave power of 10 μW applied during these measurements did not lead to saturation broadening. The modulation amplitude was set to 0.2 mT with the width of the central line of nitroxide spectrum being ∼1 mT. The sweep width was 15 mT. Ten scans were averaged, each with 4096 data points and a scan time of 60 s.

Data analysis

The 2A_zzvalues were obtained by fitting the minima and maxima of the nitroxide spectrum by fifth-order polynomials (48) using the home-written MATLAB (The MathWorks, Natick, MA)-based DynAnalysis program that is available from the authors on request. The error in these measurements is dominated by determination of these relatively broad extrema.

CW progressive power saturation measurements

The saturation measurements were performed on Bruker Elexsys EX 580 EPR spectrometer (Bruker, Billerica, MA) with a loop gap resonator (JagMar, Krakóv, Poland) at X-band frequencies. Samples were inserted into a TPX capillary and subjected to continuous N₂ or air flow at 295 K for at least 15 min before measurement. Continuous gas flow was upheld during measurements. Samples with (Cr(ox)₃)³⁻ as a relaxation agent were measured in N₂ atmosphere. A Bruker ER4111VT variable temperature unit was used for temperature control at 295 K. The microwave power was increased from 23 dB to 8 dB in 3-dB steps. The modulation amplitude was set to 0.1 mT, with the width of the central line of nitroxide spectrum at this temperature∼0.3 mT in the unsaturated spectra. The sweep width was 7.5 mT with 512 data points.

Data analysis

The CW spectra were background-corrected using a home-written MATLAB program, by subtracting a first-order polynomial fitted to the first and last 15% of the data points. The intensity of the central nitroxide peak (A) was determined manually with Origin (Microcal Software, Northampton, MA). In saturation measurements, the intensity dependence of the central nitroxide peak as a function of microwave power (P) is measured. This data was fitted to Eq. 1 by a home-written MATLAB program (49)

$$A=I\sqrt{P}\left[1+\left(2^{\frac{1}{\varepsilon }}-1\right)\frac{P}{P_{\frac{1}{2}}}\right].$$ (1)

The amplitude scaling factor, I, the homogeneity coefficient, ɛ, and the power P_1/2, where the intensity of the nitroxide peak is reduced to half of its unsaturated value, are adjustable parameters. The saturation power, P_1/2, is directly proportional to the relaxation rate of the spin label, which increases due to collision with paramagnetic species such as O₂ or (Cr(ox)₃)³⁻. This increase is directly proportional to the collision frequency and thus is a measure for relative spin-label accessibility to the paramagnetic quenchers (20). As (Cr(ox)₃)³⁻ is quite soluble in water (50), whereas oxygen is more soluble in membranes or the hydrophobic core of micelles (51–53), water or membrane accessibility of the spin label can thus be probed (20).

To factor out contributions of other relaxation mechanisms and technical parameters of the spectrometer and resonator, a dimensionless accessibility parameter Π(Quencher) is calculated using Eq. 2 (50):

$$\Pi \left(\text{Quencher}\right)=\frac{P_{\frac{1}{2}}\left(\text{Quencher}\right)-P_{\frac{1}{2}}\left(N_2\right)}{\Delta H}\mathrm{\times }\frac{\Delta H\left(\text{DPPH}\right)}{P_{\frac{1}{2}}\left(\text{DPPH}\right)},$$ (2)

where P_1/2(DPPH) is the power at which the intensity of the 2,2-diphenyl-1-picrylhydrazyl (DPPH) peak is reduced to half of its unsaturated value, ΔH(DPPH) is the line width of the DPPH line, and ΔH is taken as the average line width of the central line of nitroxide spectrum with and without quencher. Accessibility parameters for O₂ were multiplied by 5, as the measurements were performed with air rather than pure oxygen.

Pulse EPR measurements

Experimental

X-band-pulsed EPR measurements were performed on an Elexsys E580 EPR spectrometer (Bruker) at frequencies of ∼9.3 GHz using a Flexline split-ring resonator ER 4118X_MS3 (Bruker). The resonator was overcoupled to Q ∼ 100. Temperature was kept at 50 K with liquid helium cooling and was controlled by a CF935 (Oxford Instruments, Witney, Oxon, United Kingdom) cryostat with an ITC4 temperature controller (Oxford Instruments, Oxford, United Kingdom). The waiting time between repetitions was 6 ms.

Samples were loaded into 3-mm-O.D. capillaries (50–100 μL volume) home-made from Herasil tubing, were shock-frozen in liquid nitrogen and then rapidly inserted into the resonator at 50 K. EPR spectra were measured with field-swept, echo-detected EPR using a Hahn echo sequence π/2-τ-π-τ-echo (12) and a 15-mT field sweep. The interpulse delay time, τ, was 200 ns and the pulse lengths were 16 ns for the π/2 pulse and 32 ns for the π pulse.

Transversal relaxation data were acquired with a Hahn echo sequence π/2-τ-π-τ-echo and applying a ((+x) − (−x)) phase cycle to the π/2 pulse. An initial interpulse delay, τ, of 200 ns and an increment of 8 ns were used. The integrated echo intensity was measured as a function of this increment, with an integration gate of 32 ns length centered at the echo maximum. The pulse lengths were 16 ns for the π/2 pulse and 32 ns for the π pulse.

Three-pulse ESEEM measurements were performed with a π/2-τ-π/2-T-π/2-τ-echo pulse sequence with a standard phase cycle (12). The pulse length of the π/2 pulses was 16 ns and the interpulse delay τ = 344 ns, corresponding to a proton blind spot, was kept constant. Suppression of the proton modulations at the blind spot improves precision of the fitting of the deuterium modulation. The second interpulse delay, T, with an initial value of 80 ns was incremented in steps of 8 ns. The integration gate length was 32 ns.

Longitudinal relaxation data were acquired with an inversion recovery pulse sequence π-T-π/2-τ-π-τ-echo with a ((+x) − (−x)) phase cycle applied to the π/2 pulse. The delay time T, with an initial value of 2000 ns, was incremented in steps of 5800 ns, and the interpulse delay, τ = 400 ns, was kept constant. The pulse lengths were 52 ns for the π/2 pulse, 104 ns for the π pulse of the detection echo subsequence, and 24 ns for the inversion pulse. The integration gate length of 104 ns matched the longest pulse in the detection subsequence to maximize the signal/noise ratio (54). This combination of a hard inversion pulse with soft echo detection is sufficient to eliminate contributions by spectral diffusion at temperatures of 40 K and higher (55). The inversion pulse was tuned by maximizing the negative echo at delay time T = 1000 ns. Other flip angles and phases were generally adjusted with a π/2-τ-π-τ-echo pulse sequence by changing the amplitude and the phase of the pulse at τ = 400 ns, except for ESE experiments where the signal phase was tuned at τ = 200 ns.

W-band pulse EPR measurements were performed on an Elexsys EX 680 EPR spectrometer (Bruker) using a W-band EN600-1021H TeraFlex ENDOR resonator (Bruker). The resonator was not overcoupled. All pulse measurements were performed at 50 K with liquid helium cooling by a CF935 (Oxford Instruments) cryostat with an ITC4 temperature controller (Oxford Instruments).

Samples were loaded with a syringe into 0.87 mm outer diameter and 0.7 mm inner diameter home made quartz capillaries to the height of ∼3 mm, and inserted in the resonator at 50 K.

Because of a less favorable ratio between excitation bandwidth and spectral width at W-band, longitudinal relaxation data (T₁) were acquired with a saturation recovery pulse sequence saturation-T-π/2-τ-π-τ-echo and a ((+x) − (−x)) phase cycle applied to the π/2 pulse. The saturation pulse substitutes for the inversion pulse in the inversion recovery pulse sequence. Actually, this experiment is less susceptible to spectral diffusion effects than the inversion recovery experiment used at X-band. It becomes possible at W-band, as the resonator does not need to be overcoupled and the solid-state amplifier can provide much longer saturation pulses than the traveling wave tube amplifier used at X-band. The delay time, T, with an initial value of 22,000 ns, was incremented in steps of 5800 ns, and the interpulse delay τ = 400 ns was kept constant. The pulse lengths were 48 ns for the π/2 pulse and 96 ns for the π pulse for the detection subsequence and 20,000 ns for the saturation pulse. The integrator gate width was 96 ns. The saturation pulse was set to the maximum power value. The experiment was performed on the field corresponding to the maximum of the nitroxide spectrum.

The flip angles and phases for the saturation recovery experiment were adjusted with a π/2-τ-π-τ-echo pulse sequence by changing the amplitudes and the phases of the pulses at τ = 400 ns. Flip angles could not be adjusted with the same precision as at X-band. As small misadjustments of flip angles cause only slight sensitivity losses, but no changes in recovery curves, this does not lead to an additional error in the relaxation times. The waiting time between the repetitions was 15 ms.

Data analysis

Relaxation curves could not always be fitted by monoexponential decay functions. To compare different relaxation behavior among the mutants, we defined relaxation parameters τ₁ and τ₂, which serve to quantify the decay using a single number. For monoexponential fits, τ₂ was taken directly from the fit. Otherwise, it was taken as the time where echo intensity has decayed to 1/e of its initial value, which was the case for the two reference samples. To determine this value for nonexponential decay curves, we fitted transversal relaxation curves by a biexponential decay of the form

$$V\left(t\right)=A\text{exp}(-t/T_A)+B\exp (-t/T_B),$$ (3)

and longitudinal relaxation decays by the corresponding form −2 × V(t) + C. The relaxation parameter τ₁ or τ₂ is then obtained as the time where V(t) has decayed from its initial value A + B to (A + B)/e. This time is determined numerically from the four parameters A, B, T_A, and T_B by a home-written Matlab program, as the equation cannot be solved analytically. Compared to directly extracting the 1/e time from the experimental trace, this method has the advantage that it averages noise and depends less on the efficiency of echo inversion (55).

Even if nonexponential decays are nicely fitted by Eq. 3, the relaxation behavior cannot necessarily be interpreted in terms of two distinct contributions. Computation of the relaxation time distribution from a sum of exponential decays is an ill-posed problem in which apparently bimodal distributions may fit data rather well that originate from a broad monomodal distribution. Therefore, we refrain from interpreting the contributions of the two components in physical terms. A distribution of relaxation times is indeed expected in glassy samples, where local environments of the spin probes vary.

Note that transversal relaxation parameters relate to twice the interpulse delay, τ. Decay curves acquired by Hahn echo experiments were fitted over the maxima of the proton or deuterium modulation as described in Lindgren et al. (30) to minimize the influence from destructive interference of nuclear modulations.

ESEEM data were analyzed with a home-written MATLAB program. Phase, frequency, and intensity of the deuterium modulation were determined from the spectrum obtained by fitting an 11th-order polynomial background function to the primary data, subtracting this background function and dividing the difference by the background function, applying a Hamming window, zero-filling the data to four times the original length of the data set, Fourier transformation, and computation of the magnitude spectrum. By virtue of the division step that corresponds to a deconvolution, modulation depth information is preserved in the spectrum. As an alternative, modulation depth was determined by deconvolution and baseline correction of the primary data, as above, and fitting to the time domain data an oscillation with Gaussian decay envelope and fixed frequency, as well as variable amplitude, phase, and Gaussian width (see Results). As a third alternative, primary time-domain data were analyzed in terms of the number and distance of closest approach of the deuterium nuclei using the spherical shell model (21), as implemented in a home-written MATLAB program (56). All programs for data analysis are available upon request.

Results

Maximum extrema splitting 2A_zz in CW spectra at low temperature

The maximum extrema splitting 2A_zz in the solid state corresponds to twice the hyperfine coupling constant along the lobes of the p_π orbital on the ¹⁴N nucleus of the nitroxide. Localization of the unpaired electron in this orbital corresponds to a charge-separated state, whereas localization in the p_π orbital on oxygen corresponds to a neutral state. Hence, spin density in the ¹⁴N orbital and, thus, A_zz increase with polarity of the environment (17–19). In addition, hydrogen bonding of solvent molecules influences the spin-density distribution, so that A_zz depends not only on polarity but also on proticity of the solvent. Hence A_zz values can provide information about relative water accessibility of spin labels in membranes (19,23,24,57) and polarity of the spin-label environment in proteins (17). Here, we use A_zz directly as an accessibility parameter. To a first approximation, changes in A_zz between different environments are dominated by the contribution from water, and in this regime, A_zz scales roughly linearly with water concentration. Accordingly, proton donor profiles expected in membranes were found to be similar to profiles of the isotropic hyperfine coupling a₀, whose dependence on polarity and hydrogen bonding is the same as that of A_zz (19).

The dependence of A_zz on the mutation position in LHCIIb is shown in Fig. 2. As no difference in A_zz values was observed between deuterated and nondeuterated samples, the average from both measurements was taken, except for mutants S160r and V196r, where only one measurement was performed. The estimated errors are shown in the plot. The maximum error for IAA-PROXYL in different solvents was estimated to be 0.05 mT. The Reference 2 sample corresponds to the case of full water accessibility and does indeed exhibit the maximum A_zz value. Among the protein samples, the mutants S3r, S52r, and S59r form a group with large A_zz, V90r and S123r a group with intermediate A_zz, and S160r and V196r a group with low A_zz.

Figure 2.

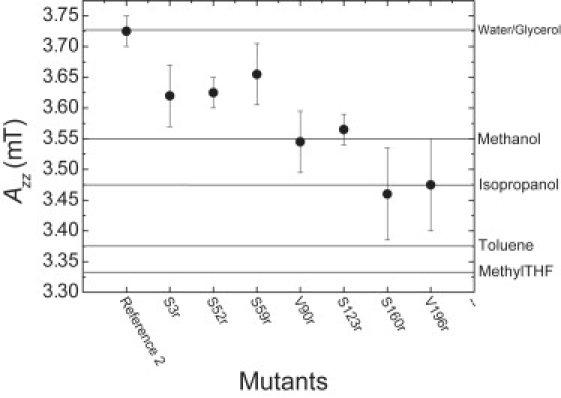
A_zz values as a function of spin label environment. Data from reference measurements on the free spin probe IAA-PROXYL in various solvents are shown as horizontal lines.

A semiquantitative estimate of the polarity of the spin label environment for the different residues in LHCIIb can be obtained by comparison to A_zz of IAA-PROXYL in solvents with different polarity. The data for several solvents are shown in Fig. 2 as horizontal lines. Although micelles are present in the reference sample, the nitroxide has an environment comparable to that in a water/glycerol mixture without detergents (dielectric constant ɛ = 64 at 25°C). Mutants S3r, S52r, and S59r have environments less polar than this mixture but more polar than methanol (ɛ = 32.6 at 25°C), V90r and S123r have an environment with a polarity comparable to that of methanol, and mutants S160r and V196r have an environment with a polarity similar to that of isopropanol (ɛ = 18 at 25°C). The range of A_zz values observed on detergent-solubilized LHCIIb labeled with IAA-PROXYL (3.45–3.65 mT) is similar to that found for membrane-solubilized bacteriorhodopsin labeled with 1-oxyl-2,2,5,5-tetramethylpyroroline-3-methyl)methanethiosulfonate (3.50–3.675 mT) (17), but differs significantly from that observed with DOXYL-labeled lipids in lipid bilayers (3.20–3.50 mT) (19). Because of the different structure of the DOXYL moiety compared to the PROXYL moiety, 2A_zz values should not be compared between these two families of spin labels. The correlation of the polarity dependence of isotropic hyperfine couplings for different spin labels was addressed in a recent study (58).

We also checked whether the EPR line shapes at 295 K, which are dominated by effects of label mobility, correlate with water accessibility. We observe intermediate mobility with rotational correlation times in the nanosecond range (1–10 ns) for most mutants, except for S123r and S160r, which exhibit slower motion (data not shown). No correlation between mobility and water accessibility was found.

CW progressive saturation measurements

The dependence of the intensity of the central nitroxide peak on microwave power is generally well fitted by Eq. 1 in both the absence and presence of relaxation agents. Typical data are shown in Fig. 3 for mutants S52r, whose environment is highly polar according to the A_zz value, and V196r, whose environment is only weakly polar. Although differences in the curves can be discerned, they are less impressive than the clear differences in A_zz.

Figure 3.

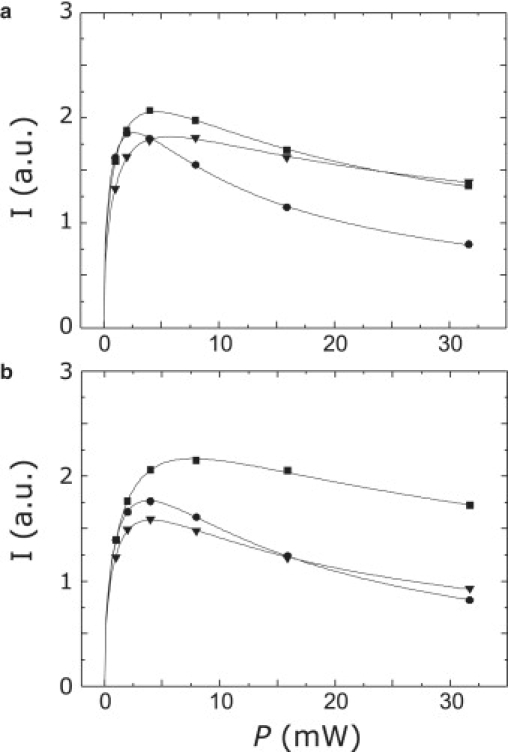
Peak-to-peak amplitude of the central nitroxide line as a function of microwave power for progressive saturation measurements on LHCIIb mutants S52r (a) and V196r (b) at 295 K. •, N₂; ▾, N₂/(Cr(ox)₃)³⁻; ■, 20% O₂ (air). Solid lines are fits by Eq. 1.

Variation of the water accessibility parameter Π(CrOx), computed by Eq. 2 for (Cr(ox)₃)³⁻ as a relaxation agent, is rather small among all the mutants, except for mutant S3r, which exhibits (Cr(ox)₃)³⁻ accessibility similar to that of unbound spin label in the buffer (Fig. 4). The negative value for (Cr(ox)₃)³⁻ accessibility of the V196r mutant is due to experimental errors in determination of P_1/2 and is interpreted as nonaccessibility to (Cr(ox)₃)³⁻.

Figure 4.

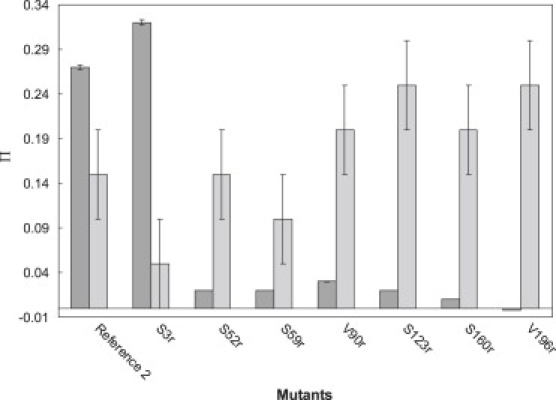
Accessibility parameters Π(CrOx) (dark gray bars) and Π(O₂) (light gray bars) determined by CW progressive saturation measurements at 295 K for different mutation positions in LHCIIb. The originally determined oxygen accessibility parameter was multiplied by a factor of 5, as measurements were performed in air with only 20% oxygen.

Variation of the oxygen accessibility parameter is generally small, although significantly larger than the experimental error. Mutants S123r, S160r, and V196r exhibit enhanced oxygen accessibility correlated with very low (Cr(ox)₃)³⁻ accessibility. Such behavior is usually interpreted as an exposure to a lipid environment, or, in our case, a location in the core of the micelle exposed to detergent alkyl chains.

The relative error of these measurements was estimated to be 1% for (Cr(ox)₃)³⁻ accessibility and 5% for oxygen accessibility. The main error is assumed here to stem from the error of quencher concentration. A systematic bias may be introduced by the bulkiness of (Cr(ox)₃)³⁻, which is much larger than a water molecule, and by its nominal charge of −3e, which can lead to repulsion by negatively charged detergent or lipid headgroups. This bias cannot be quantified as a relative error.

ESEEM

Differences in water accessibility between different mutants are clearly seen in primary three-pulse ESEEM data. Typical data sets are shown in Fig. 5, a–c. In most of our measurements, modulation depths >10% were observed, which makes the use of linearized analytical expressions for data analysis somewhat precarious (59). Therefore, our main data analysis method is based on modulation depth. Nevertheless, fits by the spherical shell model (21) were also performed and are compared to modulation depths.

Figure 5.

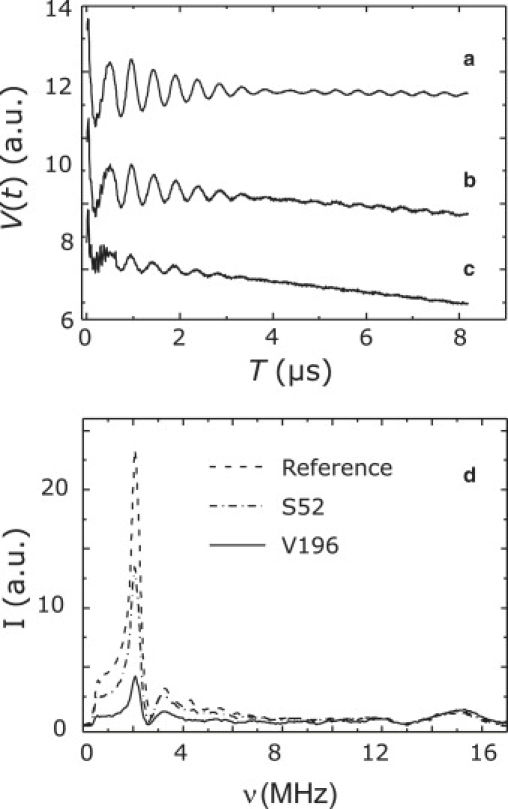
(Top) Three-pulse ESEEM time-domain data for the Reference 2 sample (a), mutant S52r (b), and mutant V196r (c). (Bottom) Spectra of the Reference 2 sample (dashed line), mutant S52r (dash-dotted line), and mutant V196r (solid line).

In previous work, ESEEM-based water accessibility parameters were defined in different ways. In a simple definition, the intensity of the deuterium ESEEM peak is normalized to the intensity of the proton peak (23). However, this definition depends on the assumption that the local concentration of non-water protons in contact with the spin label is invariable. This assumption may not apply to membrane proteins. Due to suppression effects for protons it also depends rather strongly on the choice of the first interpulse delay, τ, in the three-pulse ESEEM sequence. A more robust definition is based on the modulation depth, K, defined as the peak-to-peak amplitude between the first maximum and first minimum of the deuterium modulation (27). This parameter is a direct measure of the distance and concentration of deuterium nuclei. However, the definition by a visual fit that involves averaging of proton modulations leads to decreased precision. Furthermore, modulation depth also depends strongly on the choice of τ.

The deuterium modulation depth, k, can be determined precisely in the following way. The primary ESEEM data are corrected for the unmodulated part by fitting a polynomial function, B(t) (12), subtracting B(t) from the primary data, and dividing the difference by B(t) to obtain a deconvoluted and normalized nuclear modulation function N(t). Fourier transformation of N(t) provides the complex ESEEM spectrum, and computation of the absolute value provides the magnitude spectrum. Typical magnitude ESEEM spectra are shown in Fig. 5 d. Due to proper normalization, the amplitude, I(ν_D), of the peak at the deuterium frequency ν_D in these spectra is proportional to the modulation depth, as previously noted in Baute and Goldfarb (60).

The proportionality constant may depend on implementation of the Fourier transform algorithm and on the number of data points. For that reason, I(ν_D) is unlikely to be comparable between studies performed in different labs. From the real and imaginary peak intensities in the complex spectrum, Re(ν_D) and Im(ν_D), the phase, ϕ, of the deuterium modulation can be estimated as ϕ = atan(Im(ν_D)/Re(ν_D)). A damped harmonic oscillation,

$$D\left(t\right)=k_{\text{D}}\cos \left(2\pi {\nu }_{\text{D}}T+\varphi \right)\exp \left(-T^2/{\tau }_0^2\right),$$ (4)

is then least-square fitted to N(t) by varying the deuterium modulation depth, k_D, damping constant, τ₀, and phase, ϕ, while keeping ν_D fixed. The Gaussian damping function was found to provide good fits of the decay of the oscillation for all our samples. The modulation depth, k_D, is directly related to the primary data and is thus independent of the choice of computational algorithm. It is related to an orientation average 〈k〉 of the modulation depth, k, in the theoretical description of three-pulse ESEEM (12). The relation is given by

$$k_{\text{D}}=\frac{\langle k\rangle }{2}\left[1-\cos \left(2\pi {\nu }_{\text{D}}\tau \right)\right],$$ (5)

where time τ in the second factor on the righthand side (suppression factor) is the delay between the first two pulses. The relation of k_D to the modulation depth parameter, k as defined in Carmieli et al. (27), is expressed as k_D ≈ K/2. The suppression factor 1 − cos(2πν_Dτ) can range between 0 and 2. To minimize the influence of proton modulations on the fit of the deuterium modulation, we performed our measurements at τ = 344 ns, which corresponds to the j = 5 blind spot of proton modulation (ν_Hτ = 5, where ν_H is the proton Larmor frequency). Compared to the choice of τ = 204 ns in (25), which corresponds to the j = 3 proton blind spot, this value leads to stronger suppression of the broad wings due to hydrogen-bonded deuterons, and thus to more stable fits of the modulation that stems exclusively from non-hydrogen-bonded deuterons. For τ = 344 ns, the suppression factor has a value of 1.21, for τ = 204 ns it has a value of 1.89, and for the j = 4 blind spot at τ = 272 ns it has a value of 1.92.

According to ESEEM theory, k depends on the number, n, and distances, r_i, of nuclei coupled to the electron spin. By fitting with fixed frequency ν_D, only deuterium nuclei contribute to k_D. Neglecting effects of the small deuterium quadrupole coupling on modulation depth, and assuming sufficiently long distances, the contribution of each individual deuteron is proportional to r⁻⁶ (21). The modulation depth is thus dominated by deuterons at the distance of closest approach. However, the contribution of directly hydrogen-bonded deuterons, which leads to the low-intensity broad wings of the deuterium peaks in Fig. 5 d (25,26), is suppressed in k_D, as the Gaussian damping function guards against fitting of fast-decaying components of the modulation. Our fitting procedure thus selects the narrow spectral component whose intensity and corresponding modulation depth are proportional to the concentration of D₂O molecules that are not hydrogen-bonded to the spin label (25).

For these molecules, at sufficiently long distances, r >3 Å, the modulation depth, k, at any orientation, and thus also the orientation average, 〈k〉, scales as ν_D⁻² (12). To obtain a three-pulse ESEEM-based water accessibility parameter Π(D₂O) that is independent of the choice of interpulse delay, τ, and the exact static field, B₀, for the measurement, we define

$$\Pi \left({\text{D}}_{\text{2}}\text{O}\right)=\frac{2k_{\text{D}}}{\left[1-\cos \left(2\pi {\nu }_{\text{D}}\tau \right)\right]}\mathrm{\times }{\left(\frac{{\nu }_{\text{D}}}{2\text{MHz}}\right)}^2.$$ (6)

By normalization of the deuterium frequency to a standard value of 2 MHz, we ensure that at X-band frequencies with τ = 344 ns our accessibility parameter is similar to the parameter K defined in Carmieli et al. (27).

As the phase of the echo and the microwave frequency were checked after every experiment and were found to be stable, the main error in this parameter is assumed to result from noise. Differences in relaxation behavior between the different mutants might also introduce small errors, although most of the relaxation effects are corrected for by the deconvolution. As a rather good signal/noise ratio can be obtained, the error for these measurements is estimated to be as small as 5%.

The modulation depth is influenced by the number of nuclei and their distance of closest approach. These influences can be separated by fitting the whole modulation by the spherical shell model, since the damping of the modulation, quantified by our empirical parameter τ₀, depends on the distance, but not on the number of nuclei (21). Such an analysis provides a distance of closest approach of 0.35 nm for all LHCIIb mutants, corresponding to van-der-Waals contact of the closest non-hydrogen-bonded water molecules. As this distance does not significantly vary, variations in modulation depth are exclusively due to variations in the average number n of deuterons. This number ranges from ∼0.2 for the least accessible sites, V90r and V196r, to 0.55 for the most accessible site, S59r. Even larger values of ∼0.8 are found for the reference samples with unbound spin labels. Note that these values may not be unique, as was pointed out in previous work (25), where longer distances of closest approach were assumed. The error in the water accessibility parameter n determined by this analysis method is assumed to be larger than that in Π(D₂O), as only a few deuterium modulations were taken for analysis and only their local minima and maxima are used. The error of this evaluation method is thus assumed to be 10%.

The various water accessibilities determined from ESEEM data are presented in Fig. 6. As can be seen, the accessibility parameter, Π(D₂O), the deuterium peak intensity, I, and the average number, n, of deuterium nuclei correlate very well with each other. Among these parameters, Π(D₂O) is best suited for comparison of measurements on different proteins and in different laboratories. However, if the technique is applied at the same EPR frequency with the same interpulse delay τ, and data sets with the same number of points are background-corrected and Fourier-transformed by the same programs, Π(D₂O) is related to I by Π(D₂O) = C × I with a constant factor C.

Figure 6.

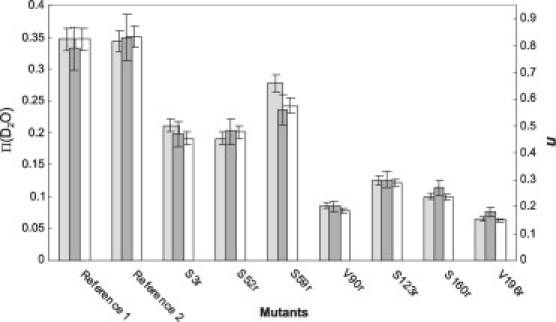
Water accessibility parameters obtained by different analysis procedures from deuterium three-pulse ESEEM data. For each sample, the left vertical scale (light gray bars) gives the Π(D₂O), the deuterium peak intensity in arbitrary units in ESEEM spectra is normalized to the Reference 1 sample (white bars), and the right vertical scale (dark gray bars) gives the average number of deuterium nuclei obtained by a spherical shell model fit.

In contrast to Π(CrOx), Π(D₂O) for all LHCIIb mutants, including mutant S3r, is significantly smaller than for the reference samples. Unlike with (Cr(ox)₃)³⁻, the slight water accessibility of the V196r mutant can still be detected. In general, differences in water accessibility between different sites are better visible than with the progressive saturation experiments. The water accessibility of mutant V90r is smaller than might have been expected from the A_zz measurement, but the difference does not significantly exceed experimental error.

Relaxation measurements

Since many stochastic processes can influence relaxation in the solid state, and mechanisms are not quantitatively understood for protein samples in glassy frozen solutions, interpretation of relaxation data is not as straightforward as interpretation of CW EPR and ESEEM data. Here, we try to understand the effects that govern electron spin relaxation of nitroxide labels in LHCIIb on the basis of empirical relaxation parameters. Such understanding would be useful, as relaxation measurements provide unique information and are technically not as demanding as many other pulse experiments.

The 1/e time τ₁ for longitudinal relaxation was determined from biexponential fits as described in the Materials and Methods section. The fits are indistinguishable from the data with bare eyes, and no particular problems were encountered in this analysis (primary data not shown). No significant differences were observed between samples prepared with normal and deuterated water (Table 1). There might be a slight trend toward shorter τ₁ values on deuteration, but the differences do not exceed experimental error. This maximum error for τ₁ determination was estimated to be 10%.

Table 1.

Longitudinal (τ₁) and transversal (τ₂) effective relaxation times at different mutation positions in LHCIIb at X-band frequencies of ∼9.4 GHz

Mutant	τ1 (μs)		τ2 (ns)
	H2O	D2O	H2O	D2O
Reference 1	1331	1350	3200	4030
Reference 2	1352	1337	3408	5063
S3r	1070	1029	2178	3893
S52r	1054	1029	2185	3532
S59r	1140	1181	2369	5174
V90r	1021	978	2140	2525
S123r	1063	1027	2118	2488
S160r	871	871	1924	2468
V196r	862	705	2000	1923

See text for a discussion of τ₁ and τ₂ relaxation times.

Determination of the effective transversal relaxation time, τ₂, which coincides with the phase memory time, T_m, for stretched exponential and monoexponential decays, is more complicated. This is because the maxima of the nuclear modulation have to be fitted in modulated echo decays (see, e.g., Lindgren et al. (30).). Furthermore, for the two protonated reference samples, decays were strongly nonexponential and were not well fitted by biexponential decays (data not shown). Such stretched exponential decays have been observed previously for surface-exposed sites in the soluble protein human carbonic anhydrase, whereas monoexponential decays were typical for buried sites (30). Because of the different decay function for the reference samples compared to the LHCIIb samples, no conclusions can be drawn from comparison of τ₂ values between these two groups. We cannot exclude the possibility that the effect is due to the presence of DMSO in the reference samples, which is required to solubilize the free spin label and might thus be associated with it. In any case, since it cannot be assumed that Eq. 7 applies to these data, local proton concentrations computed for the reference samples cannot be trusted.

The error in τ₂ for the LHCIIb mutants is estimated to be 40 ns from comparison of data obtained on two independently prepared samples of the same mutant.

In contrast to the soluble protein human carbonic anhydrase II, where labels at surface-exposed sites have much longer relaxation times than those at buried sites (32), for detergent-solubilized LHCIIb we find only minor variations of τ₂ between different mutation positions in protonated buffer. However, the change in τ₂ on deuteration of the buffer in LHCIIb depends strongly on accessibility of the site (Table 1), as is the case with carbonic anhydrase II.

This variation arises because transversal relaxation of electron spins in the low temperature limit in protonated samples is predominantly due to fluctuations of the hyperfine field at the electron imposed by the protons. These fluctuations in turn are induced by proton spin diffusion. For deuterons, with an approximately seven times smaller magnetic moment, the fluctuations are much smaller. The contribution of this mechanism to the relaxation rate is given by (12,61)

$$\Delta \left(\frac{1}{{\tau }_2}\right)=\frac{0.37{\mu }_0{\left(g{\mu }_{\text{B}}\right)}^{1/2}{\left(g_n{\mu }_n\right)}^{3/2}{\left[I\left(I+1\right)\right]}^{1/4}}{4\pi \text{h}}C,$$ (7)

where C is the number concentration of nuclear spins that induce this relaxation, I their spin quantum number, g_n their nuclear g value, g the electron spin value, μ_n the nuclear magneton, and μ_B the Bohr magneton. Eq. 7 suggests that the contribution is ∼13 times smaller for deuterons than for protons. This still neglects additional slow-down of spin diffusion for quadrupole nuclei such as deuterium due to quadrupolar broadening of their resonance line. The contribution of deuterons can thus be neglected in the difference of relaxation rates between protonated and deuterated media and a local concentration of protons can be computed by equating Δ(1/τ₂) in Eq. 7 with the experimentally determined rate difference.

Note that this approach implicitly assumes that all exchangeable protons are fixed in space. While libration of protons in hydrogen bonds can be neglected on the relevant length scales, hyperfine field fluctuations due to rotation of methyl groups may be relevant. As long as the methyl groups are protonated in both samples, as is the case in experiments with deuterated water, their contribution to transversal relaxation would be expected to cancel in the difference Δ(1/τ₂) and could be neglected. However, if this relaxation mechanism dominates, it may be impossible to extract reliable values for Δ(1/τ₂) from the data. This may be the case for our two reference samples, where we observe stretched exponential decays.

The difference in relaxation rates between protonated and deuterated samples is sensitive to proton concentration on a different lengthscale than ESEEM modulation depth. Due to its r⁻⁶ dependence, the modulation depth is strongly biased toward distances of closest approach, i.e., to water molecules in van der Waals contact with the label. Exactly those protons, as well as the hydrogen-bonded protons, are decoupled from the proton spin bath by their hyperfine splitting. Thus, there is no proton spin diffusion in direct neighborhood to the electron spin (31,32,62). Protons are effective in spin-diffusion-induced relaxation if their hyperfine coupling is comparable to or smaller than the proton-proton dipole-dipole linewidth of ∼35–100 kHz. The dipolar proton hyperfine coupling falls below 100–300 kHz at a distance range of ∼5–7 Å from the electron spin. Thus, the technique is most sensitive to the concentration of protons in a distance range of ∼6–20 Å, where protons couple both to the electron spin and to the large spin bath of remote protons.

Concentrations of exchangeable protons in this distance range, computed according to Eq. 7, range between 10 nm⁻³ for mutant S123r and 30 nm⁻³ for mutant S3r (Fig. 7). These values compare to a proton concentration in pure water of 67 nm⁻³. For mutant V196r, no relaxation suppression by deuteration is found within experimental error. In fact, due to experimental error in determining τ₂, we find an apparent slight decrease of the relaxation time on deuteration for this sample.

Figure 7.

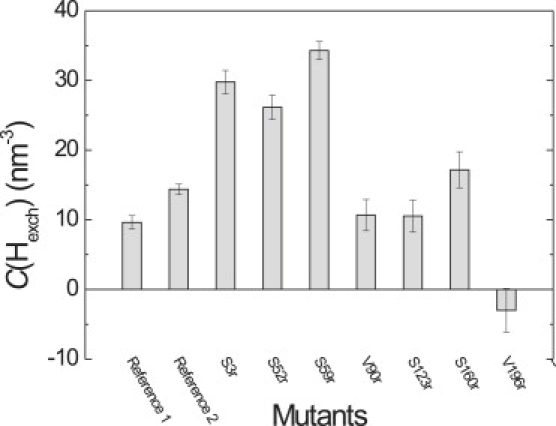
Local concentration of exchangeable protons according to Eq. 7 for different mutation sites in LHCIIb. Pure water has C(H_excH) = 67 nm⁻³.

Although effective longitudinal relaxation times, τ₁, do not exhibit significant changes on deuteration of the buffer, they vary significantly among the different sites in LHCIIb (Table 1). In general, relaxation times are longer for sites that are known to be exposed to water (reference samples) or have high water accessibility according to ESEEM.

At these low temperatures, longitudinal relaxation of nitroxides in a glassy matrix is dominated by modulation of the hyperfine field due to libration motion (63). The prolonged τ₁ for both reference samples and for mutant S59r, as well as the shortened τ₁ at sites S160r and V196r, can then be understood by considering restriction of this librational motion by the environment of the spin labels. In an aqueous environment, a stiff cage of ordered water molecules is formed around the spin label due to the hydrophobic effect. This cage hinders small-angle motion of the spin label to a larger extent than an alkyl chain solvation shell in a membrane, liposome, or micelle, or in neighboring protein side groups. This stronger hindrance of motion in turn is reflected in a longer τ₁.

This hypothesis is in line with lineshape effects in ESE spectra of the different samples that arise from anisotropy of the transversal relaxation time (33–35).

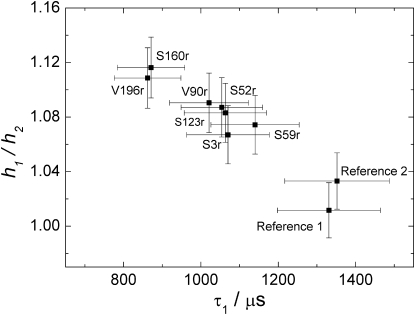
The relaxation anisotropy can be quantified most easily in terms of an anisotropy ratio, h₁/h₂, of spectral intensities at two positions in the spectrum that roughly correspond to the orientations in the nitroxide molecular frame along the orbital lobes of the nitrogen p_z orbital and perpendicular to it (33). The spectral intensity h₁ is measured at the local maximum of the absorption lineshape near the low-field edge, whereas h₂ is measured in the local minimum between the low-field edge and the central peak (global maximum). In a study on spin probes in ionomers (63) and a detailed study on a broad range of radicals and glassy matrices (35), transversal relaxation anisotropy for nitroxides was related to reordering of the solvent cage. From the ESE spectra of our samples (data not shown), we have determined the anisotropy ratio h₁/h₂. As is seen in Fig. 8, longitudinal relaxation and anisotropy ratio are correlated with each other, which indicates that both parameters are related to stiffness of the solvation cage.

Figure 8.

Anisotropy ratio h₁/h₂ for transversal relaxation obtained from ESE spectra plotted as a function of effective longitudinal relaxation time, τ₁, for different sites in LHCIIb and two reference samples.

The largest error obtained from ESE spectra analysis is assumed to originate from the selection of the position at which h₁ is determined. Comparison of h₁/h₂ values at different spectral positions provides an error estimate of 2%.

The ratio h₁/h₂ is proportional to the product of the square of the libration amplitude and the correlation time of the libration (33). Longitudinal relaxation probes the cage stiffness on a picosecond timescale in the case of a direct relaxation process, or is independent of timescale in the case of a Raman process. According to the van Vleck theory of paramagnetic relaxation (64), this independence of timescale in the Raman process arises since the energy of the electron spin transition needs to match only the difference of the energies of two quanta of lattice vibrations or modes. The typical energies of these modes at 50 K are so much larger than the Zeeman interaction that this interaction can be neglected in the computation of transition probabilities. Measurements of τ₁ at W-band frequencies of ∼94 GHz for selected mutation positions showed similar relaxation times as at X-band frequencies (Table 2).

Table 2.

Effective longitudinal relaxation time (τ₁) for different LHCIIb mutants at W-band frequencies of ∼94 GHz

Mutant	τ1 (μs)
S3r	993
S160r	800
V196r	716

Such behavior is consistent with a Raman process and inconsistent with a direct process. As differences between different spin-labeled sites are still observed, we assume that they are related to differences in libration amplitude.

Discussion

Comparative discussion of the various techniques

Different methods were presented and tested on LHCIIb mutants that provide information on the environment of a spin label in a membrane protein in general and its water accessibility in particular. The simultaneous application of well established CW EPR methods and pulse EPR methods significantly increases the amount of available information. This is, first, because these methods are based on different physical interactions and thus are influenced by different properties of the spin label environment besides water accessibility. They are also sensitive to different length scales and to different water environment types. Second, one of the CW EPR methods can be applied at ambient temperature, in a sample state that is closer to physiological conditions than a shock-frozen state, whereas the separation of interactions that is feasible with pulse techniques can provide better quantification of water accessibility. Third, solid-state methods allow for studying the kinetics of structural changes with freeze-quench techniques.

The easiest way to obtain information on water accessibility is by measuring the CW EPR spectrum of a shock-frozen sample and extracting the A_zz principle component of the hyperfine tensor that is sensitive to solvent polarity. This technique also features high concentration sensitivity, but has the disadvantage that large changes of the dielectric constant induce only small changes in A_zz. Furthermore, this parameter can be extracted only with rather low precision due to line broadening by anisotropic interaction, unresolved hyperfine splittings of protons, and heterogeneity of the spin label environment.

In addition, A_zz may be influenced by contributions to the environment other than the presence of water, as for instance charged amino acid side groups in the vicinity. Although characterization of water accessibility by that technique works well in less complex systems, such as membranes or micelles (19,23,24,57), it is thus rather inexact for membrane proteins. If complemented by high-field measurement of the principal g tensor component, g_xx, the technique can distinguish influences due to hydrogen bonding and changes in the dielectric constant of the environment (17,18). This makes interpretation more clear-cut if not unique. However, additional high-field measurements imply an experimental effort that may be higher than with the other methods discussed here and lead to decreased sensitivity at a given protein concentration. However, when other accessibility data is available, sensitivity of A_zz to charged amino acids in the vicinity of the label can be turned into an advantage, as poor correlation of A_zz with other accessibility parameters can provide a hint for their presence.

Progressive saturation measurements with CW irradiation provide information on accessibility of a spin label to paramagnetic molecules, called quenchers. This method can be applied at physiological temperatures in the presence of fluid water, which is not the case for any other method described here. Generally, we find that the saturation curves can be fitted nicely by the theoretical expression in Eq. 1, and that scatter of the data points is small. Accessibility parameters obtained from such measurements thus have a smaller relative error than the polarity-related change in A_zz.

Water-soluble quenchers, such as (Cr(ox)₃)³⁻, Ni(II) diethylene diamine diacetic acid (NiEDDA), and Ni(II) bis(acetyl acetonate) (NiAA) (62) are used in progressive saturation measurements to characterize water accessibility, or, more precisely, the immersion depth of a labeled site in the membrane or micelle. These quenchers are much larger than water molecules. They are thus most suitable to determine whether a residue is in the bulk aqueous phase outside the membrane or micelle, but not whether a residue is in contact with a single water molecule or only a few water molecules that access through a channel or cavity in the protein. This enhanced sensitivity for strongly water-exposed residues is most prominent with (Cr(ox)₃)³⁻ due to its negative charge, which in the case of LHCIIb leads to repulsion by negatively charged detergent headgroups. This may be advantageous if the water accessibility parameter from progressive saturation measurements is determined together with other water accessibility parameters that are more sensitive to local water at short length scales. Positively charged headgroups or positively charged amino acid side groups may enhance the frequency of collisions of the (Cr(ox)₃)³⁻ quencher with the label, which is generally an unwanted effect. If progressive saturation measurements are used exclusively, it may be more appropriate to select a neutral water-soluble quencher such as NiEDDA or NiAA (65). Among those quenchers, NiAA is characterized by a lower complex stability so that putative coordination sites in the protein might compete with it for the Ni²⁺ ion, thus leading to erroneous results. Due to the chelate effect, NiEDDA is more stable.

The complementary information on short-length water accessibility can be obtained most precisely by ESEEM measurements. This method directly measures the interaction of spin-labeled amino acids with water molecules by detecting deuterium hyperfine coupling. As there is no effect at all in the absence of deuterium nuclei in the vicinity of a spin label, and modulation may exceed 20% of the total echo signal for water-exposed residues (Figs. 5 and 6), this technique is very sensitive to changes in water accessibility. This improved sensitivity of ESEEM compared to CW techniques was also reported in Noethig-Laslo et al. (24). If modulation depths are obtained by time-domain fitting, or after calibration-depth-preserving Fourier transformation, they can be determined with high precision. Normalization by the square of the deuterium resonance frequency and correction for the blind spot behavior of three-pulse ESEEM (Eq. 6) ascertain that the accessibility parameter Π(D₂O) can be compared for measurements performed in different laboratories. This parameter is sensitive to the presence of deuterium nuclei at van der Waals contact distances of ∼3.5 Å.

Problems in interpretation may arise from the fact that this method does not distinguish between deuterium exchange of protons in water and of exchangeable protons in the protein backbone or nearby amino acid side groups. Whether this affects conclusions depends on the specifics of sample preparation and freezing. If exchange of the water by deuterated water is performed after reconstitution and the sample is shock-frozen immediately after preparation, exposed amide backbone and amine protons on the surface may exchange on a timescale of milliseconds to ∼100 s (66), whereas such protons in buried residues may be protected against deuterium exchange even on timescales of hundreds of minutes (67). In general, exchange of protons is expected to correlate to water accessibility on the timescale of sample preparation. Deuterium exchange before reconstitution should be avoided, as it might lead to significant background modulation from exchanged backbone amide or side-group amine protons.

The ESEEM accessibility parameter may also be influenced by contributions from deuterated glycerol. This contribution could be diminished, but not completely excluded, by using glycerol-d₃ instead of glycerol-d₈. Glycerol may penetrate somewhat more deeply into the membrane than water and may thus lead to a background signal.

Quantification of water accessibility at somewhat longer distances than with ESEEM can be obtained from measurements of transversal relaxation rate enhancement by protons. Feasibility of this technique for a large membrane protein is demonstrated here for the first time, to our knowledge. Quantitative analysis of the difference in transversal relaxation rate, 1/τ₂, between nondeuterated and deuterated samples allows us to estimate the concentration of exchangeable protons at length scales ranging from ∼6 to 20 Å. Relative errors may be somewhat larger than for the ESEEM-based accessibility parameter, Π(D₂O), but they compare favorably with measurements of changes in A_zz.

In principle, the cautionary remarks on exchangeable backbone and side-group protons in the case of ESEEM apply also to transversal relaxation enhancement. However, although an exchangeable proton can be accidentally in contact with a spin label, the concentration of such protons in a protein is much smaller than in water. Transversal relaxation rates are thus expected to be less affected by this problem, which is borne out by the fact that no enhancement is detected at position V196r in LHCIIb, whereas significant deuterium modulation is observed with ESEEM (Figs. 6 and 7 and Table 1).

Based on a theoretical expression for protons that are homogeneously distributed in space, according to Eq. 7, quantitative estimates can be derived for proton concentration near the label. For the most accessible residue in LHCIIb, mutant S3r, we find a proton concentration value of 30 nm⁻³, about half that in pure water (67 nm⁻³). This value is reasonable, although a somewhat larger value might be expected for the N-terminal domain if it resided entirely in an aqueous environment. Poorly water-accessible residues have values between 10 and 15 nm⁻³, whereas for a nonaccessible residue the error bar includes zero concentration. This quantification assumes that exchangeable protons dominate transversal relaxation at low temperatures. It failed for reference samples in a solvent that contained a small amount of DMSO.

The simultaneous use of ESEEM and transversal relaxation enhancement may be particularly important for localization of residues that are near the membrane-water interface, as these positions should be solvent-inaccessible on a short length scale, but accessible on long length scales. This effect can, however, be weakened by the ability of water to penetrate to some extent into the alkyl chain region of lipid bilayers and micelles.

The expected effects of the environment on longitudinal relaxation are hard to quantify, but the trends can be understood based on studies of orientational motion of spin labels in noncrystalline media (34,63,68). This technique detects effects on spin label libration of local rigidity of the environment. These effects appear to be strongly correlated to the formation of a rigid solvation cage for water-exposed spin labels. Line-shape analysis of ESE-detected EPR spectra, which is also sensitive to libration, supports this interpretation. The changes in ESE-detected EPR spectra could also derive from collective motion of the solvent matrix (35). Such an interpretation would be consistent with our results and picture of spin label environment, as this type of motion would also be restricted for a stiff, hydrogen-bonded solvation cage. Both techniques thus appear to probe formation of a complete solvent cage, as such cage formation is possible only for residues strongly exposed to water. These techniques might be useful for detecting water-filled cavities in a protein near a spin label. If such correlation of τ₁ with water accessibility is confirmed for other membrane proteins, this technique may even be used as a stand-alone method. The drawback of both relaxation-based techniques is that the error of the measurements is relatively large compared to the accessibility-related changes.

As a consequence of the domination of longitudinal relaxation rates by solvation effects, relaxation measurements in the solid state cannot differentiate between residues in helix and loop regions. As seen in Fig. 8, longitudinal relaxation is slower for the supposedly very mobile backbone near the N-terminus (mutant S3r) than for the supposedly rigid backbone in a helix (mutant V196r).

Accessibility parameters and structure of LHCIIb

Further insight into the specifics of each method can be obtained by comparing the respective accessibility parameters and discussing their correlation in terms of the structure of LHCIIb. Such a discussion also provides information on the structure of LHCIIb monomers reconstituted into detergent micelles, as compared to trimeric, crystalline LHCIIb. As a reference parameter for the detection of correlations, we use the three-pulse ESEEM accessibility parameter Π(D₂O), which is assumed to give the most direct water accessibility information. To relate our results to the crystal structure (38), we also compare them with a theoretical accessibility parameter determined with the Swiss-Pdb Viewer (69). All correlation plots are shown in Fig. 9.

Figure 9.

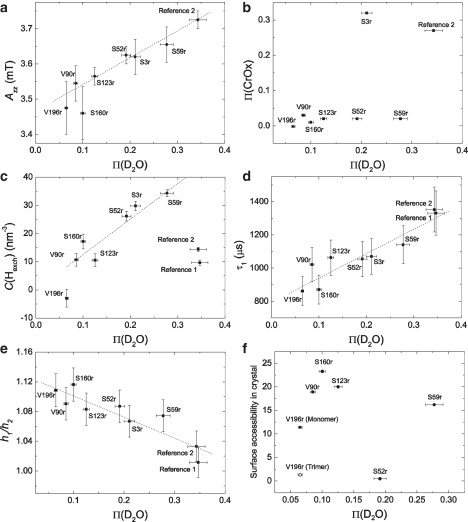
Correlation of various water accessibility parameters with the three-pulse ESEEM accessibility parameter, Π(D₂O). (a) Maximum hyperfine splitting, A_zz. (b) Progressive saturation accessibility parameter, Π(CrOx). (c) Local proton density, C(H), from the transversal relaxation rate change on deuteration. (d) Effective longitudinal relaxation time, τ₁, (e) Intensity ratio h₁/h₂ in ESE-detected EPR spectra. (f) Surface accessibility predicted by Swiss-Pdb Viewer (69) from the crystal structure (38) for an isolated monomer (solid squares) and within a trimer (open circles). Dashed lines are linear regressions of the data. In c, proportionality of C(H) to Π(CrOx) was assumed in regression analysis. If error bars are not shown, error is assumed to be within the size of the data markers. No error range is assumed for surface accessibility predicted by Swiss-Pdb Viewer.

The accessibility parameters A_zz, C(H), τ₁, and h₁/h₂ are all correlated with Π(D₂O). The correlation coefficients are 0.97 for A_zz, 0.92 for τ₁, and −0.91 for h₁/h₂ (Fig. 9, a, d, and e). For C(H), such correlation is observed only among the LHCIIb samples (Fig. 9 c). For the reference samples, this analysis fails, as explained above. If data for the reference samples are left out, the correlation coefficient is R = 0.90. For the other three parameters, the reference samples correlate as well as the LHCIIb samples and are included in the fits. Such correlation analysis presupposes that the relationship between two accessibility parameters is linear. This is strictly expected only for the relationship between C(H) and Π(D₂O), as these two parameters depend linearly on proton concentration at different length scales. Even in that case, linear correlation is expected only in the absence of distance-dependent heterogeneity of the proton distribution. We find that for LHCIIb, C(H) is proportional to Π(D₂O), except for mutant V196r and perhaps mutants S160r and S123r (Fig. 9 c). In the former case, the deviation is significant and corresponds to a situation where the density of exchangeable protons is higher in the immediate vicinity of the label (van der Waals contact) than at somewhat longer distances of 6–20 Å. As described previously, this may be caused by the exchange of protein protons by deuterium. The reason for the deviation of the S160r mutant from the linear behavior can be explained by its interfacial position between the core of the micelle and water. From an analysis of polarity of the neighboring amino acids it is not possible to say whether this loop region should reside in water or in the membrane. The measurements thus suggest that it is situated in an intermediate position. This observation indicates that by combining ESEEM measurements with those of the transversal relaxation rate we can identify residues near the interface of the lipid bilayer or micelle.

In the other cases, a linear relationship cannot be predicted from theory. Yet we find that A_zz (Fig. 9 a), τ₁ (Fig. 9 d), and h₁/h₂ (Fig. 9 e) scale linearly with Π(D₂O) within experimental error. Quality of the correlation suggests that the dependence of A_zz on mutation position is dominated by water accessibility. It remains to be seen whether this also applies to membrane proteins reconstituted into liposomes or lipid bilayers. Linear correlation of both h₁/h₂ and τ₁ with Π(D₂O) is most easily explained by assuming that the square of the libration amplitude of the spin label decreases linearly with local water concentration. However, our experimental error is too large to actually prove this relationship.

It is interesting to note that correlation of Π(CrOx) with Π(D₂O) is poor (Fig. 9 b). In agreement with expectations, reference sample 2 exhibits a high (Cr(ox)₃)³⁻ accessibility. High accessibility is also found for mutant S3r near the N-terminus that has one of the highest accessibilities according to all the other methods. However, in strong contrast to the high water accessibility implied by the deuterium modulation depth in ESEEM, the A_zz value, the transversal relaxation enhancement, the slowdown of longitudinal relaxation, and the h₁/h₂ ratio, mutant S59r appears to be only weakly accessible to (Cr(ox)₃)³⁻. Similar behavior is observed for mutant S52r. Both mutants have only intermediate oxygen accessibility (Fig. 4), which would identify them as protein-buried if the only results available were those from progressive saturation measurements. Analysis of all the other water accessibility parameters suggests that the residues are in the micelle interface and are at least partially exposed to water. It is most likely that (Cr(ox)₃)³⁻ accessibility is lowered due to electrostatic repulsion of charged detergent headgroups or to the bulkiness of the neutral maltoside detergent headgroups. Which of the two scenarios is the case could be decided by repeating accessibility measurements with a neutral water-soluble quencher such as NiEDDA.

A further possible explanation would be a change of protein conformation during shock-freezing. However, label-to-label distances of spin-labeled double mutants measured under the same conditions correlate quite nicely with simulated distance distributions based on the x-ray structure (A. Volkov, C. Dockter, Ye. Polyhach, G. Jeschke, and H. Paulsen, unpublished), which makes this explanation rather unlikely.

For the relaxation-based parameters, an influence of dissolved oxygen might be expected from observations described in Noethig-Laslo et al. (24). However, we explicitly tested for effects of sample degassing on ESEEM and relaxation measurements on both deuterated and nondeuterated samples and did not find significant changes. Degassed samples were prepared for the Reference 2 sample and the S106r mutant. The results for these samples suggest that the labels are solvent-accessible in both of them and that an effect of the dissolved oxygen in water on relaxation rates can be safely excluded.

The comparison of the τ₂ relaxation times between the deuterated and nondeuterated mutants suggests that proton spin diffusion also dominates transversal relaxation at 50 K for sites in the interior of the micelles and that oxygen dissolved in the micelle does not have a strong effect. We cannot safely exclude the possibility that such oxygen may be the reason for the decreased τ₁ relaxation time for the micelle-buried residues. However, this is rather unlikely, as the main mechanism for relaxation enhancement by oxygen in liquid solution depends on diffusional collisions with the spin label. This mechanism is not available in the solid state. Relaxation enhancement by a fast-relaxing paramagnetic species (oxygen) in the solid state due to dipole-dipole interaction with the observed slowly relaxing species (nitroxide) is relevant for transversal relaxation only in a relatively narrow temperature range (70). For longitudinal relaxation, such effects may be relevant in a broader temperature range, but their magnitude depends strongly on a matching between the longitudinal relaxation rate of the fast-relaxing species and the Larmor frequency of the slowly relaxing species. As effective longitudinal relaxation times, τ₁, are very similar at two resonance frequencies that differ by an order of magnitude (see Tables 1 and 2), a significant effect of the membrane-dissolved oxygen on τ₁ in the solid state is rather unlikely.

As we did not observe oxygen-related relaxation enhancement at a temperature of 50 K for some of the mutants and do not expect this effect for the other mutants, all measurements were performed without degassing. This makes the experiments much easier to perform, as the preparations tended to foam strongly during this procedure.

Theoretical accessibility parameters based on the x-ray structure of the LHCIIb trimer (38), considering either one LHCIIb molecule only or all three molecules in the trimer, do not correlate with the ESEEM accessibility parameter Π(D₂O) (Fig. 9 f). In fact, this is expected, as Swiss-Pdb Viewer and similar programs predict surface accessibility of residues, which for membrane proteins is a sum of lipid and water accessibility. However, predictive power of the approach remains poor even if this is taken into account. It is suggested that mutants V196r and S52r are buried sites in the trimer. Although this is in agreement with all the water accessibility parameters for V196r measured in this work, it contradicts the high oxygen accessibility of this residue (Fig. 4). This apparent contradiction can be traced back to the facts that our measurements are performed on LHCIIb monomers and that this residue is situated in the interface between LHCIIb molecules in the trimer, as is apparent from the predicted accessibility of this residue being different in monomers and trimers. All our data combined thus suggest that V196r in our samples is exposed to alkyl chains in the micelle interior.

For mutant S52r, we find moderate oxygen accessibility and water accessibility similar to that of mutant S3r, where the residue is clearly water-exposed. This is in stark contradiction to predictions for both the LHCIIb trimer and the monomer cut out of the trimer. Barring a conformational difference between LHCIIb in crystals and in the detergent micelle, this difference could be explained by the fact that the spin-labeled side groups are larger than the native side groups and may thus protrude more strongly from the protein surface. Furthermore, different rotamers may be preferred for the labels than for the native side groups. For these reasons, accessibility modeling should explicitly account for the label and should include a prediction of its conformational distribution. However, preliminary simulations based on a rotamer library approach (71) suggest that the few allowed conformers of mutant S52r are also buried (A. Volkov, C. Dockter, Ye. Polyhach, G. Jeschke, H. Paulsen, unpublished). Thus, it is likely that the conformation of the N-terminal domain in LHCIIb monomers reconstituted into detergent micelles is different from the conformation in trimers in LHCIIb crystals, as suggested previously (14).

An opposite trend in theoretically predicted surface accessibility and experimentally observed water accessibilities is found for mutants V90r, S123r, and S160r. According to all experimentally determined parameters, accessibilities are low or at best moderate for these sites, but according to predictions they are very high. In all three cases, oxygen accessibility is rather high (Fig. 4), indicating that these residues are lipid-accessible. This is indeed consistent with the x-ray structure, although this structure would also allow for positioning all three residues in the lipid headgroup layer.

It is interesting to note that mutant S59r, near the stromal end of helix A, is both predicted and found to be highly water-accessible. A closer look at the amino acid sequence shows that most of the amino acids in the direct neighborhood of this site are polar. Our data suggest that in detergent micelles, the site is water exposed. A larger protrusion length from the membrane on the stromal side was also deduced from the crystal structure (38). Thus, our data support previous results that suggest that membrane proteins reconstituted into detergent micelles behave similarly to membrane proteins in lipid bilayers (72).

For mutant S3r, accessibility cannot be predicted, as this residue is situated in the part of the N-terminal domain that is not resolved in crystal structures. This domain is known to be important for the response of the photosynthesis apparatus to changes in light conditions (40). Our results on water accessibility suggest that, at least in the monomeric state, this residue is not immersed in the micelle (or membrane), but is highly solvent-accessible at distances up to 2 nm. This observation confirms and extends previously obtained information about the N-terminal domain (14,73).

Accessibility for mutant S106r was also tested, but was not as well reproducible as for all the other mutants. For this site, high or low solvent accessibilities were obtained in analogous measurements on samples prepared in the same way (data not shown). These accessibility changes were found to be correlated with slight changes in CD spectra. This poor reproducibility might be connected to the marginal stability of a short helix near this site. To a lesser extent, we also found variations in accessibility between different preparations of mutant V90r, which is close to the flexible domain that contains the short helix with marginal stability. More detailed investigations are required to understand how each of the two states can be prepared in a controlled way.

Conclusion

Several EPR parameters that provide complementary information on water accessibility of a spin label in a membrane protein were determined on the different sites in major plant LHCIIb and compared with each other.

Detailed insight into the local environment of spin labels was obtained by simultaneous determination of the polarity-dependent ¹⁴N hyperfine splitting A_zz, the dynamics-sensitive longitudinal relaxation time and intensity ratio h₁/h₂ in ESE-detected EPR, and the ESEEM water accessibility parameter Π(D₂O) that quantifies the average number of water molecules in van der Waals contact with the label. A water accessibility parameter characterizing the average density of exchangeable protons at distances in the range of ∼6–20 Å from the label was computed from the change Δ(1/τ₂) of the relaxation rate on exchange of the water protons by deuterium. Among these parameters, the normalized ESEEM deuterium accessibility parameter Π(D₂O) appears to be the one that can be measured with the best precision and is most robust with respect to other changes in the environment of the label.

Strong correlations or negative correlations were found between all these parameters. Thus environment polarity and spin label mobility in detergent-solubilized LHCIIb appear to be dominated by water accessibility. In two reference samples consisting of free spin labels, transversal relaxation behavior was found to be qualitatively different, which hints at a qualitatively different relaxation mechanism in these samples and shows that the relaxation data should be used with care.

The parameter Π(CrOx), determined by progressive saturation measurements in the presence of the paramagnetic quencher (Cr(ox)₃)³⁻, exhibited surprisingly poor correlation with the ESEEM water accessibility parameter Π(D₂O), probably due to the negative charge of the quencher, but possibly also due to its bulkiness. This suggests that the pulse EPR methods presented here are more exact in determining the local accessibility to the small water molecule compared to saturation measurements, which are more suitable for determining the immersion depth in the membrane or micelle.

Experimental water accessibility parameters for LHCIIb were compared with theoretical predictions of surface accessibility using the oxygen accessibility parameter Π(O₂) as additional information, confirming earlier findings on structural similarity of LHCIIb monomers reconstituted into detergent micelles with LHCIIb trimers in crystals. The unexpectedly high water accessibility of residue S52 in the N-terminal domain suggests that this domain has a different conformation in detergent-solubilized monomers than in trimers in LHCIIb crystals. High water accessibility of residue S3 indicates that the first few residues of the N-terminal domain, which are not resolved by x-ray crystallography, are water-exposed in the monomers in detergent micelles.

The techniques presented in this work are applicable to any membrane protein that can be spin-labeled, regardless of its size or degree of structural order. For disordered domains of a protein or folding intermediates, these techniques can thus provide ensemble-averaged water accessibility parameters. An investigation of the kinetics of protein folding during LHCIIb self-assembly by observation of changes in water accessibility is now in progress.