Pressure-Induced Changes in the Structure and Function of the Kinesin-Microtubule Complex

Abstract

Kinesin-1 is an ATP-driven molecular motor that “walks” along a microtubule by working two heads in a “hand-over-hand” fashion. The stepping motion is well-coordinated by intermolecular interactions between the kinesin head and microtubule, and is sensitively changed by applied forces. We demonstrate that hydrostatic pressure works as an inhibitory action on kinesin motility. We developed a high-pressure microscope that enables the application of hydrostatic pressures of up to 200 MPa (2000 bar). Under high-pressure conditions, taxol-stabilized microtubules were shortened from both ends at the same speed. The sliding velocity of kinesin motors was reversibly changed by pressure, and reached half-maximal value at ∼100 MPa. The pressure-velocity relationship was very close to the force-velocity relationship of single kinesin molecules, suggesting a similar inhibitory mechanism on kinesin motility. Further analysis showed that the pressure mainly affects the stepping motion, but not the ATP binding reaction. The application of pressure is thought to enhance the structural fluctuation and/or association of water molecules with the exposed regions of the kinesin head and microtubule. These pressure-induced effects could prevent kinesin motors from completing the stepping motion.

Introduction

Protein molecules in solution are surrounded by water molecules. The hydrogen bond is formed between the water and the electric-charged residue of the protein. The water molecules of hydration work to optimize the protein structure energetically, and help molecular recognition processes proceed (1). Indeed, proteins lack activity in the absence of water molecules. An application of pressure is a powerful method for modulating intermolecular interactions between protein and water molecules. Elevated pressure was used as a thermodynamic tool to explore the biophysical properties of proteins, lipids, nucleic acids, and other macromolecules. High-pressure techniques were used to study the thermodynamic properties of biomolecules, such as structural stability and folding pathways (1–4). In general, the application of pressure of several hundred MPa (1 bar = 0.1 MPa) does not seriously affect primary and secondary structures, but it does increase the structural fluctuation of protein molecules (5). It also weakens protein-protein and protein-ligand interactions in solutions (3). These pressure-induced effects are thought to be caused by enhancement of the clustering of water molecules around hydrophobic and hydrostatic residues on the protein surface. This means that applied pressure enables modulations of the structure and function of protein molecules, without requiring the use of any chemical materials other than water molecules. In nature, pressure is an important physical factor that characterizes the physiological environment for biological species.

Application of pressure causes significant changes in the cell morphologies and activities of organisms living under ambient pressure. Muscle fiber is a good example to study for an understanding of the mechanism of how hydrostatic pressure affects its structure and function. It was reported that the application of pressure changes the mechanical behavior of muscle fibers (6,7). These findings suggest that a pressure-sensitive transition of actomyosin is directly coupled to force generation. Similar results were obtained from purified actomyosin (8,9). The polymerization and depolymerization dynamics of actin and myosin filaments were shown to be sensitive to pressure (10–12). To examine pressure-induced changes of biological systems directly, Salmon developed a high-pressure chamber for microscopy (13). It was successfully used to visualize that the application of several dozen MPa of pressure induces the spindle microtubule to depolymerize immediately and reversibly in vivo (14,15). The results also indicated that pressure affects the polymerization-depolymerization dynamics of microtubules. However, the experimental results included the effects of pressure on a variety of microtubule-associated proteins, and it was difficult at times to dissect only the pressure-induced effects on microtubules.

We studied the effects of pressure on the structure and function of cytoskeletal proteins, using the kinesin-microtubule complex as a model system. The microtubule cytoskeleton typically comprises 13 protofilaments, which form the wall of a tube (16,17). Each of the protofilaments consists of a head-to-tail arrangement of α/β-tubulin heterodimers. The filamentous structure of microtubules is thermodynamically unstable, and the length is changed through the polymerization and depolymerization of tubulin molecules (18,19). The dynamic properties are strongly affected by physical conditions, such as temperature and hydrostatic pressures (15). Thus our high-pressure microscope visualized pressure-induced effects on microtubules, revealing the dynamic features of intermolecular interactions between tubulin molecules. In addition, kinesin is a two-headed molecular motor that moves processively along a microtubule (17,20–23). The processive movement is composed of regular 8-nm steps (24–26), and the stepping motion is strongly dependent on physical and chemical conditions, such as applied force (25–27), temperature (28–30), and anesthetic agents (31). We describe here the first experiments (to the best of our knowledge) on the pressure dependency of kinesin-driven motility.

Materials and Methods

Pressure devices

The pressure apparatus consisted of a high-pressure chamber, separator, pressure gauge, and high-pressure hand pump (Fig. 1 A). These pressure devices were connected with 1/8-inch stainless tubes. The apparatus could be used with a commercially available microscope and optics for the observation of epifluorescence and bright-field images. Fig. 1 B shows a cross section of a high-pressure chamber (Sasahara Giken, Kyoto, Japan). The chamber was composed of observation and rear windows (OW and RW) and six metal parts. The outer dimensions of the main body were 60 × 60 × 34 mm, and the internal volume was ∼0.2 mL. Two windows (OW and RW) were attached to the window supports (WS1 and WS2) by epoxy resin. The observation and rear windows were fixed in the main body (MB) by the window support screws (SS1 and SS2), and sealed by the O-rings (O1 and O2).

Figure 1.

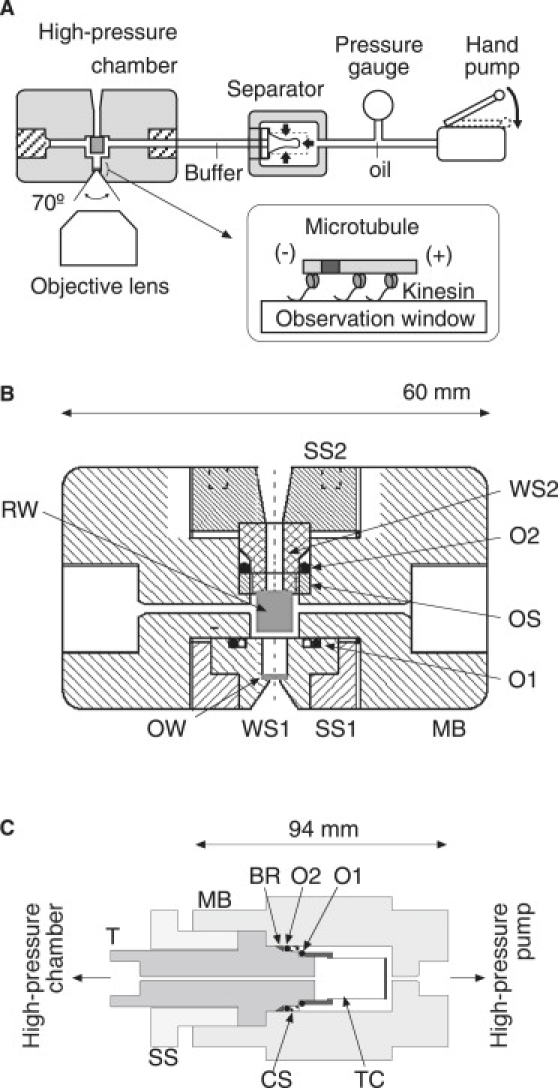
High-pressure microscope. (A) Schematic diagram of microscope apparatus (not to scale). See text for details. (Inset) A polarity-marked microtubule is immobilized above the observation window by kinesin molecules. (B) Cross section of high-pressure chamber. OW, observation window; RW, rear window; WS1 and WS2, window supports; MB, main body; SS1 and SS2, window support screws; OS, O-ring support screw; O1 and O2, O-rings. (C) Cross section of separator. MB, main body; T, transducer; SS, support screw; CS, cap screw; TC, Teflon cap; BR, backup-ring; O1 and O2, O-rings.

Microscopic observations in the chamber were performed through an observation window (OW in Fig. 1 A, optical glass (BK7), ϕ = 3.5 mm, t = 1.5 mm). The aperture diameter and critical angle were 1.5 mm and 70°, respectively. The large aperture of the OW enabled the observation of fluorescence images with both high sensitivity and resolution. The OW was made of optical glass (BK7) because this material was found to be suitable for preparing an appropriate surface condition for our experiments. Microscopic observations in the chamber could be performed using a long working distance objective lens (working distance of >4.3 mm).

Fig. 1 C shows a cross section of the separator (Sasahara Giken). The use of the separator conferred the advantage of reducing the total dead volume of the buffer solution in the pressure line. The main body (MB) of the separator was a cylindrical tube (ϕ = 60 mm, L = 94 mm, stainless steel (SUS630)). The inside was separated into two spaces by a thin Teflon cap (TC). The thickness of the cap was ∼0.2 mm, and the internal volume was ∼5 mL. The cap was attached to the transducer (T) and sealed by an O-ring (O1). These were fixed in the main body (MB) by a support screw (SS), and sealed by an O-ring (O2). This O-ring was supported by a backup ring (BR), and fixed by a cap screw (CS). The inside of the Teflon cap was filled with assay buffer, and connected to the high-pressure chamber. The gap between the Teflon cap and main body was filled with silicon oil, and connected to the high-pressure pump (Hikari Kouatsu, Hiroshima, Japan). The oil pressure was transduced to that of the buffer solution through deformation of a thin Teflon cap in the separator. The hydrostatic pressure in the pressure line was measured using a pressure gauge (KH78, Naganokeiki, Tokyo, Japan). Accuracy was verified using a Heise Bourdon tube pressure gauge calibrated against a free piston gauge (P-31, Naganokeiki).

Microscope

The high-pressure chamber was mounted on a commercially available microscope (IX71, Olympus, Tokyo, Japan), equipped with a long working distance objective lens (working distance = ≈8 mm, NA = 0.55, SLCPlan 40×, Olympus) and an intermediate magnification lens (×2, Olympus). The chamber position was adjusted in the x–y directions by manipulators. Fluorescently labeled microtubules and beads were excited by a diode-pumped Nd:YVO₄ laser (μGreen 4611 SLM, JDS Uniphase, Milpitas, CA), and epifluorescence images were captured by an EB-CCD camera (C7190-23, Hamamatsu Photonics, Hamamatsu, Japan), coupled to an image intensifier (VS4-1845 Omni-IV, Videoscope, Dulles, VA). Video images were processed by contrast enhancement and brightness offset, and recorded using a digital video recorder (DSR-11, Sony, Tokyo, Japan). All images were analyzed on a computer, using a program within Image J.

Temperature and pH measurements

The pressure-induced temperature change of the water solution was measured by a thermocouple, of which the electric probe was inserted from another port of the high-pressure chamber (Fig. 1 B, left port). Application of 200 MPa of pressure transiently increased the temperature of distilled water by 0.3°C, but it reached a thermal equilibrium within 30 s. The pressure-induced pH changes in the buffer solution for the microtubule-gliding assay were measured. The buffer solution containing a pH indicator (bromothymol blue or p-nitrophenol) was enclosed in another high-pressure chamber (32). The absorption spectrum was measured at each pressure. The corresponding pH value was calculated from the peak intensity, and each peak intensity was corrected in consideration of the pressure dependence of the solution volume and pK_a value of indicators (33,34). The application of 200 MPa of pressure increased the pH value from 6.8 to 7.0. Similar results were obtained for other good buffer solutions (ΔpH = 0.1–0.2 at 200 MPa, with 10 mM Tris, PIPES, HEPES, or MES), but not for 10 mM potassium phosphate buffer solution (ΔpH = −0.6 at 200 MPa).

Proteins and assays

Tubulin was obtained from porcine brains and labeled with tetramethylrhodamine succinimidyl ester (25). Polarity-marked microtubules were prepared by polymerizing dimly labeled tubulin molecules to the ends of brightly labeled microtubule seeds (35). The N-ethylmaleimide-treated tubulin was not used for elongation. The polarity of microtubules was confirmed by microtubule-gliding motility assays at ambient pressure. For microtubules with a total length of >10 μm, the probability that the shorter dimly labeled segment was in the leading direction of the movement was >90%. Porcine kinesin molecules (36) were diluted to 300 μg/mL (0.8 nM) in BRB80 buffer (80 mM PIPES, pH 6.8, 2 mM MgCl₂, and 1 mM EGTA), supplemented with filtered casein (∼2 mg/mL). The OW of the high-pressure chamber was incubated with the kinesin solution for 5 min. Unbound kinesin molecules were removed by washing with BRB80 buffer containing 10 μM paclitaxel. Polarity-marked microtubules were then attached to the kinesin molecules, which were densely adsorbed on the OW. Microscopic observations of fluorescence images of microtubules were performed in BRB80 buffer containing 10 μM paclitaxel and antiphotobleaching reagents (36). We added 10 μM AMP-PNP and 5–1000 μM ATP for microtubule depolymerization assays and microtubule-gliding assays, respectively. All procedures were performed at 25 ± 1°C.

Results

Performance evaluation

We confirmed the withstanding pressure of the apparatus. Pressure was increased using the hand pump. Application of 200 MPa of pressure required about half a minute, whereas the release of pressure by opening a valve was nearly instantaneous. The oil pressure was properly transduced to the buffer solution in the high-pressure chamber. High-pressure conditions were maintained properly. The stability was directly confirmed by microscopic analysis of beads undergoing Brownian motion in solution. The pressure apparatus could be used for applications of pressure up to 200 MPa (∼2000 bar).

Next, we checked the performance of the apparatus as a microscope. Because a commercial objective micrometer could not be installed in the high-pressure chamber, a micrometer scale was directly fabricated on the surface of the observation window (OW in Fig. 1 B). The micrometer pattern consisted of small voids in lattice points (Fig. 2 A). Each void was fabricated by irradiation with a femtosecond laser pulse (37,38). The custom-made objective micrometer was installed in the high-pressure chamber, with the fabricated surface located on the inside. When pressure was applied to the chamber, the microscopic image moved out of focus. After rearranging the focal position of the objective lens, the microscopic image became normally focused again. As the pressure increased, the apparent focal length clearly increased (Fig. 2 B). The displacement was almost reversible against different pressures, and may be attributable to pressure-induced deformation of the OW and chamber. We confirmed whether microscopic images were distorted under high-pressure conditions. The refocused images did not show any significant changes in image contrast or resolution (data not shown). Fig. 2 C summarizes the distances between voids under various pressure conditions, and shows that the magnification ratio was independent of the pressure. Thus the apparatus allows for the performance of microscopic analyses under high-pressure conditions.

Figure 2.

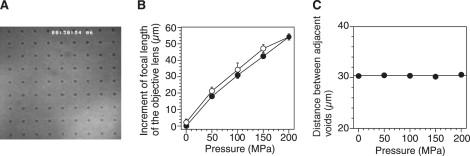
Calibration of microscopic images under pressurized conditions. (A) Bright-field image of the custom-made objective micrometer. (B) Pressure dependence of z-position of objective lens. Each plot represents average z-position of objective lens in focus with lattice pattern under pressurization (solid circles, n = 5) and depressurization (open circles, n = 5). Displacement was measured by eye, using the scale of the focusing knob. Error bars are the SD. (C) Pressure dependence of magnification ratio. Each point represents average distance between adjacent voids (n = 8). Error bars (± SD) are shown within plots.

Finally, we confirmed whether applications of pressure induced significant changes in the water solution, because pressure is a fundamental thermodynamic parameter that influences all chemical processes through effects on system volumes (34). We studied the pressure dependence of the viscous drag, temperature, and pH values of the buffer solution (see Materials and Methods). The pressure-induced change in viscous drag was measured by microscopic analysis of beads (1.03 μm in diameter; Molecular Probes, Eugene, OR) undergoing Brownian motion in distilled water (39). Fig. 3A shows two-dimensional mean square displacements (MSDs) of a bead at 0.1 and 200 MPa. The plots were fitted to the equation, MSD(t) = 4D_x–y t, with D_x–y = 0.48 and 0.42 μm² s⁻¹ at 0.1 and 200 MPa, respectively. Applications of pressure slightly decreased the diffusion constant of the bead (Fig. 3 B), consistent with previous work (40). The viscous drag of water solution was 0.88 × 10⁻³ Pa s and 1.01 × 10⁻³ Pa s at 0.1 and 200 MPa, respectively. These values were calculated according to the Stokes-Einstein relationship (41) (D_x–y = k_BT/6πηa, where k_B is the Boltzmann constant, T is the experimental temperature (= 298 K), η is the viscosity of water at each pressure, and a is the radius of the bead). In addition, the temperature and pH values were not significantly changed by applications of pressure below 200 MPa. Thus we conclude that the application of pressure did not basically alter the physical characters of the buffer solution under our experimental conditions.

Figure 3.

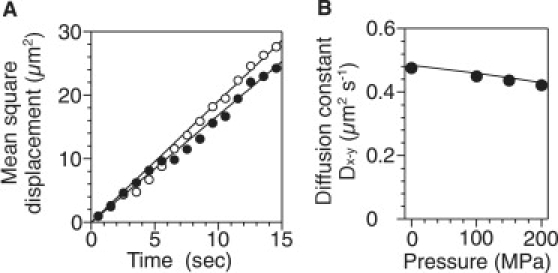
Pressure dependence of diffusion constant of beads. (A) Two-dimensional mean-square displacements (MSD) at 0.1 and 200 MPa (n = 100). Plots were fitted with equation, MSD(t) = 4D_x–yt, with D_x–y = 0.48 and 0.42 μm² s⁻¹ at 0.1 and 200 MPa, respectively. (B) Pressure dependence of diffusion constant of 1-μm bead. Plots are diffusion constants of 1-μm bead at each pressure. Solid curve represents theoretical values, as obtained from Stokes-Einstein relationship (41).

Microtubule depolymerization assay

Polarity-marked microtubules were tethered to kinesin motors on the OW of a high-pressure chamber in the presence of 10 μM paclitaxel and 100 μM AMP-PNP (Fig. 1 A, inset). Pressure-induced changes in the filamentous structure of microtubules were studied using time-lapse microscopy. Before applications of pressure to the chamber, no changes were evident in fluorescence images of the microtubules. In contrast, when pressure was applied to the sample solution, all microtubules started to shorten from both ends (Fig. 4 A and Movie S1 in the Supporting Material). Fig. 4 B shows the time courses of the length changes of the same microtubules at 125 and 150 MPa. The length changes were constant over time, irrespective of microtubule polarity. The plots at 125 MPa were fitted by straight lines of 0.34 and 0.32 μm min⁻¹ at the plus and minus ends, respectively. The shortening rates at 150 MPa increased to 1.0 and 1.1 μm min⁻¹ at the plus and minus ends, respectively. Taxol tends to drive free tubulin into small, unphysiological aggregates that can take some time to resolve into well-organized microtubules. This, rather than pressure-induced denaturation, may be the reason that pressure-induced depolymerization is apparently irreversible.

Figure 4.

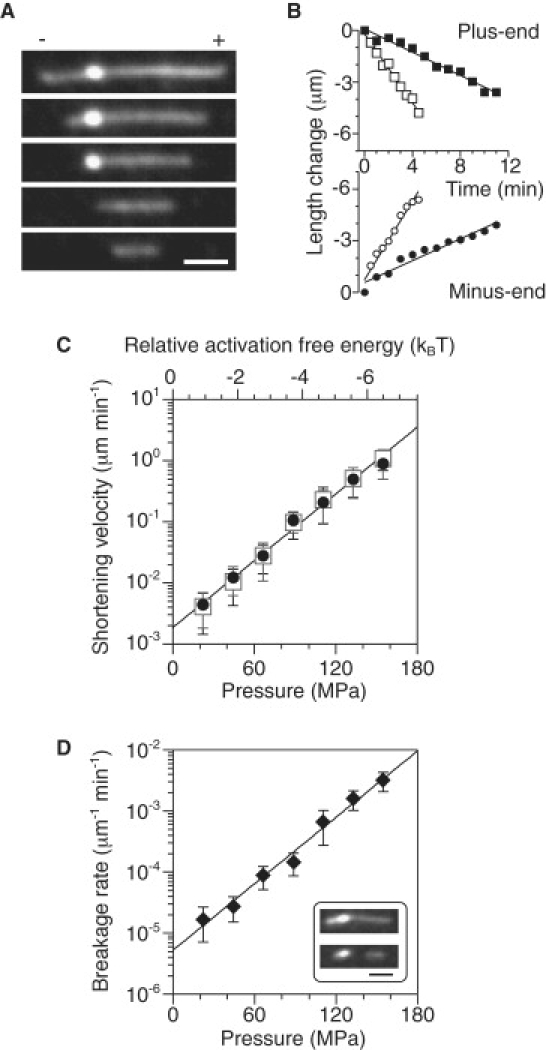
Pressure-induced microtubule depolymerization. (A) Sequential fluorescence images of same microtubule recorded at 2-min intervals. A pressure of 150 MPa was applied to a polarity-marked microtubule in the presence of 10 μM paclitaxel and 100 μM AMP-PNP. Scale bar, 5 μm. (B) Time courses of length changes from plus and minus ends of same microtubules. Pressure of 125 MPa (solid circles) or 150 MPa (open circles) was applied from t = 0 min. Plots at plus and minus ends were fitted by straight lines of 0.34 and 0.32 μm min⁻¹ at 125 MPa, respectively. Similarly, plots at plus and minus ends were fitted by straight lines of 1.0 and 1.1 μm min⁻¹ at 150 MPa, respectively. (C) Pressure dependence of shortening rates at plus (open squares) and minus (solid circles) ends (mean ± SD, n = 26–45). Shortening rates were fitted by Eq. (1), with α_shortening = 1.9 × 10⁻³μm min⁻¹ and ΔV^‡_shortening = −170 ų. (D) Pressure dependence of breakage rate of microtubules (mean ± SD, observed severing events; n = 3–8, total = 39). Breakage rates were fitted by Eq. (1), with α_breakage = 5.3 × 10⁻⁶μm⁻¹ min⁻¹ and ΔV^‡_breakage = −170 ų. (Inset) Sequential images of same microtubule at 125 MPa, recorded at 3-min intervals. Scale bar, 5 μm.

Fig. 4 C summarizes the pressure dependence of shortening rates at the plus and minus ends. The shortening rates increased exponentially with pressure, and were independent of microtubule polarity and length (data not shown). The pressure dependence of the rate, k_i, was characterized as

$$k_i={\alpha }_i\times \text{exp}[-(p-0.1)\times \Delta V^{‡}/k_{\mathrm{B}}T],$$ (1)

where α_i is the basal rate at 0.1 MPa, p is the pressure, ΔV^‡_i is the activation volume, and k_BT is the thermal energy (3) Negative and positive values of the activation volume reflect decreases and increases in the activation free energy, respectively. A large absolute value reveals the strong pressure dependence of the rate. The activation volume is analogous to the “characteristic distance” (25,42), which is frequently used for analyzing the force dependence of the rate. The shortening rates at the plus and minus end were fitted by Eq. (1) with α_shortening = 1.9 × 10⁻³ μm min⁻¹ and ΔV^‡_shortening = −170 ų, respectively. We assumed that tubulin dimers independently dissociated from the end of the outer-curled protofilament of microtubules. The tubulin dissociation rate was 4 × 10⁻³ s⁻¹ at 0.1 MPa, and increased to 2 s⁻¹ at 150 MPa. It corresponds to a 500-fold acceleration in the rate. The activation free energy change was calculated at about −6 k_BT (Fig. 4 C, upper abscissa), which is equivalent to almost one third of the free energy of ATP hydrolysis (∼20 k_BT).

Besides the shortening reaction, we occasionally observed that the tethered microtubules became severed under pressurized conditions (Fig. 4 D, inset). The breakage event was not a major occurrence under our experimental conditions. It was thought to be sensitive to the surface treatment of the OW. The breakage event was characterized by calculating the breakage events per minute per total microtubule length, including the nonsevered microtubules. The breakage rate also increased exponentially with pressure (Fig. 4 D). The plots were fitted by Eq. (1) with α_breakage = 5.3 × 10⁻⁶ μm⁻¹ min⁻¹ and ΔV^‡_breakage = −170 ų. The breakage rate per tubulin-dimer length (= 8 nm) was calculated to 7.1 × 10⁻¹⁰ (8 nm)⁻¹ s⁻¹ at 0.1 MPa, which was ∼2 × 10⁻⁷-fold smaller than the 8-nm length shortening rate (4 × 10⁻³ s⁻¹ at 0.1 MPa). On the other hand, ΔV^‡_breakage was equal to ΔV^‡_shortening, strongly suggesting a close relationship between breakage and shortening reactions.

In vitro motility assay under pressurized conditions

We studied pressure-induced effects on microtubule-based kinesin motility by performing microtubule-gliding assays under pressurized conditions. The sliding velocity was measured according to the movement of the brightly labeled segment of each polarity-marked microtubule, because microtubules driven by kinesin motors were also shortened from both ends. The shortening rates at the plus and minus ends were 0.51 ± 0.41 and 0.83 ± 0.44 μm min⁻¹ (mean ± SD, n = 14, [ATP] =1 mM, 130 MPa). The results were consistent with the values of the fixed microtubule (Fig. 4) within the experimental error. These results suggest that the motility of kinesin motors does not seriously affect the shortening rate of microtubules.

When pressure was applied to the sample, the sliding velocity of microtubules immediately decreased from 790 nm s⁻¹ at 0.1 MPa to 340 nm s⁻¹ at 130 MPa (Fig. 5 A). Most of the microtubules moved smoothly and continuously, even under pressurized conditions. The sliding velocity was constant over time for each pressure. After the release of pressure, the sliding velocity immediately returned to the original value. Thus the application of pressure acts as an inhibitor that directly and reversibly alters microtubule-based kinesin motility. Fig. 5 B shows the mean sliding velocities for each pressure and ATP concentration. The sliding velocity, v, followed normal Michaelis-Menten kinetics of v = v_max · [ATP]/([ATP] + K_m), where v_max is the sliding velocity at saturation concentrations of ATP, and K_m is the Michaelis constant. Application of pressure caused a significant decrease in v_max, but only a slight decrease in K_m (Fig. 5 B, inset). Fig. 5 C shows the pressure-velocity relationships at ATP concentrations of 1 mM and 10 μM. The sliding velocity decreased monotonically with increases in pressure. Interestingly, the pressure-velocity relationship was very close to the force-velocity relationship of single kinesin molecules (Fig. S1). The application of either ∼100 MPa (= 1 pN Å⁻²) of pressure or ∼3 pN of force decreased the sliding velocity at 1 mM ATP by half.

Figure 5.

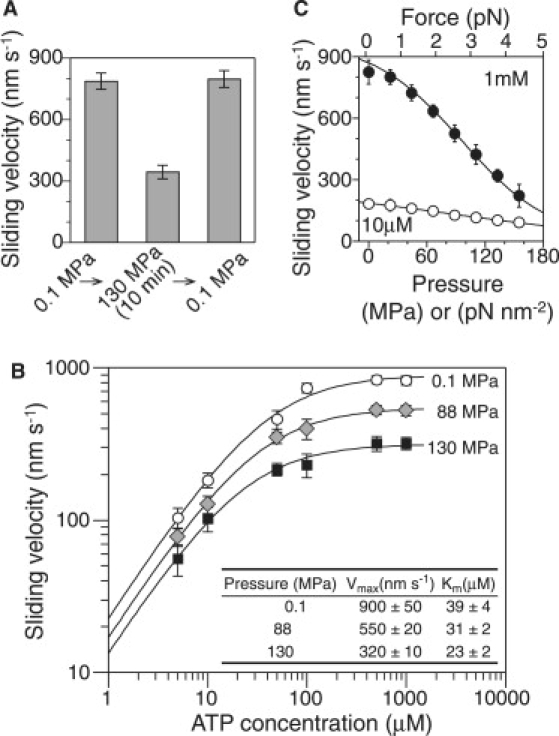
Pressure dependence of microtubule-based kinesin motility (mean ± SD, n = 5–82). (A) Reversible inhibition of sliding movement of kinesin motors. [ATP] = 1 mM. (B) Michaelis-Menten kinetics. (Inset) Fitted parameters (mean ± SD). (C) Pressure dependence of sliding velocity. [ATP] = 1 mM (solid circles) and 10 μM (open circles).

Discussion

High-pressure microscopy

The constructed instrument contained a high-pressure chamber that could be mounted on most commercially available microscopes, allowing us to perform microscopic observations under pressurized conditions. The pressure apparatus could be used for applications of pressure up to 200 MPa (∼2,000 bar), which is about twofold higher than the water pressure in the deepest part of the Mariana Trench (∼10,900 m in depth). This level of ability to withstand pressure is sufficient for studying almost all biological activities on Earth.

The high-pressure chamber was equipped with two windows at the objective and condenser lens sides. These windows enabled us to observe epifluorescence and bright-field images of an object under high-pressure conditions. By reducing the thickness of the observation window (OW in Fig. 1 B), a large aperture of the OW (∼70°), corresponding to NA = 0.57, was achieved. This allowed us to observe the epifluorescence image of individual microtubules at a video rate. On the other hand, the opening at the condenser side had room to increase the numerical aperture. The enlargement of the numerical aperture on both sides allowed us to make dark-field and phase-contrast images, and will expand the versatility of high-pressure microscopy in further applications. Another problem is that the cavity length between the two windows of the high-pressure chamber is too long, resulting in an increase in fluorescence background for microscopic observations. This problem could be solved by changing the design of the high-pressure chamber, and using confocal microscopy.

Most cellular processes are performed using biomolecules located in an aqueous environment. Our technique could be extended to study the dynamic properties of biomolecules in living cells (14,43). In general, a more complicated system is more sensitive to pressure. Cellular structure and function are thought to be suitable research targets for high-pressure microscopy.

Pressure-induced acceleration of microtubule depolymerization

We performed an in vitro assay to observe the pressure-induced effects on the filamentous structure of taxol-stabilized microtubules. When pressure was applied to the sample solution, all of the microtubules began to shorten from both ends, at a similar speed. At the end of the microtubule, the protofilament spontaneously adopts an outer-curved conformation (16,17). The tubulin molecules at the end bind to the filament, with a single tubulin-tubulin interaction in the axial direction. Thus the microtubule shortening was caused through the dissociation of one or several tubulin molecules in order. In contrast, the microtubule was hardly severed by the applied pressure. Tubulin molecules embedded in the filamentous structure are well-stabilized by tubulin-tubulin interactions not only in the axial direction, but also in the lateral direction (16,17). The multiple intermolecular interactions likely prevented the microtubule from severing.

Pressure-induced microtubule shortening could be explained by the denaturation of tubulin molecules. In general, a pressure of 100 MPa does not seriously affect the primary and secondary structures (3), but it can increase the structural fluctuation of protein molecules (5). It could also induce partial denaturation of the tertiary structure. In our case, the application of a pressure force denatured the tubulin molecules and dissociated them from both ends of the microtubule, with a resultant loss of binding capacity. After the release of pressure, tubulin molecules would not polymerize again.

Alternatively, microtubule shortening could be explained by the modulation of intermolecular interactions between tubulin and water molecules. Pressure works to enhance the clustering of water molecules around hydrostatic and hydrophobic residues (3). Pressure-induced effects are more significant on the protein surface than on the inside of the protein. Before the denaturation of tubulin molecules, water molecules could penetrate into tubulin-tubulin binding sites, resulting in a dissociation of tubulin molecules. The dissociated tubulin molecules are thought to be able to form microtubule filaments at ambient pressure. Salmon reported that the application of pressure causes the spindle microtubule in vivo to depolymerize reversibly at pressures of less than 50 MPa (15). The pressure dependence of the shortening velocity was characterized by the activation volume of −90 mL mol⁻¹ (−150 ų). This is consistent with ΔV^‡_shortening = −170 ų in our experiment (Fig. 4 C). This view is partially supported by this work, but further study must elucidate whether the microtubule is shortened by the same mechanism under pressures of more than 50 MPa.

In addition, the pressure-induced shortening reaction is similar to microtubule depolymerization by motor proteins of kinesin-8 and kinesin-13 (44–47). These molecules induce dissociation of tubulin molecules from both ends of a microtubule, with a maximum rate of several micrometers per minute. This rate is similar to the shortening rate at 150 MPa (∼1 μm min⁻¹). The application of pressure could depolymerize microtubules by a similar mechanism as with kinesin-8 and kinesin-13 molecules. Further work is necessary to understand the detailed molecular mechanism of pressure-induced microtubule shortening.

Pressure-induced deceleration of kinesin motility

Our results reveal that the application of pressure acted as an inhibitor that directly and reversibly altered microtubule-based kinesin motility. The pressure-velocity relationship (Fig. 5 C) is apparently almost the same of the force-velocity relationship of single kinesin molecules (Fig. S1). Then we characterized the pressure dependence of sliding velocity, using a mechanochemical model for kinesin motors (Fig. 6). This model was constructed on the basis of a previous three-state model (25). The three states of K, K.T, and K.D considered in the analysis correspond to kinesin without a bound nucleotide, with bound ATP, and with bound ADP (or ADP.Pi), respectively. Kinesin motors wait for a step with only a head-bound state (48,49). A single ATP hydrolysis reaction is coupled to a single step (50,51), irrespective of a wide range of force (25,27). It was assumed that chemomechanical coupling is not altered by applications of pressure. We performed a model analysis to determine the rate constants at ambient pressure and activation volumes. The rate of k₁ at each pressure was calculated from v_max divided by K_m and 8 nm. The value of k₁ decreased exponentially with pressure, and was fitted by Eq. (1), with α₁ = 2.9 μM⁻¹ s⁻¹ and ΔV^‡₁ = 15 ų. We assumed that subsequent reactions after the ATP binding reaction consisted of pressure-independent k₂, and pressure-dependent k₃, transitions. Thus v_max is given as

$$v_{\max }=8\times {[\frac{1}{{\alpha }_2}+\frac{1}{{\alpha }_3}\times \exp ((p-0.1)\times \Delta V^{‡}/k_{\text{B}}T\left)\right]}^{-1},$$ (2)

where α₂ and α₃ are the basal rates at 0.1 MPa for k₂ and k₃, respectively, and ΔV^‡₃ is the activation volume of k₃. The pressure-v_max relationship can be well-fitted by Eq. (2), where α₂ = 140 s⁻¹, α₃ = 770 s⁻¹, and ΔV^‡₃ = 88 ų.

Figure 6.

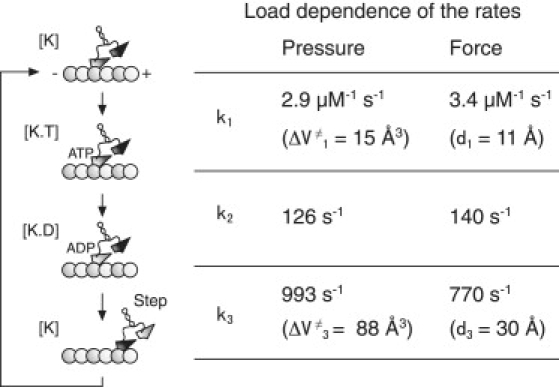
Load dependence of stepping kinetics. (Left) Mechanochemical model for kinesin motors (see text). (Right) Pressure dependence of stepping kinetics is characterized by rate constants at 0.1 MPa and activation volumes. The force dependence of a similar kinetic model is presented for comparison (25). Each rate is characterized by k_i = β_i exp(−F d_i/k_BT), where β_i is the rate constant at 0 pN, and d_i is the characteristic distance.

Our analysis revealed that the three rate constants at ambient pressure (Fig. 6) were consistent with those in previous studies (21,52,53). The activation volumes were positive values (ΔV^‡₁ = 15 ų and ΔV^‡₃ = 88 ų), meaning that the application of pressure worked to inhibit both ATP binding and stepping reactions. The value of ΔV^‡₃ was larger than that of ΔV^‡₁, indicating that the stepping reaction was sensitively changed by applied pressure, compared with the ATP binding reaction. As shown in Fig. 6, similar results were obtained for the force dependence of the rate constants. The pressure and force dependences were characterized by angstrom-order activation volumes and characteristic distances, respectively, suggesting a close relationship between them. Thus an application of pressure, as well as force, is considered to change the energy landscape for ATP binding and stepping reactions. In other words, high-pressure microscopy is a powerful and convenient method that enables us to modulate stepping kinetics without attaching any force-transmitting probes, such as an optically trapped bead (24–27) or glass needle (54,55).

Pressure is a physical parameter that is different from force. Then why do pressure and force similarly affect the stepping motion of kinesin motors? Kinesin motors “walk” along a microtubule by working two heads in a “hand-over-hand” fashion (56–58). The nucleotide hydrolysis process causes a conformational change in the kinesin head, which includes the neck-linker region (59,60). This change promotes the binding of the floating head to the next binding site on the microtubule, such that the kinesin motors complete the stepping reaction. Previous studies described force-induced effects on kinesin motility (25–27,36). When force is applied to kinesin motors in a backward direction (to the minus end of the microtubule), the stepping rate is decreased with the increment of force (Fig. S1). Applied force would strain the molecular structure of the kinesin-microtubule complex, and would perturb the energy landscape for the stepping reaction because of the mechanical work required to move against the load. On a molecular level, it is thought that the application of force inhibits the conformational change in the kinesin head and/or kinesin-microtubule interaction.

In consideration of the similarity between force-induced and pressure-induced effects on kinesin motility, applied pressure seems to cause similar changes in the energy landscape and structure, but through a slightly different mechanism. In general, the application of pressure works to enhance the structural fluctuation of protein molecules. Thus the excessive fluctuation in the kinesin head and microtubule might prevent the ordered structural change and/or binding reaction of the floating head to the microtubule from proceeding. Alternatively, pressure could enhance the association of water molecules with the exposed regions of the floating head and the microtubule. As a result, the mutual binding sites of the floating head and the microtubule are tightly covered by the water molecules of the hydration. Thus the shielding effect of hydration may have prevented the interaction between the kinesin head and the microtubule. More detailed mechanisms will be elucidated by comparisons with molecular dynamics simulations that include water molecules.

Comparison with pressure-induced effects on actomyosin systems

Previous studies described pressure-induced effects on the structure and function of actomyosin. The application of pressure induced the disassembly of myosin and actin filaments in vitro (11,12). These pressure-induced reactions are similar to the microtubule depolymerization in this study. The force-generation processes of actomyosin in vitro and in vivo were also affected by pressure. The pressure worked to perturb the binding of nucleotides to myosin and the subsequent reactions that were directly coupled to the force generation (7,10). Our results also show that pressure changes the ATP binding and stepping reactions of kinesin motors. Applications of pressure might perturb the motility of molecular motors with a similar mechanism.