The Maintained Discharge of Rat Retinal Ganglion Cells

Abstract

Action potentials were recorded from rat retinal ganglion cell fibers in the presence of a uniform field and the maintained discharge pattern was characterized. Spike trains recorded under ketamine/xylazine anesthesia were generally stationary, while those recorded under urethane anesthesia often showed slow, undriven, quasi-periodic fluctuations in firing rate. In light of these non-stationarities, interspike interval distributions and power spectral densities are reported for data collected primarily under ketamine/xylazine. The majority of cells had multi-modal interval distributions, with the first peak in the range of 25.0–38.5ms and the subsequent peaks occurring at integer multiples of the first peak. Cells with unimodal distributions were fit well by a gamma distribution function. Interval and spike count statistics showed that ON cells tended to fire faster than OFF cells and that cells with higher rates fired in a more regular manner, with the coefficient of variation covering a wide range of values across all cells (0.43–0.97). Both ON and OFF cells show serial correlations between adjacent interspike intervals, while ON cells also showed 2^nd order correlations. Cells with multi-modal interval distribution showed a strong peak at high frequencies in the power spectra in the range of 28.9–41.4Hz. Oscillations were present under both anesthetic conditions and persisted in the dark at a slightly lower frequency, implying that the oscillations are generated independent of any light stimulus but can be modulated by light level. The oscillation frequency varied slightly between cells of the same type and in the same eye, suggesting that multiple oscillatory generating mechanisms exist within the retina. Cells with high frequency oscillations were described well by an integrate-and-fire model with the input consisting of Gaussian noise plus a sinusoid where the phase was jittered randomly to account for the bandwidth present in the oscillations.

Introduction

Information about the visual world is transmitted to the brain in the form of sequences of action potentials in retinal ganglion cells that make up the optic nerve. In the presence of steady uniform illumination, most ganglion cells in the mammalian retina continually fire action potentials in an irregular pattern referred to as the maintained discharge (Kuffler et al, 1957; Rodieck, 1967). Any further stimulus must produce a change in ganglion cell firing pattern that is distinct from this background noise in order for an animal to detect it, motivating the need for a quantitative description of discharge noise statistics. To date, the maintained discharge has been analyzed for several species, including cat (Barlow and Levick; 1969; Frishman and Levine, 1983; Troy and Robson, 1992), primate (Troy and Lee, 1994), and goldfish (Levine, 1977). Here we provide the first detailed report on the maintained discharge properties of rat retinal ganglion cells.

A fundamental aspect of any description of spike train statistics is stationarity. Most studies on anesthetized animals report that the maintained discharge statistics are constant throughout the duration of a recording, presumably indicative of a stable healthy cell. Several studies though have sited a phenomenon in which ganglion cell spike rate waxes and wanes in time (Kuffler et al. 1957; Levick and Williams 1964; Rodieck and Smith, 1966; Barlow and Levick, 1969). The undulations in activity can be large in amplitude and irregular in frequency or highly rhythmic, with periods of seconds to many minutes (Rodieck and Smith, 1966). They presumably contribute to the power-law growth in discharge noise variance seen at long time scales (Teich et al, 1997). The source of the phenomenon has yet to be determined. Experimental variables, such as blood pressure, oxygenation, temperature, anesthetic, and illumination, have all been manipulated and only the latter was found to affect rhythms in the maintained discharge. However, we find that rat ganglion cell spike trains are reasonably stationary for certain anesthetics but not for others commonly used in vision experiments. The differences in anesthetic effect may provide insight into the physiological or pathological origin of the rhythms.

Another important descriptor of the maintained discharge is the distribution of intervals between spikes and the extent to which the intervals depend on the spike history of the cell. Spike trains generated by a renewal process have interspike intervals that are statistically independent, which means that they are completely described by the probability density function from which the intervals are drawn. Cat and primate retinal ganglion cell spike trains do not strictly fall within the definition of a renewal process because slight negative correlations exist among adjacent intervals (Kuffler, 1957; Rodieck, 1967; Troy and Robson, 1992; Troy and Lee, 1994), whereby short intervals tend to be followed by long intervals and vice versa. However, to a good approximation, they can be described by a renewal process with gamma-distributed interspike intervals and power spectra. We find that this description also applies to rat ganglion cell spike trains, with the caveat that most cells show a propensity for fast oscillatory discharge, which we define as oscillations in the spike train at relatively high frequencies, beyond which a typical ganglion cell can resolve in response to a light stimulus.

One of the goals in characterizing the statistical properties of the maintained discharge is to gain insight into the retinal mechanisms that generate the discharge noise and its defining features. Possible sources of spike train irregularities include phototransduction noise (Schneeweis and Schnapf, 1999), synaptic noise (Freed, 2005; Demb et al. 2004), and stimulus noise due to the stochastic nature of photon arrival (Hecht et al, 1942). Simulations have shown that a simple integrate-fire-model with a white noise input produces gamma-distributed interspike intervals and power spectra like those of mammalian retinal ganglion cells (Levine, 1991; Passaglia and Troy, 2004). This model is not sufficient for describing rat ganglion cell spike trains, however, because we find that most cells have multi-modal interval distributions. Similar shaped distributions have been reported in goldfish (Levine, 1977) and occasionally in cat (Rodieck, 1967; Ogawa et al., 1966). We show that the model can capture the maintained discharge of rat ganglion cells if it is modified to include a high frequency oscillatory input.

Methods

Physiological Preparation

Anesthesia was induced in 30 adult Brown Norway rats using one of the following protocols: (1) an intraperitoneal (I.P.) injection of urethane (1.8g/kg); (2) an I.P. injection of a urethane (500mg/kg) and chloralose (800mg/kg) mixture; (3) an I.P. injection of a mixture of ketamine hydrochloride (70mg/kg) and xylazine (2.3mg/kg); (4) 1–2% isoflurane (flowmeter set to 1L/min). Urethane has a long lasting affect and rarely needed supplemental doses. Ketamine hydrochloride and xylazine were supplemented intravenously at 60mg/kg/hr and 2mg/kg/hr, respectively. The urethane/chloralose mixture was supplemented intravenously as needed. Preparatory surgery included the insertion of tubing into the femoral vein for drug delivery and, in some experiments, into the femoral artery for measuring blood pressure. Heart rate was monitored with an EKG and body temperature maintained near 37.0°C with a heated blanket. An intramuscular injection of dexamethasone (1mg) was given to reduce brain pulsations. The pupil was dilated with atropine sulphate (1%) and a clear contact lens was placed over the eye to protect from drying. The animal was placed in a stereotaxic apparatus and the skull was surgically exposed. Hydrogen peroxide was used to clean the skull surface and allowed identification and stereotaxic calibration to bregma and lambda. A 5mm hole was drilled in the skull either directly over bregma for optic chiasm recordings or 1.5mm lateral to bregma for optic tract recordings. All experimental procedures were approved by Boston University Animal Care and Use Committee.

Recording and Visual Stimulation

Custom made tungsten-in-glass microelectrodes were used to record extracellularly from retinal ganglion cell axons (Levick, 1972). Impedances in the range of 0.7MΩ to 1.2MΩ (IMP-2 impedance tester, 30nA current, 1 kHz frequency, BAK Electronics), were sufficient to both locate visual cells and isolate single units. Electrodes were advanced into the brain either 0.5mm anterior to bregma (optic chiasm) or 1.5mm lateral to bregma (optic tract) through a protective guide tube. A video monitor (Multiscan 17se, Sony, 40.4 × 30.2cm) was placed on a moveable platform that allowed rotational movement of the screen about a 16cm arc from the eye. The monitor was positioned on its side to maximize the vertical extent of the screen. The frame rate of the monitor was 100Hz (non-interlaced) and the mean luminance was 26cd/m², which is in the photopic range for rat (Cicerone and Green, 1980). Custom software controlled the monitor output using Matlab, LabView, and the Psychophysics Toolbox (Brainard, 1997). The monitor was gamma corrected as to linearize the input-output relationship governing monitor intensity. Upon isolation of a single cell, its receptive field was located and centered on the screen. Spike times were recorded with a digital spike discriminator sampling at 10 kHz (Acquisition Processor Module, FHC Inc.).

Cells were first determined as being either ON or OFF based on their response to handheld wands. Cells were further categorized using the classification scheme in cat where X and Y-cells respond briskly when stimulated (Cleland and Levick, 1974) and W-cells generally respond in a more sluggish manner (Troy and Shou, 2002). W-cells were encountered, but were recorded too infrequently for inclusion. Differentiating X and Y-cells was done using a sinusoidal grating of high spatial frequency that reversed sinusoidally in contrast at 2Hz. Y-cell responses have a strong second harmonic (F2) component for gratings whose spatial frequency is too high to produce a modulated response (F1) from the center mechanism (Hochstein & Shapley, 1976). Thus, for spatial frequency just beyond the resolution of the center mechanism, Y-cells gave F2>F1 and X-cells did not. The maintained discharge was recorded for 2–5min for each cell, with an average number of total spikes per cell of 2775 for ON-cells and 808 for OFF-cells.

Tests of Stationarity

In order to determine whether the statistics of the maintained discharge were constant throughout the duration of a given record, the Run Test for stationarity was used (Bendat & Piersol, 1986). This is a nonparametric procedure and thus makes no assumptions about the probability distribution of the data. Negative serial correlations between adjacent intervals might be expected given findings in other animals (Troy and Robson, 1992; Troy and Lee, 1994), so the data were segmented into groups of 8, 16, 32, or 64 intervals to minimize the influence of correlations on the stationarity test. By using segments that contain various numbers of intervals, the test probes for non-stationarities that occur on differing timescales. For a spike train consisting of N segments, where the duration of each segment is given by the random variable x, the Run Test is constructed by taking the sequence of observed values x_i=1,2,3…N, and classifying each value as being above or below the median, x_m. Observations where x_i≥x_m are assigned a 1 and values where x_i<x_m are assigned a 0. Thus, an example of a set of observations would be: 011000110111. The total number of clusters of 0’s or 1’s is defined as the number of runs, r, where r = 6 in the example shown. For the case where x is generated by a stationary process, the sequence of N observations are drawn from a probability distribution that is unchanging in time, which will result in a mean and variance of the random variable, r, that are known quantities that can be calculated (Bendat & Piersol, 1986) and come out to be:

$${\mu }_r=\frac{N}{2}+1{\sigma }_r^2=\frac{N(N-2)}{4(N-1)}$$

To facilitate interpretation of the test result, we map the random variable r onto a new random variable, R, which has a zero-mean, unit-variance distribution and is referred to as the run score. The mapping is performed by subtracting off the mean and dividing by the standard deviation of r. The distribution function of R is undefined but for large values of N it follows a normal distribution to a good approximation. The end result is that stationary spike trains should give R near zero and significant deviations from zero indicate non-stationarities.

Interspike Interval and Spike Count Statistics

The statistics of the spike train were analyzed in two ways. First, the lengths of time between adjacent spikes for all spikes in a given record were collected and a histogram of the frequency of occurrence of different interspike intervals constructed. The standard deviation of interspike intervals divided by the mean interspike interval is called the coefficient of variation (CV) and was used to quantify the irregularity of the spike train. The second method was to consider the number of spikes that occur in 1sec windows over the duration of the spike train. The average number of spikes in a given window, or spike count, and the standard deviation of the spike count were computed.

Serial Correlation Coefficients

Correlations between interspike intervals were investigated using the method of Golberg et al. (1964). Records were divided up into segments of 20 intervals and the correlation between a given interval, τ_i, and (i+k)^th interval, τ_i+k, was computed. The k-th serial correlation between these two intervals, s_k, is defined as:

$$s_k=\frac{N{\displaystyle \sum _{i=1}^N{\tau }_i{\tau }_{i+k}-}{\displaystyle \sum _{i=1}^N{\tau }_i{\displaystyle \sum _{i=1}^N{\tau }_{i+k}}}}{\sqrt{[N{\displaystyle \sum _{i=1}^N{\tau }_i^2-({\displaystyle \sum _{i=1}^N{\tau }_i{)}^2][N{\displaystyle \sum _{i=1}^N{\tau }_{i+k}^2-({\displaystyle \sum _{i=1}^N{\tau }_{i+k}{)}^2]}}}}}}-\frac{k-N}{N(N-1)}$$

where N=20. The first term is the sample correlation coefficient while the second term is a correction factor that was introduced so that s_k would be zero when there is no correlation between intervals. If, for example, a short interval tends to be followed by a long interval, then the first correlation coefficient will tend to be negative. The second correlation coefficient would be a measure of how correlated an interval is with two intervals ahead, and so on with higher order coefficients.

Power Spectral Densities

The power spectral density provides information on temporal structure present in a spike train, expressing its output as a function of frequency. Power spectra were computed by first binning the spike train at 5ms and counting the number of spikes in each window and dividing by the bin size to get units that are impulses/sec. This response vector was segmented into durations of 5.12sec and each segment was processed using the Fast Fourier Transform function in Matlab. The Fourier coefficients of each segment were then squared and summed to give the average power spectral densities. Segmenting the spike trains helps reduce uncertainty in power spectral estimates (Marmarelis & Marmarelis, 1978). The spike trains were binned at 5ms because smaller bin sizes did not reveal any new or significant features above 100Hz.

Results

Stationarity

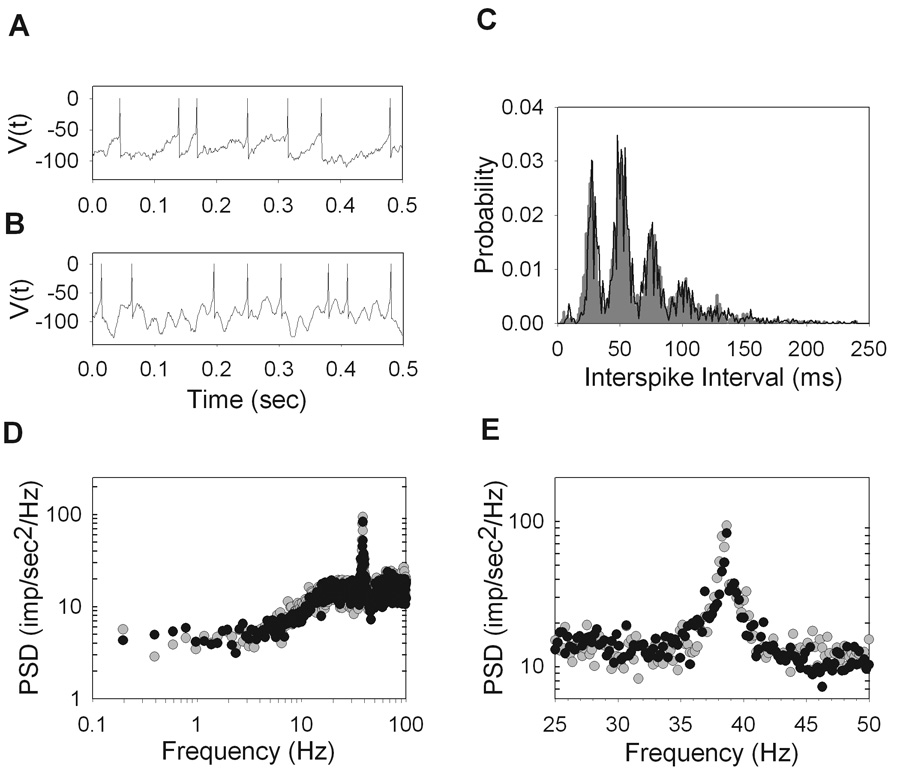
The maintained discharge of 143 cells was analyzed for stationarity. In general, cells under urethane anesthesia exhibited periods of instability, wherein the firing rate fluctuated significantly even though the receptive field was steadily and uniformly illuminated (n = 56). The fluctuations were sometimes periodic (Figure 1A), but more often they were irregular and unpredictable (Figure 1B). Similar behavior was observed in cells under urethane/chloralose (n = 2) and isoflurane anesthesia (n = 4) (Figure 1C,D). In contrast, cells under ketamine/xylazine anesthesia were very stable (n = 81) (Figure 1E,F).

Figure 1.

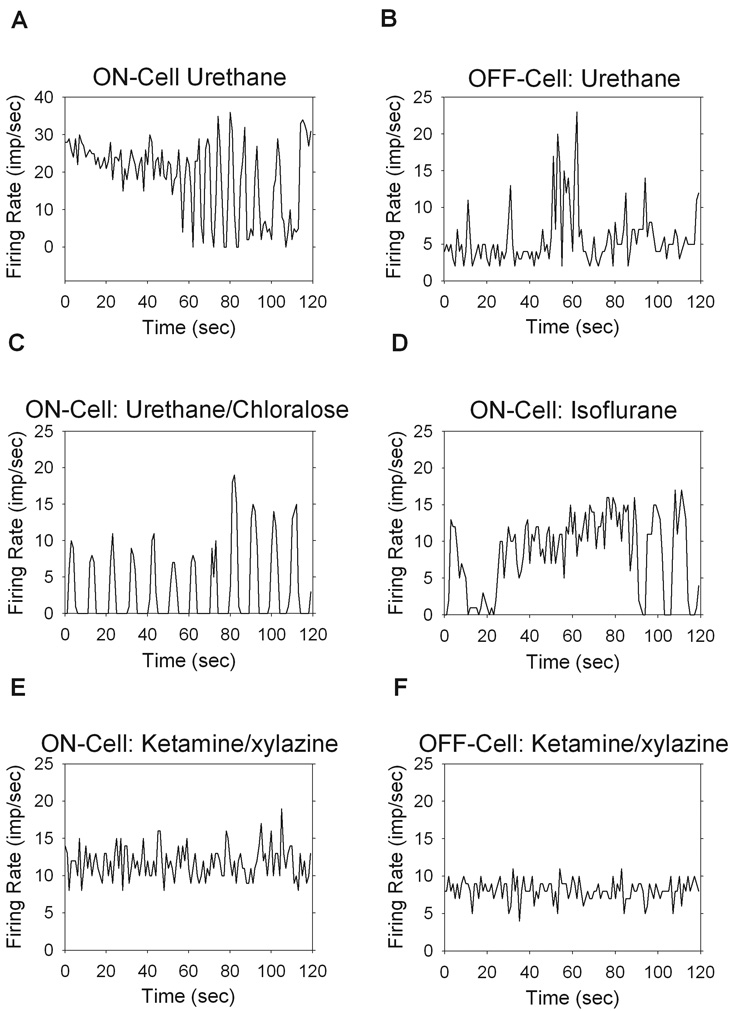
Effects of anesthesia on the maintained discharge, showing the firing rate over a 2min period (bin size = 1sec). The average run score, <R>, is given and was computed across 8, 16, 32, and 64 interval sets for each record. Examples under urethane anesthesia for an ON-cell (<R>=−1.12) (A) with periodic fluctuations in rate and an OFF-cell (<R>=−6.99) (B) showing random fluctuations in rate. Urethane/chloralose (<R>=−4.10) (C), and isoflurane (<R>=1.79) (D) anesthesia showed quasi-periodic fluctuations in rate, similar to that seen under urethane alone. Ketamine/xylazine anesthesia gave stationary discharges, with examples from a typical ON-cell (<R>=0.06) (E) and OFF-cell (<R>=0.12) (F).

Visual inspection of the spike rate record was often sufficient for identifying non-stationary behavior. To confirm this quantitatively a Run Test was performed on 8, 16, 32, and 64-segment intervals and the results are given in Table 1. The run score is a zero mean, unit variance, normally distributed variable, where significant deviations from zero indicate non-stationarity (see Methods). Averaging across all cells, the run score was significantly different from zero for all interval sizes under urethane anesthesia but not ketamine/xylazine anesthesia (P<0.05). Rat ganglion cells under urethane or isoflurane anesthesia were thus subjected to a slow time-varying input that was absent under ketamine/xylazine anesthesia. X and Y-cells were similarly effected by urethane anesthesia, both displaying non-stationarities and having run scores that were not significantly different (P<0.05). Consistent with this finding, waxing and waning has not been observed in other vision experiments that used ketamine/xylazine on rats (Girman & Lund, 2007) mice (Sagdullaev & McCall, 2005) or cats (Haider et al., 2007). However, it is unclear why the waxing and waning of firing rate was not reported in prior vision experiments that used urethane on rats (Brown and Rojas, 1965; Powers and Green, 1978; Cicerone and Green, 1980).

Table 1.

Run Test for Stationarity results under ketamine/xylazine anesthesia and urethane anesthesia. The mean and standard deviation (brackets) of the run score for 56 cells under urethane and 81 cells under ketamine/xylazine are given for segments consisting of 8, 16, 32, and 64-intervals.

	Ketamine/xylazine	Urethane
8 Intervals	0.239 [1.39]	−2.82 [4.23]
16 Intervals	−0.287 [1.43]	−2.60 [3.51]
32 Intervals	−0.497 [1.34]	−2.03 [2.63]
64 Intervals	−0.823 [1.24]	−1.99 [2.08]

Since our goal was to characterize the maintained discharge properties of ganglion cells that are in a stable and healthy condition, the subsequent analysis in this report considers data collected under ketamine/xylazine anesthesia. A total of 90 retinal ganglion cells were recorded from. The number of each cell type is given along with the mean and standard deviation of the firing rate: 38 ON-X cells (12.6 ± 6.4 imp/sec); 19 ON-Y cells (15.5 ± 5.9 imp/sec); 21 OFF-X cells (3.1 ± 3.5 imp/sec); 12 OFF-Y cells (3.4 ± 3.5 imp/sec). The mean rate was not significantly different between ON-X and ON-Y cells or between OFF-X and OFF-Y cells but it was different between ON and OFF cells (P<0.05). A total of 8 OFF-X and 1 OFF-Y cells had close to zero maintained discharge and fired only in response to dynamic visual stimulation. These cells were not included in the analysis.

Interspike Interval Distributions

Previous reports on the maintained discharge of cat and primate retinal ganglion cells have interspike interval distributions that are fit well by a gamma distribution function (Troy & Robson, 1992; Troy & Lee, 1994). The majority of cells that we encountered in rat, however, had multi-modal interval distributions (29/38 ON-X, 15/19 ON-Y, 8/13 OFF-X, 7/11 OFF-Y). The modes were all located at integer multiples of the first mode, which tended to be around 30 ms, and the initial modes were most pronounced (Figure 2A–D). Physiologically, this means that when a cell fires a spike it has a strong tendency to fire another ∼30ms later but it sometimes fails to fire a spike then. When that happens, the cell tends to fire 60ms later, or 90ms later, and so on. Hence, the cells show fast oscillatory discharges. The mean and standard deviation of the preferred interval for each cell type was estimated from the local maximum of the first mode of the interspike interval distribution. The results were 29.6 ± 2.7ms for ON-X cells, 28.5 ± 3.1ms for ON-Y cells, 31.6 ± 3.7ms for OFF-X cells, and 32.7 ± 2.7ms for OFF-Y cells. Interestingly, the location of the first mode was independent of the mean firing rate, as shown in Figure 2E. Even cells with little maintained discharge tended to fire spikes in ∼30ms intervals and multiples thereof. The preferred interval of OFF cells was statistically longer than that of ON cells (P<0.05), but the variability across cells was sufficient that the mechanism driving the fast oscillatory discharge could well be the same for all cell types.

Figure 2.

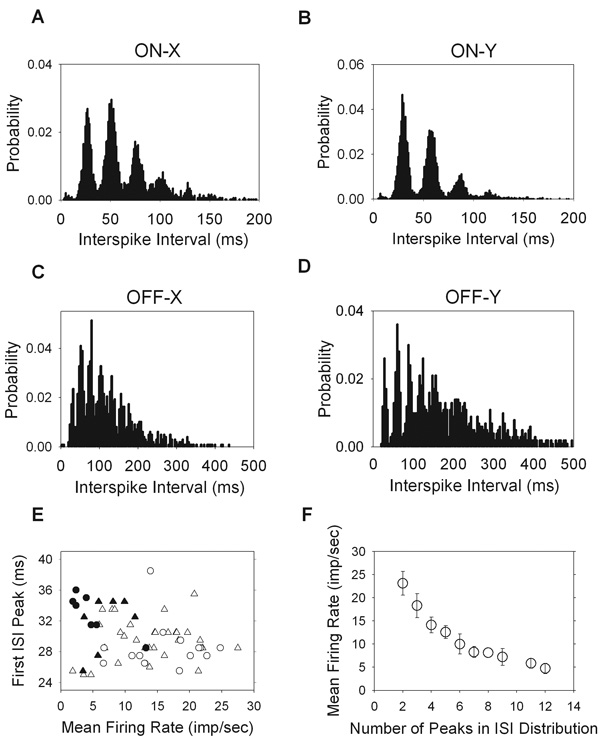
Multi-modal interspike interval distributions for all cell types. For ON cells (A, B) the bin size is 1ms, and for OFF cells (C, D) the bin size is 4ms. E. The mean firing rate of each cell is plotted against the interspike interval at which the first peak occurred. F. The number of peaks in each interval distribution is plotted against the mean firing rate of each cell (ON-X, open trianlges; ON-Y, open circles; OFF-X, filled triangles; OFF-Y, filled circles).

There was a clear dependence of the number of modes in the interval distribution on the mean firing rate (Figure 2F). Cells with low maintained discharge generally present the most modes. Presumably this is because the interval distributions are inherently broader for these cells, allowing for more modes to become apparent. It is likely that in the absence of the fast oscillatory discharge the cells would have gamma-distributed intervals like in cat and primate because other cells that have unimodal interval distributions were well fit by a gamma function, as discussed later. Related to this, a common but less striking feature of interval distributions was a small bump in the range of 4–12ms (Figure 2A–C). It was not always easy to detect, especially for low mean rate cells, given the small probabilities of interval occurrence. The feature likely reflects instances in which the fast oscillatory drive on the cell is large enough to fire a pair of spikes during a cycle. The refractory period of the spiking mechanisms then combines to make this a relatively rare event.

Interval and Spike Count Statistics

The distribution of interspike intervals in a given record provides information on the processes that underlie the generation of the maintained discharge. For cells with a lower mean firing rate, and therefore longer intervals, the variability of interval duration tended to be greater. This is illustrated in Figure 3A where the mean interspike interval is plotted versus the standard deviation of intervals for each cell. The best fit line has a slope of 1.17 and y-intercept of −0.56 (r = 0.997). The near-unity slope indicates that changes in the mean interval result in approximately equal changes in the standard deviation of intervals. This, coupled with the negative intercept, also indicates that the mean interval is larger than the standard deviation of intervals. Since the slope was not exactly 1, the coefficient of variation (CV) of the maintained discharge was generally greater for cells that fire at low rates (Figure 3B). For all cells though it is less than 1, consistent with their non-Poisson interval distributions. The result is that OFF cells, on account of their higher CV, have more irregular spike trains than ON cells.

Figure 3.

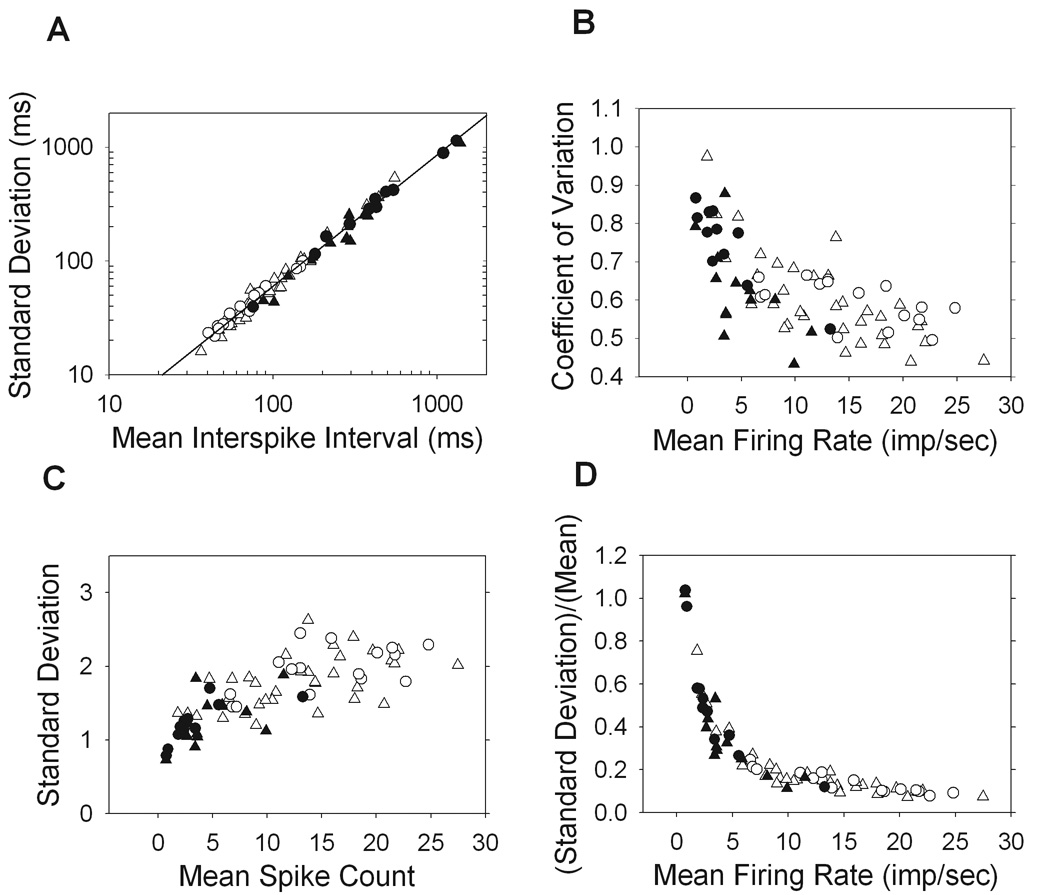
Interval and spike count statistics. A. The standard deviation of interspike intervals in the maintained discharge of each cell is plotted against the mean interval, where the line shown is the best fit with slope of 1.17 and y-intercept of −0.557 (r = 0.997). B. The coefficient of variation, or the standard deviation of intervals normalized by the mean interval, is plotted against the mean firing rate of each cell. C,D. The spike count, which is the number of spikes occurring in 1sec windows, is averaged across the maintained discharge of each cell and plotted against the standard deviation (C) as well as the standard deviation normalized by the mean (D). (ON-X, open trianlges; ON-Y, open circles; OFF-X, filled triangles; OFF-Y, filled circles).

The spike count, or the number of spikes in a given time window, was also examined. It was found that cells with a higher mean spike count tended to have a larger standard deviation of counts (Figure 3C). Expressing the relative variability as the standard deviation normalized by the mean spike count, we see that the maintained discharge becomes exponentially less variable as the mean rate increases (Figure 3D). This is a distinctly non-Poisson feature, as the mean and variance of the spike count would be equal for a Poisson process. ON and OFF cells with similar firing rates have overlapping count and interval statistics, implying that the regularity of the maintained discharge is a reflection of the discharge rate, regardless of cell polarity.

Serial Correlations

In cat, it has been shown that adjacent interspike intervals are not independent in duration, but are negatively correlated (Kuffler, 1957; Rodieck, 1967; Frishman & Levine, 1983; Robson & Troy, 1987; Troy & Robson, 1992). That is to say, a relatively short interval tends to be followed by a relatively long interval, and vice versa. The same was true for rat retinal ganglion cells where first correlation coefficient was negative for all cell types (Figure 4A, B). The second correlation coefficient was also significantly negative for ON-cells, implying that the length of a given interval will be dependent on the two previous intervals. For ON-X cells, the third coefficient was also significantly negative (P<0.05).

Figure 4.

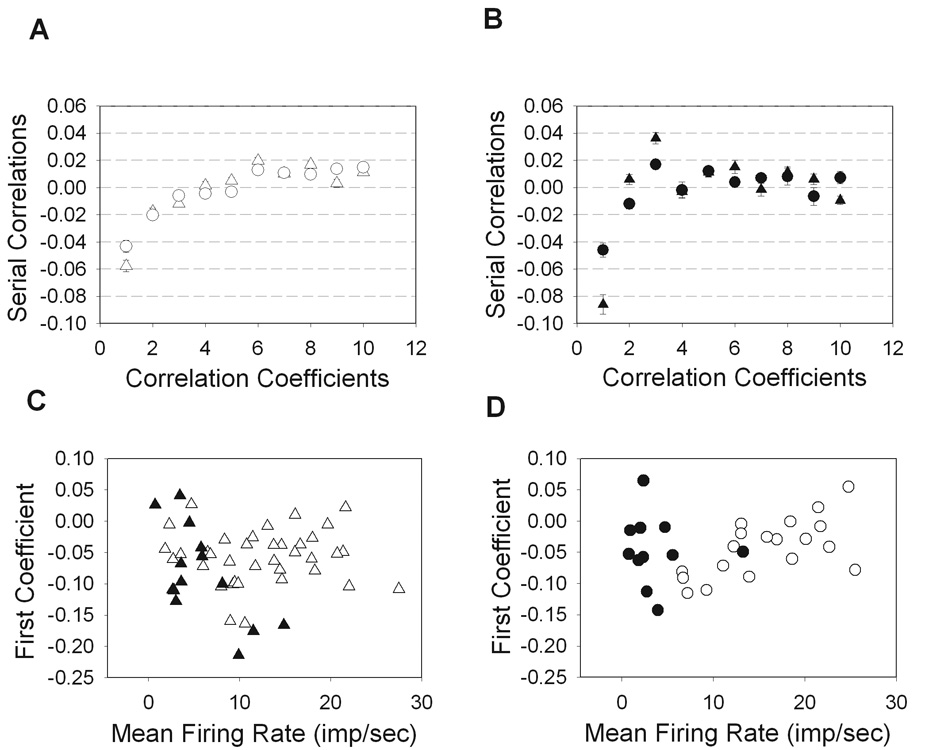
Serial correlations among interspike intervals. The magnitude of serial coefficients 1–10 were averaged over all ON cells (A) and OFF cells (B) where all cells show negative 1^st order correlations and ON-cells also showed significant 2^nd order correlations (P<0.05). The first correlation coefficient is plotted for all X-cells (C) and Y-cells (D). (ON-X, open trianlges; ON-Y, open circles; OFF-X, filled triangles; OFF-Y, filled circles).

For OFF cells the coefficients were more variable. The first correlation coefficient, for example, spanned a wider range of values across the population of cells in spite of the narrower range of their maintained discharge rate compared to ON cells (Figure 4C,D). There was a slight dependence of the first coefficient on the mean rate for OFF-X (r = −0.65) and ON-Y (r = 0.63) cells, such that adjacent intervals were more negatively correlated for the former and less so for the latter as mean rate increased. A similar relationship was not apparent for ON-X (r = 0.01) or OFF-Y (r = −0.10) cells.

Higher-order correlation coefficients were slightly positive, particularly for ON cells. The later positive coefficients could reflect a monotonic drift in their mean firing rate over time (Perkel, 1967), except that the stationarity tests which were performed would have revealed such trends. Instead, the later positive coefficients can be seen as a byproduct of the early negative correlations. For example, negative correlations imply that a very short interspike interval tends to be followed by longer intervals. Following these longer intervals, the cell will once again be allowed to fire at any interval size, and if this interval tends to be shorter than the mean interval, a positive correlation will result. However, the mean interval tends to be artificially large due to the presence of longer intervals caused by early negative correlations. Thus, when the cell is allowed to fire at any interval size, it tends to be shorter than the mean, and positive correlations result.

Power Spectral Densities

The power spectrum is another useful tool for revealing temporal structure in a spike train. The general shape of the maintained discharge spectrum of rat retinal ganglion cells resembles that reported for cat and primate, where the power density is flat at low temporal frequencies and ramps up at frequencies around 10Hz to a plateau level numerically equal to the mean firing rate (Figure 5A–D) (Troy and Robson, 1992; Troy and Lee; 1994). Since ON cells usually have high mean rates, most of their power density is concentrated at higher frequencies. OFF cells, on the other hand, due to their low mean rates have power density distributed more uniformly across temporal frequency.

Figure 5.

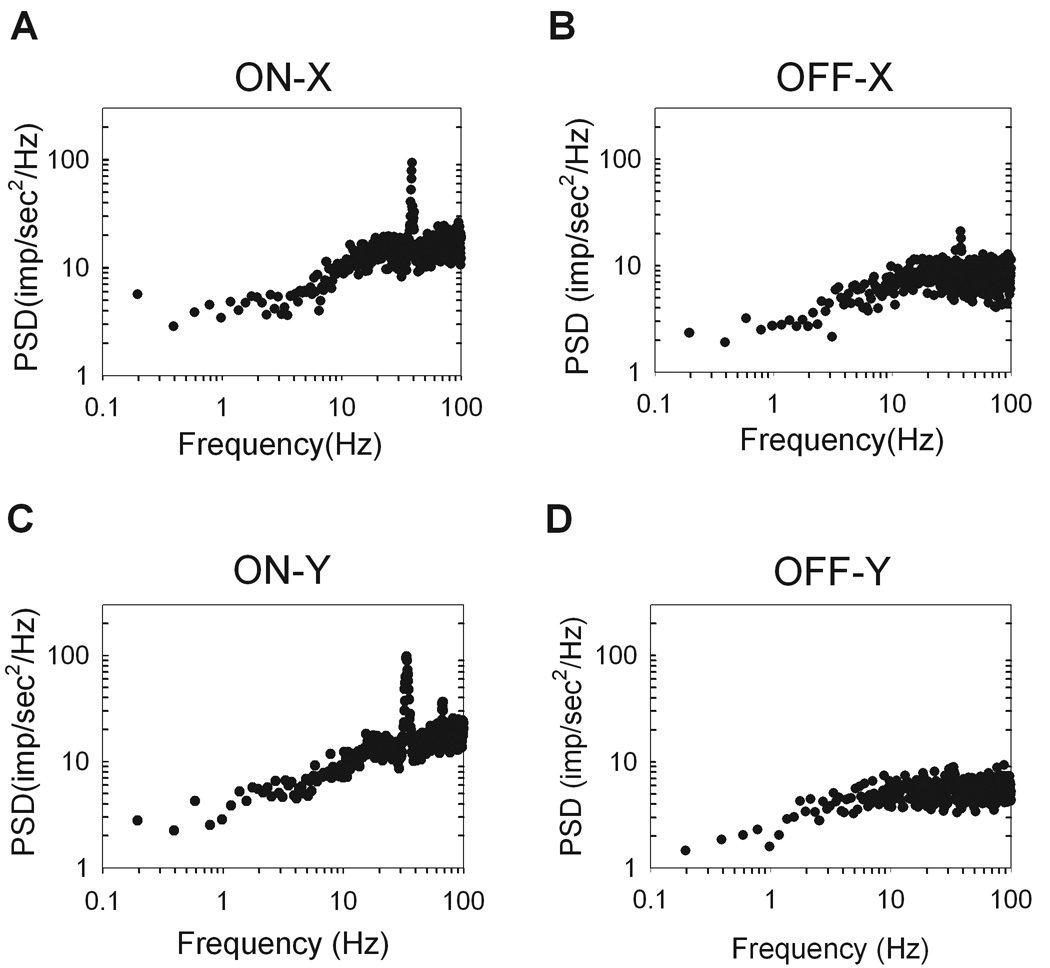
Power spectral densities (PSD) of the spike trains are plotted for each cell type. The power density is flat at low frequencies and ramps up to a value equal to the mean rate of the cell. A. ON-X cell (R81C2), mean rate: 16.1 imp/sec. B. ON-Y cell (R77C4), mean rate: 18.6 imp/sec. C. OFF-X cell (R92C11), mean rate: 8.1 imp/sec. D. OFF-Y cell (R64C8), mean rate: 6.8 imp/sec. High frequency peaks are clearer in the ON cells (A,C) than the OFF cells (B,D). The units of power density is in (impulses/sec)² per unit Hz.

Perhaps the most striking and unique feature of the power spectra of most rat ganglion cells is the large peak in the 20–40 Hz range. The peak is indicative of fast oscillations in the maintained discharge. Within the population of recorded cells an oscillatory peak was visible for 31 of 35 ON-X, 15 of 16 ON-Y, 8 of 13 OFF-X, and 6 of 11 OFF-Y cells. The oscillation frequency, which was defined as the point of maximal power density in the range of 20–50Hz, was not significantly different between any two cell types (P<0.05). Across all cell types the oscillation occurred at an average frequency of 35.2Hz ± 3.0Hz, well above the maintained discharge rate and temporal frequency response of a typical rat ganglion cell, which cuts off at 10–20Hz (unpublished observations). Lowering the frame rate of the monitor from 100Hz to 60Hz did not affect the power spectral densities or interval distributions (n=6, not shown), implying that the oscillations were not induced by the monitor. The power spectra of many ON cells (26 of 57) contained another peak at twice the oscillation frequency (Figure 5C). A plot of the oscillation frequency against the first mode of the interval distribution showed an inverse relationship with a unity-slope line (r = 0.76) (Figure 6A). Such a relationship is expected since an oscillatory discharge produces an abundance of intervals of a certain period.

Figure 6.

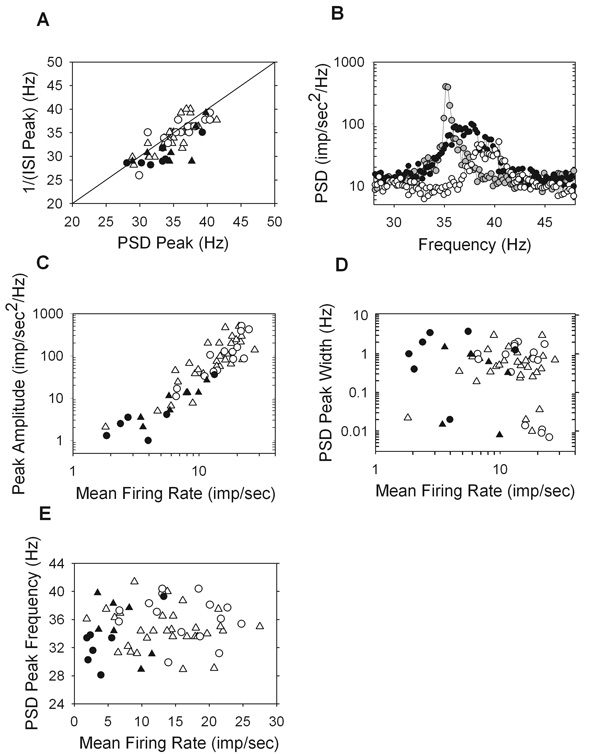
Properties of the high frequency peak in the power spectral density (PSD). A. The peak frequency of the PSD versus the inverse of the first peak of the interspike interval (ISI) distribution where the points are clustered around a line of unity slope (r = 0.76). B. Zooming in on the high frequency peaks and plotting on a linear scale for three ON-Y cells, two of which are from the same animal (R94C2, white and R94C6, gray) and one from a separate animal (R92C1, black). The mean firing rate versus amplitude (C) and width (D) of the high frequency peak, as well as versus the peak frequency (E). (ON-X, open trianlges; ON-Y, open circles; OFF-X, filled triangles; OFF-Y, filled circles).

Upon zooming in, it becomes clear that the high frequency peak has considerable bandwidth (Figure 6B), suggesting that the oscillatory driving force on the spiking mechanism is not a pure sinusoid. Also, the three cells shown in the figure are all ON-Y cells, two of which (R94C2 and R94C6) are from the same animal and eye. This illustrates that cells of the same type within the retina can oscillate at different frequencies with various bandwidths. The amplitude of the oscillatory peak was quantified as the maximum deviation of the power density from the average power density in the range of 45–50Hz, which is a flat region of the spectrum. The peak amplitude is an estimate of the strength of the oscillatory forces acting on the maintained discharge. There is a strong correlation between the mean firing rate of a cell and the amplitude of the peak (r = 0.93) (Figure 6C), meaning that the more often a cell fires the more oscillatory discharge its spike train has. The width of the high frequency peak was measured by fitting a Gaussian curve to it and the standard deviation of this best fit Gaussian is plotted against mean rate (Figure 6D). It is clear there is no correlation between bandwidth and mean firing rate (r = −0.19). There was also no correlation between mean firing rate and the oscillatory frequency (r = 0.12) (Figure 6E).

Effect of Light Level and Anesthesia on Fast Oscillatory Discharge

To determine whether the oscillatory peak was influenced by light, the maintained discharge of some ganglion cells were recorded in darkness as well as photopic illumination. Recordings in the dark were made with the stimulus monitor and room lights off with the animal behind a curtain to shield from the lights of any recording instruments. The cells were allowed several minutes to adapt when changing light level and, in every case (n = 9 ON cells), the oscillations were still present in the dark. Interestingly, though, the peak frequency consistently decreased in the dark (Figure 7A). The average frequency shift was small (2.11 ± 0.85 Hz) compared to the change in light level, but it was reproducible and statistically significant (P<0.05). Cells showing multi-modal interval distributions at photopic levels will also be multi-modal in the dark (Figure 7B), with the peaks shifted slightly towards longer intervals. Therefore, the mechanism responsible for high frequency oscillations in the maintained discharge does not require light to operate, but it is affected by light level.

Figure 7.

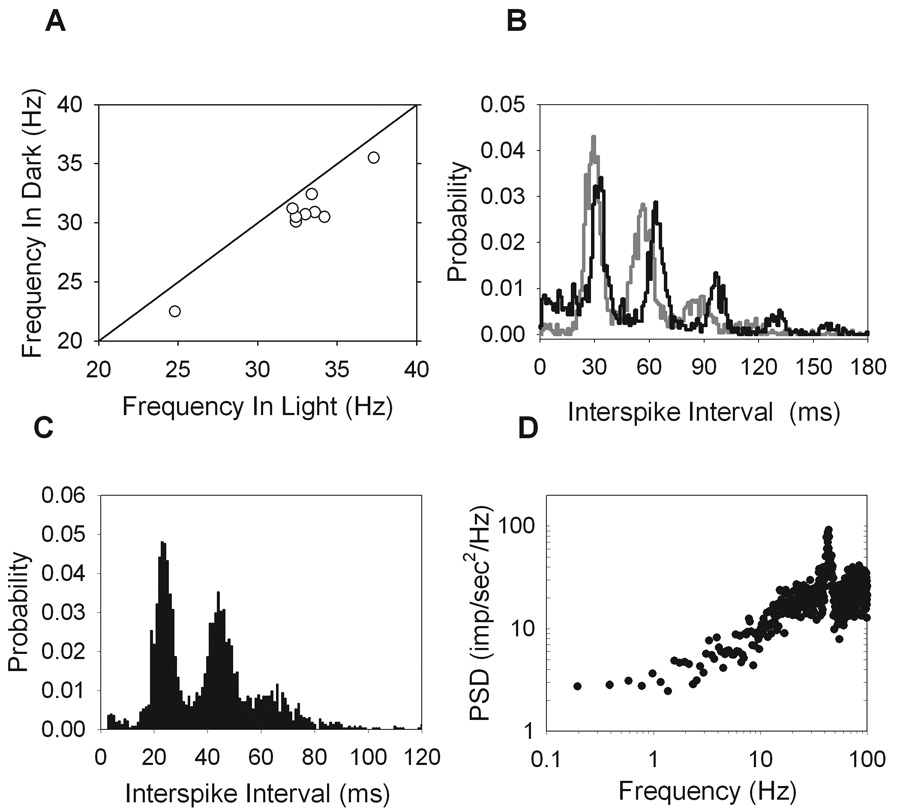
Effect of urethane and light level on the high frequency oscillations. (A) The frequency of the oscillations in the light versus the dark for 9 ON-cells with a line of unity slope showing that the frequency decreased in the dark for all cells. (B) Interval distributions from an ON-X cell (R99C2) computed in the light (gray) and in the dark (black), showing the peaks shift to slightly longer intervals in the dark. Collecting the maintained discharge under urethane anesthesia (R51C7) over a period in which the cell behaved stationary gave a multi-modal interval distribution (C) and a power spectral density showing high frequency oscillations (D), similar to the results under ketamine/xylazine anesthesia.

Although ketamine/xylazine anesthesia has been used in visual experiments in rat (Girman & Lund, 2007), mouse (Sagdullaev & McCall, 2005), and cat (Haider et al., 2007), the question of whether or not it could induce the high frequency oscillations seen here has not been engaged. Using a segment of data collected under urethane anesthesia over which the maintained discharge was stationary, it is clear that the high frequency oscillations are still present (Figure 7C, D). Both the multi-modal interval histogram and the high frequency peak in the power spectrum are features seen under both urethane and ketamine/xylazine anesthesia. It is therefore not likely that the oscillatory behavior is caused by the anesthetics.

Gamma Distributed Intervals

A subset of rat ganglion cells (13 of 81) had maintained discharges that did not show multi-modal interval histograms and oscillatory peaks in their power spectra. The interval histograms of these cells were fit well by a gamma distribution function:

$$f(\tau )=(\kappa /\mu ){\tau }^{\kappa -1}\exp (-\kappa \tau /\mu )/\mathrm{\Gamma }(\kappa )$$

where τ is the independent variable of interspike intervals, μ is the mean interval, κ is the order of the gamma distribution, and Γ(κ) is the gamma function evaluated at κ. Figure 8A gives an example of such a cell, which has best fit parameters of κ=3.01 and µ=98.20. The distribution of best fit κ and μ values on a cell-by-cell basis (Figure 8B) show a slight negative correlation (r = −0.74). This means cells with higher mean firing rates and therefore a smaller mean interval, μ, are fit by higher order gamma functions and have narrower interval distributions.

Figure 8.

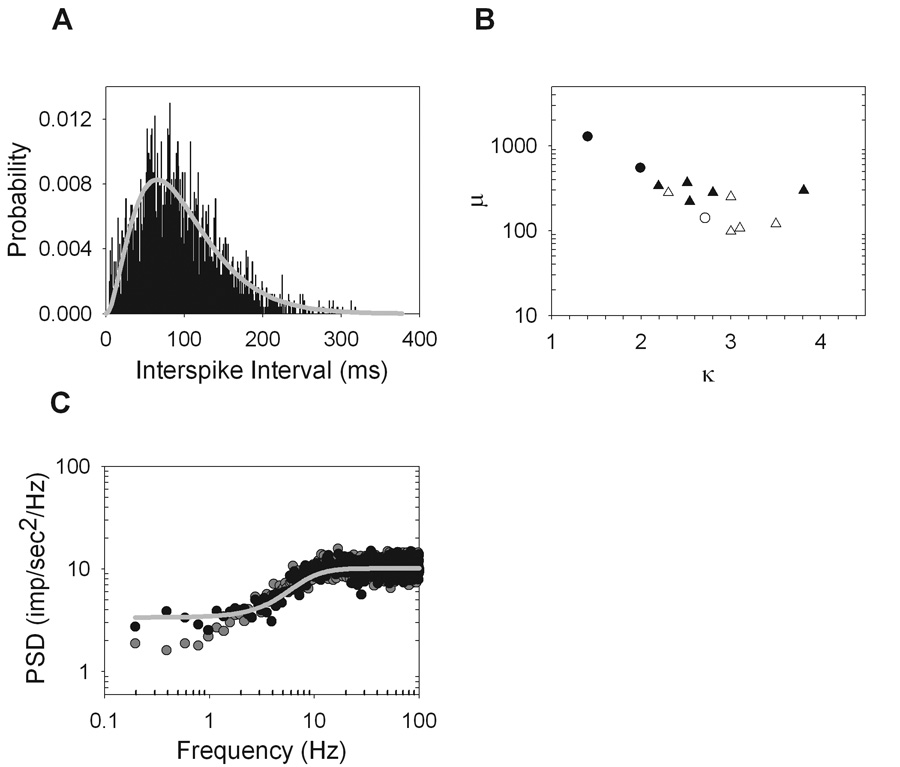
Unimodal interspike interval distributions were fit well by a gamma distribution function. A. The interval distribution for an ON-Y cell (R87C1) (black) and the best fit gamma distribution function (gray line) (κ=3.0 and µ=98.2). B. The best fit parameters κ and μ of the gamma distribution function for all cells with unimodal interval distributions show a negative correlation (r = −0.74) (ON-X, open trianlges; ON-Y, open circles; OFF-X, filled triangles; OFF-Y, filled circles). C. The power spectrum of the original spike train (gray dots) is plotted along with the spectrum of a spike train produced by randomly shuffling around the intervals (black dots) of the original spike train. The power spectrum that would have been predicted by a gamma renewal process with parameters determined by the best fit of the interval distribution is shown (gray line).

If the maintained discharge was fully described by a gamma renewal process, then randomly shuffling the order of interspike intervals would not affect the power spectrum because the intervals would already be temporally uncorrelated. This was generally not the case. While the power spectra of maintained discharge before and after shuffling overlapped at most frequencies, there is a clear deviation at low frequencies (Figure 8C), as also seen for some cat ganglion cells (Troy and Robson, 1992). The power spectrum that would result from a gamma renewal process with μ and κ determined by the best fit interval distribution is indicated by the line in Figure 8C. It follows the spectrum of the shuffled spike trains closely; indicating that the serial correlations among intervals in maintained discharge described earlier (Figure 4) caused the low frequency power density to depart slightly from that expected from a strict renewal process.

Modeling the Maintained Discharge

Studies have shown that a simple integrate-fire-model with a white noise input produces simulated spike trains that have gamma distributed intervals like those of cat retinal ganglion cells (Levine, 1991; Passaglia & Troy, 2004). We modified this model to account for the oscillatory behavior seen in most rat retinal ganglion cells. First, we considered the possible sources of this high frequency energy. The simplest explanation is that the cell intrinsically fires spikes at intervals of ∼30ms. This would produce an oscillatory peak at the appropriate frequency in the power spectrum of the maintained discharge. The multi-modal interval histograms, however, suggests that there is some oscillatory drive on the spike generator. The model was therefore modified to include a sinusoidal input.

An integrate-and-fire model was implemented with the output variable, V(t), representing the membrane voltage of the cell. The differential equation was solved numerically using a 2^nd order Runge-Kutta method in Matlab with a time step of 1ms. When V(t) reaches a given threshold, V_th, a spike is fired and the voltage is reset to a value of V_reset. The model equations are given by:

$$\frac{dV(t)}{dt}=\mu +I_n(t)+I_{osc}(t)$$

where μ sets the mean firing rate of the model cell and I_n(t) is white noise that generated by pulling independent values from a zero-mean, Gaussian distribution with standard deviation σ resulting in a bandwidth of 500Hz. I_osc(t) is a random-phase oscillatory drive on the spiking mechanism defined as:

$$I_{osc}=A\sin (2\pi f_{osc}t+\phi (t))$$

where f_osc is the frequency of oscillation, A is the amplitude, and ϕ(t) is the random phase given by low bandwidth (<1Hz), zero-mean Gaussian noise with standard deviation σ_phase. The noise signal ϕ(t) was generated in the same way as I_n(t), but was then passed through a first-order lowpass filter with 1Hz cutoff. The model output V(t) without the oscillatory drive is shown in Figure 9A. In this case, the Gaussian input noise causes jitter in the spike times that would otherwise occur at regular intervals and the result would be a unimodal gamma-distributed interval histogram. The addition of the oscillatory drive introduces subthreshold oscillations into the voltage record (Figure 9B). The result is that the interval histogram now has multiple modes and can describe the interval and spectral data of a typical rat ganglion cell very well (Figure 9B–D).

Figure 9.

Modified integrate-and-fire model. The output, V(t), is shown for the case where I_osc=0 (A) and for the case where there is an oscillatory drive (B). C. The interval distribution of an example ON-X cell (R81C2) (gray) is shown along with the best fit interval distribution of the model (black). D. The corresponding power spectra of the spike trains that produced the interval distributions shown in C. of the model to the interval distribution in C (black) for an. The high frequency peak of the power spectrum is zoomed in and plotted on a linear scale (E). The best fit parameters are f_osc=38.6, µ=710, σ=2650, σ_phase=29, A=3750, V_th=−55, and V_reset=−95.

This model also reproduced the small hump in interspike intervals in the range 4–12ms seen for many cells. A refractory period was not explicitly introduced because the integrative nature of the model eliminates very short intervals and effectively acts as a refractory period. Inspection of the spike trains confirmed that this hump in the interval histogram is caused by two spikes being occasionally fired during one cycle of the sinusoidal input. The absence of intervals in the 12–20ms range is due to the downward phase of the sinusoid moving V(t) away from spike threshold.

Discussion

Our results demonstrate that the maintained discharge of rat retinal ganglion cells is similar in many respects to that of other mammals but different in important ways as well. The similarities include higher firing rates in ON versus OFF cells, gamma distributed interval statistics for some cells, and negative serial correlations between adjacent intervals for all cells. A major difference is that most rat retinal ganglion cells have a propensity for fast oscillatory discharge. The oscillations are characterized by multi-modal interval distributions and high frequency peaks in power spectra that are rarely seen in other animals (Levine, 1977; Rodieck, 1967; Ogawa et al., 1966). Another difference is that the maintained discharge properties of rat X and Y cells are not significantly different whereas X cells tend to have higher mean rates than Y cells in cat (Troy and Robson, 1992).

Non-stationarity

The waxing and waning in maintained discharge reported here for rat retinal ganglion cells under urethane anesthesia has been observed in cat (Rodieck, 1966; Barlow and Levick, 1969) and ground squirrel (Tong, 1977). These studies considered the behavior pathological. Consistent with this interpretation Kuffler et al. (1957) observed waxing and waning in cat intraocular recordings when pressure was exerted on a ganglion cell body, a clearly abnormal state. In order to rule out possible experimental variables, different rat strains, rat ages, and anesthetics were explored in this study. Interestingly, non-stationary behavior persisted for every condition except under ketamine/xylazine anesthesia, which suggests that the phenomenon might normally be present and ketamine/xylazine acts to abolish it. If this were the case though, it is unclear why waxing and waning was not noted in prior rat optic tract recordings that also used urethane (Brown and Rojas, 1965; Cicerone and Green, 1980; Powers and Green, 1978).

Interval and Spike Count Statistics

The observed variability in both interspike intervals and spike counts is less for cells with higher mean firing rates. Thus, cells that fire more frequently tend to have a more regular discharge pattern, which is also seen in cat retinal ganglion cells (Troy and Robson, 1992). Interestingly, ON and OFF cells with similar firing rates tend to have similar discharge statistics, as evidenced by the tight overlap of points in Figure 3. This implies that the observed variability in interspike intervals and spike counts are predicted by the mean firing rate of ON and OFF cells, irrespective of cell polarity. In spite of their reported differences in intrinsic properties (Margolis et al., 2007), it would appear that the spiking mechanism and the noise that enters it are similar for ON and OFF cells since they produce the same statistics. If, for example, one cell type fired in a clocklike manner, then one would expect that for a given mean firing rate, the variability in intervals and spike counts would be very different for the two cell types.

High Frequency Oscillations

Oscillatory mechanisms are known to exist within the mammalian retina. Evidence for their existence can be readily found in the electroretinogram (ERG) of most species (Dong et al., 2004; Frishman et al., 2000), including humans (Wachemeister, 1998), in response to a light stimulus. The frequency of the oscillatory potential (OP) in rat depends on the amplitude of the stimulus, but even for weak stimuli it is much faster (>60Hz) than the oscillations we observe in the maintained discharge (Hancock and Kraft, 2004; Green and Kapousta-Bruneau, 1999). Oscillatory activity has also been seen in the subthreshold membrane potential fluctuations of retinal ganglion cells in cat (Przybyszewski et al., 1993) and mouse (Margolis and Detwiler, 2007). However, in both cases, the oscillatory strength was too weak to be observed in the spike train.

In spike recordings from cat, high frequency oscillations are absent from X and Y cells (Troy & Robson, 1992), although a clear peak in the power spectrum can be seen in the maintained discharge of Q-cells (Robson & Troy, 1987), a less frequently encountered cat ganglion cell type. However, these oscillations are different from those observed here in that they result from the very regular discharge patterns of Q-cells and not from an oscillatory drive on the ganglion cell. For example, a high order gamma process will produce spikes at fairly regular intervals, which will result in a high frequency peak in the power spectrum. Alternatively, the multi-modal interval distributions we observe can only be explained by the existence of some periodic forcing on the cell, which cause spikes to occur not just at a single preferred interval, but at integer multiples of this preferred interval.

The retinal mechanism producing the oscillatory signal does not require light to operate since the fast oscillatory discharge persisted in darkness. That the oscillation frequency decreased slightly in the dark and was not completely independent of light, suggests that it might serve a role in vision. The oscillation frequency may encode mean light level, although the change in oscillation frequency is small so it could provide only a gross estimate of light level (e.g. scotopic or photopic regime). Other ganglion cell types, such as the so-called luminance units (Barlow and Levick, 1969; Troy et al., 1995) or intrinsically photosensitive ganglion cells (Dacey et al., 2005), may signal the illumination level via the mean firing rate of the cell, while the mean firing rate of X and Y-cells are not thought to signal light level (Troy and Enroth-Cugell, 1993). Thus, changes in the oscillation frequency of X and Y-cells provide an alternative method for signaling a dramatic change in light level.

The oscillations could also be involved in population encoding of global stimulus features (Kenyon et al., 2003; Ishikane et al., 2005; Stephens et al. 2006). This idea is supported by recordings from pairs of ganglion cells, which were shown to oscillate in synchrony under stimulus-specific conditions (Ariel et al., 1983; Neuenschwander and Singer, 1996; Neuenschwander et al., 1999). The synchronization was detectable from cell pairs over 20 degrees apart in visual angle and must therefore utilize laterally-projecting amacrine or horizontal cells. However, the frequency of stimulus-induced oscillations (∼85Hz) were seen to be significantly different from that of oscillations in the maintained discharge (∼30Hz), suggesting that they may be separate phenomena. This would be consistent with the observation that light-induced OPs in the rat ERG are higher in frequency than the oscillations in maintained discharge reported here. Whether these oscillations are synchronous between ganglion cells in the rat retina requires further examination using multi-unit recordings.

The cellular origin of retinal oscillations is unclear, but there are arguments against an outer retinal component. If the photoreceptors themselves were the source, then their oscillatory outputs would need to all be in phase so that their signals do not cancel upon summation at the bipolar and ganglion cell levels. While it is conceivable that neighboring photoreceptors communicating by gap junctions could oscillate in phase, the number of photoreceptors that converge onto an individual ganglion cell in the rat retina is large (Mayhew and Astle, 1997), which would make it difficult for photoreceptors separated by large distances to oscillate in phase. Horizontal cells have been shown to oscillate under certain conditions (Foerster et al., 1977), but the oscillations are not thought to reach ganglion cells (Przybyszewski et al., 1993). The source most likely resides in the inner retina, where certain types of amacrine cell are known to oscillate both in the dark and in response to light (Vigh et al., 2003; Sakai and Naka, 1988). Or, it could be an intrinsic property of the ganglion cell membrane, though such an explanation could only account for our data and not the long-range synchronous oscillations reported in cat (Neuenschwander et al., 1999).

Modeling

The wide bandwidth of the high frequency peak in the power spectrum of most cells was captured by the model by assuming the oscillatory drive has stochastic phase. It was necessary to modulate the phase on a much slower timescale than the oscillation frequency in order for the waveform to still resemble a sinusoid. If a pure sinusoid was used for the oscillatory driving force, the resulting spike train had a spectrum with an extremely narrow high frequency peak. It was possible to incorporate an array of pure sinusoids with closely spaced in frequency in order to fit the data, but such a model seemed less physiologically plausible than the random-phase model.

Although the interspike interval distributions can be classified as being multi-modal or gamma in shape, they are not completely distinct from a functional perspective. As the model demonstrates, multi-modal interval distributions arise naturally from a gamma process by introducing an oscillatory driving force. Another interesting observation concerning the model is the extent to which the subthreshold membrane potential (V(t)) is dominated by the oscillatory driving force. The large amplitude of the oscillatory input was necessary to fit the data, suggesting the high frequency oscillations are a dominant force in governing rat retinal ganglion cell function.