Abstract
The effect of macromolecular crowding on the rates of association reactions are investigated using theory and computer simulations. Reactants and crowding agents are both hard spheres, and when two reactants collide they form product with a reaction probability, prxn. A value of prxn < 1 crudely mimics the fact that proteins must be oriented properly for an association reaction to occur. The simulations show that the dependence of the reaction rate on the volume fraction of crowding agents varies with the reaction probability. For reaction probabilities close to unity where most of encounters between reactants lead to a reaction, the reaction rate always decreases as the volume fraction of crowding agents is increased due to the reduced diffusion coefficient of reactants. On the other hand, for very small reaction probabilities where, in most of encounters, the reaction does not occur, the reaction rate increases with the volume fraction of crowding agents—in this case, due to the increase probability of a recollision. The Smoluchowski theory refined with the radiation boundary condition and the radial distribution function at contact is in quantitative agreement with simulations for the reaction rate constant and allows the quantitative analysis of both effects separately.
Introduction
The cell cytoplasm is a very crowded environment consisting of many organelles, large macromolecules, and the cytoskeletal network. The fraction of volume occupied by “crowding agents” is significant, estimated to be 20–30% of the total volume or higher. The environment of the cell cytoplasm is therefore very different from dilute solutions (1–3), where most biochemical studies are carried out. The effects of macromolecular crowding can therefore be very significant and there has been considerable effort devoted to understanding crowding effects (1–8). In this work we quantify the effect of crowding on association reactions using computer simulation and theory.
A qualitative picture for the effect of crowding agents on association reactions has been provided by the pioneering efforts by Minton (4,5). In this picture, crowding agents induce two opposing effects that impact the reaction rate. The presence of crowding agents reduces the diffusion coefficient of the reactants, and this should decrease the reaction rate. On the other hand, crowding agents can increase the equilibrium constant for the association and this thermodynamic effect should increase the reaction rate. The net reaction rate reflects a balance between these effects, and one can envisage conditions where the reaction rate might be a nonmonotonic function of the volume fraction of crowding agents.
In the diffusion-controlled limit where every encounter between reactants results in a reaction, the reduction of diffusion in the crowded environment will lead to the reduced reaction rate. In the biophysics of association reactions, however, it is important to consider that not every encounter will result in a reaction. Specific binding occurs through sites that must be properly aligned for the reaction to occur, and this is referred to as anisotropic reactivity (9–12). Therefore, the probability that an encounter results in a reaction can be quite small; for example, only ∼2% for the binding of an actin monomer to the end of a filament (13). As the probability of reactive encounter becomes smaller due to anisotropic reactivity, caging effects (which keep reactants in proximity) induced by crowding agents could increase the reaction rate by increasing the probability of reorientation and recollision. In this work, we investigate the crowding effect on the association reaction with different probability of reactive encounter, resulting in qualitatively different dependence of the reaction rate on crowding.
Although the importance of crowding effects on the reaction rate is appreciated in many different biological processes, such as protein-protein associations (14,15), actin filament elongation (13,16), and protein folding (7), it has been difficult to quantify these effects, especially in terms of the two opposing effects discussed above. For example, in a recent study, Moorthy et al. (15) studied the effect of polyacrylamide gels on the association of proteins. They found that increasing the concentration of the crowding agent (hydrogel in this case) increased the rate constant for the association reaction. The experiments could not, however, establish the mechanism for this increase in the reaction rate.
Theories developed for reaction kinetics in dense liquids can be used to understand crowding effects on protein association reactions, with the solvent replaced by the crowding agents. In the original theory of diffusion-controlled reactions, an expression for the reaction rate constant can be obtained by solving the Smoluchowski equation with so-called absorbing boundary condition. To consider a finite initial reaction rate and the structure of the solvent, refinements of the theory have been proposed, including partially absorbing boundary condition and the incorporation of a potential of mean force (17–19). We use the solution of the Smoluchowski equation with these refinements to predict the long time rate constant of protein association reactions. Computer simulations have also been used as an alternative to describe the diffusion-controlled reaction kinetics in dense liquids (20–23). However, in these studies, the reactant concentrations and the solvent densities are too high, compared with those of proteins in cells, to be directly useful for an understanding of crowding effects on the protein association reactions.
There have been simulation studies on the related problem of reaction rates in random media (24–27). Buján-Nuñez et al. (24) investigated the effect of immobile obstacles on the rates of association reaction. The presence of immobilized obstacles are often referred to as confinement effects and are distinct from crowding effects imposed by mobile crowding agents (5,8). The biophysics of the confinement problems is dominated by the fragmentation of void space due to the presence of immobile obstacles. Therefore the reaction rate goes to zero for very low volume fraction of the obstacles. Although it is not clear what fraction of the total proteins in the cytoplasm are mobile (28), comparison of the tracer diffusion in concentrated mixtures of long filaments and inert soluble particles suggests that roughly half of total cytoplasmic protein is mobile in solution and the remainder is structural (28,29). The effect of mobile crowding agents is therefore of crucial importance in understanding of biochemical reactions within cells, even though their effects might not be as dramatic as those of structural obstacles.
In this work, we investigate the effect of crowding on association reactions using computer simulation and theory. We use a simple model for the reactants and the crowding agents to isolate excluded volume effects. We model reactants and crowding agents as hard spheres, all of the same size, and propagate the system using Brownian dynamics simulations. We consider pseudo-first-order reactions, A + B → products, and keep the concentration of the B-species constant. One example of this type of reaction is actin filament elongation during membrane protrusion (30) where the concentration of actin monomers is essentially constant because the binding of monomers to one end of the filament is accompanied by a depolymerization at the other end. We investigate total volume fractions, ϕ, ranging from 0.01 to 0.4, which cover the entire regime from aqueous buffer solutions to what might be expected in a cell cytoplasmic environment.
Our model has significant technical advantages. Since the interaction between all species is identical, we can greatly amplify the volume of the data collected by labeling each of the spheres as a reactant and calculating the survival probability for all spheres. In addition, a simple analytical expression can be obtained for the long time rate constant. The Smoluchowski theory refined with the partially absorbing boundary condition and the potential of mean force provides the expression for the long time rate constant (17,18), which can be simplified with approximate results obtained for hard sphere liquids (31,32).
We investigate crowding effects for different values of the reaction probability. In general, not every encounter between reactants should lead to a reaction (9–12) because the relative orientation of proteins is essential for association. Although models of anisotropic reactivity have been considered, such as a reactive patch on a sphere (9–12), we mimic this effect via a reaction probability where an encounter results in a reaction with a probability prxn, which is less than unity. This is similar to the probability of reaction on collision considered earlier (19,33) and replaces the mixed boundary conditions dependent on the angular coordinate (9,12). We find that crowding effects are strongly dependent on the value of prxn. Simulations show that for prxn > 0.05, the reaction rate constant always decreases as the volume fraction is increased. This is the case when the encounter rate between reactants is more important in determining the reaction rate. For prxn < 0.002, the reaction rate constant increases with increasing volume fraction, which we attribute to the cage effect characterized by the increases in the pair distribution function at contact and in the recollision probability. For intermediate values of prxn, the reaction rate constant can be a nonmonotonic function of volume fraction.
An approximate expression of the long time rate constant based on the Smoluchowski theory provides a qualitatively accurate description of the crowding effect. The good agreement of the theory with simulations, especially at low values of prxn, is quite surprising given the simplicity of the theory. Furthermore, this expression allows one to separate the two opposing effects induced by crowding and suggests that the dependence of the rate constant on prxn arises from the strong dependence of the rate of product formation (from an encounter pair) on prxn.
Model and Simulation Method
We consider pseudo-first-order reactions, A + B → products, in the presence of crowding agents. All species, i.e., reactants (A and B) and crowding agents, are modeled as hard spheres of diameter σ, which is the unit of length in this work. The simulation cell is a cube of linear dimension L = 12σ with N particles. The total volume fraction, ϕ = Nπσ3/6L3, is varied by changing N which ranges from 17 at the lowest volume fraction to 1320 at the highest volume fraction investigated. The system consists of one A-reactant particle (NA = 1), 16 B-reactant particles (NB = 16), and N – NA – NB particles of the crowding agent.
We use the hard-sphere Brownian dynamics method of Strating (34) to evolve the system. Hydrodynamic interactions are not considered. After each time step Δt, the position ri(t) of particle i is obtained via
| (1) |
where R(Δt) is a random displacement with a Gaussian distribution function with zero mean and variance 6D0Δt, i.e., 〈R(Δt)〉 = 0 and 〈R2(Δt)〉 = 6D0Δt. D0 is the diffusion coefficient of the spheres in pure solvent. D0 sets the timescale, i.e., τBD = σ2/D0 is used as the unit of time in this work. If the displacement results in an overlap between any two particles, the displacements are corrected to mimic an elastic collision between particles (34). For this purpose, the velocity of each particle is calculated from the original random displacements, vi = Δri/Δt, and the collision time and the velocity after the collision are calculated (35). The corrected displacements are then determined by the position at the moment of collision and the velocity after the collision. This propagation by elastic collision is repeated until the time reaches Δt. A time step Δt = 10−4 τBD is used for all the simulations. This ensures that a particle does not move more than its radius in one time step.
In the presence of crowding agents, the diffusion coefficient, D, is a function of the total volume fraction occupied by reactants and crowding agents and is calculated from the mean-square displacement using the Einstein relation
| (2) |
where the average is over all the particles and over initial times. The diffusion coefficient is averaged over the 10 independent trajectories (starting from different initial conditions) and statistical uncertainties are one standard deviation about the mean.
To relate these parameters to experimental systems we consider the parameters for actin monomers (16,36). For this system σ = 5.4 nm (longitudinal dimension), D0 = 71.5 μm2/s, and τBD = 0.41 μs. The concentrations of A and B are 6 μM and 98 μM, respectively. A concentration of 100 μM is quite high for a single protein and actin is the most abundant protein in many eukaryotic cells (30). The number of B reactant particles (NB = 16) is chosen such that the concentration determined from these parameters does not exceed 100 μM. We investigate only one concentration of the reactant B, but this concentration is low enough that we do not expect the concentration-dependent effects noted in other work (20,21,23). For comparison we perform simulations with one particle of reactant A and two particles of reactant B (without any crowding agents at prxn = 1). The rate constant is different from that of one particle of A, 16 particles of B, by only 3%. This confirms that many-particle effects are not significant at the concentrations studied.
The reaction rate constant is obtained as follows. When reactants A and B collide, they can react with a probability prxn. In practice, a random number uniform in the range (0,1] is chosen and if this random number is <prxn the reaction is assumed to have occurred. The quantity directly obtained from the simulation trajectories is the survival probability, SA(t), which is the probability that the particle A remains unreacted after time t. The time-dependent reaction rate constant k(t) is related to the survival probability via (18,20,21),
| (3) |
or
| (4) |
where CB is the concentration of reactant B. We focus on the long time limit of the time-dependent rate constant, i.e., k∞ ≡ k(t → ∞), which we obtain from a linear least-squares fit of ln SA(t) at long times; the slope of this curve divided by CB gives k∞.
The survival probability is calculated using the method suggested by Dong et al. (20) and Zhou and Szabo (21), which has also been adopted in the recent article by Sun et al. (37). For each volume fraction a number, Ntrj, of independent trajectories are obtained. Since all the particles are identical, in the beginning of each trajectory, each of N particles is labeled A in turn and, for every choice of A, the other particles are grouped into Ngrp groups with NB number of B particles. Each group of B particles participates in the reaction independently with particle A, and hence there are NNgrpNtrj total configurations participating in the reactive events. This greatly amplifies the volume of data collected. For example, for the total volume fraction of 0.10, there are a total of 330 particles that can be labeled as a reactant A in turn, resulting in the 330 different configurations for the reaction. Once a particle is labeled as A, the rest of 329 particles are divided to 20 groups of 16 B reactants, only one group of which is considered to be reactive in turn. One single trajectory gives 6600 (= 330 × 20) reactive events, and with only 150 trajectories a total of 990,000 reactive events are recorded. In the simulations reported, the number of reactive events varies between 1,000,000 and 3,000,000.
Theory
The primary quantity in the Smoluchowski theory is time-dependent pair distribution function, ρ(r, t), of reactant pairs, which is the number density of a reactant at a distance r at time t given that its reactant pair is at the origin. The Smoluchowski equation is a stochastic equation for ρ(r, t) and is given by (17–19,21)
| (5) |
where U(r) is the potential of mean force between reactants, and Drel is the relative diffusion coefficient of a reactive pair. The potential of mean force can be obtained from the radial distribution function, i.e., g(r) = e–βU(r). where β = (kBT)−1, kB is the Boltzmann constant, and T is the temperature. Given initial and boundary conditions, Eq. 5 can be solved for ρ(r, t) and hence the reaction rate,
| (6) |
The initial condition is
| (7) |
For our model, the partially absorbing boundary condition suggested by Rice (17) and Collins and Kimball (38) takes the form
| (8) |
where k0 is the intrinsic rate of reaction between two reactants at contact. In Eq. 8, the flux of reactant pair density at contact is related to the rate of product formation.
Exact expressions for the rate constant, k(t), can be obtained in the t → 0 and t → ∞ limits (17,18),
| (9) |
and
| (10) |
where g(σ) is the value of the radial distribution function at contact, i.e., r = σ, and
| (11) |
Equation 10 can be rewritten as
| (12) |
where we can identify the diffusion-controlled reaction rate, kD = 4πσeDrel, and the initial reaction rate, k(0) = prxnk0g(σ).
The long time rate constant is also decomposed into two contributions in Minton's theory (4), i.e.,
| (13) |
where kenc is the rate constant for an encounter, and kts = kts°Γ where kts° is the transition-state limited rate constant in the absence of crowding agents and Γ is the nonideality factor defined as a ratio of activity coefficients. A comparison of this expression with Eq. 12 shows that since kenc has the same physical meaning as kD in Eq. 12, kts = kts°Γ is equivalent to k(0) (= prxnk0g(σ)) in Eq. 12. Indeed, for the case where the product is a tangent dimer, Γ = g(σ+) is an exact result. In such case, the Minton theory (4), based on the scaled particle theory for the determination of Γ, is therefore equivalent to the Smoluchowski theory. Note that for different models of the product the equivalence does not hold.
We use Eq. 12 to calculate the long time reaction rate constant and to compare the results with those obtained from simulations. The hard-sphere model allows for further simplifications via analytic forms for D and g(σ). From the Carnahan-Starling equation of state (31) and the pressure equation we have
| (14) |
and the Enskog theory predicts
| (15) |
We can also approximate Drel = 2D and σe ≈ σ. The variation of the effective collision diameter, σe, with volume fraction is not significant. Zhou and Szabo determined its value as 1.07σ for ϕ = 0.412 (21) so σ = σe is expected to be a reasonable approximation in the range of volume fractions we study. The final result for k∞ is
| (16) |
which, in units of σ and τBD for length and time, can be written as
| (17) |
The only parameter that is not known a priori for our model is k0. For its determination, it is possible to treat the cases of prxn=1 and prxn < 1 separately, since it is reasonable to assume k0 = ∞ for prxn = 1 (corresponding to the absorbing boundary condition of the original Smoluchowski theory) whereas k0 should be finite for prxn < 1. However, it is shown that the finite value of k0 determined consistently for all prxn as described below is a good approximation without making any significant change of the rate constant even at prxn = 1. Therefore, we determine k0 from the simulations consistently at all prxn with an assumption that k0 is finite even at prxn = 1. From Eq. 4, at short times,
| (18) |
or
| (19) |
It is found that the slopes of ln SA(t) for all prxn plotted as a function of prxnt collapse into one at short times which we take as an average value of k0g(σ). The value k0 determined from it varies within 5% with the volume fraction of crowding agents. We use k0 determined for ϕ = 0.01 for the analytical calculation of the reaction rate in all volume fractions for consistency, that is, k0 = 5.98 × 1026 mol σ−3 τBD−1. With σ = 5.4 nm and τBD = 0.41 μs, this corresponds to k0 = 2.31 × 1011 M−1 s−1. As mentioned above, the difference between rate constants determined using this finite value of k0 and k0 = ∞ is negligible, implying that k0 = 2.31 × 1011 M−1 s−1 is large enough for the purely diffusion-controlled case.
Results and Discussion
The diffusion coefficient decreases as the volume fraction of crowding agents is increased, as expected. Fig. 1 depicts D/D0 as a function of the volume fraction and shows that over the range studied the diffusion coefficient decreases by more than a factor of 3. The simulation results are in perfect agreement with previous Brownian dynamics simulations (39), which provide a test of the simulation algorithm. Also shown in the figure is the prediction of the Enskog theory in Eq. 15. The theory is in reasonable quantitative agreement with the simulation results for the diffusion coefficient, which justifies the use of Eq. 15 in the calculation of the long time rate constant in Eq. 12.
Figure 1.
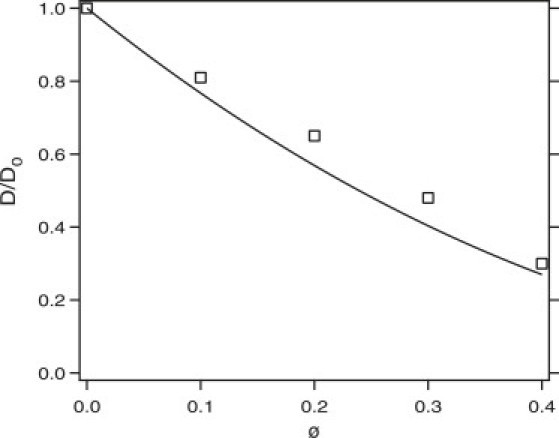
Simulation results (squares) for D/D0, as a function of total volume fraction (ϕ). The line is the prediction of the Enskog theory for hard spheres.
The reaction rate constant is obtained from the long time behavior of the survival probability. Fig. 2, a and b, depict the survival probability for prxn = 1 and 0.001, respectively, and for various volume fractions. The rate constant, k∞, is obtained from the slope of the curves divided by the concentration of B. Linear behavior is seen over several decades of the survival probability and the regime where SA(t) is between 0.1 and 10−4 is used for the calculation of the rate constant. For prxn = 1 the slope of the curve decreases as the volume fraction is increased, but for prxn = 0.001 the slope of the curve increases as the volume fraction is increased. The reaction rate constant therefore has a qualitatively different dependence on volume fraction in the two cases.
Figure 2.
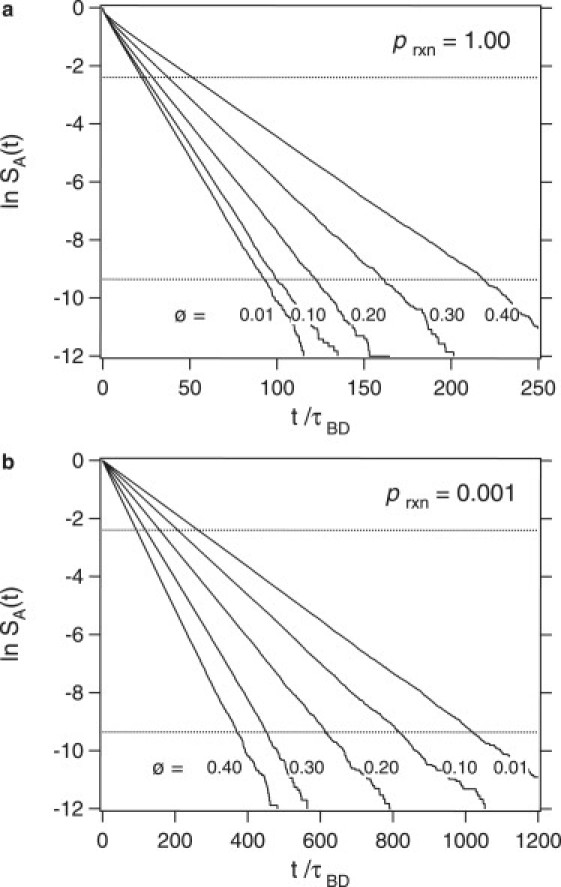
Logarithm of the survival probability as a function of time for (a) prxn = 1, and (b) prxn = 0.001, and for various total volume fractions, ϕ (numbers on each plot). For each case, the rate constant is determined from the slope in the regime marked by the horizontal dotted lines.
The qualitative dependence of the rate constant k∞ on volume fraction is different depending on the value of prxn. Fig. 3 a depicts simulation results for k∞ (in units of M−1 s−1) as a function of volume fraction for various values of prxn. For prxn ≥ 0.05, the rate constant is a monotonically decreasing function of ϕ. For prxn ≤ 0.002, the rate constant is a monotonically increasing function of ϕ. For intermediate values of prxn, the rate constant is a nonmonotonic function of ϕ. In Fig. 3 b, the rate constant is divided by the value of the rate constant for ϕ = 0.01. The trends as a function of ϕ are much clearer in this case. The line marked “Diff. Coeff.” is the relative diffusion coefficient of the spheres as in Fig. 1. The relative reaction rate constant for prxn = 1 shows roughly the same trend as the relative diffusion coefficient suggesting that diffusion limitations are important in this case. Note, however, that the decrease of the relative reaction rate constant with the increased volume fraction is less than that of the relative diffusion coefficient, which could be because of the thermodynamic effects discussed by Minton (4,8). This implies that even the prxn = 1 case does not correspond to a purely diffusion-controlled limit, where kD = 4πσeDrel (see Eq. 12). It is also interesting that the rate constant does not vanish even for ϕ = 0.40, contrary to the case of immobilized obstacles where the reaction rate decays to zero for ϕ = 0.20 (24).
Figure 3.
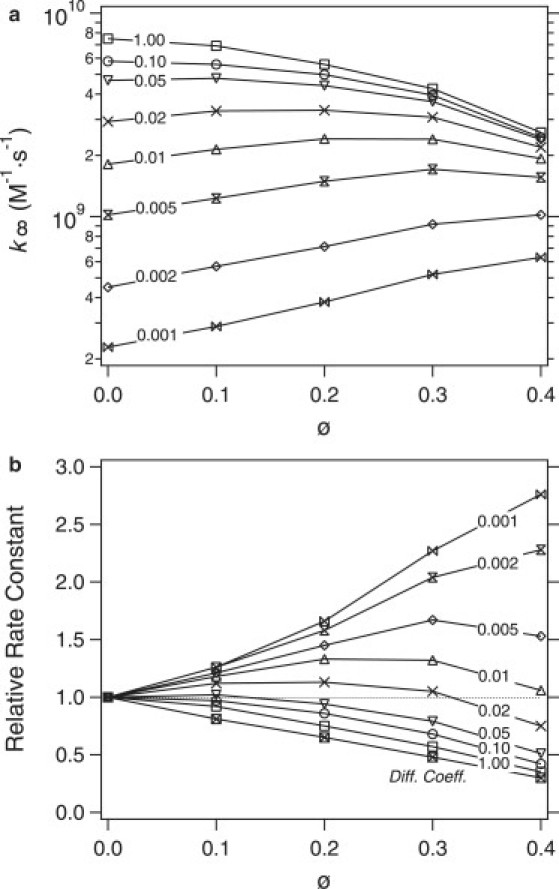
Simulations results for the rate constant (k∞) as a function of total volume fraction for various values of the reaction probability, prxn (as marked). The absolute rate constant (in units of M−1 s−1) is shown in panel a and ratio of the absolute rate constant to its value for ϕ = 0.01 is shown in panel b. Numbers on each plot are the reaction probabilities prxn. The line marked “Diff. Coeff.” is the relative diffusion coefficient of spheres.
The predictions of the Smoluchowski theory (Eq. 12) for k∞ are compared to simulation results in Fig. 4. The theory is in good qualitative agreement with the simulations in all cases, and captures the trends discussed above. With the exception of the highest volume fractions and prxn = 1, the theory is in quantitative agreement with the simulations. Note that there are no adjustable parameters in the theory and this is therefore a test of the approximations inherent to the theory. Discrepancies between theory and simulation may stem from the fact that the Smoluchowski theory of irreversible diffusion-limited reactions is exact only under the conditions that the dynamics are diffusive, A is static, and the molecules of the species B are noninteracting (18,21). These conditions are clearly not satisfied in our molecular model. In addition, the small deviations of the Enskog estimate for D from simulations as shown in Fig. 1 might also contribute to the discrepancies especially at prxn = 1, where the influence of diffusion is most important.
Figure 4.

Comparison of theoretical predictions (solid lines) to simulation results (symbols with dashed lines) for k∞ as a function of volume fraction for various values of prxn (as marked). Simulation results are the same as in Fig. 3a.
The analytical expression Eq. 12 enables a separate consideration of kD and k(0). An examination of the two contributions (kD and k(0)) to k∞ provides a qualitative understanding of the dependence of the rate constant on volume fraction. For high values of k(0) = prxnk0g(σ), the reaction is diffusion-controlled and k∞ ∼ kD, which is a monotonically decreasing function of ϕ. For low values of k(0), the reaction is not diffusion-controlled, and k∞ ∼ k(0), which is a monotonically increasing function of ϕ. When these two contributions are comparable, k∞ is a nonmonotonic function of ϕ. Fig. 5 depicts kD, k(0), and k∞ for prxn = 0.05, 0.01, and 0.002. In all cases, k(0) is an increasing function of ϕ and kD is a decreasing function of ϕ. As prxn is decreased, the contribution of k(0) becomes more significant, and this contribution is dominant for prxn ≤ 0.002. When k(0) and kD are of similar magnitude, k∞ displays a nonmonotonic dependence on ϕ.
Figure 5.

Rate constant k∞ and contributions kD and k(0) as a function of ϕ for prxn = (a) 0.05, (b) 0.01, and (c) 0.002.
The increase in k∞ with increasing ϕ for low reaction probabilities can be understood by considering the recollision probability α(t), which is the probability that a reactant pair recollide at least once in a time duration t given that they collided but did not react at time t = 0. In dense crowded media, each particle is surrounded by crowding agents that cage the particle. Although the probability of an encounter decreases with increasing volume fraction, once two reactants have encountered each other, the probability of a recollision is also greater because the cage of crowding agents makes an escape of the reactants less likely by forcing them to remain in proximity for longer. Fig. 6 depicts α(t) obtained from simulations for various volume fractions. As the volume fraction is increased so does α(t), which means that the reactants are more likely to have repeated collisions. In Fig. 6, α(t) is 0.99 at time 0.1τBD for ϕ = 0.4, compared to values of 0.979, 0.966, 0.954, and 0.946, respectively, for ϕ = 0.30, 0.20, 0.10, and 0.01. This difference does not seem large, but is significant because, for low values of prxn, the reactants have to collide many times, of order 1/prxn, for a reaction to occur. If we assume that 1000 collisions are necessary for a reaction (for prxn = 0.001) and each of these takes ∼0.1 τBD, then α1000 = 4.3 × 10−5 for ϕ = 0.40 and 7.8 × 10−25 for ϕ = 0.01. The idea of increased recollisions being responsible for the trend in the reaction rate is therefore reasonable.
Figure 6.
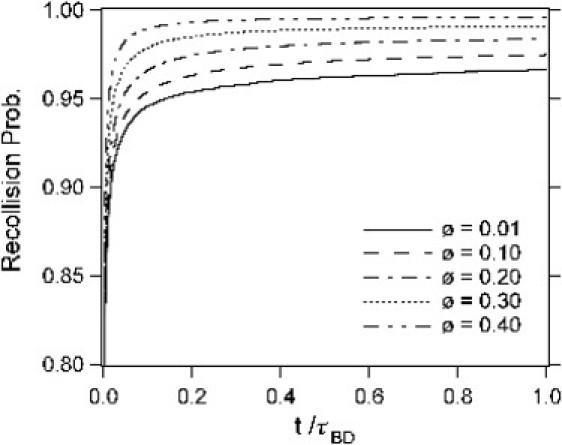
Recollision probability, α(t), as a function of time for various volume fractions.
In Fig. 7, simulation results for 1/k∞ are plotted as a function of 1/prxn. Again, good qualitative agreement is found between theoretical predictions from Eq. 12 and simulations. An interesting feature in this figure is that at high volume fractions, the increase in k∞ is modest as prxn is increased, whereas for low volume fractions it increases dramatically. This implies that although k∞ depends strongly on the intrinsic reaction probability in dilute solutions, this effect is not as important in crowded environments because cage effects make repeated encounters more likely. Therefore, the effect of anisotropic reactivity might not be as important in crowded environments as it is in buffer solutions.
Figure 7.
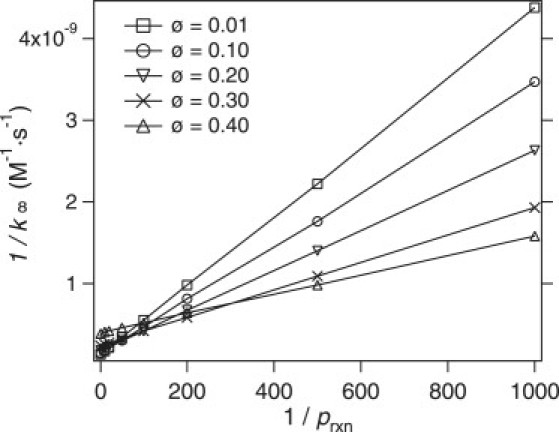
Reciprocal of rate constant, 1/k∞ as a function of the reciprocal of reaction probability, 1/prxn, determined from simulations for various volume fractions (as marked). The linear behavior is consistent with theoretical predictions (Eq. 12).
Conclusions
We study the effect of macromolecular crowding on association reactions using Brownian dynamics simulations and the Smoluchowski theory. Reactants and crowding agents are all modeled as hard spheres of the same diameter. When reactants encounter each other, via a collision, they react with a probability prxn, which mimics the fact that reactants must orient properly for a reaction to occur. We study values of prxn ranging from 0.001 to 1.
The qualitative impact of crowding agents on the reaction rate constant depends strongly on the value of prxn. For prxn > 0.05, the rate constant decreases monotonically with increasing volume fraction of crowding agents, suggesting that the reaction is dominated by diffusion limitations. The thermodynamic effect, where crowding effects are expected to increase the equilibrium constant for the associated species, does not appear to change the qualitative behavior. For prxn < 0.002, the rate constant increases monotonically with increasing volume fraction of crowding agents, attributable to the cage effect of crowding agents which increases the probability of recollisions between reactant pairs (after a collision does not result in a reaction). For 0.002 < prxn < 0.05, the rate constant can be a nonmonotonic function of the volume fraction of crowding agents.
The rate constant obtained from analytic theory is in good agreement with the simulation data, provided the short time reaction rate is input into the theory. From the standpoint of the theory the essence of the crowding effect comes from the pair correlation function between reactants (at contact), i.e., g(σ). Crowding increases the value of g(σ). In the diffusion-controlled regime, this results in a decrease in the rate constant, and in the reaction-controlled regime this results in an increase in the rate constant. Real situations lie somewhere in between these two limiting regimes.
The simulations as well as the Smoluchowski approach suggest the cage effect as a possible mechanism for the increase in reaction rate with increasing crowding seen in the experiments of Moorthy et al. (15). It is important to note, however, that this work focuses on excluded volume effects on the reaction rates. Other interactions, such as van der Waals and electrostatic interactions, could play an important role in realistic situations and it is possible, in principle, to extend this simulation protocol to investigate such effects.
Acknowledgments
J.S.K. acknowledges Prof. Mino Yang for useful discussions.
This material is based upon work supported by the National Science Foundation under grant No. CHE-0717569.
References
- 1.Zimmerman S.B., Minton A.P. Macromolecular crowding: biochemical, biophysical, and physiological consequences. Annu. Rev. Biophys. Biomol. Struct. 1993;22:27–65. doi: 10.1146/annurev.bb.22.060193.000331. [DOI] [PubMed] [Google Scholar]
- 2.Ellis J.R. Macromolecular crowding: obvious but underappreciated. Trends Biochem. Sci. 2001;26:597–604. doi: 10.1016/s0968-0004(01)01938-7. [DOI] [PubMed] [Google Scholar]
- 3.Ellis J.R., Minton A.P. Join the crowd. Nature. 2003;425:27–28. doi: 10.1038/425027a. [DOI] [PubMed] [Google Scholar]
- 4.Minton A.P. Molecular crowding: analysis of effects of high concentrations of inert cosolutes on biochemical equilibria and rates in terms of volume exclusion. Methods Enzymol. 1998;295:127–149. doi: 10.1016/s0076-6879(98)95038-8. [DOI] [PubMed] [Google Scholar]
- 5.Minton A.P. The influence of macromolecular crowding and macromolecular confinement on biochemical reactions in physiological media. J. Biol. Chem. 2001;276:10577–10580. doi: 10.1074/jbc.R100005200. [DOI] [PubMed] [Google Scholar]
- 6.Hall D., Minton A.P. Macromolecular crowding: qualitative and semiquantitative successes, quantitative challenges. Biochim. Biophys. Acta. 2003;1649:127–139. doi: 10.1016/s1570-9639(03)00167-5. [DOI] [PubMed] [Google Scholar]
- 7.Zhou H.X. Protein folding and binding in confined spaces and in crowded solutions. J. Mol. Recognit. 2004;17:368–375. doi: 10.1002/jmr.711. [DOI] [PubMed] [Google Scholar]
- 8.Minton A.P. How can biochemical reactions within cells differ from those in test tubes? J. Cell Sci. 2006;119:2863–2869. doi: 10.1242/jcs.03063. [DOI] [PubMed] [Google Scholar]
- 9.Shoup D., Lipari G., Szabo A. Diffusion-controlled bimolecular reaction rates. Biophys. J. 1981;36:697–714. doi: 10.1016/S0006-3495(81)84759-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Northrup S.H., Allison S.A., McCammon J.A. Brownian dynamics simulation of diffusion-influenced bimolecular reactions. J. Chem. Phys. 1984;80:1517–1524. [Google Scholar]
- 11.Berg O.G. Orientation constraints in diffusion-limited macromolecular association. Biophys. J. 1985;47:1–14. doi: 10.1016/S0006-3495(85)83870-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Barzykin A.V., Shushin A.I. Effect of anisotropic reactivity on the rate of diffusion-controlled reactions: comparative analysis of the models of patches and hemispheres. Biophys. J. 2001;80:2062–2073. doi: 10.1016/S0006-3495(01)76180-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Drenckhahn D., Pollard T.D. Elongation of actin filaments is a diffusion-limited reaction at the barbed end and is accelerated by inert macromolecules. J. Biol. Chem. 1986;261:12754–12758. [PubMed] [Google Scholar]
- 14.Kozer N., Schreiber G. Effect of crowding on protein-protein association rates: fundamental differences between low and high mass crowding agents. J. Mol. Biol. 2004;336:763–774. doi: 10.1016/j.jmb.2003.12.008. [DOI] [PubMed] [Google Scholar]
- 15.Moorthy J., Burgess R., Yethiraj A., Beebe D. Microfluidic based platform for characterization of protein interactions in hydrogel nanoenvironments. Anal. Chem. 2007;79:5322–5327. doi: 10.1021/ac070226l. [DOI] [PubMed] [Google Scholar]
- 16.Pollard T.D., Blanchoin L., Mullins R.D. Molecular mechanisms controlling actin filament dynamics in nonmuscle cells. Annu. Rev. Biophys. Biomol. Struct. 2000;29:545–576. doi: 10.1146/annurev.biophys.29.1.545. [DOI] [PubMed] [Google Scholar]
- 17.Rice S.A. Diffusion-Limited Reactions. Elsevier; Amsterdam: 1985. Comprehensive Chemical Kinetics 25. [Google Scholar]
- 18.Szabo A. Theory of diffusion-influenced fluorescence quenching. J. Phys. Chem. 1989;93:6929–6939. [Google Scholar]
- 19.Northrup S.H., Hynes J.T. Short range caging effects for reactions in solution. I. Reaction rate constants and short range caging picture. J. Chem. Phys. 1979;71:871–883. [Google Scholar]
- 20.Dong W., Baros F., Andre J.C. Diffusion-controlled reactions. I. Molecular dynamics simulation of a noncontinuum model. J. Chem. Phys. 1989;91:4643–4650. [Google Scholar]
- 21.Zhou H.X., Szabo A. Comparison between molecular dynamics simulations and the Smoluchowski theory of reactions in a hard-sphere liquid. J. Chem. Phys. 1991;95:5948–5952. [Google Scholar]
- 22.Van Beijeren H., Dong W., Bocquet L. Diffusion-controlled reactions: a revisit of Noyes' theory. J. Chem. Phys. 2001;114:6265–6275. [Google Scholar]
- 23.Lee J., Yang S., Kim J., Lee S. An efficient molecular dynamics simulation method for calculating the diffusion-influenced reaction rates. J. Chem. Phys. 2004;120:7564–7575. doi: 10.1063/1.1687680. [DOI] [PubMed] [Google Scholar]
- 24.Buján-Nuñez M.C., Miguel-Fernández A., López-Quintela M.A. Diffusion-influenced controlled reaction in an inhomogeneous medium: small concentration of reagents. J. Chem. Phys. 2000;112:8495–8501. [Google Scholar]
- 25.Saxton M.J. Chemically limited reactions on a percolation cluster. J. Chem. Phys. 2002;116:203–208. [Google Scholar]
- 26.Berry H. Monte Carlo simulations of enzyme reactions in two dimensions: fractal kinetics and spatial segregation. Biophys. J. 2002;83:1891–1901. doi: 10.1016/S0006-3495(02)73953-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Echevería C., Tucci K., Kapral R. Diffusion and reaction in crowded environments. J. Phys. Condens. Matter. 2007;19:065146. [Google Scholar]
- 28.Luby-Phelps K. Cytoarchitecture and physical properties of cytoplasm: volume, viscosity, diffusion, intracellular surface area. Int. Rev. Cytol. 2000;192:189–221. doi: 10.1016/s0074-7696(08)60527-6. [DOI] [PubMed] [Google Scholar]
- 29.Hou L., Lanni F., Luby-Phelps K. Tracer diffusion in F-actin and ficoll mixtures: toward a model for cytoplasm. Biophys. J. 1990;58:31–43. doi: 10.1016/S0006-3495(90)82351-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Pollard T.D., Borisy G.G. Cellular motility driven by assembly and disassembly of actin filaments. Cell. 2003;112:453–465. doi: 10.1016/s0092-8674(03)00120-x. [DOI] [PubMed] [Google Scholar]
- 31.Carnahan N.F., Starling K.E. Equation of state for nonattracting rigid spheres. J. Chem. Phys. 1969;51:635–636. [Google Scholar]
- 32.Hansen J.P., McDonald I.R. 2nd Ed. Academic Press; London: 1986. Theory of Simple Liquids. [Google Scholar]
- 33.Noyes R.M. Models relating molecular reactivity and diffusion in liquids. J. Am. Chem. Soc. 1956;78:5486–5490. [Google Scholar]
- 34.Strating P. Brownian dynamics simulation of a hard-sphere suspension. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Topics. 1999;59:2175–2187. [Google Scholar]
- 35.Allen M.P., Tildesley D.J. Oxford University Press; New York: 1976. Computer Simulation of Liquids. [Google Scholar]
- 36.Lanni F., Ware B.R. Detection and characterization of actin monomers, oligomers, and filaments in solution by measurement of fluorescence photobleaching recovery. Biophys. J. 1984;46:97–110. doi: 10.1016/S0006-3495(84)84002-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Sun J., Weinstein H. Toward realistic modeling of dynamic processes in cell signaling: quantification of macromolecular crowding effects. J. Chem. Phys. 2007;127:155105. doi: 10.1063/1.2789434. [DOI] [PubMed] [Google Scholar]
- 38.Collins F.C., Kimball G.E. Diffusion-controlled reaction rates. J. Colloid Sci. 1949;4:425–437. [Google Scholar]
- 39.Cichocki B., Hinsen K. Dynamic computer simulation of concentrated hard sphere suspensions. Physica A. 1990;166:473–491. [Google Scholar]


