Abstract
We have studied the relationship between dynamical correlations and energetic contributions in an attempt to model the transmission of information inside protein-protein complexes. The complex formed between the edema factor (EF) of Bacillus anthracis and calmodulin (CaM) was taken as an example, as the formation and stability of the complex depend on the calcium complexation level. The effect of calcium through EF-CaM residue network has been investigated with various approaches: 1), the elastic network model; 2), the local feature analysis; 3), the generalized correlations; and 4), the energetic dependency maps (EDMs), on 15-ns molecular dynamics simulations of the complex loaded with 0, 2, or 4 Ca2+ ions. The elastic network model correctly describes the basic architecture of the complex but is poorly sensitive to the level of calcium compared to the other methods. The local feature analysis allows us to characterize the local dynamics of the complex and the propagation of the calcium signal through CaM. The analyses of global dynamics and energetics—through generalized correlations and EDMs—provide a comprehensive picture of EF-CaM architecture and can be unified by using the concept of residue network connectedness. A medium connectedness, defined as the ability of each residue to communicate with all remaining parts of the complex, is observed for the 2Ca2+ level, which was experimentally identified as the most stable form of EF-CaM. The hierarchy of relative stabilities given by the EDMs sheds a new light on the EF-CaM interaction mechanism described experimentally and supports an organization of the complex architecture centered around nucleation points.
Introduction
Functional changes in protein-protein complexes are underlaid by conformational changes and concerted motions arising from information transmission through their residue networks (1). In recent years, various methods have been used to explore the collective dynamics of proteins and study their relevance for biological function, among them principal component analysis (PCA) (2–6) and normal mode analysis (1,7–10). However, the relationship between dynamical correlations and energetic contributions has not been studied extensively in protein complexes. The complex formed between the edema factor (EF) of Bacillus anthracis and calmodulin (CaM) provides a good test case for the existing methods as the complex stability depends on the number of calciums bound to CaM (2, 3, or 4 Ca2+) while the main architecture of the complex remains practically unchanged. Indeed the x-ray structures with three or four calcium ions display no significant change of the complex global architecture. Furthermore, the analysis of molecular dynamics (MD) simulations performed by Laine et al. (11) showed that the perturbation of the EF-CaM complex by adding and removing Ca2+ ions only changed the local conformations of some parts of the system, and not its overall architecture. It is thus a challenge to understand the propagation of the electrostatic effects of Ca2+ ions through the structure of EF-CaM.
EF-CaM gives an example of recruitment of an endogenous protein by a pathogen to activate its toxins (12). Indeed, upon binding of calmodulin, a ubiquitous actor of many calcium-signaling pathways (13–18), the toxin EF of B. anthracis undergoes a large conformational transition that leads to the formation and activation of its adenylyl cyclase catalytic site, which transforms ATP into cAMP. The accumulation of cAMP causes cellular dysfunction and allows EF to impair host immune defenses (19).
In the crystallographic structures of the complex (20,21) (Fig. 1), CaM displays an extended conformation—which is unusual in CaM-target complexes, and is loaded with various numbers of calcium ions: 2Ca2+ (Fig. 1 a), 3Ca2+, and 4Ca2+. Calmodulin (in red) is inserted between the catalytic core of EF and its helical domain Hel (residues 660–767, in pink). EF catalytic core is composed of domains CA (residues 292–349 and 490–622, in green) and CB (residues 350–489, in lime). The catalytic residues (in licorice) lie at the CA-CB interface. The switch A (domain CA, residues 402–551, in dark green) is in direct contact with CaM. Domain Hel is composed of four helices L, M, N, and O separated by three interhelical loops: inter L-M loop (residues 668–691), inter M-N loop (residues 706–713), and inter N-O loop (residues 738–745). A loop named switch C (residues 623–659, in blue) connects Hel to the catalytic core of EF.
Figure 1.
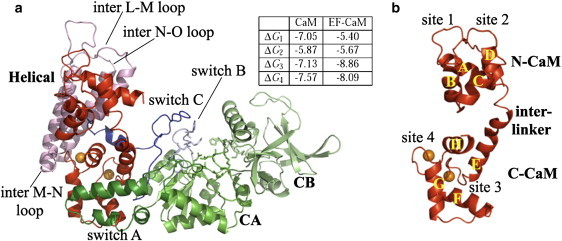
X-ray crystallographic structure of the EF-CaM complex (20), in cartoon representation. Calmodulin is displayed in red and loaded with two calcium ions (spheres in orange) on its C-terminal domain. (a) The helical domain Hel of EF is displayed in pink (residues 660–767) and composed of helices L, M, N, and O. CA is displayed in green (residues 292–349 and 490–622) with switch A in dark green (residues 502–551) and switch B in light blue (residues 579–591), and CB is displayed in lime (residues 350–489). At the interface of CA and CB, the catalytic residues are highlighted in licorice. Switch C is displayed in blue (residues 623–659). (b) CaM is composed of eight helices: A, B, and C in N-CaM; D and E in the interlinker; and F, G, and H in C-CaM. Calcium-binding loops are located between helices A and B in site 1, helices C and D in site 2, helices E and F in site 3, and helices G and H in site 4. Sites 3 and 4 are loaded with Ca2+ ions (spheres in orange). (Inset) Table gives the affinities of the four sites of CaM for calcium calculated from Ulmer et al. (28), in kcal/mol.
CaM is composed of two globular domains linked by a central flexible helix (residues 65–92) (Fig. 1 b): the N-terminal domain N-CaM (residues 5–64) and the C-terminal domain C-CaM (residues 93–147). Each domain consists in a pair of calcium-binding EF-hands (22,23) which opens upon calcium binding, exposing hydrophobic patches (24–27). However, the affinity and cooperativity of CaM calcium binding sites are affected by the presence of EF (28). In particular, EF locks N-CaM in a closed conformation, reducing its affinity for calcium (see table inset in Fig. 1), whereas it binds C-CaM in an open conformation, loaded with calcium (11). Accordingly, the predominant form of the complex is EF–(2Ca-CaM) (28), in which two Ca2+ ions are bound to the C-terminal domain of CaM.
To study the stability of EF-CaM in solution, we previously performed three 15-ns molecular dynamics (MD) simulations of the complex (11), with different levels of calcium: EF–(0Ca-CaM), EF–(2Ca-CaM), and EF–(4Ca-CaM). The analysis of these simulations helped characterize the conformational plasticity of each partner and led us to propose a model of the EF-CaM interaction in which CaM acts as a spring that maintains EF in an open active conformation.
In this work, we investigated the effect of calcium addition/removal through the structure of the whole complex. The signal propagation was studied on a simplified representation of EF-CaM, in which only C(α) were retained. The elastic network model was used first to study the natural collective dynamics of the complex and compare them to that of the MD dynamics. The effect of calcium was then characterized with approaches based on dynamical correlations on the one hand and on energetic influences on the other hand. The introduction of new concepts to describe the complex architecture gave a consensual view of the results from the two methods. These results reveal that removing calcium breaks the coupling of EF-CaM residue network, whereas calcium binding destabilizes EF within the complex.
Materials and Methods
Molecular dynamics simulations
Details concerning the preparation of initial coordinate files and the production of molecular dynamics trajectories were given previously (11). Coordinates of the EF-CaM complex with two Ca2+ were obtained from the PDB entry 1K93 (20). The EF–(0Ca-CaM) complex was generated by removing the cations and the EF–(4Ca-CaM) complex was generated by adding two Ca2+ in the N-terminal calcium loops of CaM. The Coulomb/Lennard-Jones parameters of the Ca2+ ions were taken from the parm99 parameter set of AMBER 8 (29), as a van der Waals radius R = 1.7131 Å and a well-depth ɛ = 0.459789 kcal/mol (30). These calcium parameters do not include any modeling of polarization. Nevertheless, this parameterization proves satisfactory, as in the MD simulations performed on isolated calmodulin (31) and on the EF-CaM complex (11), the systems exhibited a behavior and especially a calcium coordination geometry in agreement with the experimental observations.
The three complexes were simulated with AMBER 8 (29) during 15 ns in explicit solvent (>80,000 atoms). The MD trajectories were processed with the PTRAJ module of AMBER 9 (32). A convergence study (11) showed that the system took 3 ns to relax. The MD simulations were analyzed by Laine et al. (11) and the conformational drifts were qualitatively described. In EF–(0Ca-CaM) and EF–(4Ca-CaM), the two lobes of CaM slightly rotate with respect to each other, whereas in EF–(2Ca-CaM) the drift of CaM is very limited. Besides EF encounters collapse of its enzymatic site in EF–(0Ca-CaM) and N-CaM tends to expand in EF–(4Ca-CaM). Consequently the last 12 nanoseconds of each simulation were used for the analyzes. PYMOL (33) was used for visualization.
Elastic network model
In the elastic network theory (9,34), the complex structure is modeled as a network of N nodes, each representative of a given residue vi. Two nodes i and j are linked by a spring of constant γ∗ if they are closer than a chosen cutoff distance rc. The model can be expressed by a Kirchoff matrix Γ, defined as (34)
| (1) |
A C(α) representation of the EF-CaM complex was used to construct the elastic network model (ENM). Both experimental B-factors and MD fluctuations were predicted from the ENM according to (34)
| (2) |
| (3) |
where (ΔRk2) and Bk are the mean-square fluctuation and the temperature factor of residue k. The inverse of the Kirchoff matrix Γ−1 is the predicted covariance matrix. Predicted correlation matrices C were thus calculated by normalizing Γ−1:
| (4) |
The crystallographic structures 1K93 (20), and 1XFX, 1XFY, and 1XFZ (21), respectively loaded with 2, 3, or 4Ca2+, of the EF-CaM complex, were processed to predict the experimental B-factors. The MD fluctuations were calculated on the 12 last ns of each simulation on the one hand and were predicted using representative conformations from each simulation on the other hand. These representative conformations were identified previously (11) through a convergence analysis of the trajectories and correspond to MD snapshots taken at: 5906 ps, 9335 ps, and 12,150 ps of the EF–(0Ca-CaM) simulation, 5016 ps, 7950 ps, and 12,262 ps of the EF–(2Ca-CaM) simulation, 3529 ps, 4983 ps, 5471 ps, 11,084 ps, and 13,515 ps of the EF–(4Ca-CaM) simulation. The cutoff rc was fixed at 9 Å and γ∗ was set to 0.05 as these values permitted the best fit of predicted values on experimental B-factors.
Pearson and generalized correlation matrices
Atomic fluctuations, Pearson correlation matrices and generalized correlation matrices were calculated for the N = 619 C(α) of the EF-CaM complex, considering the 12 last ns of each MD trajectory. Atomic fluctuations and Pearson correlation matrices (N × N) were computed with the PTRAJ module of AMBER 9 (32). Correlations were quantified according to the Pearson coefficient,
| (5) |
where and are the positional fluctuation vectors of residues i and j, respectively.
Generalized correlations recently developed by Lange and Grubmüller (35) and which are based on a different metric were computed by the software g_correlation, part of the GROMACS framework (36). By analogy to the Pearson coefficient, the generalized correlation coefficient is defined as (35)
| (6) |
where is the mutual information between residues i and j (35)
| (7) |
estimated from the measure of information content , where is the probability distribution of the fluctuation vector .
Hierarchical clustering analysis was performed on the generalized correlation (GC) matrices using the statistics program R (37). Dissimilarity matrices were first determined by computing the Euclidean distances between the rows of each correlation matrix. Hierarchical clustering was performed on the dissimilarity matrices using the complete linkage method (38). The trees produced by the clustering process were cut at a given height hopt = 5 to identify clusters. The optimal value hopt of the cutting height was determined to obtain the minimum number of clusters sufficient to span the range of generalized correlations (Table 1). The same clustering analysis was applied also on the Pearson correlation matrices but no optimal cutting height could be determined as the clusters always gave the same mean correlation.
Table 1.
Hierarchical clustering analysis: mean correlation values are given for clusters identified from the generalized correlation matrices of EF–(0Ca-CaM), EF–(2Ca-CaM), and EF–(4Ca-CaM) with different cut heights h
| EF–(0Ca-CaM) | EF–(2Ca-CaM) | EF–(4Ca-CaM) | |
|---|---|---|---|
| 5.17 ≤ h < 7.1 | 0.44 ± 0.10 | 0.45 ± 0.10 | 0.46 ± 0.10 |
| 0.60 ± 0.08 | 0.60 ± 0.07 | 0.60 ± 0.08 | |
| 0.44 ± 0.10 | 0.45 ± 0.10 | 0.46 ± 0.10 | |
| 5 ≤ h < 5.17 | 0.60 ± 0.08 | 0.60 ± 0.07 | 0.56 ± 0.08 |
| 0.46 ± 0.10 | 0.46 ± 0.10 | 0.46 ± 0.10 | |
| 4.4 ≤ h < 5 | 0.46 ± 0.16 | 0.47 ± 0.22 | 0.56 ± 0.08 |
| 0.60 ± 0.08 | 0.60 ± 0.07 | 0.71 ± 0.07 |
For hopt = 5 two, two, and three clusters are identified for EF–(0Ca-CaM), EF–(2Ca-CaM), and EF–(4Ca-CaM), respectively, which display significantly different mean correlation values.
The comparison of correlation matrices were performed using the statistics program R (37). The similarity S between two correlation matrices M and N is calculated as their normalized dot product: .
Local feature analysis
In the local feature analysis (LFA) developed by Zhang and Wriggers (39), residue clusters representative of the most striking features of local dynamics are determined. A principal component analysis (PCA) was first performed on each MD trajectory with the PTRAJ module of AMBER 9 (32). Among the 3N eigenvectors Ψr associated with eigenvalues λr, r = 1, 2…3N, the first 15 ones were sufficient to describe 81–84% of the total fluctuations. These vectors were consequently used to apply the LFA formalism (39) on the C(α) motions of the complex. In brief, this formalism projects the correlation matrix in such a way that it reduces off-block diagonal correlations and identifies 15 seed degrees of freedom and hence 15 seed residues.
From the n = 15 global PCA modes one can define 3N local LFA output functions O(i) with minimum correlation (39),
| (8) |
where Ar is the projection of atomic fluctuations Δxi onto eigenvector Ψr: . The residual correlations between LFA outputs are given by (39)
| (9) |
so that in the limit n → 3N they are completely decorrelated by space: .
Rather than computing all 3N outputs O(i), the sparsification algorithm described by Zhang and Wriggers (39) was applied using the statistics program R (37) to approximate the entire 3N outputs O(i) with only a small subset of 15 outputs , where M is the ensemble of 15 seed degrees of freedom chosen to reconstruct the outputs O(i). At each iteration of the sparsification algorithm, the outputs O(i) were reconstructed given the current set M(m) of m degrees of freedom and the reconstruction mean square errors Oerr(i) were evaluated. Out of the 3N available degrees of freedom, the seed index displaying the maximum reconstruction error Oerr(im+1) and not being already picked up was chosen as the (m + 1)th index into M. Seed indexes were added to M until 15 indexes were chosen, standing for 15 seed C(α) atoms or residues. Consequently, the obtained 15 seed residues are representative of the most striking features of local dynamics. They permit us to construct a local topographic representation of the EF-CaM complex, as each seed residue and its neighboring correlated residues (residue cluster) define a local dynamic domain.
The residual correlation P(h, k) between the seed residue h and any other residue k was evaluated as (39)
| (10) |
where d is the (x,y,z) coordinate index and Ψr is the PCA eigenvector associated with eigenvalue λr.
Dependency maps
The algorithm described by Hamacher et al. in a study of the ribosomal subunit assembly (40) was used to analyze energetic dependencies inside the complex. The algorithm is based on the assumption that: “If the removal of protein Z changes the relative order from X-more-strongly-bound-than-Y to Y-more-strongly-bound-than-X, then the probabilistic assembly order is also changed” (40). This assumption was adapted to the EF-CaM case, in which pseudodomains are considered instead of proteins, and in which the stability dependency scheme of pseudodomains is considered instead of the probabilistic assembly order of proteins.
A new definition of the domains (pseudodomains) of the EF-CaM complex was derived from the LFA (Table 2). The binding free energy of a pseudodomain D to the complex C was evaluated on snapshots extracted every 10 ps from the 12 last ns of the MD trajectory of C. The binding free energy ΔΔG[D, C] is expressed as
| (11) |
where C\D stands for complex C from which domain D was removed. Within each complex, binding free energies were calculated for all pseudodomains and reference ranks were attributed accordingly, with rank 1 corresponding to the best binding energy.
Table 2.
Residues numbers delimiting 1), the EF-CaM domains in the structural biology definition by Drum et al. (20); and 2), the EF-CaM pseudodomains in the new definition with the LFA method
| Structural biology definition (20) | LFA definition | |||
|---|---|---|---|---|
| EF | CA | 294–349 and 490–622 | CA | 292–345 and 490–501 and 576–622 |
| Switch A | 502–551 | SA | 502–575 | |
| Switch B | 578–591 | |||
| CB | 350–489 | CB | 346–489 | |
| Switch C | 630–659 | SC | 623–659 | |
| Hel | 660–767 | Hel | 660–767 | |
| CaM | N-CaM | 5–64 | N-CaM | 5–84 |
| Interlinker | 65–92 | |||
| C-CaM | 93–147 | C-CaM | 85–147 | |
Residues involved in the catalytic site of EF are Arg-329 (L), Lys-346 (R), Leu-348 (R), His-351 (R), Lys-353 (R), Ser-354 (R), Lys-372 (R), Asp-491, Asp-493 (L), Thr-548 (L), His-577 (L), Thr-579 (L), Asp-582 (L), Asn-583 (L), Phe-586 (L), and Glu-588 (L) and belong either to the left side (L) or to the right side (R) of the site.
To determine the influence of a given pseudodomain D∗ on the other pseudodomains, D∗ was removed from the complex C and the binding free energy of each one of the remaining pseudodomains D to the truncated complex C\D∗ was calculated as follows:
| (12) |
The free energies of binding on C\D∗ were then ranked accordingly. When the rank of a pseudodomain D on C\D∗ was worse than its reference rank, an energetic influence was attributed to D∗ on D. The influence intensity is the number of ranks that D lost in C\D∗ context as compared to C. A total of 7 + (6∗7) = 49 binding free energy time series were calculated and energetic influences were materialized on dependency maps.
Binding free energies were evaluated by MMPBSA method (41) using the MMPBSA module of AMBER 9 (32), as
| (13) |
where ΔEMM is the molecular mechanics contribution expressed as the sum of the electrostatics (ΔEele), van der Waals (ΔEvdw), and internal (ΔEint) contributions, and ΔGsolv is the solvation free energy contribution to binding expressed as the sum of polar (ΔGsolpolar) and nonpolar (ΔGsolnonpolar) solvation free energies. The polar contribution ΔGsolpolar was calculated by solving the Poisson-Boltzmann (PB) equation with the PBSA module of AMBER 9 (32). The grid spacing was set to 0.5 Å and dielectric constants of 1 and 80 were used for the interior and exterior of the solute, respectively. The dielectric boundary was defined using a 1.6 Å probe water on the atomic surface. The nonpolar contribution ΔGsolnonpolar was calculated as the sum of a repulsive (cavity) term ΔGcavity proportional to the solvent-accessible surface area (SASA) and an attractive (dispersion) term ΔGdisp computed by surface-integration approach (Tan and Luo, in preparation quoted in (32)): ΔGsolnonpolar = ΔGdisp + ΔGcavity = ΔGdisp + 0.04356∗SASA − 1.008. Because of significant variances in computing solute entropy Ssolute using the MMPBSA approach, this term was not included in the total binding free energy value.
For most binding free energies, mean values were very close and standard deviations did not enable us to properly rank them. Nonparametric Kolmogorov-Smirnov tests (42) were therefore performed on the energy estimations time series with the statistics program R (37). The binding free energy of D was actually considered worse than that of D' when the Kolmogorov-Smirnov test gave a p-value ≤0.05.
Results
A previous analysis of the 15-ns MD simulations of the three complexes EF–(0Ca-CaM), EF–(2Ca-CaM), and EF–(4Ca-CaM) led to a model for EF-CaM interaction and to the description of the conformational changes associated with the binding or removal of two Ca2+ ions (11). In particular, binding calcium to N-CaM was shown to provoke a limited opening of the second EF-hand and both binding and removal of calcium reduced the dependence of CaM on EF while CaM interlinker underwent bending or unwinding. In this work, a scheme relating dynamics and energetics in the frame of simplified models is proposed to analyze the EF-CaM complex. Hence, the EF-CaM calcium dependence and the propagation of the calcium binding or removal signal through the residue network of the complex have been investigated. A full panel of methods for analyzing the complex dynamics was used to determine the type of dynamics analysis that agrees the most with the energetic information. The different methods used are based on: 1), elastic network theory (34); 2), local feature analysis theory (39); 3), mutual information theory (35); and 4), energetic dependency maps (40).
Elastic network model
The elastic network model (ENM) (9,34) was applied to the crystallographic structures of the EF-CaM complex (21,20). The predicted B-factors were found in agreement with the experimental values, as already demonstrated by Bahar et al. (34), with coefficients of regression R2 above 0.95 (Table 3). Fluctuations and correlation matrices were also predicted for a set of representative conformations from the MD trajectories of EF–(0Ca-CaM) (at 5906, 9335, and 12,150 ps), EF–(2Ca-CaM) (at 5016, 7950, and 12,262 ps), and EF–(4Ca-CaM) (at 3529, 4983, 5471, 11,084, and 13,515 ps), previously identified (11) through a convergence analysis. ENM fluctuations fit MD fluctuations with slightly lower R2 coefficients, in the 0.90–0.93 range (Table 3). Noticeably ENM correlation matrices from either crystallographic structures or MD conformations were very similar (Table 4). Consequently, despite high R2 coefficients with experimental values, the ENM is unable to highlight changes in internal dynamics between the different levels of calcium.
Table 3.
Slope a and coefficient of regression R2 for the linear fitting of the ENM predicted fluctuations on the experimental B-factors (x-ray) (20,21) and on the MD fluctuations (MD)
| a | R2 | ||
|---|---|---|---|
| 1K93(20) (x-ray) | 1.06 | 0.97 | |
| 1XFX(21) (x-ray) | 0.99 | 0.99 | |
| 1XFY(21) (x-ray) | 0.97 | 0.98 | |
| 1XFZ(21) (x-ray) | 0.99 | 0.98 | |
| EF-(0Ca-CaM) (MD) | 5906 ps | 0.95 | 0.90 |
| 9335 ps | 0.95 | 0.90 | |
| 12,150 ps | 0.94 | 0.90 | |
| EF-(2Ca-CaM) (MD) | 5016 ps | 0.98 | 0.93 |
| 7950 ps | 0.97 | 0.93 | |
| 12,262 ps | 0.98 | 0.92 | |
| EF-(4Ca-CaM) (MD) | 3529 ps | 1.00 | 0.91 |
| 4983 ps | 0.99 | 0.92 | |
| 5471 ps | 0.99 | 0.92 | |
| 11,084 ps | 1.01 | 0.91 | |
| 13,515 ps | 1.00 | 0.91 |
The MD fluctuations were predicted by the ENM for representative conformations extracted from the MD simulations. The snapshots' positions in the trajectories of EF–(0Ca-CaM), EF–(2Ca-CaM), and EF–(4Ca-CaM) are given in picoseconds.
Table 4.
Similarity shared by the generalized correlation matrices (upper left) and the Pearson (superscript P) and the elastic network (superscript EN) correlation matrices (lower right) between the different levels of calcium
| EF–(0Ca-CaM) | EF–(2Ca-CaM) | EF–(4Ca-CaM) | |
|---|---|---|---|
| EF–(4Ca-CaM) | 0.45 | 0.49 | 1 |
| EF–(2Ca-CaM) | 0.68 | 1 | 0.65P / 0.98EN |
| EF–(0Ca-CaM) | 1 | 0.73P / 0.98EN | 0.71P / 0.98EN |
The degree of similarity S between two matrices is evaluated as their normalized scalar product: .
The ENM correlation matrices for EF–(0Ca-CaM), EF–(2Ca-CaM), and EF–(4Ca-CaM) were compared to the Pearson correlation matrices calculated from the MD trajectories (Fig. 2). ENM correlations (upper left) are overall smaller than Pearson correlations (lower right), since ∼98% of the ENM values are within the range −0.4 to 0.4 whereas the Pearson correlations span the whole interval between −1 and 1. This is not a consequence of a smaller number of significantly contributing modes in the Pearson matrices spectra, which would make artificially high correlations (data not shown). Furthermore, the Pearson correlation patterns are much finer than those of ENM (Fig. 2), illustrating the fact that ENM describes collective motions, arising mainly from the intrinsic molecular shape of the complex.
Figure 2.
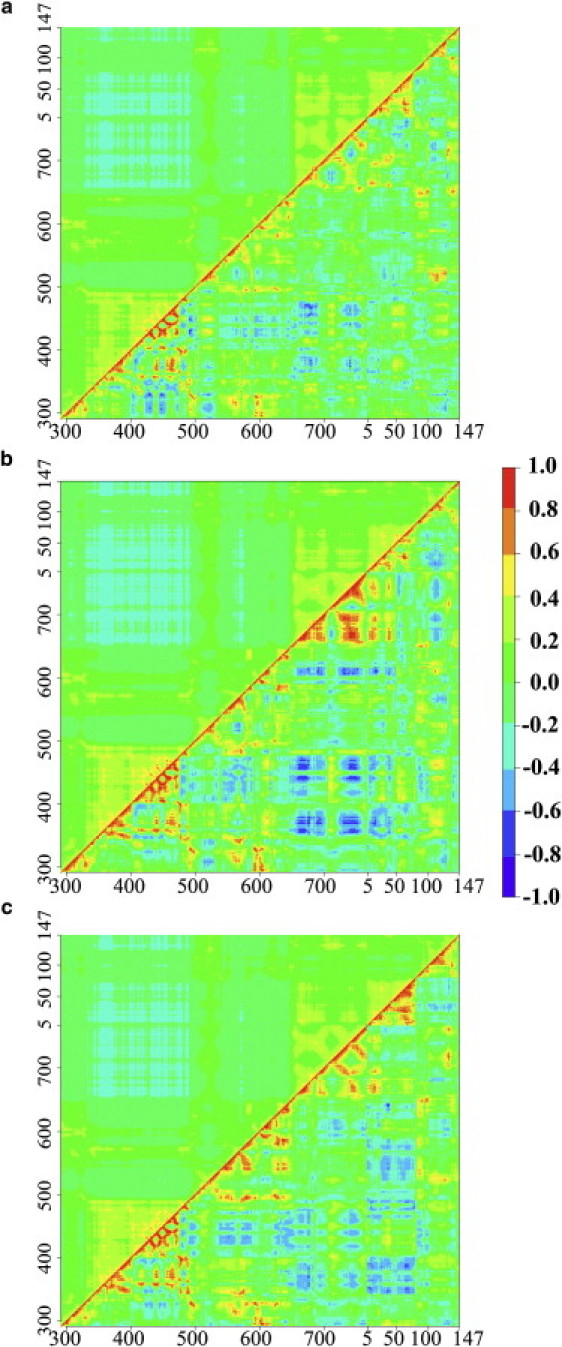
Correlation matrices predicted by the ENM (upper left) and Pearson correlation matrices (lower right). ENM correlation matrices were predicted for representative conformations extracted from the MD simulations, taken at: (a) 9335 ps for EF–(0Ca-CaM), (b) 7950 ps for EF–(2Ca-CaM), and (c) 11,084 ps for EF–(4Ca-CaM). Pearson correlation matrices were computed on the last 12 ns of each MD simulation. Residues numbers of EF (292–767) and CaM (5–147) are indicated on x and y axes.
The ENM correlation matrices unravel two anti-correlated residue blocks within EF-CaM (Fig. 2, upper left): 1), the catalytic region, formed roughly by domains CA and CB (residues 292–501); and 2), the EF-CaM interface region formed roughly by Hel of EF (residues 648–767) and N-CaM (residues 5–76). These results are in agreement with the principal component analysis of EF motions (11), which revealed a compaction and a torsion between the catalytic core and the helical domain of EF as the two first modes of EF–(2Ca-CaM) dynamics. This shows that ENM is able to predict long-range correlations to some extent, although it is based on local geometrical constraints only. Pearson correlation matrices reveal similar positive and negative correlations (Fig. 2, lower right): for instance, the anti-correlation between domains CB and Hel of EF is particularly visible in EF–(2Ca-CaM) (Fig. 2 b, lower right).
Although ENM could extract the global motions of the complex, it was not acute enough to discriminate between the various levels of calcium. To tackle that question, other methods were used: 1), post-processing of the Pearson covariance matrices by the local feature analysis theory (39); and 2), the generalized correlation coefficient (35).
Local feature analysis
To better study the local dynamics of EF-CaM, a local feature analysis (LFA) (39) was performed on the MD trajectories. Principal component analysis (PCA) was applied on the C(α) motions and then, the first 15 eigenvectors were retained for the LFA (39). The LFA sparsification algorithm (39) selected 15 seed degrees of freedom standing for 15 seed residues. As in the original article of Zhang and Wriggers (39), seed residues are mostly allocated to flexible regions within each complex (Table 5): the N- and C-tails of EF and CaM, the catalytic region and the switches A and C of EF, the calcium binding sites and the interlinker of CaM. The high flexibility of the seed residues located in the N- and C-tails (Arg-292 and Gln-767 in EF, Glu-6 in CaM) is associated with independent motions, an inherent feature of the terminal parts of a protein. Consequently these residues display flat correlation profiles, bearing little information (data not shown). More interestingly, the other seed residues are associated with locally correlated residues that form clusters representing local dynamic domains. In the three complexes, these clusters are found in regions important for the EF catalytic activity, the EF-CaM interaction, or the Ca2+-CaM interaction. They are described here in more details, focusing mainly on the EF–(2Ca-CaM) trajectory.
Table 5.
LFA seed residues
| EF–(0Ca-CaM) | EF–(2Ca-CaM) | EF–(4Ca-CaM) | ||
|---|---|---|---|---|
| Tails | Arg-292, Gln-767 (EF) | Arg-292 (EF), Glu-6 (CaM) | Glu-6 (CaM) | |
| EF | Domain CB | Thr-392, Lys-461 | Gln-376, Gly-429, Glu-449, Leu-465 | Val-380, Gly-429, Asn-450, Glu-482 |
| Switches A and C | Thr-519 (SA), Gly-638 (SC) | Thr-545 (SA) | ||
| Domain Hel | Ser-673, Asp-684, Glu-687, Pro-743, Tyr-745 | Asn-675, Ser-682, Phe-688, Pro-743 | Ser-674, Asp-684, Asp-686 | |
| CaM | N-CaM | Asp-24, Ala-57, Asn-60 | Ala-57, Gly-61 | Asp-24, Ser-38, Ala-46 |
| Interlinker | Asp-78 | Arg-74 | ||
| C-CaM | Gly-120, Met-124 | Asp-129 | Glu-104, Asp-118 |
Seed residues are located 1), in the N- and C-tails of EF and of CaM; 2), in domain CB, switches A and C and domain Hel of EF; and 3), in the N- and C-terminal domains and the interlinker of CaM. Residues locations in the structure are indicated in parenthesis when necessary: switch A is denoted SA and switch C is denoted SC.
Seed residues found in EF of EF–(2Ca-CaM), together with their associated clusters (residual correlation greater or equal to 0.03), are displayed in Fig. 3. The catalytic residues are highlighted in licorice and the whole structure is colored according to the residual correlation profile of the seed residue. The five seed residues Leu-465, Gln-376, Gly-429, Glu-449 (not shown in Fig. 3), and Gly-638 are located in the catalytic region (Table 5, Fig. 3, a–d). As shown in Fig. 3, a and b, the two clusters formed around Gln-376 and Leu-465 lie on the right edge (R) of the catalytic site and share residues 376, 379, 465, and 467 in common. Both seed residues display negative residual correlations (down to −0.03, in blue) with residues located in the left edge (L) of the catalytic site. Reciprocally the cluster formed around Gly-638 (Fig. 3 d), which includes residues from switches B and C in the left edge (L), displays anti-correlations (down to −0.03) with residues located in the right edge (R). As a consequence, the local dynamics in the catalytic region are polarized around two anti-correlated spots: Gly-638 from switch C representative of the left side and Gln-376 from CB, closely related to Leu-465, representative of the right side. This polarization, which highlights the opening/closing movement of the site, cannot be seen in EF–(0Ca-CaM), where the number of seed residues in the catalytic region is reduced (Table 5), consistent with the collapse observed in the MD simulation (11).
Figure 3.
C(α) atoms of the LFA seed residues located in the catalytic region and in the helical domain of EF–(2Ca-CaM), together with their associated clusters (residual correlation greater or equal to 0.03), represented in spheres: (a) Gln-376, (b) Leu-465, (c) Gly-429, (d) Gly-638, (e) Ser-682, and (f) Asn-675. Catalytic residues are displayed in licorice. The terms (L) and (R) stands for the left side and right side of the catalytic site, respectively. Colors follow the residual correlation profile with respect to each considered seed residue, from red down to blue.
Further away from EF catalytic site, Gly-429 is anti-correlated (down to −0.02) with most of the catalytic residues and residues at both edges of the catalytic site (Fig. 3 c). Glu-449 displays a similar correlation profile and is not shown. This region is also highlighted in EF–(4Ca-CaM) by seed residues Gly-429 and Asn-450 (Table 5).
In EF–(2Ca-CaM), seed residues were also selected in regions of EF that are contacting CaM (Table 5): 1), Thr-519 within switch A, in contact with C-CaM; and 2), Asn-675, Ser-682, Phe-688, and Pro-743 within the inter L-M loop of Hel, in contact with the first EF-hand of N-CaM (Fig. 1). Both Ser-682 (Fig. 3 e) and Asn-675 (Fig. 3 e) display positive residual correlations (up to 0.02) with the inter N-O loop (residues 738–745, Fig. 1). Additionally, Ser-682 and Phe-688 (whose correlation profile is similar to that of Ser-682, data not shown) display negative residual correlations (down to −0.03) with the entering helix C of site 2 and the interlinker of CaM. It is interesting that seed residues were found in switch A, switch C, and the inter L-M loop of Hel in EF–(2Ca-CaM), as these regions are of particular importance for the interaction between EF and CaM (20,21). Furthermore, removing or adding calcium, while affecting the stability of the complex, leads to quite different local dynamics features: no seed residue is found in switches A and C of EF–(0Ca-CaM), neither in switch C of EF–(4Ca-CaM); the number of seed residues within the inter L-M and N-O loops of Hel is increased up to 5 in EF–(0Ca-CaM) and decreased down to 3 in EF–(4Ca-CaM).
Seed residues are also located in CaM (Table 5) and their residual correlations are largely influenced by the level of calcium (Fig. 4). In EF–(2Ca-CaM), two clusters are defined in the calcium-binding loop of site 2 around Ala-57 and Gly-61. On the residual correlation matrix (Fig. 4 b), the second EF-hand of CaM appears as a block extending from residue 43 toward residue 80 of the interlinker. A correlation peak is also located in site 1 (residues 20–31) and two off-diagonal peaks demonstrate the intercorrelation between the two calcium binding loops (residues 20–31 and 56–67). No correlation is observed in the C-terminal domain, except for a narrowed peak located in the inter F-G loop between the two EF-hands (residues 108–118). Asp-129 was selected as a seed residue, but its motions are rather independent as it displays a very flat correlation profile with absolute values <0.01.
Figure 4.
LFA residual correlation matrices of CaM within (a) EF–(0Ca-CaM), (b) EF–(2Ca-CaM), and (c) EF–(4Ca-CaM). Residues numbers of CaM (5–147) are indicated on x and y axes.
Removing calcium from sites 3 and 4 in EF–(0Ca-CaM) reduces the correlation between site 1 and site 2 while inducing a new correlation peak between seed residue Asp-78 and the N-tail residues (Fig. 4 a), which is related to the unwinding of the interlinker during the simulation (11). Furthermore, residues 54–58 in site 2 are anti-correlated with Asp-78 and helix G (residues 108–129) of C-CaM (Fig. 4 a). Calcium binding in N-CaM (sites 1 and 2) induces an expansion of the correlation block of the second EF-hand toward helix B (residues 27–41) (Fig. 4 c) while seed residues are located earlier in the sequence of site 2 (Ser-38 and Ala-45). The two off-diagonal peaks located in the first EF-hand of EF–(2Ca-CaM) residual correlation matrix (Fig. 4 b) become less intense while anti-correlation peaks arise between the calcium binding loop of site 1 and the inter B-C loop (residues 39–44). As in EF–(0Ca-CaM), the interlinker (seed residue Arg-74) is correlated with the N-tail, consistent with the bending observed during the EF–(4Ca-CaM) simulation (11).
The following conclusions can be drawn regarding the effect of calcium binding/removal on the CaM residue network. The direct impact of removing calcium is observed in the interhelical F-G loop (Fig. 1 b) of C-CaM in EF–(0Ca-CaM). Additionally, motions of the F-G loop and of the interlinker become anti-correlated with that of helix C of N-CaM, which thus reveals the propagation of calcium information. On the other hand, the EF–(4Ca-CaM) correlation matrix highlights the propagation of calcium-induced conformational changes through site 2 toward helix B of site 1. Information is transmitted between the two EF-hands through anti-correlated motions of the calcium-binding loop and of the interhelical B-C loop. Overall, the LFA enables us to highlight local dynamic regions around which EF dynamics are organized and helps us to understand the propagation of calcium information along the CaM structure.
Generalized correlations
Global motions of EF-CaM were analyzed with generalized correlations calculations (35) on the MD trajectories of the three complexes. Based on mutual information theory, this correlation measure is intended to be more accurate and less biased than the commonly used Pearson correlation coefficient (35). Indeed, the Pearson measure (Fig. 5, lower right) displays >50% of absolute correlations smaller than 0.2 (in green), which is not the case for the generalized correlations (Fig. 5, upper left). The GC matrices display a larger number of intense values (>0.8) that relate larger numbers of residues far away in the proteins sequences (Fig. 5, lower right). In addition, the Pearson correlation matrices of EF–(0Ca-CaM), EF–(2Ca-CaM), and EF–(4Ca-CaM) share 65–73% similarity, while the generalized correlation matrices share 45–68% similarity (Table 4), and thus are more sensitive to the level of calcium.
Figure 5.
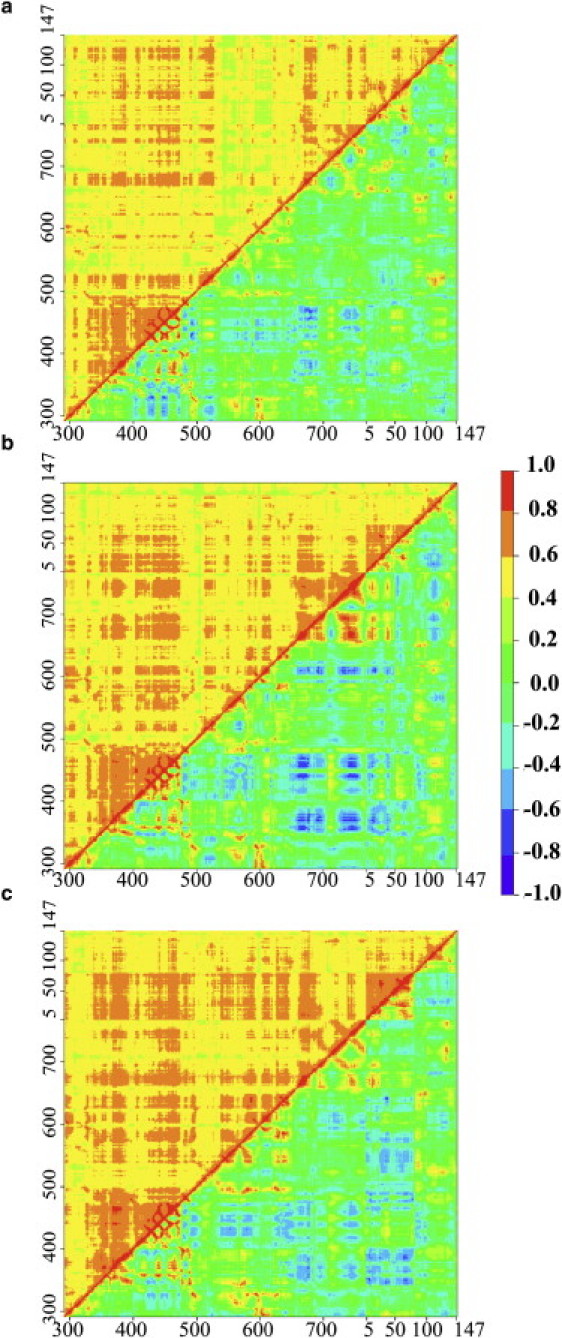
Generalized correlation matrices (upper left) and Pearson correlation matrices (lower right) for (a) EF–(0Ca-CaM), (b) EF–(2Ca-CaM), and (c) EF–(4Ca-CaM). Residues numbers of EF (292–767) and CaM (5–147) are indicated on x and y axes.
A hierarchical clustering analysis was applied to the GC matrices of the three complexes (Fig. 5). Residues were grouped based on the similarity of their correlation profiles, given that each row of a correlation matrix represents the correlation profile of a particular residue. Consequently, residues, being members of the same cluster, have the same global correlation to the remaining part of the residue network and display similar correlations to each other. The cutting height of the clustering was determined as described in Materials and Methods. Using this approach, three clusters were identified (Fig. 6 and Table 2): cluster 1 (in blue) is composed of uncorrelated residues with mean correlation below 0.5; cluster 2 (in green) is composed of slightly correlated residues with correlations in the 0.5–0.6 range; and cluster 3 (only for EF–(4Ca-CaM), in red) is composed of strongly correlated residues with a mean correlation value of 0.7.
Figure 6.
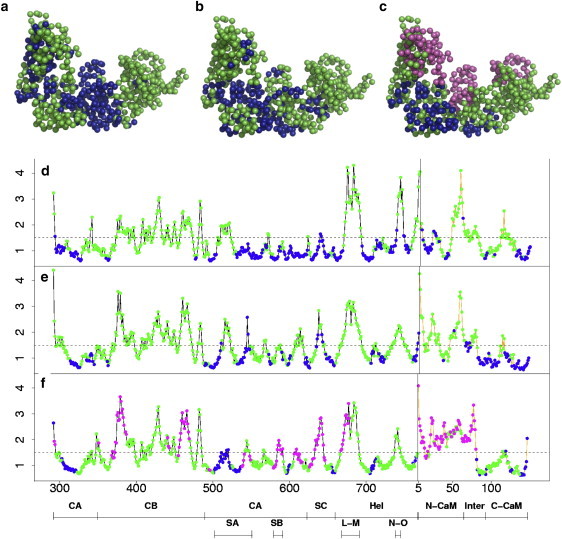
Clusters defined from the generalized correlation matrices and MD atomic fluctuations of (a and d) EF–(0Ca-CaM), (b and e) EF–(2Ca-CaM), and (c and f) EF–(4Ca-CaM). (a–c) C(α) atoms are represented as spheres and colored with respect to their cluster: cluster 1 of uncorrelated residues (<0.5) is displayed in blue, cluster 2 of slightly correlated residues (0.5–0.6) is displayed in green, and cluster 3 of highly correlated residues (0.7) is displayed in red. (d–f) C(α) atomic fluctuations of EF (black line) and of CaM (orange line), calculated on the last 12 nanoseconds of each MD trajectory. Points are colored according to the clusters color-code. The value of 1.5 Å is marked with a dotted line on each plot. The locations of the different domains CA, CB, Hel, N-CaM, the interlinker (Inter), and C-CaM of the complex, as well as those of switches A (SA), B (SB), and C (SC), and of the interhelical L-M and N-O loops along the sequence, are indicated at the bottom.
In EF–(2Ca-CaM), residues are grouped in two clusters. A large majority, 446 residues, display intermediate correlations in cluster 2 (Fig. 6 b, in green). Most of the 173 remaining uncorrelated residues of cluster 1 (in blue) have small fluctuations in the MD trajectory (Fig. 6 e). However, residues 510, 544–545 in switch A of EF, residues 636, 641–642 in switch C of EF, residues 766–767 in the C-tail of EF, and residues 50, 66–67, and 70 in site 2 of CaM display fluctuations above 1.5 Å. Consequently, the motions of these residues are relatively independent from the rest of the protein residue network.
In EF–(0Ca-CaM), a larger number of 245 residues populate cluster 1 (in blue). One-hundred-and-forty-nine of them form a large intermediate region located in CA and switch C between the catalytic core of EF and the EF-CaM interface (Fig. 6 a) and display MD fluctuations uniformly smaller than in EF–(2Ca-CaM) (Fig. 6 d). In contrast, some residues within C-CaM which were uncorrelated (cluster 1) in EF–(2Ca-CaM), become slightly correlated (cluster 2) in EF–(0Ca-CaM) while their fluctuations get larger. Furthermore, removing calcium provokes the splitting of Hel (residues 660–767) and N-CaM (residue 5–76) in four subsets of correlated flexible residues separated by uncorrelated more rigid ones (Fig. 6 d): 1), the inter L-M loop (residues 668–691); 2), the inter N-O loop (residues 738–745); 3) the C-tail of EF (residues 754–767) and the N-tail of CaM (residues 5–6); and 4), the second EF-hand together with the interlinker (residues 42–87). This finding is in agreement with the previously observed concentration of LFA seed residues in the L-M and N-O loops of EF.
In the GC matrix of EF–(4Ca-CaM) (Fig. 5 c), it was possible to group the residues into three clusters. Cluster 3 (in red) includes highly correlated residues located in three distinct regions of the complex (Fig. 6 c): 1), in CB; 2), in switch B, switch C, or CA; and 3), in helix L of Hel and N-CaM. This suggests that the conformational changes occurring in N-CaM upon calcium binding echo up to the catalytic region of EF. As opposed to these highly correlated regions, a group of uncorrelated residues (in blue) is formed around C-CaM, comprising residues 303–322 and 596–601 of CA, residues 501–537 of switch A, residues 655–659 of switch C, and residues 705–713 of Hel.
The analysis of the GC matrices enables us to draw correlation pictures of the EF-CaM complex that are sensitive to the level of calcium. The EF–(2Ca-CaM) picture displays homogeneity as most of the residues are slightly correlated except for localized regions. By contrast, correlation pictures of the two other complexes illustrate the destabilization of the EF-CaM interaction (11). For instance, EF–(0Ca-CaM) is divided in two correlated blocks separated by a region of uncorrelated residues formed by CA and switch C. The first block corresponds to CB and the second block is fragmented in several flexible correlated groups delimited by uncorrelated rather rigid residues. Therefore, calcium removal breaks the coupling between EF-CaM interface and the catalytic region, which agrees with the instability of the EF-CaM complex experimentally observed in absence of calcium (28). On the other hand, adding calcium in EF–(4Ca-CaM) induces high correlations between N-CaM and the catalytic core of EF. This suggests that calcium binding induces constraint as observed previously (11), and the information is transmitted throughout the complex, even at long distances from N-CaM. Overall, this analysis supports that moderate dynamical correlations are indicative of a stable complex.
Dependency maps
The effect of calcium on EF-CaM energetics was investigated by performing MMPBSA free energy calculations on the MD trajectories. The approach proposed by Hamacher et al. (40) and described in more details in Materials and Methods consists in calculating and ranking the binding free energy of each domain X on the rest of the complex and determining the influence of the removal of each other domain Y on the ranking. If the rank of X is lower when Y is removed, then Y is considered to have an energetic influence on the stability of X within the complex. Energetic influences are materialized by arrows on dependency maps (see Fig. 8).
Figure 8.
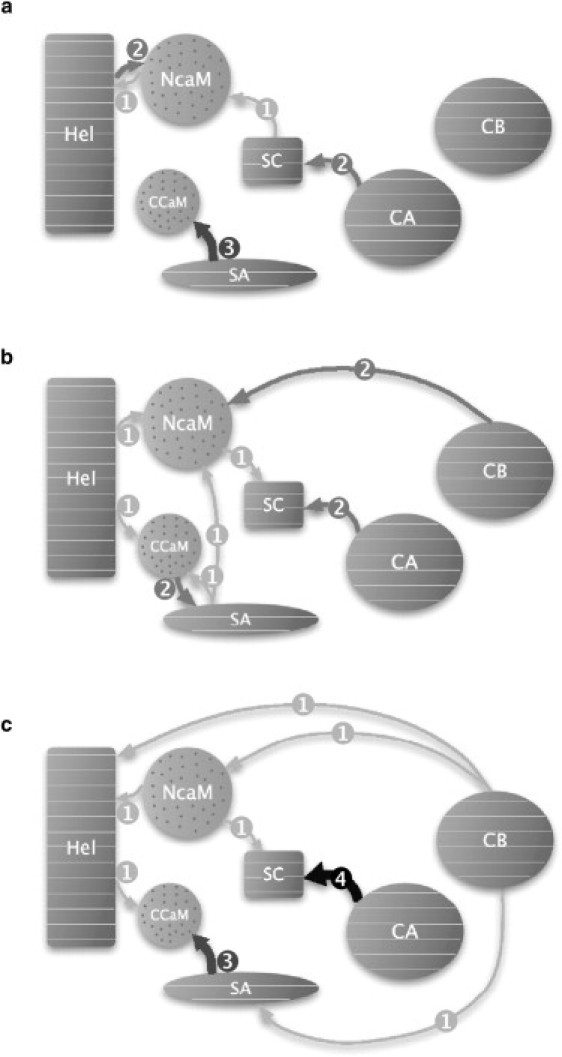
Dependency maps of (a) EF–(0Ca-CaM), (b) EF–(2Ca-CaM), and (c) EF–(4Ca-CaM). The EF-CaM complex is schematically represented by its seven pseudodomains, with CaM (pseudodomains N-CaM and C-CaM) with dots and EF (pseudodomains CA, CB, SA, SC, Hel) with horizontal lines. The arrows represent the energetic influences: the larger the greater intensity or number of lost ranks in the comparison of free binding energies (light shading is 1, medium shading is 2, dark shading is 3, and solid is 4).
Seven pseudodomains were defined inside EF-CaM with the results obtained with the LFA approach. These definitions implied some adjustments to the structural biology definition presented by Drum et al. (20) (Table 2). The matrix of EF–(2Ca-CaM) LFA residual correlations is displayed in Fig. 7 a, with our new pseudodomains delimitations. A first adjustment was made for CA and CB, defined as residues 292–349, 490–522, and residues 350–499, respectively, by Drum et al. (20). As shown in the structural biology definition (Table 2), most of the residues located in the right side of the catalytic site belong to CB and most of the residues located in the left side belong to CA. The only exceptions are observed for Lys-346 and Leu-348, which are located in the right side of the catalytic site and belong to CA. Considering the polarization of the catalytic site shown by the LFA, we thus redefined CB from residues 346 to 489. We also extracted switch A from CA, as residues 502–575 form a well-defined correlation pattern and are not correlated with the remaining part of CA (Fig. 7 a). We added residues 623–629 to the definition of switch C (residues 623–659) and we kept the original definition of Hel (residues 660–767). Since the LFA correlation pattern of CaM associates the interlinker and N-CaM (Fig. 7 a), we redefined N-CaM from residues 5 to 84 and C-CaM from residues 85 to 147. After columns and rows permutations, the LFA correlation matrix (Fig. 7 b) displays no interdomain correlations except between switch C and switch B (residues 576–591) within CA.
Figure 7.
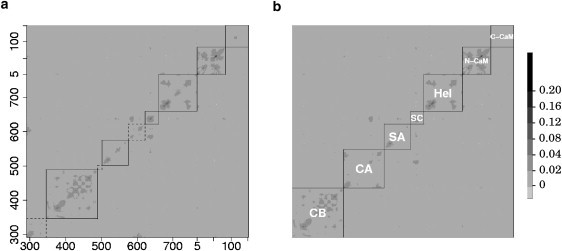
Matrix of LFA residual correlations, computed with 15 PCA eigenvectors. Pseudodomains are delimited with plain lines, except for CA on the left (a), for which dashed lines are used. In panel b, rows and columns have been permuted to group residues belonging to CA in the second block. Residue numbers of EF (292–767) and CaM (5–147) are indicated on x and y axes.
Binding free energies were calculated on each MD trajectory with MMPBSA method (41). The contributions of the different energy terms to the total binding free energy ΔΔG are given for EF–(2Ca-CaM) (Table 6). They are of the same order for the three complexes (data not shown). The largest terms are the Coulomb interaction energies ΔΔEele and the polar desolvation penalties ΔΔGsolpolar, with absolute values in the 400–2000 kcal/mol range that compensate each other. The other terms are much smaller: van der Waals energies are between −80 and −320 kcal/mol, and both nonpolar solvation terms and internal energies are between 0 and 50 kcal/mol.
Table 6.
Reference binding free energies of the seven pseudodomains of EF–(2Ca-CaM)
| ΔΔEele | ΔΔEvdw | ΔΔEint | ΔΔGsolpolar | ΔΔGsolnonpolar | ΔΔG | |
|---|---|---|---|---|---|---|
| CA | −552 ± 87 | −314 ± 11 | 52 ± 4 | 800 ± 85 | 11 ± 3 | −3 ± 22 |
| CB | −407 ± 60 | −82 ± 5 | 24 ± 3 | 497 ± 58 | 14 ± 2 | 44 ± 13 |
| SA | −1410 ± 91 | −241 ± 9 | 20 ± 3 | 1526 ± 84 | 17 ± 3 | −89 ± 24 |
| SC | −881 ± 45 | −241 ± 9 | 19 ± 3 | 1049 ± 43 | 2 ± 2 | −51 ± 20 |
| Hel | −1911 ± 78 | −161 ± 9 | 10 ± 2 | 2035 ± 75 | 21 ± 2 | −6 ± 17 |
| N-CaM | −1387 ± 86 | −101 ± 11 | 10 ± 2 | 1445 ± 82 | 25 ± 2 | −9 ± 18 |
| C-CaM | −705 ± 87 | −251 ± 12 | 10 ± 2 | 830 ± 77 | 16 ± 3 | −101 ± 29 |
The different contributions to the total free energy of binding ΔΔG are given in kcal/mol as the Coulomb interaction energy (ΔΔEele), the van der Waals energy (ΔΔEvdw), the internal energy (ΔΔEint), the polar solvation energy (ΔΔGsolpolar), and the nonpolar solvation energy (ΔΔGsolnonpolar).
As visible on Fig. 8, energetic dependency maps (EDMs) are sensitive to the level of calcium and reveal both short-range and long-range influences. Short-range influences appear to be associated with unfavorable changes in binding free energies ΔΔG (Table 7). Indeed, the positive free energy differences ΔΔΔG[CA → SC], ΔΔΔG[SA ↔ C-CaM], ΔΔΔG[Hel ↔ N-CaM] (except in EF–(2Ca-CaM)), and ΔΔΔG[Hel → C-CaM] are due to van der Waals penalties. By contrast, the Coulomb electrostatic penalty is preponderant in the positive ΔΔΔG[SC ↔ N-CaM] and the difference ΔΔΔG[SA → N-CaM] results from mixed Coulomb electrostatic and van der Waals effects. Consequently, short-range energetic influences correspond to direct hydrophobic or electrostatic interactions/contacts. However, long-range influences of CB on SA, Hel, and N-CaM are not associated with large free energy changes (Table 7). Indeed, van der Waals and nonpolar contributions are rather small while electrostatic and polar contributions compensate each other, which is not surprising since CB is >30 Å away from SA, Hel, or N-CaM. The losses of ranks for these domains are actually promoted by a favorable change in the binding energy of CA to the complex when CB is removed, of 36 and 65 kcal/mol in EF–(2Ca-CaM) and EF–(4Ca-CaM), respectively.
Table 7.
Differences in total free binding energies and in each energy term corresponding to the energetic influences identified in EF–(0Ca-CaM) (0), EF–(2Ca-CaM) (2), and EF–(4Ca-CaM) (4), given in kcal/mol below, in the legend
| ΔΔΔEele | ΔΔΔEvdw | ΔΔΔEint | ΔΔΔGsolpolar | ΔΔΔGsolnonpolar | ΔΔΔG | |
|---|---|---|---|---|---|---|
| Short-range influences | ||||||
| CA → SC (0) | 430 ± 64 | 105 ± 6 | −8 ± 2 | −478 ± 60 | 3 ± 2 | 52 ± 14 |
| CA → SC (2) | 408 ± 38 | 107 ± 7 | −9 ± 2 | −464 ± 37 | 7 ± 2 | 49 ± 14 |
| CA → SC (4) | 407 ± 34 | 116 ± 8 | −9 ± 2 | −457 ± 34 | 6 ± 2 | 63 ± 15 |
| SA → C-CaM (0) | 803 ± 47 | 82 ± 6 | 0 ± 0 | −807 ± 45 | 2 ± 2 | 80 ± 10 |
| SA ↔ C-CaM (2) | 612 ± 47 | 79 ± 8 | 0 ± 0 | −603 ± 46 | 2 ± 2 | 90 ± 14 |
| SA → C-CaM (4) | 565 ± 37 | 77 ± 5 | 0 ± 0 | −585 ± 33 | 0 ± 1 | 56 ± 9 |
| Hel ↔ N-CaM (0) | 1715 ± 82 | 84 ± 8 | 0 ± 0 | −1738 ± 89 | −7 ± 2 | 54 ± 17 |
| Hel → N-CaM (2) | 1411 ± 58 | 49 ± 8 | 0 ± 0 | −1450 ± 60 | −11 ± 2 | −1 ± 14 |
| N-CaM → Hel (4) | 1128 ± 76 | 64 ± 8 | 0 ± 0 | −1159 ± 78 | −6 ± 2 | 28 ± 11 |
| Hel → C-CaM (2) | 666 ± 39 | 55 ± 5 | 0 ± 0 | −689 ± 35 | −6 ± 1 | 25 ± 15 |
| Hel → C-CaM (4) | 768 ± 29 | 66 ± 5 | 0 ± 0 | −807 ± 32 | −8 ± 1 | 19 ± 13 |
| SC → N-CaM (0) | 552 ± 29 | 3 ± 2 | 0 ± 0 | −531 ± 28 | 0 ± 1 | 25 ± 6 |
| N-CaM → SC (2) | 473 ± 27 | 4 ± 2 | 0 ± 0 | −451 ± 27 | 0 ± 1 | 26 ± 5 |
| N-CaM → SC (4) | 442 ± 34 | 6 ± 3 | 0 ± 0 | −417 ± 31 | −3 ± 1 | 29 ± 11 |
| SA → N-CaM (2) | 692 ± 58 | 12 ± 2 | 0 ± 0 | −682 ± 56 | −4 ± 1 | 18 ± 7 |
| Long-range influences | ||||||
| CB → N-CaM (2) | 84 ± 13 | 0 ± 0 | 0 ± 0 | −80 ± 13 | 0 ± 0 | 4 ± 2 |
| CB → N-CaM (4) | 106 ± 14 | 0 ± 0 | 0 ± 0 | −105 ± 13 | 0 ± 0 | 1 ± 1 |
| CB → SA (4) | 22 ± 23 | 11 ± 4 | 0 ± 0 | −34 ± 22 | −3 ± 1 | −5 ± 7 |
| CB → Hel (4) | −55 ± 6 | 0 ± 0 | 0 ± 0 | 54 ± 7 | 0 ± 0 | −1 ± 1 |
. The arrow in indicates that removal of D∗ lowers the rank of D, and reciprocally. The arrow in indicates that removal of D also lowers the rank of D∗ (see Fig. 8). The quantity is symmetric with respect to D and D∗.
Hamacher et al. (40) used EDMs to predict the assembly ordering of the small ribosomal subunit. Here, instead of considering the assembly of proteins within a suprastructure, we considered the assembly of pseudodomains, some of which covalently bonded, within a protein-protein complex. Because of this choice, and because the establishment of the EF-CaM interaction induces conformational rearrangements not sampled in our simulations, the assembly ordering we get from the maps (Fig. 8) does not describe the actual mechanism of the EF-CaM complex formation. Instead, it gives a description of the stability dependence scheme between the different parts of the complex, as in a house-of-cards architecture: the more a pseudodomain is influenced by others, the lower the place it occupies in the hierarchy of the relative stabilities inside the complex. Accordingly, we propose that pseudodomains not subjected to any influence consist in nucleation points for the architecture of the complex.
This way, CA, CB, and Hel are the nucleation points of EF–(2Ca-CaM) (Fig. 8 b). The influences of both Hel and switch A on C-CaM correspond to direct interactions at the EF-CaM interface. Additionally, the influence of C-CaM on switch A may highlight the conformational change switch A undergoes when interacting with C-CaM (20). N-CaM is subject to the influences of switch A, CB, and Hel, which means that it plays a less important role than C-CaM in the interaction with EF, in agreement with experiments (20,21). Finally, the influences of N-CaM and CA on switch C illustrate the conformational change that switch C undergoes while interacting with N-CaM and which leads to the stabilization of the catalytic site by ordering switch B of CA (20).
In EF–(0Ca-CaM) (Fig. 8 a), the nucleation ensemble (CA, CB, and switch A) is displaced toward EF catalytic region, which reveals that EF-CaM interaction is weakened. No long-range influence is observed, so that the coupling is broken between the EF-CaM interface region and the catalytic region. This breakage is consistent with the collapse of the catalytic site observed during this simulation (11) and with the generalized correlations (Fig. 6 a). The interdependence of switch A and C-CaM is converted into a stronger influence of switch A on C-CaM. Hel is no longer linked with C-CaM: the coupling between the two CaM domains is broken.
In EF–(4Ca-CaM) (Fig. 8 c), a reduction of the nucleation ensemble (CA, CB) and new long-range influences within the EF protein, from CB to both Hel and switch A, are observed. They suggest a more constrained and unstable house-of-cards architecture and reveal a destabilization of the EF domains that contact CaM. Such a destabilization can be related to the calcium-induced conformational change of N-CaM observed during this simulation (11), which find echoes up to the catalytic region of EF according to the generalized correlations (Fig. 6 c). Noticeably, the influence of CA on switch C is reinforced. In addition, the influence of Hel on C-CaM is maintained. The interdependence of switch A and C-CaM is converted into a stronger influence of switch A on C-CaM, as observed in EF–(0Ca-CaM).
The EDMs give a model for the relative energetic dependence of the domains inside the complex and vary according to the level of calcium. The hierarchy in the domains relative stabilities sheds a new light on the EF-CaM interaction mechanism described experimentally (20,21). Indeed, in EF–(2Ca-CaM), energetic influences are centered around the EF-CaM interface. Removing or adding calcium produces different effects on the dependency maps, both leading to a destabilization. On the one hand, in EF–(0Ca-CaM), couplings within the complex are broken, especially between the catalytic core and the helical domain of EF. On the other hand, in EF–(4Ca-CaM), the number of nucleation points is decreased and new influences within EF reveal constraints that destabilize the complex architecture.
Discussion
EF-CaM is a good example of a protein-protein complex in which each partner displays remarkable conformational plasticity (11,20). The complex results from the assembly of two proteins composed of globular domains attached by a flexible linker: the N- and C-terminal domains linked by the central helix in CaM, the helical domain, and the catalytic core linked by switch C in EF. The residue network is organized into two blocks: 1), the interface region where CaM and EF contact each other, composed of Hel and switch A of EF and both domains of CaM; and 2), the catalytic region where the catalytic site lies, composed of domains CA and CB. Switch C plays an important role in maintaining the catalytic activity of the complex, as it both interacts with CaM and stabilizes switch B within the catalytic site.
We used here two different approaches to characterize the effect of Ca2+ on the global dynamics and energetics of EF-CaM, one based on dynamical correlations using generalized correlations and the other based on energetic influences using free energy calculations. Interestingly, we find good agreements between the results of the two methods, which can thus be interpreted in relation to each other in the framework of EF-CaM residue network. Both methods display an homogeneous and equilibrated picture of EF–(2Ca-CaM) architecture. Indeed, the stability of EF–(2Ca-CaM) is associated with moderate correlations over the whole residue network in the GC matrix, and with balanced nucleation points and energetic influences essentially between EF and CaM on the EDMs. Destabilization of the complex by either binding or removal of calcium ions is also revealed by both methods: in EF–(0Ca-CaM), missing correlations in the GC matrix as well as missing energetic influences in the EDMs suggest a breakage of the couplings between the different parts of the residue network while in EF–(4Ca-CaM) high correlations in the GC matrix and new energetic influences between the domains of EF highlight an imbalance in the residue network.
Consequently, the observations from analysis of GCs and EDMs support the hypothesis that the stability of the complex depends upon the organization of its residue network and particularly upon the ability of each node of the network to communicate with all remaining parts of the complex through slightly correlated motions or balanced contributions to a house-of-card architecture. This finding is in agreement with Chennubhotla and Bahar (1) and Tobi and Bahar (43), who established the relationship among protein dynamics, information transmission (1), and protein-protein association process (43). We propose to denote this property as the residue network connectedness. As previously described, the connectedness of EF-CaM residue network is affected by the level of calcium complexation. On the one hand, the coupling breakage and the imbalance of the nucleation region in EF–(0Ca-CaM) reveal a lack of communication throughout the complex residue network. On the other hand, the high correlations between N-CaM and EF catalytic core and the long-range influences inside EF in EF–(4Ca-CaM) correspond to an extended connectedness of the residue network. Because of this extended connectedness, the house-of-card architecture of the complex is destabilized. Both the lack of communication observed for EF–(0Ca-CaM) and the imbalance contributions observed for EF–(4Ca-CaM) are the signs of the complex destabilization according to the model presented here. They are thus in qualitative agreement with the relative stability of the EF-CaM interaction with different calcium levels (28).
The question remains, however: how can dynamical correlations and energetic contributions be formally related? On the one hand, the EDMs are based on relative but not necessarily absolute changes in free energies of binding, and they reveal energetic dependencies between domains within the framework of the complex stability or integrity. On the other hand, the EDMs reflect covariance dynamics to some extent through the support of domains to each other. This support is described by the action-reaction principle in classical mechanics, as the opposite directions of the action and reaction forces.
Conclusion
We used various approaches, some recently developed, to analyze the geometrical and energetic bases of the effect of calcium removal or addition on the stability and connectedness of the EF-CaM residue network. While the elastic network model gave a picture of the natural collective motions of EF-CaM, the LFA sparsification algorithm, generalized correlations and dependency maps gave information relative to the calcium level. The LFA theory highlighted local dynamic regions that may be particularly sensitive and helped us to understand the propagation of the calcium information through CaM. Generalized correlations gave comprehensive pictures of the global dynamics of the complex. Finally, dependency maps revealed the energetic influences at play between the different domains of the complex. Interestingly, information based on the generalized correlations and that based on the energetics were in good agreement and could be related to give a better understanding of the calcium-dependent interaction mechanisms. This relationship was established through the concept of residue network connectedness, indicative of the complex stability.
The edema toxin of B. anthracis has recently been shown to impair the host immune system by inhibiting the expression of anthracidal phospholipase A2 by macrophages (44). Adenylyl cyclase EF thus appears as an interesting biological target for fighting anthrax. Perspectives for this work are the modeling of the conformational transition associated with the formation of the EF-CaM complex, to describe the mechanisms of the EF activation. Specific regions involved in the internal dynamics of the complex could be targeted to disturb the stability of the catalytic site and/or block the activation of EF.
Acknowledgments
We thank Julliane Yoneda for setting up the molecular dynamics simulations. The suggestion of the word “connectedness” by a reviewer is acknowledged.
This work was supported by the French Ministry of Defense (DGA/MRIS), the National Scientific Research Center (CNRS), and the Pasteur Institute. We also acknowledge the French National Calculations Centers IDRIS (Orsay) and CINES (Montpellier) for computational resources.
References
- 1.Chennubhotla C., Bahar I. Signal propagation in proteins and relation to equilibrium fluctuations. PLoS Comput. Biol. 2007;3:1716–1726. doi: 10.1371/journal.pcbi.0030172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Amadei A., Linssen A., Berendsen H. Essential dynamics of proteins. Proteins. 1993;17:412–425. doi: 10.1002/prot.340170408. [DOI] [PubMed] [Google Scholar]
- 3.Abseher R., Nilges M. Efficient sampling in collective coordinate space. Proteins. 2000;39:82–88. doi: 10.1002/(sici)1097-0134(20000401)39:1<82::aid-prot9>3.0.co;2-s. [DOI] [PubMed] [Google Scholar]
- 4.Stepanova M. Dynamics of essential collective motions in proteins: theory. Phys. Rev. E. 2007;76:051918. doi: 10.1103/PhysRevE.76.051918. [DOI] [PubMed] [Google Scholar]
- 5.Spiwok V., Lipovová P., Králová B. Metadynamics in essential coordinates: free energy simulation of conformational changes. J. Phys. Chem. B. 2007;111:3073–3076. doi: 10.1021/jp068587c. [DOI] [PubMed] [Google Scholar]
- 6.Kubitzki M., de Groot B. Molecular dynamics simulations using temperature-enhanced essential dynamics replica exchange. Biophys. J. 2007;92:4262–4270. doi: 10.1529/biophysj.106.103101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Brooks B., Karplus M. Harmonic dynamics of proteins: normal modes and fluctuations in bovine pancreatic trypsin inhibitor. Proc. Natl. Acad. Sci. USA. 1983;80:6571–6575. doi: 10.1073/pnas.80.21.6571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Gō N., Noguti T., Nishikawa T. Dynamics of a small globular protein in terms of low-frequency vibrational modes. Proc. Natl. Acad. Sci. USA. 1983;80:3696–3700. doi: 10.1073/pnas.80.12.3696. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Tirion M. Large amplitude elastic motions in proteins from a single-parameter, atomic analysis. Phys. Rev. Lett. 1996;77:1905–1908. doi: 10.1103/PhysRevLett.77.1905. [DOI] [PubMed] [Google Scholar]
- 10.Isin B., Schulten K., Tajkhorshid E., Bahar I. Mechanism of signal propagation upon retinal isomerization: insights from molecular dynamics simulations of rhodopsin restrained by normal modes. Biophys. J. 2008;95:789–803. doi: 10.1529/biophysj.107.120691. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Laine E., Yoneda J., Blondel A., Malliavin T. The conformational plasticity of calmodulin upon calcium complexation gives a model of its interaction with the edema factor of Bacillus anthracis. Proteins. 2008;71:1813–1829. doi: 10.1002/prot.21862. [DOI] [PubMed] [Google Scholar]
- 12.Liddington R. Anthrax: a molecular full Nelson. Nature. 2002;415:373–374. doi: 10.1038/415373a. [DOI] [PubMed] [Google Scholar]
- 13.Vogel H. The Merck Frosst Award Lecture 1994. Calmodulin: a versatile calcium mediator protein. Biochem. Cell Biol. 1994;72:357–376. [PubMed] [Google Scholar]
- 14.Chin D., Means A. Calmodulin: a prototypical calcium sensor. Trends Cell Biol. 2000;10:322–328. doi: 10.1016/s0962-8924(00)01800-6. [DOI] [PubMed] [Google Scholar]
- 15.Bahler M., Rhoads A. Calmodulin signaling via the IQ motif. FEBS Lett. 2002;513:107–113. doi: 10.1016/s0014-5793(01)03239-2. [DOI] [PubMed] [Google Scholar]
- 16.Hoeflich K., Ikura M. Calmodulin in action: diversity in target recognition and activation mechanisms. Cell. 2002;108:739–742. doi: 10.1016/s0092-8674(02)00682-7. [DOI] [PubMed] [Google Scholar]
- 17.Vetter S., Leclerc E. Novel aspects of calmodulin target recognition and activation. Eur. J. Biochem. 2003;270:404–414. doi: 10.1046/j.1432-1033.2003.03414.x. [DOI] [PubMed] [Google Scholar]
- 18.Ikura M., Ames J. Genetic polymorphism and protein conformational plasticity in the calmodulin superfamily: two ways to promote multifunctionality. Proc. Natl. Acad. Sci. USA. 2006;103:1159–1164. doi: 10.1073/pnas.0508640103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Ascenzi P., Visca P., Ippolito G., Spallarossa A., Bolognesi M. Anthrax toxin: a tripartite lethal combination. FEBS Lett. 2002;531:384–388. doi: 10.1016/s0014-5793(02)03609-8. [DOI] [PubMed] [Google Scholar]
- 20.Drum C., Yan S., Bard J., Shen Y., Lu D. Structural basis for the activation of anthrax adenylyl cyclase exotoxin by calmodulin. Nature. 2002;415:396–402. doi: 10.1038/415396a. [DOI] [PubMed] [Google Scholar]
- 21.Shen Y., Zhukovskaya N., Guo Q., Florian J., Tang W. Calcium-independent calmodulin binding and two-metal-ion catalytic mechanism of anthrax edema factor. EMBO J. 2005;24:929–941. doi: 10.1038/sj.emboj.7600574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Capozzi F., Casadei F., Luchinat C. EF-hand protein dynamics and evolution of calcium signal transduction: an NMR view. J. Biol. Inorg. Chem. 2006;11:949–962. doi: 10.1007/s00775-006-0163-0. [DOI] [PubMed] [Google Scholar]
- 23.Gifford J., Walsh M., Vogel H. Structures and metal-ion-binding properties of the Ca2+-binding helix-loop-helix EF-hand motifs. Biochem. J. 2007;405:199–221. doi: 10.1042/BJ20070255. [DOI] [PubMed] [Google Scholar]
- 24.Finn B., Evenas J., Drakenberg T., Waltho J., Thulin E. Calcium-induced structural changes and domain autonomy in calmodulin. Nat. Struct. Biol. 1995;2:777–783. doi: 10.1038/nsb0995-777. [DOI] [PubMed] [Google Scholar]
- 25.Zhang M., Tanaka T., Ikura M. Calcium-induced conformational transition revealed by the solution structure of apo calmodulin. Nat. Struct. Biol. 1995;2:758–767. doi: 10.1038/nsb0995-758. [DOI] [PubMed] [Google Scholar]
- 26.Ishida H., Takahashi K., Nakashima K., Kumaki Y., Nakata M. Solution structures of the N-terminal domain of yeast calmodulin: Ca2+-dependent conformational change and its functional implication. Biochemistry. 2000;39:13660–13668. doi: 10.1021/bi000582x. [DOI] [PubMed] [Google Scholar]
- 27.Yang C., Jas G., Kuczera K. Structure, dynamics and interaction with kinase targets: computer simulations of calmodulin. Biochim. Biophys. Acta. 2004;1697:289–300. doi: 10.1016/j.bbapap.2003.11.032. [DOI] [PubMed] [Google Scholar]
- 28.Ulmer T., Soelaiman S., Li S., Klee C., Tang W. Calcium dependence of the interaction between calmodulin and anthrax edema factor. J. Biol. Chem. 2003;278:29261–29266. doi: 10.1074/jbc.M302837200. [DOI] [PubMed] [Google Scholar]
- 29.Case D., Darden T., Cheatham T., Simmerling C., Wang J. University of California; San Francisco: 2004. AMBER 8. [Google Scholar]
- 30.Aqvist J. Ion-water interaction potentials derived from free energy perturbation simulations. J. Phys. Chem. 1990;94:8021–8024. [Google Scholar]
- 31.Fiorin G., Biekofsky R., Pastore A., Carloni P. Unwinding the helical linker of calcium-loaded calmodulin: a molecular dynamics study. Proteins. 2005;61:829–839. doi: 10.1002/prot.20597. [DOI] [PubMed] [Google Scholar]
- 32.Case D., Darden T., Cheatham T., Simmerling C.I., Wang J. University of California; San Francisco: 2006. AMBER 9. [Google Scholar]
- 33.Delano, W.L. 2002. The PyMOL Molecular Graphics System. http://www.pymol.org.
- 34.Bahar I., Atilgan A., Erman B. Direct evaluation of thermal fluctuations in proteins using a single-parameter harmonic potential. Fold. Des. 1997;2:173–181. doi: 10.1016/S1359-0278(97)00024-2. [DOI] [PubMed] [Google Scholar]
- 35.Lange O., Grubmüller H. Generalized correlation for biomolecular dynamics. Proteins. 2006;62:1053–1061. doi: 10.1002/prot.20784. [DOI] [PubMed] [Google Scholar]
- 36.van Der Spoel D., Lindahl E., Hess B., Groenhof G., Mark A.E. GROMACS: fast, flexible, and free. J. Comput. Chem. 2005;26:1701–1718. doi: 10.1002/jcc.20291. [DOI] [PubMed] [Google Scholar]
- 37.R Development Core Team. 2006. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria. http://www.R-project.org, ISBN 3-900051-07-0.
- 38.Gordon A. 2nd Ed. Chapman & Hall/CRC; Boca Raton, FL: 1999. Classification. [Google Scholar]
- 39.Zhang Z., Wriggers W. Local feature analysis: a statistical theory for reproducible essential dynamics of large macromolecules. Proteins. 2006;64:391–403. doi: 10.1002/prot.20983. [DOI] [PubMed] [Google Scholar]
- 40.Hamacher K., Trylska J., McCammon J. Dependency map of proteins in the small ribosomal subunit. PLoS Comput. Biol. 2006;2:e10. doi: 10.1371/journal.pcbi.0020010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Srinivasan J., Cheatham T., Cieplak J., Kollman P., Case D. Continuum solvent studies of the stability of DNA, RNA, and phosphoramidate—DNA helices. J. Am. Chem. Soc. 1998;120:9401–9409. [Google Scholar]
- 42.Marsaglia G., Tsang W.W., Wang J. Evaluating Kolmogorov's distribution. J. Stat. Software. 2003;8:1–4. [Google Scholar]
- 43.Tobi D., Bahar I. Structural changes involved in protein binding correlate with intrinsic motions of proteins in the unbound state. Proc. Natl. Acad. Sci. USA. 2005;102:18908–18913. doi: 10.1073/pnas.0507603102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Raymond B., Leduc D., Ravaux L., Goffic R., Candela T. Edema toxin impairs anthracidal phospholipase A2 expression by alveolar macrophages. PLoS Pathog. 2007;3:e187. doi: 10.1371/journal.ppat.0030187. [DOI] [PMC free article] [PubMed] [Google Scholar]


