Abstract
A mesoscale model of DNA is presented (3SPN.1), extending the scheme previously developed by our group. Each nucleotide is mapped onto three interaction sites. Solvent is accounted for implicitly through a medium-effective dielectric constant and electrostatic interactions are treated at the level of Debye-Hückel theory. The force field includes a weak, solvent-induced attraction, which helps mediate the renaturation of DNA. Model parameterization is accomplished through replica exchange molecular dynamics simulations of short oligonucleotide sequences over a range of composition and chain length. The model describes the melting temperature of DNA as a function of composition as well as ionic strength, and is consistent with heat capacity profiles from experiments. The dependence of persistence length on ionic strength is also captured by the force field. The proposed model is used to examine the renaturation of DNA. It is found that a typical renaturation event occurs through a nucleation step, whereby an interplay between repulsive electrostatic interactions and colloidal-like attractions allows the system to undergo a series of rearrangements before complete molecular reassociation occurs.
Introduction
The breadth of available molecular-level models of DNA remains narrow. Fully atomistic models have limitations, largely due to the range of length- and timescales that are typically of interest in DNA research. The scales that characterize the solvent and ions are on the order of Ångströms and picoseconds. A DNA molecule can measure millimeters, and hybridization events can require seconds or minutes. Moreover, complete descriptions of DNA structure and dynamics become even more complex when accounting for distinct interactions that affect molecular behavior, including electrostatics, cooperative base stacking, hydrogen bonding, and the solvent. Yet this set of interactions remains incomplete, at least for in vivo systems, when no mention is made of cytosolic components that have specific roles in the processing of DNA to exert proper biological function.
Taking into account the previous considerations, and realizing that biologically relevant systems involve DNA on the scale of hundreds to thousands of basepairs, atomistic representations remain of limited utility for many common applications. As a result, increasing efforts are being devoted to the development of accurate, coarse-grain models that embody the necessary physics with a minimum number of degrees of freedom, while still being realistic at the molecular and chemical levels. Such models would facilitate access to larger spatial and temporal scales and would permit description or elucidation of some of the fundamental interactions that arise in a wide variety of biological processes.
Perhaps the simplest representation of DNA is the charged rod employed in analytically tractable linearized Poisson-Boltzmann treatments, where charge is distributed uniformly along the length of the rod. Extensions of this construct include the studies by Kornyshev and Leikin (1), as well as those by Solis and Olvera de la Cruz (2), where charges are incorporated into the cylinder model as discretized sites on the surface of the rod. Lyubartsev and Nordenskiöld (3) extended the simple charged-rod rendition to account for DNA helical grooves by using a different set of length scales to describe the cylindrical core and the charged sites. Gil Montoro and Abascal (4) included an additional neutral site between the charged beads and the cylindrical core, thereby enhancing the grooved appearance of the rod. Collectively, this class of representations emphasizes molecular stiffness, electrostatic interactions, and a cylindrical, hard-core excluded volume. The hallmark feature of these models is their ability to capture density fluctuations of ionic species at the surface of DNA and beyond, as well as to describe certain packing phenomena. However, these models are limited to studies of problems which do not depend on molecular flexibility, denaturation, or sequence-specific effects.
A different class of models has sought to capture chain backbone rigidity through a continuous elastic rod or by an effective bead-spring representation, where a single interaction site corresponds to one or several basepaired nucleotides. These constructs aim to capture the polymeric nature of DNA with minimal molecular detail. Representative applications for the elastic rod model include the study of energy in supercoiled DNA by Schlick and Olson (5), as well as the interpretation of fluorescence depolarization by Barkley and Zimm (6). Bead-spring representations were developed in an effort to allow for more detail pertaining to system dynamics. In this category, Jian et al. (7) formulated a model to treat long sequences of DNA (7). Various aspects of DNA dynamics under confined flow in channels were treated by Chopra and Larson (8). Jendrejack et al. (9,10) studied DNA dynamical properties and behavior under flow, with comparisons to experimental data. Further studies on single DNA molecules in shear flow were pursued by Hur et al. (11). Rheological properties, including polymer extension and shear viscosity, were considered by Schroeder et al. (12). Bead-spring models of this sort are useful for rather large spatial and temporal scales, but are of limited use for problems requiring a higher resolution.
In an effort to address the limitations in resolution of the previous two classes of coarse-grain representations, other models based on a distinct framework have been adopted to explore mesoscale processes. The work by Bruant et al. (13) focused on developing a construct based on quasirigid atom groups that reproduces bending, torsional, and stretching strengths, while neglecting electrostatic effects. Tepper and Voth (14) formulated a model for DNA submerged in a coarse-grain solvent, where the system is envisioned as a complex network of beads. On another front, the molecular mechanics of basepairs prompted the conception of models that use empirically measured mechanical properties of DNA to extract values for kinematic variables. For instance, Tan and Harvey (15) derived a model, where a basepair is represented by three coplanar beads, to study linear and supercoiled DNA. El Hassan and Calladine (16) also focused on treating DNA at the basepair level, but their construct adopts a rectangular unit to represent a basepair along with a more detailed set of kinematic variables.
Although former studies have been developed primarily to investigate the mechanical properties of DNA, several recent models have focused on the description of thermal effects. The model by Drukker and Schatz (17) represents each nucleotide with two beads and has been applied to treat denaturation in double-stranded sequences, but does not account for major and minor grooves in DNA. A lattice-based variant of their two-bead representation was developed by Sales-Pardo et al. (18), again with an emphasis on denaturation. Both of these models neglect electrostatic interactions in their treatment and do not attempt to describe the elastic properties of DNA. A more detailed mesoscale model was developed by Maciejczyk et al. (19), where sugar, phosphate, and key nucleic base sites are represented through pseudoatoms, some of which are characterized by internal degrees of freedom. From this construct, an effective potential of mean force was developed for Lagrangian and quaternion molecular dynamics. A specific application of this model involved a study of the transition between the A and B forms of DNA.
In recent work, Knotts et al. (20) proposed an off-lattice, coarse-grain representation for DNA in the spirit of Gō-type models. Each of the three chemical moieties comprising a nucleotide (sugar, phosphate, and nitrogenous base) is reduced to an effective, united-atom interaction site, the coordinates of which are derived from x-ray diffraction data (21). For conciseness, we refer to this model as 3-Sites-Per-Nucleotide, Ver. 0 (3SPN.0). As such, it is a much simpler construct than that encountered in more detailed superatom models (19), thereby providing significant computational advantages. A convenient attribute of the scheme behind 3SPN.0 is that it facilitates a selective atomistic reconstruction of DNA when microscopic detail is desired, or coarse-graining can be further enhanced to a lower resolution when mesoscale detail is no longer sought. In 3SPN.0, sites comprising a nucleotide are characterized by positional and orientational descriptors that yield a realistic helical arrangement. The model accounts for major as well as minor grooves, Watson-Crick basepairing, and electrostatic interactions, which together are important to the biochemistry of DNA. The 3SPN.0 force field captures DNA denaturation (as a function of chain length and ionic strength) and provides a reasonable description of other thermomechanical properties (including persistence length and bubble formation).
As useful as previous computational descriptions of DNA have been, it is important to emphasize that prior constructs aimed at treating thermal effects, including 3SPN.0, focused on the denaturation or melting of DNA. To our knowledge, mesoscopic computational models aimed at addressing the renaturation problem are not available. On the other hand, atomistic renditions have been largely restricted to small systems (22–26). DNA melting and renaturation is essential in numerous biochemical processes, where the structural stability and dynamical evolution of the molecule are closely related to biological function such as transcription, replication, and regulation of gene expression (23). Moreover, renaturation is the fundamental step in the self-assembly of DNA nanostructures. This publication presents improvements and extensions to the 3SPN.0 force field. First, intramolecular strengths have been parameterized to capture more accurately the persistence length of DNA. Second, the energy strength scales acting between basepairs have been adjusted to make contact with melting transition enthalpies of basepair groups according to the unified nearest-neighbor formalism. Third, electrostatic interactions at the level of Debye-Hückel theory have been described with a state-dependent dielectric constant, which accounts for a decrease in the polarizability of water with increasing temperature or ionic strength. Fourth, and perhaps more importantly, a weak, solvent-induced attraction has been introduced to allow for the reversible denaturation of DNA, a feature that could only be captured with the 3SPN.0 force field under a limited set of circumstances. As described below, this last contribution is both physically and biologically relevant, as it paves the way for systematic studies of DNA hybridization. Collectively, these modifications are denoted as the 3SPN.1 force field.
Our publication is organized as follows. First, we revisit key features of the coarse-grain model for DNA and develop the extensions made to the force field. We then describe the method used to parameterize the model in the context of capturing the denaturation temperature of DNA. Results are then presented and discussed in light of available experimental data and model capabilities. We conclude with a brief summary of our work.
A Mesoscale Model for DNA
The 3SPN.0 force field is constructed in the spirit of an off-lattice Gō-like model (20). Such an arrangement avoids the proper specification of site-site interactions, but instead provides realistic molecular conformations by coupling the interaction between sites to a predefined target structure. In this sense, one distinguishes between native contacts, or sites that within a region of space satisfy relative spatial and orientational constraints of the target structure, and nonnative contacts, which yield interactions that differ from the target structure. When all sites are engaged with their native contacts, the system acquires its ground state. Additional thermodynamic stability arises from steric constraints, which account for the directional character of bonds in a more realistic manner. Typically, a Lennard-Jones potential is parameterized to lower the energy of the system on approaching the ground state. A purely repulsive Lennard-Jones interaction contributes an energy penalty, on a length scale that avoids structural frustration, as configurations deviating from the native state are explored.
For our purposes, we implement the model for the study of B-DNA comprised of Nnt nucleotides per strand. The specification of standard coordinates and the 3SPN.0 force field have been previously reported (20). (We alert the reader that an entry from Table III in Knotts et al. (20) was unintentionally omitted. The missing entry is the dihedral angle S(3′)-P-(5′)S-Gb, with a value of 50.66°.) Here, we revisit the force field and introduce an extension that accounts for solvent-induced effects, the so-called 3SPN.1 force field. Moreover, the 3SPN.1 force field consists of a parameter set that improves the agreement between our mesoscale simulations and experimental data for the persistence length of DNA.
The mesoscale model for DNA is divided into bonded and nonbonded contributions. Three bonded interactions enter the force field,
| (1) |
| (2) |
| (3) |
which are typical two-, three-, and four-body contributions used to treat molecular systems. More specifically, Ubond describes covalent bonding interactions, using k1 and k2 as bond constants, together with di and d0i as instantaneous and equilibrium site-site separations for the ith bond, respectively, in the set of nbond bonds. Molecular bending is accounted for through Ubend, with a bending constant kθ, along with θi and θ0i as instantaneous and equilibrium bond angles, respectively, for the ith bend in the set of nbend bends. Torsional interactions are represented through Utors, with a torsional constant kϕ, along with instantaneous and equilibrium dihedral angles ϕi and ϕ0i, respectively, in the set of ntors torsions. The right-handed chirality in B-DNA is conserved through the scheme of Hoang and Cieplak (27).
Nonbonded, pairwise interactions are described through five contributions given by
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
The first two contributions are specific to DNA systems. Base-stacking (an intrastrand effect) is taken into account through Ustck, which acts uniformly (i.e., with a single energy scale ɛ) on all native-contact pairs nstck. In this context, a native contact is defined as a site-site interaction between a probe and all intrastrand sites found within a cutoff radius rccut = 9 Å of the target structure, following the Gō-like construct described by Hoang and Cieplak (27). An interaction-specific length scale σij between sites i and j contributes to the stiffness of the DNA backbone by controlling the instantaneous site-site separation rij. The base-stacking contribution accounts for the strong hydrophobic attraction between adjacent nucleotides and provides additional bending rigidity to the DNA molecule.
Hydrogen bonding, along with base-stacking interactions, provides structural stability in duplexed DNA or, in the case of intrastrand interactions, the formation of hairpins. In general, complementary basepairs engage in three hydrogen bonds for cytosine (C) and guanine (G) contacts, whereas only two hydrogen bonds are involved in adenine (A) and thymine (T) contacts. All other basepair contacts are mismatches which do not conform to Watson-Crick basepairing. This construct maps these interactions using a united-atom site for each base moiety that interacts through an effective single bond. More specifically, Ubase accounts for hydrogen bonding that occurs between all nbase complementary basepairs that do not participate in Ustck. Each ith basepair, characterized by the separation rij between intra- or interstrand sites i and j, is described by characteristic energies ɛi ∈ {ɛAT, ɛCG} and characteristic lengths σbi ∈ {σAT, σCG}, where ɛαβ = ɛβα and σαβ = σβα. A complementary basepair is considered to be hydrogen-bonded when the separation between bases is rij < (σbi + 2.0 Å).
At first glance, one would expect the overall relative strength between complementary basepair interactions CG:AT to be 3:2, on the basis of hydrogen bonding. The underlying assumption with this statement is that all hydrogen bonds between complementary base moieties are of equivalent strength. However, since the strength of a hydrogen bond depends on orientation (28–30), and not all of these form with identical spatial arrangements (i.e., their axis of approach differs), the CG:AT energy strength ratio is actually smaller. It has been established that base-stacking interactions play a stronger role in governing the denaturation temperature when compared solely to basepair hydrogen bonding (31). This feature has been taken into account in the 3SPN.1 force field by using the experimental enthalpies that accompany the duplex-to-single stranded (helix-coil) transition in DNA (32). Such an approach enables us to effectively map enthalpic contributions onto the relative strength between sites comprising a basepair, while reducing the number of adjustable parameters in the force field. The relative strength between basepair sites was computed as the geometric mean between contacts of a given type (either AT or CG types). Note that the arithmetic mean of this metric yields practically no distinction between AT and CG contacts. Using the unified nearest-neighbor approach and data from SantaLucia (33), which has been shown to yield good agreement with experiments for several systems (33,34), we adopt the ratio of ɛCG and ɛAT:
| (9) |
This ratio is used to assign energy strengths in Ubase.
Interactions occurring between the nnnat nonnative contact pairs (including mismatched basepairs) are assigned to Unnat. This is a purely repulsive, excluded-volume contribution (a Weeks-Chandler-Anderson interaction) characterized by a single energy scale ɛ. As such, Unnat imparts an energy penalty to the system as interparticle separations rij fall below a cutoff length scale rcoff, but otherwise does not contribute to the stability of the system. In the case of mismatched basepairs, rcoff = 1.00 Å. In all other cases, rcoff = 6.86 Å, which corresponds to a mean pairwise separation. The length scale for which the potential vanishes is given by σ0 = 2−1/6rcoff.
The remaining two contributions to the force field are related to the solvent of the system. In this work, we focus on aqueous salt (NaCl) solutions of DNA, and simulate such systems through a simple, implicit solvent approach. More specifically, electrostatic contributions, Uelec, are treated at the level of Debye-Hückel theory and account for interactions involving the nelec pairs between phosphate sites i and j that do not enter into Ubend. The Debye length, λD, which defines the spatial extent of charge screening at an interparticle separation rij, is given by
| (10) |
where ɛ0 is the permittivity of free space, ɛ(T, C) is an effective dielectric constant, β is the inverse thermal energy of the system (kBT)−1, NA is Avogadro's number, ec is the elementary charge, and I is the ionic strength of the solution. The dielectric constant specialized here for aqueous salt solutions, ɛ(T, C), includes a dependence on temperature, T, and salt concentration, C, both of which have a direct bearing on the polarizability of water. A decomposition of the effective dielectric constant into a product of contributions has been suggested in the literature (35) according to
| (11) |
where ɛ(T) is the static (zero-frequency) dielectric constant at absolute temperature T (in Kelvin), and a(C) is the salt correction for a solution with molarity C in NaCl (which is the monovalent salt we consider in our studies). These contributions are given by
| (12) |
and
| (13) |
(Note that a linear approximation for the zero-frequency dielectric constant of water with increasing temperature was published early on in (36), and is given by the expression ɛ(T) = 80 − 0.4(T − 293.15) where T is in Kelvin; this expression underestimates the value of the dielectric constant by up to ∼20%.) The expression for ɛ(T) in Eq. 12 is a quadratic regression of the tabulated data presented for the zero-frequency dielectric constant of water in Fernández et al. (37). The liquid phase data covers a temperature span from 275 K to 370 K, at 0.1 MPa, corresponding to a broader spectrum of data than that presented in Stogryn (35). We note that Catenaccio et al. (38) have implemented a modification in Onsager's equation to obtain an expression of the dielectric constant as a function of dipole moment and density. However, we present a simple empirical expression, which pools a vast amount of available experimental data for the dielectric constant of water using a range similar to that reported in Catenaccio et al. (38). The fit yields a residual standard deviation of 0.04 in the dielectric constant. The expression which corrects for salt effects is taken directly from Stogryn (35), with no extension done to account for the data used to determine ɛ(T).
Finally, the solvent-induced contribution, Usolv, is a novel addition introduced in the 3SPN.1 force field meant to represent (implicitly) many-body effects associated with the arrangement of water during the reversible denaturation of DNA. This ad hoc contribution is fully consistent with attractions seen in experiments due to correlations of electrostatic origin (39–42). Such interactions have been explained theoretically with various models (42–47), and are responsible for the association of dsDNA into bundles in the presence of multivalent ions. The more fundamental step of association involving complementary ssDNA remains elusive in the context of molecular-based descriptions. However, the utility and reliability of implicit solvent treatments, such as the one used here, continue to be illustrated in recent studies (22,48).
The contribution Usolv is represented through a Morse-like interaction characterized by an energy scale ɛs and an interparticle separation rij, while the spatial range of the potential is controlled by a length scale α−1, with a potential energy minimum set to rs. Solvent-induced interactions enter into Usolv through all possible nsolv interstrand sugar site pairs. This contribution is chosen to be compatible with the molecular geometry of DNA (namely, the sugar-sugar interstrand separation). Since the solvent-induced interaction embodies solution effects, it should depend on chain density, chain length, and electrolytic conditions.
To obtain the dependence of energy scales on solvent-induced interactions, extensive simulations of a set of short oligonucleotides were used to parameterize the force field on the basis of comparisons to experimental denaturation temperatures (systems and methodology will be presented under Replica Exchange Simulations in the next sections; here, only results relevant to the force field are summarized). First, the force field was parameterized against chain length for fixed composition (see Fig. 1 A). Next, electrostatic effects on the denaturation temperature were investigated by fixing the chain length, but varying the ionic strength (see Fig. 1 B). The resulting energy scales were fit to simple nonlinear, asymptotic functions. The interaction strength as a function of chain length can be described with the simple expression
| (14) |
where ɛ∞ = 0.504982ɛ, while the ionic strength contribution is given by
| (15) |
By construction, and as shown below, the energy scales and functional forms of Eqs. 14 and 15 yield very good agreement between the melting enthalpies and heat capacities predicted by our model and experiment.
Figure 1.

Energy strength of the solvent-induced interaction. (A) Dependence on chain length in [Na+] = 0.069 M. (B) Dependence on ionic strength for Nnt = 15. Results from exploratory simulations (circles) and corresponding nonlinear regressions (dashed lines) are also shown. For long chains (Nnt ≳ 30) and high ionic strength ([Na+] ≳ 1 M), both contributions saturate to a limiting value.
To combine the information from Eqs. 14 and 15, we investigated the parameterization of ɛs at different values of Nnt as a function of salt concentrations 0.069 M < [Na+] ≤ 0.220 M. Those results are reported in Fig. 2 and suggest that with the exception of Nnt = 10, the energy strength for the solvent-induced contribution, which is sensitive to the number of nucleotides for Nnt ≲ 30 and salt concentration for [Na+] ≲ 0.75 M, can be approximated as ɛs ≈ ɛN,AI with ɛN being a numerical prefactor and AI serving as a universal function.
Figure 2.
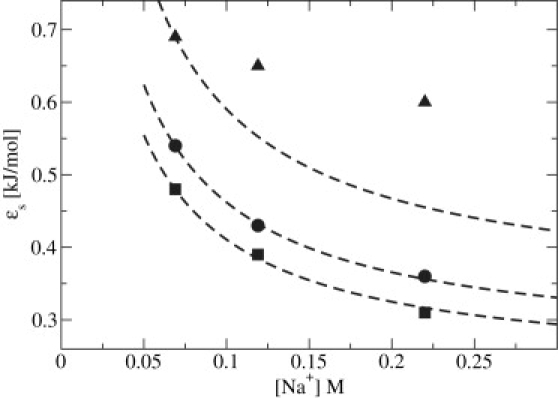
Study on combining the effects of chain length and ionic activity on the solvent-induced interaction. Data are presented for Nnt ∈ (10, triangles; 15, circles; and 20, squares). To obtain energy scale profiles for other systems, the reference system (Nnt = 15) AI is rescaled with respect to the energy strength ɛN of the corresponding chain length in [Na+] = 0.069 M (dashed lines). With the exception of the shortest chain studied, the approximation ɛs ≈ ɛNAI holds, with ɛN being a numerical prefactor and AI serving as a universal curve.
The set of parameters that enter into the 3SPN.1 force field is summarized in Table 1. Details pertaining to the molecular geometry of the model and additional constraints used in the original formulation can be found elsewhere (20). (We once again alert the reader that an entry from Table III in Knotts et al. (20) was unintentionally omitted, and that the missing entry is the dihedral angle S(3′)-P-(5′)S-Gb, with a value of 50.66°.) In the remainder of this work, we review the methods used to parameterize the model, followed by a presentation of results and a brief discussion.
Table 1.
Force-field parameters
| Parameter | Value | Units |
|---|---|---|
| ɛ | 0.769856 | kJ·mol−1 |
| ɛAT | 2.000ɛ | kJ·mol−1 |
| ɛCG | 2.532ɛ | kJ·mol−1 |
| ɛs | System-dependent | kJ·mol−1 |
| k1 | ɛ | kJ·mol−1·Å−2 |
| k2 | 100ɛ | kJ·mol−1·Å−4 |
| kθ | 1400ɛ | kJ·mol−1·rad−2 |
| kϕ | 28ɛ | kJ·mol−1 |
| α−1 | 5.333 | Å |
| rs | 13.38 | Å |
| σij | Pair-dependent | Å |
| σAT | 2.9002 | Å |
| σCG | 2.8694 | Å |
| σ0 (mismatch) | 1.00·2−1/6 | Å |
| σ0 (otherwise) | 6.86·2−1/6 | Å |
Problem of Focus and Methods
Denaturation in DNA is a reversible process. Duplexed DNA dissociates into ssDNA when interstrand hydrogen bonds break and base-stacking interactions are destabilized. This process can be induced by applying heat, or by altering solvent conditions. A key system variable in applications dealing with the handling of DNA is the denaturation or melting temperature, Tm, defined as the temperature when half of the basepairs have dissociated (opened) in dsDNA. In general, Tm depends on several factors, including chain length, base composition (through base-stacking and hydrogen-bonding interactions), topological conditions, and buffer composition (ionic strength and pH). In the case of heat-induced denaturation, ssDNA can be renatured into dsDNA by annealing the system, with a maximal rate attained at ∼25 K below Tm (49), provided solvent conditions are appropriate. Several physical changes occur when DNA denatures, including a hyperchromic response at a wavelength of 260 nm, an increase in the buoyant density, a decrease in the viscosity of the system, and an increased negative optical rotation of the solution. Theoretical and numerical studies have concluded that DNA denaturation is a first-order phase transition (50,51).
The chemistry of DNA is relatively extensive, and parameterization of any coarse-grain force field can be relatively involved. In this work, we parameterize the 3SPN.1 force field with respect to the following four aspects of DNA behavior: 1), CG content; 2), chain length; 3), ionic activity; and 4), intramolecular interactions. The first three aspects were treated by introducing adjustments to the 3SPN.0 force field, while the last item was addressed with the inclusion of a novel, solvent-induced interaction. Intramolecular interactions (bends and torsions) have been adjusted to improve agreement with the experimentally observed persistence length of DNA. Model parameterization is performed in the context of denaturation temperatures for a set of short B-form oligonucleotides (of varying fraction of CG content, fCG, chain length, Nnt, and ionic strength, [Na+]) using data from Owczarzy et al. (34,52). These systems are listed in Table 2. The method employed in this study is replica exchange molecular dynamics (REMD). Langevin dynamics (LD) simulations have been employed to effectively map simulation time to real time. Persistence length calculations have been carried out to test the ability of the 3SPN.1 force field to capture mechanical properties of DNA. (For these studies, DNA sequences of enterobacteria phage-λ have been used, the identities of which are specified later in Table 5.) In the remainder of this work, we discuss each of the techniques used in our study, followed by results and comments.
Table 2.
Series of short oligonucleotides
| Nnt | fCG | Sequence (5′to3′)∗ |
|---|---|---|
| 10 | 0.2 | ATC AAT CAT A |
| 15 | 0.2 | TAC TAA CAT TAA CTA |
| 15 | 0.4 | AGT AGT AAT CAC ACC |
| 15 | 0.6 | CGC CTC ATG CTC ATC |
| 15 | 0.8 | GCG TCG GTC CGG GCT |
| 20 | 0.2 | TAT GTA TAT TTT GTA ATC AG |
| 30 | 0.2 | TTA TGT ATT AAG TTA TAT AGT AGT AGT AGT |
Empirical data from Owczarzy et al. (52).
Table 5.
Persistence length determinations
| Nnt | fCG | 5′-Base | 3′-Base | [Na+] M | lpss [nm] | lpds [nm] |
|---|---|---|---|---|---|---|
| 68 | 0.529 | 43826 | 43893 | 0.150 | 12 ± 1 | — |
| 144 | 0.528 | 577 | 720 | 0.150 | 11 ± 1 | 42 ± 4 |
| 250 | 0.472 | 31157 | 31406 | 0.005 | — | 93 ± 5 |
| 0.010 | — | 68 ± 4 | ||||
| 0.025 | — | 53 ± 3 | ||||
| 0.050 | — | 45 ± 6 | ||||
| 0.100 | — | 40 ± 2 | ||||
| 0.150 | 12 ± 3 | 45 ± 6 | ||||
| 538 | 0.541 | 18668 | 19205 | 0.150 | — | 52 ± 2 |
| 1144 | 0.575 | 2474 | 3617 | 0.150 | — | 56 ± 2 |
Replica exchange simulations
As mentioned above, the denaturation temperature Tm of DNA is determined through replica exchange molecular dynamics (REMD) simulations in temperature. In the context of our work, we take advantage of the canonical ensemble data that are borne out of the calculation to determine the number of basepair contacts that dissociate as a continuous function of temperature, using the weighted histogram analysis method (WHAM) (53). These results are then used to obtain the melting curve, from which Tm can be calculated.
Our REMD is set up following the scheme of Rathore et al. (54). First, for a given system, a range of temperatures is selected to yield fully renatured and denatured DNA (roughly encompassing 180 K ≲ T ≲ 480 K), where replicas (seven to eight, in our case) are assigned within that range. Relatively short runs are performed on these samples to determine the average potential energy and its second moment at the temperature of each replica, subsequently interpolating between temperatures using WHAM. Then, using Eq. 15 of Rathore et al. (54), temperature allocation is determined for the replicas, taking care to allow Tm to be roughly at the middle of the range. Each replica is spaced such that the exchange acceptance ratio between neighboring replicas is ∼0.30, which corresponds to a value of
| (16) |
In this expression, 〈U(Ti)〉 is the average value of the potential energy at the temperature of the ith replica, and 〈ΔU(Ti)2〉1/2 is the corresponding standard deviation.
To implement the REMD simulation, an equilibrated configuration is placed in each replica, ensuring that the configuration corresponds to the system conditions of the ith replica. Each replica is then evolved independently and simultaneously at the corresponding temperature Ti. An exchange between adjacent replicas is proposed on a timescale sufficiently long for the thermostat to stabilize the system to sample a new set of conditions (55). When an exchange is proposed, momenta are uniformly rescaled according to the scheme described in Sugita et al. (56) and Nymeyer et al. (57). An attempt to exchange configurations {rγ} and {rδ} between neighboring replicas i and j, respectively, is accepted according to Metropolis acceptance criteria, given by
| (17) |
where
| (18) |
with βi = (kBTi)−1. Note that this form of the acceptance criteria differs slightly from standard REMD methods in that the potential energy of the exchanged coordinates must be evaluated during a proposed exchange (56). This is needed since the potential energy function across different replicas varies due to the temperature-dependent dielectric constant (see Eq. 7). By following the velocity rescaling approach in Sugita and Okamoto (58), kinetic energy contributions in the acceptance criteria based on the Hamiltonian of the system cancel out, thus recovering the one used in standard Monte Carlo (MC) schemes. This arrangement allows one to sample canonical ensemble distributions from REMD simulations (56).
At the conclusion of the REMD simulation, data from each replica are collected and analyzed with WHAM (53). The main result of this calculation is the density of states for the system determined through an iterative procedure. The density of states is then used to determine the expectation value of the fraction of dissociated interstrand basepairs, (1 − Φ), as a continuous function of temperature to obtain the melting curve, and ultimately, Tm.
Real-time mapping
In any coarse-graining approach, the replacement of atoms with effective sites reduces the number of degrees of freedom present in the original system. This leads to an averaging of timescales that must be mapped to account for the loss of frictional forces present in the atomistic representation. One way of addressing this issue is by taking empirical observations of the molecular (self) diffusion coefficient Ds, and finding the correspondence between simulation time and real time with the use of Langevin dynamics (LD) simulations.
The formulation of the LD scheme for mapping time requires a definition for the force acting on the ith particle, positioned at a point r, which reads
| (19) |
In Eq. 19, fi(r) is the total force acting on the particle, −∇Ui(r) is the force arising from the force field, γi is a damping constant (in units of reciprocal time), pi(t) is the momentum of the particle, and gi(t) represents a random force. The random force satisfies the conditions
| (20) |
and
| (21) |
where mi is the mass of the ith particle. Diffusivity data enter the LD formalism through γi. Starting with the Einstein relation,
| (22) |
a molecular friction coefficient ξs is determined and distributed equally among all coarse-grain sites N, such that
| (23) |
where ξi is the friction coefficient of the ith coarse-grain site. The development presented above permits calculation of a mass-independent friction coefficient for the ith bead, which corresponds a chemical moiety in DNA. Although this approach provides the correct molecular translational diffusion of DNA, the implicit-solvent approach used is not designed to capture faster local intramolecular dynamics. The motivation here to focus on molecular diffusivity is that it corresponds to one of the slower modes of motion of DNA (59). The damping constant per bead is then simply γi = ξi/mi, thereby providing a connection between the LD scheme and diffusivity data. In our calculations, we have implemented Eq. 19 using the propagator developed by Bussi and Parinello (60) for LD, which is implemented here as a velocity Verlet integrator.
Once a trajectory has been obtained from an LD simulation, the mean-square displacement can be computed as 〈Δr2(t)〉 = 〈|r(t) − r(0)|2〉, where r(0) is the center-of-mass coordinate of the molecule at t = 0. At sufficiently long times, the mean-square displacement scales linearly with time, yielding Fickian diffusion,
| (24) |
Under these conditions, suitable values of 〈Δr2(t)〉 can be extracted from the mean-square displacement curve and a relationship between simulation time and real time can be established using the experimental data for Ds and the time step used to integrate the equation of motion.
Persistence length
One of the several aims of our coarse-grain model for DNA is to reproduce mechanical properties, such as molecular rigidity, quantified in our study through the persistence length. From experiments, it is known that the persistence length for dsDNA is lpds ∼ 50 nm (61), whereas that of ssDNA is lpss ∼ 2 nm (62,63). To capture these length scales, long oligonucleotide sequences from the enterobacteria phage-λ genome were simulated with an LD integrator. Although several definitions exist for the persistence length (64), it is calculated here through the orientational correlation function,
| (25) |
This choice is motivated by the fact that our simulation data obey an exponential decay, as shown below, and the fact that it is often used to reduce empirical data, thereby enabling us to make direct contact with experiments. In Eq. 25, the path of the chain is parameterized by the position along the chain s; is the unit tangent vector to the chain at s. In the limit in which s is defined continuously, this expression recovers the correlation function of the wormlike chain model (65), which has been used in a number of studies to describe DNA mechanical and statistical properties (66). In the context of DNA, the path s is defined by the set of chain segments between distinct interaction sites where DNA undergoes a complete helical turn, i.e., all intrastrand sugar sites located ten nucleotide units away from a reference sugar site (20). By defining units in this manner, the inherent twist of the DNA backbone is averaged out while the net variation in the molecular orientation is captured.
The persistence length in DNA exhibits a dependence on the ionic strength of the solution. Although it is usually understood that DNA becomes more flexible with increasing salt concentration (due to an enhanced shielding of repulsive phosphate-phosphate interactions), the issue of whether to attribute the stiffness to electrostatics alone has not been fully resolved (67). A reasonable representation for the dependence of persistence length on ionic strength is attained by using the nonlinear Poisson-Boltzmann theory for uniformly charged cylinders (68),
| (26) |
where the total persistence length is taken as the sum of a nonelectrostatic length scale lp0 and an electrostatic length scale lpe. The electrostatic contribution is accounted for by the Debye length, λD, and the Bjerrum length,
| (27) |
where the relevant variables have been defined in Eq. 10. This treatment has been shown to describe experimental data for the dependence of DNA flexibility on ionic strength (61).
Persistence length calculations are demanding: long chains are required to capture the equilibrium mechanical behavior of molecules for multiple persistence lengths and the corresponding relaxation times are necessarily long. In an effort to address these difficulties, a trajectory was additionally subjected to MC pivot moves (69) in a hybrid MC/LD scheme (70). Pivot moves allow the system to undergo global molecular rearrangements in a relatively short amount of time. Upon selecting a backbone bead (a sugar or phosphate moiety) at random to serve as a pivoting site, a chain segment is defined to extend from this chosen site to either the 5′– or 3′–end of DNA with equal probability. The segment is then rotated clockwise or counterclockwise by an angle about one of the three space-fixed axes chosen at random. Post-move coordinates are generated with the direction cosine method and the angular momentum of the system is reset to zero. The move is accepted according to Metropolis acceptance criteria,
| (28) |
where ΔU = Uj − Ui denotes the difference in potential energy between the final j and initial i configurations, respectively. The hybrid scheme above is used to determine the persistence length of the proposed model of DNA as a function of Nnt and [Na+].
Results and Discussion
Here we present results for the techniques developed in the previous section. First, we discuss our REMD results for short oligonucleotides. We then address the dynamics of the model and the mapping between real and simulated time. Finally, we present results for the persistence length of DNA in the context of long sequences obtained from the genome of enterobacteria phage-λ.
Replica exchange simulations
Systems considered in the parameterization of the model are listed in Table 2; these are expressed in terms of chain length, Nnt, and fraction of CG content, fCG. A four-chain Nosé-Hoover thermostat with an integration time step of 5 fs was used in all REMD simulations. An equilibration period of ∼2.5 ns was followed by production runs consisting of 50–200 ns, depending on chain length. Exchanges between adjacent replicas were attempted every 50–100 ps. The corresponding melting temperatures, Tm, determined from WHAM as a function of [Na+] are presented in Table 3. Data were pooled from 10 independent realizations. As mentioned earlier, Tm is defined as the point when the fraction of denatured interstrand basepairs, (1 − Φ), is one-half, as determined from melting curves (see below). In Fig. 3 A, a linear regression analysis of Tm as a function of fCG is provided for the Nnt = 15 system in [Na+] = 0.069 M. As can be seen, there is good agreement between results of simulations and experimental data. In Fig. 3 B, a comparison between Tm and the effect of increasing ionic strength is given, where reasonable agreement between simulation and experiment is also observed.
Table 3.
Results for Tm from REMD for the series of short oligonucleotides
| Nnt | fCG | M[Na+] | Tm, obs∗ | Tm, sim |
|---|---|---|---|---|
| 10 | 0.2 | 0.069 | 294.4 | 296 ± 1 |
| 0.119 | 297.6 | 298 ± 3 | ||
| 0.220 | 301.0 | 301 ± 2 | ||
| 15 | 0.2 | 0.069 | 308.4 | 309 ± 2 |
| 0.119 | 313.6 | 313 ± 3 | ||
| 0.220 | 317.2 | 318 ± 3 | ||
| 0.621 | 322.4 | 320 ± 3 | ||
| 1.020 | 324.2 | 324 ± 2 | ||
| 0.4 | 0.069 | 317.4 | 317 ± 2 | |
| 0.6 | 0.069 | 326.0 | 325 ± 3 | |
| 0.8 | 0.069 | 338.0 | 340 ± 3 | |
| 20 | 0.2 | 0.069 | 317.6 | 316 ± 3 |
| 0.119 | 320.8 | 322 ± 3 | ||
| 0.220 | 325.8 | 324 ± 3 | ||
| 30 | 0.2 | 0.069 | 323.8 | 324 ± 4 |
Empirical data from Owczarzy et al. (52).
Figure 3.
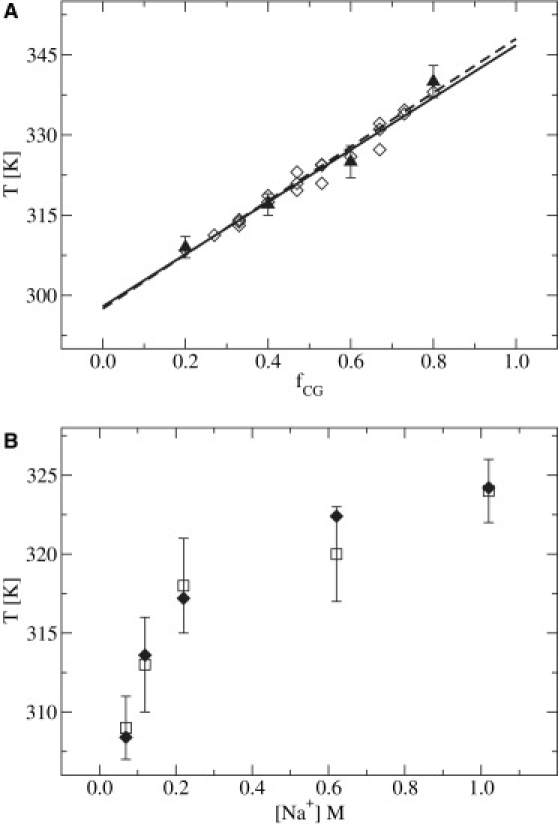
Comparison of REMD results with experimental data. (A) Tm as a function of chain composition for Nnt = 15 in [Na+] = 0.069 M for the systems studied in Table 2 (triangles, dotted line) and data from Owczarzy et al. (52) (diamonds, solid line), where lines are the corresponding linear regressions. (B) Tm as a function of [Na+] for Nnt = 15 and fCG = 0.2.
To ensure that the REMD scheme is, effectively, sampling energy regions in the vicinity of the phase transition, we examined closely the trajectory that each molecule follows in temperature space. In Fig. 4, we present a typical set of replicas from one realization. As can be seen in that figure, each molecule displays at least one denaturation or renaturation event. Moreover, there is a strong correlation between temperature and the fraction of denatured bases; as T increases, so does (1 − Φ). Note that, from the outset, replicas were spaced in temperature such that the acceptance ratio would be ∼0.30. The percentages of accepted exchanges between neighboring replicas, presented in Table 4, are consistent with our constraints.
Figure 4.
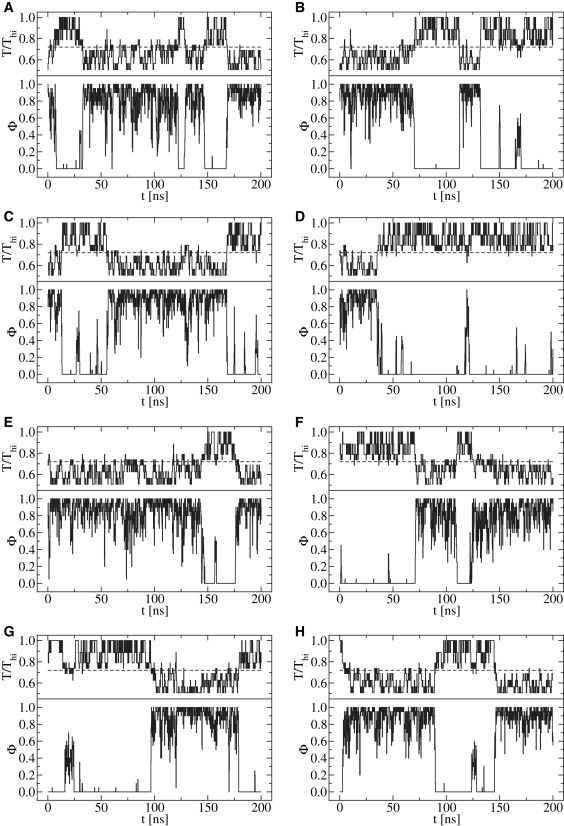
Representative molecular trajectories in T-space obtained from REMD simulation. The eight replicas used in the realization are shown for Nnt = 20 in [Na+] = 0.220 M. In each panel, the upper portion is T normalized by the highest replica temperature, Thi. For reference, Tm is also shown (dashed line). The lower portion of each panel shows the corresponding value of Φ.
Table 4.
Acceptance ratio between neighboring replicas for Nnt = 20 in [Na+] = 0.220 M
| Ti ↔ Ti+1 [K] | Acceptance ratio |
|---|---|
| 224.1 ↔ 248.8 | 0.274 |
| 248.8 ↔ 275.9 | 0.268 |
| 275.9 ↔ 303.8 | 0.295 |
| 303.8 ↔ 325.8 | 0.255 |
| 325.8 ↔ 348.4 | 0.336 |
| 348.4 ↔ 391.4 | 0.254 |
| 391.4 ↔ 441.2 | 0.272 |
In nucleic acids, base-stacking interactions promote the extension of an existing duplex tract rather than the formation of a new one (71), which leads to a cooperative response when the system is subjected to a perturbation. More specifically, cooperativity (a local effect) is expected to sharpen the denaturation transition (a global effect). Depicted in Fig. 5 A are melting curves for three systems of increasing chain length, but otherwise prepared under identical conditions. Shown in Fig. 5 B are the corresponding isochoric heat capacities, Cv, for each system. Profile widths and magnitudes of heat capacities are consistent with experiments (72,73). Although some discrepancy is expected because coarse-grain models which implicitly account for many-body effects tend to underestimate transition barriers (74,75), the process of reversible denaturation is captured well. For instance, the model exhibits a sharper transition for a larger DNA chain (Nnt = 30) when compared to that of smaller molecules (Nnt = 10,20). This signature is one of cooperativity, and has been observed experimentally in denaturation studies traced with UV absorption, optical rotation, or force-extension studies (71). Moreover, the maximal response in Cv can be inferred from bimodal energy distributions in REMD data for Tm, as shown in Fig. 5 C.
Figure 5.
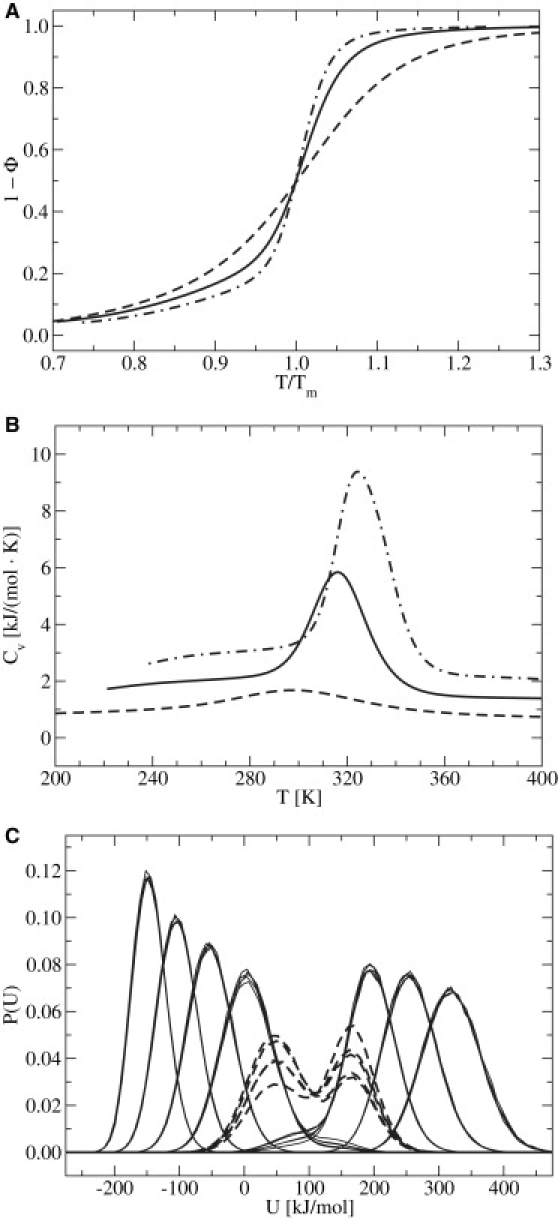
DNA denaturation becomes cooperative with increasing chain length, as evidenced by a sharper response in the transition. (A) (1 − Φ) as a function of T normalized with respect to Tm. (B) Cv as a function of T. Data are for Nnt ∈ (10, dashed line; 20, solid line; and 30, dot-dashed line), for fCG = 0.2 in [Na+] = 0.069 M. (C) Probability distributions of energy from five of ten realizations for the Nnt = 20 system. (From left to right, T = 220, 247, 272, 298, 316, 338, 378, and 408 K.) At Tm = 316 K, the system exhibits an evident bimodal probability distribution (dashed curves).
As an independent measure of our REMD-WHAM estimates of Tm, we also performed simple LD simulations on select DNA systems. In particular, Fig. 6 shows results for the Nnt = 15 system with fCG = 0.4 in [Na+] = 0.069 M. Greater than 100 independent realizations were simulated for each of the three selected temperatures, namely 301 K (small extent of denaturation), 317 K (at the transition), and 333 K (large extent of denaturation). From these calculations, we determined (1 − Φ) and made comparisons with the results from the REMD calculation. Within the statistical uncertainty of our simulations, the agreement between the REMD melting curve and straight LD simulations is satisfactory.
Figure 6.
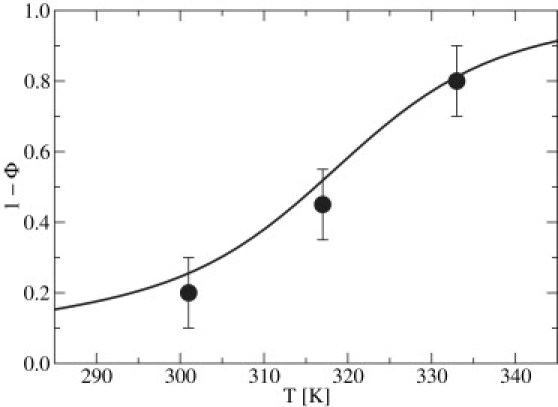
Assessing data from the melting curve obtained by REMD. The Nnt = 15 system with fCG = 0.4 in [Na+] = 0.069 M was used as a representative case. Shown are data from >100 independent realizations using LD (circles) with corresponding error bars, and data from REMD treated with WHAM (line).
After having parameterized the 3SPN.1 force field for a mesoscale model capable of describing melting in DNA, it is of interest to examine in some detail the molecular process of renaturation. Shown in Figs. 7 and 8 is a sequence of configurations corresponding to a renaturation event, wherein a molecule starts in high-temperature space and ends up sampling regions of low-temperature space. In the renaturation event, it is observed that the initial encounter may not be optimal to promote complete reassociation (e.g., DNA strands might exhibit a perpendicular orientation with one another). As solvent-induced attractions and repulsive electrostatic interactions arising from phosphate sites promote jostling between DNA strands, complete molecular reorientation is facilitated, at which point partial molecular recognition sets in (i.e., a nucleation step). Subsequently, renaturation proceeds rapidly so long as the temperature of the system is sufficiently low to yield duplexed DNA.
Figure 7.
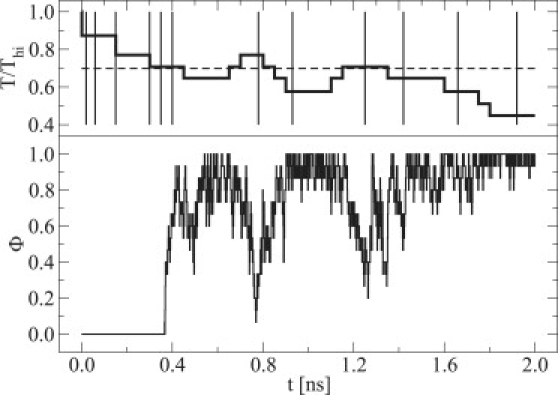
Time series data for a renaturation event in DNA. The Nnt = 15 system with fCG = 0.2 in [Na+] = 0.119 M was used as a representative case. Shown in the upper portion of the panel are selected instances (vertical lines) of T (thick line) for the analysis of the renaturation event; for reference, Tm is also shown (dashed line). The corresponding value of Φ in the time series is shown in the lower portion of the panel.
Figure 8.
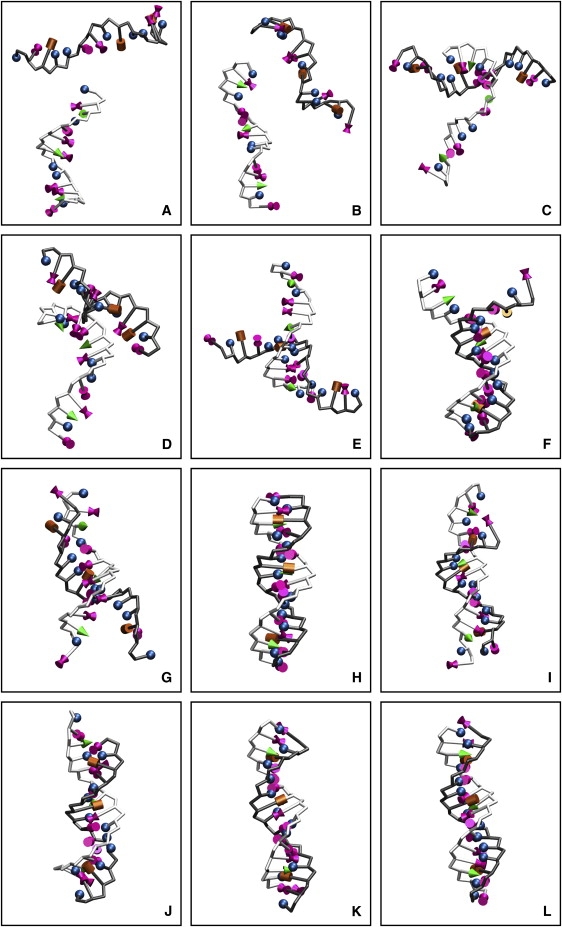
Configurations for the instances specified in Fig. 7. The backbone of each strand has been shaded differently and nucleic base moieties have been depicted as shapes as a guide to the eye. The sense strand (lighter chain) is shown with its complement (darker chain), with the nucleic bases adenine (bowtie), thymine (sphere), cytosine (cone), and guanine (cylinder). The instances selected in T-space from Fig. 7 are referenced from left to right as A–L. Initially, ssDNA molecules are found at a significant separation (A and B). As the system samples lower T, the formation of dsDNA is favored. The process first emerges with chains approaching closely (C and D), until a nucleation event sets in panels E–G, such that strands can associate to yield dsDNA (H). When the system transiently samples higher T, dsDNA is destabilized (I and J). As the system returns to lower T, dsDNA emerges again (K and L).
The mechanism borne from our model is consistent with the understanding extracted from experiments. In general, renaturation is believed to involve two main steps: the initial formation of a nucleation complex (the rate-limiting step of a second-order kinetic reaction) (49) followed by a fast zippering stage that accomplishes full complementarity (59). Moreover, it is currently thought that the initial association complex is unstable, tending to completely seal or dissociate depending on the system temperature (59). Several experimental studies can be found in the literature that support the second-order kinetics mechanism (76).
We comment that a limitation in our current parameterization concerns the treatment of long, highly repetitive (homogeneous) sequences of DNA, such as 5′–[AT]n–3′ or 5′–[A]2n–3′, and the corresponding CG sequences. A brief study on these systems indicates that the force field tends to overestimate the denaturation temperature. This effect is presumably caused by the regularity of the sequence such that a radial, isotropic potential is too permissive to account for the stringent directional requirements involved in hydrogen bonding. The sequences chosen for the parameterization have been relatively heterogeneous, and the potential we have arrived at captures melting effects rather well. The proposed force field is thus likely to perform well in most cases of biological interest, where short homogeneous sequences are flanked by heterogeneous segments. Under these circumstances, an interplay between base mismatches offsets the permissive nature of hydrogen-bonding interactions to the extent that thermal effects can be described accurately. However, to treat highly regular sequences of DNA would require an adjustment of energy strengths for basepairing, or the inclusion of angular dependence in Ubase at the expense of computational expediency.
Real-time mapping
To map simulation time to real time, we have used the experimental measurements of Eimer and Pecora (77) for the 20-basepair oligonucleotide,
| (29) |
performed in a phosphate buffer with [Na+] = 0.100 M. This system is characterized by Ds = 1.086 × 10−10 m2 s−1 at room temperature. We obtained an estimate of ξi from Eq. 23 by mapping the DNA system to the corresponding N = 118 beads of our model. Using this value of ξi to compute the respective damping constants entering into Eq. 19, we then evolved the system. The LD integrator was tested with several time steps by performing the corresponding time-mapping. From these studies, it was determined that the maximum time step that can be used, while allowing the system to remain stable, corresponds to ∼30 fs, representing a significant gain in comparison to atomistic computations, which typically require a time step of 1 fs. The variation of the Hamiltonian (Fig. 9 A) and the root mean-square deviation (Fig. 9 B) are used as stability indicators for the integrator at different time steps.
Figure 9.
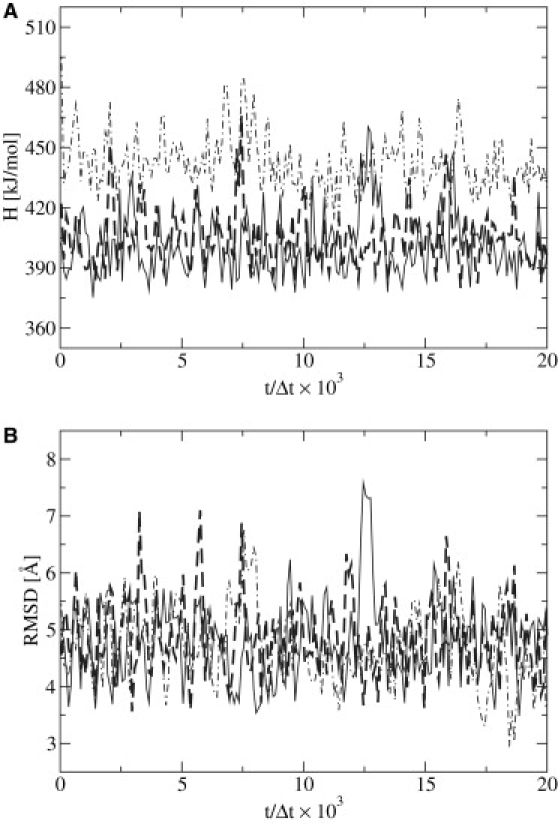
Stability of the LD integrator. (A) Hamiltonian (H) of the system. (B) Root mean-square deviation (RMSD) of configurations. Data are presented as a function of time t normalized by the simulation time step Δt ∈ (5 fs, solid line; 10 fs, heavy dashed line; and 30 fs, dot-dashed line).
Although the calibration of the simulation time step requires diffusivity data for each system of interest (given that the friction coefficient will vary according to solvent conditions), extensions are possible under certain circumstances. Provided that solvent conditions are equivalent, oligonucleotides of identical length can be treated with the same diffusivity, since there appears to be no sequence dependence provided a rodlike conformation holds in solution (78). The rigid cylinder description of Tirado-Garcia de la Torre captures well the diffusivity for oligonucleotides of low aspect ratio in the dilute, high-salt regime (77). For other solvent conditions, the viscosity of the solvent, as it relates to the friction coefficient entering Eq. 22, must be taken into account. Temperature effects in aqueous solution can be accounted for through empirical relations as a first-order approximation (79). The effect of ionic strength can be considered through scaling laws that account for electrophoretic effects (80). Finally, in the infinitely dilute limit, a thermodynamic prefactor can be applied to Eq. 22, where the equivalence of mutual diffusion and self-diffusion holds (81).
Persistence length
Persistence length calculations were performed on a series of enterobacteria phage-λ excision fragments from a digest with the TaqI restriction enzyme. The systems considered in this work are characterized in terms of the CG content, fCG, and the basepair number range within the genome in Table 5, along with the results from computer simulations of the persistence length for ssDNA (lpss) and dsDNA (lpds). Simulations were performed with an LD integrator using a time step of Δt = 0.02 ps. Pivot moves were performed every 5 ps using the scheme previously described.
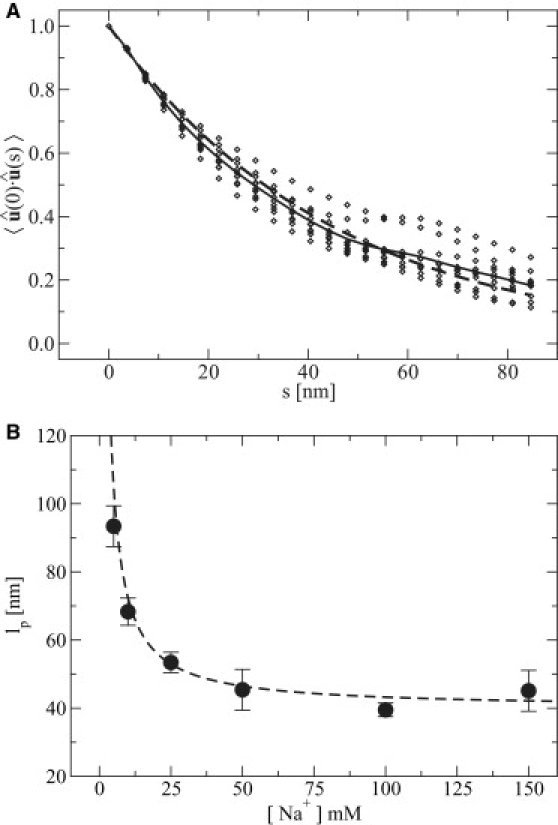
Empirically, dsDNA is observed to exhibit a persistence length lpds ∼ 50 nm at T = 300 K in [Na+] = 0.150 M (61). For these same conditions, our model yields 45 nm ≲ lpds ≲ 56 nm, which is in reasonable agreement with experiments. A representative set of data used to determine lpds is shown in Fig. 10 A, where a spread in the exponential decay of spatial correlations is evident, as has been previously observed (20,61). Chain lengths of Nnt = 144, 250, 538, and 1144 were used for our analysis of dsDNA.
Figure 10.
Persistence length calculations. (A) Plot of the orientational correlation function as a function of chain position, s, for Nnt = 250 dsDNA in [Na+] = 0.150 M. Data are shown for 10 independent realizations (diamonds), the average of the realizations (solid line), and the nonlinear regression of Eq. 25 (dashed line). (B) Effect of ionic strength on persistence length for Nnt = 250. Simulation data (circles) were fit according to Eq. 26, with lp0 = 40 nm (dashed line).
The model also captures qualitatively the trend that for ssDNA, the persistence length is shorter than that of dsDNA. From experiments, lpss ∼ 2 nm (62,63), whereas our present parameterization yields 11 nm ≲ lpss ≲ 12 nm for the same aforementioned experimental conditions of dsDNA. Chain lengths of Nnt = 68, 144, and 250 were used in our analysis of ssDNA.
To explore the ability of our model to capture the dependence of persistence length on ionic strength, a series of six simulations at T = 300 K for increasing salt concentration was used. The results are shown in Fig. 10 B. The data were fit after Eq. 26, with a bare persistence length of lp0 = 40 nm, a value consistent with our previous findings. Our model captures reasonably well the dependence that the persistence length has on ionic strength.
Summary
We have extended a coarse-grain model for DNA (20), to capture the helix-coil transition. The formulation represents each of the chemical moieties (sugar, phosphate, and nitrogenous base) as a united-atom interaction site, thereby resolving the nucleotide sequence of a given sample of DNA. Solvent is accounted for through an effective dielectric constant dependent on ionic activity and temperature, in which electrostatic interactions are treated at the level of Debye-Hückel theory. A novel component is a soft, solvent-induced attraction which partially brings about the single-to-double stranded transition. Physically, this contribution takes into account implicitly the presence of solvent degrees of freedom. Collectively, these extensions represent the 3SPN.1 force field.
The model has been parameterized as a function of chain length, chain composition, and ionic activity (with respect to NaCl) in aqueous solution. The solvent-induced interaction has been calibrated for varying conditions, the strength of which is found to approach an asymptotic value in the limit of large chains and of high-salt concentration. REMD simulations have been used to parameterize the model against empirical data. A mapping of timescales for our coarse-grain representation to real time has been accomplished with LD simulation and available experimental diffusivity data. The ability of the model to reproduce mechanical properties has also been tested in capturing the persistence length of ssDNA and dsDNA.
To our knowledge, the treatment presented in this work is the first of its kind to capture renaturation of ssDNA in the context of computer simulations. Since many biological and technological processes depend on controlling the topological conditions of DNA, this model should be useful in addressing problems related to the exploration of conditions that are meant to optimize the presentation of nucleic acids in a specific form. In addition, the modeling of biological processes is expected to be more realistic since information from the single-to-double stranded transition is built into the model. The computational advantage of this formulation is significant given that solvent and solution ions are accounted for in an implicit manner, while inherent electrostatic interactions between phosphate sites in DNA are still represented explicitly.
The 3SPN.1 force field has entailed parameterization to capture the reversible denaturation of DNA through REMD simulation. Future work along our line of research will include the determination of free energies associated with the phase transition of denaturation and the characterization of reaction kinetics through transition path sampling. In the realm of improving our implicit solvent model, an extension which takes explicit account of counterions and solution ions will also be accomplished. A thorough study relating our mesoscale formulation to that of molecular mechanics models of DNA will be undertaken, in an effort to describe the extent to which our construct captures sequence-specific information, such as that related to DNA regions where the flexibility of the double-helix is very different on a local scale. This problem is of great biological relevance in the context of DNA-protein association.
Acknowledgments
We are grateful to Thomas A. Knotts IV for addressing technical matters on the 3SPN.0 force field.
E.J.S. was supported by a National Human Genome Research Institute training grant to the Genomic Sciences Training Program (No. 5T32HG002760). D.C.S. was supported by a National Human Genome Research Institute grant (No. R01HG000225). This work was also supported by the National Science Foundation through the University of Wisconsin-Madison Nanoscale Science and Engineering Center.
References
- 1.Kornyshev A.A., Leiken S. Electrostatic interaction between helical macromolecules in aggregates: an impetus for DNA poly- and mesomorphism. Proc. Natl. Acad. Sci. USA. 1998;95:13579–13584. doi: 10.1073/pnas.95.23.13579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Solis F.J., Olvera de la Cruz M. Attractive interactions between rodlike polyelectrolytes: polarization, crystallization, and packing. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Topics. 1999;60:4496–4499. doi: 10.1103/physreve.60.4496. [DOI] [PubMed] [Google Scholar]
- 3.Lyubartsev A.P., Nordenskiöld L. Monte Carlo simulation study of DNA polyelectrolyte properties in the presence of multivalent polyamine ions. J. Phys. Chem. B. 1997;101:4335–4342. [Google Scholar]
- 4.Gil Montoro J.C., Abascal J.L.F. Ionic distribution around simple DNA models. I. Cylindrically averaged properties. J. Chem. Phys. 1995;103:8273–8284. [Google Scholar]
- 5.Schlick T., Olson W.K. Supercoiled DNA energetics and dynamics by computer simulation. J. Mol. Biol. 1992;223:1089–1119. doi: 10.1016/0022-2836(92)90263-j. [DOI] [PubMed] [Google Scholar]
- 6.Barkley M.D., Zimm B.H. Theory of twisting and bending of chain macromolecules—analysis of the fluorescence depolarization of DNA. J. Chem. Phys. 1979;70:2991–3007. [Google Scholar]
- 7.Jian H., Vologodskii A., Schlick T. A combined wormlike-chain and bead model for dynamic simulations of long linear DNA. J. Comput. Phys. 1997;136:168–179. [Google Scholar]
- 8.Chopra M., Larson R.G. Brownian dynamics simulations of isolated polymer molecules in shear flow near adsorbing and non-adsorbing surfaces. J. Rheol. 2002;46:831–862. [Google Scholar]
- 9.Jendrejack R.M., de Pablo J.J., Graham M.D. Stochastic simulations of DNA in flow: dynamics and the effects of hydrodynamic interactions. J. Chem. Phys. 2002;116:7752–7759. [Google Scholar]
- 10.Jendrejack R.M., Schwartz D.C., de Pablo J.J., Graham M.D. Shear-induced migration in flowing polymer solutions: simulation of long-chain DNA in microchannels. J. Chem. Phys. 2004;120:2513–2529. doi: 10.1063/1.1637331. [DOI] [PubMed] [Google Scholar]
- 11.Hur J.S., Shaqfeh E.S.G., Larson R.G. Brownian dynamics simulations of single DNA molecules in shear flow. J. Rheol. 2000;44:713–742. [Google Scholar]
- 12.Schroeder C.M., Teixiera R.E., Shaqfeh E.S.G., Chu S. Dynamics of DNA in the flow-gradient plane of steady shear flow: observations and simulations. Macromolecules. 2005;38:1967–1978. [Google Scholar]
- 13.Bruant N., Flatters D., Lavery R., Genest D. From atomic to mesoscopic descriptions of the internal dynamics of DNA. Biophys. J. 1999;77:2366–2376. doi: 10.1016/S0006-3495(99)77074-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Tepper H.L., Voth G.A. A coarse-grained model for double-helix molecules in solution: spontaneous helix formation and equilibrium properties. J. Chem. Phys. 2005;122:124906. doi: 10.1063/1.1869417. [DOI] [PubMed] [Google Scholar]
- 15.Tan R.K.Z., Harvey S.C. Molecular mechanics model of supercoiled DNA. J. Mol. Biol. 1989;205:573–591. doi: 10.1016/0022-2836(89)90227-1. [DOI] [PubMed] [Google Scholar]
- 16.El Hassan M.A., Calladine C.R. The assessment of the geometry of dinucleotide steps in double-helical DNA—a new local calculation scheme. J. Mol. Biol. 1995;251:648–664. doi: 10.1006/jmbi.1995.0462. [DOI] [PubMed] [Google Scholar]
- 17.Drukker K., Schatz G.C. A model for simulating dynamics of DNA denaturation. J. Phys. Chem. B. 2000;104:6108–6111. [Google Scholar]
- 18.Sales-Pardo M., Guimerà R., Moreira A.A., Widom J., Amaral L.A.N. Mesoscopic modeling for nucleic acid chain dynamics. Phys. Rev. E. 2005;71:051902. doi: 10.1103/PhysRevE.71.051902. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Maciejczyk M., Rudnicki W.R., Lesyng B. A mesoscopic model of nucleic acids. Part 2. An effective potential energy function for DNA. J. Biomol. Struct. Dyn. 2000;17:1109–1115. doi: 10.1080/07391102.2000.10506596. [DOI] [PubMed] [Google Scholar]
- 20.Knotts T.A., IV, Rathore N., Schwartz D.C., de Pablo J.J. A coarse grain model for DNA. J. Chem. Phys. 2007;126:084901. doi: 10.1063/1.2431804. [DOI] [PubMed] [Google Scholar]
- 21.Arnott S., Campbell Smith P.J., Chandrasekaran R. Atomic coordinates and molecular conformations for DNA-DNA, RNA-RNA and DNA-RNA helices. In: Fasman G.D., editor. 3rd Ed. Vol. 2. CRC Press; Cleveland, OH: 1975. (Handbook of Biochemistry and Molecular Biology: Nucleic Acids). [Google Scholar]
- 22.Hagan M.F., Dinner A.R., Chandler D., Chakraborty A.K. Atomistic understanding of kinetic pathways for single base-pair binding and unbinding in DNA. Proc. Natl. Acad. Sci. USA. 2003;100:13922–13927. doi: 10.1073/pnas.2036378100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Piana S. Atomistic simulations of the DNA helix-coil transition. J. Phys. Chem. A. 2007;111:12349–12354. doi: 10.1021/jp0756552. [DOI] [PubMed] [Google Scholar]
- 24.Perez A., Blas J.R., Rueda M., Lopez-Bes J.M., de la Cruz X. Exploring the essential dynamics of B-DNA. J. Chem. Theory Comput. 2005;1:790–800. doi: 10.1021/ct050051s. [DOI] [PubMed] [Google Scholar]
- 25.Perez A., Luque F.J., Orozco M. Dynamics of B-DNA on the microsecond time scale. J. Am. Chem. Soc. 2007;129:14739–14745. doi: 10.1021/ja0753546. [DOI] [PubMed] [Google Scholar]
- 26.Orozco M., Noy A., Perez A. Recent advances in the study of nucleic acid flexibility by molecular dynamics. Curr. Opin. Struct. Biol. 2008;18:185–193. doi: 10.1016/j.sbi.2008.01.005. [DOI] [PubMed] [Google Scholar]
- 27.Hoang T.X., Cieplak M. Molecular dynamics of folding of secondary structures in Gō-type models of proteins. J. Chem. Phys. 2000;112:6851–6862. [Google Scholar]
- 28.Schuster P., Wolschann P. Hydrogen bonding: from small clusters to biopolymers. Monatsh. Chem. 1999;130:947–960. [Google Scholar]
- 29.Legon A.C., Millen D.J. Directional character, strength, and nature of the hydrogen bond in gas-phase dimers. Acc. Chem. Res. 1987;20:39–45. [Google Scholar]
- 30.Derewenda Z.S., Lee L., Derewenda U. The occurrence of C=H⋯O hydrogen bonds in proteins. J. Mol. Biol. 1995;252:248–262. doi: 10.1006/jmbi.1995.0492. [DOI] [PubMed] [Google Scholar]
- 31.Horton R., Moran L.A., Scrimgeour K.G., Perry M.D., Rawn J.D. 4th Ed. Prentice Hall; Upper Saddle River, NJ: 2006. Principles of Biochemistry. [Google Scholar]
- 32.Breslauer K.J., Frank R., Blöcker H., Marky L.A. Predicting DNA duplex stability from the base sequence. Proc. Natl. Acad. Sci. USA. 1986;83:3746–3750. doi: 10.1073/pnas.83.11.3746. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.SantaLucia J., Jr. A unified view of polymer, dumbbell, and oligonucleotide DNA nearest-neighbor thermodynamics. Proc. Natl. Acad. Sci. USA. 1998;95:1460–1465. doi: 10.1073/pnas.95.4.1460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Owczarzy R., Vallone P.M., Gallo F.J., Paner T.M., Lane M.J. Predicting sequence-dependent melting stability of short duplex DNA oligomers. Biopolymers. 1997;44:217–239. doi: 10.1002/(SICI)1097-0282(1997)44:3<217::AID-BIP3>3.0.CO;2-Y. [DOI] [PubMed] [Google Scholar]
- 35.Stogryn A. Equations for calculating the dielectric constant of saline water. IEEE Trans. Microw. Theory Tech. 1971;19:733–736. [Google Scholar]
- 36.Curtis H.L., Defandorf F.M. Dielectric constant and dielectric strength of elementary pure inorganic compounds and air. In: Washburn E.W., editor. International Critical Tables of Numerical Data, Physics, Chemistry and Technology. McGraw-Hill; New York: 1926. [Google Scholar]
- 37.Fernández D.P., Goodwin A.R.H., Lemmon E.W., Sengers J.M.H.L., Williams R.C. A formulation for the static permittivity of water and steam at temperatures from 238 K to 873 K at pressures up to 1200 MPa, including derivatives and Debye-Hückel coefficients. J. Phys. Chem. Ref. Data. 1997;26:1125–1166. [Google Scholar]
- 38.Catenaccio A., Daruich Y., Magallanes C. Temperature dependence of the permittivity of water. Chem. Phys. Lett. 2003;367:669–671. [Google Scholar]
- 39.Rau D.C., Parsegian V.A. Direct measurement of the intermolecular forces between counterion-condensed DNA double helices: evidence for long range attractive hydration forces. Biophys. J. 1992;61:246–259. doi: 10.1016/S0006-3495(92)81831-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Rau D.C., Parsegian V.A. Direct measurement of temperature-dependent solvation forces between DNA double helices. Biophys. J. 1992;61:260–271. doi: 10.1016/S0006-3495(92)81832-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Qiu X., Kwok L.W., Park H.Y., Lamb J.S., Andersen K. Measuring inter-DNA potentials in solution. Phys Rev. Lett. 2006;96:138101. doi: 10.1103/PhysRevLett.96.138101. [DOI] [PubMed] [Google Scholar]
- 42.Raspaud E., Olvera de la Cruz M., Sikorav J.-L., Livolant F. Precipitation of DNA by polyamines: a polyelectrolyte behavior. Biophys. J. 1998;74:381–393. doi: 10.1016/S0006-3495(98)77795-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Allahyarov E., Löwen H. Effective interaction between helical biomolecules. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Topics. 2000;62:5542–5556. doi: 10.1103/physreve.62.5542. [DOI] [PubMed] [Google Scholar]
- 44.Allahyarov E., Gompper G., Löwen H. Attraction between DNA molecules mediated by multivalent ions. Phys Rev. E. 2004;69:041904. doi: 10.1103/PhysRevE.69.041904. [DOI] [PubMed] [Google Scholar]
- 45.Ha B.-Y., Liu A.J. Charge oscillations and many-body effects in bundles of like-charged rods. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Topics. 1998;58:6281–6286. doi: 10.1103/physreve.60.803. [DOI] [PubMed] [Google Scholar]
- 46.Ha B.-Y., Liu A.J. Counterion-mediated, non-pairwise-additive attractions in bundles of like-charged rods. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Topics. 1999;60:803–813. doi: 10.1103/physreve.60.803. [DOI] [PubMed] [Google Scholar]
- 47.Rouzina I., Bloomfield V.A. Macroion attraction due to electrostatic correlation between screening counterions. 1. Mobile surface-adsorbed ions and diffuse ion cloud. J. Phys. Chem. 1996;100:9977–9989. [Google Scholar]
- 48.Chocholousova J., Feig M. Implicit solvent simulations of DNA and DNA-protein complexes: agreement with explicit solvent vs experiment. J. Phys. Chem. B. 2006;110:17240–17251. doi: 10.1021/jp0627675. [DOI] [PubMed] [Google Scholar]
- 49.Anderson M.L.M. Bios Scientific; Oxford, United Kingdom: 1999. Nucleic Acid Hybridization. [Google Scholar]
- 50.Carlon E., Orlandini E., Stella A.L. Roles of stiffness and excluded volume in DNA denaturation. Phys. Rev. Lett. 2002;88:198101. doi: 10.1103/PhysRevLett.88.198101. [DOI] [PubMed] [Google Scholar]
- 51.Kafri Y., Mukamel D., Peliti L. Why is the DNA denaturation transition first order? Phys. Rev. Lett. 2000;85:4988–4991. doi: 10.1103/PhysRevLett.85.4988. [DOI] [PubMed] [Google Scholar]
- 52.Owczarzy R., You Y., Moreira B.G., Manthey J.A., Huang L. Effects of sodium ions on DNA duplex oligomers: improved predictions of melting temperatures. Biochemistry. 2004;43:3537–3554. doi: 10.1021/bi034621r. [DOI] [PubMed] [Google Scholar]
- 53.Chodera J.D., Swope W.C., Pitera J.W., Seok C., Dill K.A. Use of the Weighted Histogram Analysis Method for the analysis of simulated and parallel tempering simulations. J. Chem. Theory Comput. 2007;3:26–41. doi: 10.1021/ct0502864. [DOI] [PubMed] [Google Scholar]
- 54.Rathore N., Chopra M., de Pablo J.J. Optimal allocation of replicas in parallel tempering simulations. J. Chem. Phys. 2005;122:024111. doi: 10.1063/1.1831273. [DOI] [PubMed] [Google Scholar]
- 55.Abraham M.J., Gready J.E. Ensuring mixing efficiency of replica-exchange molecular dynamics simulations. J. Chem. Theory Comput. 2008;4:1119–1128. doi: 10.1021/ct800016r. [DOI] [PubMed] [Google Scholar]
- 56.Sugita Y., Kitao A., Okamoto Y. Multidimensional replica-exchange method for free-energy calculations. J. Chem. Phys. 2000;113:6042–6051. [Google Scholar]
- 57.Nymeyer H., Gnanakaran S., García A.E. Atomic simulations of protein folding, using the replica exchange algorithm. Methods Enzymol. 2004;383:119–149. doi: 10.1016/S0076-6879(04)83006-4. [DOI] [PubMed] [Google Scholar]
- 58.Sugita Y., Okamoto Y. Replica-exchange molecular dynamics method for protein folding. Chem. Phys. Lett. 1999;314:141–151. [Google Scholar]
- 59.Wetmur J.G., Davidson N. Kinetics of renaturation of DNA. J. Mol. Biol. 1968;31:349–370. doi: 10.1016/0022-2836(68)90414-2. [DOI] [PubMed] [Google Scholar]
- 60.Bussi G., Parrinello M. Accurate sampling using Langevin dynamics. Phys. Rev. E. 2007;75:056707. doi: 10.1103/PhysRevE.75.056707. [DOI] [PubMed] [Google Scholar]
- 61.Baumann C.G., Smith S.B., Bloomfield V.A., Bustamante C. Ionic effects on the elasticity of single DNA molecules. Proc. Natl. Acad. Sci. USA. 1997;94:6185–6190. doi: 10.1073/pnas.94.12.6185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Smith S.B., Cui Y., Bustamante C. Overstretching B-DNA: the elastic response of individual double-stranded and single-stranded DNA molecules. Science. 1996;271:795–799. doi: 10.1126/science.271.5250.795. [DOI] [PubMed] [Google Scholar]
- 63.Murphy M.C., Rasnik I., Cheng W., Lohman T.M., Ha T. Probing single-stranded DNA conformational flexibility using fluorescence spectroscopy. Biophys. J. 2004;86:2530–2537. doi: 10.1016/S0006-3495(04)74308-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Ullner M., Woodward C.E. Orientational correlation function and persistence lengths of flexible polyelectrolytes. Macromolecules. 2002;35:1437–1445. [Google Scholar]
- 65.Hagerman P.J. Flexibility of DNA. Annu. Rev. Biophys. Biophys. Chem. 1988;17:265–286. doi: 10.1146/annurev.bb.17.060188.001405. [DOI] [PubMed] [Google Scholar]
- 66.Wiggins P.A., Nelson P.C. Generalized theory of semiflexible polymers. Phys. Rev. E. 2006;73:031906. doi: 10.1103/PhysRevE.73.031906. [DOI] [PubMed] [Google Scholar]
- 67.Williams L.D., Maher L.J., III Electrostatic mechanism of DNA deformation. Annu. Rev. Biophys. Biomol. Struct. 2000;29:497–521. doi: 10.1146/annurev.biophys.29.1.497. [DOI] [PubMed] [Google Scholar]
- 68.Skolnick J., Fixman M. Electrostatic persistence length of a wormlike polyelectrolyte. Macromolecules. 1977;10:944–948. [Google Scholar]
- 69.Rathore N., de Pablo J.J. Monte Carlo simulation of proteins through a random walk in energy space. J. Chem. Phys. 2002;116:7225–7230. [Google Scholar]
- 70.Rathore N., Knotts T.A., IV, de Pablo J.J. Density of states simulations of proteins. J. Chem. Phys. 2003;118:4285–4290. doi: 10.1016/S0006-3495(03)74810-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Nelson, P. 2004. Biological Physics: Energy, Information, Life. W. H. Freeman, New York.
- 72.Mikulecky P.J., Feig A.L. Heat capacity changes associated with DNA duplex formation: salt- and sequence-dependent effects. Biochemistry. 2006;45:604–616. doi: 10.1021/bi0517178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Holbrook J.A., Capp M.W., Saecker R.M., Record M.T., Jr. Enthalpy and heat capacity changes for formation of an oligomeric DNA duplex: interpretation in terms of coupled processes of formation and association of single-stranded helices. Biochemistry. 1999;38:8409–8422. doi: 10.1021/bi990043w. [DOI] [PubMed] [Google Scholar]
- 74.Cho S.S., Weinkam P., Wolynes P.G. Origins of barriers and barrierless folding in BBL. Proc. Natl. Acad. Sci. USA. 2008;105:118–123. doi: 10.1073/pnas.0709376104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Eastwood M.P., Wolynes P.G. Role of explicitly cooperative interactions in protein folding funnels: a simulation study. J. Chem. Phys. 2001;114:4702–4716. [Google Scholar]
- 76.Wetmur J.G. Hybridization and renaturation kinetics of nucleic acids. Annu. Rev. Biophys. Bioeng. 1976;5:337–361. doi: 10.1146/annurev.bb.05.060176.002005. [DOI] [PubMed] [Google Scholar]
- 77.Eimer W., Pecora R. Rotational and translational diffusion of short rodlike molecules in solution: oligonucleotides. J. Chem. Phys. 1991;94:2324–2329. [Google Scholar]
- 78.Stellwagen N.C., Magnusdottir S., Gelfi C., Righetti P.G. Measuring the translational diffusion coefficients of small DNA molecules by capillary electrophoresis. Biopolymers. 2001;58:390–397. doi: 10.1002/1097-0282(20010405)58:4<390::AID-BIP1015>3.0.CO;2-K. [DOI] [PubMed] [Google Scholar]
- 79.Likhachev E. Dependence of water viscosity on temperature and pressure. Tech. Phys. 2003;48:514–515. [Google Scholar]
- 80.Stellwagen E., Lu Y., Stellwagen N.C. Unified description of electrophoresis and diffusion for DNA and other polyions. Biochemistry. 2003;42:11745–11750. doi: 10.1021/bi035203p. [DOI] [PubMed] [Google Scholar]
- 81.Wilk A., Gapinski J., Patkowski A., Pecora R. Self-diffusion in solutions of a 20 base pair oligonucleotide: effects of concentration and ionic strength. J. Chem. Phys. 2004;121:10794–10802. doi: 10.1063/1.1811599. [DOI] [PubMed] [Google Scholar]


