Some Cardiomyopathy-Causing Troponin I Mutations Stabilize a Functional Intermediate Actin State

Abstract

We examined four cardiomyopathy-causing mutations of troponin I that appear to disturb function by altering the distribution of thin filament states. The R193H (mouse) troponin I mutant had greater than normal actin-activated myosin-S1 ATPase activity in both the presence and absence of calcium. The rate of ATPase activity was the same as that of the wild-type at near-saturating concentrations of the activator, N-ethylmaleimide-S1. This mutant appeared to function by stabilizing the active state of thin filaments. Mutations D191H, R146G, and R146W had lower ATPase activities in the presence of calcium, but higher activities in the absence of calcium. These effects were most pronounced with mutations at position 146. For all three mutants the rates were similar to those of the wild-type at near-saturating concentrations of N-ethylmaleimide-S1. These results, combined with previous results, show that any alteration in the normal distribution of actomyosin states is capable of producing cardiomyopathy. The results of the D191H, R146G, and R146W mutations are most readily explained if the intermediate state of regulated actin has a unique function. The intermediate state appears to have an ability to accelerate the rate of ATP hydrolysis by myosin that exceeds that of the inactive state.

Introduction

Congenital cardiomyopathies are among the leading causes of sudden cardiac death and account for a large portion of cardiac fatalities in younger patients (1). Hypertrophic cardiomyopathy (HCM) is the most significant type of congenital cardiomyopathy, with an incidence of one in 500; restrictive and dilated cardiomyopathies have lower incidences. HCM is characterized by hypertrophy of the ventricular walls, fibrosis, myofibrillar disarray, hemodynamic dysfunction, arrhythmias, and death (2,3). More than 200 mutations are known to cause this disease, and the vast majority occur on sarcomeric genes. Many of the presenting clinical and pathological changes are due to the release of secondary messengers, but the underlying primary mechanism is still poorly understood (4). This underlying cause is likely to be associated with the regulation of cardiac muscle contraction at the sarcomeric level, where the mutations are present.

Cardiac muscle contraction is regulated by the troponin (I, T, and C subunits) and tropomyosin that are bound to actin (5). Activation is the result of binding of Ca²⁺ to the troponin C (TnC) subunit of troponin or to the high-affinity binding of myosin to actin. High-affinity myosin binding directly alters the position of tropomyosin on actin. Calcium binding to the single regulatory site of cardiac TnC results in a movement of the troponin I (TnI) inhibitory segment away from the actin filament (6–8). Subsequently, tropomyosin alters its position on actin (9). Changes in tropomyosin allow for transmission of the calcium-binding signal along several monomers, and are cooperatively transmitted to neighboring tropomyosin molecules (10–12).

These structural changes are highly dependent on the inhibitory segment of TnI along with its C-terminal extension in cardiac muscle. Both of these regions are largely disordered and have a greater range of motion that allows them to transition from binding to actin in the absence of calcium, to movement away from actin with calcium binding (13–15). Several mutations in these regions, including those examined in the study presented here, that cause cardiac dysfunction and disease have been identified.

The structural changes that occur in troponin and tropomyosin in response to calcium binding control contraction. Mutations in the regulatory proteins of contraction normally alter actin stimulation of myosin ATPase activity. The ATPase rate is dependent on both the fraction of myosin that is bound to actin and the functional state of regulated actin. Calcium does not have a significant effect on myosin binding to actin during ATP hydrolysis, although it does alter the binding of myosin-ADP and rigor myosin (16). The major function of Ca²⁺ may be to alter the distribution of functional states of the actin thin filament.

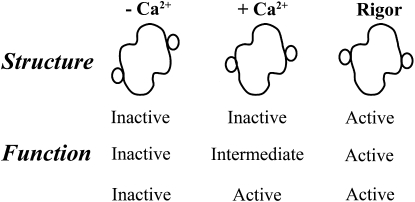
Various models have been produced that relate structure to function (16–21). Fig. 1 shows the three structural states that have been identified. The small circles show how the position of tropomyosin differs in the absence and presence of calcium, and in the rigor state (9,22,23). Although the positions of tropomyosin have been defined, the functions of these structural states have not been determined. In fact, we previously examined ATPase rates under the assumption that two of the structural states were essentially similar in function. That ability to explain function with only two states leaves the properties of the third state undefined.

Figure 1.

Possible relationships among the different known structural states of regulated actin and functional states (inactive, intermediate, and active). The structural diagrams shown are schematic representations of data presented by several groups showing tropomyosin positions on actin in the absence and presence of calcium and in the presence of bound “activating” cross bridges. In three-state models of regulation, each structure is associated with a unique function. In two-state models, two of the structures have the same function.

Actin-troponin-tropomyosin may exist in an active or inactive configuration. These states are in rapid equilibrium with each other. The active state is partially stabilized by Ca²⁺ and more so by rigor-type myosin binding. The shift in equilibrium toward more active states increases the ATPase rate (17,21,24). We previously showed that the cardiomyopathy-causing mutation Δ14 on troponin T (TnT) shifts the equilibrium toward a more active state (25). Furthermore, protein kinase C (PKC) phosphorylation of TnI shifts the equilibrium toward the inactive state (26). We hypothesize that a disruption of the normal distribution of states is a common mechanism by which many of the sarcomeric cardiomyopathy mutations cause disease. This underlying disturbance of sarcomeric regulation resulting in cardiac muscle dysfunction is a likely cause of the release of numerous secondary messengers, resulting in the observed pathology.

We studied four mutations on TnI that are known to cause restrictive cardiomyopathy and HCM: D191H, R193H, R146G, and R146W (mouse sequence) (see http://cardiogenomics.med.harvard.edu/project-detail?project_id=230#data for a comprehensive list of cardiomyopathy-causing mutations). Residue 146 is in the disordered inhibitory segment of TnI, which is unresolved in the crystal structure, and the 191 and 193 residues occur on the C-terminal portion of TnI, which is also largely unresolved because of its disordered nature (27). Some structural details of these regions have been refined with the use of nuclear magnetic resonance techniques (13–15).

We examined the effects of these mutations on the ATPase rates in the presence and absence of calcium. For the 193 mutation, we found that the rates were elevated in both the presence and absence of calcium, indicating stabilization of the active state. The results for the other three mutations were more complex, showing an increased rate versus wild-type (WT) in the absence of calcium but a decreased rate in the presence of calcium.

We also examined the actin-activated ATPase rates of the mutants in the presence of the activator N-ethylmaleimide-S1 (NEM-S1). This modified S1 shifts the regulated actomyosin to the fully activated state in the presence of ATP, but has a very low actin-activated ATPase rate itself. NEM-S1 produced similar ATPase rates for all the mutants and WT in both the absence and presence of calcium. We also showed that there is no significant alteration of troponin binding to actin due to these mutations. This means that no step within the fully activated pathway is altered by the mutants; rather, the data can be readily explained by assuming that the mutants shifted the distribution of states.

The changes in the distribution of states required for several of the mutants are most readily explained if there are three functional states of regulated actin in the case of the cardiac regulatory apparatus. Furthermore, it appears that any deviation from the normal distribution of states can result in cardiac disease.

Materials and Methods

Protein preparation

Actin and myosin were isolated from rabbit back muscle (28). Myosin-S1 was made by digestion of myosin with chymotrypsin (Worthington Biochemical, Freehold, NJ) (29). Tropomyosin was isolated from bovine cardiac tissue. Mouse cardiac troponin C and I in pET3d, and mouse cardiac troponin T in psBET were expressed as described previously (30).

Protein concentrations were determined by absorbance measurements at 280 nm, corrected at 340 nm for light scattering. The following extinction coefficients (ɛ^0.1%) were used: actin 1.15, myosin-S1 0.75, tropomyosin 0.23, and troponin 0.37.

Measuring ATPase rates

The actin-activated ATPase rates were determined by measuring the release of ³²P from γ³²P-ATP (31). Measurements were taken in the absence and presence of calcium at 25°C, pH 7.0, over a period of 10–15 min. The production of ³²P remained linear with time during this interval, so the measured velocities are initial velocities. The reaction mixture generally contained 1 mM ATP, 3 mM MgCl₂, 10 mM MOPS, 34 mM NaCl, 1 mM EGTA or 0.5 mM CaCl₂, 1 mM dithiothreitol, 10 μM actin, and 0.1 μM myosin-S1. Virtually all added NEM-S1 bound to actin under these conditions (32,33). The actin concentration was increased to the same extent as the NEM-S1 concentration, maintaining a constant level of free actin (34). All rates were adjusted by subtracting the contribution due to free S1 and NEM-S1.

Determining free troponin concentration dependencies

Plots of ATPase activity as a function of added troponin were constructed. The free concentration was determined by assuming that at the plateau of activity, one troponin and one tropomyosin were bound per seven actin monomers. The amount of troponin bound at each submaximal concentration was assumed to be proportional to the fraction of the maximum effect on ATPase activity. With this approach, the curves were transformed to ATPase rate versus free troponin.

Statistics

Data in the figures are shown as means, with error bars showing the standard deviation (SD). Statistical significance (p < 0.05) was determined using the two-sample significance t-test to compare means.

Results

Previous studies have shown that the D191H, R193H, R146G, and R146W mutations of troponin I affect ATPase activity (30,35–37). Our goal was to determine whether these effects are due to changes in the distribution of thin filament states (i.e., stabilization of either the active or inactive state) or to other factors. Mutations of troponin I could weaken the binding of troponin to actin-tropomyosin and lead to a loss of regulation. We therefore determined the concentration dependencies of ATPase rates on the various troponin types.

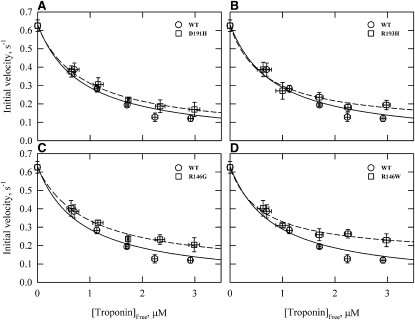
We examined the ATPase rates in the absence of calcium with increasing concentrations of the troponin complex. Fig. 2 shows initial velocities of ATP hydrolysis versus the free concentration of troponin. The estimated dissociation constants ± standard error were 0.82 ± 0.37 μM (WT), 0.96 ± 0.14 μM (D191H), 0.70 ± 0.22 μM (R193H), 0.97 ± 0.21 μM (R146G), and 0.62 ± 0.16 μM (R146W). These approximate values show that there were no large changes in the binding of troponin to actin-tropomyosin due to the mutations. Under the conditions of our experiments, the ATPase rates were near their minimum values at 3.6 μM troponin in all cases. We maintained a similar ratio of actin/tropomyosin/troponin in all other experiments to ensure that observed changes were not due to a difference in binding.

Figure 2.

TnI mutations have little effect on the concentration of free troponin required for 50% inhibition of actin-activated S1 ATPase activity. Actin-activated ATPases for WT and mutants at 0.05 M ionic strength are shown with increasing concentrations of troponin in the absence of Ca²⁺. Initial velocities (μM ATP/s/μM S1) are shown for WT and D191H (A), R193H (B), R146G (C) and R146W (D). All rates were corrected for the ATPase rate of S1 in the absence of actin (0.06 μM ATP/s/μM S1). Data are presented as mean values ± SD. Conditions: 25°C, pH 7, 0.1 μM S1, 10 μM actin, 4.3 μM tropomyosin, 1 mM ATP, 10 mM MOPS, 2 mM MgCl₂, 33 mM NaCl, 1 mM dithiothreitol, and 1 mM EGTA.

The data in Fig. 2 also show that each mutant was less inhibitory than the WT at saturating concentrations of troponin (p < 0.05). Residue 146 mutations had the greatest decreases in inhibitory function. At saturation with troponin, the rate ± SD (μM ATP/s/μM S1) for the WT was 0.12 ± .02. The rates for the mutants were 0.17 ± 0.04 for D191H, 0.18 ± 0.02 for R193H, 0.20 ± 0.04 for R146G, and 0.23 ± 0.04 for R146W. At lower concentrations of troponin, there were no significant differences between the rates of the WT and mutants (p > 0.05).

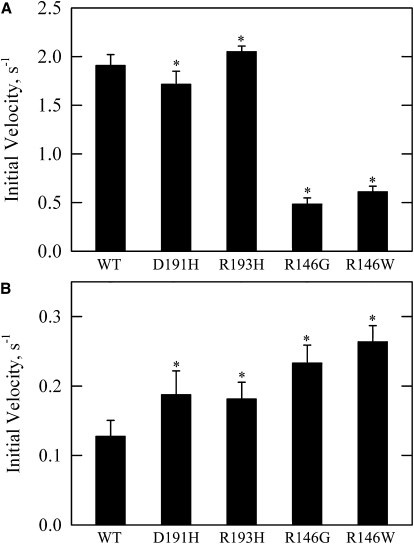
Fig. 3 compares the effects of mutant and WT troponin types on ATPase rates in the presence and absence of calcium. The rates ± SD (μM ATP/s/μM S1) in calcium were 1.91 ± 0.11 for WT, 1.72 ± 0.13 for D191H, 2.05 ± 0.06 for R193H, 0.48 ± 0.06 for R146G, and 0.61 ± 0.06 for R146W. The rates in the absence of calcium were 0.13 ± 0.02 for WT, 0.19 ± 0.03 for D191H, 0.18 ± 0.02 for R193H, 0.23 ± 0.03 for R146G, and 0.26 ± 0.02 for R146W. The differences between each mutant and WT were statistically significant in the presence and absence of calcium (p < 0.05). The R193H mutation had a small increase in rate in both the presence and absence of calcium. This indicates a stabilization of the active state.

Figure 3.

Rates of actin-activated ATPase measured at near-saturating concentrations of troponin in the presence (A) and absence (B) of calcium. The TnI C-terminal mutants show small changes in the presence of calcium and an increased rate in the absence of calcium, whereas both mutations at residue 146 show large reductions in rate in the presence of calcium and increased rates in the absence of calcium. Data are presented as mean values ± SD. All conditions and corrections are similar to Fig. 2 except that a constant and nearly saturating concentration of troponin was used and 0.5 mM CaCl₂ was substituted for EGTA in A.

The D191H mutation showed a slight decrease in ATPase rate in the presence of calcium and a significantly increased rate in the absence of calcium. The R146 mutations showed more dramatic changes, with large reductions in rate in the presence of calcium and twofold increases in the absence of calcium compared to WT. The altered rates in these mutations could not be explained by assuming stabilization of either the inactive or active state. These results require that either the mutants stabilize opposite states in the absence or presence of calcium relative to WT or they stabilize a single third regulatory state with an intermediate activity. If the intermediate state were stabilized relative to the other states, then the population of the inactive state in EGTA would be reduced. Furthermore, the population of the active state in Ca²⁺ would also be reduced relative to WT.

NEM-S1 binds tightly to actin in the presence of ATP and shifts the filament to the active state (12). By titrating with this activator, it is possible to observe the overall ATPase rate as the regulated filament is shifted to the fully active state. The actin-activated ATPase activity of NEM-S1 is very low (0.015 μM ATP/s/μM NEM-S1), and observed rates of ATP hydrolysis can be corrected for the contribution due to NEM-S1. With the fully active state stabilized with NEM-S1, we were able to screen for changes in steps that occurred during ATP hydrolysis along that pathway. If WT and mutant values were the same at full activation, it is unlikely that processes such as product release were affected by the mutation.

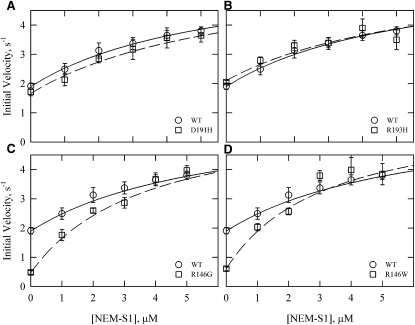
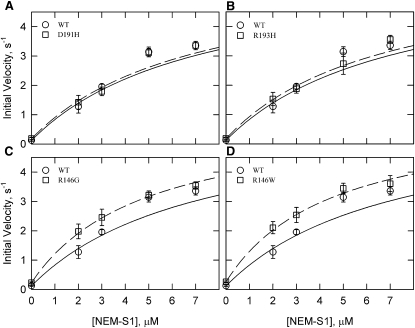
Fig. 4 shows the effect of increasing concentrations of NEM-S1 in the presence of calcium. Although there were significant differences between the WT values and those of some mutants at low NEM-S1 concentrations, the values converged at high NEM-S1 concentrations. At the highest NEM-S1 concentration used (5 μM), there was no significant difference between any of the mutants and the WT (p > 0.05). The theoretical curves shown in Fig. 4 were drawn assuming the same limiting velocities in all cases (6.04 μM ATP/s/μM S1). The data are well described by the theoretical curves. These curves also show that the mutants differed in their sensitivity to NEM-S1 concentration. The D191H and R193H mutations did not show a significant difference from WT at any NEM-S1 concentration.

Figure 4.

Actin-activated ATPase activity of S1 with increasing concentrations of the activator NEM-S1 in the presence of Ca²⁺. WT rates (circles) are the same in all four panels, with the regression shown as a solid line for the WT and a dashed line for the mutant (squares). The Michaelis-Menten equation was fit to the data using a maximal rate of 6 s⁻¹ with varying K_M values (WT = 5.5 μM, D191H = 6.1 μM, R193H = 6.1 μM, R146G = 3.4 μM, and R146W = 2.9 μM). All rates were corrected for the ATPase rate of S1 and NEM-S1 (0.015 μM ATP/s/μM NEM-S1). Data are presented as mean values ± SD. Conditions: 25°C, pH 7, 0.1 μM S1, 10 μM free actin, 1 mM ATP, 10 mM MOPS, 3 mM MgCl₂, 33 mM NaCl, 1 mM dithiothreitol, and 0.5 mM CaCl₂. Actin concentration was increased by an amount equal to the NEM-S1 added to maintain the same free actin concentration. Actin/tropomyosin/troponin ratio was 7:3:2.5.

The effects of NEM-S1 on ATPase activities in the absence of calcium are shown in Fig. 5. Under these conditions, the residue 146 mutations had ∼2-fold higher rates than WT in the absence of NEM-S1. However, the ratio between the rates of WT and the mutants began to converge to one as the NEM-S1 concentration increased. The rates for all the mutants and WT were not significantly different at the highest NEM-S1 concentration used (7 μM, p > 0.05). We could not reach the limiting rate in the absence of calcium because of the very high NEM-S1 concentrations required and the associated large errors. Fig. 5 shows theoretical curves for all low calcium data sets assuming the same limiting rate as in Ca²⁺. The curves represent the data well. As in Ca²⁺, the R146G and R146W mutants had a greater sensitivity to NEM-S1.

Figure 5.

Actin-activated ATPase activity of S1 with increasing concentrations of the activator NEM-S1 in the absence of Ca²⁺. WT rates (circles) are the same in all panels, with the regression shown as a solid line for the WT and a dashed line for the mutants (squares). The Michaelis-Menten equation was fit to the data using a maximal rate of 6 s⁻¹ with varying K_M values (WT = 9.8 μM, D191H = 9.6 μM, R193H = 9.3 μM, R146G = 7.1 μM, and R146W = 6.7 μM). All conditions and corrections are similar to Fig. 4 with the exception that CaCl₂ was replaced with 1 mM EGTA.

Discussion

Congenital cardiomyopathies remain an important cause of morbidity and mortality, with over 200 mutations identified as disease-causing mutations for HCM alone. The pathology of hypertrophy and secondary changes, such as fibrosis and myofibrillar disarray, are well established, and significant progress has been made in identifying the hormones and secondary messengers that are responsible for these changes (3,38). Reversing these secondary changes, however, remains a difficult problem due to the complex interactions and localization of the various signals. The primary treatment remains symptomatic; β-blockers and other drugs are used to reduce the load on the heart as a first line of treatment, and surgical myomectomies are performed in recalcitrant cases. In many cases the medical line of management does not significantly alter disease progression, and the surgical treatment is extremely invasive and carries a small mortality risk (39).

The most direct approach to treating the disease, short of gene manipulation, is to target the primary pathology at the level of sarcomeric regulation. Any change in the distribution of states may result in cardiac dysfunction. Phosphorylation also causes changes in the distribution of states (26). Therefore, there is the potential for altering the distribution of states toward a more normal phenotype. As we show below, the primary event can be a change in the distribution of actin states.

We screened four cardiomyopathy-causing mutations to determine whether altering the distribution between actin states is a common mechanism by which mutations cause disease. These TnI mutants were the objects of prior investigations that dealt with effects on calcium sensitivity and other functional characteristics. These earlier studies also showed that these mutants differ from WT in their ATPase rates in EGTA and calcium (30,35–37). Our primary interest was in determining the differences for these changes in rate. We first determined the saturating concentrations of troponin and tropomyosin required to achieve full inhibition. At near-saturating concentrations of troponin, all four mutants showed statistically higher ATPase rates than WT in the absence of calcium. These results also show that there are not large differences in apparent affinity between the mutants and WT.

The changes seen with the mutations could have been due to alterations in the rate of some process along the active pathway (i.e., product release). By using NEM-S1, we were able to stabilize the fully active state of the actin filaments. No differences were observed in the rates of ATP hydrolysis between the WT and mutants under these conditions. Thus it is unlikely that rates of transitions between two nucleotide bound states are affected by the mutations of TnI.

The remaining possibility is that these mutations of troponin I alter the equilibrium among states of regulated actin. For example, the increased rate in both the high and low Ca²⁺ levels seen with the R193H mutation can be rationalized by stabilization of the most active state of regulated actin. A similar shift to the active state was reported with the Δ14 mutation on TnT (25). Stabilization of the inactive state was reported in the case of protein kinase C phosphorylation of TnI (26), which reduced the ATPase rates in both the presence and absence of calcium. The D191H, R146G, and R146W mutants shown here exhibit the property of being more active in EGTA and less active than the WT at saturating calcium. These results require that either the mutants stabilize opposite states in the absence or presence of calcium relative to WT (the two-state model) or they stabilize a single third regulatory state with an intermediate activity.

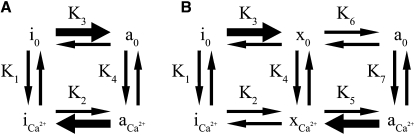
The effect of the mutations on the distribution of states in the presence and absence of calcium is shown for a two-state model (Fig. 6 A). Calcium binds more tightly to the active state (K₄ > K₁) so that the active state is stabilized by calcium. The D191H, R146G, and R146W mutants would need to shift the equilibrium constant K₃ to the right and K₂ to the left compared to WT to explain the ATPase rates (heavy arrows in Fig. 6 A). It is difficult to imagine structurally how a mutation that stabilizes the active state at low calcium relative to the WT can at the same time produce a relative stabilization of the inactive state at saturating calcium. Detailed structural studies will further clarify whether such a mechanism is possible.

Figure 6.

Possible effects of R146G and R146W mutations on the distribution of actin states in the presence (Ca²⁺) and absence (0) of calcium. In WT filaments, the equilibrium favors state i₀ in the absence of calcium and a Ca²⁺ in the presence of calcium. (A) Two-state model with inactive (i) and active (a) states. (B) Three-state model with inactive (i), intermediate (x), and active (a) states. The heavy arrows show the changes in equilibrium constants required to explain the results of the mutants.

It is more likely that conformational changes due to the mutations will cause actin filaments to favor a single structure that corresponds to a unique functional state. That is, the intermediate structural state proposed to exist in regulated actin filaments is a unique functional state. The bold arrows in Fig. 6 B indicate possible changes in equilibrium constants of TnI mutants that would give the observed ATPase rates while avoiding opposing changes of a single step. According to this scheme, the ability of the intermediate state to stimulate ATPase activity must be greater than that of the inhibited state but less than that of the fully active state. An examination of the distributions is shown further below.

It is interesting to note that the two mutations at residue 146 have similar patterns of ATPase activity. It may be the case that the significant change is the loss of the basic arginine instead of the amino acid that replaces it. It has been shown in skeletal troponin that arginine and lysine residues on the troponin mobile domain are important for stabilizing the interaction with actin (13). Examining other mutations at this site and other cardiac troponin basic amino acids may help refine this mechanism.

In the parallel pathway model, the overall actin-tropomyosin-troponin stimulated myosin ATPase rate is given by the sum of the product of the fraction of myosin bound to each actin state and the activity of each state. Because S1-ATP binds with a similar affinity to myosin in the calcium-free, calcium-bound, and NEM-S1-stabilized active states (10), this is equivalent to the sum of the product of the activity of each state times the fraction of actin in each state. In the original parallel pathway model of Hill et al. (24), we assumed that there were two states as shown in Fig. 6 A. Calcium was thought to increase the ATPase activity by increasing the population of the active state. That is, as in Fig. 6 A, the affinity of calcium for the active state is greater than that for the inactive state. Therefore, calcium increases the fraction of actin in the active state. If another state is included in the Hill model, as in Fig. 6 B, the observed ATPase rate would equal fi(vi) + fx(vx) + fa(va), where fi, fx, and fa are the fractions of total actin in each state, and vi, vx, and va are the activities of the respective states.

To place limits on the distributions of states, it is necessary to define the activities of the individual states. Because the ATPase rates at optimal concentrations of NEM-S1 are calcium-independent, it is likely that under this condition virtually all of the regulated actin is in the active state (10). This result also implies that the activity of the fully active state is calcium-independent. We made the simplifying assumption that the activities of the other states are also calcium-independent.

The activity of the inactive state must be between zero and the lowest rate we have measured (0.13/s). We assumed that the inactive state had a true rate of 0.1/s. Essentially no actin is in the fully active state in EGTA, in accord with our data obtained with a pyrene tropomyosin probe (40).

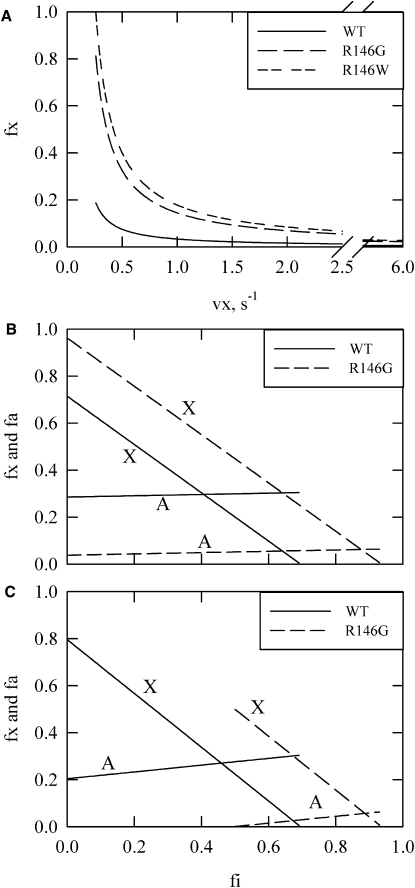
The key uncertain parameter is the activity of actin filaments in the intermediate state, vx. Fig. 7 A shows the possible values of the fractional occupancy of the intermediate state, fx, as a function of the assumed activity of the intermediate state, x, in the absence of calcium for WT and the two mutations at residue 146. The minimum value of vx that is consistent with the data for the R146W mutation is 0.26/s. At that limiting value, however, the equilibrium would be shifted totally to the intermediate state, which does not seem to be reasonable. Therefore, the value of vx is likely to be >0.26/s. The maximum value for vx is ∼0.9/s (see below), so the activity of vx is most likely 4–15% that of the active state under the conditions used in these assays.

Figure 7.

Possible distributions of states for WT and R146 mutants. (A) Occupancy of the intermediate state as a function of assumed ATPase rates for the intermediate state (vx). At any given vx, the fractional population of the intermediate state is higher for the mutations than for the WT. The activities of the inactive and active states are assumed to be 0.1/s and 6/s, respectively. An ATPase rate less than 0.26/s would require a fraction larger than 1.0 for the intermediates state in the case of R146W, limiting vx to this minimum rate. B and C show the fraction of states in the intermediate and active states for different assumed fractions in the inactive state in the presence of saturating calcium. (B) Possible distributions for the minimum possible value of vx, 0.26/s, with “X” indicating the intermediate state and “A” representing the active state. (C) The same as B but with vx = 0.85/s. At this point, the lowest possible fraction of the inactive state for the R146G mutation in saturating calcium is 0.5.

Fig. 7, B and C, show distributions for WT and R146G at two extreme possible values of vx. The maximum possible value for vx is limited by the overall rate for the R146G mutant. That rate is lower than the WT value in calcium. At values of vx >0.85/s, the major state occupied is the inactive state. At this point, the three-state model would have the same difficulty as the two-state model (Fig. 6) in that the mutation would stabilize opposite states in the absence and presence of calcium. This also means that if the absolute value of fx were determined, further restrictions would be placed on the mutant distribution; therefore, distributions where fx (mutant) < fx (WT) were not considered.

This analysis of a small number of mutations resulted in a fairly low range of values for the activity of the intermediate state. This range will change slightly once the value of the activity of actin in the inactive state is refined. Since the distribution of actin states in calcium is sensitive to the activity of the intermediate (vx) state, we can only give ranges of values at this time. Nevertheless, these constraints are already useful for relating other observables, such as binding kinetics or probe fluorescence changes, to functional actin distributions. It is important to improve the estimate of functional state distributions so that these other readily available methods can be used to confidently determine the time course of changes in functional state distributions. Such information may be critical to the understanding of familial cardiac and skeletal muscle disorders.