Coupling between Normal Modes Drives Protein Conformational Dynamics: Illustrations Using Allosteric Transitions in Myosin II

Abstract

Structure-based elastic network models (ENMs) have been remarkably successful in describing conformational transitions in a variety of biological systems. Low-frequency normal modes are usually calculated from the ENM that characterizes elastic interactions between residues in contact in a given protein structure with a uniform force constant. To explore the dynamical effects of nonuniform elastic interactions, we calculate the robustness and coupling of the low-frequency modes in the presence of nonuniform variations in the ENM force constant. The variations in the elastic interactions, approximated here by Gaussian noise, approximately account for perturbation effects of heterogeneous residue-residue interactions or evolutionary sequence changes within a protein family. First-order perturbation theory provides an efficient and qualitatively correct estimate of the mode robustness and mode coupling for finite perturbations to the ENM force constant. The mode coupling analysis and the mode robustness analysis identify groups of strongly coupled modes that encode for protein functional motions. We illustrate the new concepts using myosin II motor protein as an example. The biological implications of mode coupling in tuning the allosteric couplings among the actin-binding site, the nucleotide-binding site, and the force-generating converter and lever arm in myosin isoforms are discussed. We evaluate the robustness of the correlation functions that quantify the allosteric couplings among these three key structural motifs.

Introduction

It is important to obtain details of the conformational changes in proteins to elucidate their molecular functions. To enable efficient simulations and analysis of protein conformational dynamics, coarse-grained modeling has been successfully developed using simplified structural representations and energy functions (1). A prime example of the structure-based coarse-grained models is the elastic network model (ENM), where the C_α atoms of amino acid residues that are within a cutoff distance are connected by springs (2,3) with a uniform force constant (4). Normal mode analysis (NMA) based on the ENM has been extensively validated (5,6) and employed to describe the conformational dynamics in biomolecular structures (for reviews, see (7–10)). Remarkably, the global conformational changes (11–14), conformational transition pathways (15–20), and allosteric couplings (21–23) in complex systems are well described by few low-frequency normal modes. The ENM-based modes have also formed the basis of new computational techniques for protein structural modeling and refinements (24–27). The success of ENM-based low-resolution modeling has been attributed to the robust nature of the collective motions in multidomain proteins, which are apparently insensitive to the details of microscopic interactions. Bolstered by the robustness argument, an ENM with a uniform force constant, k₀ and a uniform cutoff distance, R_c, is typically used despite significant heterogeneity in the strength and range of physical interactions between the amino acid residues. The use of R_c values within the range 8–20 Å or other residue-contact schemes (3,28–30) generally preserves the lowest few normal modes. In addition, the lowest modes of ENM were found to be comparable with the lowest normal modes obtained from the NMA of all-atom force fields (3). Another study suggested that those few invariant or robust modes may be functionally important (31). The robustness in functionally important low-frequency modes was also discussed in the context of ribosome dynamics (32). Our recent studies have also supported the concept of robustness as a useful criterion for predicting functionally important modes (14,33).

Despite earlier studies in support of the robustness of ENM, the dynamic effects of nonuniform perturbations to the ENM force constant remain to be fully quantified. In biomolecules, such perturbations may originate from several sources, such as the approximate use of uniform elastic interactions to account for heterogeneous physical interactions between residues, and evolutionary sequence variations. To assess the effects of these complex factors, we will analyze how the normal modes are perturbed after a Gaussian random noise is added to the uniform ENM force constant. The resulting simplification allows analytic treatment of the perturbation effects (see below), and it provides a reasonable starting point for further studies of more complex perturbations.

Using a brute-force approach, one can perform NMA for a large number of ENM parameter sets with heterogeneous force constants $k_{ij}=k_0+\delta k_{ij}$ for residue pairs 〈i, j〉, whose equilibrium distance is $d_{ij}^0<R_c,$ and then statistically analyze the variations in the eigenvectors of the normal modes. Such an approach is computationally expensive for large structures typical of biological nanomachines. Therefore, it is useful to develop an approximate method that estimates the statistical variations of normal modes reliably and efficiently. The brute-force approach can be used to validate the approximate method (see below).

Recently, we introduced the structural perturbation method, based on first-order perturbation theory, to estimate the robustness of normal modes in the presence of parameter changes due to sequence variations (14,33). This method is adopted here to investigate how nonuniform errors in the ENM force constant perturb the normal modes and the normal-mode-based correlation functions (see Methods). Unlike in our earlier studies (14,33), we will add Gaussian noise to the force constant of all springs regardless of the conservation level of the residues involved. This simplification will be justified by showing that the results of mode robustness remain qualitatively unchanged even when the perturbations are restricted to nonconserved residue pairs only (see Results).

Small perturbations in the ENM force constant will mix or couple those modes whose eigenvalues are close in the unperturbed spectrum. This is evident from first-order perturbation theory, because the coupling coefficient between two modes is inversely proportional to the difference between their eigenvalues (see Methods). Such mode mixing determines the robustness of a normal mode: the more strongly a mode is coupled to other modes, the less robust it is. However, it is unclear whether the mode coupling computed from the perturbation theory is relevant to realistic situations in which the perturbations to the ENM force constant are not small. For example, the anomalous coupling between near-degenerate modes might be suppressed in the presence of finite perturbations. This issue is critical to the applicability of the perturbation theory to the robustness assessment of normal modes. In this work, we will validate the use of perturbation theory to estimate the mode robustness and the coupling between modes in the presence of finite perturbations to the ENM force constant.

The mode coupling information is useful not only for estimating the robustness of individual modes, but also for elucidating the functional significance of seemingly nonrobust modes. A mode may appear to be nonrobust if it is strongly coupled with other modes. However, superposition of the strongly coupled modes may form a robust mode group whose members are weakly coupled to those outside the group. When functional motions of proteins are deduced based on the NMA of an ENM with inaccurate force constant, it is important to analyze the modes not individually but in groups. We expect modes in the same group are strongly coupled with one another, whereas modes from different groups are only weakly coupled. Structural motions described by modes in the same group are more likely to accompany each other. The variable combinations of motions described by a mode group allow sequence variations to fine-tune allosteric couplings in proteins. Another useful application of mode coupling analysis is to build an invariant subspace spanned by a subset of low-frequency normal modes for enhanced conformational sampling (34). The invariance can be ensured by the lack of strong coupling between modes included in and modes excluded from the subset.

The concept of robustness is applicable not only to individual modes but also to quantities computed from all modes. We have recently explored the use of correlation functions to probe the allosteric coupling between a pair of functional sites in a protein structure (21). The correlation functions are computed as a weighted sum of contributions from all modes (up to a cutoff mode, see Methods). Therefore, the variations in normal modes will result in changes in the correlation functions. Here, we will investigate the robustness of correlation functions in the presence of nonuniform perturbations to the ENM force constant. A specific correlation is deemed significant or robust if its variation caused by perturbations is much smaller than its unperturbed value. This calculation will allow us to reliably predict coupled motions between a pair of protein sites, which may enable allosteric communications between them.

We illustrate the new analysis using myosin II as an example. Myosin II is a class of molecular motors that bind to and move along actin filaments by harnessing the chemical energy from ATP hydrolysis. The work cycle of myosin II consists of the following steps (35). In an ATP-bound myosin detached from actin, ATP hydrolysis produces ADP and inorganic phosphate, and it is accompanied by a large rotation of the lever arm to the prepowerstroke position (recovery stroke). Actin binding accelerates phosphate release from myosin, resulting in a force generation (powerstroke) as the lever arm rotates to the postpowerstroke position. Subsequent release of ADP is followed by the binding of a new ATP, which detaches myosin from actin and resets myosin for the subsequent cycle. Structural studies have highlighted extensive communications in the myosin motor domain (36–40), which consists of four subdomains (see Fig. 4 inset): the upper and lower 50 kDa (U50 and L50) subdoman, the N-terminal subdomain, and the converter subdomain. The nucleotide-binding site is located at the intersubdomain interface (including the P loop, switch I, and switch II—three conserved loops involved in nucleotide binding and hydrolysis). Despite the strong structural conservation of the myosin motor domain, myosin isoforms from different classes (41) vary significantly in their motor properties, pointing to variations in the functional couplings between the actin-binding site, the nucleotide-binding site, and the force-generating lever arm.

Figure 4.

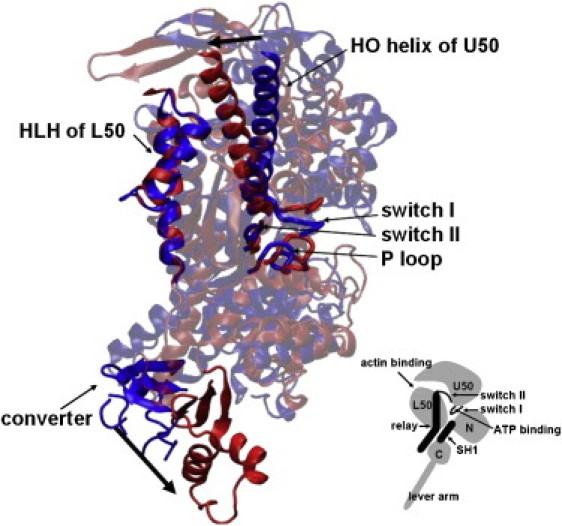
Conformational changes from the prepowerstroke myosin structure (1VOM; blue) to the rigorlike structure (1W8J; red). The two structures are aligned in the HLH motif. Local movements at the actin-binding site (HLH motif and HO helix), the nucleotide-binding site (P loop, switch I, and switch II), and the converter are highlighted by opaque cartoons. (Inset) Four subdomains—the upper and lower 50 kDa (U50 and L50), the N-terminal subdomain (N), and the converter (C)—and key structural components of myosin (relay helix, SH1 helix, lever arm, and switches I and II).

In a series of recent studies, the NMA has been employed to probe myosin's global conformational changes (12,42), local conformational changes at the nucleotide-binding site (43), allosteric coupling (21, 23), structural flexibility (42, 44), and conformational transition (19,45). Based on the NMA using the ENM constructed from a prepowerstroke structure of myosin II, we have identified two functionally important modes (21,43). Mode 1 captures a large rotation of the converter accompanying the powerstroke. Mode 7 captures a rotation of the U50 subdomain that simultaneously closes the actin-binding site and opens the nucleotide-binding site, which explains observations of a negative coupling between actin binding and nucleotide binding in myosin (38–40). Here, we assess the robustness of these modes and other low-frequency modes that are strongly coupled to the functionally important modes. By analyzing the low-frequency modes in mode groups, we will discuss how variations in myosin's functional motions can be attained thorough mode coupling.

Central to myosin motor function are allosteric couplings among actin binding, ATP binding, and product release, and the rotation of converter and lever arm. Structural comparisons have revealed two pairs of coupled structural changes in myosin: 1), the closing/opening of the actin-binding site and the opening/closing of switch I at the nucleotide-binding site (38–40); and 2), the upward/downward rotation of the converter and lever arm and the closing/opening of switch II at the nucleotide-binding site (37). By supplementing correlation analysis (21) with the robustness assessment, we will computationally validate these “structural coupling rules” between the nucleotide-binding site (including switch I and switch II) and two other key sites (the actin-binding site and converter) in the presence of nonuniform errors in the ENM force constant.

Methods

Elastic network model

In an ENM, a protein structure is represented as a network of beads, each corresponding to a C_α atom. A harmonic potential with a uniform force constant k₀ accounts for pairwise interactions between all C_α atoms that are within a cutoff distance, R_c (set here to be 10 Å), of each other. The potential energy is (2,4)

$$E=\frac{1}{2}\sum _{d_{ij}^0<R_c}{k}_0{(d_{ij}-d_{ij}^0)}^2,$$ (1)

where d_ij is the distance between C_α atoms i and j, and $d_{ij}^0$ is the equilibrium distance between C_α atoms i and j in the crystal structure.

We expand the above potential energy function to the second order:

$$E\approx \frac{1}{2}\delta X^T{H}_0\delta X=\frac{1}{2}\sum _{d_{ij}^0<R_c}{k}_0\delta X^T{H}_{ij}\delta X,$$ (2)

where δX = X - X₀, X is a 3N-dimensional vector representing the Cartesian coordinates of N C_α atoms, X₀ gives the equilibrium C_α coordinates in the crystal structure, $H_0=\sum _{d_{ij}^0<R_c}{k}_0{H}_{ij}$ is the Hessian matrix, where $H_{ij}=\frac{1}{2}{\nabla }^2\left[{(d_{ij}-d_{ij}^0)}^2\right]\text{.}$

First-order perturbation of normal modes

We consider an ensemble of ENMs with a uniform cutoff distance R_c and a hererogeneous set of force constants, k_ij, that depends on residue pair (i, j). The Hessian of each ENM is

$$H_{}=\sum _{d_{ij}^0<R_c}{k}_{ij}{H}_{ij},$$ (3)

where k_ij = k₀ + δk_ij. For simplicity, the distribution of δk_ij is assumed to be a Gaussian function centered at 0 with a standard deviation σ_k, and it is statistically independent between residue pairs. The first-order perturbation to the eigenvector V_m of mode m is (14)

$$\delta V_m=\sum _{n\ne m}\delta A_{mn}{V}_n,$$ (4)

where

$$\delta A_{mn}=\frac{V_m^T\delta H\mathrm{\times }{V}_n}{{\lambda }_m-{\lambda }_n},$$ (5)

$$\delta H=\sum _{d_{ij}^0<R_c}\delta k_{ij}{H}_{ij},$$ (6)

and λ_m is the eigenvalue of mode m.

The coupling strength C_mn between modes m and n is given by the mean-squared variation of δA_mn, which sums up contributions from all residue pairs in contact:

$$C_{mn}^{}=\langle \delta A_{mn}^2\rangle ={\sigma }_k^2\sum _{d_{ij}^0<R_c}{\left(\frac{V_m^T{H}_{ij}{V}_n}{{\lambda }_m-{\lambda }_n}\right)}^2\text{.}$$ (7)

To identify residues involved in the coupling between modes m and n, we first sort contributions from all residue pairs (see Eq. 7) from high to low and keep the top 1% of them; the residues involved in these selected pairs are defined as those involved in coupling.

The robustness of mode m is assessed using the score

$$R_m=\langle {\left|\delta V_m\right|}^2\rangle =\sum _{n\ne m}{C}_{mn}^{}\text{.}$$ (8)

High (low) robustness is indicated by a low (high) value of the above score.

Finite perturbation theory for normal modes

Next, we test how well first-order perturbation theory estimates the mode robustness score and the mode coupling strength in the presence of finite variations in the ENM force constant. For a perturbed Hessian matrix $H_{}=\sum _{d_{ij}^0<R_c}(k_0+\delta k_{ij})H_{ij},$a new set of modes (with eigenvectors represented as U_m) can be computed. The perturbed modes are numbered such that for a given m, $\left|V_n^T{U}_m\right|$ is maximal at n = m. The analog of perturbational robustness score R_m (Eq. 8)) at finite perturbations is

$$\langle {\left|U_m-V_m\right|}^2\rangle =2\left(1-\langle V_m^T{U}_m\rangle \right)\approx \sum _{n\ne m}\delta A_{mn}^2\text{.}$$ (9)

The analog of the coupling strength, C_mn, at finite perturbations is

$$\mathrm{\sim }0.5\cdot \langle \sum _i{\left(V_m^T{U}_i{V}_n^T{U}_i\right)}^2\rangle \approx 0.5\cdot \langle {\left(V_m^T{V}_m{V}_n^T\delta V_m\right)}^2+{\left(V_m^T\delta V_n{V}_n^T{V}_n\right)}^2\rangle =\delta A_{mn}^2\text{.}$$ (10)

We compute the above two quantities for 100 samples of ENMs perturbed by Gaussian noise in the ENM force constant with 0 < σ_k ≤ 1, and then compare with the corresponding quantities estimated by first-order perturbation theory (Eqs. 7 and 8).

First-order perturbation of correlation function

The correlation between two given directions of movement at site 1 (X₁) and site 2 (X₂) is given by the sum of contributions from the lowest M modes (21):

$$C_{12}=X_1^T\sum _{m\le M}\frac{V_m^{}{V}_m^T}{{\lambda }_m}{X}_2,$$ (11)

where M is the cutoff mode (with default value 100). A positive value of C₁₂ indicates that the two movements are positively correlated. Some modes contribute positively and others contribute negatively.

In the presence of perturbations to the Hessian matrix, $\delta H=\sum _{d_{ij}^0<R_c}\delta k_{ij}{H}_{ij},$ first-order perturbation theory predicts that the resulting change in C₁₂ is

$$\delta C_{12}=\sum _{d_{ij}^0<R_c}\delta k_{ij}\left\{X_1^T\sum _{m\le M}\left[\sum _{n\ne m}\frac{V_m^T{H}_{ij}{V}_n}{{\lambda }_m({\lambda }_m-{\lambda }_n)}(V_n^{}{V}_m^T+V_m^{}{V}_n^T)-\frac{V_m^T{H}_{ij}{V}_m}{{\lambda }_m^2}{V}_m^{}{V}_m^T\right]X_2\right\}=\sum _{d_{ij}^0<R_c}\delta k_{ij}{B}_{ij}\text{.}$$ (12)

Thus, the root mean-squared variation of C₁₂ is

$${\sigma }_{C_{12}}=\sqrt{\langle \delta C_{12}^2\rangle }={\sigma }_k^{}\sqrt{\sum _{d_{ij}^0<R_c}{B}_{ij}^2}\text{.}$$ (13)

The significance of a correlation function is assessed using the Z score:

$$Z=\frac{C_{12}}{{\sigma }_{C_{12}}}\text{.}$$ (14)

Here, we set σ_k = 1.0. If Z ≫1, then the correlation is robust or significant; otherwise, it is insignificant.

Dynamic domain partition

To visualize the interdomain motions described by a low-frequency mode, we decompose the conformational change given by the eigenvector of a normal mode into several movements of dynamic domains that approximately move (rotate and translate) as rigid bodies (for details, see (22)). To allow a detailed comparison of the movements of four myosin subdomains (see Fig. 4 inset) described by different modes, four initial centroids for dynamic domains are chosen at residues I581 (in L50), L429 (in U50), L106 (in the N-terminal subdoman), and K743 (in the converter).

Results

We will demonstrate the new analyses using a myosin II structure (PDB code: 1VOM) as an example. Our main goal is to validate the computational methods for assessing the robustness of and the coupling between low-frequency modes. We will also show the application of these methods to probing allosteric couplings within myosin II.

First-order perturbation theory for mode robustness and mode coupling

We will evaluate the accuracy of first-order perturbation theory in estimating mode robustness and mode coupling by comparing it with statistical estimations of these quantities for finite perturbations to the ENM force constant (see Methods). The perturbation theory is only accurate for infinitesimally small σ_k (standard deviation of the perturbations to the ENM force constant). Here we will explore how its inaccuracy increases as σ_k gradually increases from 0 to 1.

We have computed the robustness scores (see Methods) for the lowest 10 modes (see Fig. 1 a). The perturbation theory shows that modes 1–3 are the most robust (lowest robustness scores) (Fig. 1 a), whereas the least robust modes are modes 6 and 7. Comparison with the results of finite perturbations, with σ_k varying from 0.1 to 1.0, shows that the agreement is very good for σ_k = 0.1. As σ_k increases, the pronounced peak at modes 6 and 7 decreases, whereas the robustness scores of the other modes increase (Fig. 1 a). For 0.5 ≤ σ_k ≤ 1, modes 1 and 2 remain relatively robust, whereas the other eight modes have higher robustness scores. Therefore, the estimation of perturbation theory for mode robustness remains quantitatively accurate as long as σ_k < 0.3. At higher σ_k values, certain qualitative features (for example, modes 1 and 2 being the most robust) are still correctly captured. The finding of high robustness for modes 1 and 2 agrees with our recent finding that these two modes are most robust to sequence variations (14). The low robustness of mode 7 seems surprising given the previous suggestion (21) that it plays a functional role in coupling actin binding/release with nucleotide release/binding. We address this apparent paradox below, after introducing mode coupling analysis.

Figure 1.

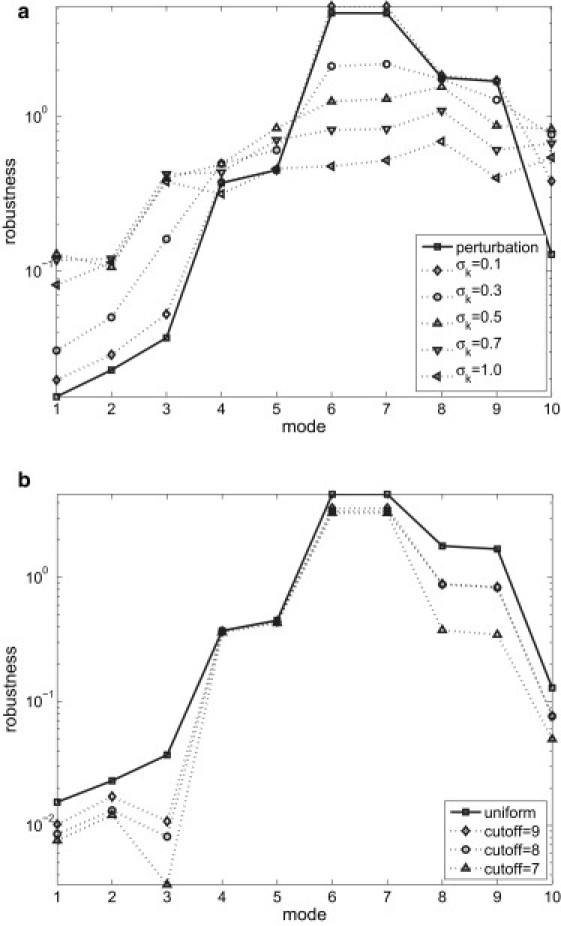
Robustness score, R_m (in logarithmic scale), for the lowest 10 modes of the myosin II structure (PDB code: 1VOM). (a) Solid lines show R_m computed using first-order perturbation theory, and dotted lines correspond to results for finite perturbations at five σ_k values. (b) Results of first-order perturbation theory in the presence of unrestricted and restricted Gaussian perturbations are shown as solid and dotted lines, respectively (the latter are restricted to nonconserved residue pairs with a given cutoff for conservation score). Note that a high (low) score means low (high) robustness.

In our earlier studies, we used first-order perturbation theory to estimate the robustness of normal modes to sequence variations (14,33). In these studies, we introduced sophisticated perturbations to residue-residue interactions, which are modulated by sequence variations. To investigate how the choices of different perturbations affect the results of mode robustness, we have modified the present perturbation protocol (see Methods) by restricting the Gaussian perturbations to those residue pairs involving at least one nonconserved residue. Here, a residue position is conserved if the conservation score from ConSurf-HSSP (46) (score ranges from 1 to 9, where 1 is most variable and 9 most conserved) is greater than or equal to a cutoff value (set to be 7, 8, or 9). Then the robustness scores are computed for the lowest 10 modes of 1VOM in the presence of the “restricted” perturbations (see Fig. 1 b). Although the robustness scores are quantitatively reduced, the relative robustness of the lowest 10 modes is qualitatively preserved. In particular, modes 6 and 7 still have the highest scores, whereas modes 1–3 have the lowest scores. Therefore, the results of mode robustness are qualitatively insensitive to the choice of different perturbations to the force constant.

We have computed the strength of coupling (see Methods) between the lowest 10 modes, and the results are shown in Fig. 2. The perturbation theory predicts three strongly coupled mode pairs, (6, 7), (4, 5), and (8, 9) (see Fig. 2 a), with the strongest coupling for mode pair (6, 7). These strong mode couplings account for the high robustness scores for modes 4∼9 (see Eq. 8 in Methods), especially modes 6 and 7. In contrast, modes 1–3 are minimally coupled with all the other modes, resulting in their low robustness scores.

Figure 2.

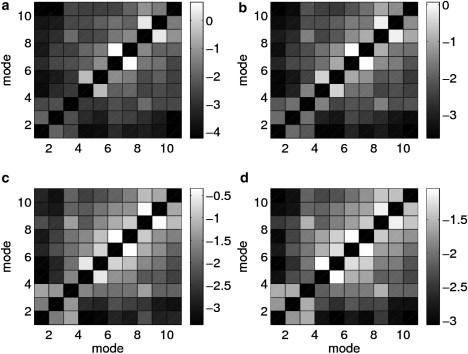
Coupling strength, C_mn (in logarithmic scale), between the lowest 10 modes of the myosin II structure (PDB code: 1VOM), which are computed using first-order perturbation theory (a), and at finite perturbations of three different magnitudes: σ_k = 0.3 (b), σ_k = 0.5 (c), and σ_k = 1.0 (d). The gray scale is used to illustrate mode coupling strength.

We compare the mode-coupling results of the perturbation theory with their counterparts for finite perturbations with σ_k varying from 0.3 to 1.0 (Fig. 2, b–d). The agreement is very good for σ_k = 0.3—the same three strongly coupled mode pairs are found (Fig. 2 b). As σ_k further increases, stronger coupling arises between the three pairs (for example, between modes 6 and 7 and mode 5), but the couplings within these pairs remain higher than the couplings between them (Fig. 2, c and d). Therefore, perturbation theory gives a qualitatively correct prediction of the three strongly coupled mode pairs that persists even for relatively large perturbations (for σ_k up to 1.0). In particular, the very high coupling between modes 6 and 7, also found for finite perturbations, is not an artifact of perturbation theory caused by near-degeneracy of these two modes.

The finding that mode 7 is strongly coupled with modes 5 and 6 explains its low robustness. Nevertheless, this does not rule out the functional relevance of mode 7. On the contrary, mode 7 is strongly coupled to modes 5 and 6 to attain variations of functional motion between different members of a protein family (see below). Indeed, if we consider perturbations to the ENM force constant due to sequence variations between myosin isoforms (33), it is very likely that the eigenvectors of the strongly coupled modes would be mixed in a perturbed normal mode spectrum. Therefore, to reliably deduce functional motions and their variations in myosin, the strongly coupled modes should be analyzed together.

Biological implications of mode couplings in myosin

Next we discuss the potential roles of mode coupling in tuning the allosteric couplings among the actin-binding site, the nucleotide-binding site and the converter/lever arm in the myosin motor domain (see Fig. 4 inset). To this end, we will dissect the motions involving the four subdomains (see Fig. 4 inset), as described by the three pairs of strongly coupled modes, by performing a dynamic domain partition analysis (see Methods).

Mode pair (6, 7)

Mode 7 describes a rotation of the U50 subdomain (Fig. 3, #7, cyan) accompanied by rotations of two other dynamic domains—one consisting of the lower half of the relay helix, part of the converter, and part of the N-terminal subdomain (green), and the other comprised of part of the converter (yellow). The first rotation of U50 appears to couple the closing of the actin-binding cleft with the opening of the nucleotide-binding site (near switch I, see (21)). The other two rotations involve the relay helix, converter, and the N-terminal subdomain. Therefore, mode 7 couples actin binding with distant movements in the N-terminal and converter subdomains, which are potentially relevant to the powerstroke. In comparison, mode 6 describes a rotation of the U50 subdomain (Fig. 3, #6, cyan) similar to that of mode 7 (the rotational axes are pointed in similar directions (Fig. 3, #7)). However, the motions of the other subdomains differ significantly between these two modes, especially in the relay helix and the converter, which belong to different dynamic domains (Fig. 3, #6, yellow, and Fig. 3, #7, green). Therefore, a variable mixing of these two modes can couple a similar rotation of the U50 subdomain with a variety of movements in the relay helix and the converter. This may allow different myosin isoforms, with varied residue-residue interactions, to couple actin binding to different movements in the converter, leading to variations in the force-generation process between myosin isoforms.

Figure 3.

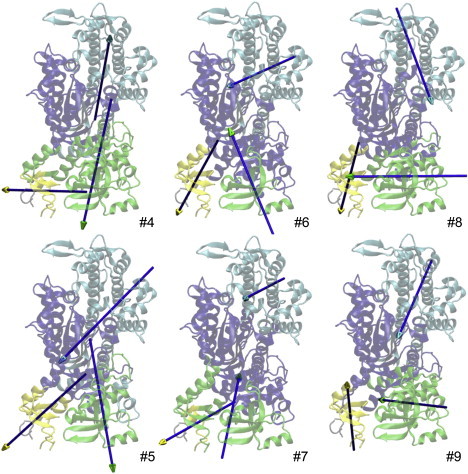
Results of dynamic domain partition for modes #4–9. Dynamic domains are shown in four different colors (see online version) (blue, cyan, green, yellow), and their directions of rotation with respect to a fixed domain (blue) are shown by arrows. The flexible parts not belonging to any domain are gray. The head (stem) of an arrow is assigned the same color as the moving (fixed) domain.

Mode pair (4, 5)

Unlike mode pair (6, 7), modes 4 and 5 describe similar rotations in the N-terminal subdomain (Fig. 3, #4 and #5, green), but different rotations in the U50 subdomain (Fig. 3, #4 and #5, cyan) and converter (Fig. 3, #4 and #5, yellow). Therefore, a combination of these two modes can couple a similar rotation of the N-terminal subdomain with a range of movements in the U50 and converter subdomains.

Mode pair (8, 9)

Modes 8 and 9 share similar rotations in the U50 subdomain (Fig. 3, #8 and #9, cyan) and the N-terminal subdomain (Fig. 3, #8 and #9, green), but they differ in the converter (Fig. 3, #8 and #9, yellow). Therefore, similar to mode pair (6, 7), this coupling can facilitate variable allosteric coupling between the converter and the U50 subdomain.

In summary, the strong couplings within the three mode pairs are likely to be functionally significant by allowing isoform-dependent tuning of allosteric couplings among the actin-binding site, the nucleotide-binding site, and the converter in myosin. The residues involved in the coupling of these three mode pairs (see Methods) are shown in Table 1. For example, residues involved in the coupling of mode pair (6, 7) are mostly distributed in the N-terminal subdomain, relay helix, SH1 helix, and converter, indicating the importance of these regions in tuning the allosteric coupling between actin binding and converter movement. The biological significance of the predicted mode coupling can be tested by mutational experiments that perturb the residues involved in the mode coupling. We propose that these targeted perturbations modulate allosteric couplings, and alter the motor properties of myosin.

Table 1.

Residues involved in the modeling coupling in myosin II

Mode pair	Residues involved in mode coupling
4, 5	7, 19, 34, 36, 37, 44, 45, 46, 47, 52, 60, 70, 71, 72, 77, 78, 79, 83, 95, 96, 97, 98, 104, 231, 233, 234, 368, 391, 392, 395, 396, 397, 398, 399, 400, 403, 404, 405, 406, 407, 408, 409, 410, 485, 508, 573, 593, 595, 646, 658, 659, 660, 662, 668, 669, 673, 674, 682, 683, 686, 723, 739 (62 total)
6, 7	7, 16, 18, 19, 21, 25, 28, 29, 36, 37, 44, 45, 46, 47, 72, 77, 78, 80, 82, 83, 84, 86, 97, 98, 104, 105, 112, 121, 397, 398, 399, 404, 407, 420, 485, 486, 488, 490, 493, 494, 496, 497, 501, 504, 505, 506, 509, 590, 591, 593, 629, 649, 650, 651, 652, 668, 669, 673, 674, 687, 690, 691, 692, 693, 695, 696, 697, 698, 699, 701, 702, 705, 706, 712, 713, 715, 720, 723, 734, 739, 741, 742, 744, 745 (84 total)
8, 9	7, 16, 18, 19, 20, 21, 25, 27, 28, 29, 32, 33, 34, 37, 45, 46, 51, 52, 53, 60, 72, 74, 76, 77, 78, 79, 80, 82, 83, 84, 86, 89, 94, 97, 99, 100, 112, 153, 194, 216, 397, 399, 404, 407, 494, 496, 499, 501, 575, 591, 629, 668, 673, 674, 677, 682, 683, 689, 690, 691, 692, 695, 699, 701, 712, 723, 731, 732, 733, 734, 735, 736, 737, 738, 739, 742, 746 (77 total)

Robustness of the allosteric couplings in myosin

Finally, we revisit the allosteric couplings in the myosin motor domain in our previous study (21). Here, we assess the robustness of four correlation functions (see Methods) that quantify the observed coupled structural changes between the nucleotide-binding site (including P loop, switch I, and switch II) and another two key sites, the actin-binding site (38–40) and the converter (37) (see Fig. 4 inset).

The directions of movement in these sites are obtained by aligning their conformations between a prepowerstroke structure of Dictyostelium myosin (PDB code: 1VOM) and a postpowerstroke rigorlike structure of myosin V (PDB code: 1W8J). The two myosins can be structurally aligned because their sequences are 41% identical. Four movements in the above sites are observed from the prepowerstroke structure to the postpowerstroke structure (see Fig. 4):

• 1.Opening of switch I (residues 233–238, using the residue numbers of Dictyostelium myosin, same below) relative to the P loop (residues 179–186);
• 2.Opening of switch II (residues 454–459) relative to the P loop;
• 3.Closing of the actin-binding cleft, indicated by a relative rotation of the HO helix of the U50 subdomain (residues 411–441) with respect to the helix-loop-helix (HLH) motif of the L50 subdomain (residues 510–553);
• 4.Downward rotation of the converter (residues 692–747) relative to the N-terminal subdomain (residues 80–178).

To test whether the above movements are coupled by the normal modes calculated from the prepowerstroke structure, we computed four correlations (see Methods) between movement 1/2 and movement 3/4, as follows:

• 1.The correlation between the opening of switch I and the closing of the actin-binding cleft (Fig. 5 a) is found to be positive and significant (C₁₂ = 0.042, ${\sigma }_{C_{12}}$ = 0.015, so Z ∼ 2.8). Its highest contribution is from mode 7, supporting the importance of this mode in allosterically coupling the actin-binding site and the nucleotide-binding site (21).
• 2.The correlation between the opening of switch II and the closing of the actin-binding cleft (Fig. 5 b) is weak and insignificant (C₁₂ = 0.0078, ${\sigma }_{C_{12}}$ = 0.0098, so Z ∼ 0.8). This weak correlation results from cancellation between positive and negative contributions from individual modes. Therefore, switch II is not directly coupled to actin binding.
• 3.The correlation between the opening of switch I and the downward rotation of the converter (Fig. 5 c) is positive and significant (C₁₂ = 0.038, ${\sigma }_{C_{12}}$ = 0.013, so Z ∼ 2.9). Its highest positive contribution is from mode 7, supporting the importance of this mode in allosterically coupling the converter and the nucleotide-binding site (21). We note that mode 2 gives a large negative contribution to this correlation that is cancelled by positive contributions from other modes, resulting in a positive net correlation. Therefore, it is important to analyze the net effects of all modes instead of focusing on a single mode.
• 4.The correlation between the opening of switch II and the downward rotation of the converter (Fig. 5 d) is also positive and significant (C₁₂ = 0.026, ${\sigma }_{C_{12}}$ = 0.011, so Z ∼ 2.4). Its highest contribution is from mode 8, supporting the importance of this mode in allosteric coupling.

Figure 5.

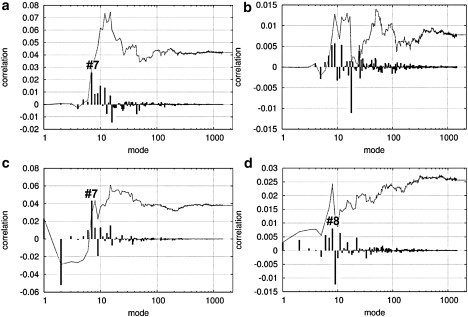
Correlation functions between (a) opening of switch I and closing of the actin-binding site (C₁₂ = 0.042, ${\sigma }_{C_{12}}$ = 0.015); (b) opening of switch II and closing of the actin-binding site (C₁₂ = 0.0078, ${\sigma }_{C_{12}}$ = 0.0098); (c) opening of switch I and downward rotation of the converter (C₁₂ = 0.038, ${\sigma }_{C_{12}}$ = 0.013); and (d) opening of switch II and downward rotation of the converter (C₁₂ = 0.026, ${\sigma }_{C_{12}}$ = 0.011). The solid line shows the cumulative correlation as a function of the cutoff mode (see Methods), and the impulses show the contributions from each mode (see Methods). The mode number is shown in logarithmic scale to clearly illustrate the positions and contributions of low-frequency modes.

Therefore, the present correlation analysis has validated in silico the “structural coupling rules” deduced from structural comparisons (37–40). In particular, the observed coupled motions from the prepowerstroke structure to the postpowerstroke structure are encoded in the former structure. Furthermore, we have uncovered a new coupling between the opening of switch I and the downward rotation of the converter. Therefore, actin binding may be indirectly coupled to the downward rotation of the converter, with the signal being transmitted through switch I.

Discussion and Conclusion

In this study, we have focused on the robustness of ENM-based normal modes to variations in the strength of elastic interactions instead of the network connectivity, because the former is amenable to quantitative comparison with first-order perturbation theory. To further explore the mode robustness to variations in network connectivity, we have examined the effects of varying the cutoff distance, R_c (with the addition of random Gaussian noise of ${\sigma }_{R_c}$ = 1 or 2 Å). The resulting robustness scores, R_m, are qualitatively similar to the curve of σ_k = 1.0 in Fig. 1 a—the lowest two modes have low R_m values, whereas the remaining eight modes have high R_m values. Therefore, our first-order perturbation theory makes qualitatively sound predictions for mode robustness to variations in both the interaction strength and the network connectivity.

Our study shows that the mode robustness analysis should be combined with the mode coupling analysis to identify groups of strongly coupled modes, which must be analyzed together to deduce meaningful information about protein functional motions. Although some functionally relevant modes are found to be robust individually (14,31), others are robust not by themselves but as a group (i.e., multiple collective motions can dominate protein functions). Mode coupling allows Nature to fine-tune protein conformational changes and thereby achieve functional diversity based on a common structural architecture. More case studies along the lines proposed here will offer a more complete understanding of both conservation and variation in protein conformational dynamics and the associated functions.

Our results are consistent with the finding by Tama and co-workers (45) that a few low-frequency normal modes can describe the observed conformational transitions, although they may be mixed by a changing coarseness of model representation. In our formulation, the modes involved in the observed conformational transitions form a “robust group”, the members of which may be strongly coupled to each other, leading to mixing between them, but are weakly coupled to outsiders, which explains the robust description of the observed conformational transitions. Therefore, it is important to use the mode coupling analysis proposed here to assess the robustness of a group of coupled modes for meaningful analysis of protein functional dynamics.

By supplementing the ENM-based NMA with the assessments of mode robustness and mode coupling of the low-frequency modes, we have found a valid and efficient way to systematically explore the effects of parameter uncertainty in ENM-based modeling, and to evaluate the statistical significance of the results. This study lays a useful framework for using ENM-based modeling to predict combinations of modes that are important for functions. In addition, our study highlights the structural mechanism by which similar proteins (such as myosin II) in various organisms carry out functions with varying efficiency.