Modeling Effects of Human Single Nucleotide Polymorphisms on Protein-Protein Interactions

Abstract

A large set of three-dimensional structures of 264 protein-protein complexes with known nonsynonymous single nucleotide polymorphisms (nsSNPs) at the interface was built using homology-based methods. The nsSNPs were mapped on the proteins' structures and their effect on the binding energy was investigated with CHARMM force field and continuum electrostatic calculations. Two sets of nsSNPs were studied: disease annotated Online Mendelian Inheritance in Man (OMIM) and nonannotated (non-OMIM). It was demonstrated that OMIM nsSNPs tend to destabilize the electrostatic component of the binding energy, in contrast with the effect of non-OMIM nsSNPs. In addition, it was shown that the change of the binding energy upon amino acid substitutions is not related to the conservation of the net charge, hydrophobicity, or hydrogen bond network at the interface. The results indicate that, generally, the effect of nsSNPs on protein-protein interactions cannot be predicted from amino acids' physico-chemical properties alone, since in many cases a substitution of a particular residue with another amino acid having completely different polarity or hydrophobicity had little effect on the binding energy. Analysis of sequence conservation showed that nsSNP at highly conserved positions resulted in a large variance of the binding energy changes. In contrast, amino acid substitutions corresponding to nsSNPs at nonconserved positions, on average, were not found to have a large effect on binding affinity. pKa calculations were performed and showed that amino acid substitutions could change the wild-type proton uptake/release and thus resulting in different pH-dependence of the binding energy.

Introduction

Each individual possesses unique characteristics reflecting their genotype, i.e., the uniqueness of the individual's DNA (1). For example, almost all nucleotide bases (99.9%) are exactly the same in all people; however, the remaining 0.1% account for ∼1.4 million individual-specific differences (single nucleotide polymorphism, SNP) that occur in humans. These differences may be within the coding or noncoding regions of DNA and may or may not result in amino acid changes, which, in turn, can either be harmless or disease causing (2). From a computational biophysics point of view, SNPs resulting in amino acid changes (nonsynonymous SNP, nsSNP) are of particular interest because such changes should affect the stability of proteins and protein-protein complexes.

From a biological perspective, the major factor contributing to the complexity of biological systems is the high degree of connectivity on the molecular scale. In particular, many proteins responsible for cellular functions rely on interactions with other proteins to perform these functions. If the structures of the corresponding protein-protein complexes are available, then we will have the opportunity to apply theoretical biophysical methods to model the energetics of protein-protein complexes (3–9) and apply the results in structure-based drug design (10). Thus, understanding protein-protein interactions and their roles in cell function will help reveal the molecular mechanisms of protein recognition and model the effect of perturbations on biological network, in particular, the effects of nsSNPs on protein-protein interactions (11–14).

The effects caused by nsSNPs can be broadly grouped into four distinctive categories (15) (although the effects may be mutually dependent) depending on what type of system or process have been affected by nsSNPs: 1), protein folding, stability, flexibility, and aggregation; 2), functional sites, reaction kinetics, and dependence on the environmental parameters, such as pH, salt concentration, and temperature; 3), protein expression and subcellular localization; and 4), protein-small molecule, protein-protein, protein-DNA, and protein-membrane interactions (see review and references within (15)). Among these categories, the effect of nsSNPs on protein stability (16–18) attracted most of the attention of the scientific community. The mechanisms of the effect of nsSNPs on protein stability could vary from geometrical constraints (the mutation of a small side chain to a bulky side chain in the protein interior), to physico-chemical effects (replacement of hydrophobic residue with polar residue), to the reversal of a charge within a salt bridge, or to the disruption of hydrogen bonds (19). For example, the nsSNPs resulting in changes of functionally important residues should be almost always deleterious as they would block protein function (20,21). However, since there are only a few functional residues within an entire protein sequence, the probability for such mutations is low (22). The possibility of an nsSNP affecting the subcellular location of a corresponding protein was reported in a recent study that showed that in ∼1% of cases the disease is caused by protein subcellular delocalization (23). In addition to the above mentioned effects, nsSNPs can change the kinetics of the corresponding reactions as was experimentally shown in patients with chronic lymphocytic leukemia (24) and inflammatory diseases (25), or they can affect pharmacokinetics (26); however modeling these effects is computationally difficult. Although studies of the consequences of nsSNPs on proteins have drawn much attention recently, the effect of nsSNPs on protein-protein interactions has not been extensively investigated. This lack of attention may be a result of an insufficient number of three-dimensional (3D) structures of protein-protein complexes for which nsSNPs are known.

The recent progress made in experimental 3D structure determination, led by the Structural Genomic Initiatives (27), in addition to advances in computational modeling (28,29), have made it possible to predict the effects of nsSNPs by mapping them on corresponding structures or on protein and protein-protein models. Indeed, structural information was used in many studies to reveal the role of SNPs on protein function and stability. A recent study on human nsSNPs and disease-associated mutations in orthologous genes revealed that ∼70% of disease-associated mutations were in protein sites that most likely affect protein function (30–33). Moreover, it was found that disease mutations are much more likely to occur at sites with low solvent accessibility (32). Recently, a structure-based approach that models residue-residue interaction networks was reported (34). It applied graph theoretical measures to predict the residues that are important for structural stability. These results imply that nsSNPs impact protein function and stability by affecting their structures, which in turn might cause changes in protein-protein or protein-ligand interactions.

It should be mentioned that most of the efforts in the field so far have been aimed at predicting deleterious mutations, since such predictions could be used for early diagnostics and potential drug discovery (23,31,32,35–38). However, the goals of our study are: 1), to investigate the possibility that disease-causing and harmless nsSNPs affect protein-protein interactions differently, and 2), to reveal the basic principles of the effects of naturally occurring interfacial nsSNPs on protein-protein interactions. The rationale behind our approach is that any mutation at a protein-protein complex interface should, in principle, somehow affect the binding energy, and even harmless nsSNPs can also cause dramatic changes in the phenotype resulting in natural differences among individuals. To deduce the effect of nsSNPs on protein function, further investigation of the effect of nsSNPs on protein-protein interaction network is needed, combined with detailed analysis of the importance of the perturbed interactions for normal cellular function.

In this study, we use homology modeling to construct 3D models of a large number of protein-protein complexes (264) with known nsSNPs at their interfaces. The effect of amino acid substitution resulted from nsSNPs on the protein-protein binding energy was calculated using a standard force field (CHARMM (39)), in contrast to previous studies that applied descriptors or semiempirical functions. In addition, specific attention was paid to possible ionization changes and charge reorganization caused by the nsSNP mutations. The calculated effects are grouped into categories that describe several distinctive mechanisms of nsSNPs affecting the energetics of protein-protein interactions. The role of charge relaxation is also investigated.

Methods

Sequence alignment, template detection, and model building

The first task was to extract query amino acid sequences associated with nsSNPs and to search for available 3D structures or for 3D structures that are homologous to the query sequences. The locus-id files for humans were downloaded from build 126 of the dbSNP database, which contains the SNPs associated with gene names and locations on genes. These files also included accessions for protein sequences associated with the SNPs. The protein sequences, which were found to be associated with SNPs, were compared against the set of human protein structures (potential structural templates) (National Center for Biotechnology Information (NCBI) Molecular Modeling DataBase (MMDB)) (40), using Blast algorithm (41). The human structures that were found at an E-value of 10E–5 or better were kept, resulting in 5.6 millions alignments. If a 3D structure of a query protein was available, no modeling was required. Query proteins that matched any of the entries in the Online Mendelian Inheritance in Man (OMIM) database (42–44) were marked as “annotated” disease-causing. The rest of the entries were considered undetermined with respect to possible disease association and are referred to in the article as “nonannotated” or “non-OMIM”.

At the second stage of processing, additional criteria were used requiring that 80% of the query sequence be mutually aligned with the structural template (nsSNPs that were not mapped in the alignment were discarded). Only templates corresponding to protein-protein (or domain-domain) complexes were used for modeling 3D structures of nsSNP-containing sequences. During this procedure, we recorded whether or not the SNP was on the interface for each chain/domain pair. It was done using query-template Blast alignments. Interface residues were defined as those being 8 Å from each other (distance was measured between Cα atoms) on different chains/domains (45). These positions were flagged as interfacial residues.

The detected templates and corresponding sequence alignments were used as input for the homology modeling. The 3D models were built with the NEST program using the sequence alignment between queries and structural templates (46). Identical alignments were discarded. The number of models built for different degrees of modeling difficulty were as follows: 1), 1257 models were built by side chain replacement where query and template sequences differed only by a few residues and the models were built by mutating corresponding residues in the original chain and 2), 5274 models were built with the NEST program. Because of the restrictive alignment criteria applied above, in most of the cases, the alignment had very few gaps/insertions, and thus the models were very close to the template structures. In total, 6531 protein models were constructed that corresponded to the first allele (the first allele in case of OMIM is the dominant allele, whereas in the case of non-OMIM it is simply the first allele in the list). Then the monomeric proteins models were joined to the corresponding partners using the 3D structure of the template protein-protein complex. The models of complexes were then evaluated according to the flagged interfacial positions, and only models with nsSNPs occurring at the interface of protein-protein complexes were retained for our study, resulting in 264 model structures.

Energy minimization

The structures of the 264 complexes were subjected to the TINKER package (47) using the CHARMM27 force field parameters (39). The minimization was done running the TINKER's minimize.x module. The minimize.x module performs energy minimization using the Limited Memory BFGS Quasi-Newton Optimization algorithm (47). The implicit solvent was modeled using the Still Generalized Born model (48), and the internal dielectric constant was set to 1.0 to be consistent with the CHARMM27 force field parameters (49). The convergence criteria applied was root mean-squared (RMS) gradient per atom = 0.01. For energy minimization calculations, we utilized a High Throughput Distributed Computing Resource, CONDOR, originally developed at the University of Wisconsin-Madison (www.cs.wisc.edu/condor), which is now available at Clemson University with more than 1080 single central processing units (CPUs) of computational power.

The minimized 3D structures of the complexes with amino acids corresponding to the first reported allele in the dbSNP database were then used to generate the corresponding nsSNP mutations. Utilizing the SCAP program (50), the mutations, corresponding to either the second allele in the dbSNP database or the disease-causing nsSNP in OMIM database, were introduced using the above minimized model 3D structures, while keeping the rest of the structure rigid, including the hydrogen atoms. In case of homooligomeric-complexes, the nsSNP mutations were introduced on both monomers. Then, the resulting 3D structures were minimized again with TINKER using the same protocol that was described above.

Binding energy calculations

The binding energy was calculated with the so-called rigid body approach keeping the structures of the monomers as they were in the complexes. Such an approach is advantageous because the internal mechanical energies of the unbound and bound monomers are the same and do not have to be included in the calculations of the binding energy. Thus, the single point calculations result in binding energy

$$\Delta \Delta G\left(\text{binding}\right)=\Delta G\left(\text{complex}\right)-\Delta G\left(A\right)-\Delta G\left(B\right),$$ (1)

where ΔG(complex), ΔG(A), and ΔG(B) are the unfolding free energy for the complex, monomer A, and monomer B, respectively. The total binding energy and its two components (electrostatics and van del Waals) were analyzed. The electrostatic component of the binding energy is the sum of the Coulombic and reaction field energies as described in detail in (51,52):

$$\Delta G_{\text{el}}\left(X\right)=G\left(\text{coul}\right)+\Delta G\left(\text{rxn}\right),$$ (2)

where X stands for the complex, A and B monomers, respectively. G(Coul) is the Coulombic interaction energy, and G(rxn) is the reaction field energy, which is calculated with Delphi program (51,52).

The total binding energy is

$$\Delta G_{\text{tot}}\left(X\right)=\Delta G\left(\text{bonds}\right)+\Delta G\left(\text{vdW}\right)+\Delta G\left(\text{el}\right),$$ (3)

where ΔG(bonds) are the bonded energy terms, ΔG(vdW) is the van der Waals energy, and ΔG(el) is the Coulombic interactions and solvation energy calculated with the Generalized Born (GB) model. However, since we adopted the rigid body approach, ΔG(bonds) for the complexes and free monomers is the same and cancels in Eq. (3). All of the above energy terms were calculated with the analyze.x module in TINKER. The nonpolar component of the binding energy was not included in the calculations because the single point mutation is not expected to change the binding interface significantly.

Changes in protein stability caused by the nsSNP mutation were calculated with respect to the energy of the target (the first reported allele or wild-type allele in case of OMIM nsSNPs) protein. The corresponding quantity is ΔΔΔG(nsSNP), as described below:

$$\Delta \Delta \Delta G\left(\text{nsSNP}\right)=\Delta \Delta G\left(\text{target:binding}\right)-\Delta \Delta G\left(\text{nsSNP:binding}\right)\text{.}$$ (4)

The changes of the total binding energy (ΔΔΔG_tot(nsSNP)), as well as the change of its vdW (ΔΔΔG_vdw(nsSNP)) and electrostatic (ΔΔΔG_el(nsSNP)) components are analyzed in this work. If the change is negative, this indicates that the nsSNP mutation weakens the affinity and destabilizes the complex, whereas if the change is positive then the mutant binding is tighter.

Multiple sequence alignment

Protein sequences from different species were downloaded from the NCBI Entrez database, using GENE search option and submitting each of the gene's ID as a query. Only cases for which a protein was found in more than four species were considered, and the multiple sequence alignments (MSAs) were built resulting in 227 out of the total 264 sequences. We used the European Bioinformatic Institute's ClustalW2 web service (http://www.ebi.ac.uk/Tools/clustalw2/index.html) to perform MSAs.

pKa calculations of the ionizable states and proton uptake/release

The pKa values of the ionizable groups were calculated using the Multi Conformation Continuum Electrostatics (MCCE) method as previously described (53–55). Recently, we demonstrated that MCCE can be utilized to calculate pKas using 3D structures that were built by homology (56). Calculations were performed for all 264 protein complexes corresponding to the first allele, and another set of pKa calculations were done for the protein complexes with corresponding nsSNP mutation. The calculations were also performed on the corresponding unbound monomers, whose structures were taken from the corresponding protein-protein complex. These results were used to predict the changes of the titratable groups' ionization states caused by complex formation. For each complex, we calculated the difference of the net charge (Δq(X)) of the complex and of the unbound monomers, called proton uptake/release:

$$\Delta q\left(X\right)=q(X:\text{complex})-q\left(X\text{:}A\right)-q(X:B),$$ (5)

where X is the first allele or nsSNP variant, and q is the net charge of the complex and of monomer A and B, respectively, calculated with MCCE at a pH of 7.0. We chose a pH of 7.0 because there was no information of what the physiological pH is for each of the proteins studied in this manuscript. In addition, we analyzed the proton uptake/release difference between complexes with the first allele and the nsSNP variant:

$$\Delta \Delta q=\text{abs}(\Delta q\left(\text{dominant allele}\right)-\Delta q\left(\text{nsSNP}\right))\text{.}$$ (6)

p-Value calculations

The p-values were calculated performing a t-test (57–59). The distributions of the corresponding changes of the binding energy and its components in case of OMIM and non-OMIM sets were checked against the null hypothesis. A large p-value indicates that the corresponding distribution is similar to the normal distribution (null hypothesis), whereas a small p-value points out a deviation from random distribution. A typical cut-off for p-value is 0.01, i.e., distribution with the p-value smaller than 0.01 is considered significantly different from random. The distribution of the variance of ΔΔΔG_tot(nsSNP) and ΔΔΔG_el(nsSNP) was checked against the null hypothesis that assumes equal variances. The SI% scale was divided into five bins, corresponding to cases with SI% smaller than 20%, 20% < SI% < 40%, 40% < SI% < 60%, 60% < SI% < 80, and 80% < SI% < 100%. The variance of the corresponding energies was calculated within each of the bins and the resulting p-value evaluated. In case of ΔΔq, six bins were considered: 0.00 < ΔΔq < 0.05, 0.05 < ΔΔq < 0.10, 0.10 < ΔΔq < 0.15, 0.15 < ΔΔq < 0.20, 0.20 < ΔΔq < 0.25, and ΔΔq > 0.25. Then, the variance of the corresponding energies within these bins and the p-value were calculated.

Results and Discussion

Distribution of binding energy

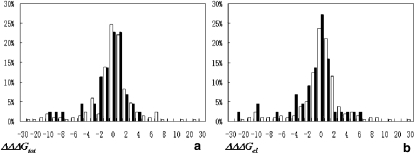
The changes in the total binding energy and its electrostatic and vdW components due to the nsSNPs were calculated for all complexes in the data set (Fig. 1, Table 1). The distributions of ΔΔΔG_tot(snSNP) for OMIM and non-OMIM cases are shown in Fig. 1 a. It can be seen that the distributions have similar shapes, showing a slight tendency toward negative values. The mean values of electrostatic (ΔΔΔG_el(snSNP)) and vdW (ΔΔΔG_vdw(snSNP)) components of the binding energy changes are statistically different for OMIM and non-OMIM cases (p-values are <0.006 and 0.01, respectively), although this is not the case for the total binding energy. Fig. 1 b shows the distribution of ΔΔΔG_el(snSNP) for both OMIM and non-OMIM cases. One can see the long negative tail of the distribution of OMIM cases for which nsSNP substitutions destabilize binding. Moreover, the mean of OMIM distribution of electrostatic energy is significantly different from zero and shifted toward negative values although this is not the case for non-OMIM distribution of electrostatic component (Table 1). This indicates that, overall, there is a tendency for OMIM nsSNP substitutions to weaken the electrostatic component of the binding energy, although there are many examples where disease nsSNPs make binding tighter as well. The effect is less pronounced for the total binding energy.

Figure 1.

Distribution of ΔΔΔG_tot(nsSNP) and ΔΔΔG_el(nsSNP) in kcal/mol for OMIM and non-OMIM cases. Solid bars, OMIM; open bars, non-OMIM.

Table 1.

Parameters of distributions of total binding energy difference and their components in kcal/mol together with the corresponding p-values (the null hypothesis that mean value ≥ 0 is rejected if p < 0.01)

Group	No.	ΔΔΔGtot			ΔΔΔGvdw			ΔΔΔGel
		Mean	Std	p-Value	Mean	Std	p-Value	Mean	Std	p-Value
OMIM	45	−1.65	3.80	0.003	−1.03	3.32	0.02	−2.35	5.51	0.003
Non-OMIM	219	−0.70	4.36	0.009	0.14	3.03	0.75	−0.45	4.39	0.06
Polar (P)	62	−0.27	3.77	0.28	0.38	3.94	0.77	−0.83	4.74	0.09
Charge (C)	76	−2.01	6.38	0.004	−0.33	2.25	0.1	−1.37	6.59	0.04
Small (S)	94	−0.74	2.39	0.002	−0.03	2.49	0.45	−0.78	2.58	0.002
Hydrophobic (H)	32	0.32	2.50	0.77	−0.36	4.46	0.32	0.74	3.23	0.09

From an electrostatic point of view, replacing the wild-type amino acid (dominant allele) at a protein-protein interface with another amino acid (amino acid which corresponds to nsSNP) is expected to be a destabilizing event. Indeed, in our previous study of 654 protein-protein and domain-domain complexes, we demonstrated that the electrostatic component of the binding energy tends to be optimized (60) with respect to random shuffling of the amino acid sequences of the corresponding binding partners. Thus, since wild-type (dominant allele) interactions across the interface are optimized, any change should make the binding affinity weaker. Indeed, the destabilization effect upon disease substitutions is the most pronounced in case of the electrostatic component of binding energy (ΔΔΔG_el distributions is shifted toward negative values with a p-value of <0.003). However, the tendency of OMIM mutations to destabilize the electrostatic component of the binding energy is not very strong, which perhaps stems from the fact that nsSNP substitutions are not random, rather they are constrained mutations accepted by the cell. At the same time, for non-OMIM substitutions the electrostatic component should be optimized for both alleles and consequently the mean of ΔΔΔG_el(nsSNP) is not statistically significantly different from zero (p-value is 0.06).

Despite the differences, in the majority of the cases, both OMIM and non-OMIM substitutions were calculated to have little effect on binding. Since we investigate nsSNP substitutions at the interface of protein complexes, this observation deserves further investigation. The next sections investigate possible patterns and correlations between different types of amino acid substitutions and their calculated effects on binding energy.

Effect of nsSNPs on binding energy with respect to amino acid characteristics

In this section, four different classes of amino acids were considered based on the amino acids' physico-chemical properties: polar (S, T, H, N, Q, Y), charged (E, D, K, R), hydrophobic (W, I, L, M, F), and small (P, A, G, C, V). We adopt this simplified classification to ensure that each class has enough representatives in our data set. Of course, many other classifications exist, including more detailed definitions of the subgroups. Below we investigate the effects of nsSNP mutations on the ΔΔΔG_tot(snSNP), ΔΔΔG_vdw(nsSNP), and ΔΔΔG_el(nsSNP) separately for each class (more detailed analysis including analysis of the effects of substitutions between classes is given in the Supporting Material).

Binding energy changes caused by a substitution of a polar amino acid

There are 62 cases in our data set for which a polar residue corresponding to the first allele and located at the interface of the protein-protein complex is substituted by another variant (Table 1). Overall, there is no statistically significant bias for energy to be shifted upon substitution toward lower or higher values.

From an electrostatic point of view, a polar→another amino acid substitution tends to be an unfavorable event in the majority of cases (p = 0.09). In another words, removal of a polar group at the interface, despite structural refinement, makes electrostatic binding energy less favorable. Further analysis of such cases showed that a removal of a polar residue disturbs the hydrogen bond network at the interface. Substitution of a polar residue with either small, charged, or hydrophobic groups tends to make the electrostatic component of binding weaker. A small residue will create energetically unfavorable cavities, a charged residue will pay a large desolvation penalty, and a hydrophobic residue will not be able to provide the required hydrogen bonds. However, exceptions are cases when a polar group is replaced by another polar residue whose side chain can satisfy the required geometry. In the last case, the electrostatics may not change or even become more favorable.

A particular example of a polar→hydrophobic substitution is shown in Fig. 2 a. It demonstrates that removal of a polar residue and substitution with a hydrophobic residue results in the placement of the hydrophobic side chain in a polar environment, an event that weakens the binding affinity. A typical case is Transthyretin (TTR), which is a plasma protein that binds retinol and thyroxine. Many distinct forms of amyloidosis are related to different nsSNPs in TTR. For example, the nsSNP (refSNP ID: rs11541784) results in a change of the polar (Ser) residue into a hydrophobic residue (Phe). The nsSNP Phe residue is located in a polar environment and reduces the binding affinity by 0.717 kcal/mol.

Figure 2.

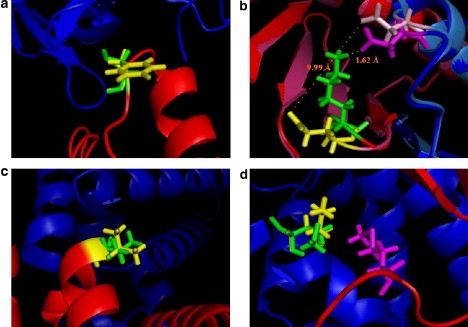
Illustration of nsSNPs at interface of protein-protein complexes: (a) TTR (transthyretin, gene ID: 4507725), red, A chain; blue, E chain; green, Ser in A85; yellow, F in A85; magenta, N in E63. (b) DYNLRB1 (Roadblock-1, gene ID: 7661822), red, A chain of target; light red, A chain of SNP variants; blue, B chain of target; sky blue, B chain of SNP variant; green, K in A75; yellow, E in A75; magenta, D in B61 of target; pink, D in B61 of SNP variant. (c) HBB (β-globin, gene ID: 4504349), red, B chain; blue, C chain; green, V in B34; yellow, L in B34. (d) GSTM2 (glutathione S-transferase M2, gene ID: 4504175), red, A chain; blue, B chain; green, M in A130; yellow, K in A130; magenta, M in B50.

Binding energy changes caused by a substitution of a charged amino acid

There are 76 cases in our data set in which a charged residue located at the interface of the target protein-protein complex is substituted in the nsSNP variant (Table 1). The values of the means of ΔΔΔG_tot(nsSNP) and its electrostatic component ΔΔΔG_el(nsSNP) are negative and this bias is statistically significant (p-values 0.004 and 0.04, respectively), which means that the target protein-protein complexes are more stable compared to the nsSNP variants.

Substituting a charged with another residue is, overall, an unfavorable event with respect to protein-protein association (Table 1). Removal of a charged residue that forms a salt bridge across the interface in the target complex leaves the charged partner without favorable pair-wise interactions. The remaining charged residue pays a huge desolvation penalty upon complex formation, which in the nsSNP variant may not be compensated by favorable pair-wise interactions. This provides an intuitive explanation why distributions of both the ΔΔΔG_tot(nsSNP) and ΔΔΔG_el(nsSNP) are shifted toward negative values.

The mutation of a charged amino acid to another charged amino acid (charged→charged) is an interesting case. The mutation could preserve the charge (Asp ↔ Glu; Lys ↔ Arg) or invert the charge (Asp,Glu ↔ Lys, Arg). Presumably, a mutation that preserves the charge should have a lesser effect on the binding energy as compared with charge-reversal mutations. However, our analysis showed that this is not always the case. Overall, all mutations of the target charged residue to another charged residue were found to be unfavorable events (Table 1). Even in the case of Glu to Asp substitutions, like aldolase B (Glu to Asp in position 64), which is a mutation (refSNP ID: 2854709) that preserves the net charge of the complex, the change of the binding energy is huge: ΔΔΔG_tot(nsSNP) = −9.06 kcal/mol, ΔΔΔG_vdw(nsSNP) = −1.58 kcal/mol, and ΔΔΔG_el(nsSNP) = −11.30 kcal/mol. This change is due to the fact that the side chain of Asp is shorter than the Glu side chain, and the nsSNP introduced Asp cannot form a strong salt bridge with the original partner Lys in position 270 of the other chain in this homo-dimer complex. Another example (Fig. 2 b) is the case of charge reversal in Roadblock-1 (DYNLRB1), which is a homo-dimeric protein that may be involved in tumor progression, as the upregulation of this gene is associated with hepatocellular carcinomas. The corresponding nsSNP (refSNP ID: rs11537531) of this protein results in the change of a Lys amino acid to a Glu amino acid at the complex's interface. In the target protein complex, the distance between Lys75 from chain A and its partner Asp61 from chain D is only 1.62 Å, resulting in a very strong hydrogen bond and pair-wise electrostatic interactions. However, in the nsSNP variant, the positively charged Lys is replaced by Glu, a negatively charged residue. Due to minimization, the distance between the nsSNP residue and the original Asp61 from chain D increases to 9.99Å because of the repulsive charge-charge interaction between the two negatively charged groups (Fig. 2 b). This reduces the effect, but the binding energy is still much less favorable as compared with the dominant allele. The corresponding energy changes are ΔΔΔG_tot(nsSNP) = −11.13 kcal/mol, ΔΔΔG_vdw(nsSNP) = −4.42 kcal/mol, and ΔΔΔG_el(nsSNP) = −3.08 kcal/mol. This is an example of a structural relaxation that reduces the effects of charge reversal.

Binding energy changes caused by a substitution of a small amino acid

There are 94 cases in our data set for which a small residue located at the interface of the target protein-protein complex is substituted into the nsSNP variant (Table 1). Overall, the total binding energy and electrostatic components are significantly (both p-values are 0.002) shifted toward negative values, which indicates that nsSNP destabilizes the complex.

Substitution of a small with another amino acid almost always will result in sterical clashes. The volume of a small amino acid is much smaller than the volume of the other residues. Thus, there will be no room for a bulky amino acid side chain at the interface. Such a replacement will cause distortion of the interface and will weaken the binding (Table 1). A typical example is the histidine triad nucleotide binding protein 1 (HINT1), Gene ID: 4885413. The nsSNP codes for Gly to Arg substitution in position 92 of B chain. The substitution introduces a new charged residue, which pays a large desolvation penalty, and the resulting change in the electrostatic component of the binding energy ΔΔΔG_el(nsSNP) is −9.23 kcal/mol).

However, there are also opposite examples, indicating that protein complexes can tolerate small amino acid substitutions at the interfaces. A typical example is Human β-globin (HBB), which regulates developmental expression. The corresponding nsSNP (refSNP ID: rs1141387) in this protein replaces a Val residue with a Leu amino acid. Despite the difference in these two amino acids' volumes, the structure of the complex does not change by much, resulting in smaller energy differences: ΔΔΔG_tot(nsSNP) = −0.98 kcal/mol, ΔΔΔG_vdw(nsSNP) = −0.01 kcal/mol, and ΔΔΔG_el(nsSNP) = −1.21 kcal/mol (Fig. 2 c). The main reason for this small difference is that both side chains are partially exposed to the solution, and there is room for a larger Leu side chain.

Binding energy changes caused by a substitution of a hydrophobic amino acid

There are 32 cases in our data set in which a hydrophobic residue located at the interface of the target protein-protein complex is substituted by the nsSNP variant (Table 1). The mean values of all energy distributions are not significantly different from zero. In general, substituting a hydrophobic residue at the interface with another residue does not have a large effect on protein-protein binding. Perhaps this is due to the fact that hydrophobic groups do not form specific interactions. Thus, the effect of a replacement of a particular hydrophobic side chain with another residue depends on the geometry of the interface and the ability of the substituted side chain to form new interactions. For example, a polar or charged residue, substituting a hydrophobic one, could increase the binding affinity only if the corresponding residue manages to create new favorable interactions across the interface. If this does not occur, then the mutation should weaken the binding. Such a case is shown in Fig. 2 d. Glutathione S-transferase M2 (GSTM2) is an important enzyme that contributes to the metabolism of phase II biotransformation of xenobiotics. The corresponding nsSNP (refSNP ID: rs1056799) changes the target amino acid Met to Lys in position A130. However, the new charged residue cannot form favorable interactions with any other residue across the interface since it is in a hydrophobic environment. As a result, the solvation loss cannot be compensated for, and the mutation weakens the binding.

Correlation of the calculated effect on the binding affinity and residue conservation

MSAs were used for phylogenetic analysis and for determining the evolutionary relationships between different species. Only positions corresponding to interfacial sites were considered. A position in the MSA that is totally or highly conserved indicates strong evolutionary constraints, and the substitution of such a highly conserved amino acid is expected to have significant effects on protein structure, function, and interactions. In contrast, an amino acid that is not conserved among different species is, perhaps, not crucial for the structure, function, and interactions of that particular protein complex.

We began our analysis with a case corresponding to a highly conserved site. Position B34 in human β-globin (HBB) is totally conserved among the species (Fig. 3 a). The nsSNP causes a mutation that changes Val residue to Leu. As result, the total binding energy, van der Waals and electrostatic components are more favorable in the target complex compared with the nsSNP variant. The corresponding changes of the binding energy are ΔΔΔG_tot(nsSNP) = −0.98 kcal/mol, ΔΔΔG_vdw(nsSNP) = −0.01 kcal/mol, and ΔΔΔG_el(nsSNP) = −1.21 kcal/mol.

Figure 3.

MSA. Blank frame is nsSNP position. (a) HBB (β-globin, gene ID: 4504349); (b) GSTM2 (glutathione S-transferase M2, gene ID: 4504175).

Another example is glutathione S-transferase M2 (GSTM2) (Fig. 3 b). Position A130 is not conserved; in humans it is a Met residue, however, in other species the same position is a Lys amino acid. The nsSNP induces a Met → Lys change in the human protein, a mutation that is already seen in other species. Perhaps this explains why such a drastic change (a hydrophobic to a charged group) has little effect on the binding affinity. The corresponding changes of the binding energy are ΔΔΔG_tot(nsSNP) = −0.53 kcal/mol, ΔΔΔG_vdw(nsSNP) = 0.28 kcal/mol, and ΔΔΔG_el(nsSNP) = −0.26 kcal/mol.

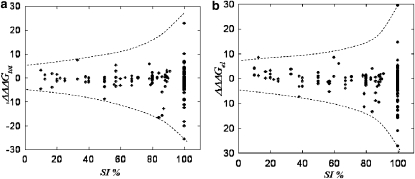
The magnitude of the binding energy change as a function of the degree of conservation is shown in Fig. 4. It can be seen that as the degree of conservation increases (calculated in terms of percent identity, SI%) the maximal amplitude of both the ΔΔΔG_tot(nsSNP) and the ΔΔΔG_el(nsSNP) increases as well (illustrated by the broken lines in Fig. 4). The effect culminates at high SI% (SI% > 80%) where the variance of the magnitude of both the ΔΔΔG_tot(nsSNP) and the ΔΔΔG_el(nsSNP) is significantly different, i.e., the null hypothesis about the equality of variances between the bins was rejected with p < 0.00001 (see Methods section). Note that this result corresponds to significant variance of the binding constant resulting to either increase/decrease or no change of the affinity. The points located close to the horizontal axis and corresponding to highly conserved positions (Fig. 4) indicate that in some cases, a mutation of a highly conserved amino acid may not affect the binding affinity. In these cases, the effect depends on the geometry of the interface and where the site is situated. These highly conserved sites are predominantly located at the periphery of the binding interface and apparently are not important for the binding affinity. Fig. 4 provides indirect support demonstrating that the calculated effects are reasonable, since no large binding energy change was calculated to be associated with nonconserved positions in the MSA.

Figure 4.

Change of the binding energy in kcal/mol as a function of the amino acid conservation (SI%). The broken lines are guides for the eye and follow the maximal amplitude of binding energy change. (a) ΔΔΔG_tot(nsSNP); (b) ΔΔΔG_el(nsSNP).

Effect of nsSNPs on proton uptake/release

Fig. 5 shows the change of the corresponding binding energy as a function of the absolute difference of the proton uptake/release for target complexes and an nsSNP variant calculated at pH = 7.0. No correlation between either the magnitude or variance of the binding energy change and ΔΔq was found. At the same time, it can be seen that most ΔΔq are close to zero, indicating that at least around a pH of 7.0 the pH-dependences of the binding energy are the same for the target complex and the nsSNP variant. However, this is not necessarily the case for the entire pH-dependence. At the same time, there is significant percentage of cases in which the ΔΔq is different from zero. This indicates that nsSNP mutations not only change the binding energy but also result in a different pH-dependence of the binding. This could have a significant physiological importance; however, there is practically no experimental data available for comparison.

Figure 5.

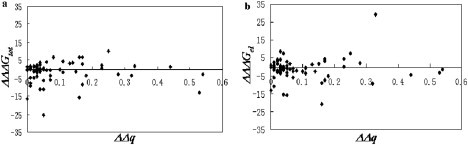
Change of the binding energy in kcal/mol as a function of calculated proton uptake/release (absolute value of ΔΔq). (a) ΔΔΔG_tot(nsSNP); (b) ΔΔΔG_el(nsSNP).

In general any substitution can lead to ionization changes. The above results indicate that amino acid substitutions corresponding to nsSNPs not only change the binding energy but could also result in changes in the ionization states of the titratable groups. Such an effect could occur not only when a titratable group is involved in the target→ nsSNP mutation but could also occur in each of the other cases as well. This is because any substitution changes the geometry of the interface and thus affects the electrostatic potential of all ionizable residues. However, in this study we did not perform charge relaxation, i.e., no attempt was made to adjust the residues' ionization states according to the pKa calculations because the calculated proton uptake/release is a fractional number. Modeling fractional ionization in single point calculations is impossible and any attempt would be an error (see for details (61)). However, a more sophisticated approach involving ensemble presentation could take into account these ionization changes and will result in a reduction of the magnitude of the energy change caused by the nsSNP mutation. Thus, all of the data points (Fig. 5) corresponding to ΔΔq that are significantly different from zero may get closer to ΔΔΔG (nsSNP) = 0, i.e., closer to the horizontal axis. Perhaps this is an effect that occurs in vivo and results in toleration of nsSNP mutations. Site-directed mutagenesis experiments and complementary numerical calculations have proven the charge-compensatory effect (62–64). Perhaps, the charge-compensatory effect is the reason that maximal ΔΔq (Fig. 5) is only ∼0.6 units, despite that some nsSNPs cause charge reversal.

Conclusion

This analysis is focused on nsSNPs located at protein-protein interfaces. Protein-protein interactions are essential for cell function, and nsSNPs affecting these interactions are expected to have significant impacts on the protein interaction network. Indeed, our analysis showed that OMIM and some non-OMIM nsSNP might have a significant effect on binding energy especially on the electrostatic component. Although the effect is statistically significant, the majority of amino acid substitutions corresponding to nsSNP does not affect the binding affinity by much. This observation should be taken with caution. A small change of the binding affinity by a kcal/mol or even less could still disrupt the functionality of the interaction network or change the kinetics of the corresponding reaction (24,25). However, investigating this effect requires modeling protein-protein networks, a task that is far beyond the goals of this study.

Two data sets were considered in this study: nsSNPs that are known to be disease-causing (OMIM data set) and nsSNPs that were not annotated to be disease-causing (non-OMIM). The distributions of the change in the binding energy and its components in both the OMIM and non-OMIM cases were found to be different although the difference is small. However, looking at the electrostatic component of the free energy we found that it is significantly shifted toward negative values for OMIM nsSNP, while this is not the case for non-OMIM nsSNPs. This indicates that disease-causing nsSNPs tend to destabilize the electrostatic component of protein-binding energy, in contrast with non-OMIM nsSNPs.

Although a large number of nsSNPs did not affect protein interactions by much (perhaps showing the plasticity of protein interfaces and their ability to tolerate amino acid changes), an even larger fraction of the nsSNPs did affect the affinity. In fact, about half of nsSNPs destabilize/stabilize the complexes by more than 1 kcal/mol. In addition, we find that 31.8% of nsSNPs affect protein-protein binding by more than 2 kcal/mol and 23.9% by more than 3 kcal/mol.

As was mentioned previously, in the case of non-OMIM complexes there is no information about which nsSNP is the dominant allele. However, our numerical protocol builds a 3D model of the first allele in the list, minimizes the structure, and then introduces a side chain mutation at the nsSNP position and minimizes the mutant structure. Could this protocol bias the calculations? Since ΔΔΔG(nsSNP) is a difference between two binding energies, the change of the order will simply change the sign of the ΔΔΔG(nsSNP). If the numerical protocol is not biased, then we should see that the effect of, for example, a P→C mutation is opposite to the effect of a C→P variation. Comparing the means reported in the Supporting Material, Table S1, we can see that this is the case, except for C→H and H→C (in both cases the means of the distributions of ΔΔΔG_tot(nsSNP) were found to be negative). However, this is the smallest subset in our study composed of only five cases, many more examples are needed to draw a conclusion.

Another important issue to address is how sensitive the results are in respect to the computational protocol and force field used. Recently we have demonstrated that the calculations of absolute value of the binding energy are very sensitive to both computational protocol and force fields (65). The same study (65), however, found that the distribution of the binding energy and the general trends are almost insensitive to the force field and protocol used. Since this study is not aimed at computing the absolute binding energy, but rather the change of the binding energy upon single amino acid substitution, the effects of force field and computational algorithm are expected to largely cancel out.

It is expected that a mutation that changes the physico-chemical property of a position at the interface of the corresponding protein-protein complex should affect binding affinity. However, our results indicate that this is not necessarily the case. The outcome of the mutation depends on a variety of factors, whose interplay determines the effects of the substitution. In addition, some positions are located in structural regions that allow for structural relaxations. From an energetics perspective, an amino acid substitution may not always affect the binding affinity. An example includes a charged residue for which the favorable pair-wise interactions are almost entirely cancelled by an unfavorable desolvation penalty. Another example is weak hydrogen bonds formed at the interface. A third example is a partially exposed hydrophobic residue at the periphery of the interface. Substitution of such residues with another may not affect the binding affinity; in fact, the nsSNP mutation could strengthen the binding.

A highly conserved position within the protein sequence is often related to an important biological function. Multiple sequence alignment analysis showed that most of the positions corresponding to interfacial nsSNPs in our data set are highly conserved. It was shown that the variance of the total binding energy and its components of the highly conserved positions is larger as compared with the variance of positions with lower conservation. However, a significant fraction of nsSNP occurring at conserved positions was calculated not to change the binding energy by much. This observation indicates that conservation of amino acids in certain interface positions does not occur to preserve binding affinity. Rather, such conservation may reflect the preservation of the binding mode or specificity. An interesting case is an nsSNP mutation that introduces an amino acid found in another species. Since such a mutation was evolutionarily accepted in the other species, the overall effect on protein-protein affinity is expected to be small. In further work, we will explore this observation and will determine the effects of introducing mutations to any other 20 amino acids.

We showed here that that the change of the binding energy from the target complex to the nsSNP variant is not related to the conservation of the net charge, hydrophobicity, or hydrogen bond network. This result implies that one cannot simply use the physical-chemical properties of amino acids to evaluate the effects an nsSNP has on protein-protein interactions. Rather, as we have done here, detailed structure-based energy calculations must be performed to predict these effects.