The Origin of Short Transcriptional Pauses

Abstract

RNA polymerases are protein molecular machines that transcribe genetic information from DNA into RNA. The elongation of the RNA molecule is frequently interrupted by pauses, the detailed nature of which remains controversial. Here we ask whether backtracking, the central mechanism behind long pauses, could also be responsible for short pauses normally attributed to the ubiquitous pause state. To this end, we model backtracking as a force-biased random walk, giving rise to a broad distribution of pause durations as observed in experiments. Importantly, we find that this single mechanism naturally generates two populations of pauses that are distinct both in duration and trajectory: long-time pauses with the expected behavior of diffusive backtracks, and a new class of short-time backtracks with characteristics similar to those of the ubiquitous pause. These characteristics include an apparent force insensitivity and immobility of the polymerase. Based on these results and a quantitative comparison to published pause trajectories measured with optical tweezers, we suggest that a significant fraction of short pauses are simply due to backtracking.

Introduction

The ability of cells to adapt to environmental conditions, to reproduce, and to serve varying roles within an organism critically depends on the control of gene expression (1). A major part of this regulation occurs at the level of transcription, which is traditionally divided into an initiation, elongation, and termination phase. During elongation, the RNA polymerase (RNAP) molecule moves along the DNA template creating an RNA copy of the genetic information. This motion typically exhibits two different modes: bursts of rapid elongation, interspersed by pauses with a vanishing mean velocity. Pauses appear to be induced by a variety of mechanisms, and pause locations and lifetimes are stochastic and biased by template sequence (2). Generally, pauses can be classified into pause states where the enzyme either forms an inactive configuration without appearing to displace along the DNA template, or pauses where the enzyme forms an inactive configuration by displacing in the rearward direction along the DNA template. Both classes of pauses have been studied extensively with biochemical and single-molecule techniques. Examples of the first type of pauses include a state that is stabilized by a RNA hairpin forming in the nascent transcript (3,4), and the ubiquitous pause (5) (both with lifetimes <25 s). The ubiquitous pause is thought to correspond to an internal structural rearrangement of the enzyme, but has not been characterized at the biochemical level (6). The second type of pause is referred to as a backtrack, manifesting itself through a displacement of the RNAP molecule in the upstream direction opposite to normal transcriptional elongation (7–10). Pauses from both classes may be preceded by yet another pause state, the elemental pause (11). This pause is not discussed here, since its lifetime is too short to show up in single molecule data. While the backtracked pause is expected to be sensitive to a force applied along the direction of the backtracking displacement, the lifetimes and density of nontranslocated pause states are insensitive to such forces (5). While nontranslocating pauses simply act to reduce the overall rate of transcription during elongation, backtracking is also implicated as a prerequisite for removing copy errors by transcript cleavage and contributes significantly to transcriptional fidelity (12–14). The general structure of the DNA-RNA-RNAP complex is maintained while backtracked, preserving the nine-basepair hybrid between the nascent RNA and the DNA template strand (see Fig. 1 a). Upon backtracking, the polymerase moves rearwards and the polymerization reaction ceases until the enzyme is realigned with the polymerizing 3′ end of the RNA molecule. However, the enzyme can reside in different translocation states while backtracked (10); and since no chemical energy is consumed, the associated motion can be described as a one-dimensional random walk along the DNA strand (15–18).

Figure 1.

(a) Schematic drawing of RNAP with an applied assisting force f. The integer n corresponds to the number of RNA bases that protrude past the active site. (b) Corresponding schematic free-energy landscape. (c) The return time distribution normalized to the particles that return within a finite time. Due to this normalization and the specific assumption that the transition state is centrally positioned, δ = a/2, the distribution is invariant with respect to f → −f. (Inset) Chance of returning within a finite time, $p_{\text{ret}}={\int }_0^{\mathrm{\infty }}\Psi \left(t\right)\mathrm{d}t$, as a function of force. For negative forces, only the fraction exp {f/f₀} returns, where f₀ = kT/a ≈ 12 pN at physiological conditions.

It has previously been suggested that backtracking may be able to account for both short- and long-time pauses, since a random-walk mechanism can give rise to a nonexponential distribution of pause durations (15,19). While this is an attractive explanation for the experimentally measured broad distribution of return times (5,15,19), it is not clear that this simple mechanism alone will generate the two distinct populations of pauses that are observed. Here we show that a random-walk pause scheme will naturally do this, and is able to account for characteristics of the short-time ubiquitous and long-time backtracked pauses. Specifically, we calculate the force dependence of such pauses and their respective average trajectories, and compare these to published experimental data. This comparison enables us to determine the basic hopping time between adjacent states while backtracked, an important parameter that directly sets the characteristic lifetime of the short pauses. Interestingly, this time coincides with the lifetime of ubiquitous pauses, thus showing that backtracking alone will generate many short pauses that are hard to distinguish experimentally from the ubiquitous pause. We therefore suggest that a significant fraction of short pauses are not caused by ubiquitous pausing but instead result from backtracking.

The Model

We model backtracking as diffusion in a one-dimensional free-energy landscape (15–19) (see Fig. 1 b), focusing on general characteristics that survive averaging over different template sequences (5,10,15). Unbounded random energy landscapes can, in principle, give rise to anomalous diffusion (20,21). Because the energy landscape of the backtracking polymerase is strictly bounded by the possible states of the nine basepair hybrid, the enzyme will undergo normal diffusion. We therefore ignore sequence dependence, and in the absence of an overall forcing, we take the free-energy landscape to be periodic. Each free-energy minimum corresponds to a displacement of the polymerase by an integer number of basepairs from the active elongation position. The application of a force f tilts the free-energy landscape by adding the energy fa per step, with a = 0.34 nm being the physical extent of a basepair. The landscape is bounded on one side by an absorbing state corresponding to the active elongation pathway. The hopping rates between the free-energy minima are given by Kramers rates (22,23) (see Fig. 1 c),

$$k_{\text{out}}=k_0\exp \left\{\frac{f\delta }{k_{\mathrm{B}}T}\right\},k_{\text{in}}=k_0\exp \left\{-\frac{f(a-\delta )}{k_{\mathrm{B}}T}\right\}\text{.}$$ (1)

Here, k₀ is the bias-free hopping rate and δ describes the physical distance along the force coordinate from a free-energy minimum to a putative transition state (see Fig. 1 b).

In this model, the duration of a backtrack corresponds to a first-passage time, the calculation of which is extensively discussed in the literature (24). The particular problem considered here is that of a discrete random walk with an absorbing boundary (see Fig. 1 b) and is easily solved for the conditional probability of being at site n at time t, given that we were at site m at time 0 (25,26),

$$P(n,t|m,0)={\left(\frac{k_{\text{in}}}{k_{\text{out}}}\right)}^{\frac{n-m}{2}}\exp \left\{-(k_{\text{out}}+k_{\text{in}})t\right\}$$

$$\left[I_{n-m}(2t/t_0)-I_{n+m}(2t/t_0)\right]\text{.}$$

Here the characteristic stepping time $t_0=1/\sqrt{k_{\text{out}}{k}_{\text{in}}}=\exp \{(a/2-\delta )f/k_{\mathrm{B}}T\}/k_0$ has been introduced, and I_n values are the modified Bessel functions (27). Independent of the direction stepped during a backtrack, the total number of paired bases in the RNA-DNA hybrid remains unchanged. Assuming that the reaction path for opening and closing basepairs is the same at both ends of the transcription bubble (see Fig. 1 a), one could argue that the transition state is likely to be positioned halfway between the free-energy minima (δ = a/2). In this case, the characteristic stepping time is simply t₀ = 1/k₀, and thus force-independent. In general, the position of the transition state might not be located halfway, and it might even depend on force, δ = δ(f).

Pause lifetimes and their force dependence

To allow for a comparison to experiments (5,15), we use the theoretical return time distribution to identify two characteristic times and discuss the effect of an externally applied force. Since the system always enters at and exits from the backtrack position n = 1, the probability distribution of first-passage return times t is given by (25)

$$\Psi \left(t\right)=k_{\text{out}}P(1,t|1,0)=k_{\text{out}}{e}^{-(k_{\text{out}}+k_{\text{in}})t}\frac{I_1(2t/t_0)}{t/t_0}\text{.}$$ (2)

This distribution has two characteristic times t₁ = t₀ and $t_2=1/{(\sqrt{k_{\text{out}}}-\sqrt{k_{\text{in}}})}^2$, which gives three asymptotic return time regimes (see Fig. 1 c). For pause durations t ≪ t₁, the probability density falls off exponentially with the rate k_out + k_in. For intermediate pause durations t₁ ≪ t ≪ t₂, the decay is algebraic with exponent −3/2. For larger t, the algebraic region is cut off by an exponential with characteristic time t₂. It should also be noted that, for opposing forces, only the finite fraction exp(f/f₀) of the pauses is able to exit, with the rest embarking on nonreturning excursions (see inset in Fig. 1 c). The distribution in Eq. 2 (see Fig. 1 c) agrees with pause-duration histograms collected in single molecule experiments (see (5), inset in Fig. 4 a; and (15), Fig. 3 c), showing that backtracking offers a simple explanation for the broad distributions observed. If backtracking was indeed the cause of most of the short pauses in this histogram (5), their characteristic duration would be of order of the hopping time t₀. The short-time regime of the experimental distribution has been fit with a time constant of ∼1 s (5), which suggests that the backtracking hopping time is of the same order. Single-molecule optical tweezer recordings of individual backtracked polymerases at basepair resolution do indicate that t₀ falls in this regime (see Fig. 5 in (28), and see below), lending credence to the above interpretation.

If backtracking was responsible for a significant fraction of all pauses, then pause lifetimes would be expected to display a dependence on externally applied force (6). However, this is not seen experimentally for short pauses with lifetimes <25 s (5). On the other hand, our theory predicts that an apparent insensitivity will arise when only the algebraic part of the distribution is sampled. If one measures pause durations larger than the maximal t₀ for the force range considered (due to experimental limitations (5,15)) and defines short pauses to be of a duration that is less than the smallest t₂, the lifetime of these short pauses will necessarily be insensitive to external force even though they are caused by backtracking.

Having discussed the general backtracking mechanism and how it could account for pauses of different durations, we now turn to an analysis of the typical trajectory, which is another characterizing feature of the different pause types. By direct comparison to published experimental data (10), we are also able to give a quantitative and independent estimate of the backtracking hopping rate t₀, which is crucial for the arguments above.

Average paths

Although the notion of a random walk mechanism underlying backtracking is generally accepted, it has not yet been fully appreciated that this implies that most backtracks must be of short duration and only go back a few bases. In what follows, we demonstrate that long and short backtracks are very different in terms of the average backtracking path traversed, and each display distinct asymptotic behaviors characteristic of the two pause classes identified in experiments. These originate from the discreteness of the lattice: while the short-time backtracks are strongly dependent on the lattice spacing a, this spacing can be absorbed into an effective diffusion constant for the long-time backtracks. Experimentally recorded traces of short and long pauses display a clear difference in their respective mean trajectories (10). We find that this is also true for backtracks: short-time random walk backtracks hardly displace from the active configuration, whereas long-time diffusive backtracks enter on average with a large number of successive backward steps, and exit the pause in the reverse manner. The steep entrance and exit can be qualitatively understood, since to avoid a rapid exit one must start off by going far into the backtrack, and remain far away from the absorbing state until just before the time of return. To make this more quantitative, consider the probability of being at position n at time t, given an exit at time T. This probability is given by

$${\Pi }_T(\mathrm{n},t)=\frac{P(1,T|n,t)P(n,t|1,0)}{P(1,T|1,0)}=\frac{T{t}_0}{t(T-t)}\frac{n^2{I}_n(2(T-t)/t_0)I_n(2t/t_0)}{I_1(2T/t_0)},$$

which is invariant with respect to t → T − t and depends on force only through a possible rescaling of the characteristic stepping time t₀. With a transition state located halfway between two adjacent backtracked positions, this force dependence also vanishes (see above). The asymptotic forms of the average trajectory in the short- (S) and long- (L) time regimes separate into a penetration depth λ_{S, L} and a shape function Λ_{S, L} according to

$${\langle n\left(t\right)\rangle }_T\sim \{\begin{array}{ll}1+{\lambda }_{\mathrm{S}}(T/t_0){\Lambda }_{\mathrm{S}}(t/T),\hfill & t,T\ll t_0\hfill \\ {\lambda }_{\mathrm{L}}(T/t_0){\Lambda }_{\mathrm{L}}(t/T),\hfill & t,T\gg t_0\hfill \end{array},$$ (3)

with the asymptotic forms given by

$$\begin{array}{ll}{\lambda }_{\mathrm{S}}\left(x\right)={(x/2)}^2,\hfill & {\Lambda }_{\mathrm{S}}\left(y\right)=4y(1-y),\hfill \\ {\lambda }_{\mathrm{L}}\left(x\right)=2\sqrt{x/\pi },\hfill & {\Lambda }_{\mathrm{L}}\left(y\right)=\sqrt{4y(1-y)}\hfill \end{array}\text{.}$$

The shape functions and penetration depths are illustrated in Fig. 2, a and b. For short excursions, the polymerase only takes a few steps into the backtrack with a well-defined average velocity, and the average penetration depth for the entire backtrack scales as T². For long excursions, the polymerase takes many steps into the backtrack, the average path starts out diffusively, and the average penetration depth scales as $\sqrt{T}$. Here, the shape function Λ_L can be split into three distinct phases (see Fig. 2 b, right-hand panel). This is in good agreement with experimental observations where long backtracks can be split into three qualitatively different regimes (10), a rapid entry into the backtrack (phase I), followed by a longer and flatter region (phase II), and a rapid exit (phase III). Shaevitz et al. (10) present experimental data for the average of the initial time evolution for pauses lasting >20 s. From the above, one can show that the backtracking path becomes independent of the pause length T in region I of the long pauses,

$${\langle n\left(t\right)\rangle }_{\mathrm{L}}\sim \{\begin{array}{ll}1+2t/t_0,\hfill & t\ll t_0\hfill \\ 4\sqrt{\frac{t}{\pi t_0}},\hfill & t_0\ll t\ll T\hfill \end{array}\text{.}$$ (4)

The absence of a T dependence enables us to make a least-square fit of t₀ to the experimental data of Shaevitz et al. (10) over the time interval from the first entrance into the backtrack up to some suitable time t_max. Instead of using the above asymptotic forms, which would have to be matched to cover the full interval, we instead fit to a numerical approximation of the asymptotic form for a T ≫ t. The estimated value of t₀ and the mean-square residue is insensitive to t_max within the range of 0.5–2 s, and is best fit by t₀ = 0.54 s (using a force of f ≈ −8 pN as applied in the experiments; see Fig. 3). This time constant sets the lower corner time t₁ (t₁ = t₀, see Fig. 1 c) for short-time backtracks, and is of the same order as the short characteristic time constant of ubiquitous pauses (1.2 ± 0.1 s; see (5)). In conclusion, the bacterial polymerase appears to step approximately twice per second while backtracked, which will naturally give rise to a large number of short-time backtracks with a lifetime comparable to the one that has previously been associated with the ubiquitous pause.

Figure 2.

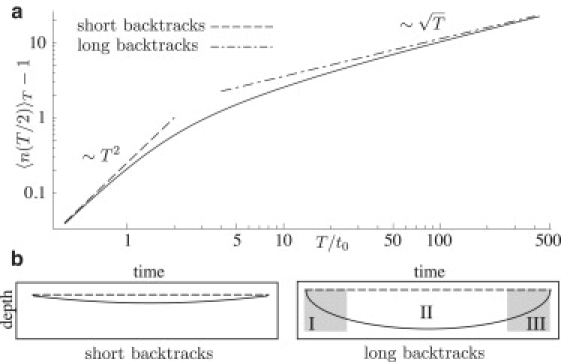
(a) The maximum depth of the average backtrack as a function of pause duration (computed numerically; solid line) and the corresponding short-time (dashed) and long-time (dash-dot) asymptotic behaviors. (b) An illustration of the average trajectory in the two regimes. Short trajectories remain shallow throughout the backtrack (left-hand panel), whereas long trajectories display the three regimes reported in Shaevitz et al. (10) (right-hand panel). They start diffusively in regime I with a steep entrance into the backtrack, remain at a distance in regime II, and return in regime III in a manner reverse to that of regime I.

Figure 3.

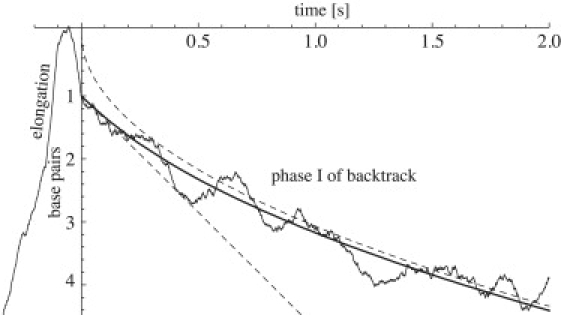
Single parameter fit of the asymptotic long-pause shape function for regime I to data from Shaevitz et al. (10), giving a characteristic time t₀ = 0.54 s (solid line). Also shown are the corresponding asymptotic curves of Eq. 4 (dashed lines). The best fit to a line has a mean-square error that is 3.5 times larger than the fit to the full theory presented here.

Discussion

Here we have asked whether backtracking, which is thought to be the central mechanism behind long pauses during transcriptional elongation, could also be responsible for short pauses normally attributed to the ubiquitous pause state. By modeling backtracking as force-biased diffusion in a periodic one-dimensional free-energy landscape, we demonstrate that the single mechanism of random walk backtracking naturally generates two classes of pauses: long-time pauses with the expected behavior of diffusive backtracks, and a novel class of short-time backtracks with characteristics similar to those ascribed to the ubiquitous pause. While sequence-induced variation in the backtracking rates will have a large effect on the lifetimes of short-time backtrack pauses, we do not expect such an effect for long-time backtracks since they sample many positions and effectively (self-) average over sequence. In accordance with this, a few sequence-specific short-time pause durations have been reported to be exponentially distributed (2) with varying time constants. To discern whether this exponential behavior crosses over to a power law behavior for longer pause durations (as we suggest here), large data sets are needed. Such large data sets are available when including data from all pauses (5,15), where the power-law regime predicted here is observed.

In summary, our analysis gives a simple explanation for the broad distribution of pause durations, the apparent force insensitivity of the lifetime of short-time pauses, as well as the distinct trajectory shapes observed in the experiment. Importantly, the characteristic time associated with short-time backtracks is similar to that of the ubiquitous pause state, as we show by a comparison to published single molecule pause trajectories. The obvious interpretation of these results is that a significant fraction of short pauses is simply due to backtracking, contrasting the view that short pauses are largely caused by the nontranslocating ubiquitous pause state. Since a couple of nontranslocating pauses of ∼1 s duration have been identified (2), exactly how many of the short pauses correspond to the ubiquitous pause state and how many correspond to a short-time backtrack remains to be determined.