Abstract
We present a biophysically based kinetic model of the cardiac SERCA pump that consolidates a range of experimental data into a consistent and thermodynamically constrained framework. The SERCA model consists of a number of sub-states with partial reactions that are sensitive to Ca2+ and pH, and to the metabolites MgATP, MgADP, and Pi. Optimization of model parameters to fit experimental data favors a fully cooperative Ca2+-binding mechanism and predicts a Ca2+/H+ counter-transport stoichiometry of 2. Moreover, the order of binding of the partial reactions, particularly the binding of MgATP, proves to be a strong determinant of the ability of the model to fit the data. A thermodynamic investigation of the model indicates that the binding of MgATP has a large inhibitory effect on the maximal reverse rate of the pump. The model is suitable for integrating into whole-cell models of cardiac electrophysiology and Ca2+ dynamics to simulate the effects on the cell of compromised metabolism arising in ischemia and hypoxia.
Introduction
Quantitative computational modeling has proven to be an important and successful tool for the analysis of electrophysiology and Ca2+ handling dynamics in cardiac myocytes during normal metabolic function (1). Recent examples of electrophysiological modeling frameworks formulated for a range of animal species include the models of Nobel et al. (2), Winslow et al. (3), Faber and Rudy (4), Matsuoka et al. (5), and ten Tusscher and Panfilov (6). These frameworks include descriptions of two key energy-dependent transporters: the Na+/K+ and the SERCA pumps, which play important roles in cell electrophysiology and Ca2+ dynamics, respectively. These models, however, become limited when attempting to simulate conditions brought about by changes in the energetic state of the myocyte such as ischemia, where cell metabolism is compromised. To overcome this issue of metabolic insensitivity, we have developed a new quantitative model of the cardiac SERCA pump following a similar approach adopted by Smith and Crampin (7) in developing a thermodynamically consistent model of the Na+/K+ pump.
The SERCA pump is a P-type ATPase enzyme found in all muscle cells, and functions to sequester Ca2+ into the sarcoplasmic reticulum (SR) to facilitate muscle relaxation. A number of different SERCA isoforms exist, and their expression is dependent on the muscle type. SERCA1a is expressed in fast twitch skeletal muscle whereas SERCA2a is found slow twitch and cardiac muscle (8). These two SERCA isoforms are functionally identical, except that in the native cardiac SR environment, SERCA2a is regulated by phospholamban. The major function of the cardiac SERCA-ATPase is to keep the cytosolic Ca2+ concentration low by pumping Ca2+ into the SR and maintaining a Ca2+ concentration gradient across the SR membrane that is approximately three orders of magnitude in size during diastole. During Ca2+-induced Ca2+ release, Ca2+ released from the SR increases the cytosolic Ca2+ concentration by an order of magnitude, which activates the contractile machinery and initiates muscle contraction. Muscle relaxation is then brought about by removal of Ca2+ from the cytosol which, under normal conditions, also results in restoration of the Ca2+ gradient across the SR membrane by the SERCA pump thereby preparing the cardiac myocyte for the next cardiac cycle. The SERCA pump is able to translocate Ca2+ against the concentration gradient by coupling the vectorial transport of Ca2+ across the SR membrane to the utilization of chemical energy via the hydrolysis of ATP. Two Ca2+ are translocated for each ATP that is hydrolyzed (9) according to the reaction
| (1) |
This reaction is fully reversible. The reversal condition depends on the relationship between the free energy of ATP hydrolysis and the energy required to transport Ca2+ against the concentration gradient (outlined in Methods, below).
Currently, there are no suitable biophysically based models of the cardiac SERCA pump that can be integrated into whole-cell and tissue frameworks for the purposes of simulating compromised metabolism. This is because existing models are not designed to be energetically sensitive and consistent with the fundamental principles of free energy transduction, or else they are simply too complex and computationally demanding. The most popular and simplest class of SERCA models is the phenomenologically based Michaelis-Menten description which typically involves three parameters: a Km; a cooperativity term, n; and a Vmax. These models depend solely on the cytosolic Ca2+ concentration and, due to their simplicity and computational efficiency, are often employed in whole-cell modeling frameworks that include descriptions of Ca2+ handling dynamics (Ca2+-induced Ca2+ release). A refinement to these models is a reversible model of the cardiac SERCA pump whose flux is a function of cytosolic and luminal Ca2+ concentrations (10). The model specifies a fixed physiological Ca2+ gradient across the SR membrane at normal physiological conditions, at odds with the thermodynamic requirement that this gradient should vary as a function of the free energy available from ATP hydrolysis and energy loss from Ca2+ leak. More-complex models typically focus on capturing, with varying success, the large number of partial reactions that make up the SERCA cycle. This is brought about by the complex interactions between the SERCA pump and various ionic species present in the cytosol (namely, Mg2+, K+, and H+) as well as its interaction with the metabolites MgATP, MgADP, and Pi. These models tend to be highly complex in terms of their structure and contain a large number of state variables and parameters. Examples of such models include those of Gould et al. (11) and Haynes and Mandveno (12). While they are highly detailed in terms of mechanism, their complex nature renders them unsuitable for whole-cell and tissue simulations.
Here we present a mathematical model of the cardiac SERCA pump that consolidates a variety of experimental data, collected from a range of modalities, and the fundamental principles of free energy transduction into a consistent single framework. We aim to develop a model of the SERCA pump in its native cardiac environment where it is intrinsically under the regulation of phospholamban. We employ a lumping scheme for rapid equilibrium partial reactions to simplify and reduce the number of model parameters, and simultaneously fit the model to a collection of experimental data that capture the dependence of the SERCA pump on Ca2+, H+, MgATP, MgADP, and Pi. This model enables integration of the SERCA function into whole-cell ventricular myocyte and continuum-based tissue models to simulate the effects on Ca2+ dynamics when cellular metabolism is compromised.
Methods
The kinetic model is based on the E1-E2 model for Ca2+ transport (13,14) with the addition of H+ binding steps (Fig. 83 of Bers (8)) to capture the pH dependence of the pump (Fig. 1). When the pump operates in the forward (clockwise) direction, two Ca2+ are bound from the cytoplasm and released into the SR lumen. This cycling is driven by the binding and hydrolysis of MgATP, followed by the release of the products MgADP, Pi, and a H+. The model has a total of 12 states, which is reduced to three states based on rapid equilibrium assumptions surrounding the ion binding steps. The model is solved as a steady-state solution and the parameters are simultaneously fitted to a diverse set of data that characterize the ionic and metabolic properties of the cardiac SERCA pump.
Figure 1.
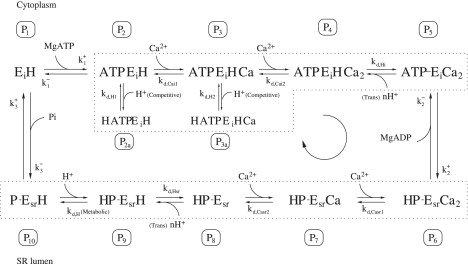
Schematic of the 12-state cardiac SERCA pump model. The binding of Ca2+ from both the cytosol and SR lumen is modeled as a partially cooperative mechanism with different Kd values for the first and second Ca2+ binding. There are five H+ binding events in the model: two for the competitive binding of H+ to the Ca2+-binding sites, two for the binding of H+ involved in the Ca2+/H+ counter-transport, and one for the release of the metabolic H+. The boxed Ps denote the probability of being in a particular state. The conformation change from E1 to E2 and back again occurs between states P5 and P6 (concomitant with ADP release), and P10 and P1 (concomitant with Pi release), respectively. For each cycle in the clockwise (forward) direction, the pump transports two Ca2+ for each ATP that is hydrolyzed. The dotted boxes indicate the partial reactions (ion binding) that are assumed to be rapid equilibrium steps (see Model Simplification: Rapid Equilibrium Assumptions). The subscripts i and sr are equivalent to 1 and 2 in the E1-E2 notation, respectively.
Ca2+ binding mechanism
In the E1-E2 model, the SERCA pump is assumed to have two Ca2+ binding sites with affinities for Ca2+ that depend on their orientations. When the binding sites are facing the cytosol, their affinity for Ca2+ is much higher than when they are facing the SR lumen, facilitating the binding, transport and subsequent release of Ca2+ into the SR. Experiments using radioactively-labeled Ca2+ have found that the Ca2+-binding sites bind Ca2+ in a sequential manner (15–19) and lead to the theorized existence of a narrow channel that consists of a deep and a superficial binding site (20). Moreover, the binding of the first Ca2+ into the deep site is followed by development of a higher binding affinity to the second superficial site, characterizing a positive cooperative binding mechanism (21). This sequential behavior is represented in the reaction scheme in Fig. 1 by the binding of Ca2+ between states P2 and P4. The second Ca2+ can bind only after the first Ca2+ has bound. The cooperative binding mechanism can be classified as being partially or fully cooperative. Cooperative binding can be represented mathematically by setting different binding constants for the first and second Ca2+ binding sites; partially cooperative binding is represented by a larger second Ca2+-binding constant while fully cooperative binding is represented by an instantaneous binding of the second Ca2+. In the case of fully cooperative binding, only one set of binding constants is necessary to characterize the reaction. A similar sequential and cooperative binding mechanism is also assumed when the binding sites orient themselves to face the SR lumen (19). We compare how well the SERCA model fits the data when the Ca2+-binding mechanism is modeled either as a partially cooperative binding scheme (Fig. 1) or as a fully cooperative binding scheme (Fig 2).
Figure 2.
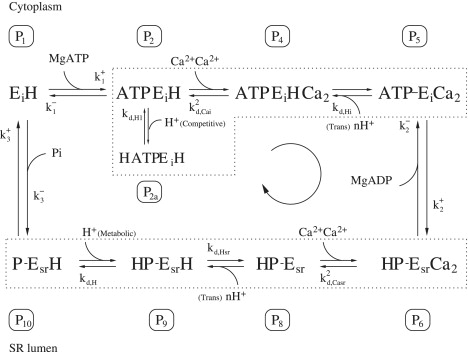
Schematic of cardiac SERCA model where the Ca2+ binding mechanism is assumed to be fully cooperative. States P3 and P3a no longer exist as they quickly evolve into P4 from the binding of the second Ca2+. Similarly in the SR lumen, state P7 has evolved into P6.
Ca2+/H+ counter-transport
The ejection of H+ from SR vesicles after the addition of Ca2+ and ATP has been observed by a number of experimental groups (22–24). The extent of the ejection is greater than can be accounted for by H+ production arising from ATP hydrolysis and is due to the counter-transport of H+ for Ca2+. A number of experimental groups have measured the stoichiometry to be 2:2 where 2 H+ are exchanged for 2 Ca2+ during each SERCA cycle at neutral pH (24,25). We incorporated this exchange of H+ into our model by assuming distinct H+ binding sites on the SERCA enzyme (between states P4 and P5 and states P8 and P9 in Fig. 1). The binding of H+ to SERCA, when the Ca2+-binding sites are facing the cytosol, has been placed between states P8 and P9, following titration experiments that have shown the ejection of H+ into the cytosol to occur after the binding of Ca2+ to the high affinity Ca2+-binding sites (23). The binding of H+ on the luminal side is assumed to be after the release of Ca2+. The stoichiometry of H+ binding in the SERCA model was left as an adjustable parameter in the fitting process as it has been suggested that the number of H+ extruded per cycle depends on pH (26). The native SR vesicle membrane is highly permeable to H+ and other monovalent ions, and abolishes the formation of any steady-state H+ gradient (27). Hence, the H+ concentration is assumed to be the same inside and outside of the SR.
Competitive H+ binding
Protons also directly compete with Ca2+ in binding to the two Ca2+ -binding sites on the SERCA enzyme (19). At decreasing pH levels, there is a progressive increase in the Km for the Ca2+ dose-response curve (28). This is modeled as a side reaction at states P2 and P3 of Fig. 1, where the enzyme can bind either Ca2+ or H+. In the model, the competitive H+ binding mechanism exists only when the Ca2+-binding sites are facing the cytosol and is not included for the case when they face the SR lumen. Whether this is sufficient to capture the pH-dependent data from Ji et al. (28) is investigated below.
Metabolite binding
When the pump is cycling in the forward direction, MgATP initially binds and phosphorylates the SERCA enzyme (29). This results in a slow conformational change in which the cytosol-facing Ca2+-binding sites now orient themselves to face the SR lumen and at the same time bring about a large decrease in Ca2+-binding affinity (13,14,27). Concomitant with the slow conformational change is a rapid dissociation of MgADP (30). This is followed by release of the other two hydrolysis products, the metabolic H+ and Pi, which is accompanied by a second conformational change that restores the Ca2+-binding sites back to their cytosol-facing orientation. The binding/unbinding of the metabolites MgATP, MgADP, and Pi along with the metabolic proton are all modeled as individual partial reactions. The MgADP dissociation step (between states P5 and P6), however, also encompasses the phosphorylation and subsequent conformational change of the enzyme, while the Pi dissociation step (between states P10 and P1) encompasses the second conformational change. In the model, MgATP binding is placed before binding of the first Ca2+. However, experimental literature suggests that Ca2+ can bind in both the presence and absence of MgATP (21,31). This implies that there may be two distinct MgATP and Ca2+ binding sites that can bind the ligands in any order. To investigate this, we have compared fitted models where MgATP binds before or after Ca2+ binding.
Thermodynamic constraints
The coupling of free energy available from the hydrolysis of ATP (ΔGMgATP) to the transport of Ca2+ into the SR lumen by the SERCA enzyme against a concentration gradient (ΔGSERCA) imposes a constraint on the system. This constraint determines the direction of the pump when the myocyte is metabolically compromised. Thermodynamic constraints are incorporated into the SERCA model following the techniques outlined in Smith and Crampin (7). Briefly, the free energy of ATP hydrolysis depends on the ratio of MgATP to its hydrolysis products as
| (2) |
where T is the temperature, R is the universal gas constant, and ΔGoMgATP is the free energy under standard conditions and is defined as ΔGoMgATP = −RTlnKMgATP (ΔGoMgATP = 11.9 kJ mol−1, taking [H+] into account). The energy required to move two Ca2+ against a concentration gradient is given by
| (3) |
The SERCA pump will cycle in the forward direction when ΔGMgATP + ΔGSERCA < 0, as is the case under normal physiological conditions and Ca2+ will be transported back into the SR, thereby allowing the muscle to relax. When the free energy of ATP hydrolysis drops, or when the Ca2+ gradient across the SR membrane changes such that the net free energy becomes zero, the pump will stop and cease to transport any more Ca2+. Should the free energy of ATP hydrolysis drop further, and the net free energy become positive, the pump will cycle in the reverse direction and generate ATP from ADP and Pi using the energy stored in the Ca2+ concentration gradient across the SR membrane. The thermodynamic considerations here indicate the point at which the pump reverses. The rate at which the pump cycles, however, is determined purely by the kinetic parameters of the model. Detailed balance enforces a further constraint on the kinetic parameters of the scheme in Fig. 1 (32). The product of the forward transition rates in the model is equal to the product of reverse transition rates
| (4) |
where Pi and Pi+1 are the fractional occupancies of adjacent states, and ki± are rate constants of first order. If the transition involves the binding or unbinding of an ion, the expression is written explicitly in terms of the ion concentration and a rate constant of higher order, ki+[Y]Pi = ki−Pi+1, where [Y] is an ion concentration. The fractional state occupancies cancel out in Eq. 4, leaving a constraint on the kinetic parameters which must hold whether or not the system is in equilibrium. Applying this to the SERCA scheme in Fig. 1 gives
| (5) |
Substituting Eqs. 2 and 3 into the equilibrium expression,
gives
| (6) |
and substituting the left-hand side of Eq. 6 with the right-hand side of Eq. 5 yields a constraint on the kinetic rate constants of the SERCA pump model,
| (7) |
Model simplification: rapid equilibrium assumptions
It is assumed in the model that the ionic reactions (binding of Ca2+ and H+) occur at a faster rate than the reactions involving the metabolites. A number of groups have proposed that Ca2+ binding is comprised of fast binding of the first Ca2+, followed by a slow conformational change that allows binding of the second Ca2+ (15,21). However, more recently, Tanford et al. (33) have proposed a sequential Ca2+ binding model, where the conformational change after binding of the first Ca2+ is assumed to be minor (compared to the E1-E2 conformation change) based on work by MacLennan et al. (34) and Brandl (35) on the structure of the SERCA enzyme. We have therefore assumed the entire Ca2+ binding process for both the cytosol and lumen-facing orientations to equilibrate rapidly in comparison to the E1-E2 conformation changes.
The assumption that the MgADP and Pi partial reactions are slow is justified on the basis that those reactions also encompass a change in the SERCA enzyme conformation, which is typically a relatively slow process (36). The MgATP reaction is also modeled as a slow process because MgATP binding has been shown to be rate-limiting at very low concentrations (20).
Application of the rapid equilibrium assumption to the partial reactions follows the technique outlined in Smith and Crampin (7). This results in a simplified three-state model, where apparent rate constants replace the forward and backward rate constants for the ionic partial reaction steps (Fig. 3). The apparent rate constants are given in the Appendix and are functions of ionic concentrations and dissociation constants for the rapid ionic reactions. The number of parameters is reduced from 24 in the 12-state model to 12 in the three-state model.
Figure 3.
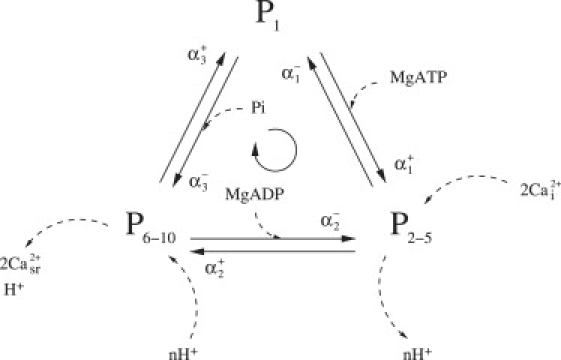
Schematic of the simplified three-state model. Application of the rapid equilibrium assumption to the ion-binding partial reactions (states within the two dotted boxes in Fig. 1) results in a simplified three-state model. The apparent rate constants (αi±, i = 1, 2, 3) replace the forward and backward rate constants and are a function of ion concentrations and dissociation constants.
The SERCA pump is assumed to be operating at a kinetic steady state in the context of a whole-cell simulation. This quasi-steady-state approximation assumes that the conformational changes of the enzyme (between states P5 and P6, and P10 and P1 in Fig. 1) are rapid compared to slower processes in the cell such as changes in ionic concentrations. The steady-state flux of the cycle is solved using the diagram method (32) and the clockwise cycle rate per pump at steady state is given by
| (8) |
in units of s−1, where Σ3 is a sum of nine positive product terms given in the Appendix. For integration into a cell model, the whole-cell pump flux will be given by
| (9) |
where ρsr is the density of the SERCA pumps per unit area of membrane, Asr is the surface area of the SR membrane, and the stoichiometric constant is due to the transport of two Ca2+ per cycle. The Ca2+ flux, JSERCA, has units of mol s−1.
Data set to constrain parameters
To characterize quantitatively the parameters for the cardiac SERCA model, a set of data was chosen that captures the metabolic and ionic dependencies of the pump. The aim was to use whole pump flux data as a function of Ca2+, H+, and each of the metabolites and, where possible, data that are derived from native cardiac SERCA preparations to capture the intrinsic influence of phospholamban on the Ca2+-sensitivity curve (which shifts to the right in the presence of phospholamban). This is achieved through the incorporation of Ca2+-dependent data from Ji et al. (28), which are derived from cardiac microsomes. Table 1 details the conditions for each of the data sets. Without reliable data on the Q10 values of the various steps in the SERCA cycle, we have chosen to correct for the differences in temperature between the data sets by normalizing the data. The entire data set was normalized to a maximum cycle rate of 5 s−1 at optimal conditions, defined as [Ca2+]sr = 0, [Ca2+]i = 10 μM, [ATP] = 5 mM, [ADP] = 0, [Pi] = 0, and pH = 7.2. These values were chosen based on a maximal flux value of 4.2 s−1 obtained from intact rabbit myocytes obtained at 22°C (37). Maximal flux values from canine and guinea pig ventricular myocytes have been estimated to be between 5 s−1 at 25°C and 7.5 s−1 at 37°C, respectively (8,38,39). Details of the data used in the parameter optimization are outlined in Table 1.
Table 1.
Description of the data used to constrain the parameters in the three-state model
| Species and preparation | Data | T | pH | ATP | ADP | Pi | [Cas+]i | [Cas+]sr | Reference |
|---|---|---|---|---|---|---|---|---|---|
| Mouse SERCA2a cardiac microsomes | Ca2+ uptake versus pH (Fig. 5) | 37 | ∗ | 3 | 0 | 0 | 0 | 0.001 | (28) |
| Mouse SERCA2a cardiac microsomes | Ca2+ uptake versus [Ca2+]i at different pH (Fig. 4) | 37 | ∗ | 3 | 0 | 0 | ∗ | 0 | (28) |
| Rabbit SERCA1a nonnative cell expression | Level of back phosphorylation versus [Pi] (Fig. 6) | 25 | 6 | 0 | 0 | ∗ | 0 | 0 | (41) |
| Rabbit SERCA1a solubilized SR fragments | ATPase activity vesus ATP and ADP (Fig. 7) | 10 | 7 | ∗ | ∗ | 0 | 5 | 5 | (42) |
The units of [ATP], [ADP], [Pi], [Cas+]i, and [Cas+]sr are in mM and temperature, T, is in °C.
Dependent variable used in the fitting process.
Parameter optimization
The parameters in the three-state model were estimated using the particle swarm optimization method. This is a population-based approach that scatters a set of solution particles into the parameter space. Each particle moves through the space with a velocity that depends on the best solution so far encountered by that particle and the best solution encountered by any particle in the swarm (40). The solutions obtained from the particle swarm optimization method were then used as initial conditions in a Levenberg-Marquardt least-squares fitting procedure to refine the solution. The fitting process was written and carried out in MatLab (The MathWorks, Natick, MA).
Results
Ca2+ binding
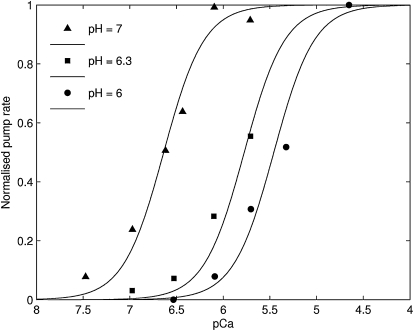
Ca2+ binding is assumed to be either partially cooperative or fully cooperative, both with a stoichiometry of two Ca2+ translocated per ATP hydrolyzed. We sought to compare these two hypotheses by fitting the data to a fully cooperative model (Fig. 2) and a partially cooperative model (Fig. 1). There are three fewer parameters in the fully cooperative model (removal of two parameters for Ca2+ binding in the cytosol and lumen-facing orientations, and one from the second competitive H+ binding). We find that there is no discernible difference between the results of the two models (difference of residuals of 3%). Fig. 4 shows the fit achieved with the fully cooperative Ca2+ binding model. The fully cooperative Ca2+ binding model is favored over the partially cooperative Ca2+ binding model as it achieves a similar quality of fit while using three fewer parameters. The fitting of data in the remainder of the results below was achieved using the fully cooperative Ca2+ binding model. The optimized parameters for the model are given in Table 2. Fig. 4 shows that the SERCA flux is a sigmoidal function of cytosolic pCa. This sigmoidal function is pH-dependent and shifts progressively to the right (increase in Km) as pH is decreased. This is due to the competitive binding of H+ to the Ca2+-binding site when both are facing the cytosol. Note that H+ binding competitively to the cytosol-facing Ca2+-binding site, alone, is required to achieve this fit, suggesting that competitive binding of H+ on the luminal side is not required to fit this set of data. Also, at a normal pH of 7, the Km for the flux-Ca2+ curve is 0.26 μM—similar to parameters employed in a reversible SERCA model (10).
Figure 4.
The fit of the three-state model with fully cooperative Ca2+ binding (Fig. 2) to the pH-dependent Ca2+ binding data from Ji et al. (28).
Table 2.
Parameters for the three-state SERCA model generated from the optimization process
| Parameter | Value |
|---|---|
| k1+ | 25,900 mM−1 s−1 |
| k2+ | 2540 s−1 |
| k3+ | 20.5 s−1 |
| k1− | 2 mM−1 s−1∗ |
| k2− | 67,200 mM−1 s−1 |
| k3− | 149 mM−1 s−1 |
| Kd,Cai | 0.91 mM |
| Kd,Casr | 2.24 mM |
| Kd,H1 | 1.09 × 10−5 mM |
| Kd,Hi | 3.54 × 10−3 mM2 |
| Kd,Hsr | 1.05 × 10−8 mM2 |
| Kd,H | 7.24 × 10−5 mM |
| n | 2.0 |
Ca2+/ H+ countertransport
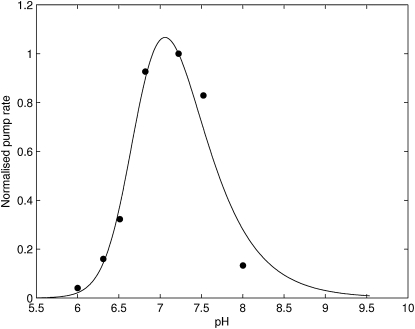
The SERCA pump flux exhibits a bell-shape dependence on pH. The pump operates optimally at a pH of ∼7.1 (Fig. 5). The bell-shaped curve results from the product of two opposing Hill-type relationships arising from the four H+ binding events in the model. Two of the H+-binding events are from the Ca2+/H+ counter-transport mechanism, one from the metabolic reaction and the other from the competition with Ca2+ for the Ca2+-binding sites. The stoichiometry for the H+ binding involved in the Ca2+/ H+ counter-transport was treated as a parameter in the optimization process. The optimal fit produced a value of 2.0, which is consistent with experimental observations of 2 (24,25). This stoichiometric relation governs the narrowness of the bell-shape relationship.
Figure 5.
The fit of the three-state model with fully cooperative Ca2+ binding (Fig. 2) to pH data from Ji et al. (28).
Metabolite dependence
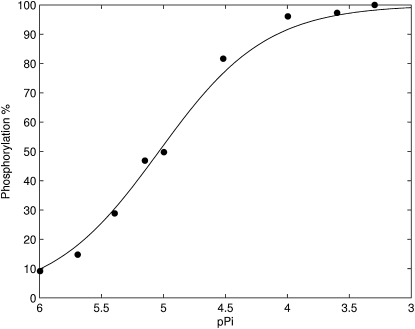
The Pi dependence of the SERCA pump is captured from data that measured the relative proportion of the enzyme that is in a phosphorylated state brought about by the addition of varying concentrations of Pi (41). The data shows that when the Pi concentration is in the mM range, almost all the SERCA enzymes are in the phosphorylated state. In the model, state P6–10 in Fig. 3 is assumed to be the phosphorylated states and the results of the optimization give a good fit to the data (Fig. 6).
Figure 6.
The fit of the three-state model with fully cooperative Ca2+ binding (Fig. 2) to Pi phosphorylation data from Dode et al. (41).
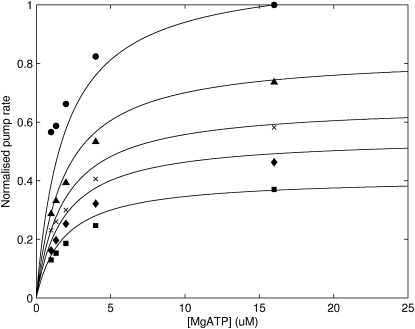
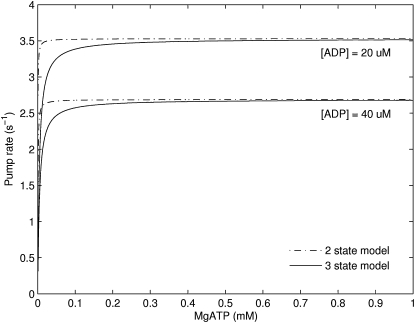
Dependence of the SERCA model on MgATP and MgADP concentrations is quantified by fitting to data from Sakamoto and Tonomura (42). The SERCA pump flux increases with increasing MgATP concentration and reaches a saturating flux that is dependent on the MgADP concentration (Fig. 7).
Figure 7.
The fit of the three-state model with fully cooperative Ca2+ binding (Fig. 2) to ATP and ADP-dependence data from Sakamoto and Tonomura (42). Descending from the top curve, the ADP concentrations are 0 mM, 20 mM, 40 mM, 60 mM, and 100 mM.
There is evidence in the literature showing MgATP to bind both before and after the binding of Ca2+ in the cytosol-facing orientation. To investigate this disparity, we fitted a model where MgATP binds before Ca2+ binding (Fig. 1) and compared it to a model where MgATP was placed immediately after Ca2+ binding. We found that when the MgATP was placed after the binding of the second Ca2+, a reasonable fit could not be achieved compared with the model where the MgATP was placed before the first binding Ca2+ (Fig. 7). The same result was observed when the MgATP binding step was placed after the dissociation of the H+ on the cytosolic side. This suggests that MgATP binds first, followed by Ca2+ and H+. To minimize the risk of missing the optimal parameter set, we took the following strategy: a large number of runs (>100) with random starting points was carried out in each case. The starting points for the parameters were within defined boundaries which were set to be the same as those in the successful fit. These boundaries were also increased but no satisfactory fit was produced. Based on this result, it was concluded that only a model with the MgATP binding site placed before binding of the first Ca2+ can produce an adequate fit to the data set.
Thermodynamic properties of the model
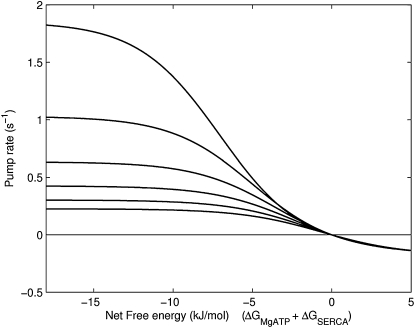
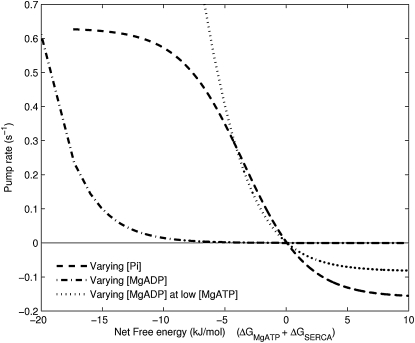
The thermodynamic properties of the pump are demonstrated by investigating the relationship between the free energy of ATP hydrolysis and the SERCA cycle flux at different levels of luminal Ca2+ concentration (Fig. 8). The free energy of ATP hydrolysis is progressively reduced by increasing the concentration of Pi. The pump stops completely at the reversal point where the net free energy is zero; i.e., the energy required by the pump to transfer Ca2+ into the SR is equal to the available free energy. Furthermore, when the energy in the Ca2+ gradient exceeds the available free energy, the model predicts a reversal of the pump where ATP is generated from ADP and Pi. The rate at which the pump operates in reverse is determined by the kinetic parameters of the model. Fig. 9 shows the effect of increasing MgADP, rather than Pi, to progressively reduce the available free energy. The cycle still reverses as net free energy goes through zero, but in this case, an increase in MgADP brings about a negligible reversal rate. Analysis of the three-state model reveals that for large values of MgADP, the maximal reverse rate is equal to . Under normal Ca2+ and pH conditions, this expression is dominated by the magnitude of α1+, the forward rate of MgATP binding, which renders the maximal reverse flux negligible as MgADP is increased (Fig. 9). This is because as MgADP tends to very large values, state P2–5 (Fig. 3) becomes saturated and progression to state P1 is restricted by the large binding constant of MgATP. A similar analysis for increasing Pi concentration shows that as Pi is greatly increased, the maximal reverse rate is equal to . The maximal reverse rate for [Pi] is therefore independent of the kinetics of MgATP binding and depends, instead, on the combined effects of Ca2+, pH, and MgADP. Increases in Pi can therefore overcome the inhibition of the large MgATP binding constant, as shown in Fig. 9, but to do so requires a very large and nonphysiological Pi concentration. The kinetics of MgATP binding therefore limits the maximum reversal rate of the pump. When the pump rate is plotted at a lower MgATP concentration, there is an appreciably larger reversal rate because the inhibitory effect of MgATP binding has been reduced.
Figure 8.
The effect of changes in the net free energy on the cycle pump rate at different luminal Ca2+ concentrations. The top curve is at [Ca2+]sr = 1 mM, increasing by 0.5 mM for each curve up to 3.5 mM for the lowest curve. The free energy of ATP hydrolysis is reduced by increasing [Pi]. Other conditions in the simulation: ATP = 5 mM, ADP = 36.3 μM, pH = 7, [Ca2+]i = 1 μM.
Figure 9.
The SERCA model predicts a reversal point when the net free energy is zero. However, the rate at which the pump reverses is a function of the model parameters. In the figure above, the free energy of ATP hydrolysis is reduced by increasing either [Pi] or [MgADP]. Increasing [Pi] causes the pump to reverse at an appreciable rate beyond the reversal point. However, increasing [MgADP] results in the pump slowing down considerably as it passes through the reversal point. [MgATP] = 5 mM for both curves. But when [MgADP] is increased while keeping [MgATP] low (10 μM), there is an appreciable reversal rate because the inhibitory effect of MgATP binding is reduced. Other conditions in the simulation: pH = 7, [Ca2+]i = 1 μM, [Ca2+]sr = 2 mM.
Simplifying to a two-state model
For physiological concentrations of metabolites, the three-state model can be further simplified by noting that the MgATP concentration in the Sakamoto and Tonomura (42) data set is in the μM range. The MgATP binding was defined as a slow step to capture these data. These low MgATP concentrations, however, are outside the physiological range: normal MgATP concentration in a healthy myocyte is ∼5 mM while, during ischemia, the MgATP concentration drops by ∼50% over the 15 min after the initial ischemic insult (43). Therefore, under physiological and even ischemic conditions, the binding of MgATP can be considered to be a rapid equilibrium reaction and, as such, the SERCA model can be further simplified to a two-state model.
Using rapid equilibrium assumptions, the slow MgATP binding step is turned into a rapid binding step (Fig. 10) by lumping the kinetic constants, k1+ and k1−, into a single dissociation constant, Kd,ATP, where Kd,ATP = k1−/k1+. This results in a two-state model (Fig. 11) where the MgATP binding step joins the cytosol-facing Ca2+ binding steps in a single state. In the limit when MgATP concentration is in the mM range, the two-state model behaves essentially the same as the three-state model. Fig. 12 shows a simulation comparing the two- and three-state models. It demonstrates that the two models are essentially identical when MgATP is in the mM range but begin to diverge when MgATP drops to the μM range.
Figure 10.
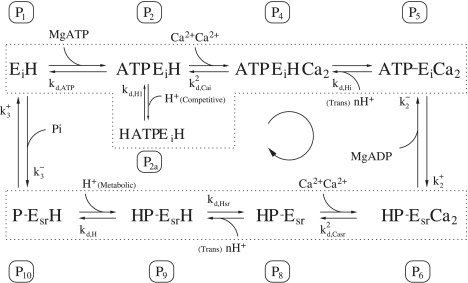
Application of the rapid equilibrium assumption to the ATP binding step reduces the forward and back binding constants (between states P1 and P2) to a single dissociation constant, Kd,ATP. The ATP binding step becomes lumped with the Ca2+ and H+ binding steps as outlined by the top dotted box.
Figure 11.
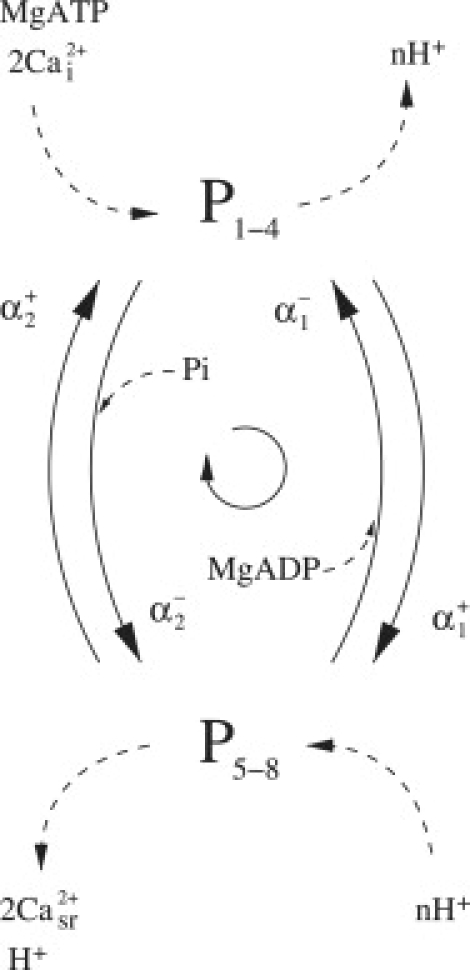
Application of the rapid equilibrium assumption to the ATP binding step reduces the three-state model further to a two-state model. The releases of ADP and Pi are assumed to be concomitant with the conformational change of the SERCA enzyme from the E1 to E2 state and are therefore modeled as relatively slower reactions. Equations for the two-state model are given in the Appendix.
Figure 12.
Simulations comparing the two- and three-state models show that they are identical when the ATP concentration is in the μM range. Conditions for simulation: pH = 7, [Ca2+]i = 1 μM, [Ca2+]sr = 1 mM, Pi = 1 mM.
Discussion
Active energy-demanding processes play key roles in all cell types by converting chemical energy in the form of ATP into useful work. In a cardiac myocyte, the major energy-demanding processes, whose functions depend critically on the cellular energetic state, are the Na+/K+ pump, the SERCA pump, and acto-myosin ATPase. The two pumps, in particular, are integral components of electrophysiological modeling frameworks that encompass Ca2+ handling dynamics (2–6). However, the omission of metabolic sensitivity in modeling these processes leads to difficulties when attempting to simulate conditions where the energetic state of a myocyte is compromised such as would be encountered during an ischemic episode (43). Recently, an energy-sensitive model of the cardiac Na+/K+ pump has been published (7,44) and used to investigate the role of the pump during ischemia. Using the approach outlined in Smith and Crampin (7), we have developed a mathematical model of the cardiac SERCA pump, which is sensitive to the metabolic state of the cell as well as the luminal and cytosolic concentrations of Ca2+ and H+. This model brings together a variety of experimental data under the framework of the biophysical E1-E2 model and enforces thermodynamic consistency by introducing a constraint on the rate constants of the model.
The analysis of the simplified model presented here does not necessarily prove that this model is unique. Rather, we have shown that this model is sufficient to describe a range of experimental data on the SERCA pump flux. Although we have ruled out several other kinetic schemes during the development of this model, there may be other kinetic schemes that, when simplified, produce similar fits to the data. Furthermore, as more data become available, these can be incorporated into an initially more complex scheme which can be subsequently simplified without loss of detail, using the method presented here.
SERCA is modeled initially as a 12-state cycle modified from de Meis and Vianna (14) to include aspects of H+ binding. Two H+ partial reactions are included to capture the Ca2+/H+ counter-transport, two more for the competitive binding to the Ca2+-binding sites, and another to account for the metabolic H+. This model is simplified based on the assumption that the reactions involving the binding/unbinding of Ca2+ and H+ occur on a timescale that is significantly faster than the conformational change of the pump as it switches between the cytosol and lumen-facing configuration. The simplified model presented here does not explicitly represent all the possible intermediate states of the cardiac SERCA pump. However, the dependencies and ions represented by these intermediate states are retained in the transition rates between states of the simplified model, which are shown to be sufficient to characterize the pump's sensitivity to Ca2+ and H+, and the metabolites, MgATP, MgADP, and Pi.
Ca2+ binding
Ca2+ is known to bind in a positive cooperative manner (21). We used our model to assess whether this binding is a partially cooperative mechanism or a fully cooperative mechanism. In the case of the partially cooperative mechanism, the binding constant of the second Ca2+ is greater than that of the first whereas in the fully cooperative case, the binding of the second Ca2+ is assumed to be instantaneous after the first Ca2+ binding to the pump. Mathematically, the fully cooperative mechanism has three fewer parameters. The results of fitting these two models to the data show negligible difference in residuals. The parsimonious approach therefore favors the fully cooperative mechanism over the partially cooperative mechanism, since, given the available data, it is impossible to distinguish between the two cases.
The Ca2+ binding characteristics of the model cannot be validated by directly comparing the dissociation constants, Kd,Cai and Kd,Casr (Table 2), which describe the affinity of Ca2+ for Ca2+-binding sites to constants reported for Ca2+ sensitivity (Km, K1/2). These latter constants reflect the apparent binding of Ca2+ to the pump and depend on the experimental conditions as illustrated in Fig. 4, which depicts the pH-dependence of the Ca2+ sensitivity curve. To make a direct comparison with values reported in the literature, we calculate the half-maximal binding concentration for [Ca2+]i from the model under given conditions. For pH values close to 7, half-maximal binding of Ca2+ from the cytosol has been measured or calculated to be between 0.5 and 10 μM (21,27,30,31,45). A comparable value is obtained from the model by isolating states P2–P5 (Fig. 2) and plotting the probability of occupying states P4 and P5 as a function of [Ca2+]i. At a pH of 7, the half-maximal point of this curve gives a Ca2+ binding constant of 4.88 μM, which is within the range of what is measured in experiments. A similar procedure gives a Ca2+ binding constant of 3.6 mM for binding of Ca2+ on the luminal side (by calculating the probability of occupying state P6 as a function of [Ca2+]sr). This is also consistent with values from the literature of 1.7 mM (46) and 1.48 mM (30). The greater binding affinity of cytosolic Ca2+ over luminal Ca2+ of approximately three orders of magnitude is a key characteristic of the pump that facilitates the binding of Ca2+ from the cytosol (at low concentrations) and the subsequent release of this Ca2+ into the luminal environment where [Ca2+] is much higher.
Variable stoichiometry of Ca2+ transport
The SERCA model is assumed to have a fixed stoichiometric coupling ratio of 2 Ca2+ for every ATP that is hydrolyzed. Yu and Inesi (47) found that in leak-proof native SR vesicles, the stoichiometry starts to drop below 2 in the absence of oxalate (a chelator of luminal Ca2+) and attribute this drop to a highly elevated luminal Ca2+ concentration. Their experiments indicate that this begins to occur ∼2 s after the addition of ATP at 25°C. In a rabbit ventricular myocyte, the Ca2+ transient lasts for no longer than 500 ms (8) as the SERCA pump is rapidly activated by the increasing cytosolic Ca2+ and inactivated when it falls. Therefore, under physiological conditions in the beating heart, it is reasonable to assume that the luminal Ca2+ levels do not approach such high levels and therefore the transport of Ca2+ is tightly coupled to the hydrolysis of ATP at a stoichiometric ratio of 2.
H+ binding
The transfer of Ca2+ into the SR lumen by the SERCA pump is also accompanied by a counter-transport of H+ out into the cytosol. At neutral pH, the stoichiometry of the counter-transport between Ca2+ and H+ is measured to be 2:2 (24–26). This is consistent with the prediction of our model of 2 H+ being counter-transported for 2 Ca2+ during each cycle of the pump.
In the enzyme cycle presented in Fig. 1 it was assumed that the H+ involved in counter-transport had distinct binding sites on the SERCA enzyme. These binding sites were separate from those of the competitive H+, which competed with Ca2+ for the Ca2+-binding sites in the cytosol-facing orientation. However, in the case of the cooperative Ca2+ binding model presented in Fig. 2, instead of binding to distinct H+-binding sites, the binding of the transported H+ can be interpreted as binding to the Ca2+-binding sites in a scheme that is a slight modification of the one proposed by Yu et al. (25). In this modified scheme, it is proposed that after the two Ca2+ have dissociated into the SR lumen, two H+ then occupy one of the two empty Ca2+ binding sites. After SERCA has undergone the conformational change so that the Ca2+-binding sites are now facing the cytosol, the Ca2+ binding site that remains empty can subsequently bind a cytosolic Ca2+ or H+. If Ca2+ binds, the second Ca2+ will rapidly follow and eject the two H+ occupying the binding site. Yu et al. (26) propose that the binding of H+ to the Ca2+-binding sites is possible because some of the residues involved in the binding of Ca2+ are acidic and are hence capable of exchanging H+ with Ca2+. Their findings suggest that, assuming the same acidic residues are involved in both H+ and Ca2+ binding, there is a lower affinity for H+ when the Ca2+-binding sites are in the cytosol-facing orientation, and a higher affinity for H+ in the luminal orientation. This is indeed the case in the SERCA model presented here where Kd,Hi and Kd,Hsr for H+ binding to the cytosol and luminal Ca2+-binding sites are 3.54 × 10−3 and 1.05 × 10−8 mM−2, respectively.
Binding order of partial reactions
The order and placement of the partial reactions involving MgATP binding was shown to be an important determinant of the ability to fit the data set, where an acceptable fit was achieved only when the MgATP binding step was placed before the first Ca2+ binding step and after the release of Pi as shown in Fig. 1. For MgATP binding either after the binding of the second Ca2+ or after the dissociation of H+, the model was found to be incompatible with the data.
Reversal of the pump
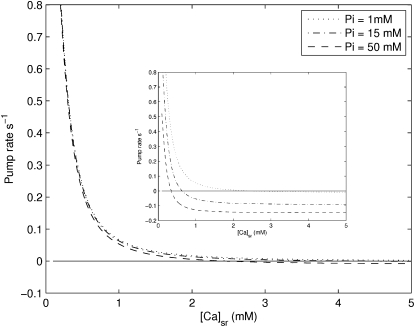
The SERCA pump has been shown experimentally to be reversible under conditions where the concentrations of MgADP and Pi are high and MgATP is kept very low (48). Under these conditions, the net free energy is positive (ΔGMgATP + ΔGSERCA > 0), resulting in the efflux of Ca2+ from the SR lumen and the synthesis of ATP as the SERCA enzyme cycles in the reverse direction. The thermodynamic constraint imposed on the model (see Methods) ensures that the pump will reverse when the net free energy is zero but the actual rate of cycling in the reverse direction is highly dependent on the kinetics of the model, particularly to the kinetics of MgATP binding (Figs. 9 and 13). At physiological concentrations of MgATP, the model predicts that the reverse rate will be negligible when ΔGnet > 0, either by increasing the products of ATP hydrolysis (Fig. 9) or by altering the Ca2+ concentrations (Fig. 13) within the physiological range. When the MgATP concentration is kept very low, however, the magnitude of the reversal rates become appreciable as the rate-limiting effect of MgATP binding is reduced. This is consistent with the results of Makinose and Hasselbach (48), where the SERCA pump was shown to reverse when the concentration of MgATP was low.
Figure 13.
An increase in the free [Ca2+]sr leads to a decrease in the pump rate until a reversal point is reached where the pump begins to cycle in the reverse direction. The model predicts that at [MgATP] = 5 mM, the rate at which the pump cycles in reverse is almost negligible over either the physiological or the ischemic range of [Pi]. The inset shows the same set of curves but at the lower [MgATP] of 100 μM. A decrease in [MgATP] reduces the inhibitive effect of MgATP binding resulting in larger reversal rates. Other conditions in the simulation: ADP = 36.3 μM, pH = 7, [Ca2+]i = 150 nM.
Data selection
The parameters of the cardiac SERCA model were constrained to a set of data which characterizes the dependence of the pump on the metabolites MgATP, MgADP, and Pi and the ions Ca2+ and H+ (28,41,42). We have sought to use data from cardiac preparations of a single mammalian species and to use data that measured the turnover rate of the pump. While not always possible, we have, within the constraints of available data, sought to maintain species consistency of the model. Considering now the origin of the data, the pH curve and pH-dependent Ca2+ curves (28) were from mouse cardiac preparations and therefore intrinsic in those (and hence in the model) is the effect of phospholamban. The ATP/ADP (42) and Pi (41) data, however, are from solubilized SR fragments and nonnative cell expressions of SERCA enzymes of rabbit skeletal muscle, respectively. The justification for using these SERCA enzyme data (from a nonnative source) is that when expressed in the presence of phospholamban, the SERCA1a isoform from skeletal muscle is functionally equivalent to the SERCA2a form in cardiac muscle (28). Because these data represent changing MgATP, MgADP, and Pi concentrations only, and not changing Ca2+ concentrations, the presence or absence of phospholamban is not relevant here. In terms of the species difference between mouse and rabbit, there is evidence to suggest their cardiac SERCA pumps have similar characteristics. Under similar pH conditions, the Km measured in mouse cardiac preparations by Ji et al. (28) of 0.25 μM is very similar to that measured from rabbit ventricular myocytes of 0.26 μM (10). There is also a difference in Vmax between species, which is due to different expression levels of the SERCA enzyme. The density of cardiac SERCA pumps in mouse is estimated to be higher than that of rabbit (8). In the modeling process, this difference in Vmax between different data sets is accounted for by normalizing all the data to a single reference point (see Methods). This normalization process also allows for the accounting of temperature differences between data sets when reliable data on Q10 values for the various reaction steps are not available. The maximum flux for the pump value was scaled to a value comparable to experiments carried out on rabbit cardiomyocytes at 22°C (see Methods).
Parameter sensitivity
A sensitivity analysis of the model parameters was performed to assess the effects of each parameter on the four data sets. Each of the parameter values in Table 2 was altered by ±10% and the deviation of the resulting curves from the optimal curves (Figs. 4–7) was calculated. The results are presented in Table 3. The sensitivity analysis shows that each of the parameters affects the model fit to at least one set of data and the ability of the model to fit each of the data sets is sensitive to more than one parameter. This is indicative of a model which is not overparameterized in respect of the data used to fit the model parameters, and reflects the whole-pump approach we have taken to fit all four sets of data simultaneously. The parameter with the greatest influence in the model is n, the number of H+ that are counter-transported for each Ca2+. This parameter has significant effects on the model fit to pH, pH-Ca2+, and ATP curves. The highly sensitive nature of this parameter reflects its importance in determining a well-constrained fit of the model to the data. Taking together the high sensitivity of this parameter and the prediction of n = 2 (which is consistent with the literature). This provides us with a good degree of confidence in the optimized model parameters.
Table 3.
The sensitivity of the parameters in the three-state model is quantified by calculating the percentage deviation from the optimal curves given a ±10% change in the parameter value
| Parameter | pH-Ca2+ curve (Fig. 4) |
pH curve (Fig. 5) |
Pi curve (Fig. 6) |
ATP/ADP curve (Fig. 7) |
||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| +10% | −10% | Avg. | +10% | −10% | Avg. | +10% | −10% | Avg. | +10% | −10% | Avg. | |
| k1+ | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3.64% | 8.51% | 6.08% |
| k2+ | 3.88% | 0.70% | 2.29% | 3.91% | 2.89% | 3.4% | 0 | 0 | 0 | 11.5% | 7.52% | 9.51% |
| k3+ | 0.40% | 4.52% | 2.46% | 32.7% | 14.1% | 23.4% | 19.1% | 9.40% | 13.4% | 0.38% | 0.37% | 0.38% |
| k2− | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 7.08% | 12.9% | 10.0% |
| k3− | 0 | 0 | 0 | 0 | 0 | 0 | 7.14% | 22.2% | 23.34% | 7.10% | 3.50% | 5.30% |
| kd,Cai | 5.09% | 13.6% | 9.35% | 3.98% | 9.97% | 6.98% | 0 | 0 | 0 | 0 | 0 | 0 |
| kd,Casr | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 8.67% | 6.22% | 7.45% |
| kd,H1 | 3.58% | 0.53% | 2.06% | 3.70% | 2.79% | 3.25% | 0 | 0 | 0 | 0 | 0 | 0 |
| kd,Hi | 3.88% | 0.71% | 2.23% | 3.89% | 2.88% | 3.39% | 0 | 0 | 0 | 0 | 0 | 0 |
| kd,Hsr | 0.46% | 0.18% | 0.32% | 3.15% | 13.74% | 8.45% | 0.07% | 0.07% | 0.07% | 2.21% | 2.87% | 2.54% |
| kd,H | 0.08% | 3.57% | 1.83% | 22.51% | 6.99% | 14.8% | 17.1% | 7.86% | 12.5% | 1.28% | 1.26% | 1.27% |
| n | 338% | 293% | 316% | 446% | 967% | 707% | 0.80% | 0.58% | 0.69% | 12.2% | 135% | 73.6% |
The model is most sensitive to n, the number of H+ that are counter-transported during each pump cycle.
The cardiac SERCA model presented here is the first model that incorporates metabolic-sensitivity, Ca2+- and H+-sensitivity, and thermodynamic constraints into a consistent biophysical framework. Along with the energy-sensitive model of the Na+/K+ ATPase (44,49), this model provides a further step toward developing a whole-cell model of cardio-myocyte electrophysiology and Ca2+ dynamics that is capable of simulating the effects of compromised metabolism such as ischemia and hypoxia.
Acknowledgments
The authors acknowledge valuable comments from Jonna Terkildsen.
This work was supported by a Tertiary Education Commission (New Zealand) Top Achiever Doctoral Scholarship and a Royal Society of New Zealand travel grant to K.T.; Royal Society of New Zealand (Marsden Fund No. 06-UoA-123) to D.S.L. and N.P.S.; National Institute of Biomedical Imaging and Bioengineering grant No. EB-005825 to E.J.C. and N.P.S.; and an Engineering and Physical Sciences Research Council grant No. EP/G007521/1 to N.P.S.
Footnotes
This is an Open Access article distributed under the terms of the Creative Commons-Attribution Noncommercial License (http://creativecommons.org/licenses/by-nc/2.0/), which permits unrestricted noncommercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Contributor Information
Kenneth Tran, Email: k.tran@auckland.ac.nz.
Edmund J. Crampin, Email: e.crampin@auckland.ac.nz.
Appendix
Equations for the three-state cooperative SERCA model
The apparent forward rate constants are
| (10) |
and the apparent backward rate constants are
| (11) |
where
| (12) |
| (13) |
ΔGoMgATP = 11.9 kJ mol−1, R = 8.314 JK−1 mol−1, and T is the temperature in K. The cycling rate (in units of s−1) is given by
| (14) |
where Σ3 is a sum of nine products given by
| (15) |
Equations for the two-state SERCA model
The apparent forward rate constants are
| (16) |
and the apparent backward rate constants are
| (17) |
where
| (18) |
| (19) |
ΔGoMgATP = 11.9 kJ mol−1, R = 8.314 JK−1 mol−1, and T is the temperature in K. The cycling rate (in units of s−1) is given by
| (20) |
where Σ2 is a sum of four terms given by
| (21) |
Model code
The model is available in the CellML database (50,51). The MatLab code for reproducing the plots in the article is available from the author.
References
- 1.Crampin E.J., Halstead M., Hunter P., Nielsen P., Noble D. Computational physiology and the physiome project. Exp. Physiol. 2004;89:1–26. doi: 10.1113/expphysiol.2003.026740. [DOI] [PubMed] [Google Scholar]
- 2.Noble D., Varghese A., Kohl P., Noble P. Improved guinea-pig ventricular cell model incorporating a diadic space, I-Kr and I-Ks, and length- and tension-dependent processes. Can. J. Cardiol. 1998;14:123–134. [PubMed] [Google Scholar]
- 3.Winslow R.L., Rice J., Jafri S., Marban E., O'Rourke B. Mechanisms of altered excitation-contraction coupling in canine tachycardia-induced heart failure, II: model studies. Circ. Res. 1999;84:571–586. doi: 10.1161/01.res.84.5.571. [DOI] [PubMed] [Google Scholar]
- 4.Faber G.M., Rudy Y. Action potential and contractility changes in [N+]i overloaded cardiac myocytes: a simulation study. Biophys. J. 2000;78:2392–2404. doi: 10.1016/S0006-3495(00)76783-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Matsuoka S., Sarai N., Kuratomi S., Ono K., Noma A. Role of individual ionic current systems in ventricular cells hypothesized by a model study. Jpn. J. Physiol. 2003;53:105–123. doi: 10.2170/jjphysiol.53.105. [DOI] [PubMed] [Google Scholar]
- 6.ten Tusscher K.H.W.J., Panfilov A.V. Alternans and spiral breakup in a human ventricular tissue model. Am. J. Physiol. Heart Circ. Physiol. 2006;291:H1088–H1100. doi: 10.1152/ajpheart.00109.2006. [DOI] [PubMed] [Google Scholar]
- 7.Smith N.P., Crampin E.J. Development of models of active ion transport for whole-cell modeling: cardiac sodium-potassium pump as a case study. Prog. Biophys. Mol. Biol. 2004;85:387–405. doi: 10.1016/j.pbiomolbio.2004.01.010. [DOI] [PubMed] [Google Scholar]
- 8.Bers D.M. 2nd Ed. Kluwer Academic Publishers; Dordrecht, The Netherlands: 2001. Excitation-Contraction Coupling and Cardiac Contractile Force. [Google Scholar]
- 9.Tanford C. Steady-state of an ATP-driven calcium-pump—limitations on kinetic and thermodynamic parameters. Proc. Natl. Acad. Sci. USA. 1982;79:6161–6165. doi: 10.1073/pnas.79.20.6161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Shannon T.R., Ginsburg K.S., Bers D.M. Reverse mode of the sarcoplasmic reticulum calcium pump and load-dependent cytosolic calcium decline in voltage-clamped cardiac ventricular myocytes. Biophys. J. 2000;78:322–333. doi: 10.1016/S0006-3495(00)76595-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Gould G.W., East J.M., Froud R.J., McWhirter J.M., Stefanova H.I. A kinetic model for the Ca2+ + Mg2+-activated ATPase of sarcoplasmic reticulum. Biochem. J. 1986;237:217–227. doi: 10.1042/bj2370217. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Haynes D.H., Mandveno A. Computer modeling of Ca2+ pump function of Ca2+-Mg2+-ATPase of sarcoplasmic-reticulum. Physiol. Rev. 1987;67:244–284. doi: 10.1152/physrev.1987.67.1.244. [DOI] [PubMed] [Google Scholar]
- 13.Makinose M. Possible functional-states of enzyme of sarcoplasmic calcium-pump. FEBS Lett. 1973;37:140–143. doi: 10.1016/0014-5793(73)80443-0. [DOI] [PubMed] [Google Scholar]
- 14.de Meis L., Vianna A.L. Energy interconversion by the Ca2+-dependent ATPase of the sarcoplasmic reticulum. Annu. Rev. Biochem. 1979;48:275–292. doi: 10.1146/annurev.bi.48.070179.001423. [DOI] [PubMed] [Google Scholar]
- 15.Dupont Y. Low-temperature studies of the sarcoplasmic-reticulum calcium-pump mechanism of calcium-binding. Biochim. Biophys. Acta. 1982;688:75–87. doi: 10.1016/0005-2736(82)90580-6. [DOI] [PubMed] [Google Scholar]
- 16.Petithory J.R., Jencks W.P. Sequential dissociation of Ca2+ from the calcium adenosine-triphosphatase of sarcoplasmic-reticulum and the calcium requirement for its phosphorylation by ATP. Biochemistry. 1988;27:5553–5564. doi: 10.1021/bi00415a025. [DOI] [PubMed] [Google Scholar]
- 17.Inesi G. Sequential mechanism of calcium-binding and translocation in sarcoplasmic-reticulum adenosine-triphosphatase. J. Biol. Chem. 1987;262:16338–16342. [PubMed] [Google Scholar]
- 18.Orlowski S., Champeil P. Kinetics of calcium dissociation from its high-affinity transport sites on sarcoplasmic-reticulum ATPase. Biochemistry. 1991;30:352–361. doi: 10.1021/bi00216a007. [DOI] [PubMed] [Google Scholar]
- 19.Forge V., Mintz E., Canet D., Guillain F. Lumenal Ca2+ dissociation from the phosphorylated Ca2+-ATPase of the sarcoplasmic-reticulum is sequential. J. Biol. Chem. 1995;270:18271–18276. doi: 10.1074/jbc.270.31.18271. [DOI] [PubMed] [Google Scholar]
- 20.Mintz E., Guillain F. Ca2+ transport by the sarcoplasmic reticulum ATPase. Biochim. Biophys. Acta Bioenerg. 1997;1318:52–70. doi: 10.1016/s0005-2728(96)00132-6. [DOI] [PubMed] [Google Scholar]
- 21.Inesi G., Kurzmack M., Coan C., Lewis D.E. Cooperative calcium-binding and ATPase activation in sarcoplasmic-reticulum vesicles. J. Biol. Chem. 1980;255:3025–3031. [PubMed] [Google Scholar]
- 22.Madeira V.M.C. Proton gradient formation during transport of Ca2+ by sarcoplasmic-reticulum. Arch. Biochem. Biophys. 1978;185:316–325. doi: 10.1016/0003-9861(78)90173-x. [DOI] [PubMed] [Google Scholar]
- 23.Chiesi M., Inesi G. Adenosine 5′-triphosphate dependent fluxes of manganese and hydrogen-ions in sarcoplasmic-reticulum vesicles. Biochemistry. 1980;19:2912–2918. doi: 10.1021/bi00554a015. [DOI] [PubMed] [Google Scholar]
- 24.Levy D., Seigneuret M., Bluzat A., Rigaud J.L. Evidence for proton countertransport by the sarcoplasmic-reticulum Ca2+-ATPase during calcium-transport in reconstituted proteoliposomes with low ionic permeability. J. Biol. Chem. 1990;265:19524–19534. [PubMed] [Google Scholar]
- 25.Yu X., Carroll S., Rigaud J.L., Inesi G. H+ countertransport and electrogenicity of the sarcoplasmic-reticulum Ca2+ pump in reconstituted proteoliposomes. Biophys. J. 1993;64:1232–1242. doi: 10.1016/S0006-3495(93)81489-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Yu X., Hao L.N., Inesi G. A pK change of acidic residues contributes to cation countertransport in the Ca-ATPase of sarcoplasmic-reticulum—role of H+ in Ca2+-ATPase countertransport. J. Biol. Chem. 1994;269:16656–16661. [PubMed] [Google Scholar]
- 27.Inesi G., Chen L., Sumbilla C., Lewis D., Kirtley M.E. Ca2+ binding and translocation by the sarcoplasmic reticulum ATPase: Functional and structural considerations. Biosci. Rep. 1995;15:327–339. doi: 10.1007/BF01788365. [DOI] [PubMed] [Google Scholar]
- 28.Ji Y., Loukianov E., Loukianova T., Jones L.R., Periasamy M. SERCA1a can functionally substitute for SERCA2a in the heart. Am. J. Physiol. Heart Circ. Physiol. 1999;276:H89–H97. doi: 10.1152/ajpheart.1999.276.1.H89. [DOI] [PubMed] [Google Scholar]
- 29.Vianna A.L. Interaction of calcium and magnesium in activating and inhibiting nucleoside triphosphatase of sarcoplasmic-reticulum vesicles. Biochim. Biophys. Acta. 1975;410:389–406. [Google Scholar]
- 30.Pickart C.M., Jencks W.P. Energetics of the calcium-transporting ATPase. J. Biol. Chem. 1984;259:1629–1643. [PubMed] [Google Scholar]
- 31.Cantilina T., Sagara Y., Inesi G., Jones L.R. Comparative-studies of cardiac and skeletal sarcoplasmic-reticulum ATPases—effect of a phospholamban antibody on enzyme activation by Ca2+ Circulation. 1993;88:624–629. [PubMed] [Google Scholar]
- 32.Hill T.L. Springer-Verlag; New York: 1989. Free Energy Transduction and Biochemical Cycle Kinetics. [Google Scholar]
- 33.Tanford C., Reynolds J.A., Johnson E.A. Sarcoplasmic-reticulum calcium-pump—a model for Ca2+ binding and Ca2+-coupled phosphorylation. Proc. Natl. Acad. Sci. USA. 1987;84:7094–7098. doi: 10.1073/pnas.84.20.7094. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.MacLennan D.H., Brandl C.J., Korczak B., Green N.M. Amino-acid sequence of a Ca2+ + Mg2+-dependent ATPase from rabbit muscle sarcoplasmic-reticulum, deduced from its complementary DNA sequence. Nature. 1985;316:696–700. doi: 10.1038/316696a0. [DOI] [PubMed] [Google Scholar]
- 35.Brandl C.J., Green N.M., Korczak B., MacLennan D.H. 2 Ca2+ ATPase genes—homologies and mechanistic implications of deduced amino-acid sequences. Cell. 1986;44:597–607. doi: 10.1016/0092-8674(86)90269-2. [DOI] [PubMed] [Google Scholar]
- 36.Peinelt C., Apell H.J. Kinetics of Ca2+ binding to the SR Ca-ATPase in the E-1 state. Biophys. J. 2005;89:2427–2433. doi: 10.1529/biophysj.105.068411. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Bassani J.W.M., Bassani R.A., Bers D.M. Relaxation in rabbit and rat cardiac-cells—species-dependent differences in cellular mechanisms. J. Physiol. 1994;476:279–293. doi: 10.1113/jphysiol.1994.sp020130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Levitsky D.O., Benevolensky D.S., Levchenko T.S., Smirnov V.N., Chazov E.I. Calcium-binding rate and capacity of cardiac sarcoplasmic-reticulum. J. Mol. Cell. Cardiol. 1981;13:785–796. doi: 10.1016/0022-2828(81)90236-4. [DOI] [PubMed] [Google Scholar]
- 39.Shigekawa M., Finegan J.M., Katz A.M. Calcium-transport ATPase of canine cardiac sarcoplasmic-reticulum—comparison with that of rabbit fast skeletal-muscle sarcoplasmic-reticulum. J. Biol. Chem. 1976;251:6894–6900. [PubMed] [Google Scholar]
- 40.Kennedy, J., and R. Eberhart. 1995. Particle swarm optimization. 1995 IEEE International Conference On Neural Networks Proceedings, Vols. 1–6:1942–1948.
- 41.Dode L., Vilsen B., Baelen K.V., Wuytack F., Clausen J.D. Dissection of the functional differences between sarco(endo)plasmic reticulum Ca2+-ATPase (SERCA) 1 and 3 isoforms by steady-state and transient kinetic analyses. J. Biol. Chem. 2002;277:45579–45591. doi: 10.1074/jbc.M207778200. [DOI] [PubMed] [Google Scholar]
- 42.Sakamoto J., Tonomura Y. Order of release of ADP and Pi from phosphoenzyme with bound ADP of Ca2+-dependent ATPase from sarcoplasmic reticulum and of Na+, K+-dependent ATPase studied by ADP-inhibition patterns. J. Biochem. (Tokyo) 1980;87:1721–1727. doi: 10.1093/oxfordjournals.jbchem.a132916. [DOI] [PubMed] [Google Scholar]
- 43.Befroy D.E., Powell T., Radda G.K., Clarke K. Osmotic shock: modulation of contractile function, pHi, and ischemic damage in perfused guinea pig heart. Am. J. Physiol. Heart Circ. Physiol. 1999;276:H1236–H1244. doi: 10.1152/ajpheart.1999.276.4.H1236. [DOI] [PubMed] [Google Scholar]
- 44.Terkildsen J.R., Crampin E.J., Smith N.P. The balance between inactivation and activation of the Na+-K+ pump underlies the triphasic accumulation of extracellular K+ during myocardial ischemia. Am. J. Physiol. Heart Circ. Physiol. 2007;293:H3036–H3045. doi: 10.1152/ajpheart.00771.2007. [DOI] [PubMed] [Google Scholar]
- 45.Meissner G. ATP and Ca2+ binding by Ca2+ pump protein of sarcoplasmic reticulum. Biochim. Biophys. Acta. 1973;298:906–926. doi: 10.1016/0005-2736(73)90395-7. [DOI] [PubMed] [Google Scholar]
- 46.Inesi G., Sumbilla C., Kirtley M.E. Relationships of molecular-structure and function in Ca2+-transport ATPase. Physiol. Rev. 1990;70:749–760. doi: 10.1152/physrev.1990.70.3.749. [DOI] [PubMed] [Google Scholar]
- 47.Yu X., Inesi G. Variable stoichiometric efficiency of Ca2+ and Sr2+ transport by the sarcoplasmic-reticulum ATPase. J. Biol. Chem. 1995;270:4361–4367. doi: 10.1074/jbc.270.9.4361. [DOI] [PubMed] [Google Scholar]
- 48.Makinose M., Hasselbach W. ATP synthesis by reverse of sarcoplasmic calcium pump. FEBS Letters. 1971;12:271–272. doi: 10.1016/0014-5793(71)80196-5. [DOI] [PubMed] [Google Scholar]
- 49.Crampin E.J., Smith N.P. A dynamic model of excitation-contraction coupling during acidosis in cardiac ventricular myocytes. Biophys. J. 2006;90:3074–3090. doi: 10.1529/biophysj.105.070557. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Lloyd C., Lawson J., Hunter P., Nielsen P. The CellML Model Repository. Bioinformatics. 2008;24:2122–2123. doi: 10.1093/bioinformatics/btn390. [DOI] [PubMed] [Google Scholar]
- 51.Terkildsen J.R., Niederer S., Crampin E.J., Hunter P., Smith N.P. Using physiome standards to couple cellular functions for rat cardiac excitation-contraction. Exp. Physiol. 2008;93:919–929. doi: 10.1113/expphysiol.2007.041871. [DOI] [PubMed] [Google Scholar]