Abstract
Coarse-grained Langevin molecular dynamics computer simulations were conducted for systems that mimic solutions of nucleosome core particles (NCPs). The NCP was modeled as a negatively charged spherical particle representing the complex of DNA and the globular part of the histones combined with attached strings of connected charged beads modeling the histone tails. The size, charge, and distribution of the tails relative to the core were built to match real NCPs. Three models of NCPs were constructed to represent different extents of covalent modification on the histone tails: (nonmodified) recombinant (rNCP), acetylated (aNCP), and acetylated and phosphorylated (paNCP). The simulation cell contained 10 NCPs in a dielectric continuum with explicit mobile counterions and added salt. The NCP-NCP interaction is decisively dependent on the modification state of the histone tails and on salt conditions. Increasing the monovalent salt concentration (KCl) from salt-free to physiological concentration leads to NCP aggregation in solution for rNCP, whereas NCP associates are observed only occasionally in the system of aNCPs. In the presence of divalent salt (Mg2+), rNCPs form dense stable aggregates, whereas aNCPs form aggregates less frequently. Aggregates are formed via histone-tail bridging and accumulation of counterions in the regions of NCP-NCP contacts. The paNCPs do not show NCP-NCP interaction upon addition of KCl or in the presence of Mg2+. Simulations for systems with a gradual substitution of K+ for Mg2+, to mimic the Mg2+ titration of an NCP solution, were performed. The rNCP system showed stronger aggregation that occurred at lower concentrations of added Mg2+, compared to the aNCP system. Additional molecular dynamics simulations performed with a single NCP in the simulation cell showed that detachment of the tails from the NCP core was modest under a wide range of salt concentrations. This implies that salt-induced tail dissociation of the histone tails from the globular NCP is not in itself a major factor in NCP-NCP aggregation. The approximation of coarse-graining, with respect to the description of the NCP as a sphere with uniform charge distribution, was tested in control simulations. A more detailed description of the NCP did not change the main features of the results. Overall, the results of this work are in agreement with experimental data reported for NCP solutions and for chromatin arrays.
Introduction
In the nucleus of the eukaryotic cell, most of the DNA exists as linear domains of uniform DNA-histone complexes, the nucleosomes. The regular central part of the nucleosome is the nucleosome core particle (NCP), which consists of 146–147 bp of DNA wrapped as a 1.70- to 1.75-turn superhelix around an octamer composed of two copies of each of the four different histone proteins H2A, H2B, H3, and H4 (1,2). Double-stranded linker DNA of variable length connects the NCPs to each other, forming nucleosomal arrays that condense into the 30-nm chromatin fibers (3–5). Each of the core histones has an unstructured, flexible, highly conserved N-terminal domain, called the “histone tail” (1,6). The tails protrude out through the DNA superhelix and can make contacts with both the wrapped and linker DNA, as well as with the other NCPs and proteins present in chromatin. Since the histone tails are necessary for both secondary and tertiary condensation (3,4), it is generally presumed that they participate in both intra- and interarray nucleosome-nucleosome interactions (7). The histone tails are essential for maintenance of the higher-order compact folded structures of chromatin and for regulation of transcription and replication (8,9).
In vitro observations show that even in the absence of another nuclear protein, the linker histone H1, folding of the array of nucleosomes into a secondary 30-nm chromatin fiber, as well as further interarray oligomerization into tertiary chromatin structures, can occur upon increase of monovalent salt (KCl, NaCl) or by addition of Mg2+ (3–5). This is a clear indication of an electrostatic mechanism (10–12). It was shown that isolated (linker-free) NCPs display similar behavior, i.e., NCP-NCP aggregation is observed upon increase of concentration of mono- and di-, tri-, and tetravalent cations (13–18). The NCP carries a net negative charge of about −148 e, as it is a highly negatively charged central particle (−236 e) to which eight flexible and positively charged (net charge +88 e) chains are attached. The underlying mechanism that leads to attraction between NCPs and subsequent aggregation is not known in detail. The NCP aggregation and nucleosomal array folding and aggregation (oligomerization) is mediated by charged histone tails, since tailless (trypsin-treated) NCPs and chromatin arrays do not show aggregation or folding, implying that tails perform a crucial role in compaction of the chromatin ((4), and references cited therein).
The picture is additionally complicated by the fact that, in vivo, these functions of the histone tails might be regulated by posttranslational covalent modifications of the amino acids. The most frequent modification is the acetylation of the lysine amino acid, which changes the distribution and net amount of charged groups in the tails (6,19,20). Acetylation of the lysine results in removal of a positive charge. Another modification, namely phosphorylation, adds negative (−2 e) charge to the histone tail. Thus, one can expect that global and local variation of electrostatic interactions between the tails and surrounding molecules is an important component of chromatin structure and dynamics.
Through many years, acetylation in the histone tails and its influence on biological, structural, and dynamic properties of chromatin has been intensively studied and reviewed in countless publications. Below, we give a limited selection of possible citations, with emphasis on early original work and on recent reviews. It is now generally acknowledged that 1), acetylation of the histone tails correlates with transcriptionally active regions in chromatin (see, e.g., (21–24)); 2), acetylated regions of chromatin are more sensitive to nuclease digestion, which indicates higher accessibility of DNA (25,26); 3), acetylated chromatin shows higher solubility in normal salt (NaCl, KCl) and in the presence of millimolar concentrations of Mg2+ (26–28).
Recently, histones have become available in large and pure quantities by the application of overexpression techniques. Reconstitution of NCPs and model chromatin arrays, resulting in large homogeneous amounts of such well-defined objects, in principle makes it possible to determine the contributions of individual tails and specific alterations within them (acetylation, mutation, phosphorylation, etc.) to the association of chromatin and its component, the NCP. The majority of published data has been obtained from averaged pooled chromatin products or from solutions of NCPs obtained by nuclease treatment of the chromatin ((4,13,18,29–32), and references cited therein), but a growing number of works focus on precisely defined chromatin and nucleosomes prepared by such recombinant methods (18,33–39). On the other hand, there is only a limited amount of data available for systems with modifications of the individual histones, such as mutants lacking tails, containing only the globular part of the histone molecule (17), or with selected tail lysines replaced by glutamine, mimicking acetylation (33–39). Available results indicate that acetylation or the absence of tails stabilize NCPs or arrays in the solution state during the course of precipitation and promote unfolding of compact chromatin arrays (17,33–35,40–42). It has been found that the H3 and H4 tails (17,34,41), and specifically the K16 lysine of H4 (33,37), are instrumental in compaction of individual arrays.
Since isolated NCPs display properties qualitatively similar to those of chromatin arrays in terms of the experimentally observed salt-induced compaction, this system is a good starting point for theoretical modeling that can address fundamental electrostatic interactions, and is also of considerable relevance for understanding the chromatin system. Interarray aggregation studies of recombinant systems, for which the standard experiment is titration with Mg2+ ions that induces precipitation, is particularly relevant in this context (33–39,43). During this titration experiment, individual arrays first compact at low amounts of added Mg2+ (<1 mM). At higher concentrations, folded arrays aggregate and the effects of linker DNA are expected to be less important (than for compaction of the individual array). The experimental work shows the importance of tail-mediated interactions between nucleosomes from different arrays during this interarray aggregation. The detailed mechanism of this electrostatically driven process is still not completely understood. In particular, the importance of the charged flexible tails, and the effects on them of covalent modifications that change their charge, have yet to be fully established. From the computational point of view, modeling the aggregation of several arrays would, however, be very demanding. The tail-mediated interactions, leading to aggregation of isolated (linker-free) NCPs, which can also be induced by Mg2+ (13,18), bears considerable resemblance to the interarray aggregation process. Computer modeling of this Mg2+-induced aggregation of NCPs, while being of interest in its own right, can shed light on chromatin interarray fiber formation, since this process, with its underlying mechanism, is very similar to the interarray aggregation.
In our view, the theoretical description of interactions in chromatin lags behind the knowledge gathered in experimental studies. In particular, when it comes to the description of the hallmark Mg2+-induced NCP and chromatin array compaction and aggregation experiment, the majority of existing chromatin and NCP models fail to describe the electrostatics at a level necessary to properly account for physics of the systems. It is notable that in this respect only, some approximate descriptions of the NCP-NCP interaction are available for models of the NCP with fully charged histone tails, and many models lack the explicit presence of flexible tails. Recent theoretical studies related to chromatin folding have begun to include descriptions of the histone tails in coarse-grained models of the NCP and nucleosomal arrays (44–50). The work by Muhlbacher et al. (46) reports a limited account of the dependence of NCP-NCP interaction on the number of charges and the charge density in the histone tails. A common drawback of all the models we know of (45–49,51), with the exception of our work, is that the electrostatic interactions and the presence of salt are treated highly approximately, either with effective potentials or within a mean-field linearized Poisson-Boltzmann (Debye-Hückel) approximation. As a result, entropically induced tail bridging, as well as ion-ion correlation attraction mechanisms, has not simultaneously been taken into consideration. A description that explicitly considers the mobile ions is crucially important, since the Mg2+-induced compaction of NCPs and intramolecular folding, as well as interarray aggregation of chromatin, is the standard experiment used to monitor the effects and properties of the tails in these processes. The distinct effects of divalent ions cannot be described by a Debye-Hückel treatment, where all effects of ion valence and salt concentration are contained in the ionic strength. In the related field of DNA compaction and aggregation induced by multivalent ions and caused by like-charge attraction, this fact has been well established for several years (52–55).
In this work, we present what to our knowledge is the first demonstration that computer modeling allows a description of the salt-dependent and histone-tail-mediated aggregation of the NCPs, including the effects of net charge and their position in the histone tails. We use a coarse-grained continuum model with explicit ions that was introduced in our previous work (44). The NCP is described as a negatively charged sphere with attached flexible chains, whose length and number of charges mimic the real system (Fig. 1). To the best of our knowledge, our approach is the only model existing in the literature about nucleosome and chromatin modeling that explicitly considers the mobile ions, which is necessary in describing the mechanisms of compaction and aggregation of these systems. We model three different states of the nucleosome core particle: “recombinant”, representing fully charged tails; “acetylated”, mimicking the tails carrying two acetylated lysines; and “acetylated + phosphorylated”, where in addition to the acetylation, one negatively charged particle (modeling a phosphorylation site) was inserted into each of the eight histone tails. Explicit presentation of the mobile ions (K+, Mg2+, and Cl−) allows description of the strong specific influence of divalent Mg2+ on the NCP-NCP interaction. The results of the simulation are in agreement with the experimentally observed increase of solubility of the nucleosomes and nucleosomal arrays upon acetylation of the histone tails. In control simulations, we also tested the importance of our approximation using the spherical model to describe the shape and charge distribution of the nucleosome core. A more detailed model with DNA described as charged beads wrapped around a spherical core, mimicking the globular part of the histone octamer, was found to maintain the major properties of the system.
Figure 1.
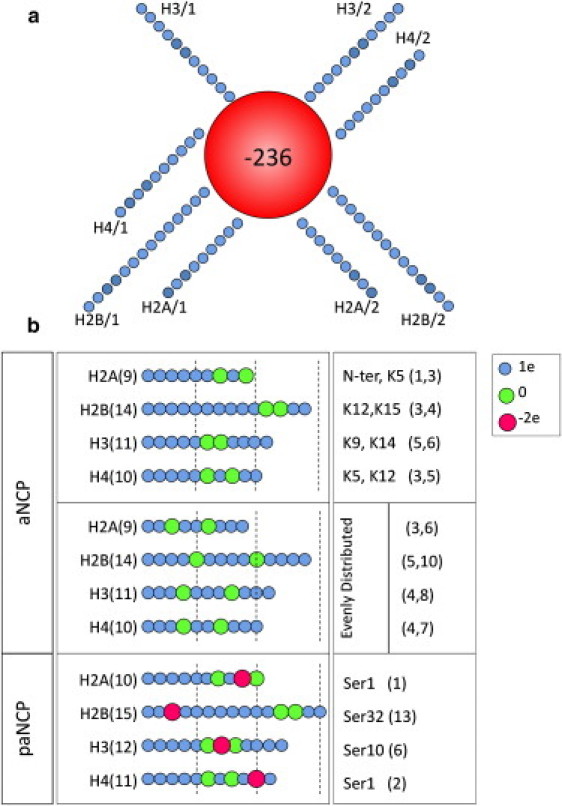
Models of the nucleosome core particle. The position of the tails relative to the core is determined from the atomic model of the NCP. (a) Top view for the model of the “recombinant” NCP. Each blue circle represents one bead (basic unit carrying charge and mass) in the model. (b) Variation in the number of beads and charges of individual beads to represent different types of histone tails in the NCP models for “acetylated” NCP (aNCP) and for phosphorylated plus acetylated NCP (paNCP). In the righthand column, the positions of the modeled modifications in the amino acid sequence of the tail are listed. Small beads with a +1 e charge (blue), larger beads with no charge (green), and largest beads with a −2 e charge (red) represent unmodified, acetylated, and phosphorylated amino acid bead positions, respectively. Four different distributions of the uncharged particles within the tails were modeled, keeping the same number of uncharged particles in each tail. In the first model, the relative positions of the neutralized sites match the sites of lysine acetylation frequently observed in vivo (upper section). In the second model, acetylation sites are evenly distributed. The two other models (not shown in figure) were designed with two uncharged beads placed at the ends of the tails (called the “head” and “root”). In the paNCP model (lower section), acetylation sites correspond to those in the native model of aNCP;, only serine phosphorylation sites are listed at right.
Methods
Coarse-grained models of the nucleosome core particle
We used a model of the NCP and salt conditions similar to that used in our previous work (44). The NCP was described as a spherical particle (“core”) of effective radius 5.1 nm with net charge −236 e combined with eight strings of linearly connected particles representing the histone tails. The charge of the central particle reflects the electrostatic balance between 147 basepairs of double-stranded DNA (charge −294 e) and the net positive charge, +58 e, of the amino acids comprising the globular domains of the histones. The volume and averaged charge density of the central sphere in our NCP model are roughly equal to those of the cylinder approximation of the real NCP. Details of the NCP model are given in our previous work (44) and in the Supporting Material for this work. The real NCP geometry, with DNA wrapped around a histone octamer core, forming a cylindrically shaped particle, as well as the known asymmetry in the charge distribution, may be important for NCP aggregation properties. The majority of the net negative charge is located on the periphery of a cylindrically shaped NCP with the top and bottom of the cylinder core being mostly neutral, with small negatively charged islets on each side. The issue of whether a very simplified presentation of the globular part of the NCP as a single negatively charged sphere can capture the major features of the salt-induced and tail-mediated NCP-NCP interaction is important to address. To tackle this problem we performed some additional simulations with a more detailed NCP model that describes the histone octamer as a sphere with negatively charged beads representing DNA wrapped around it. Some selected data from the molecular dynamics (MD) simulations are described in the Supporting Material.
The number, charge, and charge distribution of particles in the “histone tails” were varied to model three different states of the NCP, here denoted as “recombinant” (nonmodified) (rNCP), “acetylated” (aNCP), and “phosphorylated + acetylated” (paNCP) (Fig. 1). The rNCP model represents the NCP with unmodified, fully charged histone tails; the aNCP model mimics the situation where two positively charged amino acids in each of the histone tails have been acetylated. There are few accounts about the precise degree and positions of acetylation in experimental studies addressing the influence of acetylation on properties of nucleosomes or nucleosomal arrays. To a certain extent, our model of the acetylated NCP corresponds to the “hyperacetylated” fraction of NCPs studied by others (56,57) (on the average, 17 sites of acetylation per octamer), or the “highly acetylated” fraction of the nucleosomal arrays investigated by Tse et al. (28) (∼12 acetylated sites in each octamer). Most of the simulations with the NCP model carrying two acetylation sites in each histone tail were carried out with the “native” aNCP (Fig. 1 b, upper section). The relative positions for acetylation in the “native” aNCP model were assigned taking into account the information about acetylation sites most frequently occurring in vivo (58–60). When not specifically pointed out, the abbreviation “aNCP” refers to this version of distribution of the modified beads in the histone tails. To distinguish between the general (reduction of the tail charge) and specific (position of modification within the tail) influences of acetylation, three additional models of aNCP were studied. In all of these models, there were two uncharged particles in each tail, but the positions of the modification were changed compared to the “native” aNCP: in the “even” model, the uncharged beads were distributed approximately evenly inside each tail (Fig. 1 b, middle section). In the “root” model of the aNCP, two uncharged beads were placed close to the negative core; and in the “head” model, the end of each tail contains two uncharged particles. These altered models of the aNCP were studied under salt conditions similar to those in the systems of “native” aNCP.
The paNCP model addresses the situation of “extreme” modification of the NCP, where in addition to acetylation of two lysines in each tail, one serine in each histone tail has been phosphorylated (Fig. 1 b, lower section). Little is known about the degree of phosphorylation of NCPs in vivo, but it is clear that a high degree of acetylation and phosphorylation in the same nucleosome, as occurs in our paNCP model, is unlikely to occur in nature. The relative positions of the phosphorylated sites were assigned using data on serine phosphorylation within the histone tails (61–63). The rationale behind this model (paNCP) was to study the general electrostatic effect on NCP condensation for the combined reduction of positive tail charge as well as the introduction of negative charges in the tails.
The distance between the charged groups of the histone tails (0.7 nm) was evaluated assuming an extended conformation of the polypeptide chain and an even distribution of Lys+/Arg+ amino acids. The effective radius of “normal” lysine particles with charge +1 e was 0.25 nm. The “acetylated lysine” was represented as a neutral particle that had a radius of 0.45 nm. The phosphorylated amino acid was modeled as a sphere with a −2 e charge and an effective radius of 0.55 nm. This takes into account the increase in size of these amino acid side chains upon modification. To accommodate the negatively charged particle modeling the phosphorylated amino acid, the distance between “lysine” residues was increased to 1.0 nm and a particle with charge −2 e was inserted in the middle. The number of charged groups in each tail of the recombinant NCP model was set according to the charges of the real histone tails: H2A, +9 e; H2B, +14 e; H3, +11 e; H4, +10 e (using the amino acid sequence from Cheung et al. (64) and considering the N-terminal amino group to be protonated). The total charge of the histone tails in the rNCP model was +88, which, with the charge of the central unit, yields a total charge for the rNCP of −148 e, whereas the aNCP model has a net charge of −164 e, and the net charge of the paNCP model was −180 e. Additional details of the model are given in the Supporting Material.
Molecular dynamics setup
The interaction potential (force field) of the coarse-grained model had three parts: electrostatic, short-range, and bond potentials. The electrostatic interaction was defined in a standard manner, as a sum of Coulombic potentials from all the charges in the system, in dielectric media with Bjerrum length = 0.713 nm for ɛr = 78, and T = 300 K. The P3M version of the Ewald summation method (65) was used to compute the long-range part of the electrostatic forces and energies.
The short-range potential, acting between any pair of elements (NCP center particles, particles comprising the histone tails, and ions) was (44)
| (1) |
where rij is the distance between elements “i” and “j”, σij = σi + σj is the sum of their hard-core radii, and a = 0.3 nm is a parameter having the sense of effective thickness of the soft repulsion potential. For hard-core radii, we used σ = 4.7 nm for the NCP central unit and σ = 0.1 nm for ions and particles of the histone tails, except in the cases described separately below. The potential of Eq. 1 has an effective interaction radius σi + σj + a, which gives an effective size of the NCP core of ∼5.1 nm and an effective single-charged ion radius of 0.25 nm. To account for the larger size of the hydrated Mg2+ ion, the phosphate group, and the acetylated lysine in the histone tail, the corresponding hard-core sizes were σ = 0.2, 0.3, and 0.4 nm, respectively. Generally, the calibration of the force field parameters for the coarse-grained simulations was done based on comparison with all-atom molecular dynamics simulations of small fragments, though no detailed fitting of the effective potentials has been made.
The bond potential acting between connected particles had the form
The parameters were Δ = 0.1 nm with equilibrium distance req = 0.7 nm for neighboring lysines (acetylated and positively charged) and req = 0.5 nm between the phosphate group and the closest particle in the tail. The particles closest to the core of the NCP were fixed by harmonic bonds to the center of the core and to some other particles of the other tail to fix the exit points of the tails at positions close to those determined for the corresponding Cα atoms of the histone tails in the crystal structure of the NCP (1). For details, see our previous article (44) and the Supporting Material for this article.
Langevin molecular dynamics simulations were carried out using the ESPResSo package (66) with modifications to include the interacting potential described by Eq. 1. Since the solvent is not included explicitly, the molecular dynamics should be considered as a tool to generate the canonical ensemble, producing the same kind of results as Monte Carlo simulations. For strongly charged polyelectrolyte systems, the molecular dynamics method is a more efficient way to sample the configuration space compared to the standard Metropolis Monte Carlo algorithm, which displays convergence problems for simulations of highly charged systems with moving polyions. Cluster movement techniques have been developed with the Monte Carlo algorithm to overcome this problem (see (67) and references cited therein). We found the Langevin MD method within the ESPResSo package to be very effective. In the last decades, constant-temperature molecular dynamics with thermostats of different kinds was often used in polyelectrolyte and other coarse-grained simulations.
The systems were simulated at temperature 300 K using a molecular dynamics algorithm with a Langevin thermostat. Masses are given in reduced units and were set to 1 for the histone tail beads and for the ions, and to 50 for the NCP core. The ratio of the masses of the NCP core to the masses of tail beads and ions was made substantially smaller than the real one, with the purpose of providing faster sampling of the configuration space. Under the assumption that the chosen reduced mass unit corresponds to 100 a.u., the time step used in the simulations was ∼16 fs. The Langevin thermostat parameter γ was set to 0.01 in units of the time step. With such a low value, this parameter does not account for the real friction of moving particles through the solvent, but provides only a small correction to the Newtonian equations of motion, keeping the temperature constant. The dynamics in such a simulation is artificially accelerated due to the low friction and low mass of NCPs, and may be qualitatively reconstructed by scaling the time with some factor. Since we are interested only in equilibrium configurations, we do not evaluate this factor, and report only the number of MD steps made. However, it should be pointed out that the configurations generated in this way are not artificial, and do represent the equilibrium ensemble for sufficient convergence of the simulation runs.
MD simulation runs
Most of the MD simulation runs were carried out for a cubic simulation cell with a size of 40 nm, containing 10 similar NCPs starting with a configuration where the NCP particles were randomly placed and well separated from each other (>15 nm intercore distance). The number of ions in the simulation cell with 10 NCPs is listed in Table 1. The concentration of NCPs in the simulation box was 260 μM, which corresponds to 76 mM in DNA phosphate groups. This NCP concentration corresponds to the high limit of nucleosome concentration inside the eukaryotic cell nucleus recently estimated by fluorescent correlation spectroscopy and confocal imaging (68). The concentration of KCl salt in all systems with different NCP models was 65.4 mM KCl; for systems with Mg2+, the concentration of MgCl2 was 4.15 mM. Three kinds of models are coupled with two kinds of salts, resulting in six systems, referred to as nontitration systems.
Table 1.
Number of ions in nontitration systems
| System abbreviation | K | Mg | Cl |
|---|---|---|---|
| rNCP-KCl | 1480 + 2520 | 0 | 2520 |
| rNCP-MgCl2 | 0 | 740 + 160 | 320 |
| aNCP-KCl | 1640 + 2520 | 0 | 2520 |
| aNCP-MgCl2 | 160 | 740 + 160 | 320 |
| paNCP-KCl | 1800 + 2520 | 0 | 2520 |
| paNCP-MgCl2 | 320 | 740 + 160 | 320 |
The simulation box size is 40 nm.
In addition, a number of simulations have been carried out for systems with recombinant and acetylated NCPs with varying mixtures of K+ and Mg2+ ions. In this case, the system had a sum of cation charges of +1480 e for the rNCP systems and +1690 e for the aNCP systems, and it contained 50 Cl− ions. These systems are abbreviated using the indication of the NCP model and the percent of Mg2+ relative to the total positive charge of K+ + Mg2+. For example, the notation “aNCP-50Mg” is used for a simulation run with 422 Mg2+ and 846 K+ (plus 10 aNCPs and 50 Cl−). In this way, the variation of Mg2+ content from 0 to 100% may be considered to qualitatively mimic a titration experiment wherein an NCP solution starting with a low KCl salt (buffer) is titrated with magnesium salt until aggregation is detected. These are referred to as titration systems.
To investigate the relationship between participation of the histone tails in NCP-NCP interaction and the possible salt-dependent dissociation of the tails from the core of the NCP, we also performed simulations for a single NCP in a cubic simulation cell of 23-nm size in the presence of varying amounts of KCl or MgCl2. The concentration of salt in the simulations with one NCP in the cell was varied from 5 mM to 200 mM of KCl or MgCl2.
The systems were simulated for 1.6 × 107–3.2 × 107 MD time steps for nontitration system, and for 4.8 × 107 time steps or longer for titration systems. For single-NCP systems, convergence is achieved in a shorter trajectory, for 0.8 × 107 to 1.6 × 107 time steps. Configurations for analysis were collected after each 200 steps. Averages were calculated for the final 1.6 × 107 time steps or longer, after achieving convergence in the NCP-NCP radial distribution functions (RDFs) and external tail-core RDF.
Results and Discussion
Modification of the histone tails (acetylation and phosphorylation) strongly weakens NCP-NCP interaction caused by addition of K+ and Mg2+ ions
Fig. 2, a and b, displays RDFs that are highly indicative of the NCP-NCP interaction. The core-core (Fig. 2 a) and external tail-core (Fig. 2 b) distributions were calculated from the final 1.6 × 107 MD steps. The insert in Fig. 2 b shows the evolution of RDF maxima, demonstrating that convergence in all simulation systems is reached after ∼1.6 × 107 MD steps. Data obtained in the rNCP-KCl and rNCP-MgCl2 systems are practically identical to the results reported in our previous work (44), which employed a different MD program, another thermostat (Nosé-Hoover, i.e., standard MD, not Langevin dynamics), and another variant of the Ewald summation. This indicates that results are independent of the sampling algorithm and correspond to equilibrium properties of the systems within the model used. In Fig. 2, c and d, the values of the RDF maxima of the curves displayed in Fig. 2, a and b, are shown as histograms.
Figure 2.

Results of the MD simulations for rNCP, aNCP, and paNCP models for the systems with KCl and MgCl2 salts (Table 1). (a and b) RDFs of the core-core (a) and external tail-core (b) distributions collected for the converged region of the trajectories (the last 1.6 × 107 MD steps). The inset in b shows the change in the maximum intensity of the external tail-core RDF during the course of the MD simulation run. The numerical value of the RDF corresponds to the concentration of particles relative to the value expected for a uniform distribution. (c and d) Histograms of the averaged values of the maxima of the core-core (c) and external tail-core (d) RDFs under two salt conditions, 4.15 mM MgCl2 (hatched bars) and 65.4 mM KCl (gray bars). (e) Close-up view of a snapshot of three NCPs in aggregation, with each nucleosome and its core and tails in a different color, demonstrating the participation of tails in intercore interactions.
Pronounced maxima are observed in the core-core and external tail-core RDFs for the rNCP-KCl and rNCP-MgCl2 systems at a distance of close core-core and histone tail-core contact. Aggregation of the rNCPs proceeds to a different extent in the presence of K+ than in the presence of Mg2+ ions. The intensity of the first maximum in the core-core RDF of the rNCP-MgCl2 system exceeds the same peak of the rNCP-KCl system (Fig. 2, a and c). In the rNCP-MgCl2 system, a single conglomerate of 10 NCPs was formed with occasional dissociation of one to two NCPs, whereas in the rNCP-KCl system, several aggregates of two to five NCPs formed with continuous dissociation and exchange of the NCPs during the simulation. The histone tails play a decisive role in formation of the NCP-NCP contacts. The intermolecular RDFs and snapshots from the simulations demonstrate that the NCP aggregates are maintained by both cross-linking (Fig. 2 b) and screening of the negative charge of the core surface by the positive particles of the tails and K+ or Mg2+ cations. Fig. 2 e gives a close-up view of cross-linking in a cluster of three NCPs obtained from a snapshot similar to that seen in the upper part of Fig. 6 (rNCP-Mg100; note that the extended tail of the left-hand side NCP is not free but contacts the other NCP from the mirror periodic cell not shown in the snapshot).
Figure 6.
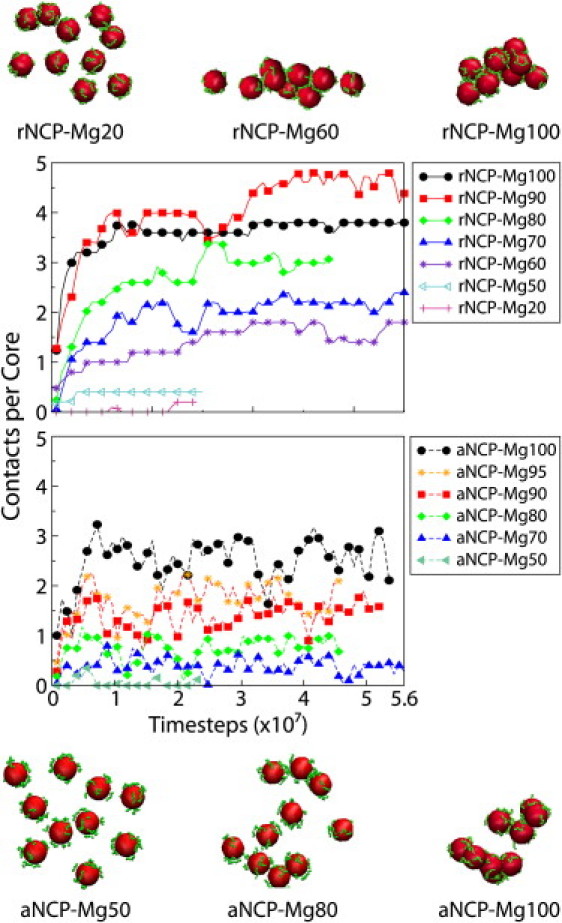
Dynamics of core-core contacts in the systems with rNCPs (a) and aNCPs (b) with varied Mg2+ content. Note the different degree of aggregation in the rNCP systems (upper snapshot) compared to the aNCP systems (lower snapshot).
On the other hand, no stable NCP-NCP contacts were observed for the NCP model with both acetylation and phosphorylation of the histone tails (paNCP model) under the same salt conditions, i.e., in the paNCP-KCl and paNCP-MgCl2 systems (Fig. 2, a and c). The paNCP system rarely forms short-lived associates consisting of two to three particles. For aNCP, only a small degree of NCP-NCP aggregation is observed in the presence of KCl. In the aNCP-MgCl2 system, the intensities of both core-core and external tail-core RDFs are lower than in the rNCP-MgCl2 system.
It may be noted that the intensity of the first maximum of the core-core RDF in the Mg2+ systems was always higher than in the corresponding K+ systems, despite the fact that the ionic strength of the Mg2+ systems (50–59 mM, including neutralizing counterions) was always below that of the K+ systems (84–89 mM). This observation once again demonstrates that the Debye-Hückel approximation, having ionic strength as the only parameter describing the effect of the ions, cannot provide an adequate description of interactions in strongly charged polyelectrolyte systems.
Intramolecular tail-core RDFs and observation of snapshots demonstrate that NCP-NCP interaction is accompanied by extension of the histone tails outside the host core, for both the rNCP and aNCP models. Still, most of the positively charged particles of the tails remain localized in the vicinity of their host core, with only a fraction taking part in cross-linking, even in the most condensed rNCP-MgCl2 system (Fig. 2 e).
For all NCP models (rNCP, aNCP, and paNCP), the mobile cations (K+ and Mg2+) accumulate near the negative surface of the core at concentrations of up to ∼1.4 M K+ and ∼1.2 M Mg2+, with no significant difference between the models; a 10–20% difference is observed between the three NCP models (data not shown). When stable NCP aggregates are formed, most of the cations are gathered inside the condensed phase and there is a drop in concentration of the cations between bulk and NCP aggregates. Interaction of oligocationic tails with chlorine anions is reduced due to the confinement of the tails in the area of the negative electrostatic field from the central particle. Although some accumulation of Cl− ions is seen in the vicinity of the tails, the intensities of the maxima in the corresponding RDFs are lower than those of the K+-Cl− and Mg2+-Cl− RDFs (data not shown).
Comparison of tail-core interaction for systems with isolated and with interacting NCPs
In Fig. 3 a, the internal tail-to-core RDFs of the systems with 10 NCPs in the simulation cell are shown. In Fig. 3 b, the intensity of the main maximum of the internal tail-core RDF for a system with a single NCP in the simulation cell is displayed as a function of salt concentration (KCl or MgCl2). In Fig. 3 b, the values of the maxima of the RDFs presented in Fig. 3 a are shown as symbols. The tail detachment is modest (albeit definitely present) for a system of a single rNCP or aNCP, even at very high Mg2+ salt. The detachment of the tails from the core is therefore not induced by increased salt concentration per se. It is the presence of other NCPs, screening of NCP-NCP repulsion, and induced fluctuation in ion distribution (mediating attraction in the presence of Mg2+) that favors bridging and thus induces the extension of tails outside their cores. Extension of tails is entropically favorable, but the electrostatic energy loss would prevent this from occurring, unless the presence of other NCPs and conditions diminishing NCP-NCP repulsion are at hand. Fig. 3 b thus clearly demonstrates that in the systems with 10 NCPs, detachment of the tails from their host cores is caused by NCP-NCP interaction and formation of tail bridges, and by an electrostatic effect due to screening of the simple salt. The two additional points at 1.8 mM KCl (vertical dashed line), the red square with a cross (rNCP) and blue triangle with a cross (aNCP), represent data from 10-NCP systems where the salt conditions favor NCP-NCP repulsion, i.e., a low concentration of K+ and an absence of Mg2+ (data are taken from simulations described below (see Fig. 5) and correspond to zero percent of Mg2+). Note that there is still a reduction in the maximum of the RDF for these 10-NCP systems, compared to the single-NCP system, even when NCPs do not aggregate in the simulation cell. This is probably because in this rather dense system, frequent random contacts between different NCPs, as well as higher ionic strength due to the neutralizing counterions, cause some extension of the tail.
Figure 3.
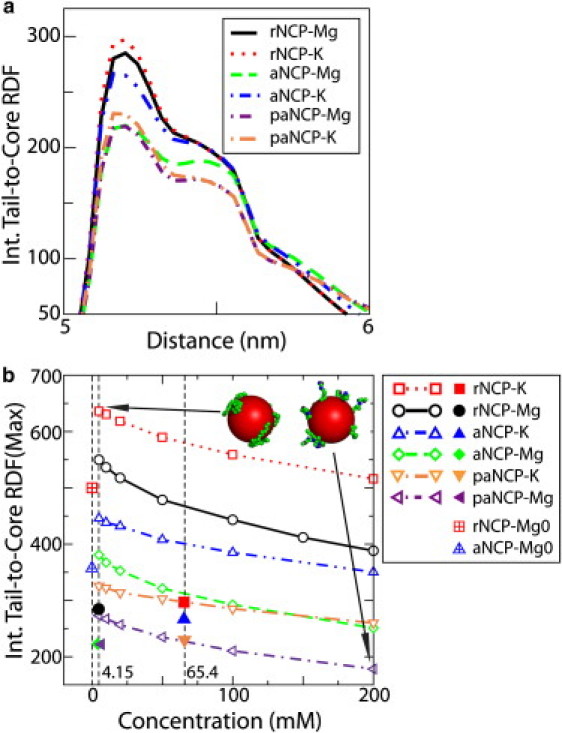
(a) Internal tail-core RDFs of the rNCP, aNCP, and paNCP in the presence of K+ and Mg2+ salts for the systems with 10 NCPs in the simulation cell. (b) Dependence of the intensity of the first maximum of the internal tail-core RDF on salt concentration (KCl or MgCl2) for a system with a single NCP particle in the simulation cell. The maxima in the 10-NCP system (a) are labeled in b with solid symbols of the same shape as the corresponding systems in the single-particle systems (b). The single red square with a cross and blue triangle with a cross represent data at zero percent Mg2+ in the systems represented in Fig. 5.
Figure 5.
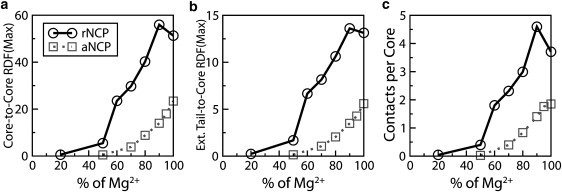
Dependence of the intensities of the RDF maxima and number of the NCP-NCP contacts determined for the rNCP (circles with solid line) and the aNCP (squares with dotted line) models on Mg2+ content in the simulation cell: (a) core-core RDF; (b) external tail-core RDF; (c) number of core-core contacts. Data were averaged for the converged region of the trajectories (the last 1.0 × 107 steps of the MD trajectory).
The data presented in Fig. 3 furthermore illustrate an important point about the mechanism of NCP-NCP interactions. Stable NCP aggregation is only possible when tail interaction with the negative core is strong. Acetylation and phosphorylation of the tails (leading to a reduction of positive charge), as well as addition of salt, allow greater extension of the tails from their cores and seem to facilitate contact of the tails with the other NCPs. However, the strength of the tail-core contact becomes weak, and the tails lose the ability to hold NCPs close to each other in acetylated and phosphorylated systems. Analysis of tail dynamics during the simulation reveals that the tails relocate from their “host” core and become associated with the neighboring nucleosome only after NCPs approach each other. It can be seen at the initial stages of the simulations with 10 NCPs in the rNCP-MgCl2 and aNCP-MgCl2 systems (when NCPs are located away from each other) that the internal RDFs of the tails are similar (data not shown) to those of the single rNCP or aNCP in the simulation cell at low salt (Fig. 3 b). Therefore, we conclude that the effect of the screening on the attractive interaction between tails and their host core is not, as previously suggested (14–16), important for the interaction between NCPs.
Importance of position of the tail modification
To understand how the position of the acetylation sites in the tails influences the NCP-NCP interaction, six additional MD simulation runs were carried out with different distributions of the uncharged beads in the histone tail (“head”, “root”, and “even”) for the aNCP model in KCl and MgCl2 salts. Values of the maximum of the core-core, external tail-core, and internal tail-core RDFs are shown in Fig. 4. Vertical bars represent the three new aNCP models; horizontal lines represent the original, “native” aNCP models. Core-core RDF indicates aggregation of the NCPs, whereas the external tail-core RDF indicates participation of the tails in the formation of bridges between close NCP pairs. In both KCl and MgCl2 solutions, a decrease in NCP-NCP interaction is observed for all four models of aNCP with two acetylation sites, compared to the rNCP model. It can be seen that neutralization of the two particles at the roots of the tails has the weakest influence on NCP aggregation. Core-core RDFs of the aNCP with “even” distribution of the uncharged beads in the tails is the most efficient in reducing NCP-NCP interaction. As observed in Fig. 4, a and b, the four models display small differences in KCl solution. In addition, in the presence of MgCl2, the “even” aNCP significantly weakens NCP aggregation and tail bridging. It is remarkable to observe, in Fig. 4 c, that despite the rather complicated behavior in NCP-NCP interactions and formation of bridges displayed by the different models for aNCP, the “native” distribution of the acetylation sites within the histone tails demonstrates the greatest decrease in interaction of the tails with their host core. Although the coarse-grained NCP model is approximate, it is clear from the data that the relative position of the charge reduction has a pronounced and complex influence on the behavior of the NCP systems. This demonstrates that the inherent electrostatics of the NCP system leaves considerable room for external regulation (by acetylation and phosphorylation) of the electrostatically induced condensation properties of the system.
Figure 4.
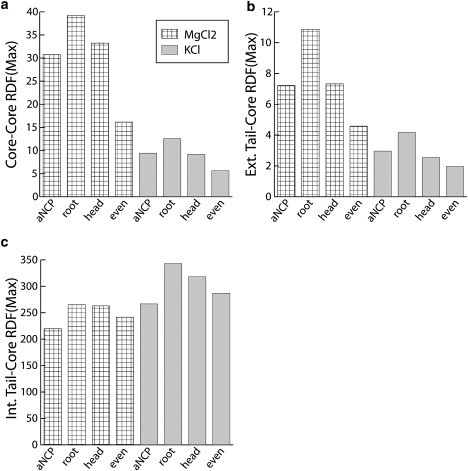
Simulation results for the aNCP model with two acetylation sites in each tail but different positions of acetylation. Values of the first maximum in the core-core RDF (a), external tail-core RDF (b), and internal tail-core RDF (c) are shown for the four aNCP models, native (aNCP), root, head, and even, under two salt conditions, 4.15 mM MgCl2 (hatched bars) and 65.4 mM KCl (gray bars).
Modeling titration of NCP solutions with Mg2+ ions
In experimental studies of NCP and chromatin array systems, the standard experiment to monitor the condensation behavior is titration by multivalent salt, in particular MgCl2 ((4), and references therein, as well as recent work (18,33,34,39,43)). To model such an experiment correctly in simulations, a very large system (large simulation cell) must be employed, or, preferably, simulations should be carried out within a grand canonical ensemble in equilibrium with a defined bulk salt solution (53). To qualitatively mimic the titration performed in experiments, we started with a system comprising K+ counterions and a small amount of added KCl (Fig. 5, 0% Mg) and made simulations of this system by replacing K+ counterions with Mg2+ (Figs. 5 and 6 show the results from such a series of MD simulations modeling the “titration” of a potassium salt solution of NCPs (NCP with K+ counterions + KCl). Since the paNCP-MgCl2 system does not show aggregation, we carried out titration by Mg2+ using only the rNCP and “native” aNCP models.
Fig. 5, a and b, shows the core-core and external tail-core RDFs, whereas Fig. 5 c presents averaged statistics of NCP-NCP contacts. The average number of NCP-NCP contacts is defined as follows: two NCPs were considered to be in contact if the core-core distance between them was <12 nm, a distance based on the position of the right border of the first maximum of the core-core RDF (see Fig. 2 a). The average number of contacts per core is defined as n = Npair/(Ncore – Nframe), where the number of pairs, Npair, was counted from one trajectory segment of Nframe frames, and Ncore = 10. The whole trajectory was divided into segments. Each segment consists of 4000 frames collected at every 10th time step. Fig. 6 shows the dynamics of the NCP-NCP contacts for the rNCP and aNCP systems with different Mg2+contents. Some illustrative snapshots showing degrees of aggregation from the MD trajectories are also presented in Fig. 6.
The extent of NCP aggregation depends on the “acetylation” state of the histone tails and on the relative amount of Mg2+. Below 50% Mg2+, no aggregation is observed for rNCP or aNCP. Aggregation of the rNCPs occurs between 60 and 80% of Mg2+ and above 80% Mg2+, a single aggregate containing all 10 rNCPs is formed. In the system with aNCP, the existence of stable NCP-NCP aggregates consisting of two to five aNCPs is seen only above 80% Mg2+ (Fig. 6, snapshots). It is of interest that there is some decrease in NCP-NCP interaction from 90 to 100% Mg2+ for the rNCP. This effect might reflect a real event of “loosening” of the NCP aggregates in excess of Mg2+ (N. Korolev and L. Nordenskiöld, unpublished experimental results) which leads to redissolution of the NCP and chromatin at high concentrations of MgCl2 (13,42).
Fig. 6 shows the “dynamics” of the NCP-NCP contacts in the rNCP and aNCP systems with different Mg2+ content. The system of a fully charged “recombinant” NCP reaches equilibrium after ∼2 × 107 MD time steps. The rNCP systems show a rather static behavior, with little fluctuation in the number of NCP-NCP contacts (Fig. 6 a). A contrasting behavior is observed in the aNCP system, where large fluctuations in the number of NCP-NCP contacts are seen during the simulations (Fig. 6 b).
Relevance of the simulation results to experimental data
To assess the validity of the predictions obtained based on the results presented here, it is desirable to make a direct comparison with biochemical data. Ideally, NCPs containing specifically neutralized lysine tails should be investigated with respect to the effects on the Mg2+-induced interparticle aggregation (precipitation). One approach to this is the preparation of histones with selective lysine-to-glutamine (K→Q) mutations, which mimics acetylation. However, no data on NCPs with well defined tail charge neutralizations (either by acetylation or by K→Q mutation) are available in the literature. On the other hand, Wang and Hayes (39,43) recently published a comprehensive study of the interarray aggregation for all combinations of the four histones, where selective K→Q mutations were introduced in each histone tail. Arrays of 12 nucleosomes with repeat lengths of 177, 207, and 208 bp were investigated. The numbers of K→Q mutations were 2, 6, 6, and 4 for H2A, H2B, H3, and H4 histones, respectively. Sixteen different histone mutant/wild-type octamer combinations were assembled to nucleosomal arrays with 4–36 quenched lysine charges in each NCP. The effect of these mutations on the EC50 values in Mg2+-induced aggregation, as detected by a precipitation assay, was established (EC50 is the concentration of Mg2+ needed to precipitate 50% of the arrays). An increase in EC50, i.e., a higher concentration of Mg2+ needed to induce aggregation, would be expected for an electrostatic mechanism and is implied for NCPs based on the above simulation results that mimic the Mg2+ “titration” experiment. Although no simple relation was found between the number of charges neutralized and EC50, the results of this study showed that, in general, the more positive charges that were neutralized, the higher was the amount of Mg2+ needed to induce aggregation. For arrays with combinations of all histones mutated (36 charges neutralized), the EC50 value increased to 16.42 mM, compared to 2.38 mM for the wild-type. The system with only H3 and H4 histones mutated (20 charges neutralized), displayed an increase of EC50 to 4.63 mM (data refer to a 12-mer nucleosomal array with a repeat length of 177 bp). Even though direct quantitative comparison with our simulation data cannot be made, the general trend observed in these experiments is in agreement with the simulation results, which indicate a higher concentration of Mg2+ needed to induce aggregation of NCPs with 16 tail charges neutralized (Figs. 5 and 6). However, the effects observed in these array experiments (including a small unexpected decrease in EC50 for the H2A single-mutant histone case) likely depend on additional factors. The relative tail exit position on the nucleosome core, as well as a possible cooperativity in the combined contributions of individual tails (39,43), may affect the aggregation process. These issues should be addressed in future simulations utilizing more detailed modeling of NCP and chromatin fiber. Nevertheless, this study illustrates the crucial importance of explicit presentation of the charged particles in the histone tails and the mobile ions in solution. This principal advantage of our model should be preserved in future studies.
It may be questioned whether the results of our simulations are relevant to and can be compared with data for array aggregation. The process of aggregation during an Mg2+ titration experiment is known to be preceded by compaction of individual arrays to a folded state (at ∼1 mM Mg2+) (41), whereas interarray aggregation then follows at higher concentrations. In the compact state, the linker DNA is folded with limited flexibility. The 12-mer arrays with linker length of 30 bp DNA can then be considered as a preaggregated cluster of 12 NCPs. The major factor that then determines the interarray aggregation of such clusters is expected to be the interactions between the nucleosomes of different arrays as they approach each other. This process is very similar to the NCP aggregation we model in the simulations. Based on this consideration, it is clear that modeling of NCP aggregation is highly relevant to the question of chromatin fiber formation (i.e., interarray aggregation).
Importance of the detailed coarse-graining in modeling salt-induced NCP aggregation
The NCP charged-sphere model used in this work encompasses a highly coarse description of the shape and charge distribution of the core (excluding the tails) of the NCP, i.e., the globular part of the histone octamer with ∼147 bp DNA wrapped around it. In reality, the shape of this core is more like a flat cylinder with the majority of the negative charges on the periphery of the cylinder jacket. The rationale for our approach is the tremendous net charge of this particle, which correspond to ∼−236 e of the DNA + globular part of the histones with an additional +88 e in the flexible tails. The electrostatic forces involved in the interaction between NCPs are of long range. It is therefore expected that the general qualitative properties of aggregation their dependence on histone tail charge, as well as on the amount of small ions present, should not be highly affected by the details of the shape and charge distribution of the core particle. On the other hand, to model the detailed structure of the ordered NCP precipitate (an issue not addressed in this work), a more refined NCP structure and distribution of charges will be of importance. For example, in phase separation from concentrated NCP solutions, liquid crystalline ordering into various columnar packing has been observed (18,29,30). Furthermore, in the folding of the individual chromatin array, the details of the core model are also expected to be highly relevant. Recent experimental studies have suggested the importance of the wedgelike NCP shape inside the so-called 30-nm chromatin fiber (38), as well as specific functions of the so-called “acidic islets” in the globular domain of the H2A histones, located on the top and bottom of the NCP cylinder (69–71).
Given the approximate nature of our NCP model, we have performed some control simulations to demonstrate the importance of the charged-sphere approximation with respect to the aggregation properties of the NCP system. Here, we give an account of the most important aspects of our results (see the Supporting Material for more details). A model of the NCP core was developed that consisted of an inner neutral sphere of diameter 7.0 nm modeling the histone octamer. Around this central sphere, ∼1.7 turns of DNA is wrapped. DNA was described as connected negatively-charged beads of 1.0 nm diameter. We also tested a model with a positively charged histone core sphere and full DNA charges, and the conclusions described below remained the same. The model is further described and illustrated in the Supporting Material (see Fig. S2). In this so-called sphere-bead NCP model, the core takes the approximate shape of a cylinder, with the negative charges on the jacket and distributed in a manner similar to that in the real system, albeit with the top and bottom of the cylinder having hemispherical caps rather than flat surfaces. We have assessed the most important aspects of the results of the sphere NCP model, namely, that in the presence of divalent ions (Mg2+), the solution of NCPs aggregate, and that in a similar system that has a reduction in tail charge, a reduced aggregation propensity is observed. Indeed, the results from simulations of this refined model display the same qualitative features as in the sphere NCP model. Although the core-core RDF for this new model is considerably broader and displays two maxima, an effect that is a result of the shape and lower symmetry compared to the spherical model, the qualitative behavior is the same as in the sphere NCP model (see Fig. 3S and Fig. 4S). The aggregates in the sphere-bead model are less compact and more extended than in the sphere model, and consequently, values of the integrated RDF are smaller. However, as illustrated by representative snapshots, there is a qualitative equivalence in the behavior of the two different models (Fig. 3S and Fig. 4S). In summary, within our approach, the following general observations are independent of the details of shape and charge distribution of the NCP core: 1), tail-mediated aggregation of NCPs is induced by Mg2+; 2), reduction of the tail charge (“acetylation”) reduces this aggregation propensity under similar conditions of Mg2+ concentration; and 3), more Mg2+ is needed to induce aggregation for “acetylated” NCP. All these observations are in agreement with available experimental observations for NCP and model nucleosomal array aggregation.
Conclusions
The approach described here captures two important features of the NCP-NCP interaction necessary to describe the mechanism of salt-induced aggregation: 1), attractive ion-ion correlation effects due to fluctuations in the ion cloud; and 2), attractive entropic and energetic tail bridging. These two physical mechanisms are necessary to describe NCP interaction. In the case of DNA, it is now well established that fluctuation-induced dynamic ion correlation gives rise to an attractive contribution to the force between DNA rods that explains experimental aggregation (52,54,72). Consequently, modeling of the multivalent ion-induced aggregation of NCPs must include this mechanism. It is also very important to incorporate flexible and charged histone tails, since their bridging contributes decisively to NCP-NCP interaction during attraction between adjacent DNA strands (44,73). Experiments with nucleosomal arrays demonstrate that tails relocate from mainly intranucleosome interaction with their own core particle in the extended array at low salt to primarily bridgelike internucleosomal interactions upon formation of condensed secondary and tertiary chromatin aggregates (41,74). Within the approximations of the coarse-grained dielectric continuum model, the simulations allow generation of the correct (within the model) equilibrium properties. There is no need to reduce the charges on the NCP and on the tails in this model. This sort of collective treatment of the polyelectrolyte and its counterions has been used in other and, from a statistical mechanical point of view, less rigorous, polyelectrolyte models. The Manning counterion condensation theory is based on this concept. Recent coarse-grained NCP/chromatin models (e.g. (47–49)) have used such “charge renormalization,” assigning some effective values to the nucleosome and tail charges. However, such a parameterized procedure becomes redundant in a model like ours, which incorporates explicit mobile counterions.
It is arguable that the model used in our approach suffers from considerable simplification, in particular with regard to the description of the shape of the nucleosome core, as well as its primitive charge distribution. However, our preliminary results with a more refined model in this respect (details of which are presented in the Supporting Material) show that the general features and conclusions from the sphere model are not affected by these approximations. In fact, the use of this model, which can be considered the simplest possible representation of the NCP that still incorporates the major aspects of the electrostatics of the system, highlights the strength in our current approach. By focusing on the simplest aspect of the system, namely the phenomenal electrostatic charges in the system, the underlying physical mechanism responsible for the nucleosome aggregation will be more clearly spelled out. A stepwise refinement of the model, the first step of which is the introduction of the sphere-bead model, to be followed by the introduction of linker DNA, can then enable a stepwise deepening of the understanding of the experimental behavior of the unique biopolyelectrolyte system that is chromatin. The results of control simulations of the more detailed sphere-bead model lend support to this approach.
As shown in our previous work (44), the results for the recombinant NCP model are in agreement with experimental data reporting a sharp change of the second virial coefficient in solutions of NCPs at salt concentration >50 mM NaCl (15,16), which is caused by NCP-NCP interactions via histone-tail cross-linking. In a similar way, in the presence of a millimolar concentration of Mg2+ and low concentration of monovalent salt, aggregation of NCPs has been observed (13). Tailless nucleosomes do not show similar aggregation properties (15), indicating the importance of an electrostatic tail bridging mechanism in NCP aggregation.
From the simulation results, comparing the dependence of tail behavior on tail modification, salt concentration, and presence of Mg2+ between the systems with 10 NCPs and those with a single NCP in the simulation cell, it becomes possible to draw conclusions about the mechanism of tail bridging and NCP-NCP attraction. In recent work performed on solutions of linker-free recombinant NCPs (16,17), it is argued that NCP-NCP interaction becomes possible when (or after) the histone tails extend from the NCP core. It is suggested that the tail extension occurs due to salt screening, which leads to the dissociation of tails from the NCPs (14–16). NMR data from an earlier work (75) reported increased dissociation of the histone tails from the chromatin array only when the salt concentration is raised well above 200 mM NaCl. It is worthy of note that aggregation and precipitation of chromatin was observed under conditions where no dissociation of the tails was registered (between 100 and 200 mM NaCl). This is in agreement with experimental data obtained in the NCP solutions (16,17) and with the results of our simulations. We propose that tails can promote NCP-NCP interaction through tail bridging only if the tail binding to the NCP (either the host or the foreign NCP) is strong. The function of salt (addition of KCl, presence of Mg2+, or other multivalent cation) is to screen the mutual repulsion of the NCPs and promote fluctuation-induced attraction. When repulsion between the NCPs is screened by salt, but the tail-core interaction is still attractive, the gain in entropy due to the possibility of tails sampling the volume outside the core makes close contacts favorable. When the tail extension from the core can occur more freely, in the case of reduction in the positive charge of the tails, formation of NCP aggregates becomes unfavorable, mainly due to the entropy decrease upon aggregation.
A positive correlation between the degree of acetylation and transcriptional activity was established in early studies of chromatin (76,77). The fraction of chromatin with a high degree of acetylation also showed higher solubility in moderate salt (100–200 mM NaCl) and in millimolar concentrations of MgCl2 (26,56,57), and differences in sedimentation coefficients (31,78). The acetylation of the histone tails does not result in noticeable alteration of conformation, stability, or dynamics of the nucleosome core particle itself (56,57). Therefore, it was suggested that modification of the histone tails either modulates interaction of the tails with linker DNA and other nucleosomes or serves as a signal for the specialized proteins. However, no detailed studies addressing the influence of histone modifications on the NCP-NCP interactions have been carried out for systems of isolated NCPs. On the other hand, the effects of histone tail-charge modifications on interarray aggregation of 12-mer chromatin arrays, has recently been studied (39,43). The general electrostatic effects of tail-charge reductions on the Mg2+-induced aggregation is supported by our results for NCP aggregation. In our previous work (44) using the same model of the NCP, we demonstrated that salt-induced aggregation of NCPs is mediated by histone tail bridging. Our results for the “acetylated” model show that this tail bridging is attenuated upon reduction in histone tail charge. To our knowledge, this work is the first theoretical demonstration of the decisive contribution of histone tail-charge modifications in the condensation of nucleosomes.
Acknowledgments
We thank Dr. Yuguang Mu for discussions on modeling and simulation.
This work was supported by a Singapore Ministry of Education University Research Committee (ARC) grant and by a grant from the Singapore Agency for Science Technology and Research (A∗STAR) through the Biomedical Research Council (BMRC).
Contributor Information
Nikolay Korolev, Email: Korolev@ntu.edu.sg.
Lars Nordenskiöld, Email: LarsNor@ntu.edu.sg.
Supporting Material
References
- 1.Luger K., Mader A.W., Richmond R.K., Sargent D.F., Richmond T.J. Crystal structure of the nucleosome core particle at 2.8 Å resolution. Nature. 1997;389:251–260. doi: 10.1038/38444. [DOI] [PubMed] [Google Scholar]
- 2.Davey C.A., Sargent D.F., Luger K., Maeder A.W., Richmond T.J. Solvent mediated interactions in the structure of nucleosome core particle at 1.9 Å resolution. J. Mol. Biol. 2002;319:1097–1113. doi: 10.1016/S0022-2836(02)00386-8. [DOI] [PubMed] [Google Scholar]
- 3.Woodcock C.L., Dimitrov S. Higher-order structure of chromatin and chromosomes. Curr. Opin. Genet. Dev. 2001;11:130–135. doi: 10.1016/s0959-437x(00)00169-6. [DOI] [PubMed] [Google Scholar]
- 4.Hansen J.C. Conformational dynamics of the chromatin fiber in solution: determinants, mechanisms, and functions. Annu. Rev. Biophys. Biomol. Struct. 2002;31:361–392. doi: 10.1146/annurev.biophys.31.101101.140858. [DOI] [PubMed] [Google Scholar]
- 5.Luger K., Hansen J.C. Nucleosome and chromatin fiber dynamics. Curr. Opin. Struct. Biol. 2005;15:188–196. doi: 10.1016/j.sbi.2005.03.006. [DOI] [PubMed] [Google Scholar]
- 6.Luger K., Richmond T.J. The histone tails of the nucleosome. Curr. Opin. Genet. Dev. 1998;8:140–146. doi: 10.1016/s0959-437x(98)80134-2. [DOI] [PubMed] [Google Scholar]
- 7.Zheng C., Hayes J.J. Structures and interactions of the core histone tail domains. Biopolymers. 2003;68:539–546. doi: 10.1002/bip.10303. [DOI] [PubMed] [Google Scholar]
- 8.Horn P.J., Peterson C.L. Chromatin higher order folding: wrapping up transcription. Science. 2002;297:1824–1827. doi: 10.1126/science.1074200. [DOI] [PubMed] [Google Scholar]
- 9.Wolffe A.P. Academic Press; San Diego, CA: 1998. Chromatin: Structure and Function. [Google Scholar]
- 10.van Holde K.E. Springer-Verlag; New York: 1989. Chromatin. [Google Scholar]
- 11.Clark D.J., Kimura T. Electrostatic mechanism of chromatin folding. J. Mol. Biol. 1990;211:883–896. doi: 10.1016/0022-2836(90)90081-V. [DOI] [PubMed] [Google Scholar]
- 12.van Holde K., Zlatanova J. What determines the folding of the chromatin fiber? Proc. Natl. Acad. Sci. USA. 1996;93:10548–10555. doi: 10.1073/pnas.93.20.10548. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.de Frutos M., Raspaud E., Leforestier A., Livolant F. Aggregation of nucleosomes by divalent cations. Biophys. J. 2001;81:1127–1132. doi: 10.1016/S0006-3495(01)75769-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Mangenot S., Leforestier A., Vachette P., Durand D., Livolant F. Salt-induced conformation and interaction changes of nucleosome core particles. Biophys. J. 2002;82:345–356. doi: 10.1016/S0006-3495(02)75399-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Bertin A., Leforestier A., Durand D., Livolant F. Role of histone tails in the conformation and interaction of nucleosome core particles. Biochemistry. 2004;43:4773–4780. doi: 10.1021/bi036210g. [DOI] [PubMed] [Google Scholar]
- 16.Mangenot S., Raspaud E., Tribet C., Belloni L., Livolant F. Interactions between isolated nucleosome core particles. A tail bridging effect? Eur. Phys. J. E. 2002;7:221–231. [Google Scholar]
- 17.Bertin A., Renouard M., Pedersen J.S., Livolant F., Durand D. H3 and H4 histone tails play a central role in the interactions of recombinant NCPs. Biophys. J. 2007;92:2633–2645. doi: 10.1529/biophysj.106.093815. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Bertin A., Mangenot S., Renouard M., Durand D., Livolant F. Structure and phase diagram of nucleosome core particles aggregated by multivalent cations. Biophys. J. 2007;93:3652–3663. doi: 10.1529/biophysj.107.108365. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Ren Q., Gorovsky M.A. The nonessential H2A N-terminal tail can function as an essential charge patch on the H2A.Z variant N-terminal tail. Mol. Cell. Biol. 2003;23:2778–2789. doi: 10.1128/MCB.23.8.2778-2789.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Wolffe A.P., Hayes J.J. Chromatin disruption and modification. Nucleic Acids Res. 1999;27:711–720. doi: 10.1093/nar/27.3.711. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Turner B.M. Histone acetylation and control of gene expression. J. Cell Sci. 1991;99:13–20. doi: 10.1242/jcs.99.1.13. [DOI] [PubMed] [Google Scholar]
- 22.Calestagne-Morelli A., Ausio J. Long-range histone acetylation: biological significance, structural implications, and mechanisms. Biochem. Cell Biol. 2006;84:518–527. doi: 10.1139/o06-067. [DOI] [PubMed] [Google Scholar]
- 23.Csordas A. On the biological role of histone acetylation. Biochem. J. 1990;265:23–38. doi: 10.1042/bj2650023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Kurdistani S.K., Tavazole S., Grunstein M. Mapping global histone acetylation patterns to gene expression. Cell. 2004;117:721–733. doi: 10.1016/j.cell.2004.05.023. [DOI] [PubMed] [Google Scholar]
- 25.Lewis P.N., Guillemette J.G., Chan S. Histone accessibility determined by lysine-specific acetylation in chicken erythrocyte nuclei. Eur. J. Biochem. 1988;172:135–145. doi: 10.1111/j.1432-1033.1988.tb13865.x. [DOI] [PubMed] [Google Scholar]
- 26.Perry M., Chalkley R. The effect of histone hyperacetylation on the nuclease sensitivity and the solubility of chromatin. J. Biol. Chem. 1981;256:3313–3318. [PubMed] [Google Scholar]
- 27.Perry M., Chalkley R. Histone acetylation increases the solubility of chromatin and occurs sequentially over most of the chromatin. A novel model for the biological role of histone acetylation. J. Biol. Chem. 1982;257:7336–7347. [PubMed] [Google Scholar]
- 28.Tse C., Sera T., Wolffe A.P., Hansen J.C. Disruption of higher-order folding by core histone acetylation dramatically enhances transcription of nucleosomal arrays by RNA polymerase III. Mol. Cell. Biol. 1998;18:4629–4638. doi: 10.1128/mcb.18.8.4629. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Mangenot S., Leforestier A., Durand D., Livolant F. X-ray diffraction characterization of the dense phases formed by nucleosome core particles. Biophys. J. 2003;84:2570–2584. doi: 10.1016/S0006-3495(03)75062-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Mangenot S., Leforestier A., Durand D., Livolant F. Phase diagram of nucleosome core particles. J. Mol. Biol. 2003;333:907–916. doi: 10.1016/j.jmb.2003.09.015. [DOI] [PubMed] [Google Scholar]
- 31.Wang X., He C., Moore S.C., Ausio J. Effects of histone acetylation on the solubility and folding of the chromatin fiber. J. Biol. Chem. 2001;276:12764–12768. doi: 10.1074/jbc.M100501200. [DOI] [PubMed] [Google Scholar]
- 32.Ausio J. Analytical ultracentrifugation and the characterization of chromatin structure. Biophys. Chem. 2000;86:141–153. doi: 10.1016/s0301-4622(00)00144-7. [DOI] [PubMed] [Google Scholar]
- 33.Shogren-Knaak M.A., Ishii H., Sun J.-M., Pazin M., Davie J.R. Histone H4–K16 acetylation controls chromatin structure and protein interactions. Science. 2006;311:844–847. doi: 10.1126/science.1124000. [DOI] [PubMed] [Google Scholar]
- 34.Kan P.-Y., Lu X., Hansen J.C., Hayes J.J. The H3 tail domain participates in multiple interactions during folding and self-association of nucleosome arrays. Mol. Cell. Biol. 2007;27:2084–2091. doi: 10.1128/MCB.02181-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Wang X., Hayes J.J. Site-specific binding affinities within the H2B tail domain indicate specific effects of lysine acetylation. J. Biol. Chem. 2007;282:32867–32876. doi: 10.1074/jbc.M706035200. [DOI] [PubMed] [Google Scholar]
- 36.Routh A., Sandin S., Rhodes D. Nucleosome repeat length and linker histone stoichiometry determine chromatin fiber structure. Proc. Natl. Acad. Sci. USA. 2008;105:8872–8877. doi: 10.1073/pnas.0802336105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Robinson P.J.J., An W., Routh A., Martino F., Chapman L. 30 nm chromatin fibre decompaction requires both H4–K16 acetylation and linker histone eviction. J. Mol. Biol. 2008;381:816–825. doi: 10.1016/j.jmb.2008.04.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Robinson P.J.J., Fairall L., Huynh V.A.T., Rhodes D. EM measurements define the dimensions of the “30-nm” chromatin fiber: evidence for a compact, interdigitated structure. Proc. Natl. Acad. Sci. USA. 2006;103:6506–6511. doi: 10.1073/pnas.0601212103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Wang X., Hayes J.J. Acetylation mimics within individual core histone tail domains indicate distinct roles in regulating stability of higher-order chromatin structure. Mol. Cell. Biol. 2008;28:227–236. doi: 10.1128/MCB.01245-07. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Pollard K.J., Samuels M.L., Crowley K.A., Hansen J.C., Peterson C.L. Functional interaction between GCN5 and polyamines: a new role for core histone acetylation. EMBO J. 1999;18:5622–5633. doi: 10.1093/emboj/18.20.5622. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Dorigo B., Schalch T., Bystricky K., Richmond T.J. Chromatin fiber folding: requirement for the histone H4 N-terminal tail. J. Mol. Biol. 2003;327:85–96. doi: 10.1016/s0022-2836(03)00025-1. [DOI] [PubMed] [Google Scholar]
- 42.Schalch, T. 2004. The 30-nm chromatin fiber: in vitro reconstitution and structural analysis. Ph.D. thesis. Swiss Federal Institute of Technology, Zurich ETH, Zurich. 179 pp.
- 43.Wang X., Hayes J.J. Site-specific binding affinities within the H2B tail domain indicate specific effects of lysine acetylation. J. Biol. Chem. 2007;282:32867–32876. doi: 10.1074/jbc.M706035200. [DOI] [PubMed] [Google Scholar]
- 44.Korolev N., Lyubartsev A.P., Nordenskiöld L. Computer modeling demonstrates that electrostatic attraction of nucleosomal DNA is mediated by histone tails. Biophys. J. 2006;90:4305–4316. doi: 10.1529/biophysj.105.080226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Muhlbacher F., Holm C., Schiessel H. Controlled DNA compaction within chromatin: the tail-bridging effect. Europhys. Lett. 2006;73:135–141. [Google Scholar]
- 46.Muhlbacher F., Schiessel H., Holm C. Tail-induced attraction between nucleosome core particles. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2006;74:031919. doi: 10.1103/PhysRevE.74.031919. [DOI] [PubMed] [Google Scholar]
- 47.Arya G., Zhang Q., Schlick T. Flexible histone tails in a new mesoscopic oligonucleosome model. Biophys. J. 2006;91:133–150. doi: 10.1529/biophysj.106.083006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Arya G., Schlick T. Role of histone tails in chromatin folding revealed by a mesoscopic oligonucleosome model. Proc. Natl. Acad. Sci. USA. 2006;103:16236–16241. doi: 10.1073/pnas.0604817103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Sun J., Zhang Q., Schlick T. Electrostatic mechanism of nucleosomal array folding revealed by computer simulation. Proc. Natl. Acad. Sci. USA. 2005;102:8180–8185. doi: 10.1073/pnas.0408867102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Voltz K., Trylska J., Tozzini V., Kurkal-Siebert V., Langowski J. Coarse-grained force field for the nucleosome from self-consistent multiscaling. J. Comput. Chem. 2008;29:1429–1439. doi: 10.1002/jcc.20902. [DOI] [PubMed] [Google Scholar]
- 51.Arya G., Schlick T. Efficient global biopolymer sampling with end-transfer configurational bias Monte Carlo. J. Chem. Phys. 2007;126:044107. doi: 10.1063/1.2428305. [DOI] [PubMed] [Google Scholar]
- 52.Oosawa F. Interaction between parallel rodlike macroions. Biopolymers. 1968;6:1633–1647. [Google Scholar]
- 53.Lyubartsev A.P., Nordenskiöld L. Monte Carlo simulation study of ion distribution and osmotic pressure in hexagonally oriented DNA. J. Phys. Chem. 1995;99:10373–10382. [Google Scholar]
- 54.Ray J., Manning G.S. Effect of counterion valence and polymer charge density on the pair potential of two polyions. Macromolecules. 1997;30:5739–5744. [Google Scholar]
- 55.Dai L., Mu Y., Nordenskiöld L., van der Maarel J.R.C. Molecular dynamics simulation of multivalent-ion mediated DNA attraction between DNA molecules. Phys. Rev. Lett. 2008;100:118301. doi: 10.1103/PhysRevLett.100.118301. [DOI] [PubMed] [Google Scholar]
- 56.Ausio J., van Holde K.E. Histone hyperacetylation: its effects on nucleosome conformation and stability. Biochemistry. 1986;25:1421–1428. doi: 10.1021/bi00354a035. [DOI] [PubMed] [Google Scholar]
- 57.Libertini L.J., Ausio J., van Holde K.E., Small E.W. Histone hyperacetylation. Its effects on nucleosome core particle transitions. Biophys. J. 1988;53:477–487. doi: 10.1016/S0006-3495(88)83126-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Hansen J.C., Tse C., Wolffe A.P. Structure and function of the core histone N-termini: more than meets the eye. Biochemistry. 1998;37:17637–17641. doi: 10.1021/bi982409v. [DOI] [PubMed] [Google Scholar]
- 59.Cheung W.L., Briggs S.D., Allis C.D. Acetylation and chromosomal functions. Curr. Opin. Cell Biol. 2000;12:326–333. doi: 10.1016/s0955-0674(00)00096-x. [DOI] [PubMed] [Google Scholar]
- 60.Turner B.M. Histone acetylation and an epigenic code. Bioessays. 2000;22:836–845. doi: 10.1002/1521-1878(200009)22:9<836::AID-BIES9>3.0.CO;2-X. [DOI] [PubMed] [Google Scholar]
- 61.Ito T. Role of histone modification in chromatin dynamics. J. Biochem. 2007;141:609–614. doi: 10.1093/jb/mvm091. [DOI] [PubMed] [Google Scholar]
- 62.Davie J.R. Covalent modification of histones: expression from chromatin templates. Curr. Opin. Genet. Dev. 1998;8:173–178. doi: 10.1016/s0959-437x(98)80138-x. [DOI] [PubMed] [Google Scholar]
- 63.Peterson C.L., Laniel M.-A. Histones and histone modifications. Curr. Biol. 2004;14:R546–R551. doi: 10.1016/j.cub.2004.07.007. [DOI] [PubMed] [Google Scholar]
- 64.Cheung P., Allis C.D., Sassone-Corsi P. Signaling to chromatin through histone modification. Cell. 2000;103:263–271. doi: 10.1016/s0092-8674(00)00118-5. [DOI] [PubMed] [Google Scholar]
- 65.Deserno M., Holm C. How to mesh up Ewald sums. I. A theoretical and numerical comparison of various particle mesh routines. J. Chem. Phys. 1998;109:7678–7693. [Google Scholar]
- 66.Limbach H.J., Arnold A., Mann B.A., Holm C. ESPResSo: an extensible simulation package for research on soft matter systems. Comput. Phys. Commun. 2006;174:704–727. [Google Scholar]
- 67.Linse P., Lobaskin V. Electrostatic attraction and phase separation in solution of like-charged colloidal particles. Phys. Rev. Lett. 1999;83:4208–4211. [Google Scholar]
- 68.Weidemann T., Wachsmuth M., Knoch T., Muller G., Waldeck W. Counting nucleosomes in living cells with a combination of fluorescent correlation spectroscopy and confocal imaging. J. Mol. Biol. 2003;334:229–240. doi: 10.1016/j.jmb.2003.08.063. [DOI] [PubMed] [Google Scholar]
- 69.Zhou J., Fan J.Y., Rangasamy D., Tremethick D.J. The nucleosome surface regulates chromatin compaction and couples it with transcriptional repression. Nat. Struct. Mol. Biol. 2007;14:1070–1076. doi: 10.1038/nsmb1323. [DOI] [PubMed] [Google Scholar]
- 70.Barbera A.J., Chodaparambil J.V., Kelley-Clarke B., Joukov V., Walter J.C. The nucleosomal surface as a docking station for Kaposi's sarcoma herpesvirus LANA. Science. 2006;311:856–861. doi: 10.1126/science.1120541. [DOI] [PubMed] [Google Scholar]
- 71.Chodaparambil J.V., Barbera A.J., Lu X., Kaye K.M., Hansen J.C. A charged and contoured surface on the nucleosome regulates chromatin compaction. Nat. Struct. Mol. Biol. 2007;14:1105–1107. doi: 10.1038/nsmb1334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Gelbart W.M., Bruinsma R.F., Pincus P.A., Parsegian V.A. DNA-inspired electrostatics. Phys. Today. 2000;53:38–44. [Google Scholar]
- 73.Korolev N., Nordenskiöld L. H4 histone tail mediated DNA-DNA interaction and effects on DNA structure, flexibility and counterion binding. A molecular dynamics study. Biopolymers. 2007;86:409–423. doi: 10.1002/bip.20749. [DOI] [PubMed] [Google Scholar]
- 74.Zheng C., Lu X., Hansen J.C., Hayes J.J. Salt-dependent intra- and inter-nucleosomal interactions of the H3 tail domain in a model oligonucleosomal array. J. Biol. Chem. 2005;280:33552–33557. doi: 10.1074/jbc.M507241200. [DOI] [PubMed] [Google Scholar]
- 75.Walker I.O. Differential dissociation of histone tails from core chromatin. Biochemistry. 1984;23:5622–5628. doi: 10.1021/bi00318a037. [DOI] [PubMed] [Google Scholar]
- 76.Marushige K. Activation of chromatin by acetylation of histone side chains. Proc. Natl. Acad. Sci. USA. 1976;73:3937–3941. doi: 10.1073/pnas.73.11.3937. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Gottesfeld J.M., Garrard W.T., Bagi G., Wilson R.F., Bonner J. Partial purification of the template-active fraction of chromatin: a preliminary report. Proc. Natl. Acad. Sci. USA. 1974;71:2192–2197. doi: 10.1073/pnas.71.6.2193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Garcia-Ramirez M., Rocchini C., Ausio J. Modulation of chromatin folding by histone acetylation. J. Biol. Chem. 1995;270:17923–17928. doi: 10.1074/jbc.270.30.17923. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


