Simultaneous Measurements of Solvent Dynamics and Functional Kinetics in a Light-Activated Enzyme

Abstract

Solvent fluctuations play a key role in controlling protein motions and biological function. Here, we have studied how individual steps of the reaction catalyzed by the light-activated enzyme protochlorophyllide oxidoreductase (POR) couple with solvent dynamics. To simultaneously monitor the catalytic cycle of the enzyme and the dynamical behavior of the solvent, we designed temperature-dependent UV-visible microspectrophotometry experiments, using flash-cooled nanodroplets of POR to which an exogenous soluble fluorophore was added. The formation and decay of the first two intermediates in the POR-catalyzed reaction were measured, together with the solvent glass transition and the buildup of crystalline ice at cryogenic temperatures. We find that formation of the first intermediate occurs below the glass transition temperature (T_g), and is not affected by changes in solvent dynamics induced by modifying the glycerol content. In contrast, formation of the second intermediate occurs above T_g and is influenced by changes in glycerol concentration in a manner remarkably similar to the buildup of crystalline ice. These results suggest that internal, nonslaved protein motions drive the first step of the POR-catalyzed reaction whereas solvent-slaved motions control the second step. We propose that the concept of solvent slaving applies to complex enzymes such as POR.

Introduction

Molecular motions are essential to the function of proteins (1). They are associated with transitions between conformational substates representing local minima in the complex energy landscape of a protein (2). The importance of solvent fluctuations in controlling protein conformational dynamics has been recognized for many years (3–5), and it has recently been proposed that different classes of protein motions are controlled by the solvent to a different extent (6–8). Slaved motions follow the dielectric fluctuations of the bulk solvent and are similar to α-fluctuations in glasses. They are considerably reduced below the glass transition temperature, T_g, when the solvent is rigid. Hydration-shell coupled motions are largely independent of bulk solvent motions. They follow the dynamics of the hydration layers and are similar to β-fluctuations in glasses. Nonslaved motions are not influenced by the solvent and follow thermally activated internal vibrations.

To gain insight into the functional significance of these protein motions, it is important to investigate how they correlate with biological activity (9). The onset of activity has been linked to a protein dynamical transition (5,10–13), although a strict correlation has sometimes been questioned (14–17). Coupling between solvent dynamics and biological function has also been demonstrated, based on manipulating solvent viscosity or composition (18–20). However, a major obstacle in accurately characterizing the relationship between solvent/protein dynamics and functional activity arises from the difficulty in measuring both types of data in a single experiment.

Here, we have used microspectrophotometry as a method to simultaneously measure solvent dynamics and functional kinetics in flash-cooled protein solution samples. Because ice clusters of size comparable to the wavelength scatter UV-visible light, and because fluorescence emission from a soluble fluorophore added to the experimental buffer is affected by solvent fluctuations (21), essential features of solvent dynamics, such as formation of crystalline ice or occurrence of a glass transition, could be identified by temperature-dependent absorption and fluorescence spectroscopy. Concurrently, the interconversion of enzymatic intermediates displaying specific spectral signatures could be measured. We studied the light-driven enzyme protochlorophyllide oxido-reductase (POR; EC 1.3.1.33), which catalyzes the β-nicotinamide adenine dinucleotide 2′-phosphate reduced tetra-sodium salt (NADPH)-dependent reduction of the C17-C18 double bond of protochlorophyllide (Pchlide) to form chlorophyllide (Chlide) (22). As the enzyme can be activated by light at cryogenic temperatures and because intermediate states that are formed during the reaction pathway are rich in optical signals (Fig. 1) (23), POR is an ideal model for studying catalysis near the solvent glass transition.

Figure 1.

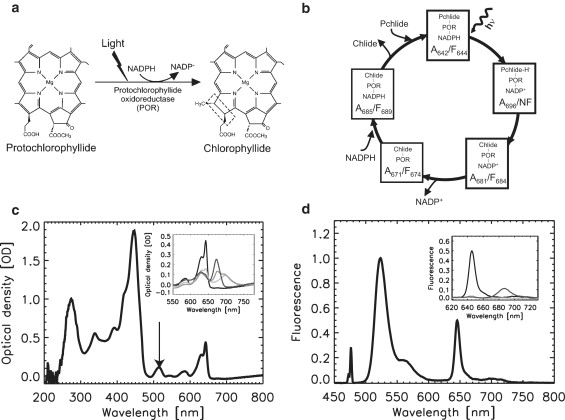
Spectral signature of POR intermediates along the catalytic cycle. (a) The light-induced POR reaction. The molecular structures of Pchlide and Chlide are shown. (b) Catalytic cycle of T. elongatus POR as proposed by Heyes et al. (41). The initial light-driven step is followed by a number of dark steps. The spectroscopic signature of the light-driven step is the consumption of the absorption/fluorescence bands from the ternary complex, centered at 642–644 nm (denoted A₆₄₂/F₆₄₄), and the concomitant buildup of a nonfluorescent A₆₉₆ intermediate displaying a broad absorption line centered at 696 nm. Temperature elevation leads to the release of Chlide via a number of thermally activated dark steps including formation of the product complex POR-Chlide-NADP⁺ (A₆₈₁/F₆₈₄). Intermediate species investigated in this work are highlighted in thick rectangles. (c) Absorption spectrum from nanovolume samples of the POR-Pchlide-NADPH complex mixed with Oregon Green, recorded at 100 K. Absorption of Oregon Green (514 nm) is indicated by the arrow. (Inset) Absorption spectra of the different species (A₆₄₂ (solid); A₆₉₆ (light shading); A₆₈₁ (medium shading); A₆₇₁ (dark shading)) before illumination (A₆₄₂) or building up upon illumination with red light followed by temperature elevation to 165 K (A₆₉₆), 195 K (A₆₈₁), and RT (A₆₇₁). The band at 630 nm (A₆₃₀) is from residual free Pchlide. (d) Fluorescence emission spectrum from nanovolume samples of the POR-Pchlide-NADPH complex mixed with Oregon Green, recorded at 100 K, obtained with 476-nm excitation. (Inset) Emission spectra of the different species (F₆₄₄ (solid); NF (dark shading); F₆₈₄ (light shading)) before illumination (A₆₄₂) or building up upon illumination followed by temperature elevation to 165 K (NF) and 195 K (F₆₈₄).

Although evidence for the concept of solvent slaving is growing for soluble proteins, including at the folding stage (24), few detailed investigations have been made in the case of enzymes (25). Our results on the POR enzyme suggest that the formation of the first intermediate along the catalytic cycle requires nonslaved protein motions, while formation of the second intermediate requires slaved motions that unlock at the solvent glass transition and involve translational motions of water molecules.

Material and Methods

Preparation of the POR-NADPH-Pchlide ternary complex

Recombinant POR from the thermophilic cyanobacterium Thermosynechococcus elongatus was overexpressed in E. coli and purified as described (23)). Concentrated POR stock solutions were prepared at ∼40 mg/mL in 30 mM Tris HCl (pH 7.5), 50 mM NaCl, and 1 mM dithiothreitol. Concentrated Pchlide stock solutions were prepared at ∼6.5 mM in 90% methanol (v/v) and 10% genapol X-080 (v/v). Samples of the POR-NADPH-Pchlide ternary complex were prepared in the dark from fresh stock solutions and contained ∼370 μM of POR, 1 mM NADPH, 33 mM dithiothreitol, 12.5% sucrose (v/v), 15 μM Oregon Green (Invitrogen, Carlsbad, CA), ∼230 μM Pchlide, and 25–40% glycerol (v/v). The concentration of Pchlide was adjusted so as to maximize the amount of bound Pchlide while minimizing the amount of unbound Pchlide, based on the previously measured dissociation constant K_d = 7.7 μM on the Synechocystis enzyme (26). The presence in the sample of residual free Pchlide as well as unbound, spectroscopically silent, POR molecules does not alter the conclusions drawn. The available range of glycerol concentration was limited by the necessity of successful flash-cooling (lower limit) while keeping sufficient POR material to provide spectroscopic data of high signal/noise ratio (higher limit). The fraction of Pchlide bound to POR was independent of the glycerol content (not shown).

Samples of ∼0.5 μL were mounted in glass microcapillaries and flash-cooled to 100 K on the microspectrophotometer of the Cryobench laboratory (Fig. 2) (27). Samples S₂₅-1, S₂₅-2, and S₄₀-1 originate from the same mother solutions, as well as S₂₅-3 and S₄₀-2.

Figure 2.

Instrumental setup. (a) Picture of the microspectrophotometer setup of the Cryobench laboratory, showing a flash-cooled Oregon Green/POR sample mounted in a microcapillary under blue laser illumination. (b) Closed view of a microcapillary-mounted sample. The sample is shown by the arrow.

Microspectrophotometry setup

The microspectrophotometer (Fig. 2) consists of a one-circle goniometer, a cryocooling device (Oxford Cryosystem 600 series, Oxford, UK), three mirror objectives, and an optical fiber holder allowing direct illumination of the sample (27). Data were collected with a charge-coupled-device-based spectrometer (S2000, Ocean-Optics, Dunedin, FL). To ensure proper flash-cooling to the glassy state and reproducible actinic excitation, extreme care was taken in precise centering of the samples on the goniometer axis. Experiments S₂₅-1 and S₂₅-2 were performed before and after the S₄₀-1 experiment, respectively, to verify the stability of the experimental setup. Indeed, slight drifts in laser alignment or power would bias the data. Absorption measurements were realized using light from a broadband halogen-deuterium source delivering 40 μW of power (Micropack DH2000-BAL, Ocean Optics). The optical path provided by the microcapillaries was 0.4 mm. For temperature-dependent absorption microspectrophotometry (TDAM) experiments, a long-pass filter (>550 nm) was inserted in the input objective to avoid actinic excitation in the Soret region by the measuring light. Actinic excitation was provided through the fiber holder with 632-nm laser light delivering a power density of 4.4 mW/cm² at sample position. Actinic excitation and absorption measurements were interleaved at 1 Hz during temperature ramping (100 K/h from 100 K to 220 K), with 800 ms of actinic excitation followed by 200 ms of dark time during which a spectrum was recorded. For temperature-dependent fluorescence microspectrophotometry (TDFM) experiments, fluorescence excitation was performed with 476-nm light. This wavelength was chosen to 1), provide sufficient penetration in the optically thick samples; 2), minimize actinic excitation and especially spurious photooxidation of free Pchlide; and 3), provide a satisfactory balance between excitation of the POR complex and Oregon Green. Actinic excitation and fluorescence measurements were interleaved at 0.1 Hz during temperature ramping (100 K/h), with 8000 ms of actinic excitation followed by 2000 ms of dark time during which fluorescence spectra were recorded with a single 20 ms pulse at 75 mW/cm².

Data processing

Spectra from TDAM/TDFM experiments were processed with a homemade routine based on the IDL software (ITT, Boulder, CO). To obtain the A₆₄₂ and A₆₈₁ plots (Fig. 3 and Fig. 4 a), absorption spectra were first corrected for background subtraction using polynomial fitting. The overlapping bands A₆₃₀/A₆₄₂ and A₆₉₆/A₆₈₁ were deconvoluted by nonlinear least-squares Gaussian fitting. Excellent fitting was obtained with reduced χ² values <10⁻⁵. The optical density at 740 nm was extracted from raw absorption spectra. Plots of A₇₄₀ (Fig. 4 b) were obtained after a linear baseline was subtracted, to account for slow drifts in the halogen source intensity. F₆₈₄ plots from TDFM experiments (Fig. 5 b) were obtained similarly to those from A₆₈₁, although no deconvolution was needed in this case. Due to the nonsymmetric shape of the fluorescence band, reduced χ² values were of lower quality (χ² <10), but this did not affect the conclusions drawn.

Figure 3.

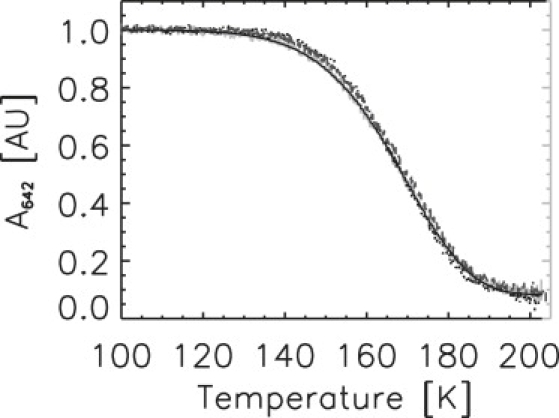
Decay of the POR ternary complex by TDAM. Decay of A₆₄₂ as a function of temperature from three consecutive TDAM experiments with samples S₂₅-1 (light shading), S₄₀-1 (dark shading), and S₂₅-2 (medium shading). Reported is the integrated area of the A₆₄₂ band fitted by a Gaussian profile and corrected for temperature dependence of the extinction coefficient. The solid curve shows the fitting of the S₂₅-1 data with a single barrier Eyring model.

Figure 4.

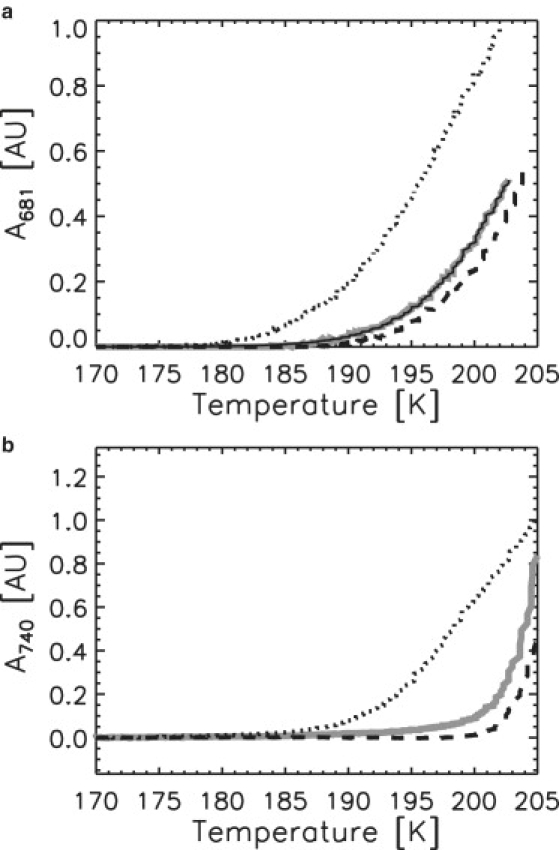
Correlation of the buildup of the POR second intermediate with crystallization of the solvent water fraction, viewed by TDAM. Formation as a function of temperature of A₆₈₁ (a) and A₇₄₀ (b) from three consecutive TDAM experiments with samples S₂₅-1 (shaded line), S₄₀-1 (dotted line), and S₂₅-2 (dashed line). In panel a, the integrated area of the A₆₈₁ band fitted by a Gaussian profile is reported. The solid curve corresponds to the fitting of the S₂₅-1 data with a single barrier Eyring model. In panel b, the raw optical density (without baseline subtraction) is reported, witnessing the buildup of crystalline ice.

Figure 5.

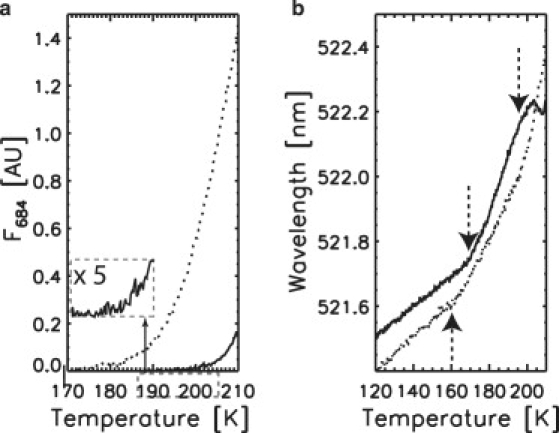
Correlation of the buildup of the POR second intermediate with the solvent glass transition, viewed by TDFM. (a) Formation as a function of temperature of F₆₈₄ from TDFM experiments with samples S₂₅-3 (solid line and inset) and S₄₀-2 (dotted line), respectively. The integrated area of the F₆₈₄ band fitted by a Gaussian profile is reported. (b) Temperature dependence of the emission wavelength of Oregon Green in the same TDFM experiments. The data from S₄₀-2 have been upshifted by a constant 1.4-nm value for clarity of the presentation. Arrows indicate the glass transition and the appearance of crystalline ice for S₂₅-3.

To quantitatively process TDAM/TDFM data, the temperature dependence of the extinction coefficients and fluorescence quantum yields should, in principle, be taken into account. To assess the influence of temperature on the A₆₄₂ absorption band, a separate experiment was performed in which no actinic excitation was used and spectra were collected at regular temperature intervals using a minimal amount of light. Band areas from these spectra were normalized to the value measured at 100 K, plotted as a function of temperature, and fitted with a second-order polynom P_corr. A₆₄₂ values from TDAM spectra (Fig. 3) were then corrected by dividing the fitted values by the value of P_corr at the corresponding temperatures. For A₆₈₁/F₆₈₄, a similar correction could not be applied. However, this was unlikely to be a serious problem since the temperature range over which A₆₈₁/F₆₈₄ were monitored was much narrower than in the case of A₆₄₂. Finally, all values in Figs. 3, 4 a, and 5 a, were normalized relative to the A₆₄₂ (or F₆₄₄) band area measured at 100 K before actinic illumination.

The temperature-dependent emission maximum from Oregon Green (Fig. 5 b) was calculated as the center-of-mass of fluorescence emission in the wavelength range 515–525 nm.

Kinetic model fitting

Thermodynamic parameters governing catalytic interconversion rates can theoretically be evaluated from TDAM and TDFM experiments. Nonlinear least-squares fitting of time/temperature-dependent absorption data with Eyring or Vogel-Tammann-Fulcher (VTF) kinetic models was realized with a homemade routine based on IDL. The two steps of the reaction ${\text{A}}_{642}\stackrel{\text{k}1}{\to }{\text{A}}_{696}\stackrel{\text{k}2}{\to }{\text{A}}_{681}$ could be decoupled as, in the used experimental conditions, A₆₈₁ started to build up after A₆₄₂ was almost entirely consumed. Thus, for the first part of the reaction (Fig. 3), the data were fitted against the model

$$A\left(t\right)=A_0\exp \left(-\upsilon {\int }_0^{t}T\left(u\right)/T_0\exp \left(-\Delta H/RT\left(u\right)\right)du\right),$$ (1)

where A(t) is the absorbance at time t, A₀ is a constant, ν has the dimension of an attempt frequency, T is the temperature, ΔH is the enthalpy barrier, and R is the gas constant. The quality of fitting was excellent, with reduced χ² values <0.005.

For the second part of the reaction (Fig. 4), the data were fitted against either a similar Eyring model or a Vogel-Tammann-Fulcher model,

$$A\left(t\right)=A_0\exp \left({\upsilon }_{\text{VTF}}{\int }_0^t\exp \left(-E_{\text{VTF}}/R\left(T\left(u\right)-T_{\text{VTF}}\right)\right)du\right),$$ (2)

where ν_VTF has the dimension of an attempt frequency, T_VTF is a temperature, and E_VTF is an energy barrier. For both models, the quality of fitting was excellent for S₂₅-1 or S₂₅-2, with reduced χ² values <0.002. In the case of S₄₀-1, models could be fitted, but reduced χ² values were of lower quality and the fitted parameters were considered less reliable, due to the extended rate distribution possibly caused by solvent demixing.

In TDAM/TDFM data, the inherent coupling between time and temperature can be expected to compromise the accuracy of the fitted thermodynamic parameters. To evaluate this potential difficulty, we fitted globally the A₆₄₂ decays from two data sets recorded with different temperature gradients (S₂₅-1, 100 K/h, and S₂₅-4, 150 K/h), instead of a single data set, so that more accurate values of ν₁ and ΔH₁ could be obtained (Supporting Material Fig. S3). The change in fitted values was only modest (Table S1). We note that global fitting from several data sets is only valid when high reproducibility from sample to sample is ensured, which would not be the case for A₆₈₁, due to sample-to-sample variations induced by flash-cooling. Finally, we refrained from processing TDAM data globally using singular value decomposition because of the intrinsic temperature dependence of the spectra.

Viscosity measurements

Viscosity measurements at room-temperature were performed with a NAR/1T refractometer (Atago, Tokyo, Japan). Refraction indices of S₂₅ and S₄₀ POR samples were reproducibly measured to be 1.400 ± 0.002 and 1.415 ± 0.002, respectively, consistent with a higher average viscosity for the S₄₀ samples.

Fluorescence anisotropy measurements

To check for potential interaction between Oregon Green and POR, fluorescence anisotropy measurements of Oregon Green were performed in the presence and absence of POR. No significant change in anisotropy was induced by the addition of the enzyme (not shown). The absence of a modification of the fluorophore tumbling time in the presence of the bulky POR molecules allowed us to conclude that Oregon Green did not bind to the enzyme.

Results

To monitor solvent dynamics simultaneously with catalytic steps in the reaction pathway of T. elongatus POR, we used a microspectrophotometer normally dedicated to the study of macromolecular crystals at cryogenic temperatures (27). This device offers the opportunity to study nanovolume solution samples, which can be easily flash-cooled to the glassy state with only a moderate amount of cryoprotectant (Fig. 2). A small amount of the fluorophore Oregon Green was added to the dark-incubated ternary complex POR-Pchlide-NADPH, as a marker of bulk solvent dynamics (21). Fluorescence anisotropy measurements revealed that the Oregon Green fluorophore did not interact with POR (not shown). The absorption spectrum of a flash-cooled sample prepared in this way (Fig. 1 c), typical of protoporphyrin-derived molecules, is composed of a broad and intense Soret band at 445 nm and of two Q-bands at 630 nm and 642 nm. These two latter bands originate from free and POR-bound Pchlide, respectively. The exogenous fluorophore produces a weak absorption band at ∼514 nm which does not overlap with absorption from the POR complex. The corresponding fluorescence spectrum (Fig. 1 d) shows a band at 644 nm originating from the POR-NADPH-Pchlide complex, and a nonoverlapping stronger band centered at ∼524 nm due to Oregon Green. Illumination of samples with red light (632 nm) combined with progressive increases in the temperature triggered the reaction cycle of POR (Fig. 1, c and d, and insets).

To investigate a potential coupling between the formation of POR catalytic intermediates and bulk solvent dynamics, we used temperature-dependent absorption and fluorescence microspectrophotometry (referred to as TDAM and TDFM, respectively), a method relatively similar to that previously developed in the infrared region to investigate globins (28)). Flash-cooled samples were heated from 100 K to 220 K at a rate of 100 K/h under pulsed red actinic excitation. Spectra were recorded continuously during this process, and spectroscopic movies of the POR reaction could be produced in absorption or fluorescence mode (Fig. S1 and Fig. S2). In TDAM experiments, the absorption at 740 nm (A₇₄₀), where no specific absorption band is present, was followed as a marker of light scattering by the sample, to probe the formation of crystalline ice at the macroscopic level. In TDFM experiments, the temperature dependence of the Oregon Green emission wavelength allowed the direct assessment of solvent dynamics at the microscopic level and on the nanosecond timescale (21).

In a first set of experiments, based on TDAM, we investigated three samples containing 25%, 40%, and again 25% glycerol (v/v) (thereafter referred to as S₂₅-1, S₄₀-1, and S₂₅-2). Fig. 3 shows the photoactivated decay of the absorption band of the ternary enzyme-substrate complex (A₆₄₂) as a function of temperature for the three samples. The formation of the first intermediate (A₆₉₆ band) exactly mirrored the decay of the substrate complex (data not shown), in agreement with previous measurements at cryogenic temperatures (26). All three decay profiles superimpose well, and are essentially independent of the glycerol concentration. In addition, they appear to be governed by Eyring (or Arrhenius) kinetics as the data can be successfully fitted to a simple Eyring model, assuming ${\text{A}}_{642}\stackrel{\text{h}\nu ,{\text{k}}_1}{\to }{\text{A}}_{696}$ with $k_1={\nu }_1\raisebox{1ex}{$T$}\!\left/ \!\raisebox{-1ex}{$T_0$}\right.\exp -\frac{\Delta H_1}{RT}$ and T(t) = T₀ + Gt, in which ν₁ is a preexponential factor (including the entropy contributions exp ΔS₁/R), ΔH₁ is the enthalpy barrier, T₀ is the starting temperature, and G is the temperature gradient. For a one-photon process, ν₁ is proportional to the intensity of the actinic light. The obtained value of 15.4 ± 1.2 kJ/mol for ΔH₁ is similar to the published value of 18.8 kJ/mol, obtained by standard cryoenzymology methods (26) (Table S1).

A different behavior was found to govern the conversion of the first intermediate (A₆₉₆) into the second one (A₆₈₁), as a significant dependence on glycerol concentration was observed (Fig. 4 a). Independent measurements carried out with a standard cryostat (Fig. S4) and at room-temperature (D. Heyes, unpublished) showed that replacing glycerol with sucrose at constant viscosity did not significantly modify the kinetics of this step of the POR reaction. Therefore, we attributed the glycerol-dependent changes observed here to changes in solvent viscosity, and not to a putative specific interaction of glycerol with POR. Furthermore, the dependence of the A₆₉₆-to-A₆₈₁ conversion step on glycerol was strikingly paralleled by the glycerol-dependent evolution of A₇₄₀, which reports the buildup of crystalline ice from the solvent water fraction (Fig. 4 b). The buildup of A₆₈₁ for S₄₀-1 started at a lower temperature (∼185 K) and grew at a slower rate than in the case of the S₂₅ samples. In addition, the data for S₂₅-1 and S₂₅-2 did not superimpose perfectly, although these samples were treated identically. The evolution of A₇₄₀ showed very similar behavior, with a slow increase starting at ∼185 K for S₄₀-1, and a steeper increase starting at ∼200 K for the S₂₅ samples, with a slight but significant difference between S₂₅-1 and S₂₅-2. The fact that differences in the buildup of A₆₈₁ were reflected in the kinetics of ice formation suggests that the two processes are connected. Whereas the build-up of A₆₈₁ could be successfully fitted with either Eyring or Vogel-Tammann-Fulcher models for both S₂₅ samples, such models could be applied less satisfactorily to S₄₀, indicative of sample heterogeneity. Assuming an Eyring model ${\text{A}}_{696}\stackrel{\text{k}2}{\to }{\text{A}}_{681}$ with ${\text{k}}_2={\nu }_2\raisebox{1ex}{$T$}\!\left/ \!\raisebox{-1ex}{$T_0$}\right.\exp -\frac{\Delta H_2}{RT},$ enthalpy barriers of ∼74 kJ/mol and ∼76 kJ/mol were found for S₂₅-1 and S₂₅-2, respectively (Table S1).

It is known that translational motions of water molecules are required during ice crystallogenesis (29). To examine whether such motions are also required to trigger the second catalytic step of POR, we performed a second set of experiments based on TDFM, with two samples containing 25% and 40% glycerol (referred to as S₂₅-3, and S₄₀-2). The formation of the second POR intermediate was monitored through the integrated F₆₈₄ band (Fig. 5 a). Simultaneously, the state of the solvent was followed at the microscopic level through the fluorescence emission wavelength of Oregon Green (Fig. 5 b). In accordance with the TDAM experiments, a clear dependence of the POR second catalytic step on glycerol concentration was observed, with F₆₈₄ starting to build up at ∼190 K and ∼170 K for S₂₅-3 and S₄₀-2, respectively. In parallel, marked deviations in the temperature-dependent emission wavelength of Oregon Green from the initial linear regime in Fig. 5 b were observed at ∼170 K and ∼160 K for S₂₅-3 and S₄₀-2, respectively. These deviations are assigned to solvent glass transitions, on the basis that at T_g the solvent dipolar relaxation time becomes shorter than the fluorescence lifetime, resulting in an abrupt red shift of the reporter emission wavelength (21). Hence, the data clearly suggest that the formation of the second intermediate in the POR-catalyzed reaction occurs above the solvent glass transition and is shifted to higher temperatures when T_g increases. In our experimental conditions, the higher 40% glycerol content gave rise to a lower observed T_g together with a formation of F₆₈₄ at lower temperature, in agreement with the finding made by TDAM.

In the case of S₂₅-3, the TDFM data of Oregon Green revealed an inflection point at ∼190 K and a blue shift at ∼200 K (Fig. 5 b). Because fluorophores interacting with rigid water molecules show little solvent relaxation (i.e., display a blue shift in their fluorescence emission), we assign these features to the onset of crystallization of the water fraction (190 K) and its massive crystallization (200 K, also observed in the TDAM data), respectively. Interestingly, the onset of crystallization corresponds to the temperature at which F₆₈₄ started to form for S₂₅-3 (Fig. 5 a). These features are not observed in the Oregon Green data of S₄₀-2, which show a continuous red shift in the spectra as the temperature increases. This corroborates the finding by TDAM that this sample might be heterogeneous, preventing the onset of crystallization to be observed in a well defined temperature range.

Discussion

The methodology developed in this work can be added to the range of techniques currently available for the investigation of protein dynamics. Temperature-dependent absorption and fluorescence UV-visible spectroscopy combined with the use of a soluble exogenous fluorophore allows the simultaneous monitoring of catalytic steps in an enzyme together with the dynamics of the surrounding solvent, in a single experiment requiring only a small amount of time. The method employs a microspectrophotomer that has been adapted to accommodate μm-sized samples. Thus, little biological material is required and samples can be easily flash-cooled to the vitreous state with only a moderate amount of cryoprotectant, in contrast to conventional cryoenzymology techniques based on slow-cooling with large amounts of cryoprotectants (26).

Our investigation of the light-induced POR reaction revealed that the first catalytic step occurs at temperatures lower than T_g, is not affected by changes in solvent viscosity nor by sample heterogeneity, and obeys Eyring kinetics with a single low energy barrier (<20 kJ/mol). Clearly, the functional protein motions that are involved in this step are independent of the solvent. In contrast, the formation of the second intermediate occurs at temperatures higher than T_g, is sensitive to changes in solvent viscosity and to sample heterogeneity, and involves a high energy barrier (>70 kJ/mol). This suggests that protein motions involved in this catalytic step are coupled to bulk solvent dynamics. Moreover, in temperature-dependent experiments, the formation of the POR second intermediate closely follows that of crystalline ice, suggesting a strong correlation between the two processes.

It has been proposed that at the solvent glass transition, the water fraction becomes liquidlike and starts to undergo translational motions (29,30). Taken together, our results suggest that these motions control both the crystallization of the solvent water fraction and the second catalytic step of the POR reaction. This hypothesis is strengthened by the TDFM plots from S₂₅-3 (Fig. 5), showing that the first noticeable signs of F₆₈₄ buildup match those of water crystallization (inflection point on the Oregon Green data, ∼190 K), some ∼20 K above T_g. The TDAM data are less precise at the microscopic level, since the increase in the absorption baseline monitored at A₇₄₀ is a macroscopic effect arising from Rayleigh scattering of ice clusters of size comparable to or larger than the scattered wavelength. Hence, the TDAM data (Fig. 4) essentially report a late state of massive crystallization.

In the course of this work, we noticed that the dynamical fate of a sample depends to some extent on its thermal history (31). Small but inevitable deviations were observed between samples prepared identically, possibly due to minute changes in sample volume or handling that affected the outcome of flash-cooling. For example, in Fig. 4, although the two S₂₅ samples were treated in exactly the same way and originate from the same aliquot of mother solution, they displayed different kinetics for ice formation. Such variations follow from the fact that flash-cooling traps the sample in an out-of-equilibrium state. The relaxation that accompanies the glass transition then drives the sample from this ill-defined out-of-equilibrium state to an equilibrium state (31). By measuring catalytic steps and solvent fluctuations simultaneously, we could turn to our advantage this sample-to-sample variability. The fact that the subtle difference in ice formation in the S₂₅ samples was reflected in the kinetics of A₆₈₁ formation indeed provided strong evidence that these two processes are coupled.

Another observation was that POR samples containing 40% glycerol repeatedly displayed lower T_g and formed crystalline ice at lower temperatures (T_x), than samples containing 25% glycerol. This behavior was unexpected, as T_g and T_x are normally found to increase with viscosity (32) and S₄₀ samples did show a higher viscosity than S₂₅ samples at room-temperature (not shown). In samples devoid of protein, however, a normal behavior was recovered, as T_g and T_x increased with the glycerol content (not shown). To explain these findings, the interactions between water, glycerol, and the protein must be considered. Neutron scattering experiments have revealed that a higher glycerol content may result in a decrease of the protein dynamical transition temperature, possibly as a result of a lubricant effect induced by glycerol (33). However, such experiments were carried out on dehydrated samples and are unlikely to account for our results. Instead, we propose the following interpretation. It is known that glycerol plays a stabilization role for a number of proteins (34). Timasheff (35) has proposed that such stabilization results from preferential hydration of the protein concomitant with exclusion of the cosolvent from the protein environment. Therefore, the fact that POR might be preferentially hydrated in the presence of a high glycerol concentration may explain why the buildup of A₆₈₁ occurred at lower temperatures for the S₄₀ samples than for the S₂₅ samples. Whereas significant demixing would normally be expected only at very high cosolvent content, we propose that the effect might be promoted here with 40% glycerol (in addition to the 12.5% sucrose) because of the high protein concentration used in this work. Indeed, under our experimental conditions, POR represented ∼2% (v/v) of the sample content, resulting in an increase of the overall sample viscosity and possibly creating conditions that favored solvent demixing. Therefore, at high initial glycerol content (40%), we propose that solvent demixing followed by flash-cooling may have resulted in heterogeneous samples made of clusters with varying contents of cryoprotectant. As a consequence, the overall rate of ice formation appeared to be slow because clusters with different glycerol concentration formed ice at different temperatures. The TDFM data also support this view, with a lower glass-transition temperature in S₄₀-2 attributable to low viscosity clusters, followed by a slow evolution, consistent with a progressive contribution from the high-viscosity clusters. In the S₄₀ samples, yet another possible phenomenon should be considered. Glycerol at relatively low concentration has been found to increase protein-protein repulsion, improving protein solubility (36). However, Gekko and Timasheff (37) have pointed out that, to minimize protein-glycerol contacts, the extent of the protein-solvent interface tends to be minimized, possibly promoting self-association reactions at high glycerol concentration. Under this latter hypothesis, the possibility that POR may have formed aggregates in S₄₀ samples should be considered. In such a case, it cannot be excluded that the POR activity be modified in the aggregated state. Further experiments employing viscogenic molecules other than glycerol are beyond the scope of this article but will be needed to further investigate this issue. Nonetheless, the remarkable point remains that, whereas the light-induced buildup of the first POR intermediate remained unaffected, formation of the second intermediate was consistently influenced by the surrounding solvent behavior.

Our data on POR, a relatively complex enzyme, are fully consistent with the theory of solvent slaving, which was elegantly elaborated from data merged from various techniques in the case of relatively simple, nonenzymatic proteins (6). The first catalytic step of the POR reaction agrees with the prediction for a nonslaved process. This step, proposed to involve hydride transfer from the pro-S face of the NADPH co-factor to the C₁₇ position of Pchlide via a charge transfer complex (38), is probably promoted by vibrationally excited protein motions of a relatively small amplitude. Interestingly, fitting a simple Eyring model to the data provided excellent agreement, suggesting a single low energy barrier (<20 kJ/mol). Although a distribution of barriers for the first catalytic step of POR, expected from the generally rugged conformational landscapes of proteins, cannot be excluded from our data, it appears that, if it exists, such a distribution is narrow. This is in contrast to previous observations made on other proteins such as heme proteins (39) or the photosynthetic reaction center (20).

The second step of the POR reaction, which is thought to involve proton transfer from a conserved tyrosine residue to the C₁₈ position of Pchlide (22), displays the properties of a solvent-slaved process. Although thermodynamic parameters governing the conversion from A₆₉₆ to A₆₈₁ can only be assessed relatively crudely, attempts to fit S₂₅ samples with an Eyring model yielded enthalpy barriers (>70 kJ/mol) that approach typical values reported for α-relaxation in glasses (7). This is in agreement with the idea that this process is under the control of solvent fluctuations. Notably, the data could be fitted equally well with a Vogel-Tammann-Fulcher model (it is known that the two models cannot be easily distinguished), consistent with the hypothesis that the second catalytic step of POR could be coupled to fluctuations of the solvent with a relation of the type k₂(T) = k_α(T) / n(T), where k_α(T) is the rate of bulk solvent relaxation and n(T) is a proportionality factor slowly varying with temperature (6).

It would have been highly informative to monitor a protein dynamical transition putatively connecting the solvent glass transition with the second catalytic step in POR (30). In principle, TDFM measurements of a protein's endogenous fluorophore (such as Pchlide in our case) could detect such a transition, in the form of an abrupt red shift of the emission wavelength associated with enhanced flexibility of the immediate environment. Unfortunately, changes in the fluorescence emission wavelength of the Pchlide substrate (F₆₄₄) were obscured by the consumption process in the relevant temperature window (Fig. S1), and the A₆₉₆ intermediate is nonfluorescent. Therefore, we can only postulate that the occurrence of a POR dynamical transition at a temperature close to T_g might be required to allow the second catalytic step to proceed. We argue that the primary event, however, remains the solvent glass transition.

In conclusion, Fig. 6 shows a proposed scheme of the POR reaction pathway that incorporates the solvent dependence of individual catalytic steps. Catalysis starts from excited state S1 and intersystem crossing leading to the triplet state T1 (40). Depending on the available thermal energy, T1 may either convert to A₆₉₆ through a nonslaved process, or return to the ground state via radiationless relaxation. Once A₆₉₆ is formed, solvent-slaved protein motions are necessary to form A₆₈₁/F₆₈₄ as well as the ensuing product-complex species, as recently demonstrated (41). Future experiments using the proposed technique will involve either naturally photosensitive proteins, or proteins engineered with exogenous dyes, or caged-compounds.

Figure 6.

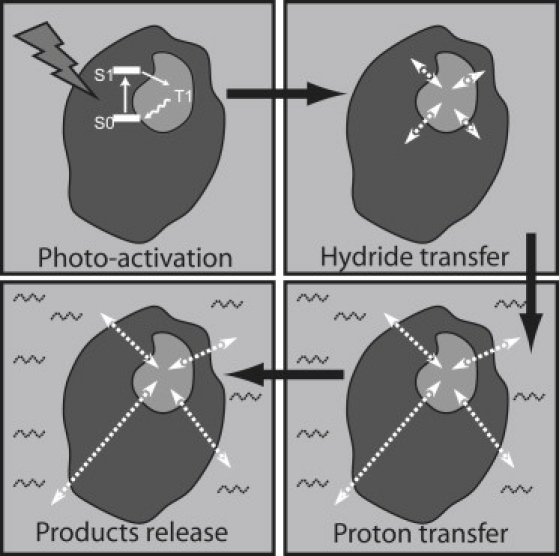
Dependence of the POR reaction pathway on solvent dynamics. Small-amplitude vibrationally excited motions characterizing the hydride transfer step are depicted by small arrows localized at the enzyme active site. Protein motions of larger amplitude characterizing the subsequent proton transfer and product release steps are depicted as long arrows linking the enzyme active site to the solvent in a liquidlike state (shaded waves).