A Theoretical Model for the Mechanical Unfolding of Repeat Proteins

Abstract

We consider the mechanical stretching of a polypeptide chain formed by multiple interacting repeats. The folding thermodynamics and the interactions among the repeats are described by the Ising model. Unfolded repeats act as soft entropic springs, whereas folded repeats respond to a force as stiffer springs. We show that the resulting force-extension curve may exhibit a pronounced force maximum corresponding to the unfolding of the first repeat. This event is followed by the unfolding of the remaining repeats, which takes place at a lower force. As the protein extension is increased, the force-extension curve of a sufficiently long repeat protein displays a plateau, where the force remains nearly constant and the protein unfolds sequentially so that the number of unfolded repeats is proportional to the extension. Such a sequential mechanical unfolding mechanism is displayed even by the repeat proteins whose thermal denaturation is highly cooperative, provided that they are long enough. By contrast, the unfolding of short repeat progressions can be cooperative.

Introduction

Proteins containing repeated folded units of the same or similar structure are common in nature (1–4). Their folding kinetics and thermodynamics have attracted considerable attention (1–5). As certain repeat proteins are believed to have a mechanical function (6), their mechanical response has also received recent attention. In particular, two experimental groups have used AFM to pull on individual ankyrin repeat proteins (7,8). The purpose of this article is to present a simple theoretical model describing the mechanical response of such proteins. The model is shown in Fig. 1. Each subunit can be in either a folded or an unfolded conformation. Unfolded subunits respond to the force as soft, entropic springs. Folded subunits act like springs that have a higher stiffness. We are particularly interested in the effect of the interactions among the subunits on the mechanical response of the entire chain. To describe those, we adopt an Ising-type model (2,4), which has already been applied to describe the folding of repeat proteins.

Figure 1.

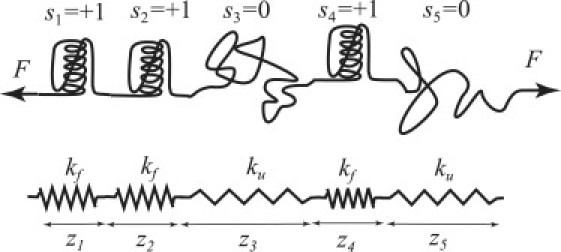
Illustration of the model used. The protein is described as a sequence of folded ($s_i=+1$) and unfolded ($s_i=0$) repeat units. The folded and unfolded repeats behave as Hookean springs with stiffnesses $k_{\mathrm{f}}$ and $k_{\mathrm{u}}$, respectively.

Our model is related to those of Buhot and Halperin (9) and Tamashiro and Pincus (10), who considered the stretching of a polymer undergoing a helix-coil transition. This transition was described using the Zimm-Bragg model (11,12), in which each monomer is in either a helical or a coil conformation. The model presented here uses a similar two-state representation for each repeat rather than for each individual monomer. Mathematically, the Zimm-Bragg model is equivalent to the Ising model, and thus, many results reported by others (9,10) can be adapted for our purpose. However, the situation considered there differs from this study in a number of ways. First, whereas in those studies (9,10) helical segments were considered to be rigid rods, it is important in the context of our study to consider the elasticity of individual folded repeats. Second, those works (9,10) focused on the infinite chain limit, $N\to \mathrm{\infty }$. In contrast, typical repeat proteins only contain a finite number of repeats, often N ∼ 5–30. As will be seen later, finite-size effects are responsible for a pronounced peak in the force-extension curves of certain repeat proteins. This peak would disappear in the limit of an infinitely long chain. Third, individual helical residues are unstable, so a sufficiently long helix has to be nucleated for the transition to the helical state to occur (11,12). In contrast, a more general situation, where individual repeats can be stable on their own, will be considered here.

We show here that if the ends of a repeat protein chain are pulled apart, its unfolding can proceed according to two scenarios. In both scenarios, the chain behaves as a stiff spring at low extensions. In the first scenario, a pronounced peak in the dependence of the force, f, on the extension, z, is observed when the first repeat becomes unfolded. After this event, the chain yields at a much lower force and the remaining repeats unfold one after another. The second scenario is similar to that found in the studies of the helix-coil transition (9,10): the force-extension curve is monotonic and levels out at a certain plateau value.

We further show that although interactions among repeats can lead to highly cooperative thermal/chemical denaturation (3), mechanical denaturation of the same protein may remain noncooperative and involve sequential unfolding of repeats one at a time. However because short progressions of folded repeats are often thermodynamically unstable, simultaneous unfolding of several repeats may be observed at the end of a pulling experiment.

The rest of this article is organized as follows. In the Model section, we describe the model. This is followed by the Results section and then the Discussion section, where we highlight key findings and discuss their implications for single-molecule AFM pulling experiments. We conclude with a summary of the results and their potential generalizations.

Model

We consider a chain of N identical repeats shown in Fig. 1. Each repeat can be in a folded state, f, or unfolded state, u. The (free) energy of the repeats is given by an Ising-like expression:

$$E\left[\left\{s_i\right\}\right]/k_{\mathrm{B}}T=-\sum _{i=1}^{N}H{s}_i-J\sum _{i=1}^{N-1}{s}_i{s}_{i+1}\text{.}$$ (1)

Here, $s_i=0$ if the ith repeat is unfolded and $s_i=1$ if it is folded. The parameter H is the free energy of folding for an isolated repeat, and the parameter J > 0 represents the coupling between two adjacent repeats, which stabilizes the folded conformation of each. We will assume that parameters H and J are such that in the absence of stretching, the repeats are predominantly folded. In other words, the expectation value $\langle s_i\rangle$ is close to 1.

Equation 1 does not contain the free energy associated with the stretching of the chain. To include this, consider the ensemble of the chain conformations with the given value of the overall extension,

$$z=z_1+z_2+\dots +z_N,$$ (2)

which is measured in the z direction (here, this direction will coincide with the direction of the stretching force). Then, the free energy of the chain is (9,10,13,14)

$$G=-k_{B}T\text{ln}p\left(z\right),$$ (3)

where the probability distribution of z is given by

$$p\left(z\right)=\sum _{\left\{s_i\right\}}\text{exp}\left(-\frac{E\left[\left\{s_i\right\}\right]}{k_{\mathrm{B}}T}\right)p_{\left\{s_i\right\}}\left(z\right)/\sum _{\left\{s_i\right\}}\text{exp}\left(-\frac{E\left[\left\{s_i\right\}\right]}{k_{\mathrm{B}}T}\right)$$ (4)

Here $p_{\left\{s_i\right\}}\left(z\right)$ is the probability distribution of z with the variables $\left\{s_i\right\}$ fixed. This distribution can be expressed in terms of the probability distributions $p_{s_i}\left(z_i\right)$ for the extensions $z_i$ of individual repeats as

$$p_{\left\{s_i\right\}}\left(z\right)=\int d{z}_{1}d{z}_2\dots d{z}_N{p}_{s_1}\left(z_1\right)p_{s_2}\left(z_2\right)\dots p_{s_N}\left(z_N\right)\delta (z-z_1-z_2-\dots z_N)\text{.}$$ (5)

Note that Eqs. 4 and 5 take advantage of the assumption that the interdomain interaction energy (Eq. 1) is a function of the internal variables, $\left\{s_i\right\}$, only and does not depend on$\left\{z_i\right\}$, thus allowing the factorization of the integrand in Eq. 5.

We further assume that each unfolded repeat is a Gaussian chain, so that for $s_i=0$, we have

$$p_0\left(z\right)=\frac{1}{\sqrt{2\pi b_{\mathrm{u}}^2}}\text{exp}\left(-\frac{z^2}{2b_{\mathrm{u}}^2}\right),$$ (6)

where $b_{\mathrm{u}}$ is the root mean-squared extension. Thus, it is mechanically equivalent to a Hookean spring with a spring constant $k_{\mathrm{u}}=k_{\mathrm{B}}T/b_{\mathrm{u}}^2$. Likewise, we will assume that each folded repeat acts as a stiffer Hookean spring with a stiffness of $k_{\mathrm{f}}\equiv k_{\mathrm{B}}T/b_{\mathrm{f}}^2$, so that for $s_i=1$, we have

$$p_1\left(z\right)=\frac{1}{\sqrt{2\pi b_{\mathrm{f}}^2}}\text{exp}\left(-\frac{z^2}{2b_{\mathrm{f}}^2}\right)\text{.}$$ (7)

With these assumptions, the integral of Eq. 5 can be evaluated to give

$$p_{\left\{s_i\right\}}\left(z\right)=\frac{1}{\sqrt{2\pi \left(n_{\mathrm{f}}{b}_{\mathrm{f}}^2+n_{\mathrm{u}}{b}_{\mathrm{u}}^2\right)}}\text{exp}\left(-\frac{z^2}{2\left(n_{\mathrm{f}}{b}_{\mathrm{f}}^2+n_{\mathrm{u}}{b}_{\mathrm{u}}^2\right)}\right),$$ (8)

Here $n_{\mathrm{f}}=\sum _{i=1}^N{s}_i$ and $n_{\mathrm{u}}=N-\sum _{i=1}^N{s}_i$ are, respectively, the numbers of folded and unfolded repeats in the chain.

Although the Gaussian chain approximation for unfolded repeats is reasonable as long as their extension is much shorter than their contour length, the assumptions made in Eq. 7 deserve further discussion. This equation effectively ignores that the end-to-end distance for each folded repeat is finite. More generally, we could model those repeats as deformable solid objects. If we were to do so, there would be additional entropic elasticity associated with aligning them in the direction of the force, which would be the dominant contribution to the overall chain elasticity at very low forces (10). Because adjacent folded units in repeat proteins often form superstructures, it may be more realistic in certain cases to model such superstructures, as opposed to individual repeats, as elastic objects, in which case the factorization assumption of Eq. 5 would be violated. These choices would depend on details of the specific protein under study and could be straightforwardly incorporated in our model if desired. Here, we have chosen the simplest possible model that accounts for the difference in the elasticity of folded and unfolded repeats. In an earlier study (13), the extension of folded repeats was neglected altogether. In contrast, two studies (9,10) dealing with polymers that exhibit helix-coil transition treated the helical segments as inextensible rods whose contribution to the overall chain elasticity was only through the aforementioned entropic effect associated with the alignment of the rods along the direction of the force.

Results

Analytical approximations

For sufficiently small N, Eq. 4 can be computed through exact enumeration. Before showing such exact results, we present here simple analytical approximations, which turn out to capture much of the physics of the problem.

Suppose that of the N repeats, $n_{\mathrm{f}}$ are folded and $n_{\mathrm{u}}=N-n_{\mathrm{f}}$ are unfolded. Further suppose that the number of contiguous blocks of folded repeats is n. In other words, the sequence $\left\{s_i\right\}$ contains n uninterrupted subsequences of the form 111…1 with the total number of 1s adding up to $n_{\mathrm{f}}$. A single folded repeat counts as a contiguous block, and the number of such repeats is included in n. For example, in Fig. 1, $n_f=3$ and n = 2. The free energy of Eq. 1 can then be rewritten in the form

$$E/k_{\mathrm{B}}T=-(H+J)n_{\mathrm{f}}+Jn\text{.}$$ (9)

If one starts with a fully folded conformation, unfolding an outer repeat (i = 1 or i = N) will reduce $n_f$ by 1 and thus increase the energy by $J+H$. Likewise, the energy is increased by $J+H$ whenever a repeat at either end of a contiguous folded block (containing more than one repeat) is unfolded. By contrast, the unfolding of an inner repeat within a contiguous folded block will change the energy by 2J + H, because n will increase from 1 to 2. Using the terminology of Buhot and Halperin (9), we can think of J as the interfacial energy associated with creating a pair of “domain boundaries” between sequences of folded and unfolded repeats, whereas $\mathrm{\Delta }G=J+H$ can be regarded as the free energy cost of unfolding a repeat without creating additional domain boundaries (i.e., by propagating an existing domain boundary). For any given $n_{\mathrm{f}}$, n, and chain extension, z, the free energy of the chain can be written as

$$G(z,n_{\mathrm{f}},n)/k_{\mathrm{B}}T\approx \frac{z^2}{2\left[n_{\mathrm{f}}{b}_{\mathrm{f}}^2+(N-n_{\mathrm{f}})b_{\mathrm{u}}^2\right]}-(H+J)n_{\mathrm{f}}+Jn-S(n_{\mathrm{f}},n)\text{.}$$ (10)

Here, the first term is the elastic part corresponding to Eq. 8, and $S(n_{\mathrm{f}},n)=k_{\mathrm{B}}\text{ln}\Omega (n_{\mathrm{f}},n)$ is an entropy term that can be calculated by counting the number $\Omega (n_{\mathrm{f}},n)$ of the sequences $\left\{s_i\right\}$ that correspond to the same values $n_f$ and n. Equation 10 neglects the logarithmic corrections that result from the $n_{\mathrm{f}}$ dependence of the prefactor in Eq. 8.

Following the arguments of Buhot and Halperin (9), we now neglect the entropy term in Eq. 10. The free energy for the protein, for a given value of the extension z, can then be estimated as

$$G\left(z\right)/k_{\mathrm{B}}T\approx \underset{n,n_{\mathrm{f}}}{\text{min}}\left\{\frac{z^2}{2\left[n_{\mathrm{f}}{b}_{\mathrm{f}}^2+(N-n_{\mathrm{f}})b_{\mathrm{u}}^2\right]}-(H+J)n_{\mathrm{f}}+Jn\right\}$$ (11)

If any folded repeats are present, the minimum with respect to n is achieved at n = 1 (n = 0 would imply that the protein is completely unfolded, which would be inconsistent with a finite value of $n_{\mathrm{f}}$). If $1\ll n_{\mathrm{f}}\ll N,$ then we can treat $n_{\mathrm{f}}$ as a continuous variable, which gives the condition $\partial G(z,n_{\mathrm{f}},n)/\partial n_{\mathrm{f}}=0$, or

$$n_{\mathrm{f}}=N\frac{b_{\mathrm{u}}^2}{b_{\mathrm{u}}^2-b_{\mathrm{f}}^2}-\frac{z}{\sqrt{2(J+H)}}\frac{1}{\sqrt{b_{\mathrm{u}}^2-b_{\mathrm{f}}^2}}\text{.}$$ (12)

Substituting this back into Eq. 11 gives

$$G\left(z\right)/k_{\mathrm{B}}T=J+z\sqrt{\frac{2(J+H)}{b_{\mathrm{u}}^2-b_{\mathrm{f}}^2}}\text{.}$$ (13)

This means that the repeat protein will yield at a force equal to

$$F_{\text{yield}}=G\prime \left(z\right)=k_{\mathrm{B}}T\sqrt{\frac{2(J+H)}{b_{\mathrm{u}}^2-b_{\mathrm{f}}^2}}\text{.}$$ (14)

The force-extension curve of the protein thus exhibits a plateau where the force $F=F_{\text{yield}}$ does not depend on the extension. This situation is similar to fluid-vapor coexistence, which is manifested by a plateau in the pressure-volume diagram. In our case, the coexistence is between the unfolded and folded conformations of the repeats (15).

The condition $0<n_{\mathrm{f}}\ll N$ results in the following range of acceptable extensions where this regime is valid:

$$\begin{array}{l}{z}_{\text{min}}\ll z<z_{\text{max}},\\ z_{\text{min}}=N{b}_{\mathrm{f}}^2\sqrt{\frac{2(J+H)}{b_{\mathrm{u}}^2-b_{\mathrm{f}}^2}},z_{\text{max}}=N{b}_{\mathrm{u}}^2\sqrt{\frac{2(J+H)}{b_{\mathrm{u}}^2-b_{\mathrm{f}}^2}}\end{array}\text{.}$$ (15)

When $z>z_{\text{max}}$, all the repeats are unfolded and the protein is an entropic spring with a spring constant equal to $k_{\mathrm{B}}T/N{b}_{\mathrm{u}}^2$.

Let us now consider the case of a nearly folded protein, where $n_{\mathrm{f}}$ is close to N. Within this limit, the continuous approximation for $n_{\mathrm{f}}$ breaks down. For small enough z, the minimum of Eq. 11 is achieved when n = 1 and $n_{\mathrm{f}}=N$. This means that each repeat will likely remain folded, and thus the protein will respond to stretching as a linear spring with a stiffness equal to $k_{\mathrm{f}}/N$. Thus, for small enough z,

$$G\left(z\right)=\frac{k_{\mathrm{f}}{z}^2}{2N}(+\text{constant}),$$ (16)

and the corresponding force-extension curve is Hook's law:

$$F=G\prime \left(z\right)=(k_{\mathrm{f}}/N)z\text{.}$$ (17)

As z is increased beyond a certain critical $z_{\mathrm{u}}$ value, the value $n_{\mathrm{f}}=N-1$ will provide the minimum to Eq. 11. This means that at $z\ge z_{\mathrm{u}},$ one of the repeats will unfold. The value of $z_{\mathrm{u}}$ is readily obtained from Eq. 11:

$$z_{\mathrm{u}}=b_f\sqrt{2N(J+H)}\sqrt{1+\frac{N{b}_{\mathrm{f}}^2}{b_{\mathrm{u}}^2-b_{\mathrm{f}}^2}}\text{.}$$ (18)

The corresponding rupture force is

$$F_{\mathrm{u}}=k_{\mathrm{f}}{z}_{\mathrm{u}}/N=\frac{k_{\mathrm{B}}T}{b_{\mathrm{f}}}\sqrt{2(J+H)/N}\sqrt{1+\frac{N{b}_{\mathrm{f}}^2}{b_{\mathrm{u}}^2-b_{\mathrm{f}}^2}}\text{.}$$ (19)

If we further assume that the discrete nature of $n_{\mathrm{f}}$ is only important for $n_{\mathrm{f}}=N,N-1$, and that a continuous approximation is good for $n_{\mathrm{f}}<N-1$, then we arrive at a force-extension law that consists of a linear segment at short extensions, a plateau at longer extensions, and another linear segment corresponding to a fully unfolded protein:

$$F=G\prime \left(z\right)=\{\begin{array}{c}(k_{\mathrm{f}}/N)z,z<z_{\mathrm{u}}\\ F_{\text{yield}},z_{\mathrm{u}}\le z<z_{\text{max}}\\ (k_{\mathrm{u}}/N)z,z\ge z_{\text{max}}\end{array}\text{.}$$ (20)

Numerical results and their comparison with analytical approximations

Fig. 2 shows the dependence of the force $G\prime \left(z\right)$ on the extension z calculated numerically from Eqs. 3 and 4 and by using the simple formulas of Eq. 20. The numerically computed force exhibits a large van der Waals loop, which is well approximated by the peak predicted by the first line of Eq. 20 (see Fig. 2 a). Smaller oscillations observed in Fig. 2 are not captured by Eq. 20, since the latter assumes that the number of repeats changes continuously. These oscillations are recovered if one uses Eq. 11 directly, without making a continuous $n_{\mathrm{f}}$ assumption, as shown in Fig. 2 b. Consistent with the notion that for larger extensions we can treat the number $n_{\mathrm{u}}$ of unfolded repeats as continuous, and so that the accuracy of Eq. 20 should become better, we observe the oscillations to decay and converge to a plateau value that is well approximated by $F_{\text{yield}}$ given by Eq. 14 (Fig. 2 a, dashed line). However, when the extension is further increased, a drop in the force is observed before it begins to rise and follow the linear dependence predicted by the last line in Eq. 20. This drop will be explained in the next section.

Figure 2.

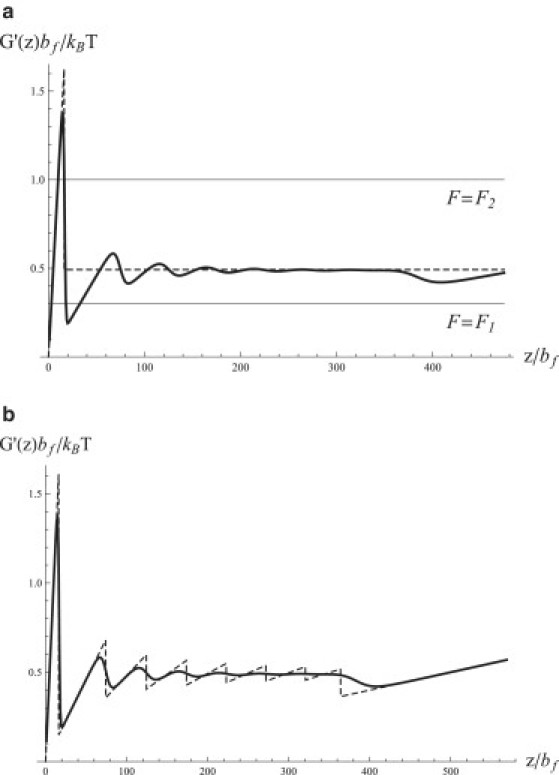
Force-extension curve of a repeat protein computed numerically and estimated using the approximations described in the first part of the Results section. The parameters of the model used are: H = 4, J = 8, N = 10, and $b_{\mathrm{u}}=10b_{\mathrm{f}}$. (a) Numerical data (solid line) versus the approximation using Eq. 20. Two horizontal lines show two different values of the force, F. For $F=F_1$, the equation $G\prime \left(z\right)=F$ has three solutions (three crossings of the horizontal line), and for $F=F_2$, there are two solutions. (b) Numerical data (solid line) compared with the force-extension curve obtained directly from Eq. 11 without invoking a continuous approximation for the number of folded repeats (dashed line).

One has to be careful interpreting the curve $F=G\prime \left(z\right)$ versus z as the “true” force-extension law describing the protein's elasticity. When a constant stretching force, F, is applied to the protein, the latter experiences the effective potential $G_F\left(z\right)=G\left(z\right)-Fz$ (16–18). The points where ${G\prime }_F\left(z\right)=0$, i.e., those described by the equation $F=G\prime \left(z\right)$, are the minima (if $G″>0$) or the maxima (if $G″<0$) of this potential. At low enough forces, there is only one solution satisfying $F=G\prime \left(z\right)$. The situation is different in the van der Waals loop region. At intermediate force values (see, e.g., the case $F=F_1$ in Fig. 2 a), this equation has three solutions. The smallest and the largest solutions correspond to free-energy minima and the one in the middle corresponds to the barrier separating those minima. Thus if the protein is held at constant tension $F_1$, it will undergo thermally activated hopping between the minima over the barrier, and the thermodynamic expectation value of z will be an appropriate thermal average over the two basins of attraction. Such thermal hopping can indeed be observed in pulling experiments (19). If we continue to increase the force past the value $F_1$ we will find that more than three solutions, corresponding to multiple minima separated by barriers, are possible at certain force values. Finally, when F becomes larger than a certain value (close to $F_{\text{yield}}$ from Eq. 14), there are only two solutions ($G\prime \left(z_l\right)=F$, $G\prime \left(z_{\mathrm{h}}\right)=F$, $z_l<z_{\mathrm{h}}$), as shown in Fig. 2 a for the case $F=F_2$. The lower value, $z_l$, corresponds to a metastable minimum, from which the system can escape over the barrier located at $z=z_{\mathrm{h}}$. This means that the folded protein cannot sustain such a high force and will eventually unfold. Whether or not the force peak will be observed then depends on the pulling timescale relative to that of barrier crossing. If, for example, force F is quickly increased, then the system may not have enough time to escape the metastable folded states, and thus the initial peak in the curve $G\prime \left(z\right)$ versus z (or its part) will be observed. When van der Waals loops are traversed in nonequilibrium pulling experiments, the resulting unfolding dynamics are generally stochastic (20,21), exhibiting force peaks and drops corresponding to barrier crossings. The statistics of such events and their dependence on the pulling rate are beyond the scope of our model, which contains no information about kinetics.

Discussion

Mechanical unraveling of long repeat proteins is not cooperative. The unfolding of short repeat series can exhibit cooperative behavior

Equations 14, 15, and 18–20 suggest that the mechanical response of the repeat protein does not depend individually on the values of J and H but rather on the sum J + H. To test this, we plot in Fig. 3 the dependence of the force $G\prime \left(z\right)$ on z for different values of J and H chosen such that the sum J + H stays constant. As long as the extension z is not too large, this dependence is indeed nearly the same. In particular, at modest extensions, the mechanical response of a protein formed by noninteracting repeats (H = 12, J = 0) is virtually the same as that in the case H = −15, J = 27. A negative value of H means that the folding of an individual repeat is unfavorable thermodynamically. As is known in the context of the helix-coil transition theory (11,12), folding in this case requires nucleation of a sufficiently long contiguous block of folded repeats such that the favorable interaction between neighboring units outweighs the initial cost of folding. This situation results in a highly cooperative, sharp transition between the folded and unfolded states, which can, indeed, be observed in thermal or chemical denaturation experiments (3). However, this cooperative behavior with respect to thermal unfolding makes no difference when the same protein is denatured mechanically. The unraveling of the chain in this case starts with the unfolding of the first or last repeat (requiring the lowest free-energy cost) and proceeds sequentially. The protein responds to stretching by unfolding more repeats such that the number of unfolded repeats increases linearly with the extension (cf. Eq. 12). As a result, the tension in the chain exhibits a plateau at a force close to $F_{\text{yield}}$. A similar scenario has been previously reported by us for the J = 0 case (13), the only difference being that the order in which the repeats unfold does not matter in that case, since there is no interfacial free-energy cost associated with unfolding. The lack of cooperativity in the mechanical unfolding of repeat proteins has already been pointed out in the experimental study by Li et al. (8).

Figure 3.

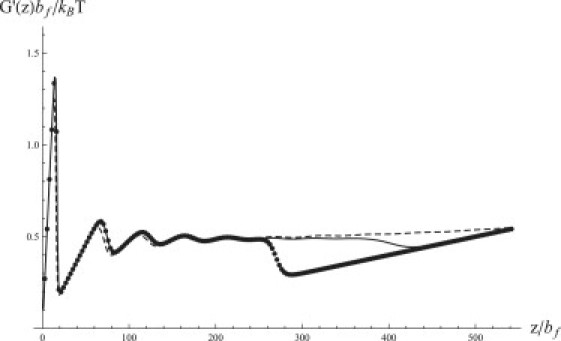
Force-extension curve of a repeat protein with the same J + H but different J and H. Solid line, J = H = 6; dashed line, J = 0, H = 12; points, H = −15, J = 27. The number of repeats is N = 10 and $b_{\mathrm{u}}=10b_{\mathrm{f}}$.

At large extensions, however, the three curves plotted in Fig. 3 begin to diverge. In particular, a significant drop in the force is observed for the case H = −15, followed by linear dependence with a slope corresponding to the fully unfolded protein (cf. the last line of Eq. 20). This implies that complete unraveling of the protein occurs sooner than in the other two cases. To understand this behavior, note that if H < 0, then isolated folded repeats are unstable thermodynamically. Consequently, once the number of folded repeats, $n_{\mathrm{f}},$ drops below a certain value, the remaining repeats will lose their stability and unfold spontaneously. Further insight into such spontaneous unfolding is gained by considering the free energy of the chain (Eq. 11). Although at sufficiently small extensions z, the free-energy minimum is attained at a finite value of $n_{\mathrm{f}}$ and at n = 1, for higher values of z, the minimum can be provided by $n_{\mathrm{f}}=n=0$. When the transition between the two regimes happens at a value $n_{\mathrm{f}}$ such that $n_{\mathrm{f}}$ < N, the remaining $N-n_{\mathrm{f}}$ repeats must unfold spontaneously, resulting in a drop in the force. Indeed, Eq. 11 predicts the small drop in force observed in Fig. 2 a and mentioned in the section comparing numerical results with approximations. Moreover, Eq. 11 predicts eight peaks (Fig. 2 a, dashed line), in contrast to N = 10 repeats in the chain, indicating that the last three repeats unfold simultaneously. Reducing the stability of individual repeats will promote early spontaneous unfolding of multiple repeats, which is indeed seen in Fig. 3, where the most prominent drop is observed for H = −15.

From these considerations, it is also clear that if the length, N, of the repeat protein only slightly exceeds the number of repeats needed to nucleate a stable folded structure, its mechanical unfolding will take place in a cooperative fashion, as the unfolding of the first repeat will destabilize the rest of the molecule.

Conditions for the existence of the force peak

As found in the Results section, the initial rupture event drastically lowers the stiffness of the chain and can lead to a sharp peak in the force followed by subsequent unfolding of the remaining repeats that takes place at much lower forces. This initial peak is pronounced when the rupture force, $F_{\mathrm{u}}$ (Eq. 19), is much higher than the yield force, $F_{\text{yield}}$ (Eq. 14). When Eqs. 14 and 19 are compared, these two forces become identical in the $N\to \mathrm{\infty }$ limit. Thus, the initial rupture peak is a finite-size effect that disappears for long chains. Numerical calculations using Eq. 4 also confirm this finding. This, of course, is consistent with the notion that van der Waals loops cannot exist in infinite systems. The requirement $F_{\mathrm{u}}\gg F_{\text{yield}}$ gives the following condition for the existence of a significant rupture peak:

$$b_{\mathrm{f}}^2\ll b_{\mathrm{u}}^2/(N+1)\text{.}$$ (21)

This means that stiffer folded repeats (i.e., those with a lower $b_{\mathrm{f}}$) will produce a higher rupture peak. Longer repeat proteins will generally have a less pronounced peak. Since the mean-square end-to-end distance, $b_{\mathrm{u}}^2$, of the unfolded chain grows linearly with its contour length, L, longer contour length stored in a repeat will also result in a more pronounced peak.

The validity of Eq. 21 can be verified for a typical AFM protein stretching experiment. Using a typical number, $k_{\mathrm{f}}=50\text{pN}/\text{nm},$ for the stiffness of an individual repeat (6,7), we estimate $b_{\mathrm{f}}\sim \sqrt{k_{\mathrm{B}}T/k_{\mathrm{f}}}\sim 0.2\text{nm}$. Lee et al. (7) found that unfolded repeats behave as wormlike chains with a contour length L ∼ 12 nm and persistence length p ∼ 2 nm. For such a chain, we estimate $b_{\mathrm{u}}\sim \sqrt{Lp}\sim 5\text{nm}$. Equation 21 thus holds if $N\ll {(b_{\mathrm{u}}/b_{\mathrm{f}})}^2\sim 300$. This condition is satisfied in Lee et al. (7), where $N\le 24$. The authors indeed observed a pronounced rupture peak (7), although it was not found in another study, by Li et al. (8). Consistent with the model proposed here, the peak observed in Lee et al. (7) had a shape corresponding to a Hookean spring. The initial high peak was followed by a series of much lower force peaks attributed to the unfolding of individual repeats. This behavior is consistent with the calculated shape of $G\prime \left(z\right)$ (see Fig. 2 b), which shows oscillations reflecting the unfolding of subsequent repeats.

We note that the estimate of Eq. 21 gives, at best, the necessary but not a sufficient condition for the peak to be actually observed. For example, in the idealized scenario discussed in the section about numerical results, above, the force on the chain is raised and the chain extension is measured. It then follows that this peak corresponds to a metastable state of the chain and will only be observed if the pulling is sufficiently fast. The situation is even more complicated in real experiments, where the protein is attached to a cantilever and to a surface. The stiffness of the cantilever and the linker must also be considered and may change the conditions for the peak (22). Differences in the parameters $b_{\mathrm{f}}$, $b_{\mathrm{u}}$, and N, as well as in the pulling method, could explain why a large peak appears in some experiments but not in others.

The high strength and toughness exhibited by many load-bearing proteins existing in nature is commonly attributed to the existence of “sacrificial bonds” (23–25), whose rupture releases “hidden length” of the polypeptide chain, allowing the system to dissipate large amounts of energy. Recently, there has been considerable progress in engineering and controlling protein constructs that display such behavior (26–30). For a protein to act as a sacrificial bond when it unfolds, a large free-energy barrier must exist, delaying its unfolding and allowing the folded protein to generate a force that is higher than the force that would destabilize the native state thermodynamically (13,31). The existence of such a barrier is equivalent to having a large peak (van der Waals loop) in the dependence of $G\prime \left(z\right)$ on z (see Results). Equation 21 thus provides a recipe for designing a repeat protein with potentially interesting sacrificial bond properties.

The yield force is proportional to the square root of the unfolding free energy

Scaling properties of rupture/unfolding forces in AFM pulling experiments have attracted considerable theoretical attention in the past (32–35), although most of the related work has focused on the irreversible unfolding regime, where those forces are controlled by barriers rather than by thermodynamic stability of proteins. Here, we can address the opposite regime of very slow pulling, where we found the yield force to be proportional to $\sqrt{J+H}$. This is a rather general result that arises when the thermodynamic stability of a sacrificial bond system is considered. When a sacrificial bond is broken, a contour length, L, becomes liberated. If we assume that the polymer is a Gaussian chain with a Kuhn segment of length p, then the entropic cost for stretching it by an amount z is $\mathrm{\Delta }S\sim -z^2/\left(2Lp\right)$. Thus, if a stretching force F is applied, the corresponding free-energy change is $\mathrm{\Delta }G\sim {\text{min}}_z{k}_{\mathrm{B}}T{z}^2/\left(2Lp\right)-Fz=-F^{2}Lp/2k_{\mathrm{B}}T$. The lowering of the free energy comes at the cost, $\mathrm{\Delta }E$, of breaking the bond. Therefore, the bond is destabilized thermodynamically when

$$\mathrm{\Delta }E\approx F^{2}Lp/2k_{\mathrm{B}}T,$$ (22)

which gives a square-root dependence of the force on the bond energy, $\mathrm{\Delta }E$. Setting $Lp=b_{\mathrm{u}}^2$ and $\mathrm{\Delta }E/k_{\mathrm{B}}T=J+H$ in Eq. 22, and assuming $b_{\mathrm{f}}=0$, one recovers the result of Eq. 14 for the yield force. It is also clear from the above arguments that the square root dependence is contingent on Gaussian polymer statistics. For example, if excluded volume effects are included, this would result in a slightly different scaling (13), $F\propto \mathrm{\Delta }{E}^{3/5}$.

Conclusions

In this article, we have studied a simple model for the mechanical unfolding of repeat proteins, in which the interactions among individual repeats are described by the Ising model. We find that although thermal denaturation of such a protein may be highly cooperative, its mechanical unfolding is sequential as long as the number of folded repeats is sufficient to ensure that the chain does not unfold spontaneously. We further show that the unfolding of the first repeat may produce a rupture force significantly higher than the force associated with the unfolding of subsequent repeats. These findings can be understood by employing simple analytic approximations for the protein's free energy as a function of its extension and the number of folded repeats.

Structural information about repeat proteins can be incorporated into this model to make it more realistic. Specifically, consider the free energy of a stretched, partially unfolded protein given by Eq. 10. The first term describes the elastic response of the chain. The next two terms describe the interactions among repeats. As long as the elastic part is independent of n, the free-energy minimum with respect to n is achieved at n = 1. This means that the mechanical unfolding pathway predominantly involves partially unfolded structures that consist of a single folded block flanked by fully unfolded chains. One can use this fact to replace the first term in Eq. 10 by a more realistic description of the protein's elastic response. Such a description could utilize, e.g., a wormlike chain model for the unfolded tails (36) combined with input from atomistic simulations to account for the elasticity of the folded block as a function of its length, $n_{\mathrm{f}}$ (6). Thermal unfolding data can further be used to estimate parameters H and J.

Finally, note that our model can also be applied to the unfolding of naturally occurring or engineered “polyprotein” constructs containing multiple repeats of the same (or several different) protein domains, which are commonly used in single-molecule AFM pulling studies (21). Unlike ankyrin repeat proteins, where individual repeats are often unstable, individual domains within polyproteins can fold independently. Although the assumption of noninteracting, individually stable domains (corresponding to the case H > 0, J = 0 within the model presented here) is often adequate for the interpretation of AFM pulling experiments (37–40), a more general case of interacting domains may be of interest, e.g., in the context of unfolding and refolding of polyubiquitin chains, where a cooperative folding mechanism has been suggested (41–43).