Abstract
It has been theoretically suggested that when a bacterium swims in a fluid, the disturbance it creates is long-ranged and can influence its locomotion. The contribution of these long-range hydrodynamic interactions to swimming cells is examined herein for a number of bacterial strains with well-defined flagellar geometries. We show experimentally for the first time that long-range hydrodynamic interactions are important for an accurate description of the swimming of a single cell, and the effect is more pronounced for bacteria with a large cell body. The commonly used local resistive force theory assumes a stationary background fluid while ignoring flows induced due to other moving parts of the cell. Although pedagogically attractive, resistive force theory is not generally applicable to experiment.
Introduction
Bacteria swim at low Reynolds numbers (Re ∼ 10−5) by rotating one or more helical filaments called flagella. The original work of Gray and Hancock (1) assumed local interactions, i.e., fluid disturbances generated by a moving segment of the flagellum do not interact with other parts of the swimming cell. Within this approximation, swimming characteristics such as the thrust F, the torque T, and the swimming speed V, can be predicted by the normal Kn and the tangential Kt resistive coefficients for a slender segment of the flagellum, and the geometry of the cell. Specifically, these parameters include the pitch λ, the length and the radius R of the flagellum, and the effective radius aE of the cell body (see Fig. 1). Lighthill (2) and others (3–5) recognized the shortcoming of such an approximation and their calculations incorporated long-range hydrodynamic interactions (LRHI), also known as the slender-body theory (SBT). The version of the SBT adopted by Lighthill (2) placed a uniform distribution of stokeslets along the length of a helical flagellum. To satisfy the nonslip boundary condition, a corresponding uniform distribution of source doublets was also included. The essence of the SBT was to construct a self-consistent local velocity field neighboring each segment of the flagellum due to contributions from moving parts of the bacterium, such as the cell body and other parts of the flagellum (2). To our knowledge, however, this important theoretical development has not been scrutinized by laboratory experiments. The central finding of our work presented herein demonstrates the significance of the local field corrections due to the flagellum/flagellum interaction while the flagellum/cell body interaction plays a relatively minor role.
Figure 1.
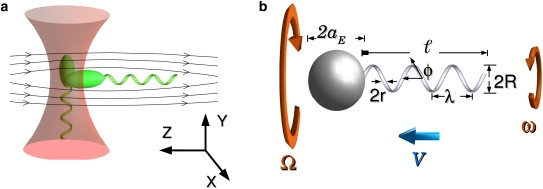
(a) An optical tweezers traps a bacterium horizontally in the presence of a flow, while in its absence the cell aligns with the optical axis. (b) Geometrical parameters of a bacterium, and the definitions of the dynamical variables: the swimming speed V, and the angular velocities of the flagellum ω, and the cell body Ω.
Methods
It was recently demonstrated that swimming bacteria can be stably trapped in optical tweezers, and many of its swimming properties, such as F, T, V, and the rotation speeds of the flagellum ω and the cell-body Ω can be determined precisely (6). The technique thus allows us to differentiate theories with various approximations. The optical trap in the experiment is formed by focusing an infrared laser (1064 nm, ∼50 mW) into a flow chamber using a 100× oil immersion objective. In the absence of an externally imposed flow, the bacterium is trapped along the optical axis whereas by applying a flow field, the bacterium can be held perpendicular to the optical axis. Both situations are depicted in Fig. 1. The position of the bacterial body in the trap is determined by a position-sensitive detector and is digitized at 5 kHz with a 12-bit resolution. Bacterial swimming causes this position (x, z) to fluctuate and is recorded as a function of time t, where z is along the swimming direction and x is transverse to it (see Fig. 1). A power spectrum analysis of x(t) yields two sharp peaks, giving the rotation frequency of the flagellum (ω/2π) and cell body (Ω/2π) (6). In a typical measurement, a bacterium is trapped for a couple of seconds, during which the time traces x(t) and z(t) are acquired. The cell is then released from the trap by temporarily switching off the laser and is video-recorded for a few seconds. From the bright-field video images, we determined the semi-minor (a) and semi-major axis (b) of the bacterium, and the free swimming speed V. The scale of the image is calibrated with an Olympus microscale (Melville, NY). The thrust F is determined from the measured V using F = A0V, where A0 = 4πηb/[ln(2b/a) − 1/2] is the linear drag coefficient for an elliptical cell body and η is the fluid viscosity (note that, for minicells, which have a spherical cell body of radius a, we set A0 = 6πηa and D0 = 8πηa3). The above measurements also permit us to deduce the torque acting on the cell body T = D0Ω and the rotational drag coefficient D() of the flagellum; the latter is due to torque balance. In the above, the rotational drag coefficient D0 of the body is given by . Aside from trapping the bacterium (which is pursued and captured manually by moving a computer-controlled stage), all the other data acquisition steps are automated by the computer. To minimize boundary effects, all of our measurements were performed at a distance ∼100 μm away from the chamber surface.
For stringent modeling of swimming, we performed measurements using bacteria with a simple geometry, namely cells possessing a single polar flagellum. The three bacterial strains studied were Vibrio alginolyticus YM42 (a marine bacterium), Caulobacter crescentus YB4038 (a fresh water bacterium), and Escherichia coli P678-54 (a mini-cell producing bacterium). Wild-type E. coli were not included because of complications arising from bundling of multiple flagella.
An important part of this work was the determination of flagellar dimensions. Since the flagellum of V. alginolyticus has a membrane sheath, the fluorescent dye Nano-Orange was used (7). The flagella of the other two strains were labeled with Cy3 (8). As displayed on the top row of Fig. 2, the flagella of all strains are clearly visible, allowing the helical length ℓ, the pitch λ, and the radius R to be determined. These quantities uniquely define the helical geometry, i.e., other quantities such as the pitch angle ϕ = tan−1(2πR/λ) and the contour length L = ℓ/cos ϕ can be derived. Measurements were carried out for a large number of cells, and the results are summarized in Table 1. Our measured ℓ, λ, and R for YM42, YB4038, and P678-54 are in reasonable agreement with those published in the literature (8–10). A parameter that is not accessible to optical microscopy is the radius r of the filament. This quantity can be determined by electron microscopy, and we used the published values (8–10) shown in Table 1.
Figure 2.
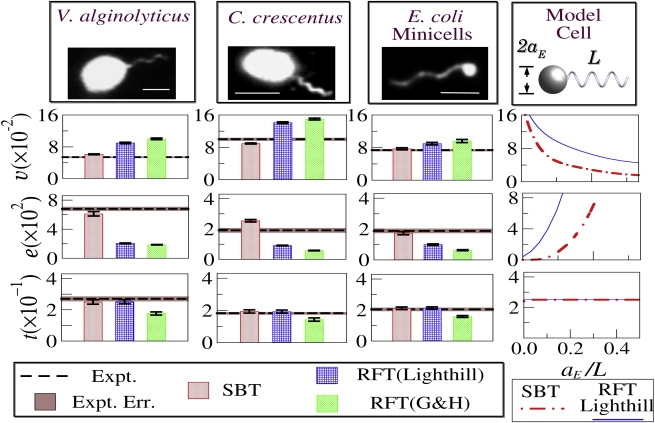
The top row shows the fluorescent images of the bacterial strains. The scale bars correspond to 2 μm. Experimental data are indicated by dashed lines. The bars are theoretical predictions with uncertainties being errors propagated from the spreads in geometrical parameters of the bacteria. The last column shows variations of v, e, and t for a hypothetical bacterium with an increasing load aE/L, where L = ℓ/cos ϕ is the contour length of the flagellum.
Table 1.
Parameters for the three bacterial strains studied
| Bacterial strain |
Dynamic variables |
Flagellar dimensions |
Cell size |
Cell No. |
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Genus | Name | ℓ(μm) | λ(μm) | 2R(nm) | r(nm) | a(μm) | b(μm) | nD | nG | ||||||
| V. alginolyticus | YM42 | 34 (1) | 571 (12) | 26 (1) | 3.7 (1) | 1.2 (0.02) | 280 (1) | 16 | 0.35 (0.01) | 2.3 (0.05) | 140 | 40 | |||
| C. crescentus | YB4038 | 30 (1) | 311 (10) | 31 (1) | 4.5 (0.6) | 0.96 (0.01) | 280 (1) | 7 | 0.42 (0.01) | 0.96 (0.03) | 80 | 40 | |||
| E. coli minicell | P567-48 | 14 (0.4) | 78 (2) | 31 (1) | 6.2 (0.2) | 2.3 (0.02) | 380 (5) | 12 | 0.41 (0.01) | 0.41 (0.01) | 75 | 40 | |||
The uncertainties quoted in parenthesis are standard errors of the mean. The values nD and nG are, respectively, the numbers of cells used in the dynamic and geometric measurements. The values for r were obtained from the literature (8–10) for V. alginolyticus, C. crescentus, and E. coli minicells, respectively.
Results and Discussion
For a bacterium swimming along a straight line, three dynamic quantities, V, ω, and Ω are sufficient to specify its motion. However, due to the torque balance condition, , the number of degrees of freedom is only two; that is, only two of the three quantities above are independent. To specify the motion, Lighthill chose the dimensionless velocity v = V/VW and the torque t = T/4πηR2Lω. Since the power generation is an important characteristic of bacterial locomotion, the dimensionless power e = E/ηV2 was also calculated by Lighthill. Here VW = ωλ/2π is the wave velocity of the helix, and E = Tω/L is the power delivered per flagellar length. The three quantities (v, e, t) are functions of the geometric parameters of the flagellum (ℓ, λ, R, r) and the cell body (a, b). Since they are all measured experimentally, it allows quantitative comparisons between theory and experiment. Within the resistive force theory (RFT), a simple calculation shows
| (1) |
| (2) |
| (3) |
where AT = (A + A0) is the total linear drag coefficient on the bacterium, A (D) is the linear (rotational) drag coefficient of the flagellum, and B is the cross-coupling coefficient relating the linear and rotational motions. A, B, and D are functions of Kt = 4πη/[2 ln(2λQ/r) − δ1] and Kn = 8πη/[2 ln(2λQ/r) + δ2] (6). Different versions of RFT assume different values for Q, δ1, and δ2. For example, Gray and Hancock (1) assumed Q = 1, δ1 = 1, and Kn/Kt = 2, implying δ2 = −1. Lighthill (2) found it more appropriate to set Q = 0.09λ/cos ϕ, δ1 = 0, and δ2 = 1. The SBT calculations for v, e, and t are more tedious, but closed forms can still be found ((2), S. Chattopadhyay and X. L. Wu, unpublished). Specifically, we used the integral equations, Eqs. 56, 95, and 103 of Lighthill (2), and performed the calculations numerically for a given bacterial geometry (1). For convenience, the relevant equations are summarized in Appendix A. Lighthill's calculation consisted of three steps:
-
Step 1.
The zero-thrust limit, where the flagellum propels itself without a cell body;
-
Step 2.
A finite thrust, when a cell body is attached but without hydrodynamic interactions between the flagellum and the cell body; and
-
Step 3.
Inclusion of the LHRI between the flagellum and the cell body.
In the second step, the load A0V due to the cell body is taken into account explicitly using the elliptical shape of the cell. For simplicity in the calculation of Step 3, Lighthill approximated the elliptical cell body as a sphere with an effective radius aE = 2b/3[ln(2b/a) − 1/2], which is obtained by equating 6πηaE with A0.
The bacterial strains YM42, YB4038, and P678-54 were grown according to the protocols in the literature ((10–12), respectively). Among the three strains, V. alginolyticus (YM42) is the fastest swimmer; under optimal conditions, it can swim up to ∼100 μm/s with a flagellar frequency f(= ω/2π) ≈ 2 kHz. At room temperature (23 °C) and a NaCl concentration of ∼30 mM, we found the average velocity to be V ≈ 35 μm/s (11). C. crescentus (YB4038) swims at V ≈ 30 μm/s in distilled water, which is consistent with a previous observation (10). E. coli mini cells are the slowest bacteria in this study, with V ≈ 14 μm/s. They were isolated from cultures containing mutant bacteria that produce uneven cell divisions (12). The mini cells have surprisingly uniform spherical bodies and possess a single flagellum if they swim.
In Fig. 2, the measured quantities (v, e, t) for the three bacterial strains are plotted by dotted horizontal lines and the errors of the mean are indicated by the shaded bands. We found that the reduced swimming speed v of YM42 is nearly a factor-of-two smaller than YB4038, despite the small difference in the mean swimming speeds V of the two bacteria. This suggests that for each rotation of the flagellum, YB4038 swims a longer distance than YM42, indicating that Caulobacter is a more efficient swimmer. By all our measures, the mini cells behave quantitatively similar to C. crescentus despite their very different cell geometry (see Table 1). In the case of C. crescentus, cells have a slightly curved body, making it rotate around the swimming axis with a small offset (10). We found that the torque balance equation was not satisfied if the half-width of the cell (a ≈ 0.3 μm) was used. However, upon using the apparent width (a ≈ 0.42 μm) measured directly via bright-field microscopy, the torque balance was satisfied. We noted that the calculation of v is negligibly affected by a, as A0 depends on a logarithmically (A0 ∝ 1/[ln(2b/a) − 1/2]), which should be compared with the strong a dependence of D0 (D0 ∝ a2).
Next, we turn our attention to theoretical predictions, which are presented as colored bars in Fig. 2. The uncertainties in the calculations, resulting from the spread in the measured geometric parameters, are indicated by the error bars. We found that, while all models predict t to within ∼30% of each other and are in reasonable agreement with each strain tested, such consistency is absent for v and e. Specifically, RFT of Lighthill or Gray and Hancock predicted higher v than SBT, and in the case of V. alginolyticus, the discrepancy is approximately a factor of two. This should be compared with the ∼15% difference between the measurement and the predictions of SBT. A more conspicuous difference is the reduced power dissipation e, resulting largely from its V2 dependence. As shown, LRHI significantly increases e, and for V. alginolyticus the difference between RFT and SBT is four times. The underlying physics that gives rise to this huge difference can be understood as the result of the local velocity field experienced by the flagellum. In RFT, the surrounding fluid is assumed to be static; however, in the SBT, this field is calculated self-consistently, giving rise to an overall rotational movement. This reduces the relative velocity between the flagellum and the fluid. Consequently, for the same motor speed, the flagellum will experience a larger slip or a smaller v, and the swimming efficiency e−1 correspondingly decreases. Although the above comparisons between theory and experiment were made using the reduced quantities v, t, and e, the conclusion remains the same if instead the dimensional quantities V, T, and E were used. As delineated in Fig. 2, for all bacteria studied, SBT works considerably better than the RFT, suggesting SBT has captured the essential physics of bacterial swimming. Moreover, this agreement is achieved without a single free parameter in the model.
An interesting feature of Fig. 2 is that the discrepancy between RFT and our measurements becomes progressively worse as the bacterial swimming speed increases. For instance, with the mini cells, although the measured v agrees better with SBT (within ∼7%), the difference with RFT is only ∼20%. However, this difference is ∼100% for V. alginolyticus, giving the impression that RFT may be a reasonable approximation for slow swimming cells but not for fast ones. This interpretation, however, is incorrect. According to SBT, the relevant quantity to gauge the importance of LRHI is the load defined as g = A0V/L (2), i.e., the thrust/length that a flagellum must provide to propel the cell at velocity V. This is because the net contribution of thrust—i.e., g multiplied by the length of the flagellum—does not vanish. This is in sharp contrast with the zero-thrust limit, where the number of stokeslets integrated along the flagellum is zero, significantly reducing the hydrodynamic effect. Since A0 ∝ aE and V/VW is constant, it follows that the dimensionless load is given by aE/L. To illustrate this point, we show, in the last column of Fig. 2, RFT and SBT calculations of v, e, and t for a hypothetical bacterium with a variable load aE/L. The calculation was performed using the flagellar geometry of V. alginolyticus and with aE varying. One observes that for v and e, the difference between RFT (solid line) and SBT (dotted line) decreases with decreasing aE/L, and the two theories converge as aE/L → 0, indicating that no LRHI is needed for a zero-thrust swimmer. As mentioned in the Introduction, LRHI results from flagellum/flagellum and flagellum/cell body interactions. However, because LRHI between the cell body and the flagellum is relatively weak (see Appendix B), it can be concluded that the primary contribution is due to interactions between different segments of the flagellum. We note, on the other hand, that both theories predict constant t, independent of aE/L, and the difference between the two is negligible. It is thus expected that with everything being equal, bacteria swim slower and need more power in the presence of LRHI. For instance, for a bacterium with a large cell body, say aE/L = 0.15, the reduced speed v without LRHI is approximately a factor-of-two higher whereas the reduced energy dissipation e is approximately a factor-of-four lower. The observed trend for the three bacteria is consistent with this physical picture. Similar qualitative features were also found by Johnson and Brokaw when they compared the predictions of RFT and SBT for swimming of spermatozoa, which has a load ∼1/10 of V. alginolyticus, or aE/L ≈ 0.015 (13).
Conclusion
In conclusion, we have performed measurements of bacterial swimming using optical tweezers and compared the measurements with mathematical models of propulsion based on helical-wave propagation along a single polar flagellum. It has been demonstrated that SBT works considerably better than RFT for all strains tested, and for cells with a heavy load, the use of SBT becomes essential. RFT is commonly used by experimenters to calculate bacterial swimming speed and efficiency. Here we showed that such practice is only qualitative, and can lead to erroneous results for bacteria with a large body/flagellar length ratio. Because of the simplicity in the implementation of RFT, previous theoretical studies (1,13) have made attempts to reconcile the discrepancy between RFT and SBT by setting Kn/Kt = 2 and using Q as an adjustable parameter. For instance, the choice of Q = 1 suggested by Gray and Hancock was purely empirical, as this value appeared to fit the experimental data of spermatozoa (1). Johnson and Brokaw (13) similarly found that an overall increase of Kt and Kn by 35–40% but without a significant change in their ratio could also make RFT to agree with the observations of spermatozoa swimming. If such a phenomenological approach is used for our data, we found that no value of Q could produce good fits for v, e, and t for any bacterium tested. This is perhaps not surprising, as RFT should agree with experiments only at the zero-thrust limit, and prior agreements with experiments (1,13) have been primarily due to the fact that spermatozoa swam very close to the that limit with aE/L ∼ 0.02. The smallest load in our experiment is for the minicells, which have aE/L ∼ 0.06.
Acknowledgments
We thank M. Homma and Y. Brun for providing us with bacterial strains.
This work is supported by the National Science Foundation under grant No. BP-0646573.
Appendix A: Formulation of Lighthill's SBT
According to Lighthill's 1976 article (2), the dimensionless velocity v, the torque t, and the energy dissipation rate e are given by (Eqs. 57–59, 95, and 103 of (2))
| (4) |
| (5) |
| (6) |
where α = cos ϕ is the directional cosine of the helix, aE is the effective radius of the cell body, and L is the total length of the flagellum. The other quantities, Y, Z, ψ, and Ψ are functions of α and are given by
In the above equation, ɛ = 5.2αr/λ with r the radius of the flagellum, with ℓ = L cos ϕ, and A1(α), and A2(α), and A3(α) are given by the definitive integrals
where and represent the ends of the flagellum with L1 + L2 = L. For a long flagellum, the term ln(θ1θ2) in the above equation can be replaced by averaging L1 over the length of the flagellum with the result 〈ln(θ1θ2)〉 = 2 ln(kL) − 2.
Appendix B: The Effect of Cell Body-Flagella Interactions
Lighthill calculated the effect of LRHI between the cell body and the flagellum on bacterial swimming (2). To perform this complicated calculation, he replaced the elliptical cell body with an equivalent sphere of radius aE, and the flow field it created near each flagellum segment was calculated by a single stokeslet located at the center of the sphere. Likewise, the local flow field experienced by the cell body due to the rotating flagellum was calculated by a uniform distribution of stokeslets along the center line of the flagellum. Solving these equations self-consistently, the swimming velocity V was obtained, which yielded a slight deviation from the swimming speed assuming no cell-body/flagellum interaction. It was further shown that the net effect of the cell-body/flagellum interaction was to reduce the value of Ψ by a factor of (see the definition in Appendix A, where this term is included). In other words, if this term is set to unity, one attains the result without cell-body/flagellum interaction. For the three bacterial strains measured, we evaluated the relative importance of cell-body/flagellum interaction, and the results are presented in Fig. 3. It is shown that including this long-range effect only marginally changes the reduced speed v by ∼5% for V. alginolyticus and by ∼2% for the mini cells. It is interesting to point out that the effect of the cell body/flagellum interaction is to increase v, making swimming more efficient. The effect is more noticeable for bacteria with a larger load aE/L, and hence V. alginolyticus has the greatest effect and the mini cells the smallest. Physically, the improved swimming efficiency may be understood as a hydrodynamic screening effect, i.e., the presence of the cell body modifies the local velocity field around the flagellum such that the relative wave velocity between the flagellum and its surrounding fluid is increased. However, because g ∝ A0 or aE, this lamination effect cannot compensate LRHI resulting from thrust generation by the flagellum, and it will represent a relatively small correction to swimming.
Figure 3.
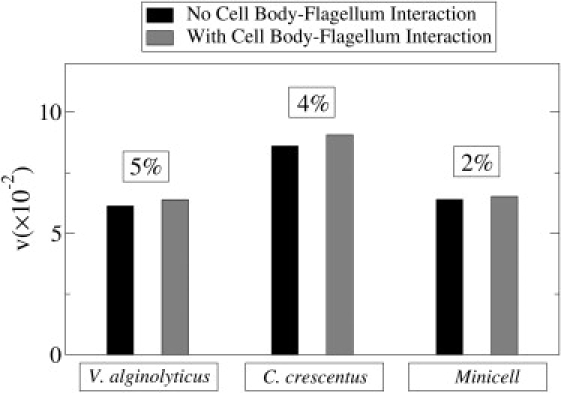
Calculations of v for the three different bacteria with and without the LRHI between the cell body and the flagellum. The difference for each strain is indicated in the box above the respective plots.
We note that because the effect of cell body/flagellum interaction is small, imposing a more realistic cell-body shape in the calculation of Step 3 (see the main text) will not alter our above conclusion significantly. Moreover, as the stokeslets that account for the finite load are all along the swimming direction, LRHI will not significantly affect the torque balance.
References
- 1.Gray J., Hancock G.J. The self-propulsion of microscopic organisms through liquids. J. Exp. Biol. 1955;32:802–814. [Google Scholar]
- 2.Lighthill J. Flagellar hydrodynamics. SIAM Rev. 1976;18:161–230. [Google Scholar]
- 3.Johnson R.E. An improved slender-body theory for Stokes flow. J. Fluid Mech. 1980;99:411–431. [Google Scholar]
- 4.Keller J.B., Rubinow S.I. Slender-body theory for slow viscous flow. J. Fluid Mech. 1976;75:705–714. [Google Scholar]
- 5.Childress S. 1st Ed. Cambridge University Press; New York: 1981. Mechanics of swimming and flying. Cambridge Studies in Mathematical Biology. [Google Scholar]
- 6.Chattopadhyay S., Moldovan R., Yeung C., Wu X.L. Swimming efficiency of bacterium Escherichia coli. Proc. Natl. Acad. Sci. USA. 2006;103:13712–13717. doi: 10.1073/pnas.0602043103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Grossart H., Steward G., Martinez J., Azam F. A simple, rapid method for demonstrating bacterial flagella. Appl. Environ. Microbiol. 2000;66:3632–3636. doi: 10.1128/aem.66.8.3632-3636.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Darnton N.C., Turner L., Rojevsky S., Berg H.C. On torque and tumbling in swimming Escherichia coli. J. Bacteriol. 2007;189:1756–1764. doi: 10.1128/JB.01501-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Magariyama Y., Sugiyama S., Kazamasa M., Kawagishi I., Imae Y. Simultaneous measurement of bacterial flagellar rotation rate and swimming speed. Biophys. J. 1995;69:2154–2162. doi: 10.1016/S0006-3495(95)80089-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Li G., Tang J. Low flagellar motor torque and high swimming efficiency of Caulobacter crescentus swarmer cells. Biophys. J. 2006;91:2726–2734. doi: 10.1529/biophysj.106.080697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Sowa Y., Hotta H., Homma M., Ishijima A. Torque-speed relationship of the Na+-driven flagellar motor of Vibrio alginolyticus. J. Mol. Biol. 2003;327:1043–1051. doi: 10.1016/s0022-2836(03)00176-1. [DOI] [PubMed] [Google Scholar]
- 12.Adler H., Fisher W., Cohen A., Hardighee A. Miniature Escherichia coli cells deficient in DNA. Proc. Natl. Acad. Sci. USA. 1967;57:321–326. doi: 10.1073/pnas.57.2.321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Johnson R.E., Brokaw C.J. Flagellar hydrodynamics. A comparison between resistive-force theory and slender-body theory. Biophys. J. 1979;25:113–127. doi: 10.1016/S0006-3495(79)85281-9. [DOI] [PMC free article] [PubMed] [Google Scholar]


