Interaction of Cellular and Network Mechanisms in Spatiotemporal Pattern Formation in Neuronal Networks

Abstract

Spatiotemporal patterning of neuronal activity is considered to be an important feature of cognitive processing in the brain as well as pathological brain states, such as seizures. Here, we investigate complex interactions between intrinsic properties of neurons and network structure in the generation of network spatiotemporal patterning in the context of seizure-like synchrony. We show that membrane excitability properties have differential effects on network activity patterning for different network topologies. We consider excitatory networks consisting of neurons with excitability properties varying between type I and type II that exhibit significantly different spike frequency responses to external current stimulation, especially at firing threshold. We find that networks with type II-like neurons show higher synchronization and bursting capacity across a range of network topologies than corresponding networks with type I-like neurons. These differences in activity patterning are persistent across different network sizes, connectivity strengths, magnitudes of random external input, and the addition of inhibitory interneurons to the network, making them highly likely to be relevant to brain function. Furthermore, we show that heterogeneous networks of mixed cell types show emergent dynamical patterns even for very low mixing ratios. Specifically, the addition of a small percentage of type II-like cells into a network of type I-like cells can markedly change the patterning of network activity. These findings suggest that cellular as well as network mechanisms can go hand in hand, leading to the generation of seizure-like discharges, suggesting that a single ictogenic mechanism alone may not be responsible for seizure generation.

Introduction

Spatiotemporal patterning of neuronal activity is considered to be an underlying feature of many cognitive as well as pathological phenomena. For example, epilepsy is characterized by spontaneous recurrent seizures generated by synchronized bursting of neuronal populations. A wide range of molecular and cellular mechanisms, as well as synaptic pathologies are implicated in seizure generation. Synaptic abnormalities are centered around reduced inhibition or increased excitatory transmission, causing an imbalance between cortical excitation and inhibition (Dudek et al., 1999). Examples of cellular mechanisms include specific ion channel abnormalities or resultant changes in the relationship between the adapted spike frequency and applied current (f–I curve) as observed in cortical neurons from an epileptic animal model (Prince and Tseng, 1993). This latter type of cellular change can make individual cells more responsive to an imbalance in network excitation and thus promote seizure-like activity.

At the same time, much less is known about network underpinnings of different forms of this disease. The potential network mechanisms proposed to underlie excessive excitatory neurotransmission during epileptogenesis in acquired focal epilepsies span from loss of inhibitory interneurons to aberrant axonal reorganization. In mesial temporal lobe epilepsy, for example, excitatory dentate granule cells sprout axons (mossy fibers) onto neighboring granule neurons (for review, see Parent and Lowenstein, 1997). Evidence suggests that mossy fiber sprouting leads to abnormal recurrent excitation that may be critical for seizure initiation or propagation in the network (Lysetskiy et al., 2005). In addition, studies of epilepsy models provide evidence for increased recurrent excitation in other brain areas, including in the CA1 region of the hippocampus (Derchansky et al., 2008) and among cortical pyramidal cells (Jin et al., 2006).

During recent years, many studies have focused on understanding the role of network topology and/or its community structure on network dynamics (Boccaletti et al., 2006). It has been shown that network reorganization, often modeled using the small-world network (SWN) paradigm (Watts and Strogatz, 1998) (see supplemental material, available at www.jneurosci.org), can lead to dramatic changes in dynamical activity patterns generated by its elements (Netoff et al., 2004; Percha et al., 2005). Relatively little work has focused on understanding the interactions between cellular and network properties and their combined effect on spatiotemporal patterning in the network, with the notable exception of the studies by Santhakumar et al. (2005), Dyhrfjeld-Johnsen et al. (2007), and Morgan and Soltesz (2008).

In this study, we investigate underpinnings of the combination of intrinsic cell and network mechanisms in spatiotemporal pattern formation in excitatory neuronal networks. Using multicompartmental neurons modeled in the Hodgkin–Huxley formalism (Hodgkin and Huxley, 1952), we construct networks consisting of four different cell types with various membrane excitability properties as described by their frequency–current (f–I) relationships. At the same time, we modify network topology and connectivity to mimic aberrant network reorganization. We first explore response properties of homogeneous networks that consist of model neurons of the same excitability type. We show that the network response is strongly affected by cellular properties for different topologies. We then investigate spatiotemporal pattern formation in heterogeneous networks consisting of cells of different excitability types. We find that the introduction of very few cells with different excitability properties can profoundly influence spatiotemporal activity. We believe that our results highlight the combined interaction of intrinsic neuronal properties and overall network structure in the generation of complex patterns of network activity.

Materials and Methods

Neuronal properties

The model neurons were based on a hippocampal CA1 pyramidal neuron with simplified dendritic morphology and a minimum number of active currents. CA1 pyramidal cells were chosen as this region is commonly implicated in generating seizures and is often used for in vitro studies of interictal to ictal transition (Dzhala and Staley, 2003; Derchansky et al., 2008). Each model cell was composed of a five-compartment, 1200-μm-long dendritic cable electrotonically coupled to a soma compartment (equivalent to a 35 μm sphere) (Shao et al., 1999). The cable dendrite contained only passive kinetics and the current balance equation in each compartment was given by the following:

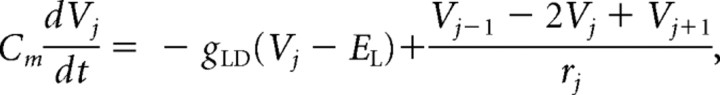where V_j is the membrane potential in dendritic compartment j = {1, 2, 3, 4, 5}. The compartmental coupling term for the first compartment contained V_s instead of V_{j − 1} and for the last compartment reflected a sealed-end boundary condition. The soma compartment contained the following active currents modeled in Hodgkin–Huxley formalism: a transient, inward Na⁺ current; an outward, K⁺-delayed rectifier current; a transient outward K⁺ A-type and an inward, hyperpolarization-activated, mixed Na⁺ and K⁺ h current (Migliore et al., 1999; Poolos et al., 2002). The current balance equation for the soma compartment was given by the following:

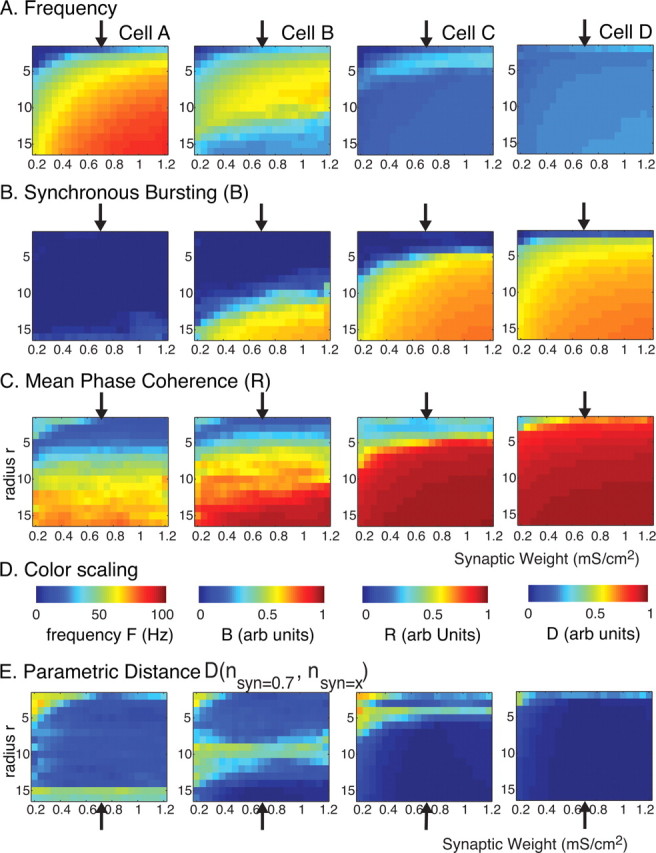
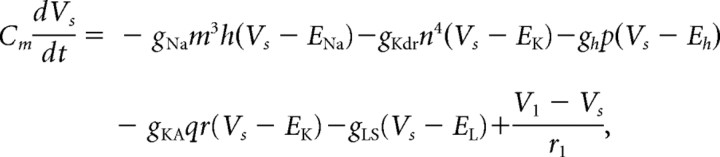where V_s is membrane voltage in the soma compartment. The model cells and network were implemented in the NEURON, version 5.9, simulation environment (Hines and Carnevale, 2001). Equations for the gating kinetics of the ionic currents and parameter values are listed in the supplemental material (available at www.jneurosci.org).

Cells were connected through synaptic currents that targeted the most distal dendritic compartment of the postsynaptic neuron. As such, the current balance equation for the fifth dendritic compartment contained the additional term − Σ I_syn, reflecting the sum of synaptic currents from all impinging synapses. On activation of synaptic current by a presynaptic cell crossing threshold (set at −20 mV), it decayed following a single exponential with time constant τ = 0.5 ms:

where I_syn (nA/cm²) is the synaptic current, defined for t > t_i, resulting from a presynaptic spike at time t_i, and w is the synaptic weight (mS/cm²). The reversal potential E_syn was 0 mV for excitatory synapses and −75 mV for inhibitory synapses. Synaptic weight values were homogeneous across all synapses in a network. In Figures 3, 5, and 7–9, all synaptic weights w were set to the default value of 0.7 mS/cm², whereas the value of w was varied in Figures 4 and 6.

Figure 3.

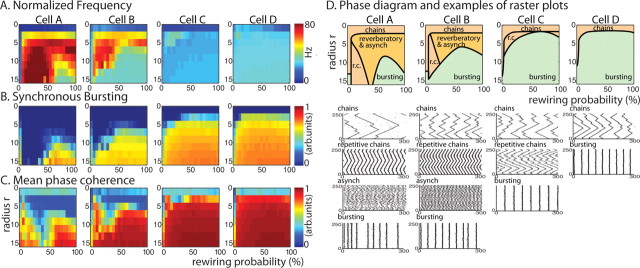
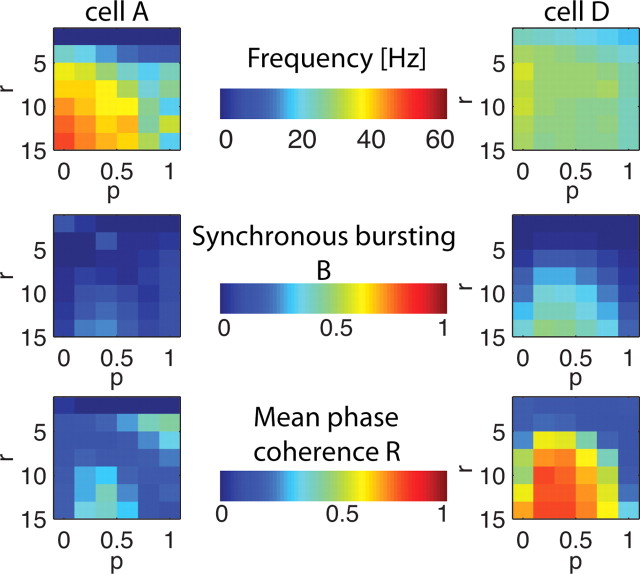
Spatiotemporal pattern formation in 250 cell excitatory networks with homogeneous cell type as described by our three measures; average frequency F (A), bursting B (B), and mean phase coherence R (C) for network topologies with rewiring parameter p between 0 and 100% (horizontal axis) and radius of connectivity r between 0 and 16 (vertical axis) for all four cell types (columns cell A to cell D). Warm colors denote high values and cool colors denote low values. D, E, Summary plots showing network activity patterns obtained in different regions of rewiring p and connectivity r parameter space as derived from our three measures for networks consisting of each cell type (top row, columns cell A to cell D). Raster plots showing 300 ms of network activity in each parameter region of summary plots (bottom rows, columns cell A to cell D). In the raster plots, we have removed the initial 100 ms of network activity to ignore initialization transients.

Figure 5.

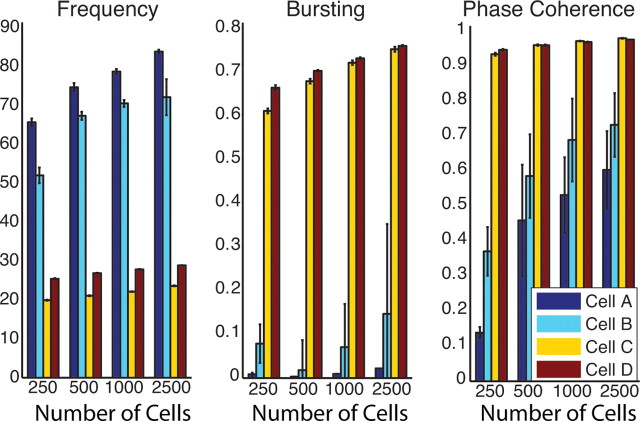
Spatiotemporal pattern formation in excitatory networks as a function of number of cells N (N = 250, 500, 1000, 2500). Values of network frequency (left panel) (in hertz), bursting (B; middle panel) and phase coherence (R; right panel) for networks composed of cell types A (dark blue), B (light blue), C (yellow), and D (red). In all networks, connectivity fraction was 4% and synaptic strength was 0.7 mS/cm². Rewiring parameter p was adjusted (for N = 250, p = 0.4; for N = 500, p = 0.2; for N = 1000, p = 0.1; and for N = 2500, p = 0.04), so that the mean pathlength (which depends on p and number of connections per element) is constant.

Figure 7.

Spatiotemporal pattern formation as a function of the noise frequency (horizontal axes) (in hertz) and radius of connectivity r (vertical axes) for excitatory networks of 250 neurons of cell types A, B, C, and D (columns from left to right). A–D, Measures of network frequency (A), bursting (B), and mean phase coherence (C) in which color reflects measure value (D). E, Parametric distance D (see Materials and Methods) of the three measures between the case when synaptic noise was at its default value of 1 Hz and the other values as indicated on x-axis. The arrows in all panels denote the default noise frequency (1 Hz).

Figure 8.

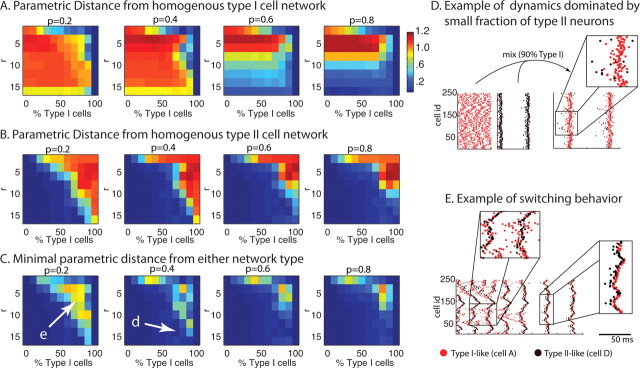
Effects of cell type heterogeneity on network spatiotemporal patterning in 250 cell excitatory networks. A, B, Parametric distance D_i,cellA from homogeneous type I (cell A) networks (A) and D_i,cellD from homogeneous type II (cell D) networks (B) for heterogeneous network i with mixture ratio of type I and type II cells on horizontal axis and connectivity radius r on vertical axis. C, Minimum of D_i,cellA and D_i,cellD. The warm colors denote high values, whereas the cool colors denote low values. D, Activity in a mixed network of 10% type II neurons, which dominate activity and promote stable global synchrony (right panel) for r–p parameter values (parameter values at arrow in C, 2nd panel) that display asynchronous activity in a homogeneous type I network (left panel, left plot) and synchronous bursting in a homogeneous type II network (left panel, right plot). E, Activity of mixed network (parameter values at arrow in C, 1st panel) exhibiting unreliable switching behavior that continues throughout run. Note in D and E the network synchronizes when type II cells lead bursts (see insets D and right E), and that leading type I cells do not promote network synchrony (see E, top inset). In all raster plots, we have removed the initial 100 ms of network activity to ignore initialization transients.

Figure 9.

Spatiotemporal pattern formation as a function of rewiring probability p (horizontal axes) and connectivity radius r (vertical axes) in excitatory networks of 250 neurons of cell types A (panels in right column) and D (panels in left column) coupled to homogeneous inhibitory networks of 250 neurons (see text for description). Measures of network frequency (top panels) (in hertz), bursting (middle panels), and mean phase coherence (bottom panels) in which color reflects measure value (middle column).

Figure 4.

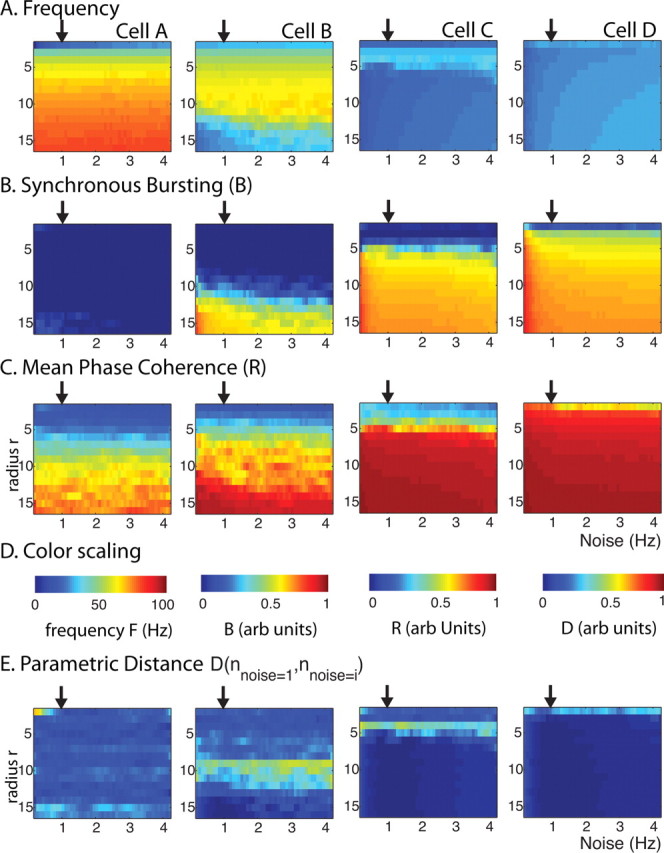
Spatiotemporal pattern formation as a function of synaptic weight (horizontal axes) (in mS/cm²) and radius of connectivity r (vertical axes) for excitatory networks of 250 cells of type A, B, C, and D (columns from left to right). The rewiring parameter was fixed at p = 0.2 (20%). A–D, Measures of network frequency (A), bursting (B), and mean phase coherence (C) in which color reflects measure value (D). E, Parametric distance D (see Materials and Methods) of the three measures between networks with synaptic weight fixed at the default value (0.7 mS/cm²). The arrows in all panels denote this default synaptic strength.

Figure 6.

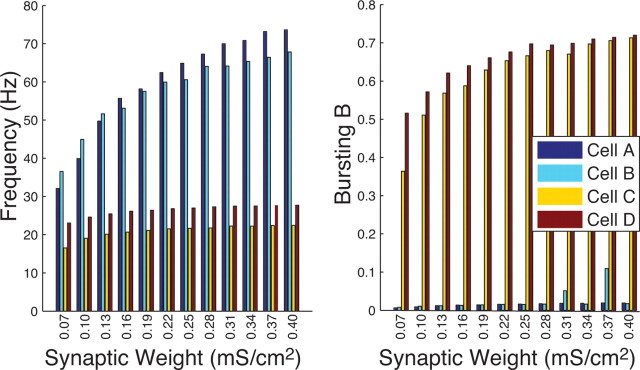
Network frequency (in hertz) (left) and bursting (B) (right) for varied synaptic weight values (in mS/cm²) in excitatory networks consisting of 2500 neurons of cell types A (dark blue), B (light blue), C (yellow), and D (red). Connectivity fraction in the networks was 4% and rewiring p = 0.2.

Additionally, to simulate synaptic noise, every cell in the network was randomly stimulated by a synaptic current, identical in synapse location, amplitude, and decay dynamics to the synaptic current caused by spike firing of a presynaptic cell, but randomly occurring with an average frequency of 1 Hz.

Network connectivity

The network was constructed using the SWN paradigm (see supplemental material, available at www.jneurosci.org). The small-world phenomenon provides a convenient framework to systematically modify network topology. Moreover, emerging evidence suggests that networks of similar topology exist in the brain (Sporns and Zwi, 2004). In the SWN paradigm, the rewiring parameter p allows for exploration of network topologies that lie between local and random. The parameter p ranges from 0 to 1, and is the probability of replacing a local, nearest neighbor connection with a connection randomly assigned elsewhere in the network. Thus, the network has only nearest neighbor connections for p = 0 and has completely random topology for p = 1 (Watts and Strogatz, 1998). It is well understood that for low, nonzero values of p, small-world networks exhibit strong clustering, but with a relatively small mean path length.

Our networks consisted of 250 or more cells with a uniform number of outbound synaptic connections emanating from each cell and periodic boundary conditions. We varied the radius of connectivity, r, to consider connectivity fractions (i.e., the ratio of the total number of actual outbound connections to the number of all possible connections in the network) between 0 and 15%. Specifically, the connectivity fraction for a one-dimensional network is calculated as 2r/(N − 1) × 100%, where N is the number of cells in the network. Physiological connectivity is considered to be between 1 and 5%, with the higher percentages meant to represent abnormally dense connectivity perhaps observed near a seizure focus. Spatiotemporal activity patterns obtained for connectivity levels outside this range did not vary significantly from those presented here. The topology of network connectivity varied by considering all values of the rewiring parameter p € [0,1]. All simulations were run for at least 3000 ms, whereas many runs were much longer to explore the stability of behavior.

Measures

To quantify observed spatiotemporal patterning of network activity and distinguish between various network behaviors, we applied three measures: average frequency (F), mean phase coherence (R), and a measure of synchronous bursting (B). The combination of these three measures allowed us to compare network dynamics quantitatively, and also detect behavior switching within a single simulation run.

Frequency.

The average frequency of cell n, F_n, was defined as the inverse of the average interspike interval over the duration of the simulation run:

where S is the total number of spikes fired at times t_k of cell n. The network average frequency, F, was the average of F_n over the number of cells in the network.

Mean phase coherence.

To quantify phase locking between cells, we adapted the mean phase coherence, R, of an angular distribution (Mormann et al., 2000). The value of R ranged between 0 and 1, and increased as phase locking increased between cells. We measured the time dependence of R with a sliding window of 750 ms. R is defined as follows:

where S denotes the number of samples in the array of cell n spike times, and φ_n,m is the phase between cells n and m for interspike interval j. This was determined as follows: the period for interspike interval j, τ_nj ≡ t_nj+1 − t_nj, for cell n was taken to be 2π. The cell m spike associated with interval j, t_mj, was selected such that t_nj ≤ t_mj+1 ≤ t_nj+1 so the phase between spikes at time t_nj and t_mj (interval τ_nj,mj ≡ t_mj − t_nj) could be calculated at time t_nj by φ_n,m≡(τ_nj,mj/τ_nj)2π.

Synchronous bursting.

We used an interspike distance synchrony measure (Tiesinga and Sejnowski, 2004) to monitor the degree of spiking synchrony in the network. The metric, B, is based on the time-ordered, complete set of network spikes and relies on the fact that the variance between firing times of all cells in the network during a synchronous event is smaller than during asynchronous events. B is defined as follows:

where N is the number of cells in the network. The combined, time-ordered set of network spike times t_υ was labeled by the index ν, whereas the set of network interspike intervals was labeled τ_υ with τ_υ = t_{υ + 1} − t_υ. Note that these interspike intervals are between different cells in the network. Thus, assuming that every neuron fires independently with a constant rate, the combined spike train for a large asynchronous network will have a Poisson spike distribution with the term $\sqrt{\langle {\tau }_v^2\rangle -{\langle {\tau }_v\rangle }^2}/\langle {\tau }_v\rangle \to 1$. However, in the limit of large N and if the network is fully synchronized with neurons firing with a period T, the term $\sqrt{\langle {\tau }_v^2\rangle -{\langle {\tau }_v\rangle }^2}/\langle {\tau }_v\rangle \to \sqrt{N}$. Thus, the relatively atypical form of B provides a normalized measure of degree of synchronized bursting in the network, where low values of B are indicative of asynchronous activity, whereas B = 1 indicates strong, highly synchronous bursting.

Parametric distance.

To determine overall dissimilarity between network states, we formulated a parametric distance, D, between simulation runs 1 and 2 as determined from all three measures:

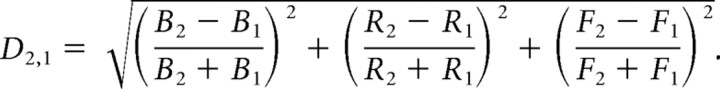D was small if the behavior of runs 1 and 2 was similar and was large between dissimilar runs.

Results

Model cell excitability properties

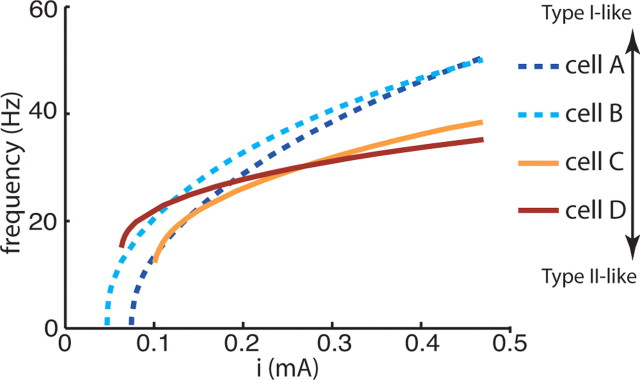
By modulating the activation characteristics of the delayed rectifier K⁺ current and the maximal conductances of the ionic currents, we created four model cells having various membrane excitability properties as described by their f–I curves (Fig. 1). Both cells A and B had characteristic type I membrane excitability properties (Rinzel and Ermentrout, 1998; Izhikevich, 2001). They displayed a continuous f–I curve indicating the appearance of arbitrarily low firing frequencies at firing threshold. Cells C and D exhibited type II excitability with a nonzero, “critical” firing frequency at threshold (Rinzel and Ermentrout, 1998). Another distinguishing characteristic of type I and II excitability is the slope of the f–I curve at high applied current: uniformity of firing frequency at high input currents is typical of type II cells. Thus, cell B, whose f–I curve at high current tended toward a shallower slope, was less type I-like than cell A, which had a steeper f–I slope typical of type I excitability. However, cell C had a lower critical firing frequency at threshold than cell D and displayed a steeper f–I slope, reminiscent of type I excitability. Thus, with these four cells types, we were able to explore network effects resulting from a transition in neuronal excitability from type I to type II behavior. Model parameter values that were varied to create the four cell types are listed in Table 1.

Figure 1.

Frequency–current (f–I) curves of the four model neurons computed by injecting sustained currents of varying amplitudes (x-axis) into the soma compartment. Neuronal excitabilities transition from type I-like (cells A and B), to type II-like (C and D). Both cells A and B were characteristically type I with a continuous f–I curve at firing threshold corresponding to arbitrarily low firing frequencies. Cell A frequency increased steadily at high input currents, whereas cell B frequencies were more uniform (typical of type II dynamics). Cells C and D were type II-like with a high, “critical” frequency at firing threshold. Cell C had a lower critical frequency and a steeper f–I slope at high input currents than cell D.

Table 1.

Model cell parameters altered to construct four cell types

	Vhalf K+dr (mV)	gKdr (S/cm2)	gNa (S/cm2)	gKa (S/cm2)	gh (mS/cm2)	EK (mV)	ENa (mV)	Eh (mV)
Cell A	13	0.2	0.3	0.048	0.5	−90	55	−30
Cell B	13	0.5	0.5	0.048	0.1	−77	50	0
Cell C	0	0.08	0.3	0.048	0.75	−90	55	−30
Cell D	0	0.7	1.5	0.03	0.5	−77	50	0

Changes in the steady-state, half-activation of the K_dr current (V_half K⁺_dr) eliminated low-frequency firing at threshold for type II-like cells. Changes in maximal conductances of Na⁺ (g_Na) and K⁺-dr (g_Kdr) currents promoted spiking. Changes in maximal conductances of K⁺ A-type (g_Ka), and h (g_h) currents modulated resting membrane potential and rheobase current.

Phase response curve analysis

For periodically firing neurons, phase response curves (PRCs) describe how small, brief inputs given at different phases of the periodic cycle affect the timing of subsequent spikes (see supplemental material, available at www.jneurosci.org). It has been suggested that PRCs may help to elucidate the mechanisms by which some cells tend to synchronize when coupled, whereas others tend toward antisynchrony (Hansel et al., 1995; Ermentrout, 1996; Izhikevich, 1999; Ermentrout et al., 2001). To obtain the phase response curves for our model cells, we elicited a fixed background firing frequency by injecting an appropriate applied current (as determined by the f–I curve of the cell). We then injected small, EPSP-like inputs at different times between periodically occurring spikes. Figure 2 shows the PRCs for all cell models with background firing at 40 Hz. The EPSP-like stimulus was a current pulse with amplitude of 0.21 nA/cm² and duration of 2 ms.

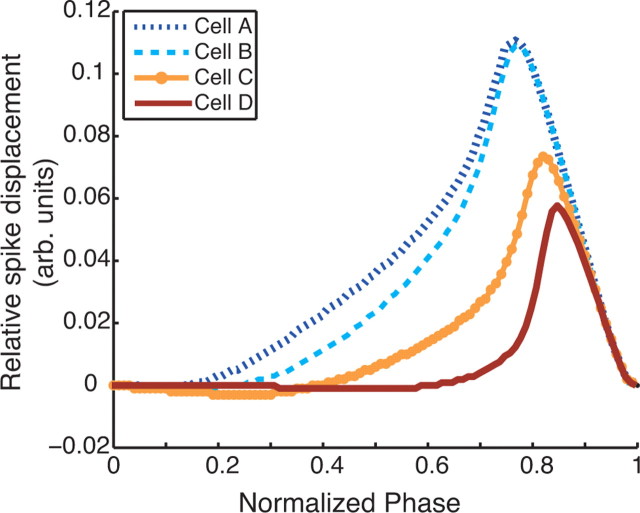
Figure 2.

Phase response curves of model cells. Positive (negative) displacement indicates an advance (delay) of the subsequent spike. Note increasingly greater shift in spike advance to later in period from cell A to cell D. Also, note the expected negative region (spike delay) early in the period for both type II cells C and D.

There was an obvious shift in the shape of the PRC as cells transitioned from type I-like to type II-like. Type I-like cells A and B had positive PRCs and displayed an advance in spike firing earlier in the period than both type II-like cells C and D. Both cells C and D showed a negative, spike-delaying region early in the period, with a positive spike-advancing peak highly skewed to the right. These distinctions are in fact consistent with the responses of classic type I and type II dynamics: cells with a firing threshold described by a saddle-node on a circle bifurcation (type I) (see supplemental material, available at www.jneurosci.org) have strictly non-negative phase response curves (Reyes and Fetz, 1993), whereas those described by a subcritical Hopf bifurcation (type II) (see supplemental material, available at www.jneurosci.org) have a negative region in their phase response curves (Brown et al., 2004).

Analysis of coupled pairs of oscillating type I and type II neurons has determined the properties of their PRCs that contribute to the firing patterns in such two-cell networks. In particular, when coupled with excitatory synapses, the spike-delaying, negative region early in the cycle together with the spike-advancing, positive peak late in the cycle of the type II PRCs promote synchronization of these cells (Hansel et al., 1995). However, the strictly spike-advancing, positive PRCs of type I cells do not promote synchronization in pairs of neurons coupled with excitatory synapses (Ermentrout, 1996; Izhikevich, 1999). For our results, these theories are not directly applicable because we consider much larger networks in which cells are not in an intrinsically oscillatory state. Nevertheless, the propensities for desynchronization or synchronization of type I and type II neurons, respectively, suggest how intrinsic neuronal properties contribute to network spatiotemporal patterning.

Homogeneous networks

First, we explored the effects of neuron excitability and network topology on activity patterns in homogenous networks composed of only one cell type. In homogeneous networks, cellular membrane excitability was found to have a significant impact on the spatiotemporal patterning observed for a given network connectivity radius and wiring topology (Fig. 3). Figure 3A–C shows the phase plot of our three measures [frequency (A), degree of synchronous bursting (B), and mean phase coherence (C)] computed for networks with topologies characterized by rewiring parameter p values between 0 and 100% (horizontal axis) and radius of connectivity r values between 0 and 16 (vertical axis) in which the color denotes the values of the different measures. Based on these measures, we created summary plots describing network activity patterns in different regions of p–r parameter space (Fig. 3D). For very low connectivity radius r levels, networks of each cell type exhibited propagating chains of activity (network raster plots for each network type shown in first row below summary plots). The low number of connections supported propagation of these activity chains because termination occurred when two chains propagating from opposite directions met. However, as connectivity radius r levels were increased, network responses varied dramatically for the four cell types. Networks of type II-like cells (cells C and D) displayed synchronous bursting for most values of connectivity radius and rewiring suggesting that subtleties of network topology are not reflected in activity patterns. Networks of type I-like cells (cells A and B), however, display different high-frequency activity patterns before the constraints of high connectivity r and rewiring p force synchronous bursting behaviors. For cell A and B networks, these high-frequency activity patterns took two forms: high-frequency, temporally locked, wave-like propagation that we called repetitive chain activity, or random asynchronous firing. The propagating activity chains seen for low r values transitioned to the higher frequency repetitive chains with the increase in the number of connections in the network. In this topology, one chain was able to initiate multiple chains of activity farther out in the network and back connections allowed a higher frequency of initiation. But as the rewiring parameter p was increased, disrupting the local coupling between cells, such chain activity could no longer be supported and activity dissolved into high-frequency, asynchronous patterning. For the highest values of r and p, the effective path length in the network was sufficiently decreased to force synchronous bursting activity.

The conditions that lead to synchronous bursting in these homogeneous networks highlight the interaction of intrinsic cell properties and network topology. Generally, our excitatory network with high connectivity radius levels and a random wiring pattern will promote synchronization. However, depending on the intrinsic propensity of the cell for synchronization, a variety of different network activity patterns are possible. In cell A networks, the intrinsic cell properties resisting synchronization are dominant for a wide range of network topologies. Network structure forces synchronization only when the connectivity radius is very high, random rewiring is abundant, and the effective path length in the network is short. In the cell D networks, however, intrinsic cell properties as well as network structure tend toward synchronization. It is only when the network topology is restricted to low radius of connectivity or low rewiring and the effective pathlength in the network is too long to support synchronization that the network does not fall into this activity pattern. The introduction of only a few random connections is sufficient to permit synchronous bursting. In this case, network topology plays only a minimal role in the spatiotemporal patterning.

Effect of synaptic weight and network size

Spatiotemporal activity in our excitatory network will clearly depend on the overall synaptic input individual cells receive, which, in turn, is a function of the magnitude of the synaptic weight as well as the number of cells in the network for a given connectivity percentage. We found, however, that the activity patterns (i.e., formation of propagating chains, asynchronous reverberatory activity, or synchronous bursts) obtained in the different homogeneous networks were overall robust to changes in synaptic weight and network size. In particular, we investigated the effect of network connectivity and synaptic weight on spatiotemporal pattern formation in the four homogeneous networks of 250 cells for a fixed network rewiring (p = 0.2) (Fig. 4). We have chosen this particular value of p as the network exhibited the most dramatic differences in its dynamics for different cell types. The x-axis on the color plot represents changing values of synaptic strength, whereas the y-axis represents the value of connectivity radius (i.e., connectivity fraction) (see Materials and Methods). In the three top rows, the color denotes the values of the measures used (frequency, bursting, mean phase coherence). Activity patterning was consistent across the range of synaptic weights compared with network behaviors shown in Figure 3A–C, across networks having different cell types (Fig. 4A–C, columns). The black arrow indicates the value of the synaptic strength used in the previous set of the simulations. This consistency, evidenced by uniform values for each of our measures horizontally across each panel in Figure 4A–C, was true across most values of the synaptic weights and connectivities. The discrepancies observed at the lowest synaptic weights and low connectivity radius values are attributable to the fact that the network dynamics could not be supported (i.e., network was inactive) for these values and are driven only by the external noise. To further emphasize parameter regions in which differences in activity patterns were obtained, we plot the parametric distance D based on our three measures of network behavior compared with the behavior when the synaptic weight was at the default level (Fig. 4D). As we mentioned above for all four cell types, largest differences in network behaviors occurred for low synaptic weight and low connectivity radius values (top left corner of each panel) because of much lower network activity in these parameter regions compared with default synaptic weight. In each panel, there is also a band of relatively higher distance values that occurs at progressively lower values of connectivity radius r with the transition from cell type A to D. This band reflects the variability of network patterning in these parameter regions in which network behavior transitioned to bursting, as summarized in Figure 3D. For example, with rewiring p = 0.2 (20%), cell A networks transitioned to bursting only near the highest connectivity radius r values, cell B networks transitioned near r = 10, whereas cell C networks transitioned near r = 5 and cell D networks transitioned at the lowest values of r. We note that the difference occurs even at the default synaptic weight value (indicated by the arrow in each panel), reflecting the variability in network patterning with each random instantiation of the network in these parameter regions.

We also found that network size did not affect the basic differences in activity patterns in homogeneous networks composed of the four different cell types (Fig. 5). We simulated networks consisting of 500, 1000, and 2500 cells, and compared network activity using our measures of frequency, bursting, and phase coherence when the connectivity fraction in each network was 4%, the synaptic weight was at the default value of 0.7 mS/cm², and the rewiring parameter p was set to conserve mean pathlength (which depends on p and the number of connections per element) in each network (Newman, 2003). Increasing network size did not qualitatively alter the differences in network patterning with cell type. In the 250 cell networks, type I networks (cell types A and B) displayed high-frequency asynchronous firing characterized by low values of B and R at these parameter values, whereas type II networks (cell types C and D) were synchronously bursting at lower frequencies but with higher values for B and R. As network size increased, frequency and phase coherence of the asynchronous activity in the type I networks increased, but bursting remained low, indicating a consistency of activity patterning.

Because in a larger network, synaptic weights can vary over a larger range for a fixed connectivity, and still maintain network activity, we investigated spatiotemporal patterning for the network with 2500 cells for synaptic weights down to an order of magnitude smaller than the values used in other simulations. We found that the differences in activity patterns in networks of different cell types were maintained across the range of synaptic weights (Fig. 6). In this set of simulations, the connectivity fraction was fixed at 4% and rewiring p = 0.2. As synaptic weight was decreased, type I networks (cell types A and B) maintained high-frequency asynchronous patterning characterized by high average frequency and low B, whereas type II networks (cell types C and D) continued to burst synchronously as indicated by the low values of average frequency and high B. At the lowest synaptic weight values, scaling of frequency of type I networks and of bursting B of type II networks can be observed. This represents completely different responses of networks having different cell types to the increased input. The type I cell network modulated its frequency response maintaining nonbursting type of the dynamics, whereas in type II cell network one can observe increased burst synchrony without an apparent change in frequency. For simplicity, we did not include the values of phase coherence (R) for these results because the frequency and bursting measures better reflected spatiotemporal dynamics in these cases.

Effect of synaptic noise

Synaptic noise was included in our networks to maintain a low level of random background activity. Our results on the differences in network activity patterns with cell type were not affected by different frequencies of this background synaptic noise (Fig. 7). We simulated 250 cell homogeneous networks of each cell type with rewiring parameter p = 0.2, synaptic weight set to 0.7 mS/cm², and varied the frequency of the random synaptic input (x-axis) each cell received from our default value of 1 Hz (indicated by the arrow in each panel) up to 4 Hz. For each network type, activity patterns were consistent across noise frequencies for values of connectivity radius r between 0 and 16 (y-axis) as evidenced by the horizontal uniformity in the values of our measures in each panel of Figure 7A–C as shown by the color. Differences in activity patterns arising from different noise frequencies are highlighted in Figure 7D, in which the parametric distance between networks with the default noise frequency are plotted. For cell type A networks, a high distance value occurs for the lowest connectivity radius r and noise frequency values (top left-hand corner) because of the overall low activity level in these networks. As in Figure 4, horizontal bands of higher distance values occur for networks of each cell type at the connectivity radius r values, in which the networks transition to bursting, reflecting the variability of network patterning in this transition region.

Heterogeneous networks

To further understand the interaction between intrinsic neuronal properties and network topology, we investigated activity patterning in heterogeneous networks, composed of varying ratios of type I and type II cells. Beginning with a homogeneous type I (cell A) network, we randomly switched a fraction of the neurons to type II (cell D). The results of these simulations are presented in Figure 8. Figure 8, A and B, show the parametric distance D_i,cellA (A) and D_i,cellD (B) of the behavior of a simulated heterogeneous network i to the behavior of a homogenous network composed solely of cell types A and D, respectively. For example, a low value of D_i,cellA reflects high similarity between the activity pattern in the heterogeneous network and that in a homogeneous network composed of only cell type A (type I), whereas a low value of D_i,cellD reflects high similarity with a homogeneous network composed of only cell type D (type II). The vertical axis denotes the radius of connectivity r of the network, whereas the horizontal axis denotes the percentage of type I cells in the mixture ratio, varying from 0% type I cells (100% type II cells) to 100% type I cells (0% type II cells). Thus, the rightmost columns of all panels in Figure 8A have low distance values, whereas the leftmost columns of all panels in Figure 8B have low distance values. The networks are simulated for four values of the rewiring parameter p = 0.2, 0.4, 0.6, 0.8. Each data point represents the average over 10 simulation runs, each run with a different instantiation of network wiring topology. Figure 8C, however, displays the minimum of the two distances plotted in Figure 8, A and B, to focus on the parameter regions in which qualitatively new behavior of the heterogeneous network emerges (i.e., behaviors not similar to either of the homogenous networks for given network topology).

We found that small changes in cell type composition could have an immense effect on spatiotemporal patterning observed in the network. We observed two basic patterns of emergent behavior: (1) one of the cell types dominated the behavior of the network even for mixture ratios of a few percentage, or (2) activity patterns switched between different behaviors characteristic of the homogeneous networks. Figure 8, D and E, depicts examples of those two behaviors, respectively. Replacing as few as 10% of type I cells with type II cells invoked synchronous bursting even in regions of r–p parameter space in which the homogenous network of type I cells did not burst. Such an example is shown in Figure 8D (Fig. 8C, arrow; same point in Fig. 8A,B) in which the left panels show asynchronous activity in the homogeneous type I network and synchronous bursting in the homogeneous type II network for network topology of the same r and p values. But in the heterogeneous network of 90:10 type I–type II mixture ratio, those 10% of type II cells lead firing and dictate synchronous bursting (see inset). This dominance of type II activity in heterogeneous networks is apparent in the low values of D_i,cellD in a large region of r–p parameter space (Fig. 8B). As suggested by the homogeneous network results, all networks converge to synchronous bursting activity at high radius of connectivity r and high rewiring p, as evident by a drop in D_i,cellA at high p values.

Only when the percentage of type I cells is close to 100 and connectivity radius r values are low does activity vary from type II-dominated behavior. In this parameter region, networks displayed unreliable, alternating switching between activity patterns characteristic of homogeneous type I networks and homogeneous type II networks. This switching is reflected in the larger values of the minimum distance in Figure 8C. An example of pattern switching is shown in Figure 8E (Fig. 8C, arrow; same point in Fig. 8A,B) in which repetitive chain activity, characteristic of type I networks, transitions to synchronous bursting, which is a more predominant behavior in type II networks. It is interesting to note that type I cells lead firing during the repetitive chains, but type II cells lead firing that results in a synchronous burst (see insets). Generally, switching between behaviors occurred on a variety of timescales, but faster timescale switching (on the order of hundreds of milliseconds) tended to be more periodic.

Excitatory and inhibitory networks

In this study, we concentrate on exclusively excitatory networks as a first step in understanding the interaction of intrinsic cell properties and network topology in generating spatiotemporal network patterning. However, in hippocampal-type networks that we aim to simulate, inhibitory interneurons are integrated throughout the network and contribute to network activity, both under normal and pathological conditions. Here, we investigate whether the addition of inhibitory interneurons alters our basic observation that membrane excitability differentially affects spatiotemporal patterning in networks with different structural properties. We coupled 250 cell excitatory networks to separate 250 cell inhibitory networks with a fixed topology and homogeneous cell population (composed of cell type A; intranetwork rewiring parameter, p = 0.2; intranetwork inhibitory synaptic weight, 0.5 mS/cm²). For simplicity of computation, every inhibitory cell was paired with an excitatory cell such that the distance between these two cells was considered to be zero. This pairing allowed us to easily compute the distances between inhibitory and excitatory cells to achieve appropriate connectivity. The intranetwork radius of connectivity for the inhibitory network was set to be always the same as that of the excitatory one. The inhibitory network made inhibitory synaptic connections onto cells in the excitatory network with the same parameters as its intranetwork topology (i.e., the same number of connections and their distribution). At the same time, the excitatory network made excitatory synaptic connections to cells in the inhibitory network with the equivalent topology of its intranetwork excitatory connections.

Figure 9 shows our three measures of frequency, bursting, and phase coherence of the excitatory network activity patterns in a homogeneous type I network (left column; cell type A) and type II network (right column; cell type D) as connectivity radius r and rewiring parameter p are varied in the excitatory network. These results indicate that, although the actual pattern observed in the excitatory–inhibitory network differed from that of an exclusively excitatory network, the underlying observation was the same. Namely, the excitatory–inhibitory networks with type D excitatory cells showed significantly higher capacity to synchronize and burst than the corresponding networks with type A excitatory cells.

Major differences in the patterning compared with solely excitatory networks include lower spiking frequencies and a shift of the parameter regions for which synchronous bursting occurs to higher r and p values. Also, note that overall levels of the measures for bursting and phase synchrony were decreased compared with levels measured in exclusively excitatory networks (Fig. 3).

Discussion

We explored how neuronal membrane properties interact with network topology to affect spatiotemporal pattern formation in a network. Until now, most of the work exploring the dynamical properties of networks has studied these effects separately. These studies centered around molecular or cellular mechanisms underlying single-cell responses (Steinlein and Noebels, 2000) or topological network properties in which network elements have extremely reduced dynamics (Netoff et al., 2004; Percha et al., 2005; Boccaletti et al., 2006). A notable exception is the recent work focusing on studying epileptogenic cellular and topological changes in a large-scale network model of the dentate gyrus containing biologically realistic cell types and network structure (Santhakumar et al., 2005; Dyhrfjeld-Johnsen et al., 2007; Morgan and Soltesz, 2008).

We have shown how the intrinsic properties of membrane excitability contribute to the behavior of the network for different network topologies. Our results are persistent across different network sizes, connectivity strengths, and magnitudes of random external input, making them highly likely to be relevant to brain function. At the same time, our results are predominantly applicable to local networks that do not have significant axonal transmission delays, because our simulations do not incorporate existence and variability of such delays over large distances.

Although our studies focused mainly on excitatory networks, the spatiotemporal patterns we found under different network conditions will be indicative of behaviors in more general networks, especially when excitatory interactions are prominent. This is further supported by the fact that, when we added inhibitory neurons into our model, we still saw higher synchronization and bursting capacity for the networks with type D excitatory cells in the corresponding networks with type A excitatory neurons. However, inhibitory interneuron networks can also exhibit complex spatiotemporal patterning by themselves and, for example, can lead to network synchronization (Kopell and Ermentrout, 2004; Bathellier et al., 2006; Klaassen et al., 2006). Thus, more sophisticated models will be necessary to elucidate the relative contributions of cellular and network properties to recurrent excitation and inhibitory drive.

In our results, we observed that, with a change in membrane excitability toward type II behavior, network dynamics transition from a three-phase behavior to a two-phase behavior, effectively abolishing the high-frequency, asynchronous state. This high activation, asynchronous state can be linked to the occurrence of “on” states of persistent cortical activity (Tahvildari et al., 2007, 2008; Galloway et al., 2008). It is generally assumed that such enhanced spiking activity in the form of persistent reverberation for several seconds is the neural correlate of working memory (Funahashi et al., 1989; Fuster, 1990; Goldman-Rakic, 1995; Mongillo et al., 2008). Our results indicate that local network mechanisms in the form of the introduction of a minimal number of random connections or of cells with type II-like membrane properties can abolish this state in favor of synchronous bursting. Additionally, in our heterogeneous networks, activity spontaneously switched from more asynchronous patterns to synchronous bursting depending on the specific cells that initiated the firing episode.

Our simulation results also show that the extent of the effects of network topology varies with the properties of the network elements, suggesting that a single ictogenic mechanism alone may not be responsible for seizure generation. Conversely, we show that a combination of network and cellular mechanisms leads more robustly to synchronous discharges in our model. This could indicate that changes in a single (cellular or network) parameter would have to be pretty large in the context of known anatomical and physiological data to induce seizure-like activity. However, a combination of smaller changes in both network and cellular properties may lead to dramatic dynamical changes in network activity patterns. This idea is further underscored by our finding that adding even a small percentage of cells with certain characteristics to create a heterogeneous network markedly changes the patterning of network activity.

Specifically, our heterogeneous networks show emergent behavior, even for very small mixture ratios of type I and type II cells, suggesting the possible importance of the identity and/or location of pathologically modified cells in epileptogenesis. As in the brain, the combination of small world and, possibly, scale free network topologies (see supplemental material, available at www.jneurosci.org) supports the formation of local cellular hubs (cells or local cell communities with large numbers of incoming and outgoing connections). Recent modeling results in large-scale realistic models of the dentate gyrus suggest that pathological changes in those hubs alone may lead to seizure-like network dynamics (Morgan and Soltesz, 2008). Moreover, our results indicate that the mixture ratio can be effectively smaller for more global network topologies to obtain the observed transitions. This further underscores the potential importance of combined network and cellular mechanisms underlying formation of synchronous discharges.

Together, these results point to extremely complex interactions between cellular and molecular properties, as well as network properties underlying spatiotemporal patterning observed, for example, during the transition from bursting to seizure-like discharges. This further indicates that insight into the synergy of these very different scales may be crucial in understanding function in the healthy and pathological brain.