Solvation effect on conformations of 1,2:Dimethoxyethane: Charge dependent nonlinear response in implicit solvent models

Abstract

We provide an improvement in the Langevin-Debye model currently being used in some implicit solvent models for computer simulations of solvation free energies of small organic molecules, as well as of biomolecular folding and binding. The analysis is based on the implementation of a charge-dependent Langevin-Debye (qLD) model that is modified by subsequent corrections due to Onsager and Kirkwood. The physical content of the model is elucidated by discussing the general treatment within the LD model of the self-energy of a charge submerged in a dielectric medium for three different limiting conditions and by considering the nonlinear response of the medium. The modified qLD model is used to refine an implicit solvent model (previously applied to protein dynamics). The predictions of the modified implicit solvent model are compared with those from explicit solvent molecular dynamics simulations for the equilibrium conformational populations of 1,2-dimethoxyethane (DME), which is the shortest ether molecule to reproduce the local conformational properties of PEO, a polymer with tremendous technological importance and a wide variety of applications. Because the conformational population preferences of DME change dramatically upon solvation, DME provides a good test case to validate our modified qLD model.

I. Introduction

The solvation of molecular systems is of primary importance in determining the physical, chemical and biological properties of the solute. Two principal approaches exist for modeling solvation. The first method represents the solvent molecules explicitly in full atomistic detail, but this approach is computationally very expensive.¹ The second approach treats the solvent as a continuum and is termed an implicit solvent model.^2,3 By greatly reducing the number of degrees of freedom, implicit solvent models offer the promise of a cheap and efficient way to model solvation, provided the physics is properly described. Implicit solvent models require several essential components, each of which contributes to determining the success and limitations of these models.⁴ Although continuum models are seldom perfect, it is possible to diminish the errors sufficiently to make them quite useful for studying the dynamics and structure of proteins, nucleic acids, and docking.^5–8 Cramer and Truhlar review the wide use of different types of implicit solvent models for describing equilibrium solvation, spectra (electronic and vibration), nonequilibrium solvation, and for treating systems in inhomogeneous media.⁴ It must also be noted that many explicit solvent models are themselves imperfect in, for instance, not including the solvent electronic polarization which further augments the computational cost. In both the explicit and implicit approaches, however, the solute charge distribution and its response to the reaction field of the solvent can be modeled either by assigning partial atomic charges in molecular dynamics descriptions or by using quantum mechanical calculations.

Many continuum models focus heavily on modeling the dielectric response of the continuum solvent. The core features of these electrostatic models have been developed by Debye, Born, Onsager, and Kirkwood in the early part of the last century.^9–12 Most dielectric models treat the solvent as a continuous, homogeneous, isotropic medium characterized by a scalar, static dielectric constant ε as follows: Consider, for simplicity, a charged, spherical solute with radius a embedded in a volume of a dielectric medium with a bulk dielectric constant ε. Then, for any point at a distance r > a in the solvent, the dielectric constant is set to the bulk value. There is ambiguity associated with the physical meaning of the radius a, i.e., in the interpretation of the boundary between the solute and the bulk solvent. The common use of a sharp boundary, separating regions with a bulk dielectric constant from those with the solute’s value, is clearly a gross oversimplification since the solvent molecules in the vicinity of the solute respond to the external field of the solute to a different degree than those more distant in the bulk. One approach to overcoming this simplification is to choose an “appropriate” value for a, which is interpreted as an “effective” atomic radius that differs from actual atomic radii close to 76% on average for cations.^13,14 The use of an effective radius in some ways compensates for the failure of the continuum models to provide a satisfactory description of the first solvation shell. Additionally, this simple dielectric model assumes a linear response of the solvent to any applied external field, corresponding to the solution of Poisson’s equation for the system. However, the model fails to capture accurately the interactions of the solute with those solvent molecules lying in the region close to the solute where the solvent has properties that differ from those of the bulk. In this proximal region which also includes the first solvation shell, the assumption of linear response to the ion’s electric field may break down.¹¹ Consequently, the continuum model typically overestimates the dielectric response in regions close to the solute where the local electric field may be very strong. Additional issues related to the interactions associated with the first solvation shell include the representation of their dispersion interactions, hydrogen bonding, hydrophobic effects, role in charge transfer, and solvent Lewis acidity or basicity.⁴

Cramer and Truhlar review the many different methods employed to evaluate the contributions to the free energy associated with the inner solvation shells that may be poorly represented by the continuum models. Some implicit solvent models attempt to approximate the inner solvation effects by computing the electrostatic interactions using a linear or quadratic model for the distance dependent dielectric “constant”.^2,15 Warshel introduces derivations of a distance dependent dielectric function for surface charges but cautions against its usage for buried charges.¹⁶ While the dielectric continuum methods may achieve varying degree of success, these ad hoc approximations are quite severe and fail to address the main reasons (beyond the use of linear response mentioned above) behind the failure of continuum model to capture the influence of interactions with proximal solvent molecules that behave differently from those in the bulk. Therefore, a better treatment of the solvation shell is essential to the development of improved continuum solvent models.

Improved models clearly must relax simplifying approximations concerning the surrounding medium. Due to strong electric fields in proximity to charged solute atoms, the solvent polarization becomes saturated, and the proximal solvent dipoles no longer respond linearly to the applied field. This nonlinear effect is well described by the Langevin-Debye (LD) model which introduces the concept of dielectric saturation.¹¹ Dielectric saturation is more generally related to the notion of a microscopic permittivity field whose value at any point in space is a local effective dielectric constant that differs from the bulk dielectric constant near the solute. Based on the LD theory of ionic saturation, Hingerty et al. have proposed a sigmoidal form of distance dependent dielectric constant to study binding and conformational changes in nucleic acids upon metal binding.¹⁷ Ramstein and Lavery (RL) have reformulated the function presented by Hingerty et al. with an analytical fit that depends on two parameters, the dielectric constant of the bulk and the slope of the sigmoidal portion of the dielectric constant function in their study of the distortion of nucleic acids.¹⁸ Subsequently, fits to the model by RL have been applied successfully to simulations for protein systems.^5,8 However, the LD equation has been derived for unit charges as present in nucleic acids and a few amino acids under certain conditions. However, most constituent atoms of DNA, protein, polymer, etc., carry partial charges assigned,¹⁹ and it is unclear whether the present LD equations are suitable.

In this work, we present, analyze, and implement improved versions of the Langevin-Debye (LD) model that is modified to describe the nonlinear solvent response as a function of the magnitude of the charge. We begin with a description of the Langevin-Debye (LD) theory of ionic saturation in section II, while section III discusses the corrections to the model as proposed by Onsager and Kirkwood. Several commonly used dielectric models are compared with the resultant modified Langevin-Debye model in Section IV. The charge-dependent version of the Langevin-Debye (qLD) model is presented in Section V, followed by a treatment that includes the corrections due to Onsager (qLD+O) and Kirkwood (qLD+OK). In Section VI, the physical content of the qLD model is elucidated by considering the self-energy of a charge submerged in a nonlinear dielectric medium for three different limiting conditions: (i) solids where the dipoles are unable to orient, (ii) systems where dipoles can reorient but only with a linear response, and (iii) the general situation where the dipoles can reorient and the response is nonlinear. The general qLD model yields the usual Born self-energy¹² along with an additional term which originates from the nonlinear response of the solvent to the external applied field. In Section VII we describe the performance and implementation of the qLD, qLD+O and qLD+OK models when they are introduced into the Shen-Freed implicit solvent model.⁵ The predictions of this model are compared with explicit solvent simulations for the equilibrium conformational populations of 1,2-dimethoxyethan (DME), which is the shortest ether molecule to reproduce the local conformational properties of polyethylene oxide (PEO).²⁰ Because the conformational population preferences of DME change dramatically upon solvation,²⁰ DME provides an excellent system for validating the modified LD (qLD) model. Finally, Section VIII discusses the features of qLD and their relation to other commonly used continuum dielectric models in implicit solvent simulations.

II. Langevin-Debye theory of ionic saturation

Ionic saturation theory is discussed at length Debye’s book Polar Molecules,¹¹ so we only briefly summarize the necessary equations using the same notation as Debye. The model contains an ion that is placed in an infinite medium (so that boundary effects can be ignored) of a continuous distribution of point molecules, each with an electric polarizability α₀ and an electric dipole moment μ. These surrounding solvent molecules can be polarized in two ways: (a) their charge distribution distorts in presence of an external field due to the solute, and (b) the applied field tends to align the randomly oriented permanent dipole moments. The first effect produces an induced dipole moment in each molecule, the magnitude of which depends linearly on the electric polarizability α₀ and on the applied field (Fig. 1). A thermal average is performed over the random distribution of dipoles at each point in order to determine the net effect of alignment of these induced dipoles in presence of a charged solute.

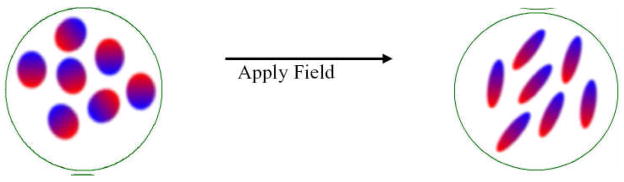
Figure 1.

Two dimensional cartoon representation of fictive mathematical device called “Lorentz sphere”.

The Langevin-Debye model assumes the “Lorentz sphere” to be homogeneous and isotropic. This assumption implicitly implies that the electric field from the dipoles vanishes inside the Lorentz sphere. The volume of the sphere, represented in the figure by the circle, is large compared to the solvent molecule size. The ovals in the circle represent the polar solvent molecules that can be polarized in two ways, (a) due to the distortion of the charge distribution of the molecules in presence of an external field and (b) from the alignment by the applied field of the randomly oriented permanent dipole moment of the molecules. These effects are represented by elongation and alignment, respectively.

Consider a small volume element of the solvent situated at a distance r from the position of the ion with unit charge e, such that the volume element is large compared the dimensions of solvent molecules but small macroscopically. These microscopic, isotropic, homogeneous volume elements are called “Lorentz spheres”(Fig 1).²¹ We now compute the dielectric constant of this volume element in the presence of the electric field of the unit charge e at the origin. The analysis of Debye produces two coupled equations for the electric displacement D, electric field E, local field F, and polarization P,

$$\mathbf{D}=\mathbf{E}+4\pi \mathbf{P}$$ (1)

$$\mathbf{F}=\mathbf{E}+\frac{4\pi }{3}\mathbf{P},$$ (2)

where implicit in the definition of F is the assumption that no dipole-dipole interactions are present inside the “Lorentz sphere”. It now remains to compute the polarization P.

The volume element under consideration responds to the local field F by acquiring the electric moment m,

$$\mathbf{m}={\alpha }_0\mathbf{F}+\mu L(\beta \mu \text{F})\widehat{\mathbf{F}},$$ (3)

where β is 1/kT, k is Boltzmann’s constant, T is the absolute temperature, μ is the magnitude of the electric dipole moment of the solvent molecules, and F̂ is a unit vector in the direction of the local field F. The function L appearing in the above equation is the Langevin function L(x) = coth(x) − 1/x and arises from the thermal average over all orientations of the dipole moment. The first term on the right hand side of Eq. (3) is the induced dipole due to the local field F and is proportional to the electronic polarizability α₀, while the second term corresponds to the average electric moment in the direction of the local electric field and arises from the average orientation of the dipoles in response to the local electric field. The polarization of the volume element under consideration, thus, emerges as,

$$\mathbf{P}=\text{n}\mathbf{m}=\text{n}({\alpha }_0\mathbf{F}+\mu L(\beta \mu \text{F})\widehat{\mathbf{F}}),$$ (4)

where n is the number density of solvent molecules. Equation (4) implies that P and F are parallel, which, in turn, implies from Eq. (1) and (2) that D, E and F are collinear. Thus, Eqs. (1)–(4) reduce to scalar equations. Using Eq. (4) enables elimination of P from Eqs. (1) and (2) to yield

$$\text{D}-\text{F}=\frac{8\pi }{3}[\text{n}{\alpha }_0\text{F}+\text{n}\mu L(\beta \mu \text{F})]$$ (5)

$$\text{and F}-\text{E}=\frac{4\pi }{3}[\text{n}{\alpha }_0\text{F}+\text{n}\mu L(\beta \mu \text{F})].$$ (6)

The determination of the dielectric constant in a volume element at a distance r from the ion requires knowledge of the ratio of D and E, which is obtained by eliminating the local field F between Eqs. (5) and (6). Upon specifying a particular value for F as a parameter, Eqs (5) and (6) may be solved to produce the corresponding values of D and E for the given F. The computed values of D and E are then assigned to spatial coordinates by using the solution to Maxwell’s equations to express the dielectric displacement at a radial distance r from the location of the unit charge e as,

$$\text{D}=\frac{e}{r^2}.$$ (7)

After eliminating F using Eqs. (5) through (7), we tabulate values of r and the corresponding values of D(r) and E(r) for a central ion with unit charge and thereby compute D/E or the dielectric constant as a function of distance. Debye distinguishes between a radial and tangential dielectric constant, depending upon whether the polarization and dielectric displacements are along the radial line or perpendicular to it. Calculations demonstrate that both are very similar. Hence, we restrict attention to the tangential dielectric constant, i.e., small displacements at constant r, and the radial permittivity function is not presented.

Before determining the dielectric constant ε(r) from the ratio of D(r) and E(r), the molecular parameters, α₀, and μ, the isotropic electrical polarazibility and the dipole moment, respectively, in the equations are expressed in terms of the bulk optical ε_∞ and static ε₀ dielectric constants. These transformations of α₀ and μ can be accomplished by invoking the following assumptions that are consistent with the Langevin-Debye model. First of all, the Lorenz-Lorentz equation gives the relation,^11,22

$${\alpha }_0=\frac{3n}{4\pi }\left(\frac{{\epsilon }_{\infty }-1}{{\epsilon }_{\infty }+2}\right).$$ (8)

In the low field limit, the local field F can be eliminated by taking the ratio of Eqs. (1) and (2) to yield,

$$\frac{\text{D}}{\text{E}}=\frac{1+\frac{8\pi }{3}n\left[{\alpha }_0+\beta \frac{{\mu }^2}{3}\right]}{1-\frac{4\pi }{3}n\left[{\alpha }_0+\beta \frac{{\mu }^2}{3}\right]}.$$ (9)

When the field is weak, the ratio of D and E can be replaced by the bulk dielectric constant ε₀ of the solvent. In order to express μ in terms of the bulk parameters, Eq. (9) is rearranged to produce,

$${\mu }^2=\frac{27}{4\pi \beta }n\left(\frac{{\epsilon }_0-{\epsilon }_{\infty }}{({\epsilon }_0+2)({\epsilon }_{\infty }+2)}\right).$$ (10)

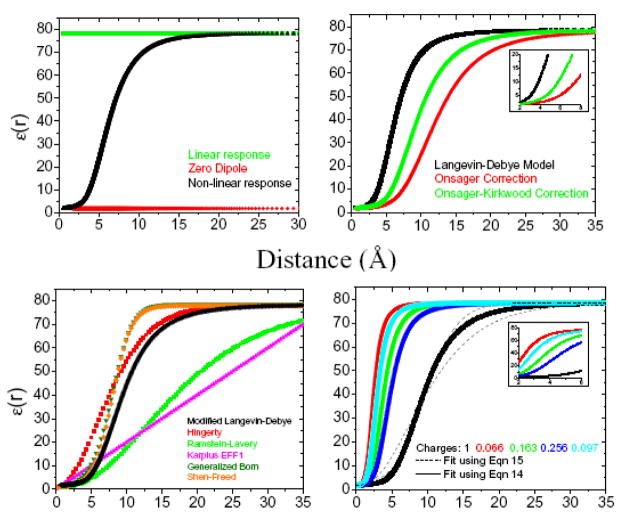
The curves in Fig. 2a therefore depend only on the choice of the bulk optical and static dielectric constants of the solvent and the solvent number density, and the caption to Fig. 2 presents the parameters used in the plots. The behavior of ε(r) is sigmoidal and approaches the bulk dielectric constant ε₀ for large distances r from the ion, while near the charge, i.e., for small r, the dielectric constant ε(r) is much smaller due to the nonlinear response to the field. In the limit of linear response, i.e., where βμF ≪ 1 and the Langevin’s function L(βμF) can be approximated by $\frac{\beta \mu \text{F}}{3}$, ε(r) reduces in the entire medium to a constant that corresponds to the bulk static dielectric constant ε₀ (green points in Fig. 2a). When the solvent dipole moment vanishes, the temperature is high, or the dipoles cannot reorient as in the solid state, ε(r) becomes the high frequency, optical dielectric constant ε_∞ (red points in Fig. 2a).

Figure 2.

(a) Curves are derived from the Langevin-Debye formalism with the input values, n = 3.33*10²² for the number density of molecules per cc (for a molecular weight of 18.0g/mol and a mass density of 0.997g/cc for water), optical dielectric constant, ε₀= 1.77, static dielectric constant; ε_∞ = 78.5; and T = 298K. The black data points correspond to the general solution, whereas the red and green points are obtained for the limiting cases of zero dipole and linear response regime of the solvent, respectively. (b) The radial permittivity following corrections in the LD model due to Onsager (red) and Kirkwood (green). The parameters C_μ = 0.0695 and g = 2.80 are used to give the water dipole moments of $\frac{\mu }{{(g{C}_{\mu })}^{0.5}}=1.85\text{D}$ and $\frac{\mu }{{(C_{\mu })}^{0.5}}=3.11\text{D}$ in the gas phase and liquid phase. The inset is a magnified view of region from 2–8 Å. (c) The different functional forms used to model the distance dependence of the dielectric constant. The parameters used for each functional form are described in the text. (d) The modified Langevin-Debye model calculated for all the four charges for the atoms of DME. We use the fits from Eq. (14) (long dash –––) and Eq. (15) (short dash– – –) and the parameters in Table 1. The curves fit for q=1 are displayed. The inset is a magnified view of regions from 2–6 Å.

III. Correction due to Onsager and Kirkwood

The permanent dipole moments predicted by the LD model for polar species are smaller in the liquid state than those in the gas phase (0.82 D for water from Eq. (8) vs. 1.85 D observed in the gas phase and 3.09 D in the liquid state). Onsager noted that this error in the Langevin-Debye treatment arises from the assumption in the definition Eq. (2) of the local field F that dipole-dipole interactions are neglected.¹⁰ Onsager proposed that only a portion of the field produced by the solute, namely the directing field, contributes to the dipole orientation and, hence, to the Boltzmann averaged orientation polarization in the second term on the right hand side of Eq. (3). Therefore, the directing field is obtained by scaling the local field by a constant correction factor C_μ, such that the correct liquid state dipole moment is obtained, Specializing to water, the computations yield $\frac{\mu }{C_{\mu }}=3.09\text{D}$, which corresponds to the magnitude of liquid state dipole moment for water.^13,23 Using the constant scaling approximation Eqs. (5) and (6) of the Langevin-Debye model are re-expressed as

$$\begin{array}{l}\text{D}-C_{\mu }\text{F}=\frac{8\pi }{3}\left[\text{n}{\alpha }_0{C}_{\mu }\text{F}+\text{n}{C}_{\mu }\mu L\left(\beta \mu F{C}_{\mu }\right)\right]\\ \text{and}{C}_{\mu }\text{F}-\text{E}=\frac{4\pi }{3}\left[\text{n}{\alpha }_0{C}_{\mu }\text{F}+\text{n}{C}_{\mu }\mu L\left(\beta \mu F{C}_{\mu }\right)\right]\\ \text{where}{C}_{\mu }^2=\frac{\left(2{\epsilon }_{\infty }+{\epsilon }_0^2\right)({\epsilon }_{\infty }+2)}{{\epsilon }_{\infty }{({\epsilon }_0+2)}^2}.\end{array}$$ (11)

This approach can be understood as an approximation to the more general reaction field treatment of Onsager. However, the more rigorous reaction field calculation in which C_μ depends on r yields almost identical result, so we restrict attention to the computationally simpler constant C_μ approximation.

The Onsager correction modifies the contribution from long distance correlations between dipoles. The theory has been further generalized and improved for strong polar liquids by Kirkwood and Frohlich by including a Kirkwood correlation factor g to describe the influence of the local solvent density change near the solute.^9,24 We again assume the correction factor C_μ to be constant, for simplicity, because the more general reaction field treatment yields almost identical results.^9,13,25 After incorporating this additional correlation term, we obtain,

$$\begin{array}{l}\text{D}-C_{\mu }\text{F}=\frac{8\pi }{3}\left[\text{n}{\alpha }_0{C}_{\mu }\text{F}+g\text{n}{C}_{\mu }\mu L\left(\frac{\mu \text{F}}{\text{kT}}{C}_{\mu }\right)\right],\\ C_{\mu }\text{F}-\text{E}=\frac{4\pi }{3}\left[\text{n}{\alpha }_0{C}_{\mu }\text{F}+g\text{n}{C}_{\mu }\mu L\left(\frac{\mu \text{F}}{\text{kT}}{C}_{\mu }\right)\right],\end{array}$$ (12)

where g can be calculated in advance or determined from the weak-field limit of the equations using the known bulk dielectric constant to solve for g. The simple limiting case of g=1 reduces the equations to those of Onsager.

The same technique applied above to solve the Langevin-Debye equations for a self-consistent local field F can also be used to obtain the permittivity from the Eq. (11). The three curves in Fig 2b (black, red and green) have been determined for the parameters, g = C_μ =1; C_μ = 0.0695 and g = 1; and C_μ = 0.0695 and g = 2.80, respectively, where C_μ and g have been chosen in the last curve to reproduce the correct dipole moment of water in both the gas phase $\frac{\mu }{{(g{C}_{\mu })}^{0.5}}=1.85\text{D}$ and the liquid phase $\frac{\mu }{{(C_{\mu })}^{0.5}}=3.11\text{D}$. The black curve is derived from the original Langevin-Debye model (Eqs. (5) and (6)), and the red and green curves correspond to the modifications by Onsager and corrections due to Kirkwood to the LD models, respectively. Interestingly, the qualitative behavior of the solvent’s dielectric response is unaltered upon introduction of the corrections due to Onsager (red) and Kirkwood (green). Both modifications maintain a sigmoidal profile, which clearly emerges from the Langevin function. However, all three curves in Fig 2b differ in the steepness or the rate of change of ε with r. Onsager’s correction primarily accounts for the long distance correlations between the dipoles and increases the saturation of proximal solvent molecules, i.e., lowers ε(r) for small r more than the original LD model (red points). The modifications due to Kirkwood include the short range dipole correlations in addition to Onsager’s correction, and the saturation is slightly weakened compared to the case of Onsager’s modification alone. The most significant differences appear at small r, in a region that might be critical to represent the short range solute-solvent interactions more accurately. For example, in the neighborhood of the first solvent shell in aqueous solutions at r ~ 5A, the three models yield widely varying values for the dielectric “constant” of ~23 (LD), ~4 (with Onsager correction) and ~7 (with Onsager-Kirkwood corrections). The inset of Fig 2b exhibits the difference in the permittivity of the solvent for the region corresponding to the first and second solvation shells.

IV. Continuum models and nonlinear response

Several forms of distance dependent dielectric functions have been developed to approximate the effects described by the LD theory. The present section presents comparisons of the Langevin-Debye model, modified due to Onsager and Kirkwood, with other distance dependent dielectric functions that are commonly used in continuum solvent models (Fig. 2c). Generally speaking, two forms of distance dependence are used, (i) linear and (ii) sigmoidal. The sigmoidal functions have two advantages over the linear models. The linear distance-dependent dielectric model (ε = 2r as in the effective energy function 1 (EFF1) model²) does not approach the correct bulk dielectric constant as r approaches infinity in contrast to the sigmoidal dependence. Secondly, the linear model fails to provide a balanced description between long and short range interactions. As mentioned earlier, the short range solvent dielectric response is critical to describe the interactions in the first solvation shells and associated features like hydrogen bonding and the “hydrophobic effect”. The sigmoidal dielectric dependence is a consequence of the nonlinear solvent response and therefore describes the short and long range interactions more faithfully.

The sigmoidal form of Hingerty et al.¹⁷ is given by,

$$\epsilon (r)=78-77{\left(\frac{r}{2.5}\right)}^2\frac{e^{r/2.5}}{{\left(e^{r/2.5}-1\right)}^2},$$ (13)

where the single parameter is set to 2.5 for comparative purposes in Fig. 2c. Hingerty et al. use this function to study binding and conformational changes in nucleic acids upon metal binding. In a subsequent analysis of the distortion of nucleic acids, Ramstein and Lavery¹⁸ have reformulated the function of Hingerty et al., so that ε(r) depends on two parameters, the bulk dielectric constant D and the slope s of the sigmoidal segment of the function,

$$\epsilon (r)=D-\frac{D-D_0}{2}\left({(sr)}^2+2sr+2\right)e^{-sr}.$$ (14)

The green curve in Fig. 2c is constructed using the same values s=0.16, D=78.5 and (the “inside” dielectric constant) D₀=1 as Ramstein and Lavery. The Ramstein and Lavery parameters yield an ε(r) that poorly agrees with the LD model but which seems to agree better with the linear form of the dielectric “constant” used in EFF1. Shen and Freed employ the same functional form as in Eq. (14) but with different parameters (s = 0.30, D = 78.5 and D₀=1) in their implicit solvent model to investigate the dynamics of proteins.⁵ Another functional form for ε(r) can be deduced from the ad hoc interpolation model introduced to model the effective interactions of two charges in the Generalized Born model,¹⁴ producing a function in good agreement with the Langevin-Debye model as evident from the olive curve in Fig. 2c using both Born radii of 3 A. An alternate functional form used by Shen-Freed (SF),^8,26

$$\epsilon (r)=D-(D-D_0)\frac{1+e^{2h}}{e^{2h}+e^{\mathit{hsr}}}$$ (15)

has a very similar quality of agreement with the Langevin-Debye model as illustrated in Fig. 2c for D=78, D₀=1, s=0.25 and h=3.0.

Clearly the linear model used in EFF1 is a poor representation of the dielectric response of the solvent in presence of charged solutes. However, its use lowers the computational cost since the electrostatic energy term is now ∝ $\frac{1}{r^2}$; thus, using a linear form of dielectric constant saves an expensive square root operation to evaluate $\frac{1}{r}$. Additional arguments supporting the use of the linear model are as follows: Many simulation protocols apply a distance based cutoff for electrostatic interactions. Moreover, at large distances, the contribution due to electrostatic interactions almost vanishes, while for small distances, the Langevin-Debye model can be approximated by a linear dependence². Hence, even though the dielectric response is unphysical in the linear model, it has been used with reasonable success. The Ramstein-Lavery model describes a flatter distance-dependent dielectric response, which might introduce too strong long range interactions and perhaps weaker hydrogen bonds. The Generalized Born model and the Shen-Freed functional forms are far more plausible physically and yield the correct long range limit for the bulk dielectric constant. Both models describe the nonlinear response of the solvent due to the presence of the external field produced by the solute.

However, all models presented so far in this paper, employ a unit charge which is not realistic for most solutes. We, therefore, consider a modified version of the Langevin-Debye (qLD) model for partial charges which follows from the simple scaling noted by Hassan²⁷. Such a partial charge model would be better suited for simulations of polymers and proteins where the constituent atoms of the solute have partial charges. The model is tested by comparing the conformational populations of DME that are obtained from explicit and implicit solvent simulations. This test is very stringent because the conformational populations of DME are dramatically altered by solvation.

V. Charge-dependent Langevin-Debye model

This section presents the straightforward extension of Debye’s theory of ionic saturation to treat partial charges. Given a partial charge qe at the origin, the displacement field is simply,

$$\text{D}=\frac{qe}{r^2}.$$ (16)

Following exactly the development of the modified Langevin-Debye model in Eq. (11) we can determine the permittivity as a function of q and r.

The field generated by an ion induces structure in the proximal solvent molecules, leading to the phenomena of dielectric saturation as described by Langevin-Debye model. The smaller the charge, the weaker the structure induced in the inner solvation shells, and the extent of dielectric saturation is, consequently, diminished. The behavior of ε(r) for partial charges is displayed in Fig 2d and is consistent with the physical picture presented by the Langevin-Debye theory of ionic saturation. The curves in Fig 2d demonstrate how ε(r) reaches the asymptotic bulk dielectric constant faster for smaller charges, where the values used for q are taken from the force field charge parameters for DME of Bedrov et al. discussed further in Section VI. While the nonlinear response may be thought to be negligible for neutral solutes, in fact, the cumulative contribution from the partial charges of the solute to the solvent’s dielectric response may be significant since the local field is still strong, particularly at small distances. The inset in Fig 2d exhibits the wide variation with charge in the dielectric “constant” for the proximal solvent distance range 2–6 Å for the values of each of the partial charges present in DME.

Introducing the simple change in variables $r^{\prime }\to \frac{r}{q^{1/2}}$ in Eq. (16) converts the equations for the partial charged systems identically into the original unit charge equations of Debye.²⁷ Thus, this substitution can be introduced into the analytical approximations used for the function ε(r) to produce a charge-dependent functional form for the dielectric response of the solvent. Because the constant factor of $\frac{1}{q^{1/2}}$ can be absorbed into the steepness parameter associated with the sigmoidal fits, the theory effectively produces a charge dependent parameter s. Both Eqs. (14) (one parameter, s) and (15) (two parameters, h and s) are fit to the predictions of the modified LD model to produce charge dependent parameters for each functional form. The curve obtained after fitting the more flexible two-parameter model of Eq. (15) agrees better with the LD equations than the one-parameter curve obtained from Eq. (14) (lower χ), especially in the most important region for small r. The results for partial charges are tabulated in Table 1 where s scales inversely proportional to square root of the magnitude of the partial charge. We note that the fits for all the curves in Fig. 2d differ in the value of s, the parameter that controls the steepness of the sigmoid curve. The fitted s is in descending order for the LD, qLD+OK and qLD+O models, respectively. Thus, the description of more detailed physical interactions in the Onsager and Kirkwood theories is very conveniently implemented without any additional computational cost simply by adjusting the steepness parameter s.

VII. General expression for self-energy of a charge

The physical content of the qLD, qLD+O and qLD+OK models, as well of the nonlinear electrostatic response, is illustrated by analyzing the electrostatic polarization energy W incurred when a charge qe is submerged in a volume V of a dielectric medium. W is given by the general result,

$$\begin{array}{l}W=\frac{1}{8\pi }\int (\mathbf{E}•{\mathbf{D}}_0-\mathbf{D}•{\mathbf{E}}_0)d\tau \\ =-\frac{1}{8\pi }\underset{V}{\int }(\frac{1}{\epsilon (r)}-\frac{1}{{\epsilon }_{\mathit{vac}}})\frac{{(qe)}^2}{r^4}d\tau ,\end{array}$$ (17)

where D and E are the fields in the dielectric medium and the subscript 0 denotes the fields in vacuum with the dielectric constant ε_vac. The simplification in Eq. (17) follows because D is unchanged from D₀ since the charge density remains constant before and after placing the charge in the dielectric medium, where $\mathbf{D}=\frac{qe}{r^2}\widehat{\mathbf{r}}=\epsilon \mathbf{E}$.

We now compute the self-energy of a charge qe from Eq. (17) under various limiting conditions to understand the physics inherent in different solvent models. First consider W in the limit where the nonlinear response due to the field is neglected. When βμF ≪ 1, the Langevin function L(βμF) can be approximated by $\frac{\beta \mu \text{F}}{3}$ and, Eq. (11) reduces to

$$\begin{array}{l}\text{D}-C_{\mu }\text{F}=\frac{8\pi }{3}\text{n}\left[{\alpha }_0{C}_{\mu }+\beta g{\left(\mu C_{\mu }\right)}^2\right]\text{F}\\ \text{and }{C}_{\mu }\text{F}-\text{E}=\frac{4\pi }{3}\text{n}\left[{\alpha }_0{C}_{\mu }+\beta g{\left(\mu C_{\mu }\right)}^2\right]\text{F.}\end{array}$$ (18)

Eliminating F from Eq. (18) as before produces the ratio

$$\frac{\text{D}}{\text{E}}=\frac{1+2\alpha }{1-\alpha }\text{where}\alpha =\frac{4\pi }{3}\text{n}\left[{\alpha }_0+\beta g{C}_{\mu }{\mu }^2\right].$$ (19)

As mentioned earlier, the gas phase dipole moment is $\frac{\mu }{{(g{C}_{\mu })}^{0.5}}={\mu }_{\mathit{gas}}$; hence, the static, low frequency bulk dielectric constant ε₀ is related to the molecular electrical polarizability and the dipole moment of the molecules through,

$$\alpha =\frac{{\epsilon }_0-1}{{\epsilon }_0-2}\text{where}\alpha =\frac{4\pi }{3}\text{n}\left[{\alpha }_0+\frac{{\mu }_{\mathit{gas}}^2}{3\text{kT}}\right].$$ (20)

Combining the two equations (19) and (20) to eliminate α yields $\frac{\text{D}}{\text{E}}={\epsilon }_0$. Introducing this relationship into Eq. (17) produces,

$$W=\frac{{(qe)}^2}{2a}\left(\frac{1}{{\epsilon }_0}-\frac{1}{{\epsilon }_{\mathit{vac}}}\right),$$ (21)

which is the well known form of the Born self-energy for a charge qe and radius a immersed in a medium of bulk dielectric constant ε₀. Repeating the calculation for the case of vanishing dipole moment in the surrounding molecules of the dielectric solvent (i.e., where no reorientation is possible in response to an external field as in a solid medium) results in the same expression as in Eq. (18) with ε₀ replaced by the high frequency dielectric constant ε_∞.

Retaining the full nonlinear response of the dipoles in the solvent leads to the more general expression for the self-energy, containing the sum of the traditional Born self-energy and a nonlinear electrostatic correction,

$$W=\frac{{(qe)}^2}{2a}\left(\frac{1}{{\epsilon }_0}-\frac{1}{{\epsilon }_{\mathit{vac}}}\right)-\frac{s{(qe)}^2}{2{\epsilon }_o}\underset{as}{\overset{\infty }{\int }}\left[\frac{1}{1-\gamma \left[x^2+2x+2\right]e^{-x}}-1\right]\frac{dx}{x^2}\text{where}\gamma =\frac{{\epsilon }_0-{\epsilon }_{\infty }}{2{\epsilon }_0}.$$ (22)

Equation (22) uses the approximate analytical fit in Eq. (14) for ε(r) that is obtained from computed values of D/E as a function of r. The use of the fit is convenient because the ratio of the nonlinear correction to the standard Born self-energy then becomes a function of the single parameter as for specified bulk dielectric constants (ε₀ and ε_∞) of a given solvent. The ratio of the second term on the right hand side of Eq. (22) to the first Born term is presented as a function the parameter as in Fig 3 for the case of water. Noting that small as corresponds to a high charge and/or small radius of the charged ion, the relative contribution from the nonlinear term with respect to the usual Born term is more significant for small as, a result in agreement with earlier studies and with observed deviations of experimental solvation energies from the Born theory for small and highly charged ions.¹³ The red asterisks on the curve correspond to the three charged atoms found in DME and are labeled accordingly. The magnitude of the relative contributions varies from ~10% to ~1% for the partial charges of the atoms in DME. Thus, even small neutral molecules with partial charges on constituent atoms yield non-negligible nonlinear contributions to the free energy of solvation for the whole molecule.²⁸ Because the relative contribution of nonlinear effects from the charges (Fig 3) is averaged over all distances, for some conformations of the solute the contribution can be significant.

Figure 3.

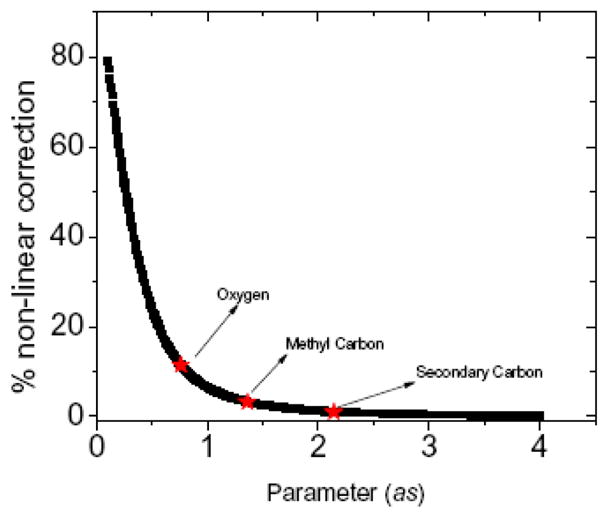
Relative magnitude of nonlinear contribution to the self energy.

The contribution of the nonlinear term to the self energy of a charge placed in aqueous medium (Eq. (22)). The red points correspond to the three atom types in DME.

VII. Application to conformational populations of 1,2: Dimethoxyethane

One common method for assessing improved continuum solvation models has been to compare predicted solvation energies with experiments. For example, recent excellent papers by Sandberg et al. study how solvation energies are affected by the nonlinear dielectric model.^13,28 However, the extraction of the free energy of hydration of ions requires a fair bit of “massaging” of experimental data to describe the gross changes between gas phase and solution. A more direct and perhaps more sensitive test of the nonlinear dielectric model is pursued here and involves comparing equilibrium conformational populations of solvated small molecules computed from implicit solvent models with those obtained from explicit solvent MD simulations.

Our modified charge-dependent Langevin-Debye models (qLD, qLD+O and qLD+OK) are implemented in the Shen-Freed implicit solvent model to compare the equilibrium conformational populations of 1,2-dimethoxyethane (DME) obtained from Langevin dynamics simulations using the modified and original implicit solvent models with explicit solvent simulations. Oligomers of DME form poly(ethylene oxide) PEO, which has applications in drug delivery and which is also under development as prosthetic devices, artificial skin, and as scaffolds for tissue engineering.²⁹ All these applications involve interactions of PEO with an aqueous environment. The PEO/water system has been extensively studied by Smith and coworkers with molecular dynamics simulations.²⁰ The use of an implicit solvent model would reduce the computational cost of simulating the dynamic and equilibrium properties of PEO by at least two orders of magnitude and would facilitate the study of more complex systems. As a first step towards developing an implicit solvent model for describing the structure and dynamics of PEO in aqueous solutions, we consider its building block, namely DME, the shortest ether molecule that reproduces the local conformations of PEO. In addition to being small –and, therefore, ideal for computational methods development, –explicit water simulations are available for DME, and DME undergoes a qualitative change in conformational preferences upon solvation, so it proves to be a sensitive test of the solvation model.

Langevin dynamics simulations have been performed for DME at 298K using the simulation protocol described briefly in the Appendix. The solvent contributions are modeled using a distance dependent dielectric “constant” ε to screen charge-charge interactions and a solvation potential with parameters σ derived by us using empirical free energies of solvation for several primary ethers at 298K (details in Appendix). The last two terms of the left hand side of equation (A1) correspond to the polar and non-polar contribution to the solvation, respectively. The polar or charge-charge interaction is expressed in terms of atomic partial charges q_i and a distance dependent dielectric constant ε(r). The interaction energy for a pair of charges assumes the functional form to be the harmonic mean of the charge dependent dielectric constant ε(q_i, r_ij) and ε(q_j, r_ij) evaluated with the individual charges q_i and q_j at the given distance r_ij. The Born self-interaction energy for each charge is effectively included in the solvation parameters σ_i, so these Born energies do not appear explicitly in the expression for the total energy in Eq. (A1). The non-polar or microscopic solvation potential is modeled using the Ooi-Scheraga solvent–accessible surface area (SASA) potential which is described in more detail in the Appendix.

The implicit solvent simulations capture the dominant trends concerning the stability and populations of major conformations (triads of three consecutive dihedral angles of main chain atoms) for DME. The original unit charge, implicit solvent model successfully captures the stabilization of the tgt conformation in the aqueous phase and the destabilization of ttt and tg+g− upon solvation (Table II), where t denotes trans and g is the gauche conformation. Important hydrophilic (tgt and ggt) and hydrophobic conformers (ttt and tg+g-) are also grouped together as separate entries in the table to describe the qualitative influence of the solvation of DME predicted by different models. The implicit solvent model exhibits good agreement with explicit solvent molecular dynamics (MD) simulations by Bedrov et al. for these conformational populations of DME,²⁰ but room still exists for improving the solvation potential model. The original Shen-Freed model captures the qualitative order of stability for the different conformations (except for tgg and tg+g-). However, we find improved quantitative agreement with the explicit solvent MD simulations (Table II) for the dielectric model that contains an additional dependence on partial charges (qLD, qLD+O and qLD+OK). The order of preference for tgg and tg+g− is corrected when using the charge dependent qLD. The data in Table II are obtained using the charge dependent qLD+OK model. Repeating the simulations with the charge dependent qLD (but omitting the corrections proposed by Onsager and Kirkwood) yields basically the same improvements over the original Shen-Freed implicit solvent model (data not shown). A portion of the discrepancy between the implicit and explicit solvent simulations arises because the former uses empirical data for the free energies of solvation for normal ethers (see appendix), so the solvation potential would differ if derived from computations of the free energies of solvation with the potentials used for the explicit solvent simulations.

Table II.

Comparison of implicit and explicit solvent simulations for DME. The charge dependent dielectric model used corresponds to the parameters shown in Table I, while the implicit model uses s = 0.27.

Triads	Gas Phase	Explicit	Implicit	Implicit (with q-dependent dielectric model)
ttt	22.75	2.66	8.15	1.5
tgt	27.65	74.11	53.38	70.83
tgg	3.70	14.48	9.23	13.5
tg+g−	33.18	6.28	22.63	11.6
Hydrophobic	55.93	8.94	30.78	13.1
Hydrophillic	31.35	88.0	62.61	83.88

VIII. Discussion

A range of different implicit solvent models is currently being used to render many biologically interesting problems accessible to computational studies. A common class of implicit solvent methods uses variations of the Generalized Born model to account for electrostatic effects in simulation of structure and dynamics of biomolecules with varying degree of success.^3,7,30 However, recently several investigators have concluded that the generalized Born/solvent accessibility method (GB/SA) often produces erroneous results. As shown by Lazaridis and coworkers,³¹ the seemingly sophisticated generalized Born (GB) method, which omits dielectric saturation, provides as accurate an approximation of the Poisson equation as the very crude model with a linearly varying distance dependent dielectric “constant”. Moreover, comparisons by Shea of implicit³² and explicit solvent³³ simulations of the coil to helix transition in Ala₇ using this linearly varying distance dependent dielectric “constant” model yield poor agreement. Furthermore, some implicit solvent models either completely omit a solvation potential or, as in the GB/SA method treat the surface area contributions of all solute atoms as identical. Not surprisingly, these models lead to rather poor comparisons with explicit solvent simulations. For example, Zhou and Berne³⁴ find that the GB method in the proprietary IMPACT package poorly describes the free energy landscape from explicit solvent MD simulations: some non-native states are too heavily weighted, and the native β-hairpin is not the lowest free energy state. More recent GB/SA simulations for the more complex 28-residue 1PSV, a protein with an αββ structure, completely fail to locate the native structure due to an overestimate of the salt bridge interactions between side groups.³⁵ Instead, the simulations find free energy minima corresponding to misfolded states. Likewise, free energy surfaces for a three-stranded β-sheet, calculated by Brooks using a GB/constant dielectric constant implicit solvent method,³⁶ depart from explicit solvent MD simulations, so quite different dynamics would emerge from the two approaches. Finally, Garcia shows that the GB/SA method fares rather poorly compared to explicit solvent simulations for the helix-coil transition in alanine rich peptides.³⁷

Our approach has been to develop a computationally facile solvation model for the Shen-Freed implicit solvent model. The non-polar contribution to solvation is modeled by the atom dependent influences of protein-solvent interactions, a dependence that is omitted in implicit solvent models such as the GB/SA. Protein-solvent van der Waals interactions obviously depend on the protein atom type, whereas some models merely distinguish between hydrophobic and hydrophilic atoms and thus are likewise wholly inadequate. In addition, our solvation potential describes the entropic effects of solvent reorganization that likewise vary with solute atom type.³⁸ The polar component of our solvation model accounts for non-linear effects, such as dielectric saturation. The phenomenon of dielectric saturation is inherent in the distance dependent dielectric “constant” in our implicit solvent model, but the model has originally been introduced for describing electrostatic interactions between the unit charges in DNA based on calculations of Debye for a single unit charge.¹⁸ On the other hand, protein force fields have interactions with many small charges, so the distance dependent dielectric “constant” model introduced for DNA has been further optimized for protein force fields by introducing a charge dependence (i.e., by extending Debye’s theory to partial charges). Since the distance dependence of the LD distance dependent dielectric “constant” model is similar to that for the GB models when a single Born radius is used, the introduction of a charge dependence in the qLD model corresponds to allowing for the equivalent of different Born radii and should, therefore, lead to improvements of the LD model. More fundamentally, the qLD model provides a means to derive the interaction term between pairs of charges, as opposed to the form of the interaction term in our implicit solvent model (i.e., the use of a harmonic mean of ε_i(r_ij) and ε_j(r_ij)) and in the GB methods which employ purely phenomenological interpolation between known limits that has been optimized with respect to the solution to the PB equation.¹⁴ In an ongoing project, we have used the Langevin-Debye model derive the distance and charge dependence of the interaction energy between two charges in the continuous medium, and only the difficult numerical calculations remain. The development of this model for the interaction will enable us to extend the implicit solvent model to nucleic acids and other charged bimolecular systems, and the advances should prove useful in improving the Generalized Born methods.

IX Conclusion

We briefly review the Langevin-Debye model of ionic saturation and the subsequent corrections due to Onsager and Kirkwood. However, these models have been derived for unit charges, whereas most solutes comprise a combination of partial charges as well as perhaps unit charges. A more physically reasonable way to capture the solvation effects in continuum models would require developing a charge dependent version of the Langevin-Debye model (qLD). We present qLD and discuss the physical content of this model by evaluating the electrostatic self-energy in three different limiting conditions. The first example is that of a solid in which dipoles are unable to reorient. This example produces the Born self-energy with the high frequency optical dielectric constant, which for water, would result in the Born energy being computed with a dielectric constant of 1.77 which is obviously a poor description. Next, allowing the dipoles to reorient but retaining only their linear response to the ion leads again to the Born self-energy but now with the correct bulk water dielectric constant of 78.5, reflecting the well-known fact that reorientation of water molecules provides the dominant contribution to the dielectric constant of water and hence to the solvation of ions. Lastly, the nonlinear response arises because the reorienting water dipoles modify the local field acting on other dipoles. The relative magnitude of the nonlinear response term with respect to the Born contribution can be quite significant for highly charged small ions, fairly high for some partial charges, and very important for small distances, such as those within the first solvation shell (Fig. 3).

We find improved agreement with the explicit solvent simulations for the conformational populations of DME when the qLD, qLD+O and qLD+OK models are used in the Shen-Freed implicit solvent model. The conformational population of DME changes dramatically upon solvation as demonstrated by comparing explicit water and gas phase simulations. Therefore, this comparison provides a good test for any implicit solvent model. We find a significant improvement when using the charge dependent model (qLD). The qualitative order of preference of different conformations is in excellent agreement with explicit water simulations when qLD is used, since it captures many major features of the solute-solvent interaction. Not only is there a significant stabilization of tgt and tgg and a destabilization of ttt and tg+g− upon solvation in our implicit solvent model, but there is also good quantitative agreement with the explicit water simulation populations for these conformations. Most importantly, the analysis of the explicit solvent simulations partially attributes the destabilization of tg+g− to unfavorable dipole-dipole interactions of the water molecule that is hydrogen bonded to DME and other water molecules in the first hydration shell of DME as well with the DME dipole itself. Interestingly these first shell solvation effects are captured better by the charge dependent implicit solvent model than the original solvent model with all charges effectively the same. The correction introduced by introducing the dependence on charge captures the first shell solvation effects better. Thus, we provide a version of the Shen-Freed implicit solvent model that is physically more realistic and that describes the solvation effects better without any additional computational cost. In addition, our analysis provides encouragement that the derivation of the interaction energy of two charges within the LD model will be useful in improving a wide range of implicit solvent models.

Table I.

Parameters for the functional forms of the distant-dependent dielectric “constant” obtained by fitting to the Langevin-Debye model with corrections due to Onsager-Kirkwood. The magnitudes of the partial charges are those for the atoms in DME. The parameters D and D₀ are fixed to the static and optical dielectric constants of water, respectively.

Charge (q)	Parameters for Eq. (14)
	D	D0	s
1	78.5	1.77	0.274
0.066	78.5	1.77	1.07
0.163	78.5	1.77	0.68
0.256	78.5	1.77	0.541
0.097	78.5	1.77	0.88

Appendix I: Langevin dynamics simulations

The Langevin dynamic simulations take the total system energy as the sum of the usual different types of interaction potentials between individual atoms, while the solvent contributions is modeled with dielectric screening U_ch (ε) and solvation terms U_solv (σ),

$$\begin{array}{l}{U}_{\mathit{total}}=U_b+U_{\mathit{bend}}+U_{\mathit{tors}}+U_{\mathit{imp}-\mathit{tors}}\\ +U_{\mathit{vdW}}+U_{ch}(\epsilon )+U_{\mathit{solv}}(\sigma ),\end{array}$$ (A1)

in which the bonding interactions U_b and bond-bond bending interactions U_bend are modeled by harmonic potentials, the regular and improper torsional energies U_tors and U_imp–tors by standard periodic functions, and the van der Waals interaction by using Buckingham exponential-6 potentials.³⁹ The last two terms of equation A1 correspond to the polar and non-polar contribution to the solvation. The polar or charge-charge interaction is expressed in terms of atomic partial charges q_i and a distance dependent dielectric constantε(r), $U_{ch}(\epsilon )={\displaystyle \sum _{i>j}}\frac{q_i{q}_j}{\epsilon (r_{ij})r_{ij}}$. The interaction energy for a pair of charges uses $\frac{1}{\epsilon (r_{ij})}$ as the harmonic mean of the charge dependent dielectric constant ε(q_i, r_ij) and ε(q_j, r_ij) evaluated with the individual charges q_i and q_j at the given distance r_ij. The self-energy term for each charge is not included in U_ch(ε) because its effects are already included in the solvation potential. The microscopic solvation potential is modeled using the Ooi-Scheraga solvent–accessible surface area (SASA) potential, $U_{\mathit{solv}}(\sigma )={\displaystyle \sum _{i=1}^N}{g}_i{\sigma }_i$, where σ_i is the accessible surface area on a hypersurface formed by the first solvent shell surrounding protein atom i, and the empirical parameter g_i depends on the atom type and contains the electrostatic self-energy.⁴⁰ Accessible surface areas (ASA) are computed for 4 classes of atoms or groups, namely (i) methyl carbon, (ii) polar secondary carbon, (iii) non-polar secondary carbon, and (iv) oxygen. The hydrogen atoms are not treated as a separate class because they have nearly vanishing ASAs. The empirical parameters g_i for the four atom types are determined by fits the free energy of solvation⁴¹ for six primary ethers (di-methyl, di-ethyl, methyl-n-propyl, ethyl-n-propyl, di-n-propyl, and di-n-butyl ethers) following the methods and using the same atom radii as Ooi et al.⁴⁰ The details of the computation of the solvation parameters will be published elsewhere along with the treatment of the dynamics of larger PEO oligomers.

Langevin dynamics simulations are generated by integrating the atom positions and velocities using the standard velocity Verlet algorithm, using the Shen-Freed modified version⁴² of the TINKER package⁴³ and solute force field parameters developed by Smith and co-workers.³⁹ The Pastor-Karplus accessible surface area model is used to compute the frictional forces due to the implicit water molecules and the corresponding random forces (necessary by virtue of the fluctuation-dissipation theorem to assure the proper equilibrium limit at long times).⁴⁴ The LD simulations use an integration time step of Δt= 2.0 fs. Except for the hydrogen atoms, whose presence is ignored in computing theσ_i, the solvent accessible surface area σ_i is calculated from the exposed surface area of intersecting spheres centered on each atom, using a probe sphere of radius 1.4 Å, which corresponds to the effective radius of a water molecule. To save computational time, the accessible surface area, the atomic friction coefficients, and the solvation potential are updated every 100 dynamical steps (0.20 ps) instead of every step. (Tests show that updating every 100 steps yields almost no difference from updating every step because conformational variations occur on a much longer time scale).⁵ No nonbonding force cutoff is applied, and the RATTLE method is not applied to stabilize the simulation.⁴⁵ A constant temperature is maintained using a Berendsen-type thermal bath coupling throughout the simulation, and the data are saved every 2000 steps (10 ps) for subsequent analysis.⁴⁶ The explicit water simulations have been performed by Smith and coworkers.²⁰