Mutations reveal voltage gating of CNGA1 channels in saturating cGMP

Abstract

Activity of cyclic nucleotide–gated (CNG) cation channels underlies signal transduction in vertebrate visual receptors. These highly specialized receptor channels open when they bind cyclic GMP (cGMP). Here, we find that certain mutations restricted to the region around the ion selectivity filter render the channels essentially fully voltage gated, in such a manner that the channels remain mostly closed at physiological voltages, even in the presence of saturating concentrations of cGMP. This voltage-dependent gating resembles the selectivity filter-based mechanism seen in KcsA K⁺ channels, not the S4-based mechanism of voltage-gated K⁺ channels. Mutations that render CNG channels gated by voltage loosen the attachment of the selectivity filter to its surrounding structure, thereby shifting the channel's gating equilibrium toward closed conformations. Significant pore opening in mutant channels occurs only when positive voltages drive the pore from a low-probability open conformation toward a second open conformation to increase the channels' open probability. Thus, the structure surrounding the selectivity filter has evolved to (nearly completely) suppress the expression of inherent voltage-dependent gating of CNGA1, ensuring that the binding of cGMP by itself suffices to open the channels at physiological voltages.

INTRODUCTION

Cyclic nucleotide–gated (CNG) cation channels in photoreceptors are activated by intracellular cGMP, whose concentration varies with light intensity (Stryer, 1986; Yau and Baylor, 1989). The activity of these channels thereby translates light signals into electric signals. External divalent cations block the channels and, consequently, reduce the contribution of individual channels to the overall light-sensitive current, a feature critical to the high sensitivity and reliability of phototransduction (Yau and Baylor, 1989).

Given that the role of CNG channels in the retina is to convert cGMP concentration changes into electric signals, these channels should be gated primarily by ligands, not voltage. Indeed, retinal CNGA1 channels exhibit essentially no voltage gating in the presence of high concentrations of cGMP. However, in the presence of low concentrations of cGMP, they do display modest voltage sensitivity of unknown physical origin (Karpen et al., 1988; Benndorf et al., 1999; Nache et al., 2006). Specifically, at low cGMP concentrations, depolarization-induced currents undergo noticeable relaxation, and the steady-state macroscopic I-V relation exhibits modest outward rectification. The degree of rectification decreases with increasing cGMP concentration and eventually becomes negligible. This modest voltage gating at low but not high cGMP concentrations is interpreted as follows (Karpen et al., 1988; Benndorf et al., 1999; Nache et al., 2006): a step in the ligand-gating sequence is modestly voltage sensitive with an effective valence (Z) of ∼0.2, and the apparent voltage sensitivity decreases when the gating equilibrium is already biased toward the open state in the presence of saturating cGMP concentrations.

The cGMP-binding sites are formed by the carboxy terminus, whereas the primary activation gate, in the current view, is located within the ion selectivity filter (Sun et al., 1996; Bucossi et al., 1997; Becchetti et al., 1999; Becchetti and Roncaglia, 2000; Liu and Siegelbaum, 2000; Flynn and Zagotta, 2001; Contreras et al., 2008). In the present study, we find that many mutations around the selectivity filter render the channels practically fully voltage gated, even in the presence of saturating concentrations of cGMP. We present a simple model to account for these observations.

MATERIALS AND METHODS

Molecular biology and oocyte preparation

Complementary DNA for CNGA1 (Kaupp et al., 1989) was cloned into the pGEM-HESS plasmid (Liman et al., 1992). Mutant cDNAs were obtained through PCR-based mutagenesis and confirmed by DNA sequencing. The cRNAs were synthesized with T7 polymerase (Promega) using linearized cDNA as a template. Oocytes harvested from Xenopus laevis were incubated in a solution containing (in mM): 82.5 NaCl, 2.5 KCl, 1.0 MgCl₂, 5.0 HEPES, pH 7.6, and 2–4 mg/ml collagenase (Worthington). The oocyte preparation was agitated at 100 rpm and 30°C for 40–60 min. It was then rinsed thoroughly and stored in a solution containing (in mM): 96 NaCl, 2.5 KCl, 1.8 CaCl₂, 1.0 MgCl₂, 5 HEPES, pH 7.6, and 50 mg/ml gentamicin. Defolliculated oocytes were selected and injected with RNA at least 2 and 16 h, respectively, after collagenase treatment. All oocytes were stored at 18°C.

Recordings and solutions

Currents were recorded from inside-out membrane patches of Xenopus laevis oocytes previously injected with the desired cRNA using an Axopatch 200B amplifier (MDS Analytical Technologies). Macroscopic currents were filtered at 5 kHz and sampled at 50 kHz using an analogue-to-digital converter (Digidata 1322A; MDS Analytical Technologies) interfaced to a personal computer. Single-channel currents were filtered at 1 kHz and sampled at 10 kHz. pClamp 8 software was used for amplifier control and data acquisition.

Channels were activated with intracellular cGMP, and unless specified otherwise, the currents were elicited by stepping the voltage from the −80-mV holding potential to voltages between −200 and 200 mV in 10-mV increments. The currents in the absence of cGMP were used as template for subsequent off-line background current corrections. Both internal and external solutions contained (in mM): 130 NaCl, 0.1 EDTA, and 5 HEPES, pH 7.6. All chemicals were purchased from Sigma-Aldrich.

Data analysis

G-V curves were calculated by dividing the steady-state current value at each voltage by the electrochemical driving force, and then normalizing to the value at 200 mV. In the case of the F380A mutant, the G-V curve was also obtained by isochronal measurements of the tail currents at −80 mV and normalized to the maximum value. Data analysis and curve fitting were performed with Origin 8.0 (OriginLab Corp.). Molecular models were prepared with PyMOL 1.0 (DeLano Scientific). I-V curve simulations were performed using New Barrier (http://tedlab.urmc.rochester.edu/BarrierModel.htm). The figures were made with Origin 8.0 (OriginLab Corp.) and CorelDRAW X4 (Corel Corp.).

Online supplemental material

Fig. S1 shows macroscopic currents and corresponding G-V curves for 10 E363 mutant channels. Figs. S2–S6 show macroscopic currents and corresponding G-V curves for 59 mutants with point alanine (or valine) mutations in the region from the N terminus of the pore helix to the C terminus of S6. Fig. S7 shows simulated I-V curves of wild-type and the F387A mutant channels with a permeation model harboring three ion-binding sites. Figs. S1–S7 are available at http://www.jgp.org/cgi/content/full/jgp.200910240/DC1.

RESULTS

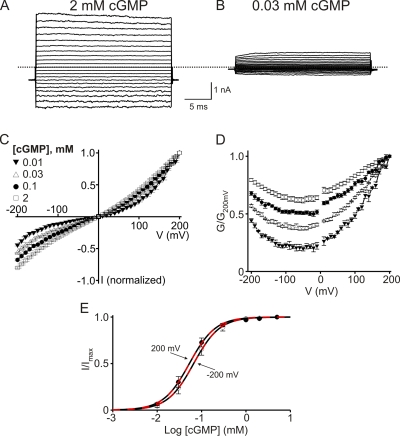
For ease of later comparison, we first illustrate some known properties of CNGA1 channels. Fig. 1 (A and B) shows current records of retinal CNGA1 channels in the presence of saturating (2 mM) and subsaturating (30 µM) concentrations of intracellular cGMP. At 2 mM, currents develop instantaneously after a voltage step, whereas at 30 µM they develop slowly. The macroscopic I-V relation is nearly linear at 2 mM but tends toward outward rectification with decreasing cGMP concentration (Fig. 1 C). To better illustrate the voltage dependence of the macroscopic conductance (G), we calculated the conductance from the current/electrochemical driving force ratio and plotted it against voltage (Fig. 1 D). The CNGA1 conductance exhibits insignificant voltage sensitivity at high concentrations of cGMP and modest sensitivity at low concentrations of cGMP. Also, the cGMP dose–response curves barely differ between −200 and 200 mV (Fig. 1 E). These results confirm previous reports (Karpen et al., 1988; Kaupp et al., 1989; Benndorf et al., 1999; Nache et al., 2006).

Figure 1.

cGMP activation of wild-type CNGA1 channels. (A and B) Macroscopic current traces recorded in symmetric 130 mM Na⁺ from inside-out patches containing CNGA1 channels in the presence of 2 mM (A) or 30 µM (B) of intracellular cGMP. Currents were elicited by stepping from the −80-mV holding potential to voltages between −200 and 200 mV in 10-mV increments. Only traces every 20 mV are shown for clarity. Dotted line indicates zero current level. (C) I-V curves (mean ± SEM; n = 3–6) in the presence of 0.01 mM (filled inverted triangles), 0.03 mM (open triangles), 0.1 mM (filled circles), and 2 mM (open squares) cGMP, each normalized to the current at 200 mV. (D) Corresponding normalized G-V curves (mean ± SEM; n = 3–6). (E) Fraction of maximal current (I/I_max; mean ± SEM; n = 7) plotted against cGMP concentration for −200 mV (open circles) and 200 mV (filled circles). Black dashed curves are Hill equation fits with a common Hill coefficient (n) yielding EC₅₀ = 66 ± 2 µM at −200 mV, EC₅₀ = 53 ± 1 µM at 200 mV, and n = 1.48 ± 0.03. Red dashed curves are fits of Eq. 1 to both datasets simultaneously, with a single adjustable K_L and all other parameters fixed (n = 1.48; K₁ = 0.62, K₂ = 1.04, and Z_K2 = 0.25), which yield K_L = 96 ± 2 µM at −200 mV and K_L = 182 ± 5 µM at 200 mV.

Mutations around the external end of the selectivity filter render the channels voltage gated, even at saturating cGMP

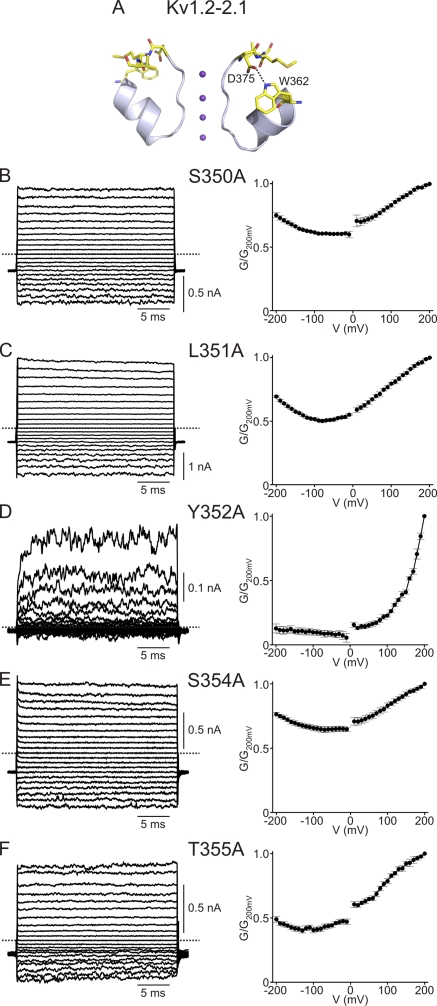
The modest voltage sensitivity of CNGA1 at low cGMP concentrations signifies that the conformation of part of the ion conduction pore, e.g., the selectivity filter, is directly or indirectly influenced by membrane voltage. In Kv channels and bacterial KcsA channels, the external end of the selectivity filter is structurally attached to the pore helix (Perozo et al., 1993; Yang et al., 1997; Doyle et al., 1998; Zhou et al., 2001; Long et al., 2005, 2007; Blunck et al., 2006; Cordero-Morales et al., 2007). Disruption of that interaction affects voltage gating in these channels (e.g., C-type inactivation; López-Barneo et al., 1993; Cordero-Morales et al., 2006b). We therefore wondered whether similar disruption of the analogous contact in CNG channels would also affect their voltage sensitivity. To test this idea, we mutated six residues (³⁵⁰SLYWST³⁵⁵) in the pore helix of CNGA1, one at a time, to alanine; five mutants express sufficient current for examination. The macroscopic conductance of the S350A, L351A, S354A, and T355A mutants, like that of wild type, exhibits little voltage sensitivity (Fig. 2, B, C, E, and F). In stark contrast, the Y352A pore helix mutant becomes strongly voltage sensitive, even in the presence of saturating cGMP concentrations (Fig. 2 D): depolarization elicits large outward currents with resolvable time courses, but hyperpolarization induces little inward current. We note that some residual current persists at extreme negative voltages.

Figure 2.

A point mutation in CNGA1's pore helix renders the channel voltage sensitive. (A) Partial crystal structure model of the Kv1.2-Kv2.1 chimeric channel (PDB 2R9R) featuring the pore helix and the selectivity filter in two diagonally opposite subunits. An oxygen in the side chain of the chimera's D375 is hydrogen-bonded to the nitrogen of W362. (B–F; Left) Macroscopic currents in 2 mM cGMP for the S350A, L351A, Y352A, S354A, and T355A mutants. Each current trace for Y352A or T355A is the average of five or three individual traces. (Right) Corresponding G-V curves (mean ± SEM; n = 4–6).

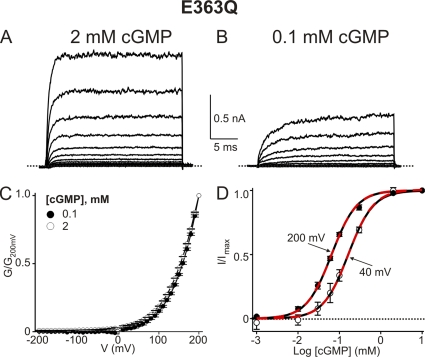
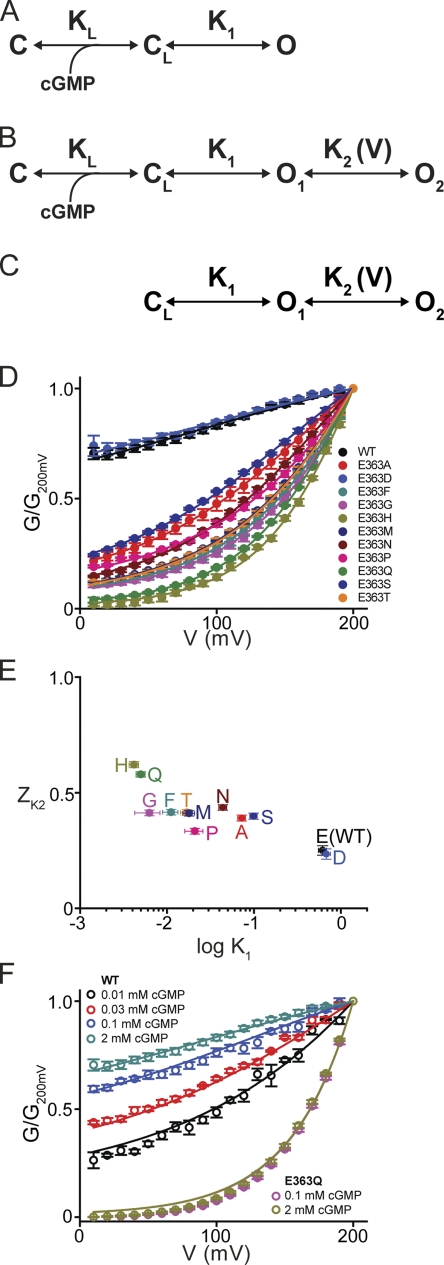
CNGA1's Y352 corresponds to Shaker's W434, whose mutation profoundly affects the ability of voltage to switch the selectivity filter between conducting and nonconducting conformations (Perozo et al., 1993; Yang et al., 1997). Intriguingly, the corresponding residue W362 in Kv1.2 of known structure is within hydrogen-bonding reach of D375 (Fig. 2 A), a residue that corresponds to E363 in CNGA1. The, by analogy, likely spatial proximity of Y352 and E363 in CNGA1 suggests that mutation of E363 too, like that of Y352 shown above, might render the channels voltage sensitive. We thus mutated E363 to all 19 other natural variants; 11 mutants express detectable currents. Only the E363D channels exhibit wild-type–like behavior (Fig. S1 B), whereas the remaining 10 E363 mutants display strong outward rectification (E363Q is shown in Fig. 3, A and C; all others are in Fig. S1). At negative voltages the conductance of these E363 mutants is greatly reduced, and in the case of E363Q and E363H, dramatically so (E363H expresses much less well). These latter two mutants are essentially completely shut down by hyperpolarization (see below); i.e., they appear to be fully voltage gated, even in the presence of a saturating concentration of cGMP. The kinetics of E363Q current development after a voltage jump become faster with increasing cGMP concentration (compare Fig. 3, A with B). However, the shape of the steady-state G-V curves at saturating and subsaturating concentrations of cGMP is superimposable (Fig. 3 C). Depolarization lowers the EC₅₀ for channel activation by cGMP only modestly (Fig. 3 D). Therefore, cGMP and voltage are unlikely to affect the same gating step(s).

Figure 3.

The E363Q mutant channel shows extreme outward rectification at saturating cGMP concentrations. (A and B) Macroscopic currents of the E363Q mutant in 2 mM (A) and 0.1 mM (B) cGMP. (C) G-V curves (mean ± SEM; n = 5) for 2 mM (open circles) and 0.1 mM (filled circles) cGMP. (D) I/I_max (mean ± SEM; n = 3–7) plotted against cGMP concentration for 40 mV (open circles) and 200 mV (filled circles). Black dashed curves are Hill equation fits with a common Hill coefficient (n) yielding EC₅₀ = 163 ± 10 µM at 40 mV, EC₅₀ = 65 ± 3 µM at 200 mV, and n = 1.44 ± 0.01. Red dashed curves are fits of Eq. 1 to both datasets simultaneously, with a single adjustable K_L and all other parameters fixed (n = 1.44; K₁ = 5 × 10⁻³, K₂ = 1.04, and Z_K2 = 0.58), which yield K_L = 166 ± 6 µM at 40 mV and K_L = 67 ± 2 µM at 200 mV.

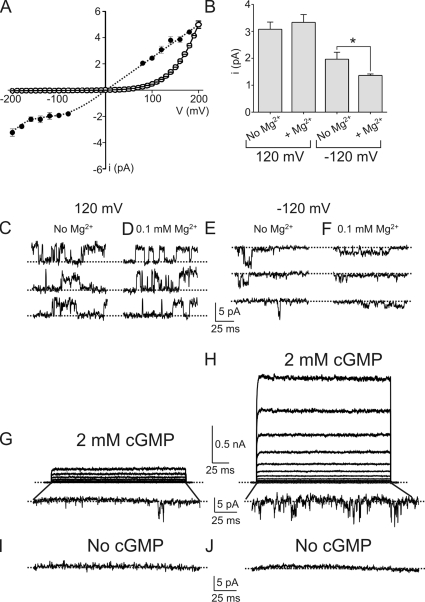
We further investigated the mechanism underlying the voltage sensitivity of the fully gated E363Q mutant by comparing the single-channel and macroscopic current–voltage relations. The single-channel i-V curve rectifies only mildly over the −200 to 200–mV range (Fig. 4 A, filled symbols). For illustration, single-channel currents at 120 and at −120 mV are shown in Fig. 4 (C and E). In sharp contrast, the macroscopic I-V curve rectifies steeply (Fig. 4 A, open symbols). The dramatic difference in the degree of rectification seen in these two current–voltage relations indicates that the rectification of the macroscopic I-V curve is due mainly to voltage gating. As expected, an E363Q channel–containing membrane patch carries large macroscopic outward currents at positive voltages, but only brief individual channel events at very negative voltages (Fig. 4, G and H). The following criteria confirm that the latter are indeed individual E363Q mutant channel events. First, the events occur only when patches are exposed to intracellular cGMP (compare Fig. 4, G and H with I and J). Second, we observe inward current events only in patches containing a large number of channels; i.e., carrying outward macroscopic currents. Third, the frequency of individual channel events at negative voltages correlates with the amount of macroscopic current in the same patch at positive voltages (compare Fig. 4, G with H). Lastly, the single-channel events are less strongly inhibited by Mg²⁺ than the wild-type current. The wild-type channel is known to be blocked by Mg²⁺ in a voltage-dependent manner, such that mainly the inward current is blocked. Neutralizing E363 reduces the apparent Mg²⁺ affinity (Root and MacKinnon, 1993; Eismann et al., 1994; Park and MacKinnon, 1995). As expected for single-channel currents presumably carried by E363Q mutant channels, their amplitude at −120 mV is reduced 37% by 100 µM of external Mg²⁺ (Fig. 4, B–F). This yields an estimated K_i of 170 µM, compared with 20 µM for the wild type (Root and MacKinnon, 1993; Eismann et al., 1994; Park and MacKinnon, 1995). We conclude, therefore, that the extreme macroscopic rectification of some E363 mutants over the wide voltage range mostly reflects voltage gating, not single-channel rectification.

Figure 4.

Macroscopic rectification of the E363Q mutant reflects voltage gating, not asymmetric ion conduction. (A) Single-channel i-V curve (mean ± SEM; n = 4–7) of the E363Q mutant (filled circles) and the (arbitrarily scaled) macroscopic I-V curve (mean ± SEM; n = 5) in the presence of 2 mM cGMP (open circles). The dotted line through the single-channel data points is hand drawn. (B) Single-channel current amplitude of the E363Q mutant (mean ± SEM; n = 5–20) at 120 or −120 mV and in the presence or absence of 0.1 mM of extracellular Mg²⁺. *, P < 0.001 (one-way ANOVA). (C–F) Representative single-channel currents of the E363Q mutant recorded at 120 mV (C and D) or −120 mV (E and F) and in the absence (C and E) or presence (D and F) of 0.1 mM of extracellular Mg²⁺; each trace was recorded from a separate inside-out patch. (G–J) Longer-duration macroscopic current traces recorded in 2 mM cGMP (G and H) from membrane patches of two oocytes expressing different densities of E363Q channels. Traces at −200 mV were magnified to show individual channel activity; the control traces recorded from the same patches at −200 mV and in the absence of cGMP are shown below (I and J).

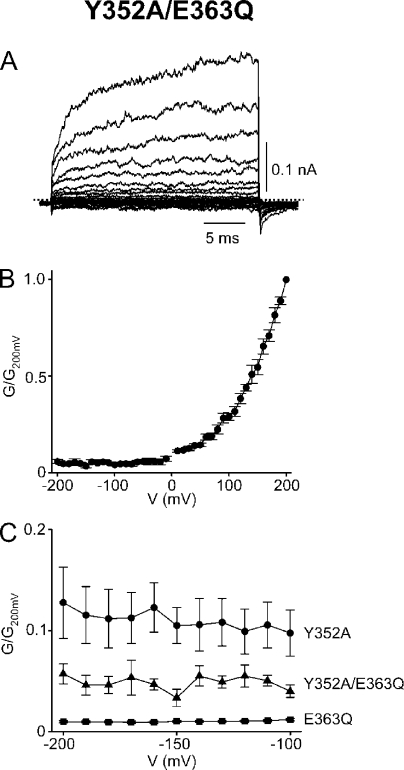
To recapitulate, we find that the Y352A pore helix mutant becomes strongly voltage sensitive; that mutation of its putative structural contact, residue E363, similarly reveals strong rectification; and that this latter behavior reflects voltage gating, not single-channel rectification. To confirm that E363 does interact with Y352, we produced the Y352A/E363Q double-mutant channel (Fig. 5, A and B). Were the two mutations to act independently and therefore additively, the residual voltage-independent conductance of the double mutant at extreme negative voltages would be even lower than that of either single mutant. Instead, it falls between those of the single mutants (Fig. 5 C; also compare Figs. 2 D, 3 C, and 5 B). The finding that the two mutations affect gating in an energetically non-additive manner confirms that Y352 and E363 indeed interact.

Figure 5.

Gating effects of mutations at Y352 and E363 are not additive. (A) Macroscopic currents of the Y352A/E363Q double mutant in 2 mM cGMP; each trace is the average of nine individual traces. (B) Corresponding G-V curve (mean ± SEM; n = 5). (C) Residual conductance (mean ± SEM; n = 4–5) at very negative voltages of the channels containing a single E363Q (squares) or Y352A (circles) mutation, or a Y352A/ E363Q double mutation (triangles).

Mutations in S6 near the internal end of the selectivity filter also render the channels voltage gated in saturating cGMP

Whereas the selectivity filter's external end is attached to the pore helix, its internal end, which extends from the pore helix, is attached to S6 (Fig. 6 A). To test whether perturbing the relevant part of S6 also enhances voltage sensitivity, we mutated seven S6 residues near the internal end of the selectivity filter (³⁸⁰FLIGVLI³⁸⁶), one at a time, to alanine. Among the five mutants that express sufficient current for examination, those with F380A and G383A substitutions (colored red in Fig. 6 A) are also voltage gated (Fig. 6, B and D). The tail current kinetics of the F380A mutant are sufficiently slow to be measured, and as expected, the G-V curve obtained directly from tail currents (Fig. 6 B, open circles) matches that calculated from the I-V curve (filled circles). In contrast, the remaining three mutants, with substitutions (I382A, V384A, and I386A, colored gray in Fig. 6 A) internal to the filter and/or on the other side of the helix, exhibit little voltage sensitivity (Fig. 6, C, E, and F). This spatial distribution pattern of S6 mutations that result in voltage gating further supports the notion that proper attachment of the selectivity filter to the surrounding shell is essential to minimize voltage gating in CNG channels.

Figure 6.

S6 mutations and voltage gating. (A) Partial crystal structure model of the Kv1.2-Kv2.1 chimeric channel (PDB 2R9R) featuring the selectivity filter, the pore helix, and the external part of S6 in two diagonally opposite subunits. Residue numbers are those of the corresponding residues in CNGA1. Mutations at red- and gray-colored S6 residues produce voltage-gated and non-voltage–gated channels, respectively, whereas those at blue-colored ones produce nonconductive channels. (B–F) Macroscopic currents in 2 mM cGMP (left) and corresponding G-V curves (right; mean ± SEM; n = 3–7) for various CNGA1 mutants. The normalized conductance values were calculated from the current/electrochemical driving force ratio, except for those indicated by open circles in B, which were determined from isochronal tail current measurements.

Alanine scan of the entire region from the pore helix to S6

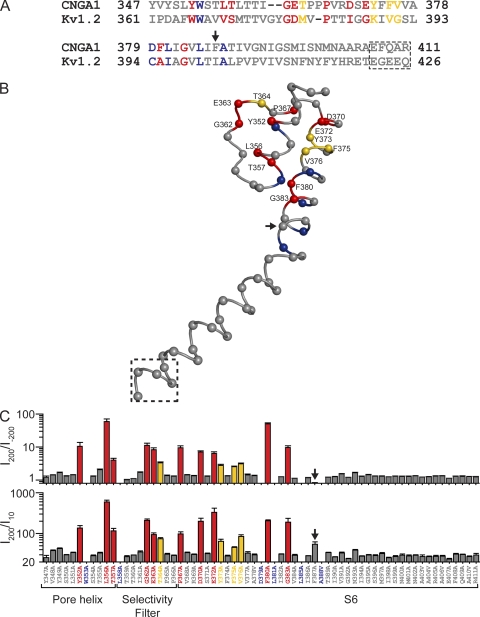
The hypothesis that proper anchoring of the selectivity filter to the surrounding structural shell prevents undesirable voltage gating implies that mutations that result in voltage gating (in saturating cGMP) will be confined to the external part of the pore around the selectivity filter. In particular, no S6 mutations in the internal part of the pore should confer voltage sensitivity, even though architectural similarities with Kv channels suggest the possible existence of an intracellular gate. To test this prediction, we replaced each of the remaining 53 residues in the region from the N-terminal end of the pore helix to the C-terminal end of S6, one at a time, with alanine (native alanine residues were replaced with valine; Fig. 7 A). Of the 65 mutant channels (including those already discussed), 59 express sufficient current for examination (Figs. S2–S6). Phenotypically, the 65 mutant channels fall into four categories, characterized by their degree of rectification, which we express as the ratio of currents at 200 and −200 mV (I₂₀₀/I₋₂₀₀) or, for comparison (see below), that at 200 and 10 mV (I₂₀₀/I₁₀) (Fig. 7 C). The first category, colored gray in the sequence alignment (Fig. 7 A) and in the chimeric Kv channel structure (Fig. 7 B), exhibits, like the wild type, no significant voltage gating in saturating cGMP. The second group (colored red in Fig. 7) is strongly voltage gated; i.e., little or no macroscopic current remains at hyperpolarized potentials. The third group (colored yellow in Fig. 7) exhibits modest voltage gating; i.e., the channels conduct significant, if diminished, macroscopic current at very hyperpolarized potentials. The fourth group (colored blue in Fig. 7) expresses no or insufficient current for examination.

Figure 7.

Distribution pattern of point mutations that produce voltage gating in the CNGA1 channel. (A) Partial sequence alignment of the CNGA1 (GI 31342442) and Kv1.2 (GI 1235594) channels for the region in which the alanine scan was performed. Mutations at red- and yellow-colored positions produce strongly and modestly voltage-gated currents, respectively, whereas those at blue-colored ones produce no or unmeasurable currents. The remaining mutations (gray-colored positions) produce non-voltage–gated currents. Residues in the dashed box are absent from the crystal structure model of the Kv1.2-Kv2.1 chimeric channel. (B) Partial crystal structure model of the Kv1.2-Kv2.1 chimeric channel (PDB 2R9R) corresponding to the entire alignment shown in A, featuring the selectivity filter, the pore helix, and S6 in one subunit. Labeled positions (numbering is that of corresponding residues in CNGA1) indicate the mutations that produce voltage-gated or partially voltage-gated channels. Structure within the dashed box, absent from the crystal structure, is arbitrary. (C) I₂₀₀/I₋₂₀₀ (top) and I₂₀₀/I₁₀ (bottom) values (mean ± SEM; n = 3–7) of mutant channels. Red bars signify I₂₀₀/I₋₂₀₀ > 5, yellow bars are 4 > I₂₀₀/I₋₂₀₀ > 2.5, and gray bars are I₂₀₀/I₋₂₀₀ for near unity in the top panel, whereas in the bottom panel they signify I₂₀₀/I₁₀ > 95, 85 > I₂₀₀/I₁₀ > 45, and I₂₀₀/I₁₀ < 35, respectively, except for the F387A mutant (arrow), which is discussed in Results.

Structural mapping of these phenotypes yields an informative pattern (Fig. 7 B). All mutations that cause the appearance of voltage gating in saturating concentrations of cGMP (Fig. 7 B, labeled positions) are located in the external part of the pore around the selectivity filter. Thus, if voltage gating arises from the ion conduction pore, it must arise from this external region, not from a more internal one, such as the C-terminal part of S6 that in Kv channels constitutes the activation gate. This pattern reinforces the view that proper anchoring of the selectivity filter is critical in minimizing voltage gating.

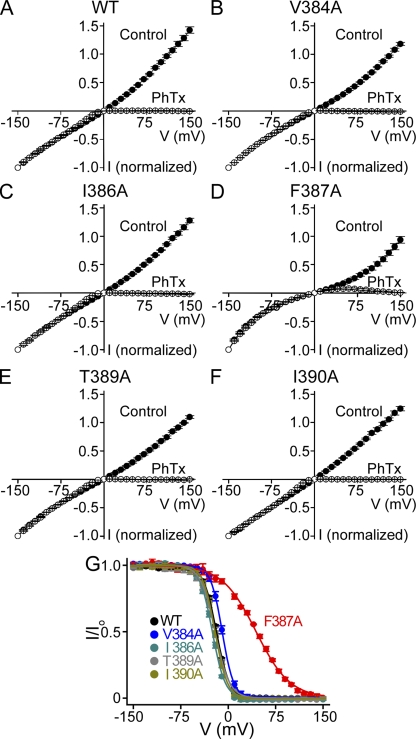
It is noteworthy that the F387A mutation in the cavity, unlike mutations at neighboring residues, renders the I-V relation “super-linear” (compare Fig. 8, A with D, filled symbols). As a result, the current exhibits little rectification as judged from the I₂₀₀/I₋₂₀₀ value but partial rectification based on the I₂₀₀/I₁₀ value (categorization of all other mutants is qualitatively the same in both cases). In principle, the phenyl ring of F387 may be involved in forming an ion-binding site in the cavity of the channel. As illustrated in Fig. S7, the super-linearity of this mutant's I-V curve may simply result from the disruption of an ion-binding site. If that were the case, block of the mutant's pore should exhibit reduced voltage dependence because it contains fewer Na⁺ ions that can be displaced by a blocker across the electric field (Armstrong, 1971; Spassova and Lu, 1998; Shin et al., 2005). Indeed, the F387A mutation, but not those at neighboring residues, reduces voltage dependence of channel block by philanthotoxin (PhTx) (Fig. 8 and Table I; see Guo and Lu, 2000 for PhTx block of CNGA1). For this reason, we did not categorize the F387A mutant as modestly voltage gated.

Figure 8.

Voltage-dependent block of wild-type and mutant CNGA1 channels by intracellular PhTx. (A–F) I-V curves (mean ± SEM; n = 4–6) of wild-type (WT) and mutant channels in the presence (open circles) and absence (filled circles) of 10 µM of intracellular PhTx. (G) Fraction of current not blocked (I/I_o; mean ± SEM; n = 4–6) by 10 µM PhTx for wild-type and mutant channels, plotted against membrane voltage. Curves are fits of a Boltzmann function, I/I_o = 1/(1 + [PhTx]/^appK_dexp^−ZFV/RT); the fitted parameter values are listed in Table I.

Table I.

Best-fit values obtained from Fig. 8 G

	appKd (M)	Z
WT	1.6 ± 0.1 × 10−6	2.48 ± 0.07
V384A	3.5 ± 0.2 × 10−6	2.81 ± 0.09
I386A	8.3 ± 0.6 × 10−7	2.55 ± 0.07
F387A	5.2 ± 0.2 × 10−5	0.96 ± 0.02
T389A	1.6 ± 0.1 × 10−6	2.25 ± 0.06
I390A	1.2 ± 0.1 × 10−6	2.67 ± 0.08

Charge-neutralizing mutations at arginine residues in S4 do not affect the voltage sensitivity of E363Q mutant channels

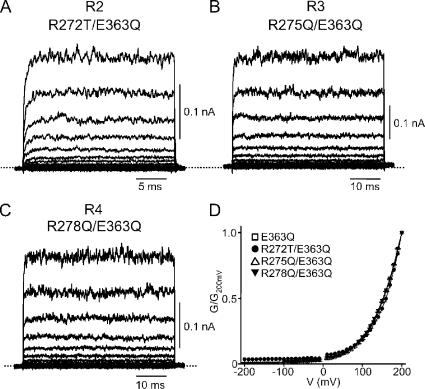
Voltage sensitivity in K⁺ channels originates from two regions: the S4 voltage sensor and the ion selectivity filter. The S4 in CNGA1 channels resembles that of Kv channels in that it contains the four arginines that in Kv channels sense voltage (Kaupp et al., 1989; Jan and Jan, 1990; Aggarwal and MacKinnon, 1996; Seoh et al., 1996; Tang and Papazian, 1997). This similarity naturally raises the question of whether the voltage sensitivity that we find to be brought out by numerous mutations around the selectivity filter arises, not from the filter after all, but from the arginines in S4. To address this issue, we made neutral substitutions at R1 through R4 on the background of the E363Q mutation and observed the following. R1 is intolerant of mutation, as all 19 mutants fail to produce detectable currents (a result consistent with R1's involvement in a critical hydrogen bond). R2 is so poorly tolerant that among the 19 possible substitutions, only lysine and threonine yield measurable currents. R3 and R4 are more tolerant. If the voltage sensitivity of E363Q channels originates, as our results thus far suggest, mainly from the selectivity filter region rather than from S4, neutral substitutions (R2T, R3Q, or R4Q; Fig. 9, A–C) should have little effect on voltage sensitivity. This is indeed the case, as the G-V curves of the E363Q mutant with or without neutral substitutions for any one of these three arginine residues are all superimposable (Fig. 9 D). That is, these positive charges on S4 play no role in conferring voltage sensitivity to the mutants described above.

Figure 9.

Effect of S4 mutations on voltage gating induced by the E363Q mutation. (A–C) Macroscopic currents recorded in 2 mM cGMP from E363Q mutant channels containing an additional substitution in S4: R272T (R2T; A), R275Q (R3Q; B), or R278Q (R4Q; C). (D) G-V curves (mean ± SEM; n = 3–8) for the E363Q mutants without (open squares) or with an additional S4 substitution: R272T (filled circles), R275Q (open triangles), or R278Q (filled inverted triangles). The four curves are superimposed.

DISCUSSION

Here, we report four main findings. First, mutations at several sites render macroscopic CNGA1 currents strongly outwardly rectifying in the presence of saturating concentrations of cGMP. Second, the rectification mainly reflects voltage gating, not single-channel current rectification. Third, mutations that bring out voltage gating are exclusively confined to the region around the ion selectivity filter. Fourth, the acquired voltage sensitivity is not affected by neutralizing any of the (second through fourth) positively charged residues in S4. We will analyze the characteristic features of the voltage-gated mutant channels using mainly the E363Q mutant as an example. This mutant not only is practically fully voltage gated, but it also expresses sufficient current for a relatively more detailed characterization. Additionally, E363 mutations have been extensively studied in the context of ion conduction.

Over a decade ago, mutations at E363 were shown to render the macroscopic I-V curve outwardly rectifying (Root and MacKinnon, 1993; Eismann et al., 1994; Sesti et al., 1995). These studies were performed with voltage ramp protocols between −100 and 100 mV. Within this relatively restricted voltage range, rectification is not as extreme as we report here over a much wider (−200 to 200 mV) range. On the assumption that the glutamate residue is located near the external mouth of the ion conduction pore, and given the fact that the single-channel i-V curve exhibits rectification (although less than the macroscopic I-V curve), a natural conclusion is that neutralizing a negatively charged residue near the external end of the pore would lower the local electrostatic potential. This reduced potential could in turn lower the permeant ion concentration at the external mouth of the pore, causing the pore to conduct ions in an outwardly rectifying manner. As detailed below, our voltage pulse protocols over a much wider voltage range reveal that the extreme rectification after neutralization of E363 mainly reflects voltage gating, not single-channel current rectification. First, if macroscopic rectification caused by neutralizing E363 were mainly due not to channel gating, but to asymmetric ion conduction, the current induced by a voltage step should develop instantaneously without relaxation. On the contrary, several neutral E363 mutant channels, like other voltage-gated ones with mutations in the pore helix or in S6, clearly exhibit current relaxation. Second and as already mentioned, among those E363 mutants, E363Q channels display extreme outward rectification; i.e., they carry no significant inward current. If macroscopic rectification were mainly due to asymmetric conduction rather than gating, the single-channel i-V curve should exhibit a similar degree of outward rectification. Fig. 4 A shows that this is not the case: the single-channel i-V curve (filled symbols) rectifies only mildly over the −200 to 200–mV range, compared with the much more steeply rectifying macroscopic I-V curve (open symbols). This result leads to the conclusion that the rectification of the macroscopic I-V curve must mainly reflect voltage gating, a conclusion that is further supported by the observation that an E363Q channel–containing membrane patch carries large macroscopic outward current at positive voltages, but only brief individual channel events at very negative voltages (Fig. 4, G and H).

To estimate the magnitude of the voltage-induced change in open probability of the E363Q channel, one could attempt to determine, from single-channel current recordings, the open probability at various voltages. This conceptually straightforward undertaking is very difficult in practice because, given the extremely low open probability at negative voltages, there is no reliable way to ensure that a membrane patch contains only a single channel. Alternatively, we can obtain the information by comparing outward macroscopic current (=iNP_o) at a positive voltage with inward current at the corresponding negative voltage. At negative voltages where the open probability is extremely low, the inward current was calculated from the product of unitary current and the fraction of total open time for all channels (iNP_o) present in the patch. With this simple approach, we obtained a ratio of channel open probabilities at −200 and at 200 mV of 1.6 ± 0.5 × 10⁴ (mean ± SEM; n = 8), reflecting a valence of ∼0.6. A comparable value of 0.5 was estimated from the limiting slope (Almers, 1978) of the semilogarithmic plot of macroscopic conductance against voltage (Fig. 10 A). Finally, a Boltzmann function fit to the entire experimentally accessible portion of the G-V curve yielded Z = 0.5 and V_1/2 = 240 mV, and a projected maximum around 400 mV (Fig. 10 B). Indeed, the experimental G-V curve shows no sign of saturation at 200 mV, the limit of our recording system. In biophysical terms, the voltage sensitivity (valence of ∼0.5) of CNGA1 mutants is rather modest, much lower than that of Kv channels, which originates from S4 (Schoppa et al., 1992), but is comparable to that of KcsA K⁺ channels, which originates from the region around the selectivity filter (Heginbotham et al., 1999; Cordero-Morales et al., 2006a). In biological terms, however, a G-V relation with a Z of ∼0.5 and V_1/2 of ∼240 mV would pose significant problems, as it would surely result in closure of the channels at physiological voltages.

Figure 10.

Voltage dependence of the activation of E363Q mutant channels exposed to a saturating cGMP concentration. (A) Semilogarithmic plot of relative conductance against voltage between 10 and 200 mV (taken from Fig. 3 C). The data points from 10 to 150 mV were fitted with a straight line, yielding a valence of 0.47 ± 0.01 (mean ± SEM; n = 5); the rest of the line was extrapolated. (B) Entire G-V curve (mean ± SEM; n = 5) of the E363Q mutant in the presence of 2 mM cGMP taken from Fig. 3 C. Black curve superimposed on the plot of relative conductance against voltage is a Boltzmann function fit yielding Z = 0.51 ± 0.01 and V_1/2 = 240 ± 7 mV. Red dashed curve is a simulation of Eq. 2 with K₁ = 5 × 10⁻³, K₂ = 1.04, and Z_K2 = 0.58 (taken from Table II). The asymptotic maximum was rescaled to one to produce the plot.

E363 located at the external end of the selectivity filter appears to interact with Y352 in the pore helix (Fig. 5). Neutralizing E363 could therefore conceivably loosen the attachment of the filter to the pore helix, thereby decreasing the probability of the filter remaining in a stable, open conformation. In fact, the loosening of structural contacts between the selectivity filter and the pore helix of K⁺ channels has been shown to affect voltage gating (Alagem et al., 2003; Cordero-Morales et al., 2006a,b). Mutations at E363 and at other sites around the selectivity filter of CNGA1 channels evidently keep the gating equilibrium biased toward closed states, whereas positive voltages appear to help stabilize an open conformation of the selectivity filter. Voltage sensitivity may arise from ion movement within the selectivity filter as its conformation changes to an open state. In addition, given that the pore helix bears no charges but has a dipole moment and is located in a low-dielectric environment (Roux and MacKinnon, 1999), its motion may be voltage sensitive.

Sequential binding of cGMP to four potential sites of a wild-type CNGA1 channel drives it through a series of closed states to open states (Karpen et al., 1988; Tanaka et al., 1989; Goulding et al., 1994; Gordon and Zagotta, 1995; Varnum and Zagotta, 1996; Benndorf et al., 1999; Nache et al., 2006). This gating sequence consists of (at least) two processes: a ligand-binding transition followed by a closed-open channel transition (Fig. 11 A). Kinetic analyses have suggested that the closed-open transition is voltage dependent (valence of ∼0.2), and that this could account for the voltage gating observed at low concentrations of cGMP. Although a voltage-sensitive step anywhere along the ligand-initiated gating sequence could mediate the observed enhancement of activation of certain mutant channels by depolarization, it cannot explain the failure of a sufficiently strong hyperpolarization to reduce conductance to zero. For any residual current to remain at extreme negative potentials (as is the case for most rectifying mutants described here; e.g., Figs. 2 D, 5 B, and 6 D, and Fig. S1), the voltage-sensitive transition must be between open states. In fact, more than one open state has been observed in wild-type channels under low cGMP conditions, or in channels with neutral substitutions at E363 (Sesti et al., 1995, 1996; Bucossi et al., 1996, 1997; Fodor et al., 1997; Becchetti et al., 1999; Kusch et al., 2004).

Figure 11.

Analysis of voltage gating of wild-type and E363 mutants. (A–C) Schemes representing gating of the CNGA1 channel, in which C and C_L represent closed-channel states without and with cGMP bound, respectively, whereas O₁ and O₂ (lumped into a single open state in A) are two sequential open states in voltage-sensitive equilibrium. (D) G-V relations (mean ± SEM; n = 4–7) between 10 and 200 mV for wild-type and E363 mutant channels. Curves correspond to a simultaneous fit of Eq. 2 to the datasets with common K₂. Best-fit parameters were (common) K₂ = 1.04 ± 0.14 and individual K₁ and Z_K2 values for each mutant (listed in Table II). (E) Z_K2 for each wild-type and mutant channel plotted against the channel's K₁, both obtained from the simultaneous fit described above and listed in Table II. (F) G-V relations (mean ± SEM; n = 4–7) between 10 and 200 mV for WT and E363Q channels at saturating and subsaturating cGMP concentrations (taken from Figs. 1 D and 3 C). Curves are fits of Eq. 1 with adjustable parameters K_L = 78 ± 4 µM and n = 1.44 ± 0.06. Fixed parameters are K₂ = 1.04 (taken from D and common to all curves), K₁ = 0.62 and Z_K2 = 0.25 for WT, and K₁ = 5 × 10⁻³ and Z_K2 = 0.58 for E363Q channels (taken from Table II).

A model to describe voltage gating of mutant CNGA1 channels requires at least four states (Fig. 11 B): two closed (C and C_L) and two open (O₁ and O₂). Sequential binding of cGMP brings the mutant channel, like the wild type, to the final closed state (C_L), from which it may proceed to the first open state (O₁). None of the gating transitions to this point is assumed to be voltage sensitive. However, state O₁ is in voltage-sensitive equilibrium with a second open state, O₂. Whereas in wild-type channels the (voltage-insensitive) transition from the last closed to the first open state is energetically favorable (i.e., high-probability), in mutant channels the first open state is energetically unstable (i.e., low-probability) with respect to the last closed state. Strong depolarization (favoring O₂) will therefore be required to pull a sizeable fraction of channels into an open configuration. For the scheme in Fig. 11 B, relative conductance (G/G_max) is given by the ratio of the open states to the sum of all states:

$$\frac{G}{G_{\text{max}}}=\frac{\left[O_1\right]+\left[O_2\right]}{\left[C\right]+\left[C_L\right]+\left[O_1\right]+\left[O_2\right]}$$

The equilibrium constants in the absence of an electric field are defined as K_L = [C][cGMP]ⁿ/[C_L], K₁ = [O₁]/[C], and K₂ = [O₂]/[O₁]. Assuming for simplicity that only the transition between open states is voltage sensitive, we define K₂(V) = K₂exp(Z_K2FV/RT), where Z_K2 is the effective valence associated with the O₁–O₂ transition, V is the membrane voltage, and F, R, and T have their usual meaning. The relative conductance is then given by:

$$\frac{G}{G_{\text{max}}}=\frac{1}{1+\frac{1+{\left(\frac{K_L}{\left[\mathrm{cGMP}\right]}\right)}^n}{K_1\left(1+K_2{e}^{\frac{Z_{K2}\mathrm{FV}}{\mathrm{RT}}}\right)}}.$$ (1)

At saturating concentrations of cGMP, the ligand-binding transition is extremely biased toward the C_L state and scheme B (Fig. 11 B) is then reduced to scheme C (Fig. 11 C), and Eq. 1 to

$$\frac{G}{G_{\text{max}}}=\frac{1}{1+\frac{1}{K_1\left(1+K_2{e}^{\frac{Z_{K2}\mathrm{FV}}{\mathrm{RT}}}\right)}}.$$ (2)

At sufficiently negative voltages, K₂exp(Z_K2FV/RT) vanishes and Eq. 2 reduces to:

$$\frac{G}{G_{\text{max}}}=\frac{1}{1+\frac{1}{K_1}},$$ (3)

that is, K₁ governs the height of the asymptotic, voltage-insensitive plateau at negative voltages; i.e., the fraction of conductance that will not be further reduced by any degree of hyperpolarization. The remaining, voltage-sensitive fraction is described by a Boltzmann function with valence Z = Z_K2 and V_1/2 = (RT/Z_K2F)ln[(K₁+1)/K₁K₂]. In the limit where K₁ becomes very small (i.e., state O₁ has very low probability), the conductance plateau at extreme negative voltages vanishes, and the conductance becomes voltage gated over its entire range, such that Eq. 2 (red dashed curve in Fig. 10 B) reduces to a Boltzmann function (black curve). The valence Z_K2 governs the steepness of the G-V curve; K₂ influences only V_1/2, not the height of the plateau.

Fig. 11 D shows G-V plots (normalized to the conductance at 200 mV) at saturating cGMP concentrations for wild-type and 11 E363 mutant channels. We restricted our analysis to the voltage range between 10 and 200 mV, where the single-channel i-V curve is linear (Fig. 4 A) and variations in macroscopic conductance therefore primarily reflect changes in channel open probability, not confounded by altered ion conduction. Given the saturating cGMP concentrations, the relevant scheme is model C in Fig. 11, governed by Eq. 2. A simultaneous fit of Eq. 2 to the entire dataset yields K₂ = 1.04 ± 0.14, common to all 12 channels, as well as K₁ and Z_K2 values for each individual channel. These best-fit K₁ and Z_K2 values are listed in Table II, and their relationship is plotted in Fig. 11 E. Generally, a mutation that has a greater destabilizing effect on the O₁ state (i.e., smaller K₁) seems to exhibit a somewhat larger Z_K2. This trend suggests that a larger voltage-driven conformational change can occur around the selectivity filter of mutants with a more disrupted interaction between selectivity filter and pore helix—a not implausible scenario. Of all viable mutations, E363H has the largest effect on both parameters, lowering K₁ 150-fold and raising Z_K2 2.5-fold from the wild-type values. These sole changes account for the appearance of nearly full-range voltage gating in E363H channels. Thus, mutations produce voltage gating not just by modestly increasing the valence associated with the open–open transition, but mainly by lowering the stability of an open state. The latter effect creates a condition in which strong depolarization is now needed to achieve high open probability.

Table II.

Best-fit values of Eq. 2

	K1	ZK2
WT	6.2 ± 0.6 × 10−1	0.25 ± 0.02
E363A	7.2 ± 0.7 × 10−2	0.39 ± 0.01
E363D	6.8 ± 0.8 × 10−1	0.23 ± 0.02
E363F	1.1 ± 0.2 × 10−2	0.42 ± 0.01
E363G	6.3 ± 2.0 × 10−3	0.41 ± 0.01
E363H	4.2 ± 0.5 × 10−3	0.62 ± 0.01
E363M	1.8 ± 0.3 × 10−2	0.41 ± 0.01
E363N	4.4 ± 0.5 × 10−2	0.44 ± 0.01
E363P	2.1 ± 0.5 × 10−2	0.33 ± 0.01
E363Q	5.0 ± 0.9 × 10−3	0.58 ± 0.01
E363S	9.9 ± 0.9 × 10−2	0.40 ± 0.01
E363T	1.7 ± 0.3 × 10−2	0.41 ± 0.01

To recapitulate, our analysis is consistent with a model where the whole range of observed voltage sensitivities, from barely detectable in wild-type channels to full-fledged in certain mutants, reflects a common property inherent in all channels, including wild type. In the case of wild-type channels in the presence of saturating ligand concentrations, where the closed–open gating equilibrium is already biased to approach maximal open probability, inherent voltage gating is largely obscured because depolarization cannot further enhance open probability to any significant extent. Extension of this model for saturating cGMP concentrations (Fig. 11 C, governed by Eq. 2) to include a ligand-binding transition of negligible voltage sensitivity (Fig. 11 B, governed by Eq. 1) also adequately accounts for—without any adjustments of K₁, K₂(V), or Z_K2—the voltage gating behavior of wild-type and E363Q mutant channels at subsaturating ligand concentrations. We fit the data of Fig. 11 F with Eq. 1, keeping K₁, K₂(V), and Z_K2 fixed at their values obtained from Fig. 11 D. The resulting best-fit values for the two remaining adjustable parameters are K_L = 78 ± 4 µM and Hill coefficient = 1.44 ± 0.06. This Hill coefficient value is comparable to those obtained from Hill fits of the cGMP dose–response curves in Figs. 1 E and 3 D.

To assess the voltage sensitivity, if any, of the ligand-binding step, we fitted Eq. 1 to the cGMP dose–response relations at −200 and 200 mV simultaneously. The fits of the wild-type data yield K_L (−200 mV) = 96 ± 2 µM and K_L (200 mV) = 182 ± 5 µM, a twofold variation over 400 mV (Fig. 1 E, red dashed lines), which corresponds to K_L (0 mV) = 132 µM with a valence factor of 0.04. Similar fits to the E363Q data yield K_L (40 mV) = 166 ± 6 µM and K_L (200 mV) = 67 ± 2 µM, a 2.5-fold variation over a 160-mV range (Fig. 3 D), which corresponds to K_L (0 mV) = 196 µM with a valence factor of −0.1. The relatively small variation of K_L with voltage further supports the notion that the observed voltage sensitivity is mainly associated with the open–open transition, whereas cGMP binding per se exhibits little voltage sensitivity.

In summary, we have found that certain mutations around the selectivity filter render CNGA1 channels practically fully voltage gated. These mutations loosen the attachment of the selectivity filter to the surrounding structures. As a result, saturated binding of cGMP by itself can only help the channel enter a low-probability, i.e., unstable open state. Membrane depolarization, which favors a second open state in equilibrium with the first, is required to move a sizeable fraction of the channels into an open configuration. In other words, the channels become voltage gated, even in the presence of saturating concentrations of cGMP. Such voltage gating would have a profoundly adverse functional consequence, as the mutant channels could remain mostly closed at physiological voltages. Thus, proper attachment of the selectivity filter to the surrounding supporting structure is essential to ensure that the CNGA1 channel remains primarily gated by ligands, not voltage.